Hybrid Superconducting/Magnetic Multifunctional Devices in Two-Dimensional Systems
Abstract
:1. Introduction
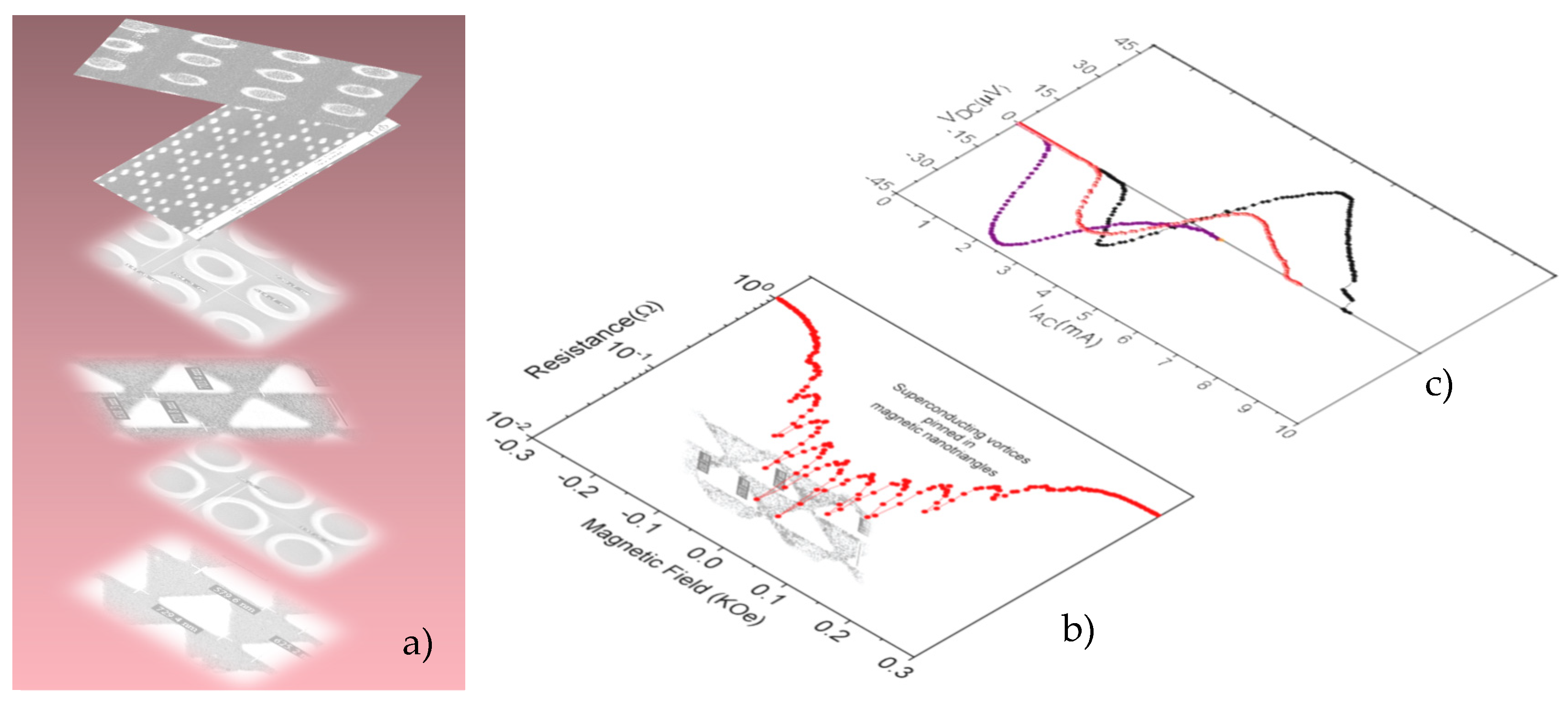
- Superconducting/Hybrid Devices at the Nanoscale
2. Magnetic and Superconducting Two-Dimensional Materials
2.1. Emerging Two-Dimensional Magnets
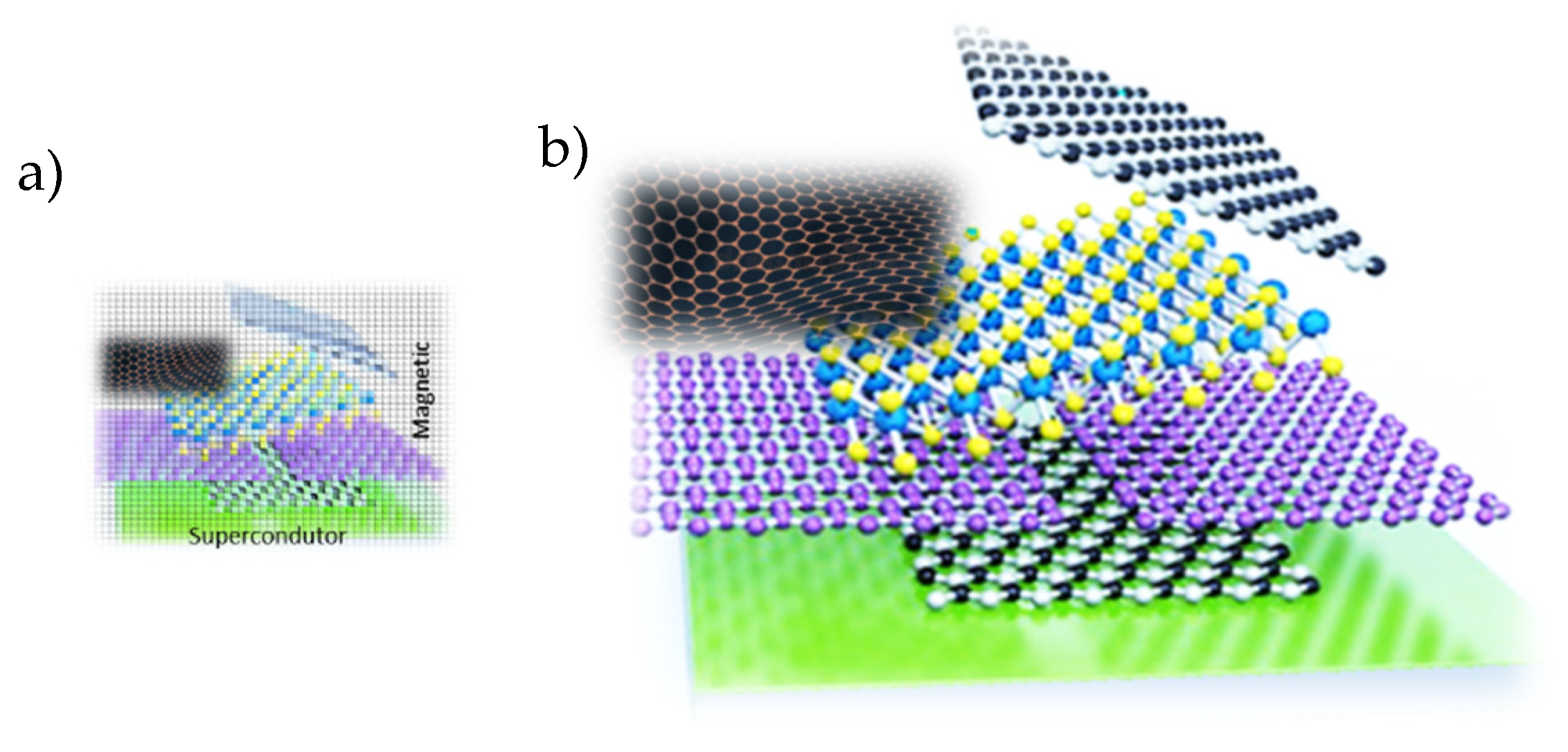
2.2. Two-Dimensional Superconductors and Interfaces
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Fernández-Pacheco, A.; Streubel, R.; Fruchart, O.; Hertel, R.; Fischer, P.; Cowburn, R.P. Three-dimensional nanomagnetism. Nat. Commun. 2017, 8, 15756. [Google Scholar] [CrossRef] [Green Version]
- Haviland, D.B.; Liu, Y.; Goldman, A.M. Onset of superconductivity in the two-dimensional limit. Phys. Rev. Lett. 1989, 62, 2180. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-Like Two-Dimensional Materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Choi, W.; Choudhary, N.; Han, G.H.; Park, J.; Akinwande, D.; Lee, Y.H. Recent development of two-dimensional transition metal dichalcogenides and their applications. Mater. Today 2017, 20, 116–130. [Google Scholar] [CrossRef]
- Geim, A.; Grigorieva, I. Van der Waals heterostructures. Nature 2013, 499, 419–425. [Google Scholar] [CrossRef] [Green Version]
- Frisenda, R.; Navarro-Moratalla, E.; Gant, P.; De Lara, D.P.; Jarillo-Herrero, P.; Gorbachev, R.V.; Castellanos-Gomez, A. Recent progress in the assembly of nanodevices and van der Waals heterostructures by deterministic placement of 2D materials. Chem. Soc. Rev. 2017, 47, 53–68. [Google Scholar] [CrossRef] [Green Version]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Guo, Y.; Cheng, H.; Dai, J.; An, X.; Zhao, J.; Tian, K.; Wei, S.; Zeng, X.C.; Wu, C.; et al. Signature of coexistence of superconductivity and ferromagnetism in two-dimensional NbSe2 triggered by surface molecular adsorption. Nat. Commun. 2016, 7, 11210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Xu, S.; Huang, B.; Duan, W. Emergent Phenomena in Magnetic Two-Dimensional Materials and van der Waals Heterostructures. ACS Appl. Electron. Mater. 2022, 4, 3278–3302. [Google Scholar] [CrossRef]
- Baert, M.; Metlushko, V.V.; Jonckheere, R.; Moshchalkov, V.V.; Bruynseraede, Y. Composite Flux-Line Lattices Stabilized in Superconducting Films by a Regular Array of Artificial Defects. Phys. Rev. Lett. 1995, 74, 3269–3272. [Google Scholar] [CrossRef]
- Harada, K.; Kamimura, O.; Kasai, H.; Matsuda, T.; Tonomura, A.; Moshchalkov, V.V. Direct Observation of Vortex Dynamics in Superconducting Films with Regular Arrays of Defects. Science 1996, 274, 1167–1170. [Google Scholar] [CrossRef]
- Buzdin, A. Mixing superconductivity and magnetism. Nat. Mater. 2004, 3, 751–752. [Google Scholar] [CrossRef] [PubMed]
- Golovchanskiy, I.A.; Abramov, N.N.; Stolyarov, V.S.; Bolginov, V.V.; Ryazanov, V.V.; Golubov, A.A.; Ustinov, A. Ferromagnet/Superconductor Hybridization for Magnonic Applications. Adv. Funct. Mater. 2018, 28, 1802375. [Google Scholar] [CrossRef]
- Baek, B.; Rippard, W.H.; Benz, S.P.; Russek, S.E.; Dresselhaus, P.D. Hybrid superconducting-magnetic memory device using competing order parameters. Nat. Commun. 2014, 5, 3888. [Google Scholar] [CrossRef] [Green Version]
- De Simoni, G.; Strambini, E.; Moodera, J.S.; Bergeret, F.S.; Giazotto, F. Toward the Absolute Spin-Valve Effect in Superconducting Tunnel Junctions. Nano Lett. 2018, 18, 6369–6374. [Google Scholar] [CrossRef] [Green Version]
- Golubov, A.A.; Kupriyanov, M.Y. Controlling magnetism. Nat. Mater. 2017, 16, 156–157. [Google Scholar] [CrossRef]
- Alija, A.; Pérez de Lara, D.; Gonzalez, E.M.; Kakazei, G.N.; Sousa, J.B.; Araujo, J.P.; Hierro-Rodriguez, A.; Martín, J.I.; Alameda, J.M.; Vélez, M.; et al. Ferromagnetic proximity effect in a-CoxSi1−x/Nb bilayers: Role of magnetic disorder and interface transparency. Phys. Rev. B 2010, 82, 184529. [Google Scholar] [CrossRef]
- Tagirov, L.R. Low-Field Superconducting Spin Switch Based on a Superconductor/Ferromagnet Multilayer. Phys. Rev. Lett. 1999, 83, 2058–2061. [Google Scholar] [CrossRef]
- Gu, J.Y.; You, C.-Y.; Jiang, J.S.; Pearson, J.; Bazaliy, Y.B.; Bader, S.D. Magnetization-Orientation Dependence of the Superconducting Transition Temperature in the Ferromagnet-Superconductor-Ferromagnet System: CuNi/Nb/CuNi. Phys. Rev. Lett. 2002, 89, 267001. [Google Scholar] [CrossRef] [PubMed]
- Gingrich, E.C.; Niedzielski, B.M.; Glick, J.A.; Wang, Y.; Miller, D.L.; Loloee, R.; Pratt, W.P., Jr.; Birge, N.O. Controllable 0–π Josephson junctions containing a ferromagnetic spin valve. Nat. Phys. 2016, 12, 564–567. [Google Scholar]
- Bill, A.; de Rojas, J.; Baker, T.E.; Richie-Halford, A. Properties of Magnetic-Superconducting Proximity Systems. J. Supercond. Nov. Magn. 2012, 25, 2177–2182. [Google Scholar] [CrossRef]
- Zhang, T.; Cheng, P.; Li, W.-J.; Sun, Y.-J.; Wang, G.; Zhu, X.-G.; He, K.; Wang, L.; Ma, X.; Chen, X.; et al. Superconductivity in one-atomic-layer metal films grown on Si(111). Nat. Phys. 2010, 6, 104–108. [Google Scholar] [CrossRef]
- Takashi, U.; Puneet, M.; Masakazu, A.; Tomonobu, N. Macroscopic Superconducting Current through a Silicon Surface Reconstruction with Indium Adatoms: Si (111)−(√7×√3)−In. Phys. Rev. Lett. 2011, 107, 207001. [Google Scholar]
- Wang, Q.Y.; Li, Z.; Zhang, W.H.; Zhang, Z.C.; Zhang, J.S.; Li, W.; Ding, H.; Yun-Bo, O.; Deng, P.; Xue, Q.K.; et al. Interface-Induced High-Temperature Superconductivity in Single Unit-Cell FeSe Films on SrTiO3. Chin. Phys. Lett. 2012, 29, 037402. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Yankowitz, M.; Fallahazad, B.; Kang, S.; Movva, H.C.P.; Huang, S.; Larentis, S.; Corbet, C.M.; Taniguchi, T.; Watanabe, K.; et al. van der Waals Heterostructures with High Accuracy Rotational Alignment. Nano Lett. 2016, 16, 1989–1995. [Google Scholar] [CrossRef]
- Kim, K.; DaSilva, A.; Huang, S.; Fallahazad, B.; Larentis, S.; Taniguchi, T.; Watanabe, K.; LeRoy, B.J.; MacDonald, A.H.; Tutuc, E. Tunable moiré bands and strong correlations in small-twist-angle bilayer graphene. Proc. Natl. Acad. Sci. USA 2017, 114, 3364–3369. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.-X.; Zhang, Y.-H.; Morissette, E.; Wang, Z.; Liu, S.; Rhodes, D.; Watanabe, K.; Taniguchi, T.; Hone, J.; Li, J.I.A. Spin-orbit–driven ferromagnetism at half moiré filling in magic-angle twisted bilayer graphene. Science 2022, 375, 437–441. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.I.-J.; Yamoah, M.A.; Li, Q.; Karamlou, A.H.; Dinh, T.; Kannan, B.; Braumüller, J.; Kim, D.; Melville, A.J.; Muschinske, S.E.; et al. Hexagonal boron nitride as a low-loss dielectric for superconducting quantum circuits and qubits. Nat. Mater. 2022, 21, 398–403. [Google Scholar] [CrossRef] [PubMed]
- Kravets, V.G.; Jalil, R.; Kim, Y.-J.; Ansell, D.; Aznakayeva, D.E.; Thackray, B.; Britnell, L.; Belle, B.D.; Withers, F.; Radko, I.; et al. Graphene-protected copper and silver plasmonics. Sci. Rep. 2014, 4, 5517. [Google Scholar] [CrossRef] [Green Version]
- Britnell, L.; Ribeiro, R.M.; Eckmann, A.; Jalil, R.; Belle, B.D.; Mishchenko, A.; Kim, Y.-J.; Gorbachev, R.V.; Georgiou, T.; Morozov, S.V.; et al. Strong Light-Matter Interactions in Heterostructures of Atomically Thin Films. Science 2013, 340, 1311–1314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.W.; Hu, Y.H.; Li, Y.; Fang, Z.Y. Light–matter interaction of 2D materials: Physics and device applications. Chin. Phys. B 2017, 26, 036802. [Google Scholar] [CrossRef]
- Vélez, M.; Martín, J.I.; Villegas, J.E.; Hoffmann, A.; González, E.M.; Vicent, J.L.; Schuller, I.K. Superconducting vortex pinning with artificial magnetic nanostructures. J. Magn. Magn. Mater. 2008, 320, 2547–2562. [Google Scholar] [CrossRef]
- Aladyshkin, A.Y.; Silhanek, A.V.; Gillijns, W.; Moshchalkov, V.V. Nucleation of superconductivity and vortex matter in superconductor–ferromagnet hybrids. Supercond. Sci. Technol. 2009, 22, 053001. [Google Scholar] [CrossRef]
- Pérez de Lara, D.; Castaño, F.J.; Ng, B.G.; Körner, H.S.; Dumas, R.K.; Gonzalez, E.M.; Liu, K.; Ross, C.A.; Schuller, I.K.; Vicent, J.L.; et al. Magnetic pinning of flux lattice in superconducting-nanomagnet hybrids. Appl. Phys. Lett. 2011, 99, 182509. [Google Scholar] [CrossRef] [Green Version]
- De Lara, D.P.; Erekhinsky, M.; Gonzalez, E.M.; Rosen, Y.; Schuller, I.K.; Vicent, J.L. Vortex ratchet reversal: Role of interstitial vortices. Phys. Rev. B 2011, 83, 174507. [Google Scholar] [CrossRef]
- De Lara, D.P.; Alija, A.; Gonzalez, E.M.; Velez, M.; Martin, J.I.; Vicent, J.L. Vortex ratchet reversal at fractional matching fields in kagomélike array with symmetric pinning centers. Phys. Rev. B 2010, 82, 174503. [Google Scholar] [CrossRef] [Green Version]
- De Lara, D.P.; Alija, A.; Gonzalez, E.M.; Martin, J.I.; Velez, M.; Colino, J.M.; Anguita, J.V.; Vicent, J.L. Enhancement of synchronized vortex lattice motion in hybrid magnetic/amorphous superconducting nanostructures. Appl. Phys. Lett. 2009, 94, 122506. [Google Scholar] [CrossRef] [Green Version]
- Gillijns, W.; Silhanek, A.V.; Moshchalkov, V.V.; Reichhardt, C.J.O. Origin of Reversed Vortex Ratchet Motion. Phys. Rev. Lett. 2007, 99, 247002. [Google Scholar] [CrossRef] [Green Version]
- Perez de Lara, D.; Castaño, F.J.; Ng, B.G.; Körner, H.S.; Dumas, R.K.; Gonzalez, E.M.; Liu, K.; Ross, C.A.; Schuller, I.K.; Vicent, J.L. Rocking ratchet induced by pure magnetic potentials with broken reflection symmetry. Phys. Rev. B 2009, 80, 224510. [Google Scholar] [CrossRef]
- Dinis, L.; De Lara, D.P.; Gonzalez, E.M.; Anguita, J.V.; Parrondo, J.M.R.; Vicent, J.L. Transverse ratchet effect and superconducting vortices: Simulation and experiment. New J. Phys. 2009, 11, 073046. [Google Scholar] [CrossRef]
- Villegas, J.E.; Savel’ev, S.; Nori, F.; Gonzalez, E.M.; Anguita, J.V.; García, R.; Vicent, J.L. A Superconducting Reversible Rectifier That Controls the Motion of Magnetic Flux Quanta. Science 2003, 302, 5648. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, B.; Clark, G.; Navarro-Moratalla, E.; Klein, D.R.; Cheng, R.; Seyler, K.L.; Zhong, D.; Schmidgall, E.; McGuire, M.A.; Cobden, D.H.; et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Lu, Q.; Liu, W.; Niu, W.; Sun, J.; Cook, J.; Vaninger, M.; Miceli, P.F.; Singh, D.J.; Lian, S.-W.; et al. Room-temperature intrinsic ferromagnetism in epitaxial CrTe2 ultrathin films. Nat. Commun. 2021, 12, 2492. [Google Scholar] [CrossRef]
- Deng, Y.; Yu, Y.; Song, Y.; Zhang, J.; Wang, N.Z.; Sun, Z.; Yi, Y.; Wu, Y.Z.; Wu, S.; Zhu, J.; et al. Gate-tunable room-temperature ferromagnetism in two-dimensional Fe3GeTe2. Nature 2018, 563, 94–99. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Sapkota, D.; Taniguchi, T.; Watanabe, K.; Mandrus, D.; Morpurgo, A.F. Tunneling spin valves based on Fe3GeTe2/hBN/ Fe3GeTe2 van der Waals heterostructures. Nano Lett. 2018, 18, 4303–4308. [Google Scholar] [CrossRef] [Green Version]
- Gong, C.; Li, L.; Li, Z.; Ji, H.; Stern, A.; Xia, Y.; Cao, T.; Bao, W.; Wang, C.; Wang, Y.; et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature 2017, 546, 265–269. [Google Scholar] [CrossRef] [Green Version]
- Zhong, D.; Seyler, K.L.; Linpeng, X.; Cheng, R.; Sivadas, N.; Huang, B.; Schmidgall, E.; Taniguchi, T.; Watanabe, K.; McGuire, M.A.; et al. Van der Waals engineering of ferromagnetic semiconductor heterostructures for spin and valleytronics. Sci. Adv. 2017, 3, e1603113. [Google Scholar] [CrossRef] [Green Version]
- Bonilla, M.; Kolekar, S.; Ma, Y.; Diaz, H.C.; Kalappattil, V.; Das, R.; Eggers, T.; Gutierrez, H.R.; Phan, M.-H.; Batzill, M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289–293. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Li, L.; Wang, Z.; Mak, K.F.; Shan, J. Controlling magnetism in 2D CrI3 by electrostatic doping. Nat. Nanotechnol. 2018, 13, 549–553. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Clark, G.; Klein, D.R.; MacNeill, D.; Navarro-Moratalla, E.; Seyler, K.L.; Wilson, N.; McGuire, M.; Cobden, D.H.; Xiao, D.; et al. Electrical control of 2D magnetism in bilayer CrI3. Nat. Nanotechnol. 2018, 13, 544–548. [Google Scholar] [CrossRef] [PubMed]
- Tse, W.-K.; Qiao, Z.; Yao, Y.; MacDonald, A.H.; Niu, Q. Quantum anomalous Hall effect in single-layer and bilayer graphene. Phys. Rev. B 2011, 83, 155447. [Google Scholar] [CrossRef] [Green Version]
- Kuo, C.-T.; Neumann, M.; Balamurugan, K.; Park, H.J.; Kang, S.; Shiu, H.W.; Kang, J.H.; Hong, B.H.; Han, M.; Noh, T.W.; et al. Exfoliation and Raman Spectroscopic Fingerprint of Few-Layer NiPS3 Van der Waals Crystals. Sci. Rep. 2016, 6, 20904. [Google Scholar] [CrossRef] [Green Version]
- Du, K.-Z.; Wang, X.-Z.; Liu, Y.; Hu, P.; Utama, M.I.B.; Gan, C.K.; Xiong, Q.; Kloc, C. Weak Van der Waals Stacking, Wide-Range Band Gap, and Raman Study on Ultrathin Layers of Metal Phosphorus Trichalcogenides. ACS Nano 2015, 10, 1738–1743. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-U.; Lee, S.; Ryoo, J.H.; Kang, S.; Kim, T.Y.; Kim, P.; Park, C.-H.; Park, J.-G.; Cheong, H. Ising-Type Magnetic Ordering in Atomically Thin FePS3. Nano Lett. 2016, 16, 7433–7438. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Du, K.; Liu, Y.Y.F.; Hu, P.; Zhang, J.; Zhang, Q.; Owen, M.H.S.; Lu, X.; Gan, C.K.; Sengupta, P.; et al. Raman spectroscopy of atomically thin two-dimensional magnetic iron phosphorus trisulfide (FePS 3 ) crystals. 2D Mater. 2016, 3, 031009. [Google Scholar] [CrossRef]
- Lin, M.-W.; Zhuang, H.L.; Yan, J.; Ward, T.Z.; Puretzky, A.A.; Rouleau, C.M.; Gai, Z.; Liang, L.; Meunier, V.; Sumpter, B.G.; et al. Ultrathin nanosheets of CrSiTe3: A semiconducting two-dimensional ferromagnetic material. J. Mater. Chem. C 2015, 4, 315–322. [Google Scholar] [CrossRef]
- Liu, J.; Shi, M.; Lu, J.; Anantram, M.P. Analysis of electrical-field-dependent Dzyaloshinskii-Moriya interaction and magnetocrystalline anisotropy in a two-dimensional ferromagnetic monolayer. Phys. Rev. B 2018, 97, 054416. [Google Scholar] [CrossRef]
- Cortie, D.L.; Causer, G.L.; Rule, K.C.; Fritzsche, H.; Kreuzpaintner, W.; Klose, F. Two-Dimensional Magnets: Forgotten History and Recent Progress towards Spintronic Applications. Adv. Funct. Mater. 2019, 30, 1901414. [Google Scholar] [CrossRef]
- Matsukura, F.; Tokura, Y.; Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 2015, 10, 209–220. [Google Scholar] [CrossRef]
- Heron, J.T.; Trassin, M.; Ashraf, K.; Gajek, M.; He, Q.; Yang, S.Y.; Nikonov, D.E.; Chu, Y.-H.; Salahuddin, S.; Ramesh, R. Electric-Field-Induced Magnetization Reversal in a Ferromagnet-Multiferroic Heterostructure. Phys. Rev. Lett. 2011, 107, 217202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, S.M.; Cybart, S.; Yu, P.; Rossell, M.D.; Zhang, J.X.; Ramesh, R.; Dynes, R.C. Reversible electric control of exchange bias in a multiferroic field-effect device. Nat. Mater. 2010, 9, 756–761. [Google Scholar] [CrossRef] [PubMed]
- Novoselov, K.S.; Mishchenko, A.; Carvalho, A.; Neto, A.H.C. 2D materials and van der Waals heterostructures. Science 2016, 353, aac9439. [Google Scholar] [CrossRef] [Green Version]
- Novoselov, K. Nobel Lecture: Graphene: Materials in the Flatland. Rev. Mod. Phys. 2011, 83, 837–849. [Google Scholar] [CrossRef]
- Portolés, E.; Iwakiri, S.; Zheng, G.; Rickhaus, P.; Taniguchi, T.; Watanabe, K.; Ihn, T.; Ensslin, K.; de Vries, F.K. A tunable monolithic SQUID in twisted bilayer graphene. Nat. Nanotechnol. 2022, 17, 1159–1164. [Google Scholar] [CrossRef]
- Kim, M.; Park, G.H.; Lee, J.; Lee, J.H.; Park, J.; Lee, H.; Lee, G.H.; Lee, H.J. Strong Proximity Josephson Coupling in Vertically Stacked NbSe2 -Graphene-NbSe2 van der Waals Junctions. Nano Lett. 2017, 17, 6125–6130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Walsh, E.D.; Efetov, D.K.; Lee, G.-H.; Heuck, M.; Crossno, J.; Ohki, T.A.; Kim, P.; Englund, D.; Fong, K.C. Graphene-Based Josephson-Junction Single-Photon Detector. Phys. Rev. Appl. 2017, 8, 024022. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Nojima, T.; Iwasa, Y. Highly crystalline 2D superconductors. Nat. Rev. Mater. 2016, 2, 16094. [Google Scholar] [CrossRef] [Green Version]
- Saito, Y.; Nojima, T.; Iwasa, Y. Quantum phase transitions in highly crystalline two-dimensional superconductors. Nat. Commun. 2018, 9, 778. [Google Scholar] [CrossRef] [Green Version]
- Ugeda, M.M.; Bradley, A.J.; Zhang, Y.; Onishi, S.; Chen, Y.; Ruan, W.; Ojeda-Aristizabal, C.; Ryu, H.; Edmonds, M.T.; Tsai, H.-Z.; et al. Characterization of collective ground states in single-layer NbSe2. Nat. Phys. 2015, 12, 92–97. [Google Scholar] [CrossRef]
- Xi, X.; Wang, Z.; Zhao, W.; Park, J.-H.; Law, K.T.; Berger, H.; Forró, L.; Shan, J.; Mak, K.F. Ising pairing in superconducting NbSe2 atomic layers. Nat. Phys. 2015, 12, 139–143. [Google Scholar] [CrossRef] [Green Version]
- Heersche, H.B.; Jarillo-Herrero, P.; Oostinga, J.B.; Vandersypen, L.M.K.; Morpurgo, A.F. Bipolar supercurrent in graphene. Nature 2007, 446, 56–59. [Google Scholar] [CrossRef] [Green Version]
- Ge, J.-F.; Chen, W.-J.; Xu, Y.; Gao, C.-L.; Guan, D.-D.; Liu, C.-H.; Qian, D.; Zhang, S.-C.; Jia, J. Epitaxial growth of two-dimensional stanine. Nat. Mater. 2015, 14, 285–289. [Google Scholar] [CrossRef] [PubMed]
- Özer, M.M.; Thompson, J.R.; Weitering, H.H. Hard superconductivity of a soft metal in the quantum regime. Nat. Phys. 2006, 2, 173–176. [Google Scholar] [CrossRef]
- Kinoshita, K.; Moriya, R.; Okazaki, S.; Zhang, Y.; Masubuchi, S.; Watanabe, K.; Taniguchi, T.; Sasagawa, T.; Machida, T. Resonant Tunneling between Quantized Subbands in van der Waals Double Quantum Well Structure Based on Few-Layer WSe2. Nano Lett. 2022, 22, 4640–4645. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-C.; Ghosh, R.K.; Addou, R.; Lu, N.; Eichfeld, S.M.; Zhu, H.; Li, M.-Y.; Peng, X.; Kim, M.J.; Li, L.-J.; et al. Atomically thin resonant tunnel diodes built from synthetic van der Waals heterostructures. Nat. Commun. 2015, 6, 7311. [Google Scholar] [CrossRef] [Green Version]
- Bisri, S.Z.; Shimizu, S.; Nakano, M.; Iwasa, Y. Endeavor of Iontronics: From Fundamentals to Applications of Ion-Controlled Electronics. Adv. Mater. 2017, 29, 1607054. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.F.; Bao, X.Y.; Han, T.Z.; Tang, Z.; Zhang, L.X.; Guang, W.; Wang, Z.G.; Niu, Q.; Xue, Q.K.; et al. Superconductivity Modulated by Quantum Size Effects. Science 2004, 306, 1915–1917. [Google Scholar] [CrossRef]
- Bollinger, A.T.; Dubuis, S.G.; Yoon, J.; Pavuna, D.; Misewich, J.; Božović, I. Superconductor–insulator transition in La2 − xSrxCuO4 at the pair quantum resistance. Nature 2011, 472, 458–460. [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.-S.; Jaccard, D.; et al. Superconducting Interfaces Between Insulating Oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Ueno, K.; Nakamura, S.; Shimotani, H.; Ohtomo, A.; Kimura, N.; Nojima, T.; Aoki, H.; Iwasa, Y.; Kawasaki, M. Electric-field-induced superconductivity in an insulator. Nat. Mater. 2008, 7, 855–858. [Google Scholar] [CrossRef]
- Ye, J.T.; Inoue, S.; Kobayashi, K.; Kasahara, Y.; Yuan, H.T.; Shimotani, H.; Iwasa, Y. Liquid-gated interface superconductivity on an atomically flat film. Nat. Mater. 2009, 9, 125–128. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro-Palau, R.; Zhang, C.; Watanabe, K.; Taniguchi, T.; Hone, J.; Dean, C.R. Twistable electronics with dynamically rotatable heterostructures. Science 2018, 361, 690–693. [Google Scholar] [CrossRef] [Green Version]
- de Vries, F.K.; Portolés, E.; Zheng, G.; Taniguchi, T.; Watanabe, K.; Ihn, T.; Ensslin, K.; Rickhaus, P. Gate-defined Josephson junctions in magic-angle twisted bilayer graphene. Nat. Nanotechnol. 2021, 16, 760–763. [Google Scholar] [CrossRef] [PubMed]
- Rodan-Legrain, D.; Cao, Y.; Park, J.M.; de la Barrera, S.C.; Randeria, M.T.; Watanabe, K.; Taniguchi, T.; Jarillo-Herrero, P. Highly tunable junctions and non-local Josephson effect in magic-angle graphene tunnelling devices. Nat. Nanotechnol. 2021, 16, 769–775. [Google Scholar] [CrossRef]
- Diez-Merida, J.; Díez-Carlón, A.; Yang, S.Y.; Xie, Y.M.; Gao, X.J.; Watanabe, K.; Taniguchi, T.; Lu, X.; Law, K.T.; Efetov, D.K. Magnetic Josephson junctions and superconducting diodes in magic angle twisted bilayer graphene. arXiv preprint 2021, arXiv:2110.01067. [Google Scholar]
- Golod, T.; Krasnov, V.M. Demonstration of a superconducting diode-with-memory, operational at zero magnetic field with switchable nonreciprocity. Nat. Commun. 2022, 13, 3658. [Google Scholar] [CrossRef]
- Golubov, A.A.; Kupriyanov, M.Y.; Il’Ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411–469. [Google Scholar] [CrossRef] [Green Version]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nat. Phys. 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Zhu, Y.; Pal, A.; Blamire, M.G.; Barber, Z.H. Barber, Superconducting exchange coupling between ferromagnets. Nat. Mater. 2017, 16, 195–199. [Google Scholar] [CrossRef] [PubMed]
- Tedrow, M.; Meservey, R. Spin-Dependent Tunneling into Ferromagnetic Nickel. Phys. Rev. Lett. 1971, 26, 192. [Google Scholar] [CrossRef]
- Giazotto, F.; Taddei, F. Superconductors as spin sources for spintronics. Phys. Rev. B 2008, 77, 132501. [Google Scholar] [CrossRef] [Green Version]
- Huertas-Hernando, D.; Nazarov, Y.V.; Belzig, W. Absolute Spin-Valve Effect with Superconducting Proximity Structures. Phys. Rev. Lett. 2002, 88, 047003. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ningrum, V.P.; Liu, B.; Wang, W.; Yin, Y.; Cao, Y.; Zha, C.; Xie, H.; Jiang, X.; Sun, Y.; Qin, S.; et al. Recent Advances in Two-Dimensional Magnets: Physics and Devices towards Spintronic Applications. AAAS Res. 2020, 2020, 1768918. [Google Scholar] [CrossRef]
- Kulić, M.L.; Endres, M. Ferromagnetic-semiconductor–singlet-(or triplet) superconductor–ferromagnetic-semiconductor systems as possible logic circuits and switches. Phys. Rev. B 2000, 62, 11846–11853. [Google Scholar] [CrossRef] [Green Version]
- Holmes, D.S.; Ripple, A.L.; Manheimer, M.A. Energy-Efficient Superconducting Computing—Power Budgets and Requirements. IEEE Trans. Appl. Supercond. 2013, 23, 1701610. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perez de Lara, D. Hybrid Superconducting/Magnetic Multifunctional Devices in Two-Dimensional Systems. Physchem 2022, 2, 347-356. https://doi.org/10.3390/physchem2040025
Perez de Lara D. Hybrid Superconducting/Magnetic Multifunctional Devices in Two-Dimensional Systems. Physchem. 2022; 2(4):347-356. https://doi.org/10.3390/physchem2040025
Chicago/Turabian StylePerez de Lara, David. 2022. "Hybrid Superconducting/Magnetic Multifunctional Devices in Two-Dimensional Systems" Physchem 2, no. 4: 347-356. https://doi.org/10.3390/physchem2040025
APA StylePerez de Lara, D. (2022). Hybrid Superconducting/Magnetic Multifunctional Devices in Two-Dimensional Systems. Physchem, 2(4), 347-356. https://doi.org/10.3390/physchem2040025





