Examining the Hydration Behavior of Aqueous Calcium Chloride (CaCl2) Solution via Atomistic Simulations
Abstract
1. Introduction
2. Simulation Methods
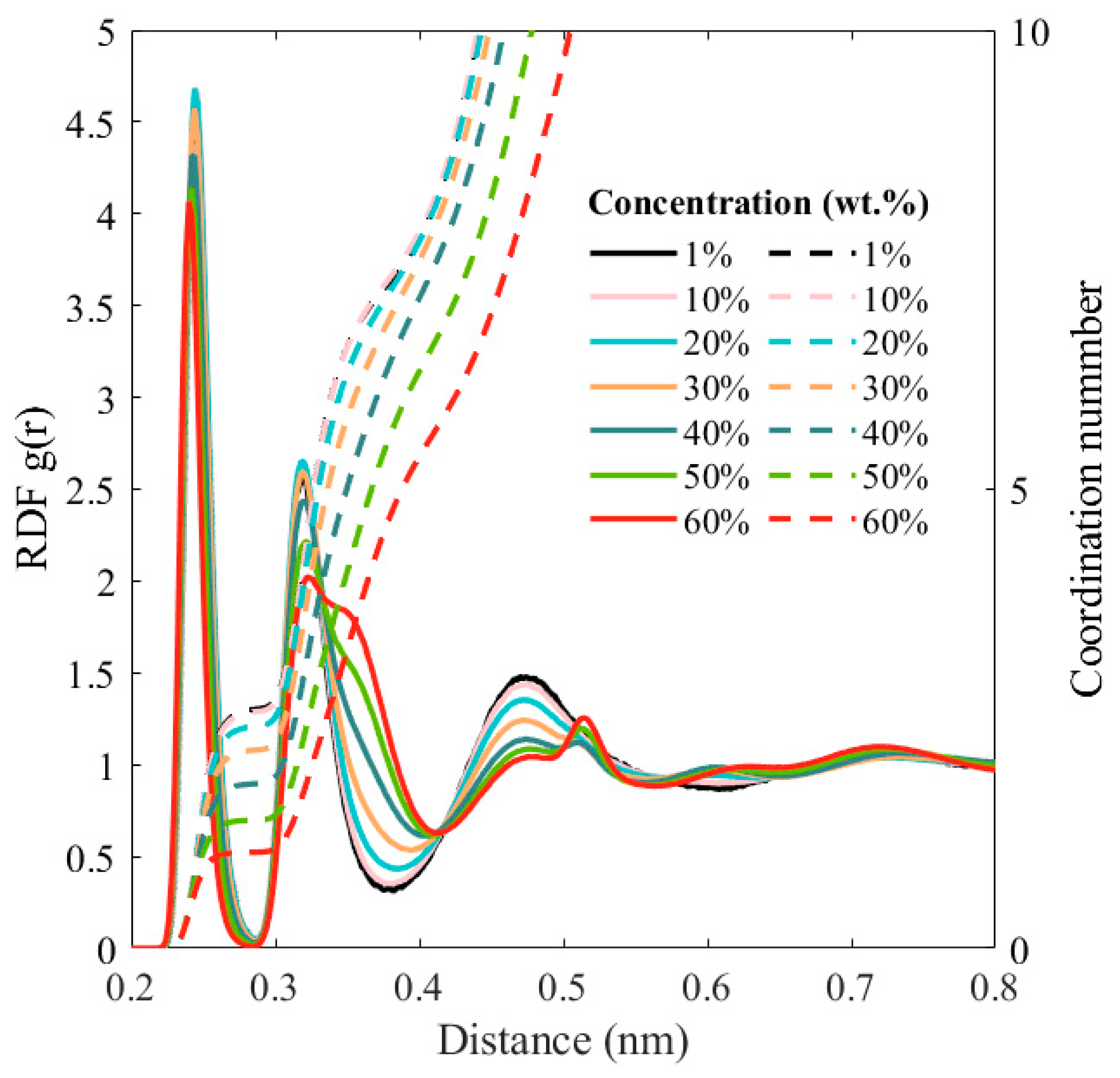
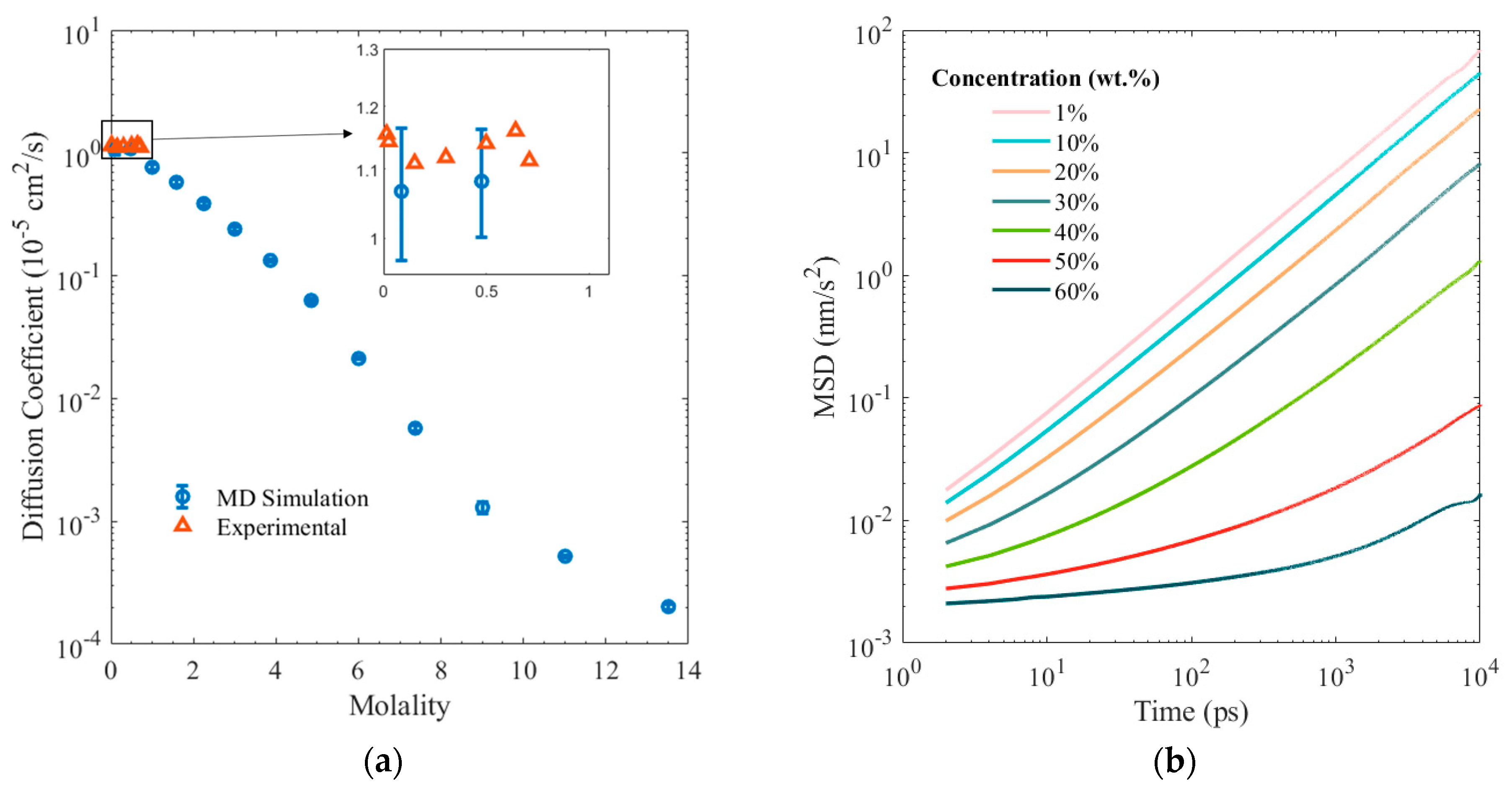
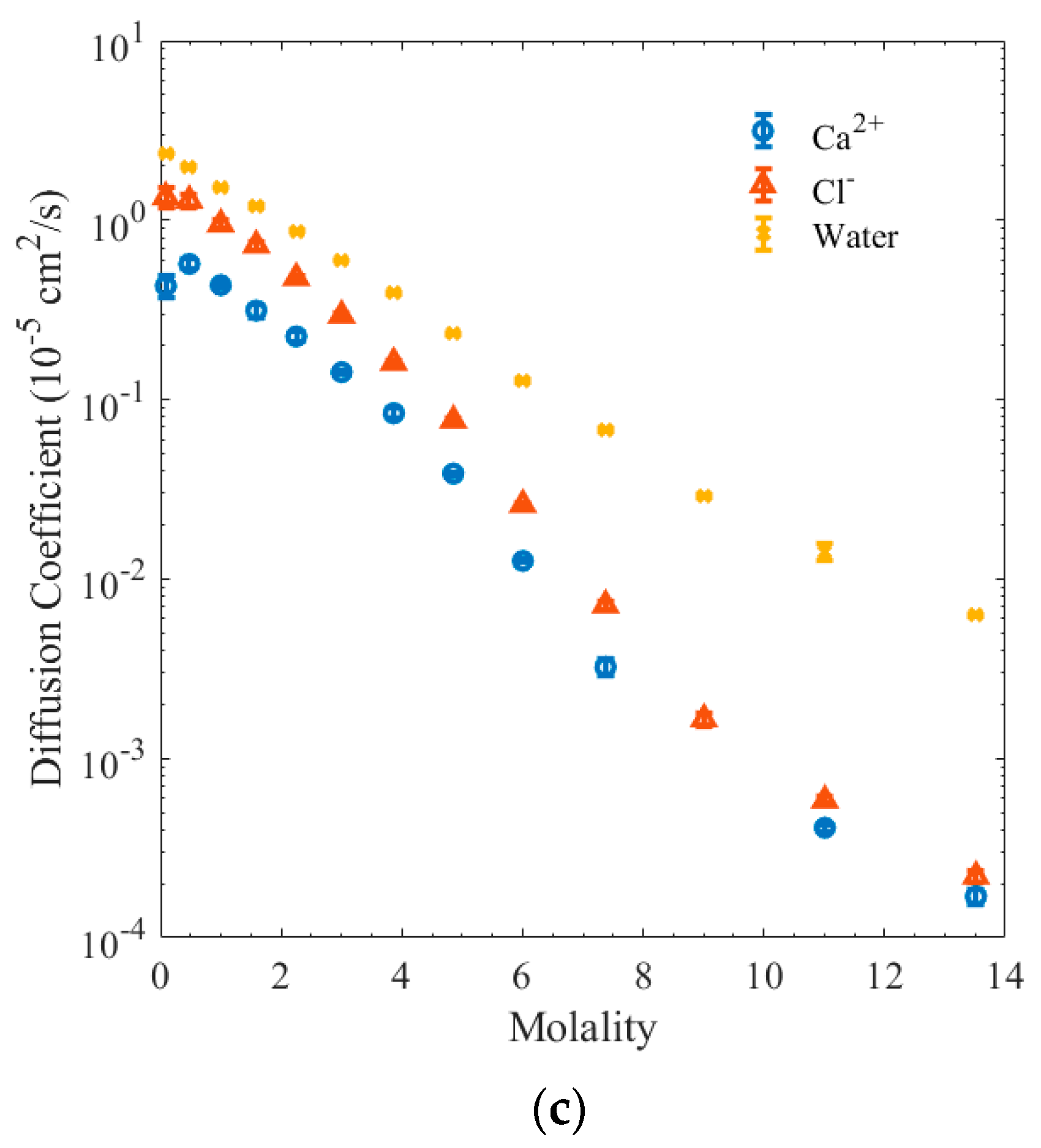
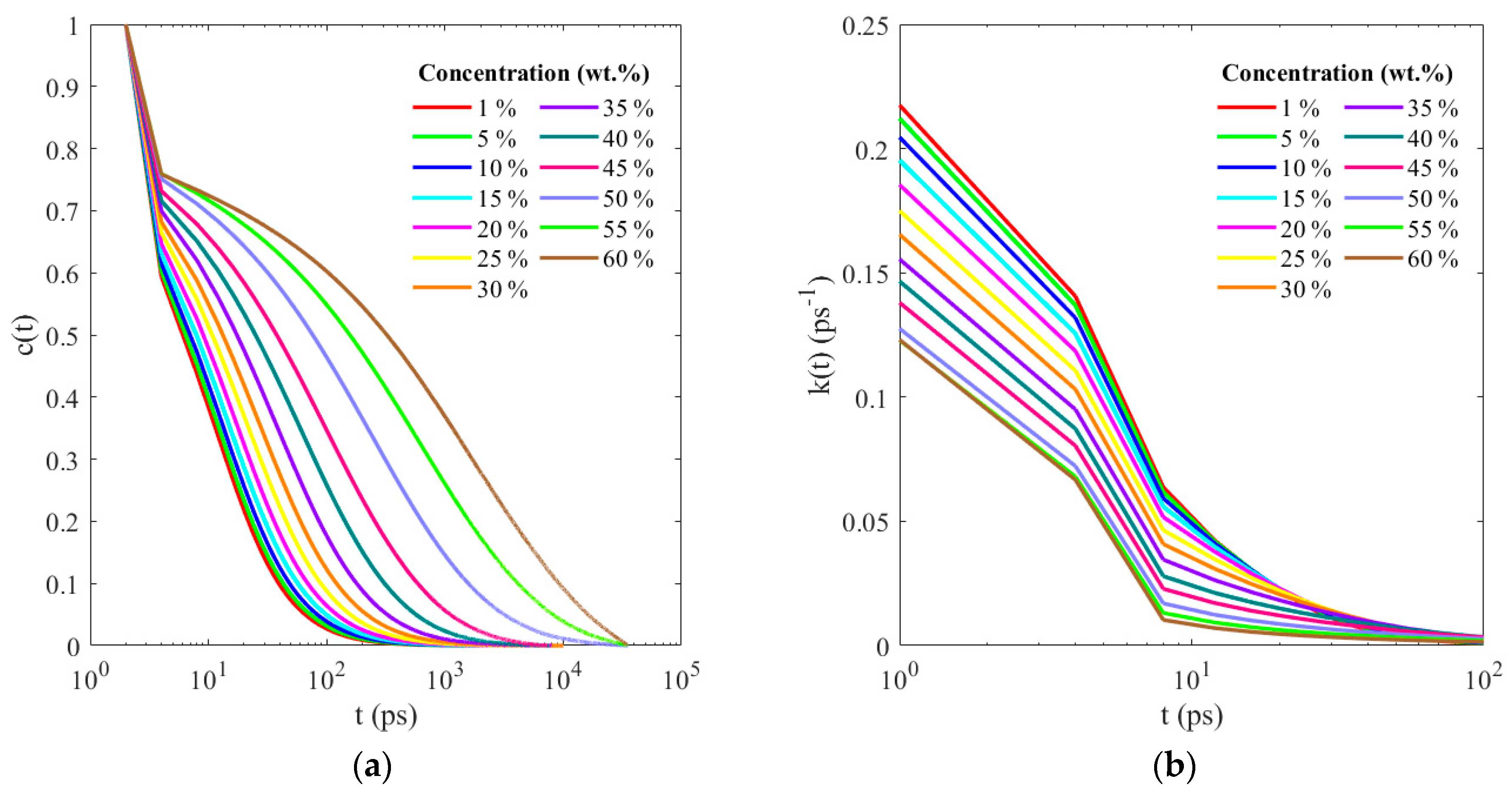
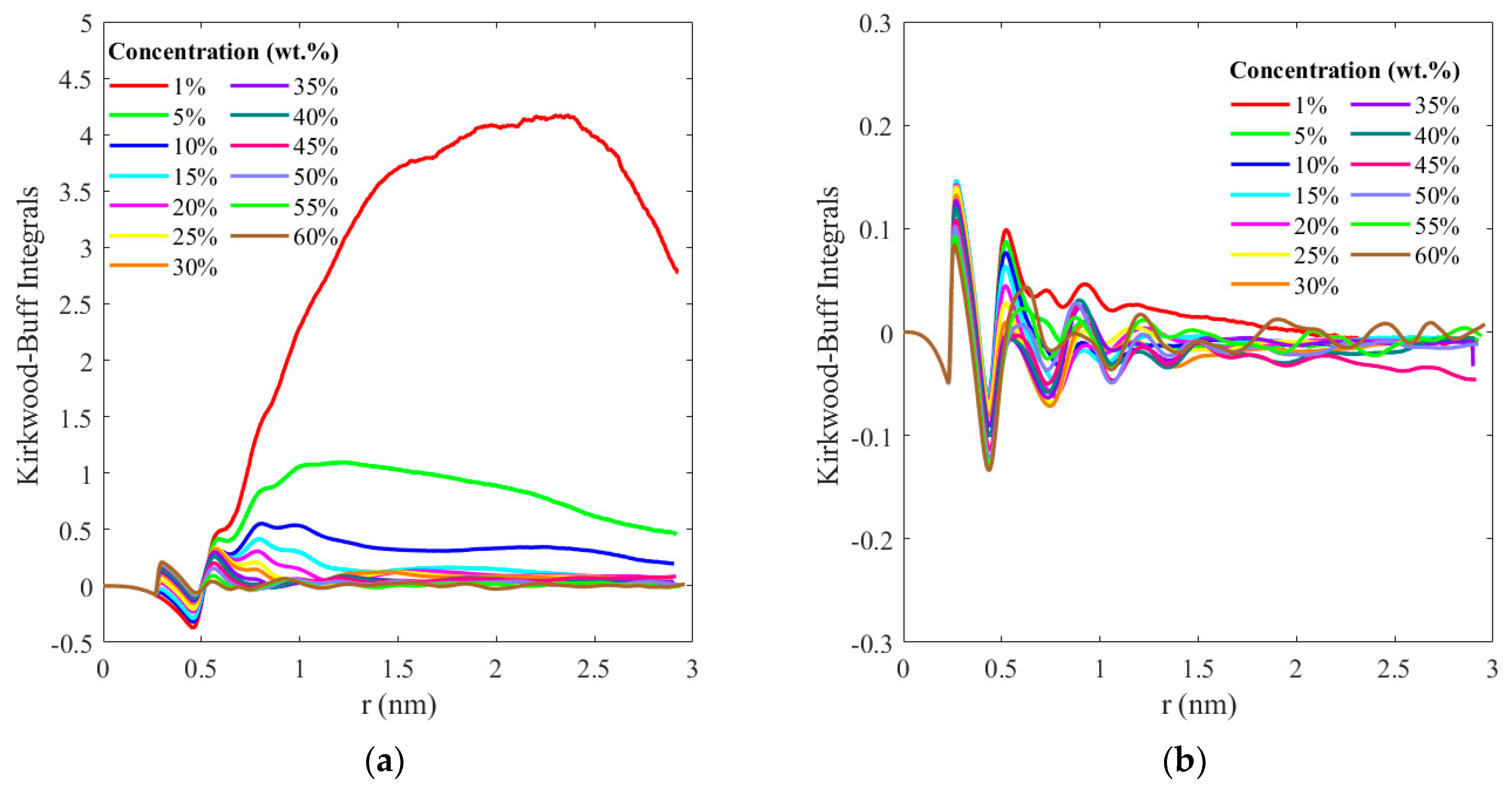
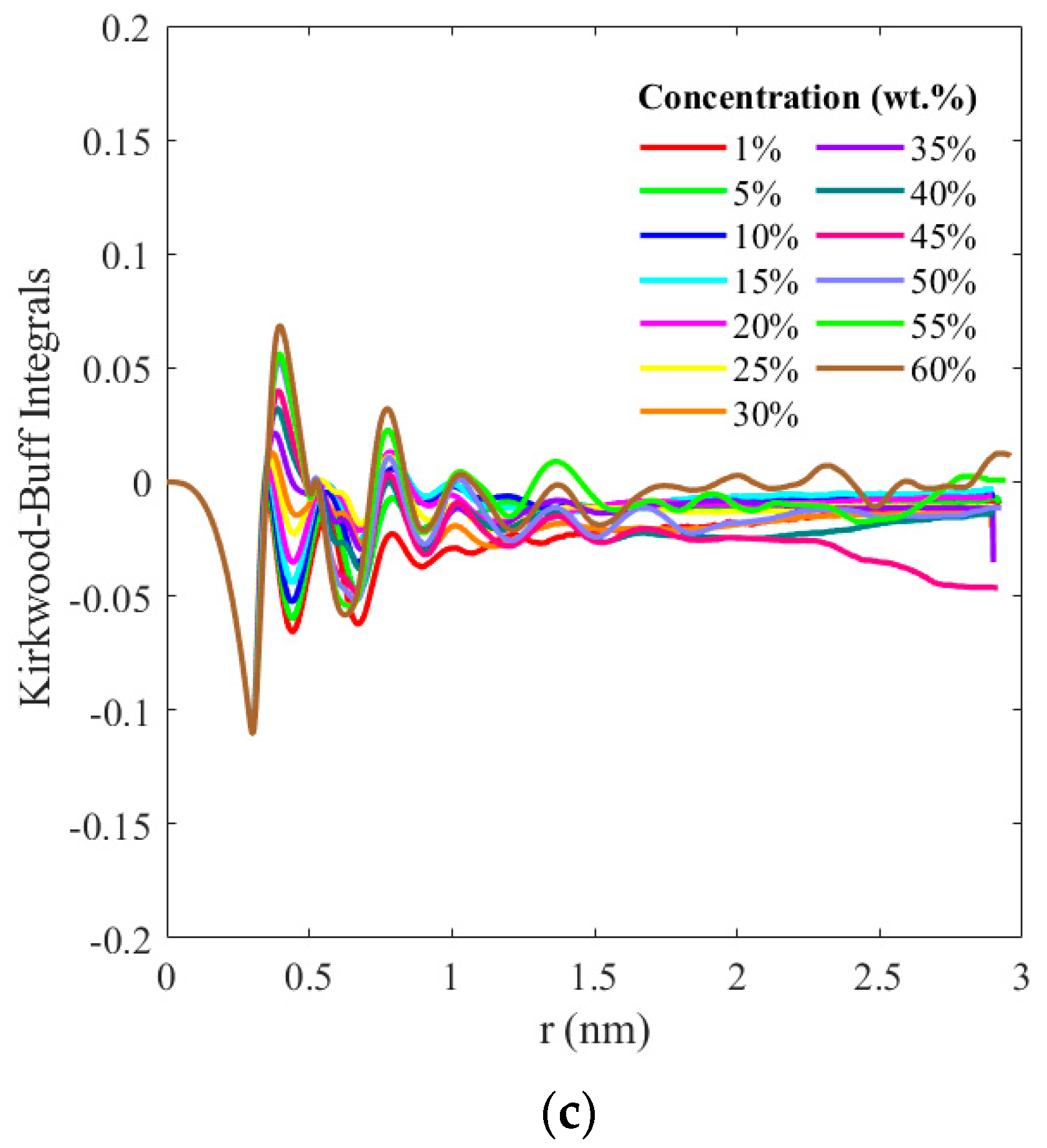
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yu, K.; Liu, Y.; Yang, Y. Review on form-stable inorganic hydrated salt phase change materials: Preparation, characterization and effect on the thermophysical properties. Appl. Energy 2021, 292, 116845. [Google Scholar] [CrossRef]
- Gerkman, M.A.; Han, G.G. Toward Controlled Thermal Energy Storage and Release in Organic Phase Change Materials. Joule 2020, 4, 1621–1625. [Google Scholar] [CrossRef]
- Bruni, F.; Imberti, S.; Mancinelli, R.; Ricci, M.A. Aqueous solutions of divalent chlorides: Ions hydration shell and water structure. J. Chem. Phys. 2012, 136, 064520. [Google Scholar] [CrossRef]
- Balasubramanian, G.; Murad, S.; Kappiyoor, R.; Puri, I.K. Structure of aqueous MgSO4 solution: Dilute to concentrated. Chem. Phys. Lett. 2011, 508, 38–42. [Google Scholar] [CrossRef]
- Hemalatha, B.; Vasantharani, P.; Vijayakumari, K.K. Ion-Ion and Ion-Solvent Interactions of Tetraalkyl Ammonium Bromide in Mixed DMF-Water Systems at Different Temperatures. J. Solut. Chem. 2009, 38, 947–955. [Google Scholar] [CrossRef]
- Botamanenko, D.Y.; Jarrold, M.F. Ion-Ion Interactions in Charge Detection Mass Spectrometry. J. Am. Soc. Mass Spectrom. 2019, 30, 2741–2749. [Google Scholar] [CrossRef] [PubMed]
- Dakua, V.K.; Sinha, B.; Roy, M.N. Ion–solvent and ion–ion interactions of sodium molybdate salt in aqueous binary mixtures of 1,4-dioxane at different temperatures. Phys. Chem. Liq. 2007, 45, 549–560. [Google Scholar] [CrossRef]
- Kournopoulos, S.; Santos, M.S.; Ravipati, S.; Haslam, A.J.; Jackson, G.; Economou, I.G.; Galindo, A. The Contribution of the Ion–Ion and Ion–Solvent Interactions in a Molecular Thermodynamic Treatment of Electrolyte Solutions. J. Phys. Chem. B 2022, 126, 9821–9839. [Google Scholar] [CrossRef]
- van der Vegt, N.F.A.; Haldrup, K.; Roke, S.; Zheng, J.; Lund, M.; Bakker, H.J. Water-Mediated Ion Pairing: Occurrence and Relevance. Chem. Rev. 2016, 116, 7626–7641. [Google Scholar] [CrossRef]
- Biriukov, D.; Wang, H.-W.; Rampal, N.; Tempra, C.; Kula, P.; Neuefeind, J.C.; Stack, A.G.; Předota, M. The “good”, the “bad”, and the “hidden” in neutron scattering and molecular dynamics of ionic aqueous solutions. J. Chem. Phys. 2022, 156, 194505. [Google Scholar] [CrossRef]
- Megyes, T.; Grósz, T.; Radnai, T.; Bakó, I.; Pálinkás, G. Solvation of Calcium Ion in Polar Solvents: An X-ray Diffraction and ab Initio Study. J. Phys. Chem. A 2004, 108, 7261–7271. [Google Scholar] [CrossRef]
- Megyes, T.; Bakó, I.; Bálint, S.; Grósz, T.; Radnai, T. Ion pairing in aqueous calcium chloride solution: Molecular dynamics simulation and diffraction studies. J. Mol. Liq. 2006, 129, 63–74. [Google Scholar] [CrossRef]
- Todorova, T.; Hünenberger, P.H.; Hutter, J. Car–Parrinello Molecular Dynamics Simulations of CaCl2 Aqueous Solutions. J. Chem. Theory Comput. 2008, 4, 779–789. [Google Scholar] [CrossRef] [PubMed]
- Friesen, S.; Hefter, G.; Buchner, R. Cation Hydration and Ion Pairing in Aqueous Solutions of MgCl2 and CaCl2. J. Phys. Chem. B 2019, 123, 891–900. [Google Scholar] [CrossRef]
- Wang, G.; Zhou, Y.; Toshio, Y.; Liu, H.; Zhu, F.; Wu, Z. Structure of Aqueous CaCl2 Solutions by X-ray Scattering and Density Functional Theory. Russ. J. Phys. Chem. A 2022, 96, S68–S76. [Google Scholar] [CrossRef]
- Smith, W.R.; Nezbeda, I.; Kolafa, J.; Moučka, F. Recent progress in the molecular simulation of thermodynamic properties of aqueous electrolyte solutions. Fluid Phase Equilibria 2018, 466, 19–30. [Google Scholar] [CrossRef]
- Lísal, M.; Smith, W.R.; Kolafa, J. Molecular Simulations of Aqueous Electrolyte Solubility: 1. The Expanded-Ensemble Osmotic Molecular Dynamics Method for the Solution Phase. J. Phys. Chem. B 2005, 109, 12956–12965. [Google Scholar] [CrossRef]
- Moučka, F.; Lísal, M.; Škvor, J.; Jirsák, J.; Nezbeda, I.; Smith, W.R. Molecular Simulation of Aqueous Electrolyte Solubility. Osmotic Ensemble Monte Carlo Methodology for Free Energy and Solubility Calculations and Application to NaCl. J. Phys. Chem. B 2011, 115, 7849–7861. [Google Scholar] [CrossRef]
- Moučka, F.; Lísal, M.; Smith, W.R. Molecular Simulation of Aqueous Electrolyte Solubility. 3. Alkali-Halide Salts and Their Mixtures in Water and in Hydrochloric Acid. J. Phys. Chem. B 2012, 116, 5468–5478. [Google Scholar] [CrossRef]
- Moučka, F.; Kolafa, J.; Lísal, M.; Smith, W.R. Chemical potentials of alkaline earth metal halide aqueous electrolytes and solubility of their hydrates by molecular simulation: Application to CaCl2, antarcticite, and sinjarite. J. Chem. Phys. 2018, 148, 222832. [Google Scholar] [CrossRef]
- Deublein, S.; Reiser, S.; Vrabec, J.; Hasse, H. A Set of Molecular Models for Alkaline-Earth Cations in Aqueous Solution. J. Phys. Chem. B 2012, 116, 5448–5457. [Google Scholar] [CrossRef] [PubMed]
- Mamatkulov, S.; Fyta, M.; Netz, R.R. Force fields for divalent cations based on single-ion and ion-pair properties. J. Chem. Phys. 2013, 138, 024505. [Google Scholar] [CrossRef] [PubMed]
- Zeron, I.M.; Abascal, J.L.F.; Vega, C. A force field of Li+, Na+, K+, Mg2+, Ca2+, Cl−, and SO42− in aqueous solution based on the TIP4P/2005 water model and scaled charges for the ions. J. Chem. Phys. 2019, 151, 134504. [Google Scholar] [CrossRef] [PubMed]
- Kohagen, M.; Mason, P.E.; Jungwirth, P. Accurate Description of Calcium Solvation in Concentrated Aqueous Solutions. J. Phys. Chem. B 2014, 118, 7902–7909. [Google Scholar] [CrossRef]
- Martinek, T.; Duboué-Dijon, E.; Timr, Š.; Mason, P.E.; Baxová, K.; Fischer, H.E.; Schmidt, B.; Pluhařová, E.; Jungwirth, P. Calcium ions in aqueous solutions: Accurate force field description aided by ab initio molecular dynamics and neutron scattering. J. Chem. Phys. 2018, 148, 222813. [Google Scholar] [CrossRef]
- Bernal-Uruchurtu, M.I.; Ortega-Blake, I. A refined Monte Carlo study of Mg2+ and Ca2+ hydration. J. Chem. Phys. 1995, 103, 1588–1598. [Google Scholar] [CrossRef]
- Probst, M.M.; Radnai, T.; Heinzinger, K.; Bopp, P.; Rode, B.M. Molecular dynamics and x-ray investigation of an aqueous calcium chloride solution. J. Phys. Chem. 1985, 89, 753–759. [Google Scholar] [CrossRef]
- Lindahl, E.; Abraham, M.J.; Hess, B.; van der Spoel, D. GROMACS 2020 Manual; GROMACS Development Team: Stockholm, Sweden, 2020. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Van Der Spoel, D.; Van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Sayle, R.A.; Milner-White, E. RASMOL: Biomolecular graphics for all. Trends Biochem. Sci. 1995, 20, 374–376. [Google Scholar] [CrossRef]
- Hoover, W.G.; Holian, B.L. Kinetic moments method for the canonical ensemble distribution. Phys. Lett. A 1996, 211, 253–257. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Beveridge, D.L.; DiCapua, F.M. Free Energy Via Molecular Simulation: Applications to Chemical and Biomolecular Systems. Annu. Rev. Biophys. Biophys. Chem. 1989, 18, 431–492. [Google Scholar] [CrossRef] [PubMed]
- Naik, R.R.; Gandhi, N.S.; Thakur, M.; Nanda, V. Analysis of crystallization phenomenon in Indian honey using molecular dynamics simulations and artificial neural network. Food Chem. 2019, 300, 125182. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Di Pierro, M.; Elber, R.; Leimkuhler, B. A Stochastic Algorithm for the Isobaric–Isothermal Ensemble with Ewald Summations for All Long Range Forces. J. Chem. Theory Comput. 2015, 11, 5624–5637. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Evaluation of the grand-canonical partition function using expanded Wang-Landau simulations. III. Impact of combining rules on mixtures properties. J. Chem. Phys. 2014, 140, 104109. [Google Scholar] [CrossRef]
- Chialvo, A.A.; Simonson, J.M. The structure of CaCl2 aqueous solutions over a wide range of concentration. Interpretation of diffraction experiments via molecular simulation. J. Chem. Phys. 2003, 119, 8052–8061. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017; pp. 1–626. [Google Scholar] [CrossRef]
- Hall, J.R.; Wishaw, B.F.; Stokes, R.H. The Diffusion Coefficients of Calcium Chloride and Ammonium Chloride in Concentrated Aqueous Solutions at 25°. J. Am. Chem. Soc. 1953, 75, 1556–1560. [Google Scholar] [CrossRef]
- Young, J.M.; Tietz, C.; Panagiotopoulos, A.Z. Activity Coefficients and Solubility of CaCl2 from Molecular Simulations. J. Chem. Eng. Data 2020, 65, 337–348. [Google Scholar] [CrossRef]
- Luzar, A. Resolving the hydrogen bond dynamics conundrum. J. Chem. Phys. 2000, 113, 10663–10675. [Google Scholar] [CrossRef]
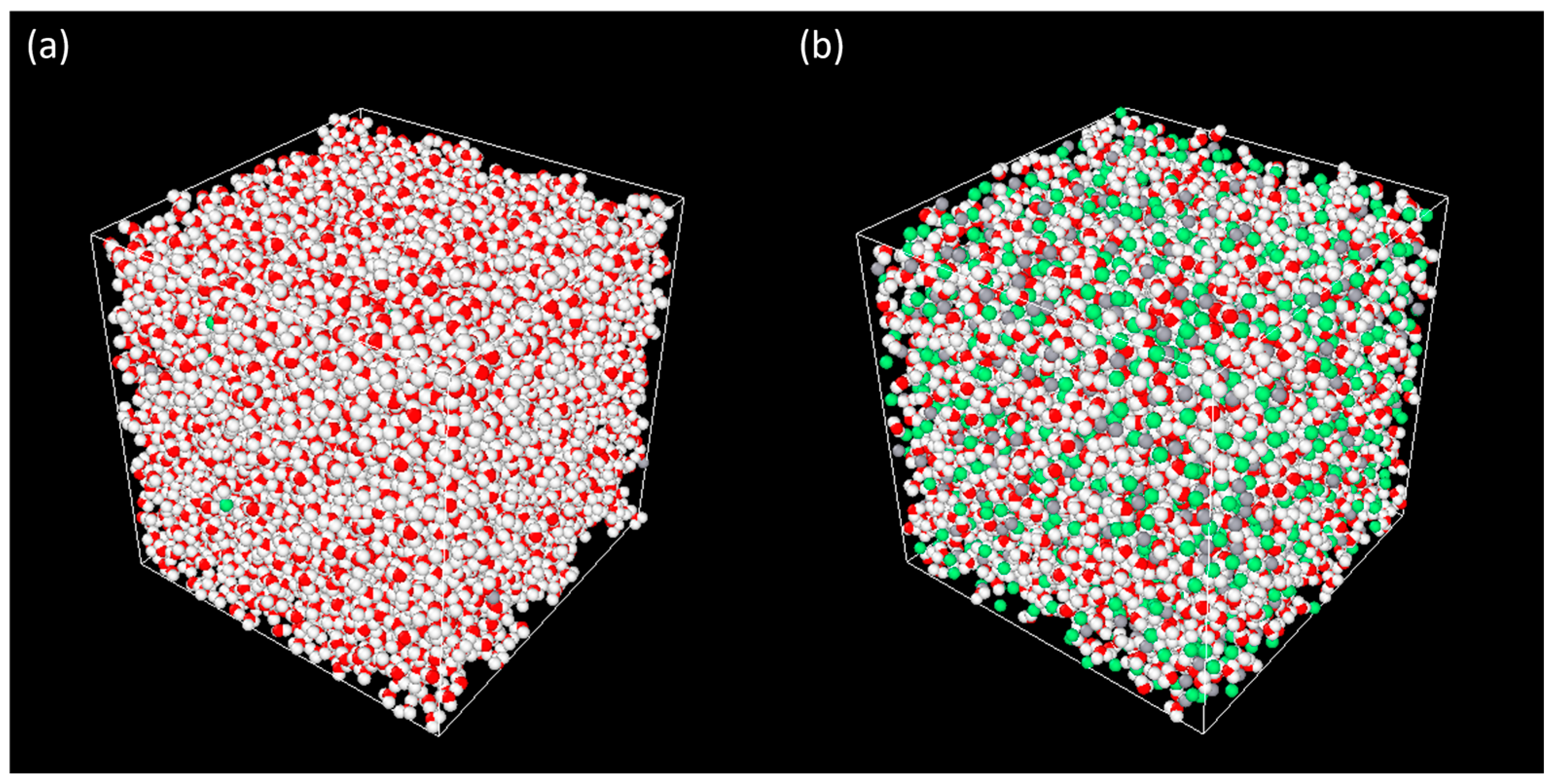
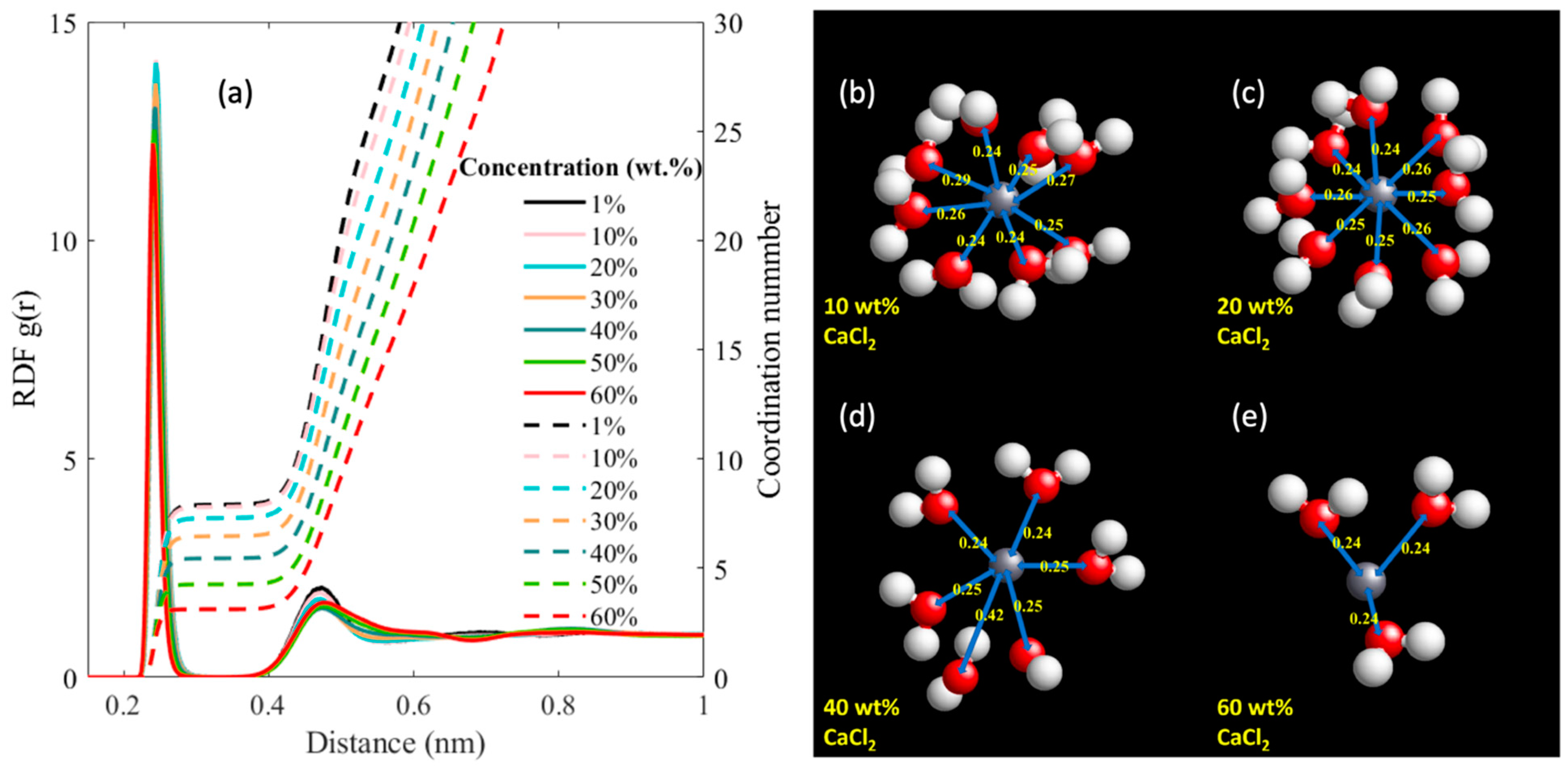
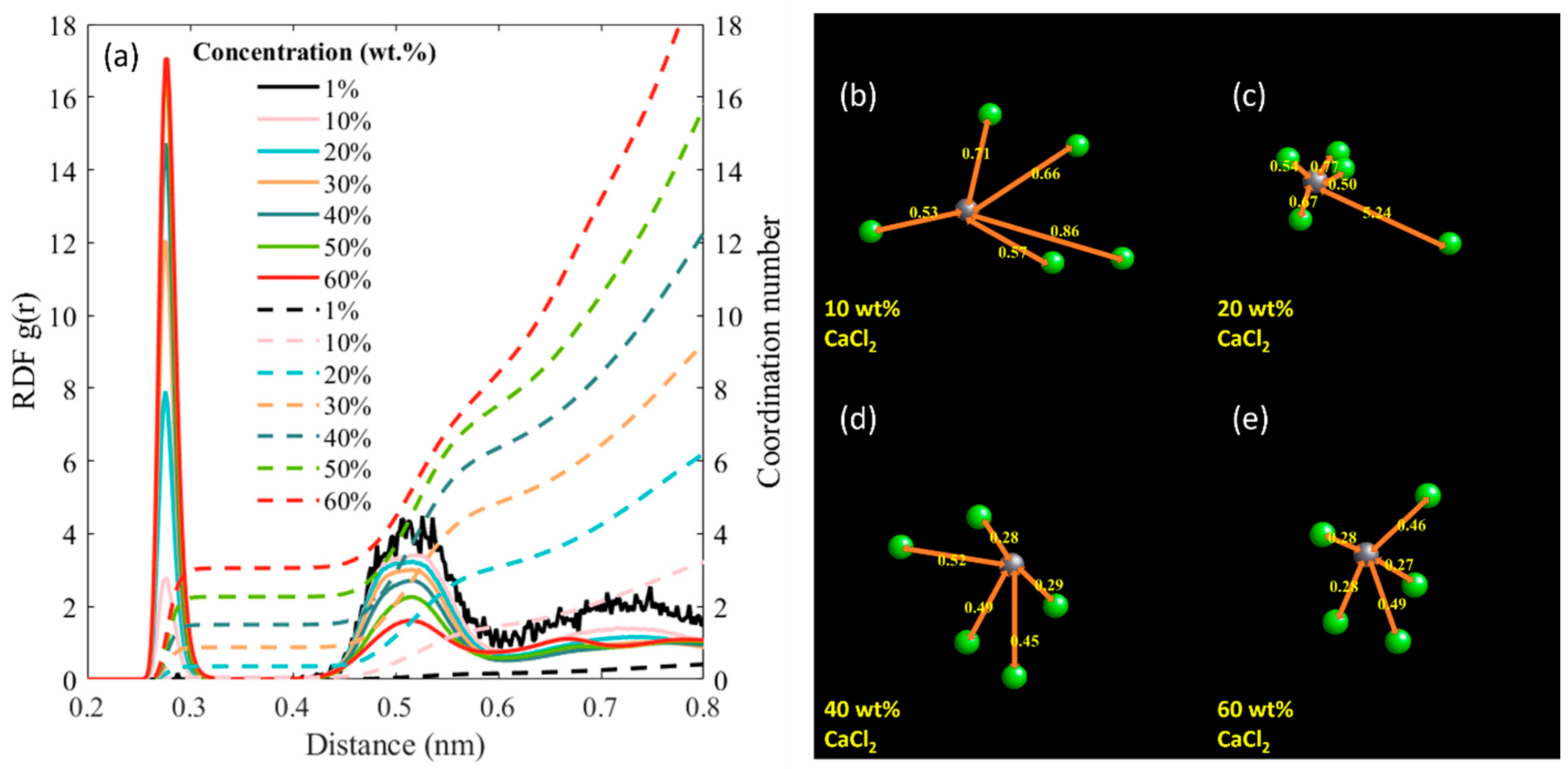
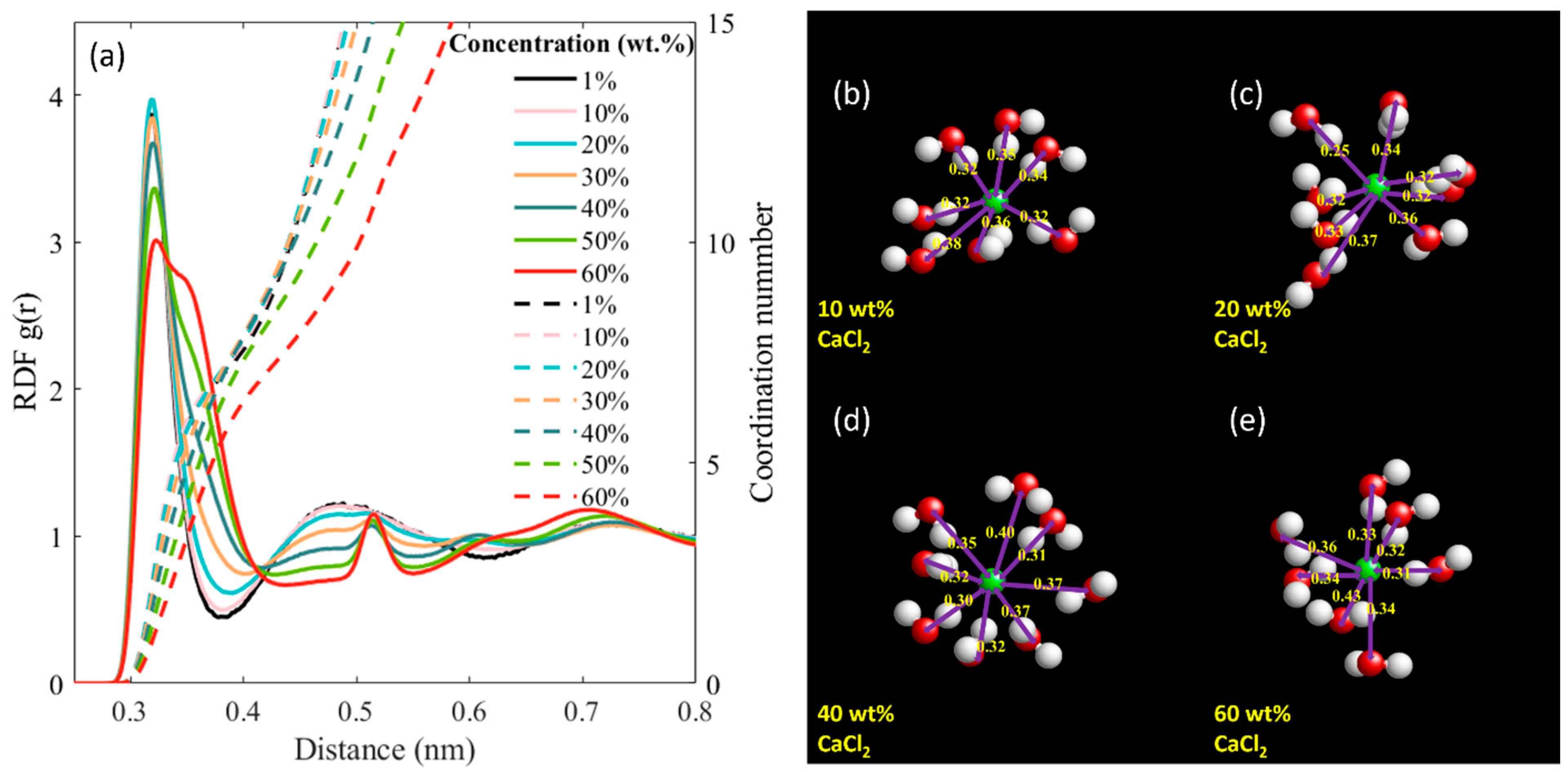

| CaCl2 wt.% | Molality (mol/kg) | Number of Molecules/Ions | ||
|---|---|---|---|---|
| Water | Ca2+ | Cl− | ||
| 1.00% | 0.1 | 6996 | 11 | 22 |
| 5.00% | 0.5 | 6852 | 59 | 118 |
| 10.00% | 1.0 | 6669 | 120 | 240 |
| 15.00% | 1.6 | 6474 | 185 | 370 |
| 20.00% | 2.3 | 6267 | 254 | 508 |
| 25.00% | 3.0 | 6048 | 327 | 654 |
| 30.00% | 3.9 | 5814 | 405 | 810 |
| 35.00% | 4.9 | 5568 | 487 | 974 |
| 40.00% | 6.0 | 5307 | 574 | 1148 |
| 45.00% | 7.4 | 5025 | 668 | 1336 |
| 50.00% | 9.0 | 4728 | 767 | 1534 |
| 55.00% | 11.0 | 4407 | 874 | 1748 |
| 60.00% | 13.5 | 4062 | 989 | 1978 |
| Sites | σ (nm) | ε (kJ/mol) | q (e) |
|---|---|---|---|
| Ca | 0.2813 | 0.5069 | 2.000 |
| Cl | 0.4448 | 0.4571 | −1.000 |
| Ow | 0.3166 | 0.6502 | −0.820 |
| H | 0.0000 | 0.0000 | 0.410 |
| Bond types | Interaction function | r0 (nm) | kb (kJ·mol−1·nm−4) |
| Ow-H | 0.1 | 2.32 × 107 | |
| Angle types | Interaction function | ϴ0 degrees | kϴ kJ mol−1 rad−2 |
| H-Ow-H | 109.5 | 434 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, L.; Balasubramanian, G. Examining the Hydration Behavior of Aqueous Calcium Chloride (CaCl2) Solution via Atomistic Simulations. Physchem 2023, 3, 319-331. https://doi.org/10.3390/physchem3030022
Yan L, Balasubramanian G. Examining the Hydration Behavior of Aqueous Calcium Chloride (CaCl2) Solution via Atomistic Simulations. Physchem. 2023; 3(3):319-331. https://doi.org/10.3390/physchem3030022
Chicago/Turabian StyleYan, Lida, and Ganesh Balasubramanian. 2023. "Examining the Hydration Behavior of Aqueous Calcium Chloride (CaCl2) Solution via Atomistic Simulations" Physchem 3, no. 3: 319-331. https://doi.org/10.3390/physchem3030022
APA StyleYan, L., & Balasubramanian, G. (2023). Examining the Hydration Behavior of Aqueous Calcium Chloride (CaCl2) Solution via Atomistic Simulations. Physchem, 3(3), 319-331. https://doi.org/10.3390/physchem3030022





