Modelling Photoionisations in Tautomeric DNA Nucleobase Derivatives 7H-Adenine and 7H-Guanine: Ultrafast Decay and Photostability
Abstract
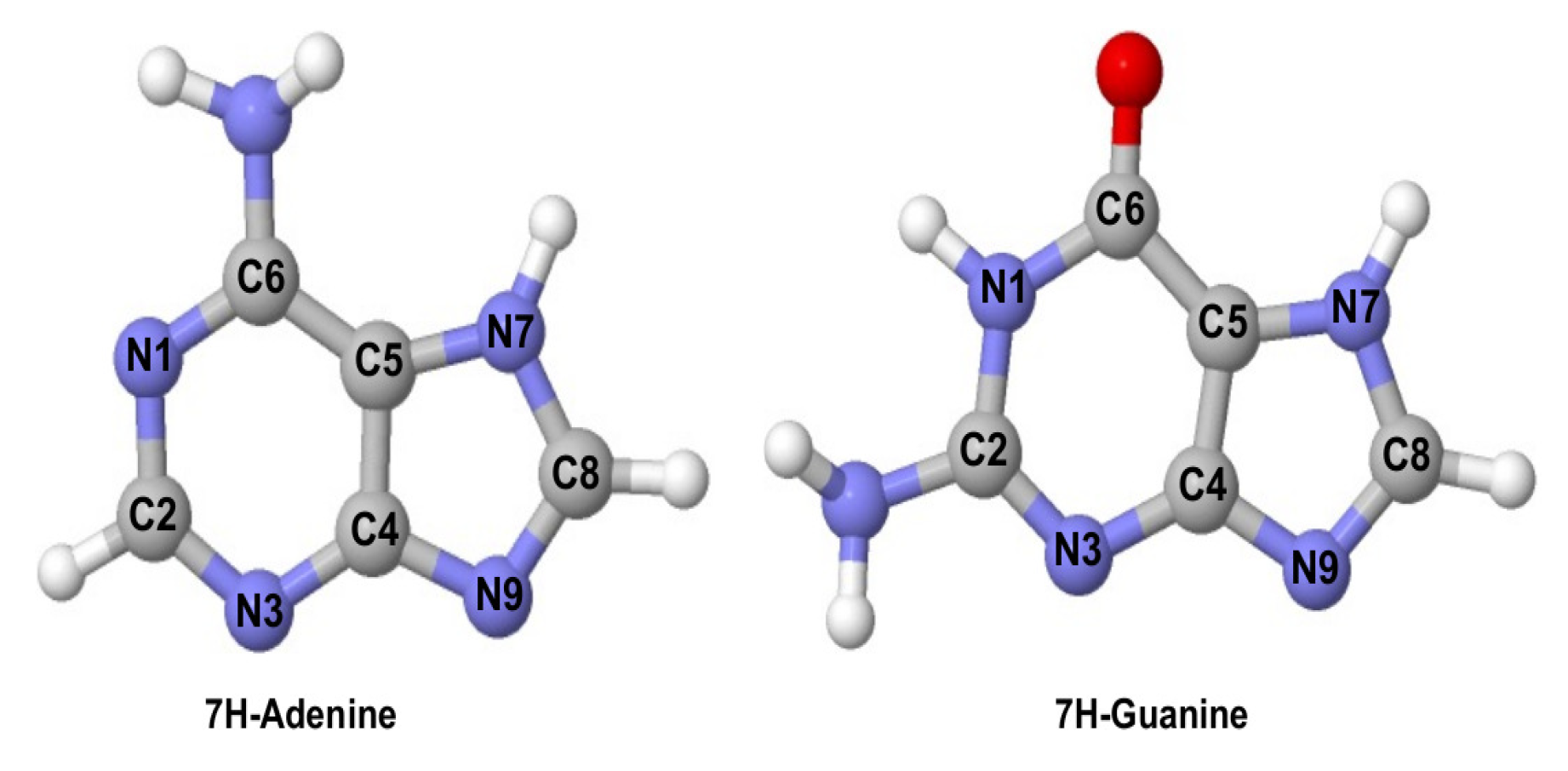
:1. Introduction
2. Results
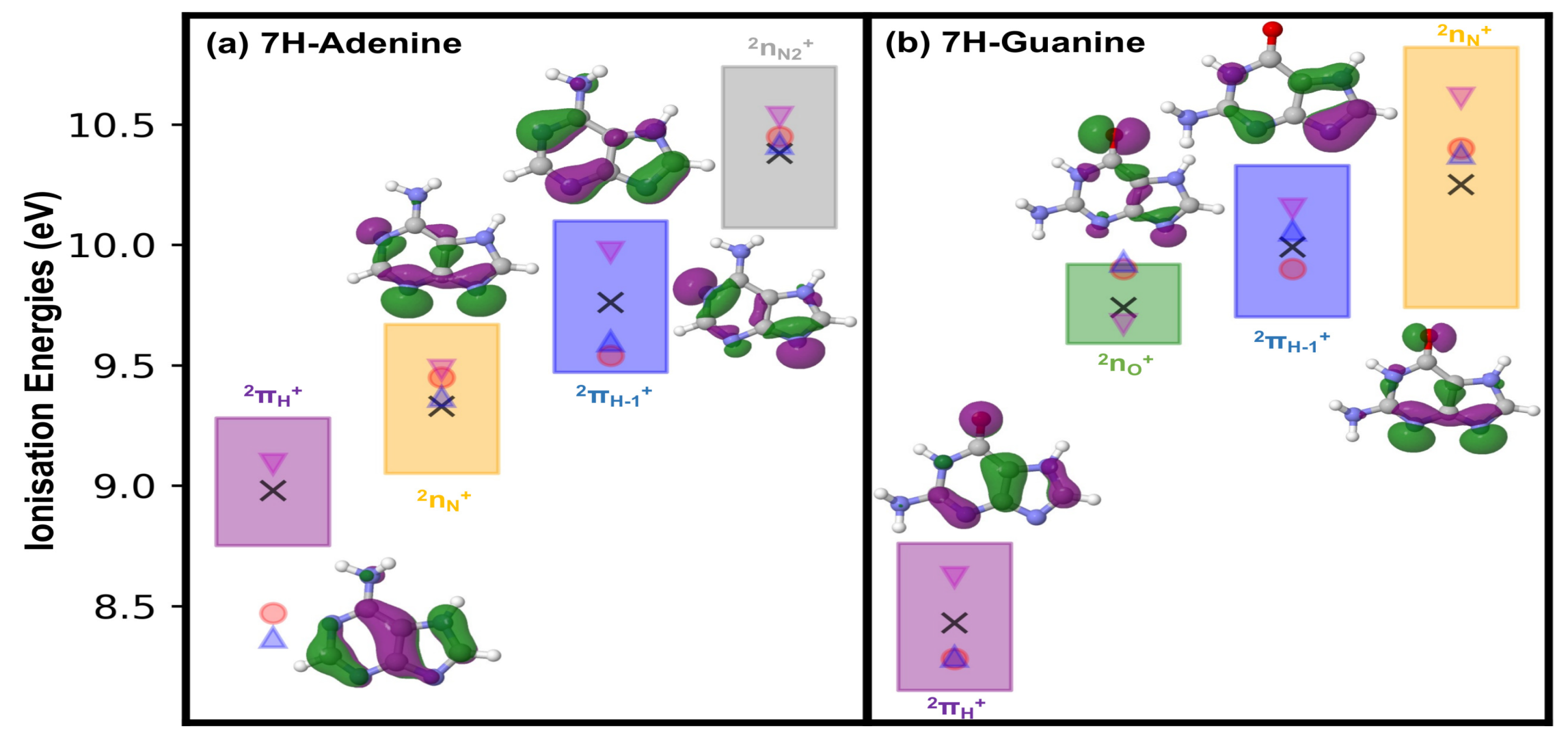
2.1. Ionisation Potentials
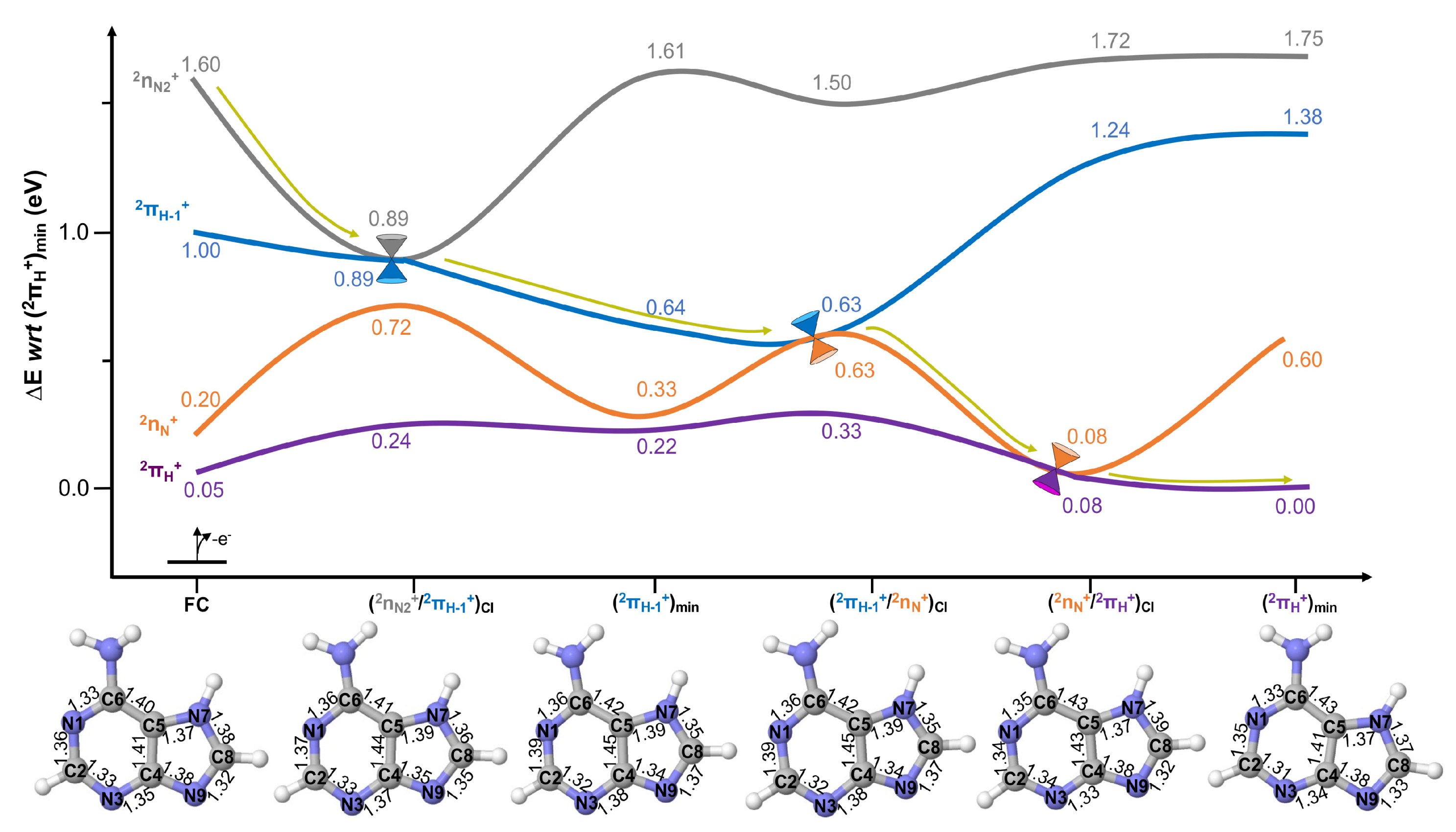
2.2. Excited State Decays
Conical Intersection Characterisation
3. Discussion
4. Computational Details
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schreier, W.J.; Gilch, P.; Zinth, W. Early Events of DNA Photodamage. Annu. Rev. Phys. Chem. 2015, 66, 497–519. [Google Scholar] [CrossRef]
- Noonan, F.P.; Zaidi, M.R.; Wolnicka-Glubisz, A.; Anver, M.R.; Bahn, J.; Wielgus, A.; Cadet, J.; Douki, T.; Mouret, S.; Tucker, M.A.; et al. Melanoma induction by ultraviolet A but not ultraviolet B radiation requires melanin pigment. Nat. Commun. 2012, 3, 884. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Improta, R.; Santoro, F.; Blancafort, L. Quantum Mechanical Studies on the Photophysics and the Photochemistry of Nucleic Acids and Nucleobases. Chem. Rev. 2016, 116, 3540–3593. [Google Scholar] [CrossRef]
- Middleton, C.T.; de La Harpe, K.; Su, C.; Law, Y.K.; Crespo-Hernández, C.E.; Kohler, B. DNA Excited-State Dynamics: From Single Bases to the Double Helix. Annu. Rev. Phys. Chem. 2009, 60, 217–239. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crespo-Hernández, C.E.; Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast Excited-State Dynamics in Nucleic Acids. Chem. Rev. 2004, 104, 1977–2020. [Google Scholar] [CrossRef] [PubMed]
- Spata, V.A.; Lee, W.; Matsika, S. Excimers and Exciplexes in Photoinitiated Processes of Oligonucleotides. J. Phys. Chem. Lett. 2016, 7, 976–984. [Google Scholar] [CrossRef] [PubMed]
- Markovitsi, D.; Gustavsson, T.; Vayá, I. Fluorescence of DNA Duplexes: From Model Helices to Natural DNA. J. Phys. Chem. Lett. 2010, 1, 3271–3276. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Zhang, Y.; Kohler, B. Excited States in DNA Strands Investigated by Ultrafast Laser Spectroscopy. Top. Curr. Chem. 2015, 356, 39–87. [Google Scholar]
- Martínez-Fernández, L.; Esposito, L.; Improta, R. Studying the excited electronic states of guanine rich DNA quadruplexes by quantum mechanical methods: Main achievements and perspectives. Photochem. Photobiol. Sci. 2020, 19, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Balanikas, E.; Banyasz, A.; Douki, T.; Baldacchino, G.; Markovitsi, D. Guanine Radicals Induced in DNA by Low-Energy Photoionization. Acc. Chem. Res. 2020, 53, 1511–1519. [Google Scholar] [CrossRef]
- Gustavsson, T.; Markovitsi, D. Fundamentals of the Intrinsic DNA Fluorescence. Acc. Chem. Res. 2021, 54, 1226–1235. [Google Scholar] [CrossRef]
- Kleinermanns, K.; Nachtigallová, D.; de Vries, M.S. Excited state dynamics of DNA bases. Int. Rev. Phys. Chem. 2013, 32, 308–342. [Google Scholar] [CrossRef]
- Beckstead, A.A.; Zhang, Y.; de Vries, M.S.; Kohler, B. Life in the light: Nucleic acid photoproperties as a legacy of chemical evolution. Phys. Chem. Chem. Phys. 2016, 18, 24228–24238. [Google Scholar] [CrossRef] [PubMed]
- Boldissar, S.; de Vries, M.S. How nature covers its bases. Phys. Chem. Chem. Phys. 2018, 20, 9701–9716. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pfeifer, G.P.; Besaratinia, A. UV wavelength-dependent DNA damage and human non-melanoma and melanoma skin cancer. Photochem. Photobiol. Sci. 2012, 11, 90–97. [Google Scholar] [CrossRef] [Green Version]
- Cadet, J.; Mouret, S.; Ravanat, J.L.; Douki, T. Photoinduced Damage to Cellular DNA: Direct and Photosensitized Reactions†. Photochem. Photobiol. 2012, 88, 1048–1065. [Google Scholar] [CrossRef] [PubMed]
- Nisoli, M.; Decleva, P.; Calegari, F.; Palacios, A.; Martín, F. Attosecond Electron Dynamics in Molecules. Chem. Rev. 2017, 117, 10760–10825. [Google Scholar] [CrossRef]
- Calegari, F.; Trabattoni, A.; Palacios, A.; Ayuso, D.; Castrovilli, M.C.; Greenwood, J.B.; Decleva, P.; Martín, F.; Nisoli, M. Charge migration induced by attosecond pulses in bio-relevant molecules. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 142001. [Google Scholar] [CrossRef]
- Bucher, D.B.; Pilles, B.M.; Carell, T.; Zinth, W. Charge separation and charge delocalization identified in long-living states of photoexcited DNA. Proc. Natl. Acad. Sci. USA 2014, 111, 4369–4374. [Google Scholar] [CrossRef] [Green Version]
- Takaya, T.; Su, C.; de La Harpe, K.; Crespo-Hernández, C.E.; Kohler, B. UV excitation of single DNA and RNA strands produces high yields of exciplex states between two stacked bases. Proc. Natl. Acad. Sci. USA 2008, 105, 10285–10290. [Google Scholar] [CrossRef] [Green Version]
- Vayá, I.; Gustavsson, T.; Douki, T.; Berlin, Y.; Markovitsi, D. Electronic Excitation Energy Transfer between Nucleobases of Natural DNA. J. Am. Chem. Soc. 2012, 134, 11366–11368. [Google Scholar] [CrossRef] [PubMed]
- Bucher, D.B.; Kufner, C.L.; Schlueter, A.; Carell, T.; Zinth, W. UV-Induced Charge Transfer States in DNA Promote Sequence Selective Self-Repair. J. Am. Chem. Soc. 2016, 138, 186–190. [Google Scholar] [CrossRef]
- Banyasz, A.; Ketola, T.; Martínez-Fernández, L.; Improta, R.; Markovitsi, D. Adenine radicals generated in alternating AT duplexes by direct absorption of low-energy UV radiation. Faraday Discuss. 2018, 207, 181–197. [Google Scholar] [CrossRef]
- Roca-Sanjuán, D.; Rubio, M.; Merchán, M.; Serrano-Andrés, L. Ab initio determination of the ionization potentials of DNA and RNA nucleobases. J. Chem. Phys. 2006, 125, 084302. [Google Scholar] [CrossRef] [Green Version]
- Wolf, T.J.A.; Gühr, M. Photochemical pathways in nucleobases measured with an X-ray FEL. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2019, 377, 20170473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, T.J.A.; Holzmeier, F.; Wagner, I.; Berrah, N.; Bostedt, C.; Bozek, J.; Bucksbaum, P.; Coffee, R.; Cryan, J.; Farrell, J.; et al. Observing Femtosecond Fragmentation Using Ultrafast X-ray-Induced Auger Spectra. Appl. Sci. 2017, 7, 681. [Google Scholar] [CrossRef]
- Assmann, M.; Köppel, H.; Matsika, S. Photoelectron Spectrum and Dynamics of the Uracil Cation. J. Phys. Chem. A 2015, 119, 866–875. [Google Scholar] [CrossRef] [PubMed]
- Assmann, M.; Weinacht, T.; Matsika, S. Surface hopping investigation of the relaxation dynamics in radical cations. J. Chem. Phys. 2016, 144, 034301. [Google Scholar] [CrossRef] [Green Version]
- Segarra-Martí, J.; Tran, T.; Bearpark, M.J. Ultrafast and radiationless electronic excited state decay of uracil and thymine cations: Computing the effects of dynamic electron correlation. Phys. Chem. Chem. Phys. 2019, 21, 14322–14330. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Segarra-Martí, J.; Tran, T.; Bearpark, M.J. Computing the Ultrafast and Radiationless Electronic Excited State Decay of Cytosine and 5-methyl-cytosine Cations: Uncovering the Role of Dynamic Electron Correlation. ChemPhotoChem 2019, 3, 856–865. [Google Scholar] [CrossRef]
- Crespo-Hernández, C.E.; Martínez-Fernández, L.; Rauer, C.; Reichardt, C.; Mai, S.; Pollum, M.; Marquetand, P.; González, L.; Corral, I. Electronic and Structural Elements That Regulate the Excited-State Dynamics in Purine Nucleobase Derivatives. J. Am. Chem. Soc. 2015, 137, 4368–4381. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Vries, M.S. Tautomer-Selective Spectroscopy of Nucleobases, Isolated in the Gas Phase. In Tautomerism; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; Chapter 7; pp. 177–196. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Merchán, M. Are the five natural DNA/RNA base monomers a good choice from natural selection?: A photochemical perspective. J. Photochem. Photobiol. C Photochem. Rev. 2009, 10, 21–32. [Google Scholar] [CrossRef]
- Huang, Y.; Kenttamaa, H. Theoretical Estimations of the 298 K Gas-Phase Acidities of the Purine-Based Nucleobases Adenine and Guanine. J. Phys. Chem. A 2004, 108, 4485–4490. [Google Scholar] [CrossRef]
- Bravaya, K.B.; Kostko, O.; Dolgikh, S.; Landau, A.; Ahmed, M.; Krylov, A.I. Electronic Structure and Spectroscopy of Nucleic Acid Bases: Ionization Energies, Ionization-Induced Structural Changes, and Photoelectron Spectra. J. Phys. Chem. A 2010, 114, 12305–12317. [Google Scholar] [CrossRef] [Green Version]
- Marian, C.M. The Guanine Tautomer Puzzle: Quantum Chemical Investigation of Ground and Excited States. J. Phys. Chem. A 2007, 111, 1545–1553. [Google Scholar] [CrossRef]
- Zaytseva, I.L.; Trofimov, A.B.; Schirmer, J.; Plekan, O.; Feyer, V.; Richter, R.; Coreno, M.; Prince, K.C. Theoretical and Experimental Study of Valence-Shell Ionization Spectra of Guanine. J. Phys. Chem. A 2009, 113, 15142–15149. [Google Scholar] [CrossRef]
- Dolgounitcheva, O.; Zakrzewski, V.G.; Ortiz, J.V. Electron Propagator Theory of Guanine and Its Cations: Tautomerism and Photoelectron Spectra. J. Am. Chem. Soc. 2000, 122, 12304–12309. [Google Scholar] [CrossRef]
- Mons, M.; Piuzzi, F.; Dimicoli, I.; Gorb, L.; Leszczynski, J. Near-UV Resonant Two-Photon Ionization Spectroscopy of Gas Phase Guanine: Evidence for the Observation of Three Rare Tautomers. J. Phys. Chem. A 2006, 110, 10921–10924. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Yu, C.; Peng, S.; Akiyama, I.; Li, K.; Lee, L.K.; LeBreton, P.R. Ultraviolet photoelectron studies of the ground-state electronic structure and gas-phase tautomerism of hypoxanthine and guanine. J. Phys. Chem. 1980, 84, 1006–1012. [Google Scholar] [CrossRef]
- Trofimov, A.B.; Schirmer, J.; Kobychev, V.B.; Potts, A.W.; Holland, D.M.P.; Karlsson, L. Photoelectron spectra of the nucleobases cytosine, thymine and adenine. J. Phys. B At. Mol. Opt. Phys. 2005, 39, 305–329. [Google Scholar] [CrossRef]
- Shiozaki, T.; Woywod, C.; Werner, H.J. Pyrazine excited states revisited using the extended multi-state complete active space second-order perturbation method. Phys. Chem. Chem. Phys. 2013, 15, 262–269. [Google Scholar] [CrossRef] [Green Version]
- Kotur, M.; Zhou, C.; Matsika, S.; Patchkovskii, S.; Spanner, M.; Weinacht, T.C. Neutral-Ionic State Correlations in Strong-Field Molecular Ionization. Phys. Rev. Lett. 2012, 109, 203007. [Google Scholar] [CrossRef] [Green Version]
- Kotur, M.; Weinacht, T.; Zhou, C.; Matsika, S. Following Ultrafast Radiationless Relaxation Dynamics With Strong Field Dissociative Ionization: A Comparison Between Adenine, Uracil and Cytosine. IEEE J. Sel. Top. Quantum Electron. 2012, 18, 187–194. [Google Scholar] [CrossRef]
- Segarra-Martí, J.; Bearpark, M.J. Modelling photoionisation in isocytosine: Potential formation of longer-lived excited state cations in its keto form. ChemPhysChem 2021. [Google Scholar] [CrossRef]
- Matsika, S. Two- and three-state conical intersections in the uracil cation. Chem. Phys. 2008, 349, 356–362. [Google Scholar] [CrossRef]
- Brash, D.E.; Goncalves, L.C.; Bechara, E.J. Chemiexcitation and Its Implications for Disease. Trends Mol. Med. 2018, 24, 527–541. [Google Scholar] [CrossRef]
- Fdez. Galván, I.; Delcey, M.G.; Pedersen, T.B.; Aquilante, F.; Lindh, R. Analytical State-Average Complete-Active-Space Self-Consistent Field Nonadiabatic Coupling Vectors: Implementation with Density-Fitted Two-Electron Integrals and Application to Conical Intersections. J. Chem. Theory Comput. 2016, 12, 3636–3653. [Google Scholar] [CrossRef] [Green Version]
- Atchity, G.J.; Xantheas, S.S.; Ruedenberg, K. Potential energy surfaces near intersections. J. Chem. Phys. 1991, 95, 1862–1876. [Google Scholar] [CrossRef]
- Hall, K.F.; Boggio-Pasqua, M.; Bearpark, M.J.; Robb, M.A. Photostability Via Sloped Conical Intersections: A Computational Study of the Excited States of the Naphthalene Radical Cation. J. Phys. Chem. A 2006, 110, 13591–13599. [Google Scholar] [CrossRef]
- Tokmachev, A.M.; Boggio-Pasqua, M.; Bearpark, M.J.; Robb, M.A. Photostability via Sloped Conical Intersections: A Computational Study of the Pyrene Radical Cation. J. Phys. Chem. A 2008, 112, 10881–10886. [Google Scholar] [CrossRef]
- Segarra-Martí, J.; Garavelli, M.; Aquilante, F. Multiconfigurational second-order perturbation theory with frozen natural orbitals extended to the treatment of photochemical problems. J. Chem. Theory Comput. 2015, 11, 3772–3784. [Google Scholar] [CrossRef] [PubMed]
- Segarra-Martí, J.; Francés-Monerris, A.; Roca-Sanjuán, D.; Merchán, M. Assessment of the Potential Energy Hypersurfaces in Thymine within Multiconfigurational Theory: CASSCF vs. CASPT2. Molecules 2016, 21, 1666. [Google Scholar] [CrossRef] [Green Version]
- Segarra-Martí, J.; Mukamel, S.; Garavelli, M.; Nenov, A.; Rivalta, I. Towards Accurate Simulation of Two-Dimensional Electronic Spectroscopy. Top. Curr. Chem. 2018, 376, 24. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Merchán, M.; Lindh, R. Computation of conical intersections by using perturbation techniques. J. Chem. Phys. 2005, 122, 104107. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Tinoco, M.; Dolgounitcheva, O.; Zakrzewski, V.G.; Ortiz, J.V. Composite electron propagator methods for calculating ionization energies. J. Chem. Phys. 2016, 144, 224110. [Google Scholar] [CrossRef] [PubMed]
- Dolgounitcheva, O.; Zakrzewski, V.G.; Ortiz, J.V. Vertical Ionization Energies of Adenine and 9-Methyl Adenine. J. Phys. Chem. A 2009, 113, 14630–14635. [Google Scholar] [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef] [Green Version]
- Krylov, A.I. Equation-of-Motion Coupled-Cluster Methods for Open-Shell and Electronically Excited Species: The Hitchhiker’s Guide to Fock Space. Annu. Rev. Phys. Chem. 2008, 59, 433–462. [Google Scholar] [CrossRef] [Green Version]
- Roca-Sanjuán, D.; Aquilante, F.; Lindh, R. Multiconfiguration second-order perturbation theory approach to strong electron correlation in chemistry and photochemistry. WIRES Comput. Mol. Sci. 2012, 2, 585–603. [Google Scholar] [CrossRef]
- Giussani, A.; Segarra-Martí, J.; Nenov, A.; Rivalta, I.; Tolomelli, A.; Mukamel, S.; Garavelli, M. Spectroscopic fingerprints of DNA/RNA pyrimidine nucleobases in third-order nonlinear electronic spectra. Theor. Chem. Acc. 2016, 135, 121. [Google Scholar] [CrossRef]
- Segarra-Martí, J.; Zvereva, E.; Marazzi, M.; Brazard, J.; Dumont, E.; Assfeld, X.; Haacke, S.; Garavelli, M.; Monari, A.; Léonard, J.; et al. Resolving the Singlet Excited State Manifold of Benzophenone by First-Principles Simulations and Ultrafast Spectroscopy. J. Chem. Theory Comput. 2018, 14, 2570–2585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Close, D.M.; Crespo-Hernández, C.E.; Gorb, L.; Leszczynski, J. Ionization Energy Thresholds of Microhydrated Adenine and Its Tautomers. J. Phys. Chem. A 2008, 112, 12702–12706. [Google Scholar] [CrossRef]
- Slavíček, P.; Winter, B.; Faubel, M.; Bradforth, S.E.; Jungwirth, P. Ionization Energies of Aqueous Nucleic Acids: Photoelectron Spectroscopy of Pyrimidine Nucleosides and ab Initio Calculations. J. Am. Chem. Soc. 2009, 131, 6460–6467. [Google Scholar] [CrossRef]
- Pluhařová, E.; Jungwirth, P.; Bradforth, S.E.; Slavíček, P. Ionization of Purine Tautomers in Nucleobases, Nucleosides, and Nucleotides: From the Gas Phase to the Aqueous Environment. J. Phys. Chem. B 2011, 115, 1294–1305. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Proton-Coupled Electron Transfer in DNA on Formation of Radiation-Produced Ion Radicals. Chem. Rev. 2010, 110, 7002–7023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altavilla, S.F.; Segarra-Martí, J.; Nenov, A.; Conti, I.; Rivalta, I.; Garavelli, M. Deciphering the photochemical mechanisms describing the UV-induced processes occurring in solvated guanine monophosphate. Front. Chem. 2015, 3, 29. [Google Scholar] [CrossRef] [Green Version]
- Weingart, O.; Nenov, A.; Altoè, P.; Rivalta, I.; Segarra-Martí, J.; Dokukina, I.; Garavelli, M. COBRAMM 2.0—A software interface for tailoring molecular electronic structure calculations and running nanoscale (QM/MM) simulations. J. Mol. Model. 2018, 24, 271. [Google Scholar] [CrossRef] [Green Version]
- Tomaník, L.; Muchová, E.; Slavíček, P. Solvation energies of ions with ensemble cluster-continuum approach. Phys. Chem. Chem. Phys. 2020, 22, 22357–22368. [Google Scholar] [CrossRef]
- Zhao, H.Y.; Lau, K.C.; Garcia, G.A.; Nahon, L.; Carniato, S.; Poisson, L.; Schwell, M.; Al-Mogren, M.M.; Hochlaf, M. Unveiling the complex vibronic structure of the canonical adenine cation. Phys. Chem. Chem. Phys. 2018, 20, 20756–20765. [Google Scholar] [CrossRef]
- Martinez-Fernandez, L.; Gavvala, K.; Sharma, R.; Didier, P.; Richert, L.; Segarra Martì, J.; Mori, M.; Mely, Y.; Improta, R. Excited-State Dynamics of Thienoguanosine, an Isomorphic Highly Fluorescent Analogue of Guanosine. Chem. Eur. J. 2019, 25, 7375–7386. [Google Scholar] [CrossRef]
- Serrano-Andrés, L.; Merchán, M.; Borin, A.C. Adenine and 2-aminopurine: Paradigms of modern theoretical photochemistry. Proc. Natl. Acad. Sci. USA 2006, 103, 8691–8696. [Google Scholar] [CrossRef] [Green Version]
- Barbatti, M. Photorelaxation Induced by Water–Chromophore Electron Transfer. J. Am. Chem. Soc. 2014, 136, 10246–10249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Serrano-Andrés, L.; Merchán, M.; Borin, A.C. A Three-State Model for the Photophysics of Guanine. J. Am. Chem. Soc. 2008, 130, 2473–2484. [Google Scholar] [CrossRef]
- Cohen, B.; Hare, P.M.; Kohler, B. Ultrafast Excited-State Dynamics of Adenine and Monomethylated Adenines in Solution: Implications for the Nonradiative Decay Mechanism. J. Am. Chem. Soc. 2003, 125, 13594–13601. [Google Scholar] [CrossRef] [PubMed]
- Barbatti, M.; Aquino, A.J.A.; Szymczak, J.J.; Nachtigallová, D.; Hobza, P.; Lischka, H. Relaxation mechanisms of UV-photoexcited DNA and RNA nucleobases. Proc. Natl. Acad. Sci. USA 2010, 107, 21453–21458. [Google Scholar] [CrossRef] [Green Version]
- Yarkony, D.R. Nonadiabatic Quantum Chemistry—Past, Present, and Future. Chem. Rev. 2012, 112, 481–498. [Google Scholar] [CrossRef] [PubMed]
- Domcke, W.; Yarkony, D.R. Role of Conical Intersections in Molecular Spectroscopy and Photoinduced Chemical Dynamics. Annu. Rev. Phys. Chem. 2012, 63, 325–352. [Google Scholar] [CrossRef]
- Blancafort, L. Photochemistry and Photophysics at Extended Seams of Conical Intersection. ChemPhysChem 2014, 15, 3166–3181. [Google Scholar] [CrossRef] [Green Version]
- Pepino, A.J.; Segarra-Martí, J.; Nenov, A.; Improta, R.; Garavelli, M. Resolving Ultrafast Photoinduced Deactivations in Water-Solvated Pyrimidine Nucleosides. J. Phys. Chem. Lett. 2017, 8, 1777–1783. [Google Scholar] [CrossRef]
- Pepino, A.J.; Segarra-Martí, J.; Nenov, A.; Rivalta, I.; Improta, R.; Garavelli, M. UV-induced long-lived decays in solvated pyrimidine nucleosides resolved at the MS-CASPT2/MM level. Phys. Chem. Chem. Phys. 2018, 20, 6877–6890. [Google Scholar] [CrossRef]
- Schuurman, M.S.; Stolow, A. Dynamics at Conical Intersections. Annu. Rev. Phys. Chem. 2018, 69, 427–450. [Google Scholar] [CrossRef]
- Schalk, O.; Boguslavskiy, A.E.; Stolow, A. Substituent Effects on Dynamics at Conical Intersections: Cyclopentadienes. J. Phys. Chem. A 2010, 114, 4058–4064. [Google Scholar] [CrossRef] [Green Version]
- Fdez. Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Fdez. Galván, I.; et al. Modern quantum chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef] [PubMed]
- Olsen, J. The CASSCF method: A perspective and commentary. Int. J. Quantum Chem. 2011, 111, 3267–3272. [Google Scholar] [CrossRef]
- Robb, M.A. Theoretical Chemistry for Electronic Excited States; Theoretical and Computational Chemistry Series; The Royal Society of Chemistry: London, UK, 2018; pp. P001–P225. [Google Scholar] [CrossRef] [Green Version]
- Widmark, P.O.; Malmqvist, P.Å.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. I. First row atoms. Theor. Chim. Acta 1990, 77, 291. [Google Scholar] [CrossRef]
- Widmark, P.O.; Persson, B.J.; Roos, B.O. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. II. Second row atoms. Theor. Chim. Acta 1991, 79, 419. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.A.; Roos, B.O.; Sadlej, A.J.; Wolinski, K. Second-order perturbation theory with a CASSCF reference function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.Å.; Roos, B.O. Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
- Finley, J.; Malmqvist, P.Å.; Roos, B.O.; Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Granovsky, A.A. Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory. J. Chem. Phys. 2011, 134, 214113. [Google Scholar] [CrossRef]
- Forsberg, N.; Malmqvist, P.Å. Multiconfiguration perturbation theory with imaginary level shift. Chem. Phys. Lett. 1997, 274, 196–204. [Google Scholar] [CrossRef]
- Ghigo, G.; Roos, B.O.; Malmqvist, P.Å. A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2). Chem. Phys. Lett. 2004, 396, 142–149. [Google Scholar] [CrossRef]
- Shiozaki, T. BAGEL: Brilliantly Advanced General Electronic-structure Library. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1331. [Google Scholar] [CrossRef] [Green Version]
- Park, J.W.; Al-Saadon, R.; MacLeod, M.K.; Shiozaki, T.; Vlaisavljevich, B. Multireference Electron Correlation Methods: Journeys along Potential Energy Surfaces. Chem. Rev. 2020, 120, 5909. [Google Scholar] [CrossRef]
- Bearpark, M.J.; Robb, M.A.; Schlegel, H.B. A direct method for the location of the lowest energy point on a potential surface crossing. Chem. Phys. Lett. 1994, 223, 269–274. [Google Scholar] [CrossRef]
- Shiozaki, T.; Gyorffy, W.; Celani, P.; Werner, H.J. Communication: Extended multi-state complete active space second-order perturbation theory: Energy and nuclear gradients. J. Chem. Phys. 2011, 135, 081106. [Google Scholar] [CrossRef]
- MacLeod, M.K.; Shiozaki, T. Communication: Automatic code generation enables nuclear gradient computations for fully internally contracted multireference theory. J. Chem. Phys. 2015, 142, 051103. [Google Scholar] [CrossRef] [Green Version]
- Vlaisavljevich, B.; Shiozaki, T. Nuclear Energy Gradients for Internally Contracted Complete Active Space Second-Order Perturbation Theory: Multistate Extensions. J. Chem. Theory Comput. 2016, 12, 3781–3787. [Google Scholar] [CrossRef] [Green Version]
- Park, J.W.; Shiozaki, T. Analytical Derivative Coupling for Multistate CASPT2 Theory. J. Chem. Theory Comput. 2017, 13, 2561–2570. [Google Scholar] [CrossRef] [Green Version]
- Schaftenaar, G.; Noordik, J. Molden: A pre- and post-processing program for molecular and electronic structures*. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]

| Intersection Type [48] | |||||||
|---|---|---|---|---|---|---|---|
| 7H-adenine | |||||||
| 0.060 | 0.784 | 1.486 | 0.005 | 1.237 | 1.171 | Sloped, single-path | |
| 0.129 | 0.904 | 1.374 | 3.693 | 1.069 | 1.092 | Sloped, single-path | |
| 0.054 | 0.594 | 0.459 | 1.712 | 0.132 | 0.657 | Peaked, bifurcating | |
| 7H-guanine | |||||||
| 0.059 | 0.866 | 5.780 | 0.018 | 17.899 | 2.754 | Sloped, single-path | |
| 0.056 | 0.572 | 3.906 | 0.020 | 9.709 | 2.646 | Sloped, single-path | |
| 0.063 | 0.934 | 0.239 | 0.297 | 0.029 | 0.319 | Peaked, bifurcating |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Segarra-Martí, J.; Nouri, S.M.; Bearpark, M.J. Modelling Photoionisations in Tautomeric DNA Nucleobase Derivatives 7H-Adenine and 7H-Guanine: Ultrafast Decay and Photostability. Photochem 2021, 1, 287-301. https://doi.org/10.3390/photochem1020018
Segarra-Martí J, Nouri SM, Bearpark MJ. Modelling Photoionisations in Tautomeric DNA Nucleobase Derivatives 7H-Adenine and 7H-Guanine: Ultrafast Decay and Photostability. Photochem. 2021; 1(2):287-301. https://doi.org/10.3390/photochem1020018
Chicago/Turabian StyleSegarra-Martí, Javier, Sara M. Nouri, and Michael J. Bearpark. 2021. "Modelling Photoionisations in Tautomeric DNA Nucleobase Derivatives 7H-Adenine and 7H-Guanine: Ultrafast Decay and Photostability" Photochem 1, no. 2: 287-301. https://doi.org/10.3390/photochem1020018
APA StyleSegarra-Martí, J., Nouri, S. M., & Bearpark, M. J. (2021). Modelling Photoionisations in Tautomeric DNA Nucleobase Derivatives 7H-Adenine and 7H-Guanine: Ultrafast Decay and Photostability. Photochem, 1(2), 287-301. https://doi.org/10.3390/photochem1020018






