Correction: Ocádiz Flores et al. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133
Text Correction
Error in Tables
Error in Figures
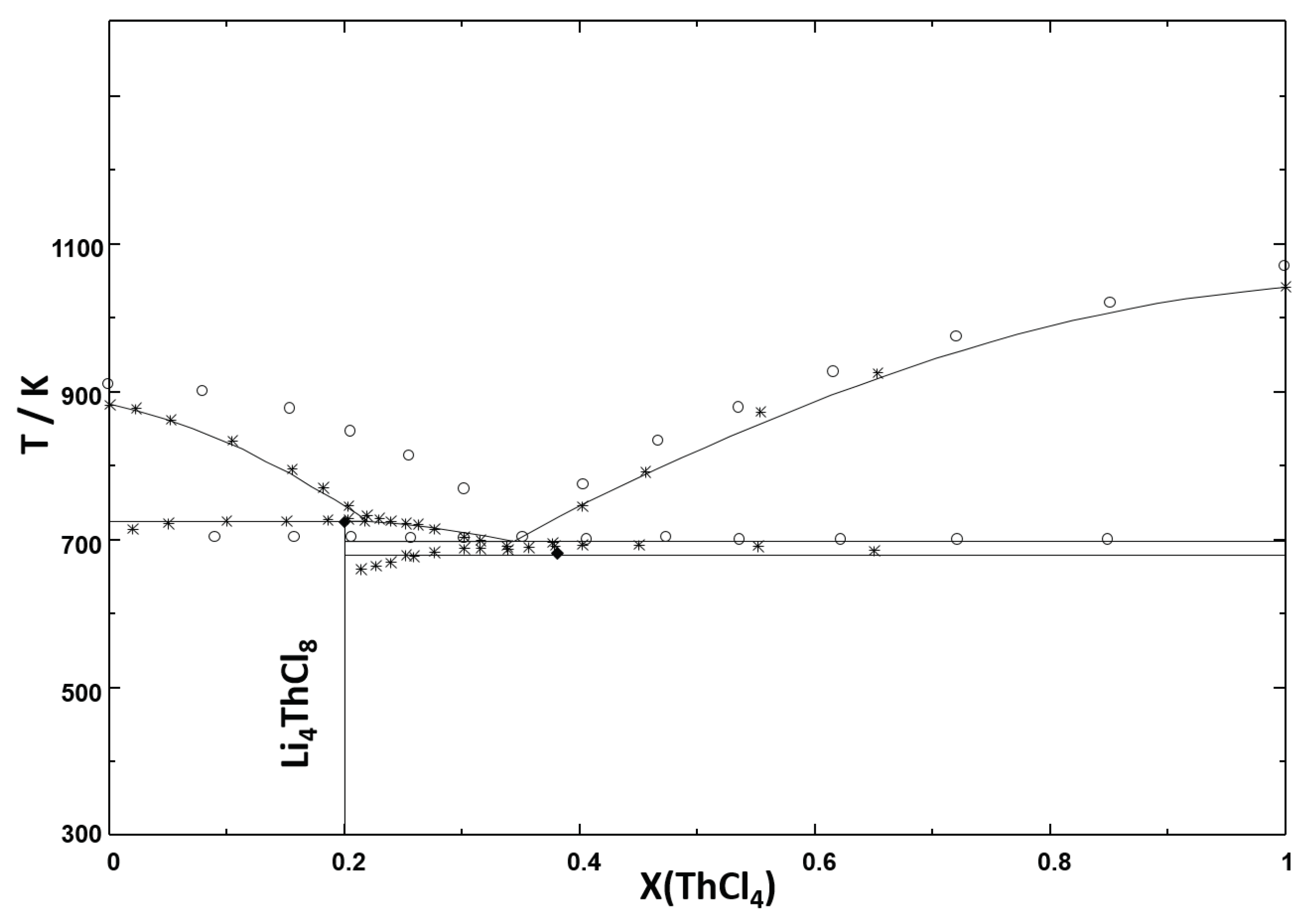
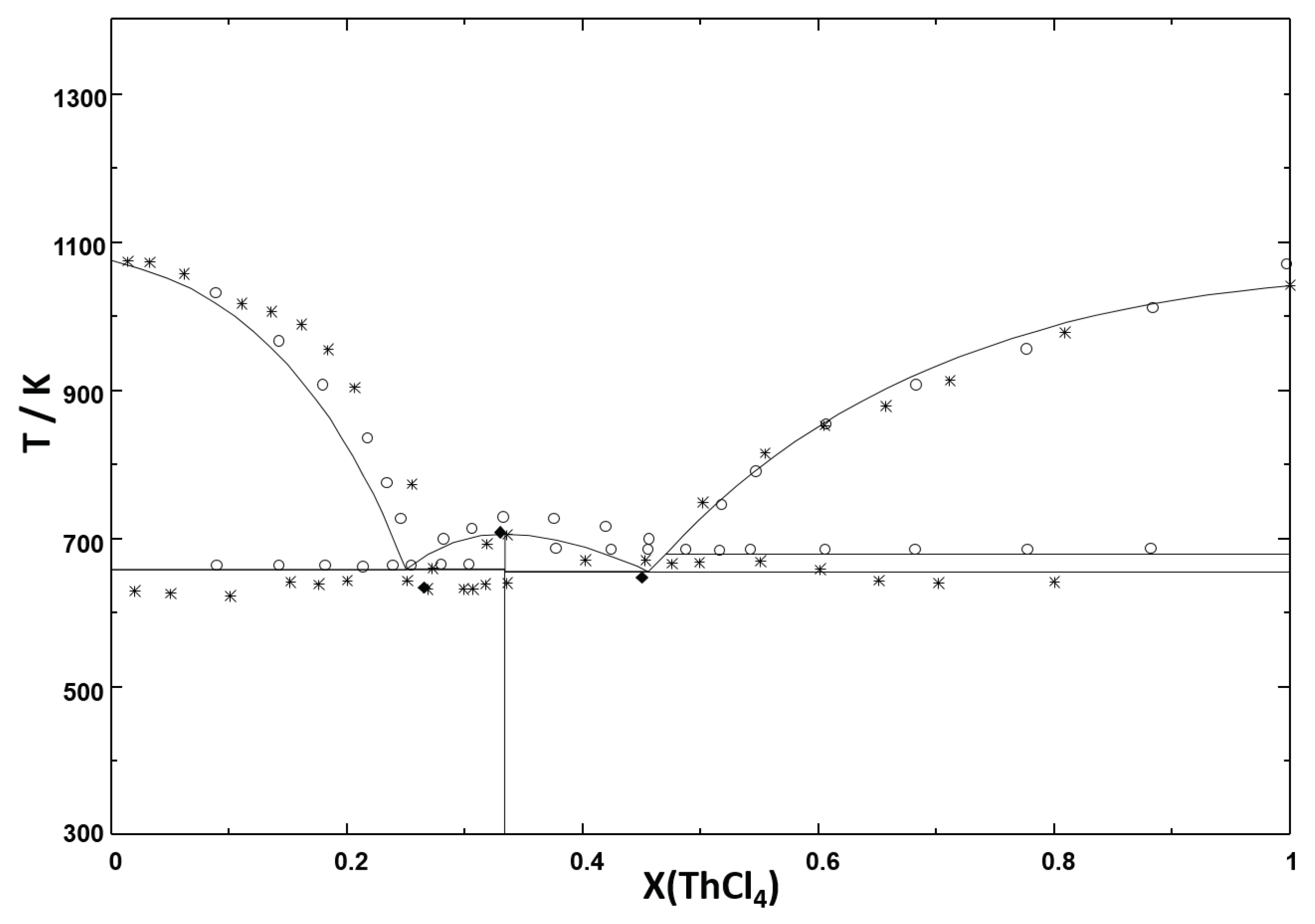
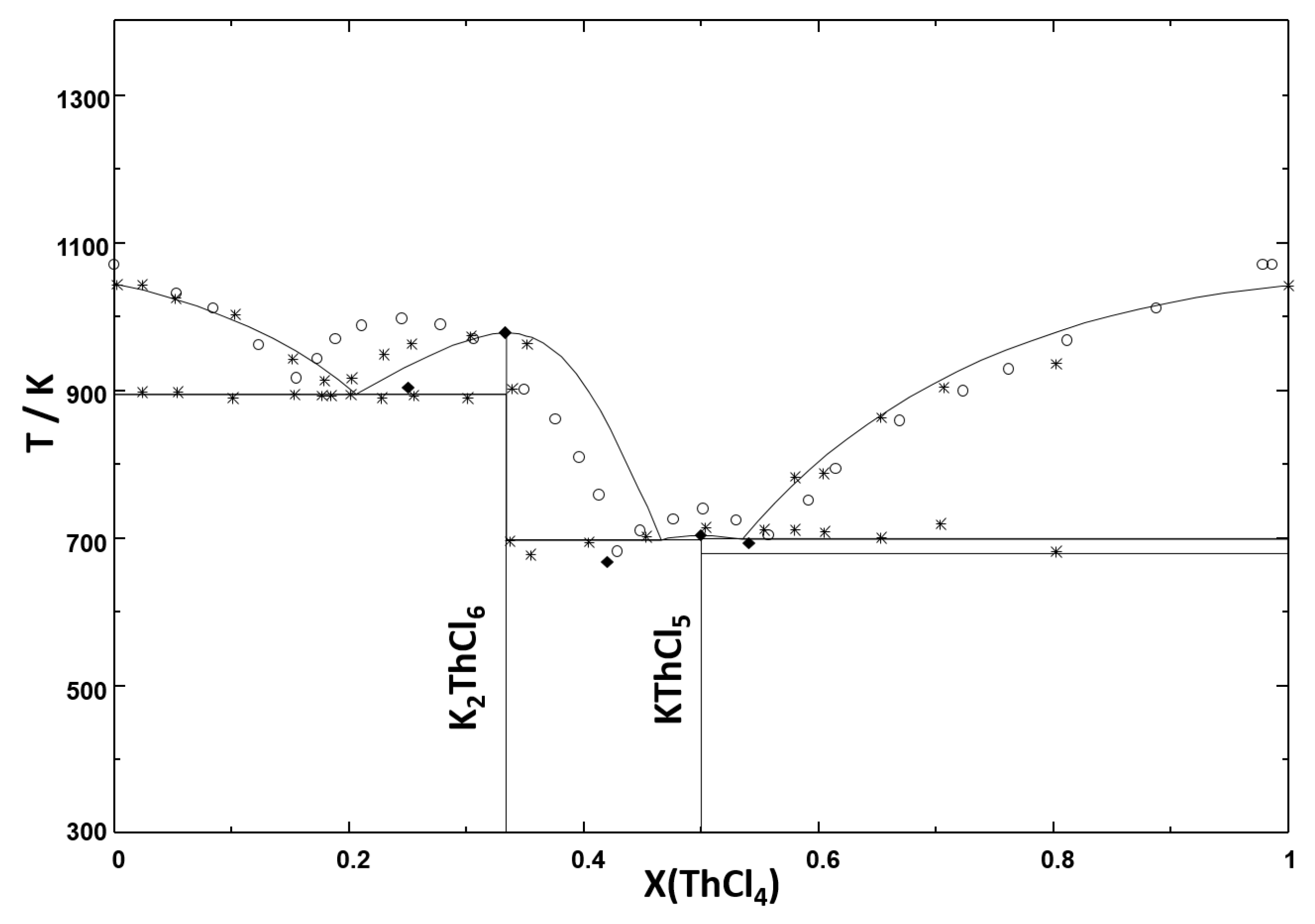
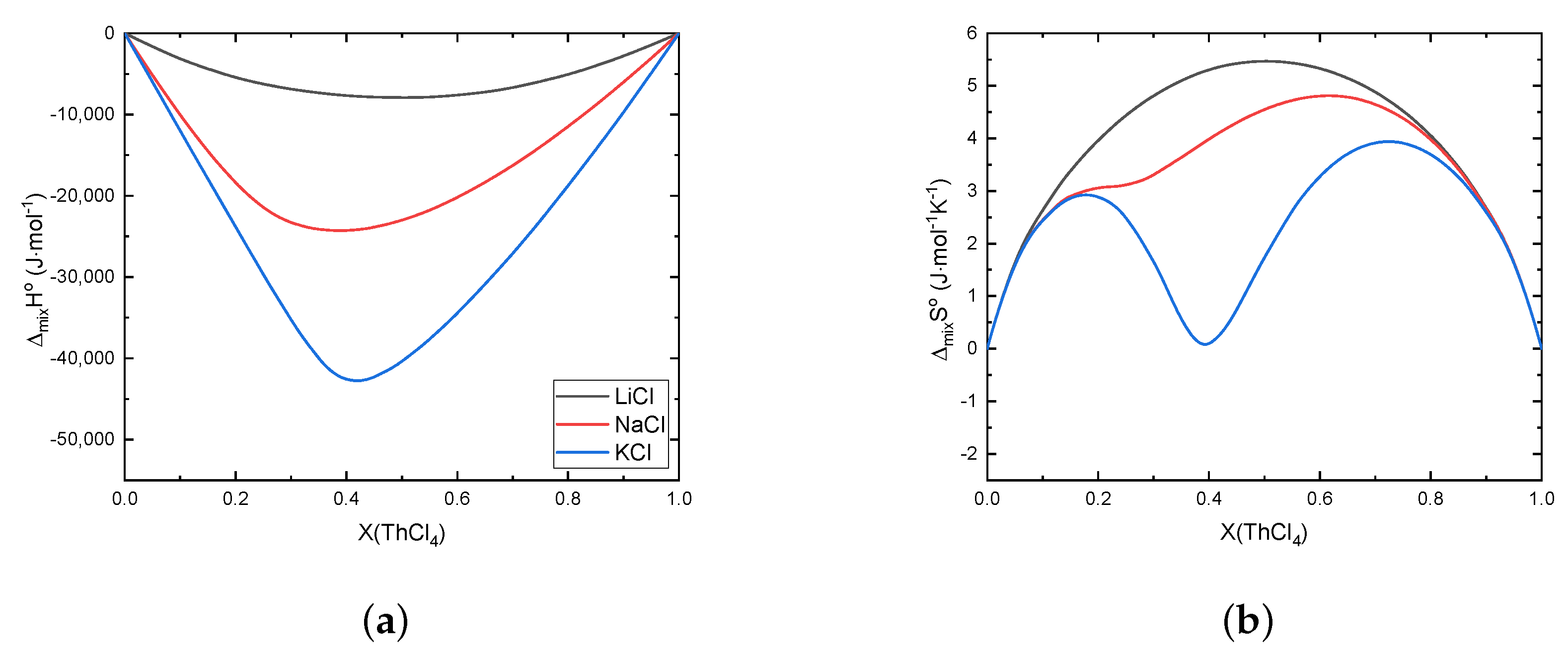
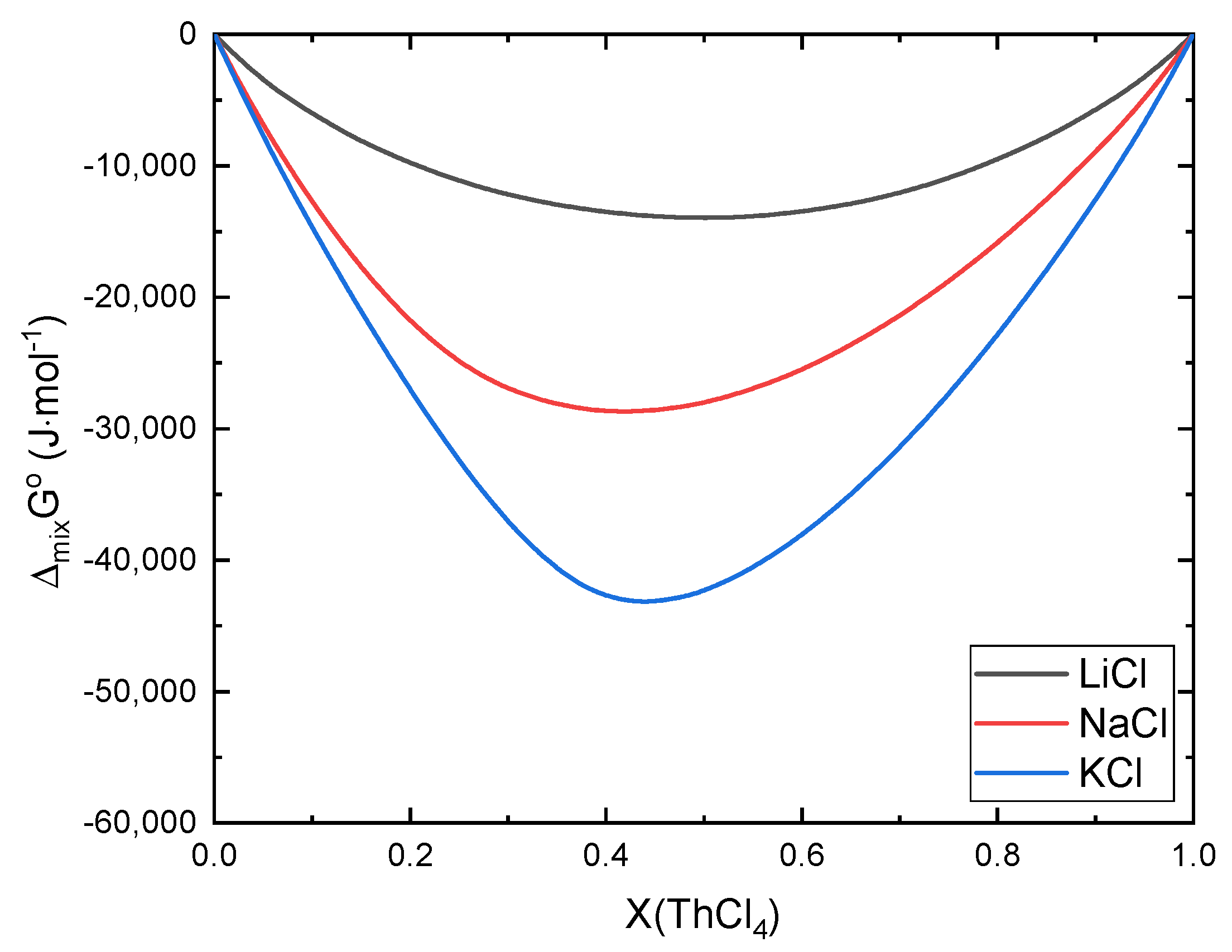
Reference
- Ocádiz Flores, J.A.; Rooijakkers, B.A.S.; Konings, R.J.M.; Smith, A.L. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133. [Google Scholar] [CrossRef]
| Compound | H(298 K)/ (kJ·mol) | S(298 K)/ (J·Kmol) | C(T/K)/(J·Kmol) = a + b·T + c·T + d·T | Range | Reference | |||
|---|---|---|---|---|---|---|---|---|
| a | b | c | d | |||||
| LiCl(cr) | −408.266 | 59.3 | 44.70478 | 0.01792765 | 1.863482 × 10 | −194,457.7 | 298–883 | [27] |
| 73.30619 | −0.009430108 | 33,070.5 | 883–2000 | [27] | ||||
| LiCl(l) | −388.4342 | 81.76 | 44.70478 | 0.01792765 | 1.863482 × 10 | −194,457.7 | 298–883 | [27] |
| 73.30619 | −0.009430108 | 33,070.5 | 883–2000 | [27] | ||||
| NaCl(cr) | −411.260 | 72.15 | 47.72158 | 0.0057 | 1.21466 × 10 | −882.996 | 298–1074 | [28] |
| NaCl(l) | −390.853 | 83.302 | 68.0 | 298–2500 | [28,29] | |||
| KCl(cr) | −436.6841 | 82.555 | 50.47661 | 0.005924377 | 7.496682 × 10 | −144,173.9 | 298–700 | [27] |
| 143.5698 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 700–1044 | [27] | |||
| 73.59656 | −8,217,836 | 1044–2000 | [27] | |||||
| KCl(l) | −410.4002 | 107.7311 | 50.47661 | 0.005924377 | 7.496682 × 10 | −144,173.9 | 298–700 | [27] |
| 143.5698 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 700–1044 | [27] | |||
| 73.59656 | 1044–2000 | [27] | ||||||
| -ThCl(cr) | −1191.3012 | 176.135 | 120.293 | 0.0232672 | −615,050 | 298–1042 | this work, [35] | |
| -ThCl(cr) | −1186.300 | 183.499 | 120.293 | 0.0232672 | −615,050 | 298–1042 | [5,34] | |
| ThCl(l) | −1149.740 | 197.626 | 167.4 | 298–1500 | [5,34] | |||
| LiThCl(cr) | −2834.966 | 413.34 | 299.11212 | 0.0949778 | 7.453928 × 10 | −1,392,880.8 | 298–883 | this work |
| 413.51776 | −0.014453232 | −482,768 | 883–1042 | |||||
| 437.1957 | −0.037720432 | 132,282 | 1042–2000 | |||||
| NaThCl(cr) | −2051.540 | 328.0 | 215.73616 | 0.0346672 | 2.42932 × 10 | −616,815.992 | 298–1042 | this work |
| 239.41 | 0.0114 | 2.42932 × 10 | −1765.992 | 1042–1074 | ||||
| KThCl(cr) | −1685.000 | 258.69 | 170.76961 | 0.029191577 | 7.496682 × 10 | −759,223.9 | 298–700 | this work |
| 263.8628 | −0.1447727 | 9.965702 × 10 | −8,832,886 | 700–1042 | ||||
| 287.5408 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 1042–1044 | ||||
| 217.568 | 1044–2000 | |||||||
| KThCl(cr) | −2139.850 | 380.5 | 221.24622 | 0.035115954 | 1.4993364 × 10 | −903,397.8 | 298–700 | this work |
| 407.4326 | −0.3128126 | 1.9931404 × 10 | −17,050,722 | 700–1042 | ||||
| 431.1106 | −0.3360798 | 1.9931404 × 10 | −16,435,672 | 1042–1044 | ||||
| 291.16408 | 1042–2000 | |||||||
| System | Equilibrium | Invariant Reaction | This Study (calc.) | Tanii et al. [21] | Vokhmyakov et al. [20] | Oyamada [19] | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| X(ThCl) | T / K | X(ThCl) | T / K | X(ThCl) | T / K | X(ThCl) | T / K | |||
| LiCl-ThCl | Congruent Melting | LiCl = L | 1 | 883 | 1 | 881 | 1 | 910 | ||
| Peritectic | LiThCl = LiCl + L | 0.2 | 723 | 0.2 | 725 | 0.2 | 723 | - | - | |
| Eutectic | LiThCl + -ThCl = L | 0.343 | 695 | - | 690 | 0.38 | 681 | 0.35 | 703 | |
| - transition | -ThCl = -ThCl | 1 | 679 | |||||||
| Congruent Melting | -ThCl = L | 1 | 1042 | 1 | 1041 | 1 | 1070 | |||
| NaCl-ThCl | Congruent melting | NaCl = L | 0 | 1074 | 0 | 1074 | 0 | 1097 | ||
| Eutectic | NaCl + NaThCl = L | 0.251 | 657 | - | 639 | 0.255 | 633 | 0.26 | 667 | |
| Congruent Melting | NaThCl = L | 1/3 | 703 | 1/3 | 708 | 1/3 | 708 | 1/3 | 729 | |
| Eutectic | NaThCl + -ThCl = L | 0.457 | 654 | - | 637 | 0.45 | 648 | 0.49 | 686 | |
| KCl-ThCl | Congruent melting | KCl = L | 0 | 1044 | 0 | 1043 | 0 | 1070 | ||
| Eutectic | KCl + KThCl = L | 0.206 | 894 | - | 895 | 0.25 | 903 | 0.15 | 917 | |
| Congruent melting | KThCl = L | 1/3 | 977 | 1/3 | 988 | 1/3 | 978 | 0.25 | 997 | |
| Eutectic | KThCl + KThCl = L | 0.467 | 697 | - | 705 | 0.42 | 668 | 0.43 | 681 | |
| Congruent melting | KThCl = L | 0.5 | 702 | 0.5 | 703 | 0.5 | 741 | |||
| Eutectic | KThCl + -ThCl = L | 0.536 | 699 | 0.54 | 693 | 0.56 | 706 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocádiz Flores, J.A.; Rooijakkers, B.A.S.; Konings, R.J.M.; Smith, A.L. Correction: Ocádiz Flores et al. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133. Thermo 2022, 2, 394-400. https://doi.org/10.3390/thermo2040027
Ocádiz Flores JA, Rooijakkers BAS, Konings RJM, Smith AL. Correction: Ocádiz Flores et al. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133. Thermo. 2022; 2(4):394-400. https://doi.org/10.3390/thermo2040027
Chicago/Turabian StyleOcádiz Flores, Jaén A., Bas A. S. Rooijakkers, Rudy J. M. Konings, and Anna Louise Smith. 2022. "Correction: Ocádiz Flores et al. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133" Thermo 2, no. 4: 394-400. https://doi.org/10.3390/thermo2040027
APA StyleOcádiz Flores, J. A., Rooijakkers, B. A. S., Konings, R. J. M., & Smith, A. L. (2022). Correction: Ocádiz Flores et al. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122–133. Thermo, 2(4), 394-400. https://doi.org/10.3390/thermo2040027





