Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems
Abstract
1. Introduction
2. Thermodynamic Modelling
2.1. Pure Compounds
2.2. Liquid Solution
3. Results and Discussion
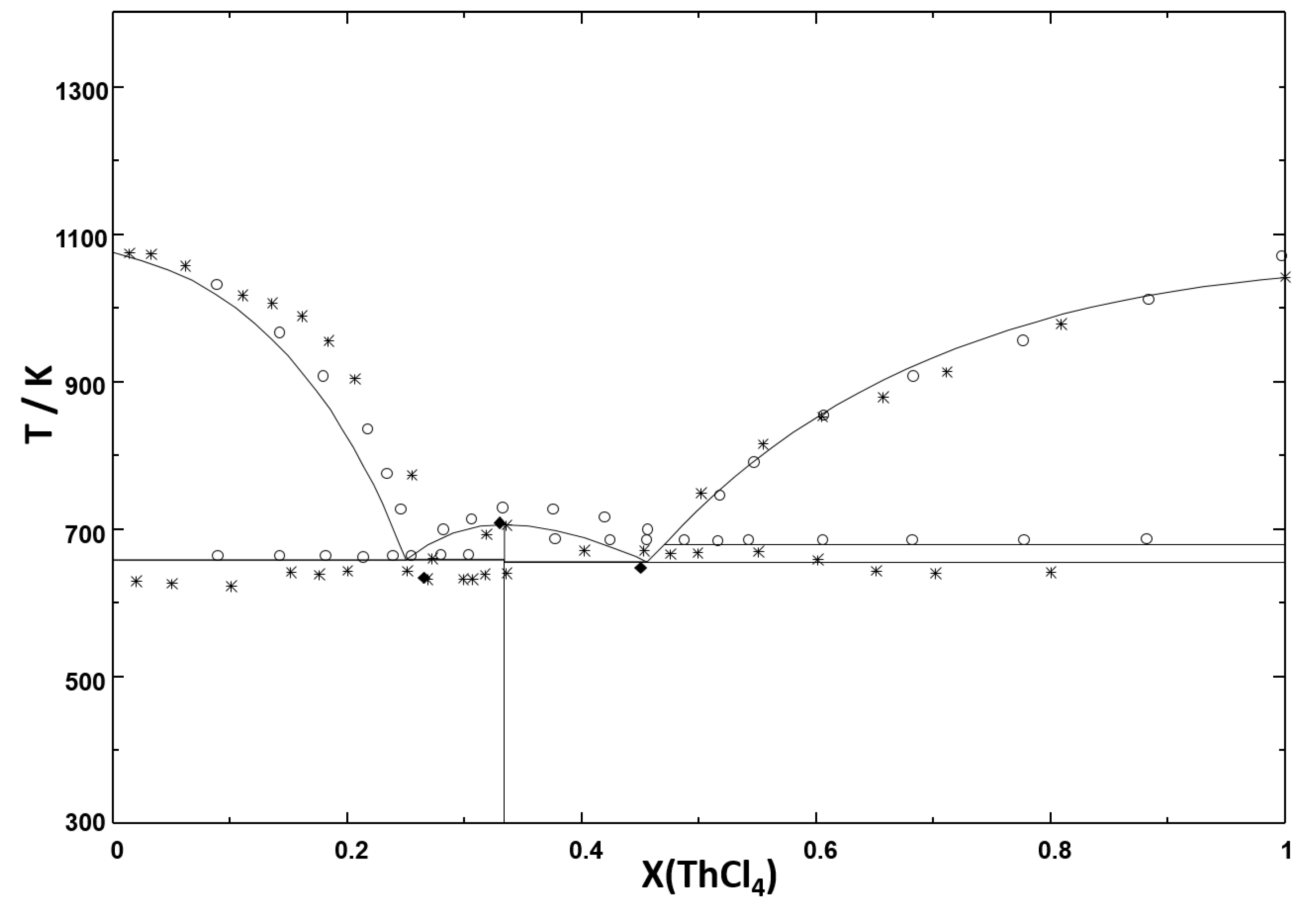
3.1. Phase Diagrams
3.2. Enthalpy of Mixing
4. Conclusions
- Isolate the intermediate phases LiThCl, NaThCl, and KThCl and elucidate their crystal structures;
- Derive their standard enthalpies of formation and standard entropies;
- Obtain novel phase equilibrium data with calorimetry, particularly for the KCl-ThCl system;
- Measure enthalpies of mixing for the liquid solutions.
Author Contributions
Funding
Conflicts of Interest
References
- Martin, R. Superfuel: Thorium, the Green Energy Source for the Future; St. Martin’s Press: New York, NY, USA, 2012. [Google Scholar]
- Haas, D.; Hugon, M.; Verwerft, M. Overview of European Experience with Thorium Fuels. In Nuclear Back-End and Transmutation Technology for Waste Disposal; Springer: Tokyo, Japan, 2015; p. 197. [Google Scholar]
- Beaver, W.; Wikle, K. Powder Metallurgy of Thorium. In Proceedings of the Powder Metallurgy in Nuclear Engineering: The Conference on Powder Metallury in Atomic Energy, Philadelphia, PA, USA, 1 January 1958; p. 82. [Google Scholar]
- Hombourger, B. Thermochemical Investigation of Molten Fluoride Salts for Generation IV Nuclear Applications—An Equilibrium Exercise. Ph.D. Thesis, Swiss Federal Institute of Technology Lausanne (EPFL), Lausanne, Switzerland, 2018. [Google Scholar]
- Rand, M.; Fuger, J.; Grenthe, I.; Neck, V.; Rai, D. Chemical Thermodynamics of Thorium; OECD Nuclear Energy Agency: Paris, France, 2008. [Google Scholar]
- Mooney, R. The crystal structure of ThCl4 and UCl4. Acta Crystallogr. 1949, 2, 189–191. [Google Scholar] [CrossRef]
- Elson, R.; Fried, S.; Sellers, P.; Zachariasen, W. The tetravalent and pentavalent states of Protactinium. J. Am. Chem. Soc. 1950, 72, 5791. [Google Scholar] [CrossRef]
- Sellers, P.; Fried, S.; Elson, R.; Zachariasen, W. The Preparation of Some Protactinium Compounds and the Metal1. J. Am. Chem. Soc. 1954, 76, 5935–5938. [Google Scholar] [CrossRef]
- Mucker, K.; Smith, G.; Johnson, Q.; Elson, R. Refinement of the crystal structure of ThCl4. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1969, 25, 2362–2365. [Google Scholar] [CrossRef]
- Brown, D.; Hall, T.; Moseley, P. Structural parameters and unit cell dimensions for the tetragonal actinide tetrachlorides (Th, Pa, U, and Np) and tetrabromides (Th and Pa). J. Chem. Soc. Dalton Trans. 1973, 6, 686–691. [Google Scholar] [CrossRef]
- Schleid, T.; Meyer, G.; Morss, L. Facile synthesis of UCl4 and ThCl4, metallothermic reductions of UCl4 with alkali metals and crystal structure refinements of UCl3, UCl4 and Cs2UCl6. J. Less Common Met. 1987, 132, 69–77. [Google Scholar] [CrossRef]
- Mason, J.; Jha, M.; Chiotti, P. Crystal structures of ThCl4 polymorphs. J. Less Common Met. 1974, 34, 143–151. [Google Scholar] [CrossRef]
- Eyring, L.; Westrum, E.F., Jr. The Heat of Formation of Thorium Tetrachloride. J. Am. Chem. Soc. 1950, 72, 5555–5556. [Google Scholar] [CrossRef]
- Fuger, J.; Brown, D. Thermodynamics of the actinide elements. Part IV. Heats and free energies of formation of the tetrachlorides, tetrabromides, and tetraiodides of thorium, uranium, and neptunium. J. Chem. Soc. Dalton Trans. 1973, 4, 428–434. [Google Scholar] [CrossRef]
- Smith, B.; Thakur, L.; Wassef, M. Thermochemical Studies of Thorium (IV) and Uranium (IV) Chlorides; Technical Report; London University: London, UK, 1969. [Google Scholar]
- Konings, R. The heat capacity and entropy of actinide (IV) compounds. J. Chem. Thermodyn. 2004, 36, 121–126. [Google Scholar] [CrossRef]
- Atomic Energy Review, Special Issue No. 5 Thorium: Physic-Chemical Properties of Its Compounds and Alloys; Atomic Energy Review, Special Issue; International Atomic Energy Agency: Vienna, Austria, 1975.
- Hubert, S.; Delamoye, P.; Lefrant, S.; Lepostollec, M.; Hussonnois, M. Observation of a phase transition in ThBr4 and ThCl4 single crystals by far-infrared and Raman spectroscopy study. J. Solid State Chem. 1981, 36, 36–44. [Google Scholar] [CrossRef]
- Oyamada, R. Phase Diagrams of ThCl4 Systems Containing NaCl, KCl and LiCl and the Limitation of the Congruently Melting Compounds Formation. Denki Kagaku Oyobi Kogyo Butsuri Kagaku 1971, 39, 2–5. [Google Scholar] [CrossRef][Green Version]
- Vokhmyakov, A.; Desyatnik, V.; Kurbatov, N. Interaction of thorium tetrachloride with chlorides of the alkali metals. Sov. At. Energy Engl. Transl. 1973, 35, 1122–1123. [Google Scholar] [CrossRef]
- Tanii, S. Phase Diagrams of the systems Thorium Chloride-Alkali Chlorides and Thorium Chloride-Alkali Chlorides. Denki Kagaku Oyobi Kogyo Butsuri Kagaku 1964, 32, 167–170. [Google Scholar]
- Edelstein, N.; Katz, J.; Fuger, J.; Morss, L. The Chemistry of the Actinide and Transactinide Elements; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Vdovenko, V.; Gershanovich, A.; Suglobova, I. Thermal and X-ray diffraction studies of thorium chloride-lithium chloride and thorium chloride-sodium chloride binary systems. Radiokhimiya 1974, 166, 886–889. [Google Scholar]
- Gershanovich, A.; Suglobova, I. Thermographic and X-ray diffraction studies of binary systems formed by thorium tetrachloride with potassium, rubidium, and cesium chlorides. Radiokhimiya 1980, 22, 265–270. [Google Scholar]
- Bale, C.W.; Chartrand, P.; Degterov, S.; Eriksson, G.; Hack, K.; Mahfoud, R.B.; Melançon, J.; Pelton, A.; Petersen, S. FactSage thermochemical software and databases. Calphad 2002, 26, 189–228. [Google Scholar] [CrossRef]
- Leitner, J.; Voňka, P.; Sedmidubský, D.; Svoboda, P. Application of Neumann–Kopp rule for the estimation of heat capacity of mixed oxides. Thermochim. Acta 2010, 497, 7–13. [Google Scholar] [CrossRef]
- SGPS-SGTE Pure Substances Database (v13.1); Accessed via FactSage (Version 7.2); Scientific Group Thermodata Europe: Saint-Martin-d’Hères, France, updated 2018.
- Glushko, V.; Gurvich, L.V.; Weitz, V.; Medvedev, V.; Hachkuruzov, G.; Jungmann, V.; Bergman, G.; Baibuz, V.; Yorish, V. The IVTAN Data Bank on the Thermodynamic Properties of Individual Substances; Chemical Thermodynamics of Thorium; Nauka Publishing House: Moscow, Russia, 1978. [Google Scholar]
- van Oudenaren, G.; Ocádiz-Flores, J. Coupled structural modelling of the molten salt system NaCl-UCl3. J. Mol. Liq. 2021, Submitted. [Google Scholar]
- Plato, W. Erstarrungserscheinungen an anorganischen Salzen und Salzgemischen. I. Z. Für Phys. Chem. 1906, 55, 721–737. [Google Scholar] [CrossRef]
- Pyashyenko, B. Unknown. Metallurgiya 1935, 10, 85. [Google Scholar]
- Murgulescu, I. Heat Capacities in Molten Alkaline Halides. Rev. Roum. Chim. 1977, 22, 683–689. [Google Scholar]
- Dawson, R.; Brackett, E.; Brackett, T. A high temperature calorimeter; the enthalpies of α-aluminum oxide and sodium chloride. J. Phys. Chem. 1963, 67, 1669–1671. [Google Scholar] [CrossRef]
- Capelli, E.; Konings, R. Halides of the Actinides and Fission Products Relevant for Molten Salt Reactors. In Comprehensive Nuclear Materials; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Chiotti, P.; Gartner, G.; Stevens, E.; Saito, Y. Heats of Fusion and Transformation for Some Metals and Compounds. J. Chem. Eng. Data 1966, 11, 571–574. [Google Scholar] [CrossRef]
- Pelton, A.D.; Degterov, S.A.; Eriksson, G.; Robelin, C.; Dessureault, Y. The modified quasichemical model I—Binary solutions. Metall. Mater. Trans. B 2000, 31, 651–659. [Google Scholar] [CrossRef]
- Beneš, O. Thermodynamics of Molten Salts for Nuclear Applications. Ph.D. Thesis, Institute of Chemical Technology, Prague, Czech Republic, 2008. [Google Scholar]
- Capelli, E. Thermodynamic Characterization of Salt Components for Molten Salt Reactor Fuel. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Ard, J.; Johnson, K.; Christian, M.; Yingling, J.; Besmann, T.M.; Mcmurray, J.W.; Peng, J. FY20 Status Report on the Molten Salt Thermodynamic Database (MSTDB) Development; Technical Report; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2020. [Google Scholar]
- Smith, A.; Capelli, E.; Konings, R.; Gheribi, A. A new approach for coupled modelling of the structural and thermo-physical properties of molten salts. Case of a polymeric liquid LiF-BeF2. J. Mol. Liq. 2020, 299, 112165. [Google Scholar] [CrossRef]
- Robelin, C.; Chartrand, P. Thermodynamic evaluation and optimization of the (NaF+AlF3+CaF2+BeF2+Al2O3+BeO) system. J. Chem. Thermodyn. 2013, 57, 387–403. [Google Scholar] [CrossRef]
- Thoma, R. Phase Diagrams of Nuclear Reactor Materials; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 1959; Volume 2548. [Google Scholar]
- Bendall, P.; Fitch, A.; Fender, B. The structure of Na2UCl6 and Li2UCl6 from multiphase powder neutron profile refinement. J. Appl. Crystallogr. 1983, 16, 164–170. [Google Scholar] [CrossRef]
- Kraus, C. Phase Diagram of Some Complex Salts of Uranium with Halides of the Alkali and Alkaline Earth Metals; Technical Report; Naval Research Laboratory: Washington, DC, USA, 1943. [Google Scholar]
- Kuroda, T.; Suzuki, T. The Equilibrium State Diagrams of UCl4-NaCl, UCl4-KCl, UCl4-CaCl2 and UCl4-BaCl2 Systems. J. Electrochem. Soc. Jpn. 1958, 26, E140–E141. [Google Scholar] [CrossRef]
- Blander, M. Thermodynamic properties of molten salt solutions. In Molten Salt Chemistry; Springer Netherlands: Dordrecht, Netherlands, 1987; pp. 17–62. [Google Scholar]
- Liu, J.; Chen, X.; Lu, J.; Cui, H.; Li, J. Polarizable force field parameterization and theoretical simulations of ThCl4–LiCl molten salts. J. Comput. Chem. 2018, 39, 2432–2438. [Google Scholar] [CrossRef]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Danek, V. Physico-Chemical Analysis of Molten Electrolytes; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Papatheodorou, G.; Kleppa, O. Enthalpies of mixing of liquid nickel (II) chloride-alkali chloride mixtures at 810 C. J. Inorg. Nucl. Chem. 1970, 32, 889–900. [Google Scholar] [CrossRef]
- Papatheodorou, G.; Kleppa, O. Enthalpies of mixing in the liquid mixtures of the alkali chlorides with MnCl2, FeCl2 and CoCl2. J. Inorg. Nucl. Chem. 1971, 33, 1249–1278. [Google Scholar] [CrossRef]
- Kleppa, O.; Papatheodorou, G. Enthalpies of mixing of binary liquid mixtures of cadmium chloride with cesium and lithium chlorides. Inorg. Chem. 1971, 10, 872–873. [Google Scholar] [CrossRef]
- Gruen, D.; McBeth, R. Tetrahedral NiCl4− Ion in Crystals and in Fused Salts. Spectrophotometric Study of Chloro Complexes of Ni (II) in Fused Salts. J. Phys. Chem. 1959, 63, 393–398. [Google Scholar] [CrossRef]
- Smith, G.; Boston, C.; Brynestad, J. Electronic Spectra and Coordination Geometry in Molten Mixtures of CsCl and NiCl2 Containing up to 60 Mole% NiCl2. J. Chem. Phys. 1966, 45, 829–834. [Google Scholar] [CrossRef]
- Photiadis, G.; Papatheodorou, G. Co-ordination of thorium (IV) in molten alkali-metal chlorides and the structure of liquid and glassy thorium (IV) chloride. J. Chem. Soc. Dalton Trans. 1999, 20, 3541–3548. [Google Scholar] [CrossRef]
- Capelli, E.; Beneš, O.; Beilmann, M.; Konings, R.J.M. Thermodynamic investigation of the LiF–ThF4 system. J. Chem. Thermodyn. 2013, 58, 110–116. [Google Scholar] [CrossRef]
- Manzoor, A.; Pandey, S.; Chakraborty, D.; Phillpot, S.R.; Aidhy, D.S. Entropy contributions to phase stability in binary random solid solutions. NPJ Comput. Mater. 2018, 4, 1–10. [Google Scholar] [CrossRef]
- Forsberg, C.W. Reactors with molten salts: Options and missions. In Frederick Joliot & Otto Hahn Summer School on Nuclear Reactors, Physics and Fuels Systems; Cadarache: Saint-Paul-lez-Durance, France, 2004. [Google Scholar]
- Deubner, H.; Rudel, S.; Kraus, F. A simple access to pure thorium (IV) halides (ThCl4, ThBr4, and ThI4). Z. Anorg. Und Allg. Chem. 2017, 643, 2005–2010. [Google Scholar] [CrossRef]




| System | Compounds | References |
|---|---|---|
| LiCl-ThCl | LiThCl | [20,21,23] |
| none | [19] | |
| NaCl-ThCl | NaThCl | [19,20,21] |
| NaThCl | [23] | |
| KCl-ThCl | KThCl | [19,24] |
| KThCl | [21,24] | |
| KThCl | [19,24] |
| Compound | H(298 K)/ (kJ·mol) | S(298 K)/ (J·Kmol) | C(T/K)/(J·Kmol) = a + b·T + c·T + d·T | Range | Reference | |||
|---|---|---|---|---|---|---|---|---|
| a | b | c | d | |||||
| LiCl(cr) | −408.266 | 59.3 | 44.70478 | 0.01792765 | 1.863482 × 10 | −194,457.7 | 298–883 | [27] |
| 73.30619 | −0.009430108 | 33,070.5 | 883–2000 | [27] | ||||
| LiCl(l) | −388.4342 | 81.76 | 44.70478 | 0.01792765 | 1.863482 × 10 | −194,457.7 | 298–883 | [27] |
| 73.30619 | −0.009430108 | 33,070.5 | 883–2000 | [27] | ||||
| NaCl(cr) | −411.260 | 72.15 | 47.72158 | 0.0057 | 1.21466 × 10 | −882.996 | 298–1074 | [28] |
| NaCl(l) | −390.853 | 83.302 | 68.0 | 298–2500 | [28,29] | |||
| KCl(cr) | −436.6841 | 82.555 | 50.47661 | 0.005924377 | 7.496682 × 10 | −144,173.9 | 298–700 | [27] |
| 143.5698 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 700–1044 | [27] | |||
| 73.59656 | −8,217,836 | 1044–2000 | [27] | |||||
| KCl(l) | −410.4002 | 107.7311 | 50.47661 | 0.005924377 | 7.496682 × 10 | −144,173.9 | 298–700 | [27] |
| 143.5698 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 700–1044 | [27] | |||
| 73.59656 | 1044–2000 | [27] | ||||||
| -ThCl(cr) | −1191.3012 | 176.135 | 120.293 | 0.0232672 | −615,050 | 298–1042 | this work, [35] | |
| -ThCl(cr) | −1186.300 | 183.499 | 120.293 | 0.0232672 | −615,050 | 298–1042 | [5,34] | |
| ThCl(l) | −1149.740 | 197.626 | 167.4 | 298–1500 | [5,34] | |||
| LiThCl(cr) | −2834.966 | 413.34 | 299.11212 | 0.0949778 | 7.453928 × 10 | −1,392,880.8 | 298–883 | this work |
| 413.51776 | −0.014453232 | −482,768 | 883–1042 | |||||
| 437.1957 | −0.037720432 | 132,282 | 1042–2000 | |||||
| NaThCl(cr) | −2051.540 | 328.0 | 215.73616 | 0.0346672 | 2.42932 × 10 | −616,815.992 | 298–1042 | this work |
| 239.41 | 0.0114 | 2.42932 × 10 | −1765.992 | 1042–1074 | ||||
| KThCl(cr) | −1685.000 | 258.69 | 170.76961 | 0.029191577 | 7.496682 × 10 | −759,223.9 | 298–700 | this work |
| 263.8628 | −0.1447727 | 9.965702 × 10 | −8,832,886 | 700–1042 | ||||
| 287.5408 | −0.1680399 | 9.965702 × 10 | −8,217,836 | 1042–1044 | ||||
| 217.568 | 1044–2000 | |||||||
| KThCl(cr) | −2139.850 | 380.5 | 221.24622 | 0.035115954 | 1.4993364 × 10 | −903,397.8 | 298–700 | this work |
| 407.4326 | −0.3128126 | 1.9931404 × 10 | −17,050,722 | 700–1042 | ||||
| 431.1106 | −0.3360798 | 1.9931404 × 10 | −16,435,672 | 1042–1044 | ||||
| 291.16408 | 1042–2000 | |||||||
| A | B | Z | Z |
|---|---|---|---|
| Li | Li | 6 | 6 |
| Na | Na | 6 | 6 |
| K | K | 6 | 6 |
| Th | Th | 6 | 6 |
| Li | Th | 4 | 6 |
| Na | Th | 3 | 6 |
| K | Th | 4 | 6 |
| System | Equilibrium | Invariant Reaction | This Study (calc.) | Tanii et al. [21] | Vokhmyakov et al. [20] | Oyamada [19] | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| X(ThCl) | T / K | X(ThCl) | T / K | X(ThCl) | T / K | X(ThCl) | T / K | |||
| LiCl-ThCl | Congruent Melting | LiCl = L | 1 | 883 | 1 | 881 | 1 | 910 | ||
| Peritectic | LiThCl = LiCl + L | 0.2 | 723 | 0.2 | 725 | 0.2 | 723 | - | - | |
| Eutectic | LiThCl + -ThCl = L | 0.343 | 695 | - | 690 | 0.38 | 681 | 0.35 | 703 | |
| - transition | -ThCl = -ThCl | 1 | 679 | |||||||
| Congruent Melting | -ThCl = L | 1 | 1042 | 1 | 1041 | 1 | 1070 | |||
| NaCl-ThCl | Congruent melting | NaCl = L | 0 | 1074 | 0 | 1074 | 0 | 1097 | ||
| Eutectic | NaCl + NaThCl = L | 0.251 | 657 | - | 639 | 0.255 | 633 | 0.26 | 667 | |
| Congruent Melting | NaThCl = L | 1/3 | 703 | 1/3 | 708 | 1/3 | 708 | 1/3 | 729 | |
| Eutectic | NaThCl + -ThCl = L | 0.457 | 654 | - | 637 | 0.45 | 648 | 0.49 | 686 | |
| KCl-ThCl | Congruent melting | KCl = L | 0 | 1044 | 0 | 1043 | 0 | 1070 | ||
| Eutectic | KCl + KThCl = L | 0.206 | 894 | - | 895 | 0.25 | 903 | 0.15 | 917 | |
| Congruent melting | KThCl = L | 1/3 | 977 | 1/3 | 988 | 1/3 | 978 | 0.25 | 997 | |
| Eutectic | KThCl + KThCl = L | 0.467 | 697 | - | 705 | 0.42 | 668 | 0.43 | 681 | |
| Congruent melting | KThCl = L | 0.5 | 702 | 0.5 | 703 | 0.5 | 741 | |||
| Eutectic | KThCl + -ThCl = L | 0.536 | 699 | 0.54 | 693 | 0.56 | 706 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocádiz Flores, J.A.; Rooijakkers, B.A.S.; Konings, R.J.M.; Smith, A.L. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo 2021, 1, 122-133. https://doi.org/10.3390/thermo1020009
Ocádiz Flores JA, Rooijakkers BAS, Konings RJM, Smith AL. Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo. 2021; 1(2):122-133. https://doi.org/10.3390/thermo1020009
Chicago/Turabian StyleOcádiz Flores, Jaén A., Bas A. S. Rooijakkers, Rudy J. M. Konings, and Anna Louise Smith. 2021. "Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems" Thermo 1, no. 2: 122-133. https://doi.org/10.3390/thermo1020009
APA StyleOcádiz Flores, J. A., Rooijakkers, B. A. S., Konings, R. J. M., & Smith, A. L. (2021). Thermodynamic Description of the ACl-ThCl4 (A = Li, Na, K) Systems. Thermo, 1(2), 122-133. https://doi.org/10.3390/thermo1020009






