Feature Extraction and Classification of Canopy Gaps Using GLCM- and MLBP-Based Rotation-Invariant Feature Descriptors Derived from WorldView-3 Imagery
Abstract
:1. Introduction
2. Materials and Methods
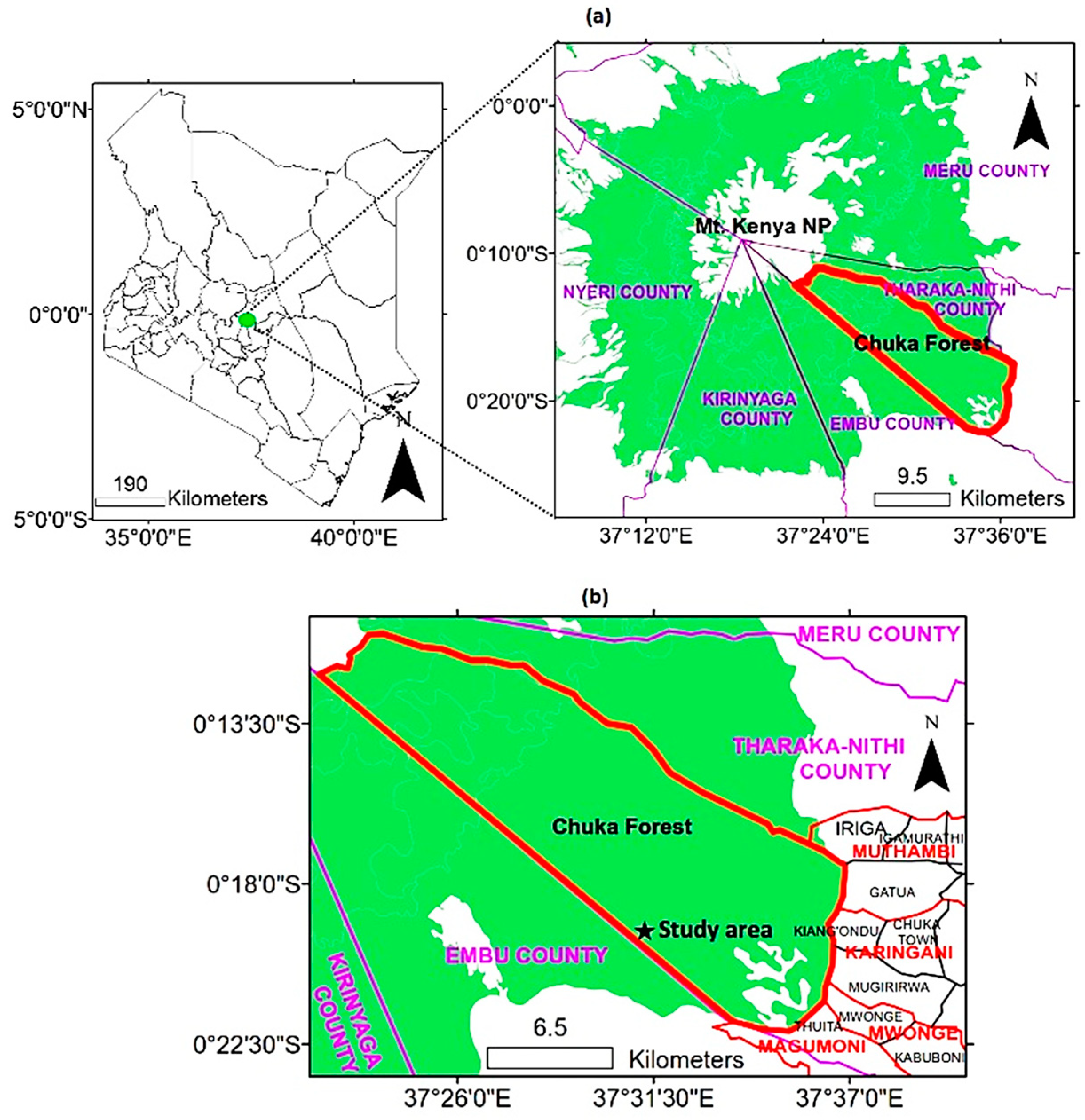
2.1. Study Area
2.2. Acquisition and Pre-Processing of Satellite Data
2.3. Acquisition of Field Data
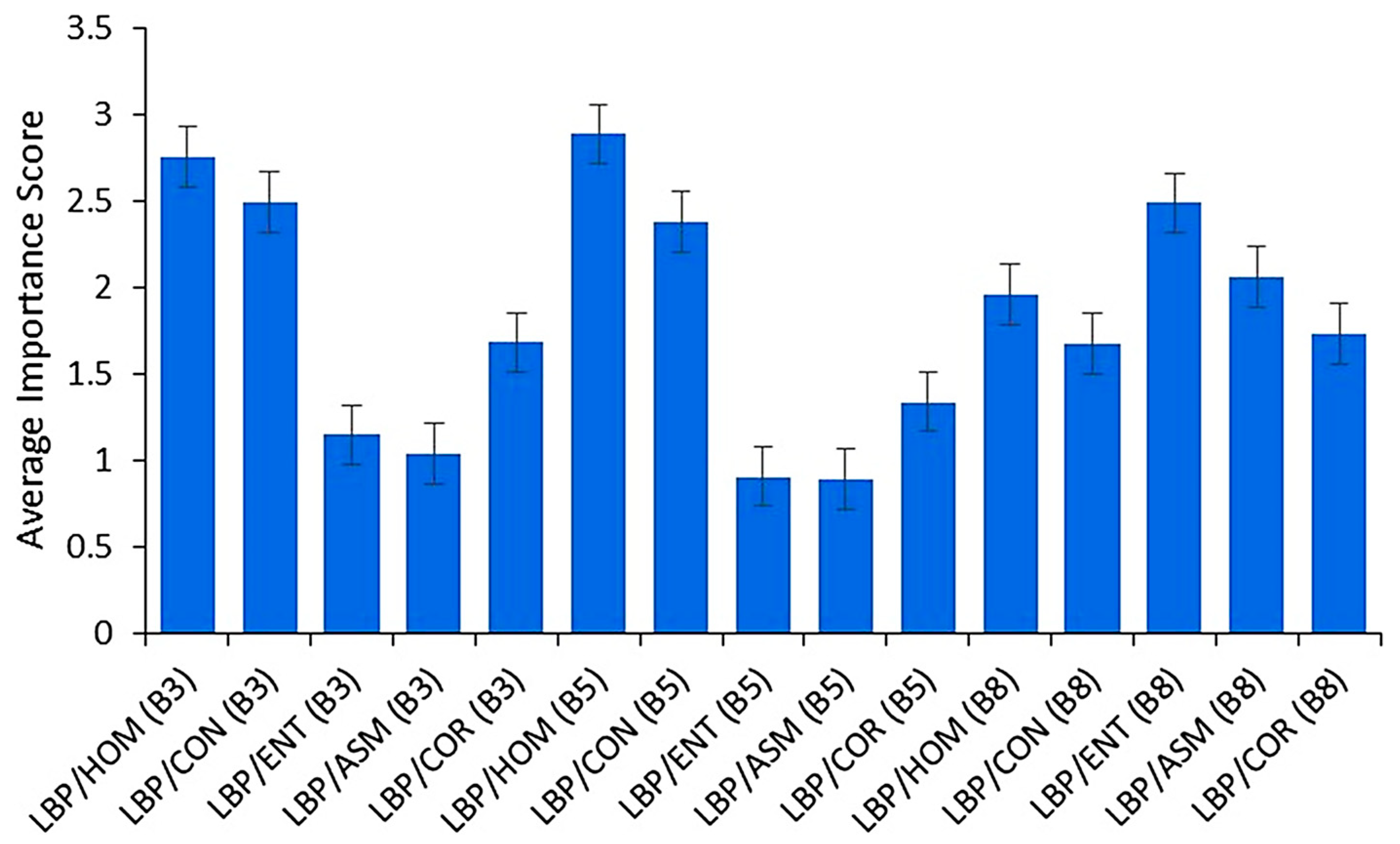
2.4. Feature Extraction and Selection
2.5. Similarity and Separability between Training Signatures
2.6. Training of Random Forest and Support Vector Machine Classifiers
2.7. Classification Post-Processing
2.8. Measures of Model Performance
3. Results
3.1. Similarity and Separability between Training Signatures
3.2. Optimisation of Random Forest and Support Vector Machine Classifiers
3.3. Model Performance
3.4. Image Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solberg, R.; Malnes, E.; Amlien, J.; Danks, F.; Haarpaintner, J.; Høgda, K.-A.; Johansen, B.E.; Karlsen, S.R.; Koren, H. State of the art for tropical forest monitoring by remote sensing. In A Review Carried Out for the Ministry for the Environment of Norway and the Norwegian Space Centre; Norwegian Computing Centre: Oslo, Norway, 2008; p. 11. [Google Scholar]
- Gibson, L.; Lee, T.M.; Koh, L.P.; Brooks, B.W.; Gardner, T.A.; Barlow, J.; Peres, C.A.; Bradshaw, C.J.A.; Laurance, W.F.; Lovejoy, T.E.; et al. Primary forests are irreplaceable for sustaining tropical biodiversity. Nature 2011, 478, 378–381. [Google Scholar] [CrossRef] [PubMed]
- Miettinen, J.; Stibig, H.J.; Achard, F. Remote sensing of forest degradation in Southeast Asia-Aiming for a regional view through 5-30 m satellite data. Glob. Ecol. Conserv. 2014, 2, 24–36. [Google Scholar] [CrossRef]
- Jackson, C.M.; Adam, E. Remote sensing of selective logging in tropical forests: Current state and future directions. iForest 2020, 13, 286–300. [Google Scholar] [CrossRef]
- Andersen, H.E.; Reutebuch, S.E.; McGaughey, R.J.; D’Oliveira, M.V.; Keller, M. Monitoring selective logging in western Amazonia with repeat lidar flights. Remote Sens. Environ. 2014, 151, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Achard, F.; Eva, H.D.; Stibig, H.-J.; Mayaux, P.; Gallego, J.; Richards, T.; Malingreau, J.-P. Determination of deforestation rates of the world’s humid tropical forests. Science 2002, 297, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Edwards, D.P.; Tobias, J.; Sheil, D.; Meijaard, E.; Laurance, W.F. Maintaining ecosystem function and services in logged tropical forests. Trends Ecol. Evol. 2014, 29, 511–520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- KWS. Mt Kenya Ecosystem Management Plan 2010–2020. Available online: https://www.kws.go.ke/file/1470/download?token=1lO6G3zI (accessed on 16 February 2019).
- NEMA. Kenya State of the Environment and Outlook 2010; Supporting the Delivery of Vision 2030. Available online: http://www.enviropulse.org/documents/Kenya_SOE.pdf (accessed on 3 January 2019).
- Kigomo, B.N. The growth of camphor (Ocotea usambarensis Engl.) in plantation in the eastern Aberdare range, Kenya. East Afr. Agri. For. J. 1987, 52, 141–147. [Google Scholar] [CrossRef]
- Dalagnol, R.; Phillips, O.L.; Gloor, E.; Galvao, L.S.; Wagner, F.H.; Locks, C.J.; Luiz, E.O.C.; Aragao, L.E. Quantifying canopy tree loss and gap recovery in tropical forests under low-intensity logging using VHR satellite imagery and airborne lidar. Remote Sens. 2019, 11, 817. [Google Scholar] [CrossRef] [Green Version]
- Betts, H.D.; Brown, L.J.; Stewart, G.H. Forest canopy gap detection and characterisation by the use of high-resolution Digital Elevation Models. N. Z. J. Ecol. 2005, 29, 95–103. [Google Scholar]
- Runkle, J.R. Guidelines and Sample Protocol for Sampling Forest Gaps; General technical report, PNW-GTR-283, USDA Forest Service; Pacific Northwest Research Station: Portland, OR, USA, 1992; 44p. [Google Scholar]
- Nakashizuka, T.; Katsuki, T.; Tanaka, H. Forest canopy structure analyzed by using aerial photographs. Ecol. Res. 1995, 10, 13–18. [Google Scholar] [CrossRef]
- Masiliūnas, D. Evaluating the Potential of Sentinel-2 and Landsat Image Time Series for Detecting Selective Logging in the Amazon. Master’s Thesis, Report GIRS-2017-27. Wageningen University and Research, Wageningen, The Netherlands, 2017. [Google Scholar]
- Hamunyela, E.; Verbesselt, J.; Herold, M. Using spatial context to improve early detection of deforestation from Landsat time series. Remote Sens. Environ. 2016, 172, 126–138. [Google Scholar] [CrossRef]
- Costa, O.B.; Matricardi, E.A.T.; Pedlowski, M.A.; Miguel, E.P.; Gaspar, R.O. Selective logging detection in the Brazilian Amazon. Floresta Ambient. 2019, 26, e20170634. [Google Scholar] [CrossRef] [Green Version]
- Ellis, P.; Griscom, B.; Walker, W.; Gonçalves, F.; Cormier, T. Mapping selective logging impacts in Borneo with GPS and airborne lidar. For. Ecol. Manag. 2016, 365, 184–196. [Google Scholar] [CrossRef] [Green Version]
- Spaias, L.; Suomlainen, J.; Tanago, J.G.D. Radiometric detection of selective logging in tropical forest using UAV-borne hyperspectral data and simulation of satellite imagery. In Proceedings of the 2016 European Space Agency Living Planet Symposium, Prague, the Czech Republic, 9–13 May 2016. [Google Scholar]
- Ota, T.; Ahmed, O.S.; Minn, S.T.; Khai, T.C.; Mizoue, N.; Yoshida, S. Estimating selective logging impacts on aboveground biomass in tropical forests using digital aerial photography obtained before and after a logging event from an unmanned aerial vehicle. For. Ecol. Manag. 2019, 433, 162–169. [Google Scholar] [CrossRef]
- Rex, F.; Silva, C.; Paula, A.; Corte, A.; Klauberg, C.; Mohan, M.; Cardil, A.; da Silva, V.S.; de Almeida, D.R.A.; Garcia, M.; et al. Comparison of statistical modeling approaches for estimating tropical forest aboveground biomass stock and reporting their changes in low-intensity logging areas using multi-temporal LiDAR data. Remote Sens. 2020, 12, 1498. [Google Scholar] [CrossRef]
- Kamarulzaman, A.; Wan Mohd Jaafar, W.S.; Abdul Maulud, K.N.; Saad, S.N.M.; Omar, H.; Mohan, M. Integrated segmentation approach with machine learning classifier in detecting and mapping post selective logging impacts using UAV imagery. Forests 2022, 13, 48. [Google Scholar] [CrossRef]
- Ghasemi, N.; Sahebi, M.R.; Mohammadzadeh, A. Biomass estimation of a temperate deciduous forest using wavelet analysis. IEEE Trans. Geosci. Remote Sens. 2013, 51, 765–776. [Google Scholar] [CrossRef]
- Zhou, J.; Guo, R.Y.; Sun, M.; Di, T.T.; Wang, S.; Zhai, J.; Zhao, Z. The effects of GLCM parameters on LAI estimation using texture values from Quickbird satellite imagery. Sci. Rep. 2017, 7, 7366. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.I.; Jung, K.; Park, S.H.; Kim, H.J. Support vector machines for texture classification. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1542–1550. [Google Scholar] [CrossRef] [Green Version]
- Suruliandi, A.; Jenicka, S. Texture-based classification of remotely sensed images. Int. J. Signal Imaging Syst. Eng. 2015, 8, 260–272. [Google Scholar] [CrossRef]
- Lucieer, A.; Stein, A.; Fisher, P. Multivariate texture-based segmentation of remotely sensed imagery for extraction of objects and their uncertainty. Int. J. Remote Sens. 2005, 26, 2917–2936. [Google Scholar] [CrossRef]
- Jenicka, S.; Suruliandi, A. Comparison of soft computing approaches for texture-based land cover classification of remotely sensed image. Res. J. Appl. Sci. Eng. Technol. 2015, 10, 1216–1226. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmuga, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cyber. 1973, 3, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Cross, G.R.; Jain, A. Markov random field texture models. IEEE Trans. Pattern Anal. Mach. Intell. 1983, 5, 25–39. [Google Scholar] [CrossRef] [PubMed]
- Unser, M. Texture classification and segmentation using wavelet frames. IEEE Trans. Image Process. 1995, 4, 1549–1560. [Google Scholar] [CrossRef] [Green Version]
- He, D.C.; Wang, L. Texture unit, texture spectrum, and texture analysis. IEEE Trans. Geosci. Remote Sens. 1990, 28, 509–513. [Google Scholar] [CrossRef]
- Arivazhagan, S.; Ganesan, L. Texture classification using wavelet transform. Pattern Recognit. Lett. 2003, 24, 1513–1521. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikäinen, M.; Mäenpää, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Rakwatin, P.; Longépé, N.; Isoguchi, O.; Shimada, M.; Uryu, Y. Mapping tropical forest using ALOS PALSAR 50m resolution data with multiscale GLCM analysis. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1234–1237. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, H.; Lin, H.; Fang, C. Textural-spectral feature-based species classification of mangroves in Mai Po Nature Reserve from Worldview-3 imagery. Remote Sens. 2016, 8, 24. [Google Scholar] [CrossRef] [Green Version]
- Marissiaux, Q. Characterizing Tropical Forest Dynamics by Remote-Sensing Using Very High Resolution and Sentinel-2 Images. Master’s Thesis, Faculty of Bioengineers, Catholic University of Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2018. [Google Scholar]
- Burnett, M.W.; White, T.D.; McCauley, D.J.; De Leo, G.A.; Micheli, F. Quantifying coconut palm extent on Pacific islands using spectral and textural analysis of very high-resolution imagery. Int. J. Remote Sens. 2019, 40, 1–27. [Google Scholar] [CrossRef]
- KFS. Mt. Kenya Forest Reserve Management Plan 2010–2019. Available online: http://www.kenyaforestservice.org/documents/MtKenya.pdf (accessed on 3 January 2019).
- Lange, S.; Bussmann, R.W.; Beck, E. Stand structure and regeneration of the subalpine Hagenia abyssinica of Mt. Kenya. Bot. Acta. 1997, 110, 473–480. [Google Scholar] [CrossRef]
- Bussmann, R.W.; Beck, E. Regeneration- and cyclic processes in the Ocotea-Forests (Ocotea usambarensis Engl.) of Mount Kenya. Verh. GfÖ. 1995, 24, 35–38. [Google Scholar]
- DigitalGlobe. The Benefits of the 8 Spectral Bands of WorldView-2. Available online: https://dg-cms-uploads-production.s3.amazonaws.com/uploads/document/file/35/DG-8SPECTRAL-WP_0.pdf (accessed on 2 February 2019).
- DigitalGlobe. WorldView-3. Above + Beyond. Available online: http://worldview3.digitalglobe.com/ (accessed on 2 February 2019).
- Li, H.; Jing, L.; Tang, Y. Assessment of pansharpening methods applied to worldview-2 imagery fusion. Sensors 2017, 17, 89. [Google Scholar] [CrossRef] [PubMed]
- Jackson, C.M.; Adam, E. A machine learning approach to mapping canopy gaps in an indigenous tropical submontane forest using WorldView-3 multispectral satellite imagery. Environ. Conserv. 2022, 49, 255–262. [Google Scholar] [CrossRef]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Fox, T.J.; Knutson, M.G.; Hines, R.K. Mapping forest canopy gaps using air-photo interpretation and ground surveys. Wildl. Soc. Bull. 2000, 28, 882–889. [Google Scholar] [CrossRef]
- Kupidura, P. The comparison of different methods of texture analysis for their efficacy for land use classification in satellite imagery. Remote Sens. 2019, 11, 1233. [Google Scholar] [CrossRef] [Green Version]
- Cui, H.; Qian, H.; Qian, L.; Li, Y. Remote sensing experts classification system applying in the land use classification in Guangzhou City. In Proceedings of the 2nd International Congress on Image and Signal Processing, CISP’09, Tianjin, China, 17–19 October 2009. [Google Scholar] [CrossRef]
- Cohen, W.B.; Spies, T.A. Estimating structural attributes of Douglas fir/western hemlock forest stands from Landsat and SPOT imagery. Remote Sens. Environ. 1992, 41, 1–17. [Google Scholar] [CrossRef]
- Bianconi, F.; Fernández, A. Rotation invariant co-occurrence features based on digital circles and discrete Fourier transform. Pattern Recognit. Lett. 2014, 48, 34–41. [Google Scholar] [CrossRef]
- Sokal, R.; Rohlf, J. Introduction to Biostatistics, 2nd ed.; Freeman and Company: New York, NY, USA, 1987. [Google Scholar]
- Tuominen, J.; Lipping, T. Spectral characteristics of common reed beds: Studies on spatial and temporal variability. Remote Sens. 2016, 8, 181. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Guo, X.; Yu, H. Variable selection using mean decrease accuracy and mean decrease Gini based on random forest. In Proceedings of the 7th IEEE International Conference on Software Engineering and Service Science (ICSESS), Beijing, China, 26–28 August 2016. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for landcover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Odindi, J.; Abdel-Rahman, E.M. Land-use/cover classification in a heterogeneous coastal landscape using RapidEye imagery: Evaluating the performance of random forest and support vector machines classifiers. Int. J. Remote Sens. 2014, 35, 3440–3458. [Google Scholar] [CrossRef]
- Negrón-Juárez, R.I.; Chambers, J.Q.; Marra, D.M.; Ribeiro, G.H.P.M.; Rifai, S.W.; Higuchi, N.; Roberts, D. Detection of subpixel treefall gaps with Landsat imagery in Central Amazon forests. Remote Sens. Environ. 2011, 115, 3322–3328. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High-density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Hethcoat, M.G.; Edwards, D.P.; Carreiras, J.M.B.; Bryant, R.G.; França, F.M.; Quegan, S. A machine learning approach to map tropical selective logging. Remote Sens. Environ. 2019, 221, 569–582. [Google Scholar] [CrossRef]
- Clausi, D.A. An Analysis of Co-Occurrence Texture Statistics as a Function of Grey Level Quantization. Can. J. Remote Sens. 2002, 28, 45–62. [Google Scholar] [CrossRef]
- Asner, G.P.; Kellner, J.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Anderson, C.; Martin, R.E. Forest canopy gap distributions in the southern Peruvian Amazon. PLoS ONE 2013, 8, e60875. [Google Scholar] [CrossRef] [Green Version]
- Baldauf, T.; Köhl, M. Use of TerraSAR-X for forest degradation mapping in the context of REDD. In Proceedings of the World Forestry Congress XIII, Buenos Aires, Argentina, 23 October 2009. [Google Scholar]
- Di Ruberto, C.; Fodde, G.; Putzu, L. Comparison of statistical features for medical colour image classification. In International Conference on Computer Vision Systems; Springer: Cham, Switzerland, 2015; Volume 9163, pp. 3–13. [Google Scholar] [CrossRef]



| Class # | Class | Sample | Description |
|---|---|---|---|
| Class 1 | Vegetated gap |  | Low-lying vegetation in the forest canopy |
| Class 2 | Shaded gap |  | Gaps in the forest canopy that are darker because of the shadows cast by the nearby tree crowns |
| Class 3 | Forest canopy |  | The topmost layer of a forest, mostly tree crowns with a few emergent trees having heights that shoot above the canopy. |
| (a) G-Statistic | (b) Euclidean Distance | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NCG | SG | VG | FC | NCG | SG | VG | FC | ||
| NCG | 9.01 | 7.15 | 1.43 | NCG | 106 | 77 | 49 | ||
| SG | 8.02 | 2.53 | SG | 96 | 55 | ||||
| VG | 0.38 | VG | 41 | ||||||
| FC | FC | ||||||||
| Block ID | Feature | Random Forest | Support Vector Machine | Block ID | Feature | Random Forest | Support Vector Machine | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mtry | ntree | OOB Error | Gamma | Cost | CV Error | mtry | ntree | OOB Error | Gamma | Cost | CV Error | ||||
| A | MLBP/MHOM | 3 | 1500 | 0.108 | 0.1 | 1000 | 0.103 | D | MLBP/MHOM | 3 | 1500 | 0.097 | 0.01 | 10 | 0.091 |
| MLBP/MCON | 2 | 4500 | 0.128 | 1 | 10 | 0.129 | MLBP/MCON | 2 | 5500 | 0.121 | 0.01 | 1000 | 0.116 | ||
| MLBP/MENT | 2 | 2500 | 0.204 | 0.1 | 100 | 0.202 | MLBP/MENT | 2 | 4500 | 0.165 | 1 | 100 | 0.159 | ||
| MLBP/MASM | 3 | 3500 | 0.210 | 0.1 | 100 | 0.212 | MLBP/MASM | 3 | 500 | 0.199 | 0.01 | 1000 | 0.191 | ||
| MLBP/MCOR | 2 | 2500 | 0.140 | 0.01 | 1000 | 0.132 | MLBP/MCOR | 3 | 3500 | 0.136 | 0.1 | 10 | 0.127 | ||
| B | MLBP/MHOM | 2 | 4500 | 0.109 | 0.01 | 1000 | 0.110 | E | MLBP/MHOM | 2 | 500 | 0.101 | 1 | 10 | 0.109 |
| MLBP/MCON | 2 | 3500 | 0.129 | 1 | 100 | 0.122 | MLBP/MCON | 2 | 1500 | 0.116 | 0.1 | 100 | 0.112 | ||
| MLBP/MENT | 3 | 1500 | 0.177 | 0.1 | 1000 | 0.174 | MLBP/MENT | 3 | 5500 | 0.184 | 1 | 10 | 0.179 | ||
| MLBP/MASM | 2 | 2500 | 0.197 | 0.01 | 10 | 0.190 | MLBP/MASM | 2 | 1500 | 0.208 | 0.1 | 100 | 0.214 | ||
| MLBP/MCOR | 2 | 5500 | 0.140 | 1 | 10 | 0.136 | MLBP/MCOR | 2 | 6500 | 0.149 | 0.01 | 100 | 0.136 | ||
| C | MLBP/MHOM | 3 | 3500 | 0.109 | 0.01 | 10 | 0.102 | F | MLBP/MHOM | 3 | 5500 | 0.106 | 1 | 100 | 0.108 |
| MLBP/MCON | 3 | 4500 | 0.126 | 0.1 | 10 | 0.119 | MLBP/MCON | 3 | 1500 | 0.124 | 0.01 | 1000 | 0.119 | ||
| MLBP/MENT | 3 | 6500 | 0.210 | 0.01 | 1000 | 0.204 | MLBP/MENT | 3 | 4500 | 0.205 | 1 | 10 | 0.201 | ||
| MLBP/MASM | 2 | 3500 | 0.200 | 0.01 | 1000 | 0.197 | MLBP/MASM | 2 | 500 | 0.199 | 1 | 10 | 0.194 | ||
| MLBP/MCOR | 2 | 2500 | 0.139 | 1 | 10 | 0.134 | MLBP/MCOR | 3 | 1500 | 0.135 | 0.1 | 100 | 0.138 | ||
| MLBP/MHOM | |||||||||||
| Random Forest | Support Vector Machine | ||||||||||
| FC | SG | VG | Total | UA (%) | FC | SG | VG | Total | UA (%) | ||
| FC | 28 | 1 | 3 | 32 | 88 | FC | 28 | 0 | 2 | 30 | 93 |
| SG | 0 | 29 | 0 | 29 | 100 | SG | 1 | 30 | 1 | 32 | 94 |
| VG | 2 | 0 | 27 | 29 | 93 | VG | 1 | 0 | 27 | 28 | 96 |
| Total | 30 | 30 | 30 | 90 | Total | 30 | 30 | 30 | 90 | ||
| PA (%) | 93 | 97 | 90 | PA (%) | 93 | 100 | 90 | ||||
| Overall accuracy = 93.3% Kappa = 0.90% | Overall accuracy = 94.4% Kappa = 0.92% | ||||||||||
| MLBP/MCON | |||||||||||
| Random Forest | Support Vector Machine | ||||||||||
| FC | SG | VG | Total | UA (%) | FC | SG | VG | Total | UA (%) | ||
| FC | 27 | 1 | 3 | 31 | 90 | FC | 28 | 1 | 2 | 31 | 90 |
| SG | 1 | 28 | 1 | 30 | 91 | SG | 0 | 29 | 2 | 31 | 94 |
| VG | 2 | 1 | 26 | 29 | 82 | VG | 2 | 0 | 26 | 28 | 93 |
| Total | 30 | 30 | 30 | 90 | Total | 30 | 30 | 30 | 90 | ||
| PA (%) | 90 | 93 | 87 | PA (%) | 93 | 97 | 87 | ||||
| Overall accuracy = 90.0% Kappa = 0.85% | Overall accuracy = 92.2% Kappa = 0.88% | ||||||||||
| MLBP/MENT | |||||||||||
| Random Forest | Support Vector Machine | ||||||||||
| FC | SG | VG | Total | UA (%) | FC | SG | VG | Total | UA (%) | ||
| FC | 25 | 3 | 4 | 32 | 78 | FC | 25 | 3 | 3 | 31 | 81 |
| SG | 3 | 26 | 1 | 30 | 87 | SG | 3 | 27 | 1 | 31 | 87 |
| VG | 2 | 1 | 25 | 28 | 89 | VG | 2 | 0 | 26 | 28 | 93 |
| Total | 30 | 30 | 30 | 90 | Total | 30 | 30 | 30 | 90 | ||
| PA (%) | 83 | 87 | 83 | PA (%) | 83 | 90 | 87 | ||||
| Overall accuracy = 84.4%; Kappa = 0.77% | Overall accuracy = 86.7%; Kappa = 0.80% | ||||||||||
| MLBP/MASM | |||||||||||
| Random Forest | Support Vector Machine | ||||||||||
| FC | SG | VG | Total | UA (%) | FC | SG | VG | Total | UA (%) | ||
| FC | 23 | 2 | 3 | 28 | 82 | FC | 25 | 3 | 4 | 32 | 78 |
| SG | 4 | 25 | 3 | 32 | 78 | SG | 3 | 27 | 1 | 31 | 87 |
| VG | 3 | 3 | 24 | 30 | 80 | VG | 2 | 0 | 25 | 27 | 93 |
| Total | 30 | 30 | 30 | 90 | Total | 30 | 30 | 30 | 90 | ||
| PA (%) | 77 | 83 | 80 | PA (%) | 83 | 90 | 83 | ||||
| Overall accuracy = 80.0% Kappa = 0.70% | Overall accuracy = 85.6% Kappa = 0.78% | ||||||||||
| MLBP/MCOR | |||||||||||
| Random Forest | Support Vector Machine | ||||||||||
| FC | SG | VG | Total | UA (%) | FC | SG | VG | Total | UA (%) | ||
| FC | 26 | 3 | 4 | 33 | 85 | FC | 26 | 2 | 3 | 31 | 84 |
| SG | 2 | 27 | 1 | 30 | 90 | SG | 2 | 28 | 0 | 30 | 93 |
| VG | 2 | 0 | 25 | 27 | 78 | VG | 2 | 0 | 27 | 29 | 93 |
| Total | 30 | 30 | 30 | 90 | Total | 30 | 30 | 30 | 90 | ||
| PA (%) | 87 | 90 | 83 | PA (%) | 87 | 93 | 90 | ||||
| Overall accuracy = 86.7% Kappa = 0.80% | Overall accuracy = 89.0% Kappa = 0.84% | ||||||||||
| Image Blocks | |||||||
|---|---|---|---|---|---|---|---|
| Texture Descriptor | A | B | C | D | E | F | |
| RF classifier | MLBP/MHOM | 91.4 | 89.8 | 91.0 | 93.3 | 92.9 | 92.4 |
| MLBP/MCON | 83.9 | 83.2 | 85.3 | 90.0 | 92.3 | 86.7 | |
| MLBP/MENT | 82.6 | 83.9 | 82.4 | 84.4 | 83.4 | 82.6 | |
| MLBPMASM | 81.1 | 81.4 | 81.1 | 80.0 | 82.9 | 80.0 | |
| MLBP/MCOR | 84.4 | 84.4 | 84.5 | 86.7 | 83.5 | 85.5 | |
| Average OA | 84.7 ± 4.0 | 84.5 ± 3.2 | 84.9 ± 3.8 | 86.9 ± 5.1 | 87.0 ± 5.1 | 85.4 ± 4.7 | |
| SVM classifier | MLBP/MHOM | 92.6 | 90.8 | 93.1 | 94.4 | 91.2 | 91.8 |
| MLBP/MCON | 83.2 | 88.1 | 90.2 | 92.2 | 95.1 | 90.2 | |
| MLBP/MENT | 82.8 | 85.7 | 80.3 | 86.7 | 83.7 | 82.8 | |
| MLBP/MASM | 81.1 | 85.9 | 81.4 | 85.6 | 80.9 | 81.3 | |
| MLBP/MCOR | 87.5 | 85.5 | 86.5 | 90.0 | 85.5 | 84.5 | |
| Average OA | 85.4 ± 4.6 | 87.2 ± 2.3 | 86.3 ± 5.5 | 89.9 ± 3.7 | 87.3 ± 5.8 | 86.1 ± 4.6 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackson, C.M.; Adam, E.; Atif, I.; Mahboob, M.A. Feature Extraction and Classification of Canopy Gaps Using GLCM- and MLBP-Based Rotation-Invariant Feature Descriptors Derived from WorldView-3 Imagery. Geomatics 2023, 3, 250-265. https://doi.org/10.3390/geomatics3010014
Jackson CM, Adam E, Atif I, Mahboob MA. Feature Extraction and Classification of Canopy Gaps Using GLCM- and MLBP-Based Rotation-Invariant Feature Descriptors Derived from WorldView-3 Imagery. Geomatics. 2023; 3(1):250-265. https://doi.org/10.3390/geomatics3010014
Chicago/Turabian StyleJackson, Colbert M., Elhadi Adam, Iqra Atif, and Muhammad A. Mahboob. 2023. "Feature Extraction and Classification of Canopy Gaps Using GLCM- and MLBP-Based Rotation-Invariant Feature Descriptors Derived from WorldView-3 Imagery" Geomatics 3, no. 1: 250-265. https://doi.org/10.3390/geomatics3010014
APA StyleJackson, C. M., Adam, E., Atif, I., & Mahboob, M. A. (2023). Feature Extraction and Classification of Canopy Gaps Using GLCM- and MLBP-Based Rotation-Invariant Feature Descriptors Derived from WorldView-3 Imagery. Geomatics, 3(1), 250-265. https://doi.org/10.3390/geomatics3010014








