Advances in Remote Sensing and Deep Learning in Coastal Boundary Extraction for Erosion Monitoring
Abstract
1. Introduction
2. Methodology
3. Remote Sensing
3.1. Passive Sensors
- Blue band: Used for monitoring water quality, turbidity and shallow water characteristics.
- Green band: Differentiates vegetation from water and aids in land use mapping.
- Red band: Assesses vegetation health, crop conditions and soil properties.
- NIR: Monitors vegetation health, detects water bodies and supports land use mapping.
- SWIR: Measures soil moisture, identifies fires and differentiates materials such as minerals and rocks.
- MWIR: Tracks land and sea surface temperatures, monitors thermal variations and detects fires.
- LWIR: Analyzes surface temperature, soil composition, urban activity and heat stress.
3.2. Active Sensors
- Single-polarization: Usually sends and receives signals in one orientation (HH or VV) but can also generate HV and VH signals.
- Dual-polarization: Transmits in one orientation and receives in two (HH and HV or VH and VV), providing higher-quality data which can be used to distinguish different types of surfaces.
- Full-polarization: Transmits and receives signals in both orientations, producing all four combinations (HH, HV, VH, VV) simultaneously.
- X-band: Short wavelength for detecting small changes and urban monitoring.
- C-band: Suitable for global mapping and identifying crops, with moderate canopy penetration.
- L-band: Long wavelength for biomass monitoring, with better canopy and soil penetration but lower resolution.
3.3. Remote Sensing Platforms
3.4. Datasets
4. Artificial Intelligence
Metrics
5. Coastal Segmentation
5.1. Neural Network
5.2. Pulse-Coupled Neural Network
5.3. CNNs
| Method | 1998 (Kappa) | 2015 (Kappa) | 2023 (Kappa) | 1998 (OA) | 2015 (OA) | 2023 (OA) |
|---|---|---|---|---|---|---|
| PBIA-RF | 0.88 | 0.87 | 0.90 | 90% | 89% | 92% |
| OBIA-RF-MSS | 0.93 | 0.92 | 0.93 | 92.7% | 95% | 95% |
| OBIA-RF-MRS | 0.71 | 0.63 | 0.74 | 71% | 69% | 70% |
| CNN-OBIA | 0.67 | 0.76 | 0.79 | 67% | 77% | 78% |
5.4. Encoder-Decoder
5.4.1. UNet
| Name | LP (%) | LR (%) | OP (%) | OR (%) | F1-Score (%) |
|---|---|---|---|---|---|
| DeepUNet | 98.58 | 98.91 | 99.04 | 99.04 | 98.74 |
| UNet | 96.68 | 97.42 | 97.57 | 97.57 | 97.05 |
| SegNet | 97.52 | 96.50 | 97.81 | 97.81 | 97.01 |
| SeNet | 96.71 | 96.54 | 97.03 | 97.03 | 96.83 |
5.4.2. Dual-Loop
| Algorithm | R | |
|---|---|---|
| Canny | 6.44 | 470.90 |
| HED | 100.54 | 458.21 |
| Single-loop UNet | 0.62 | 117.69 |
| Markov random field | 0.59 | 60.62 |
| Dual-loop FCN | 0.51 | 67.30 |
| Dual-loop UNet | 0.52 | 51.2 |
5.4.3. Residual Blocks
| Models | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) |
|---|---|---|---|---|
| RF | 69.42 | 69.94 | 69.87 | 70.61 |
| SVM | 64.31 | 64.47 | 64.50 | 64.84 |
| UNet | 94.80 | 94.89 | 93.47 | 94.22 |
| SegNet | 94.13 | 94.62 | 93.36 | 94.41 |
| ResNet | 94.11 | 94.57 | 93.66 | 94.49 |
| Basaeed et al. [122] | 95.92 | 96.19 | 95.62 | 96.12 |
| FusionNet | 95.95 | 96.21 | 95.62 | 96.13 |
| DenseNet | 95.98 | 96.35 | 95.72 | 96.41 |
| Nogueira et al. [125] | 96.35 | 96.80 | 95.97 | 96.45 |
| DeepUNet | 96.42 | 96.87 | 96.03 | 96.51 |
| RDUNet | 97.13 | 97.06 | 97.19 | 97.39 |
5.4.4. DeepLabV3+
5.4.5. Comparison Studies
| Model | Acc. (%) | Land Acc. (%) | Sea Acc. (%) | Precision (%) | Recall (%) | F1-Score (%) | IoU (%) |
|---|---|---|---|---|---|---|---|
| RGB Bands | |||||||
| RefineNet | 99.04 | 98.36 | 89.27 | 98.79 | 99.05 | 98.86 | 92.42 |
| FC-DenseNet | 99.55 | 98.65 | 88.18 | 99.60 | 99.55 | 99.55 | 92.72 |
| DeepLabV3+ | 99.40 | 98.59 | 89.30 | 99.45 | 99.40 | 99.39 | 92.98 |
| PSPNet | 99.50 | 98.47 | 88.39 | 99.50 | 99.51 | 99.49 | 92.63 |
| SegNet | 98.64 | 99.25 | 87.83 | 98.02 | 98.64 | 98.28 | 91.21 |
| UNet | 99.38 | 98.56 | 89.16 | 99.32 | 99.38 | 99.32 | 92.79 |
| NIR-SWIR-Red Bands | |||||||
| RefineNet | 99.45 | 98.80 | 89.08 | 99.42 | 99.45 | 99.41 | 92.89 |
| FC-DenseNet | 99.58 | 98.75 | 88.10 | 99.60 | 99.58 | 99.58 | 92.85 |
| DeepLabV3+ | 99.52 | 98.83 | 89.80 | 99.52 | 99.52 | 99.50 | 93.36 |
| PSPNet | 99.56 | 98.71 | 89.43 | 99.59 | 99.57 | 99.56 | 93.15 |
| SegNet | 66.53 | 98.79 | 54.09 | 67.48 | 66.53 | 66.56 | 59.11 |
| UNet | 99.51 | 98.78 | 89.32 | 99.50 | 99.51 | 99.49 | 93.11 |
5.4.6. Ensemble Learning
| Model | Accuracy (%) | IoU (%) | F1-Score (%) | Precision (%) | Recall (%) |
|---|---|---|---|---|---|
| Standard UNet | 99.721 | 99.429 | 99.714 | 99.671 | 99.756 |
| Dilated UNet | 99.721 | 99.429 | 99.714 | 99.706 | 99.722 |
| Fractal UNet | 99.576 | 99.137 | 99.566 | 99.278 | 99.857 |
| FC-DenseNet | 99.759 | 99.506 | 99.753 | 99.788 | 99.717 |
| Pix2Pix | 99.722 | 99.432 | 99.715 | 99.637 | 99.794 |
| WaterNet | 99.797 | 99.585 | 99.792 | 99.726 | 99.858 |
| AWEIsh | 99.180 | 98.344 | 99.165 | 98.455 | 99.885 |
| AWEInsh | 99.601 | 99.185 | 99.591 | 99.581 | 99.601 |
5.5. Attention Mechanisms
5.5.1. Squeeze-and-Excitation
| Methods | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) |
|---|---|---|---|---|
| NDWI | 80.13 | 79.79 | 77.31 | 78.53 |
| Multiresolution | 93.03 | 89.84 | 91.26 | 89.29 |
| SVM | 94.74 | 87.03 | 91.96 | 89.28 |
| UNet | 94.90 | 96.06 | 97.19 | 94.50 |
| SegNet | 95.21 | 93.95 | 95.46 | 94.75 |
| DeepLabV3+ | 95.22 | 94.04 | 95.46 | 94.75 |
| DeepUNet | 95.88 | 95.61 | 95.66 | 95.63 |
| SANet | 98.63 | 98.44 | 98.65 | 98.55 |
| Method | IoU (%) | Network Parameters (M) | Prediction Time (s) |
|---|---|---|---|
| UNet | 94.62 | 34.53 | 4.78 |
| Attention UNet | 94.57 | 34.88 | 5.11 |
| SegNet | 94.52 | 29.44 | 3.42 |
| DeepLabV3+ (Xception16) | 94.41 | 54.61 | 3.40 |
| SDW-UNet | 95.20 | 12.62 | 4.31 |
5.5.2. Convolutional Block Attention Module
| Input | Model | Mean Distance | RMSE | F1-Score (%) |
|---|---|---|---|---|
| S1SAR | Original UNet | 0.3272 | 0.7034 | 92.13 |
| UNet + BN | 0.3201 | 0.6922 | 94.62 | |
| Modified UNet | 0.2514 | 0.6071 | 98.62 | |
| S1SAR + DEM | Original UNet | 0.2516 | 0.5026 | 93.81 |
| UNet + BN | 0.2246 | 0.4194 | 98.97 | |
| Modified UNet | 0.1984 | 0.3845 | 99.02 |
5.5.3. FMPNet
| Method | SLS Dataset | SLSGF1 | ||||
|---|---|---|---|---|---|---|
| OA (%) | F1-Score (%) | IoU (%) | OA (%) | F1-Score (%) | IoU (%) | |
| FCN8 | 98.58 | 98.72 | 97.18 | 93.59 | 92.99 | 87.88 |
| UNet | 98.22 | 98.40 | 96.47 | 91.10 | 89.14 | 83.50 |
| SegNet | 93.94 | 94.36 | 88.51 | 91.36 | 90.24 | 83.92 |
| LinkNet | 96.47 | 96.77 | 93.14 | 93.06 | 92.37 | 86.94 |
| PSPNet | 98.57 | 98.70 | 97.16 | 92.32 | 91.49 | 85.63 |
| Attention UNet | 97.22 | 97.47 | 94.55 | 90.01 | 88.33 | 81.52 |
| DeepLabV3+ | 98.65 | 98.79 | 97.31 | 94.39 | 93.03 | 89.34 |
| DeepUNet | 98.91 | 99.02 | 97.83 | 83.92 | 79.53 | 71.32 |
| SENet | 96.29 | 96.60 | 92.81 | 92.01 | 91.14 | 84.12 |
| FNNN | 97.86 | 98.07 | 95.77 | 93.04 | 92.63 | 86.95 |
| MFDAN [157] | 95.25 | 95.57 | 90.89 | 94.22 | 93.74 | 89.02 |
| FMPNet | 99.09 | 99.18 | 98.19 | 97.64 | 96.12 | 95.38 |
5.5.4. Attention-UNet
5.5.5. Dual-Branch
| Method | SLS Dataset | HRSC2016 Dataset | ||||||
|---|---|---|---|---|---|---|---|---|
| IoU (%) | Recall (%) | Accuracy (%) | F1-Score (%) | IoU (%) | Recall (%) | Accuracy (%) | F1-Score (%) | |
| DeepUNet | 90.34 | 94.92 | 94.97 | 94.92 | 92.46 | 95.96 | 96.86 | 96.05 |
| SANet | 87.83 | 93.75 | 93.53 | 93.53 | 91.20 | 95.50 | 96.28 | 95.36 |
| MSUNet | 91.41 | 95.56 | 95.53 | 95.52 | 89.54 | 96.04 | 95.59 | 94.42 |
| FCN | 85.91 | 92.11 | 92.55 | 92.41 | 89.21 | 94.49 | 95.38 | 94.24 |
| U-Net | 91.16 | 95.28 | 95.34 | 95.37 | 90.96 | 94.76 | 96.23 | 95.22 |
| SegNet | 89.40 | 94.37 | 94.46 | 94.40 | 91.38 | 95.85 | 96.34 | 95.46 |
| PSPNet | 91.48 | 95.46 | 95.02 | 95.04 | 91.29 | 96.06 | 95.61 | 95.41 |
| DeepLabV3+ | 96.98 | 96.93 | 95.06 | 95.50 | 92.84 | 96.25 | 96.56 | 96.26 |
| DFA-Net | 86.98 | 93.46 | 95.06 | 95.04 | 87.56 | 92.95 | 96.26 | 93.28 |
| U2-Net | 92.31 | 95.99 | 96.09 | 95.99 | 92.77 | 96.49 | 96.99 | 96.24 |
| LANet | 91.98 | 95.77 | 95.85 | 95.83 | 92.84 | 96.25 | 97.02 | 96.26 |
| DBENet | 93.05 | 96.35 | 96.42 | 96.40 | 93.59 | 96.74 | 97.34 | 96.67 |
5.5.6. DeepSA-Net
| Dataset | Bands | Model | IoU (%) | Recall (%) | Precision (%) | Accuracy (%) |
|---|---|---|---|---|---|---|
| SLS | Red-Green-Blue | UNet | 98.25 | 98.45 | 99.51 | 99.14 |
| SCUNet | 98.30 | 98.65 | 99.37 | 99.16 | ||
| DenseUNet | 98.78 | 99.13 | 99.45 | 99.40 | ||
| DeepLabV3+ | 99.02 | 99.48 | 99.50 | 99.51 | ||
| Proposed | 99.31 | 99.46 | 99.74 | 99.66 | ||
| SLS | Red-Blue-NIR | UNet | 98.15 | 98.85 | 99.04 | 99.08 |
| SCUNet | 98.25 | 98.51 | 99.29 | 99.21 | ||
| DenseUNet | 98.53 | 98.86 | 99.46 | 99.27 | ||
| DeepLabV3+ | 98.81 | 99.15 | 99.50 | 99.41 | ||
| Proposed | 99.07 | 99.34 | 99.60 | 99.54 | ||
| YTU-WaterNet | NIR-SWIR-Red | UNet | 98.95 | 99.24 | 99.63 | 99.48 |
| SCUNet | 99.06 | 99.26 | 99.74 | 99.53 | ||
| DenseUNet | 98.43 | 98.72 | 99.58 | 99.21 | ||
| DeepLabV3+ | 99.14 | 99.58 | 99.51 | 99.57 | ||
| Proposed | 99.37 | 99.56 | 99.73 | 99.69 |
5.5.7. ENet
| Method | SLS test Dataset | HRSC2016 Test Dataset | ||||
|---|---|---|---|---|---|---|
| IoU (%) | Accuracy (%) | F1-Score (%) | IoU (%) | Accuracy (%) | F1-Score (%) | |
| UNet | 91.44 | 95.66 | 95.54 | 90.40 | 95.31 | 94.91 |
| FCN | 89.64 | 94.81 | 94.91 | 89.55 | 95.72 | 94.65 |
| SegNet | 88.98 | 94.21 | 94.17 | 88.90 | 95.19 | 94.33 |
| PSPNet | 91.06 | 95.32 | 95.37 | 90.21 | 95.07 | 94.30 |
| DeepLabV3+ | 91.56 | 95.76 | 95.83 | 91.03 | 96.05 | 94.90 |
| U2-Net | 92.12 | 95.96 | 95.94 | 91.46 | 96.32 | 94.98 |
| LANet | 91.89 | 96.11 | 96.02 | 91.30 | 96.19 | 94.91 |
| ACC-UNet | 92.04 | 96.19 | 96.11 | 91.97 | 96.29 | 95.03 |
| DCSAUNet | 91.78 | 96.19 | 95.94 | 91.42 | 96.11 | 94.91 |
| DeepUNet | 92.03 | 96.19 | 96.17 | 91.17 | 96.19 | 94.97 |
| SANet | 92.22 | 96.39 | 96.36 | 92.01 | 96.39 | 95.03 |
| MSUNet | 91.96 | 95.45 | 95.40 | 91.03 | 96.35 | 94.97 |
| DBENet | 92.27 | 96.28 | 96.26 | 92.36 | 96.38 | 96.48 |
| E-Net | 92.78 | 96.28 | 96.26 | 92.62 | 96.38 | 96.68 |
5.5.8. EMA-Net
5.5.9. DANet-SMIW
| Model | Pixel Accuracy (%) | IoU (%) |
|---|---|---|
| FCN32s-VGG | ||
| DeepLabV3-Xception65 | ||
| PSPNet-Resnet50 | ||
| DenseASPP-Densenet121 | ||
| PSANet-Resnet50 | ||
| ICNet-Resnet50 | ||
| DuNet-Resnet50 | ||
| PIDNet | ||
| DANet-SMIW |
5.6. Multi-Branch (CNN + Transformer)
| Model | GF-HNCD | BSD | ||
|---|---|---|---|---|
| F1-Score (%) | IoU (%) | F1-Score (%) | IoU (%) | |
| UNet | 93.61 | 93.72 | 94.29 | 94.33 |
| DeepLab v3+ | 94.97 | 94.15 | 95.58 | 94.81 |
| SwinUNet | 94.18 | 94.02 | 94.59 | 94.21 |
| TransUNet | 94.97 | 94.85 | 95.06 | 94.71 |
| SegFormer | 95.84 | 95.96 | 96.37 | 95.46 |
| STIRUNet | 96.85 | 96.72 | 97.44 | 96.78 |
| Method | Backbone | Accuracy (%) | IoU (%) | F1-Score (%) |
|---|---|---|---|---|
| Gaofen-6 Dataset | ||||
| UNet | - | 96.95 | 92.15 | 95.96 |
| DeepLabV3+ | ResNet50 | 96.87 | 91.98 | 95.77 |
| DANet | ResNet50 | 96.68 | 91.52 | 95.52 |
| Segformer | MiT-B1 | 97.16 | 92.71 | 96.18 |
| SwinUNet | Swin-Tiny | 96.88 | 91.95 | 95.92 |
| TransUNet | ViT-R50 [189] | 97.07 | 92.41 | 96.03 |
| ST-UNet | - | 97.23 | 92.99 | 96.34 |
| UNetformer | ResNet18 | 97.15 | 92.67 | 96.15 |
| TCUNet | - | 97.52 | 93.53 | 96.63 |
| Landsat-8 Dataset | ||||
| UNet | - | 64.63 | 41.55 | 61.25 |
| DeepLabV3+ | ResNet50 | 91.75 | 83.82 | 91.13 |
| DANet | ResNet50 | 88.23 | 76.84 | 86.72 |
| Segformer | MiT-B1 | 80.88 | 67.83 | 80.63 |
| SwinUNet | Swin-Tiny | 81.04 | 68.03 | 80.96 |
| TransUNet | ViT-R50 | 75.10 | 60.60 | 74.92 |
| ST-UNet | - | 84.82 | 73.41 | 84.65 |
| UNetformer | ResNet18 | 90.17 | 80.20 | 88.89 |
| TCUNet | - | 95.46 | 90.84 | 95.19 |
6. Coastal Extraction
| Methods | Recall (%) | Precision (%) | ||
|---|---|---|---|---|
| 16 m | 50 m | 16 m | 50 m | |
| Sobel | 66.5 | 45.6 | 64.7 | 43.3 |
| Canny | 82.4 | 78.3 | 85.0 | 75.2 |
| HED | 89.7 | 88.2 | 92.9 | 89.5 |
| RCF | 92.5 | 90.9 | 93.6 | 92.3 |
| Proposed + ReLU | 94.3 | 91.9 | 94.7 | 93.7 |
| Proposed + leaky-ReLU | 94.8 | 92.6 | 95.4 | 94.2 |
7. Dual Approach
| Model | Wilkes Land | Antarctic Peninsula | ||||||
|---|---|---|---|---|---|---|---|---|
| IoU (%) | F1 ODS (%) | F1 OIS (%) | Acc. (%) | IoU (%) | F1 ODS (%) | F1 OIS (%) | Acc. (%) | |
| Gaussian | 63.0 | 23.5 | 31.8 | 77.4 | 28.0 | 20.8 | 29.6 | 58.8 |
| UNet | 80.6 | 41.0 | 41.6 | 92.0 | 58.6 | 29.0 | 29.2 | 79.3 |
| HED | 76.7 | 38.4 | 41.0 | 90.1 | 54.7 | 27.8 | 29.6 | 77.6 |
| SCNN | 70.6 | 31.6 | 34.1 | 87.1 | 48.5 | 23.0 | 25.4 | 77.7 |
| HED-UNet | 84.9 | 39.7 | 41.6 | 92.0 | 67.2 | 27.1 | 29.1 | 80.5 |
| Method | Accuracy (%) | Recall (%) | IoU (%) | F1-Score (%) |
|---|---|---|---|---|
| UNet | 94.64 | 98.68 | 90.76 | 94.69 |
| DeepLabV3+ | 95.02 | 97.05 | 91.13 | 95.14 |
| SANet | 93.53 | 93.75 | 87.83 | 93.53 |
| MSUNet | 95.53 | 95.56 | 91.41 | 95.35 |
| LANet | 94.82 | 97.87 | 91.87 | 97.05 |
| DBENet | 96.42 | 96.35 | 93.05 | 96.40 |
| HED-UNet | 97.12 | 97.50 | 95.40 | 97.69 |
| CSAFNet | 98.28 | 99.17 | 96.72 | 98.36 |
8. Erosion Assessment
9. Discussion
9.1. Data
9.2. Coastal Segmentation
| Method | Data | Annotation | Resolution (m/pixel) | Region | Best Results (Metric) |
|---|---|---|---|---|---|
| NN [85] | ALOS-2 SAR (HH-polarized) | Manual | 10 m | Japan | 95% accuracy |
| PCNN [87] | RADARSAT-2 SAR (HH, VV, HV, VH) | Landsat-7 PAN | 15 m | Niger Delta, Mississippi-Horn Island | 1.57–2.71 pixels (distance score) |
| CNN [90] | Pleiades RGB + NIR | GPS Survey | 0.5 m | Algeria | 94% segmentation accuracy |
| OBIA + RF [92] | Landsat-5, Sentinel-2 (RGB + MIR, RGB + NIR) | Field survey | 10–30 m | Tunisia | 5.5–7.8 m (shoreline distance) |
| Unet [94] | Sentinel-1 SAR (VV, VH) | Morphological operations | 10 m | Taiwan | 97.24% F1-Score (5-pixel tolerance) |
| Unet [97] | GE Images | Manual | 0.7 m | Vietnam | 98% validation accuracy |
| Unet [99] | GF-2 RGB-NIR | Manual | 4–10 m | China | 93.65% accuracy |
| DeepUnet [104] | Orbview-3 (RGB-NIR) | Manual | 4 m, resampled to 1 m | Micronesia | 99.04% overall precision |
| DeepUnet [102] | Google Earth (RGB) | Manual | 3–50 m | Various | 99.04% overall precision |
| Unet [60] | Sentinel-2 (SWED Dataset) | Manual | 10 m | Sweden | 93.7% accuracy |
| Unet + QD [106] | Google Maps (RGB) | Navigational Charts | 2–64 m | Hong Kong | 95.5% pixel accuracy |
| Unet [110] | Landsat-8, SLS (NDWI, RGB, NIR) | LabelMe, QGIS | 10–30 m | Caspian Sea | 98.87% IoU |
| Unet [113] | GE satellite images | Manual | 0.7 m | China | 98% validation accuracy |
| Dual-Loop Unet [117] | Gaofen-2 (RGB) | Manual | 0.8 m | China | 67.30 Chamfer distance (R = 0.52) |
| RDUNet [120] | GE, ISPRS benchmark | Manual | 3.5 m | Global | 97.39% accuracy |
| Res-UNet [119] | GE (RGB) | Manual | 3–5 m | China | 98.15% F1-Score |
| DeepLabV3+ [126] | Sentinel-1 (SAR VV) | Sentinel-2 CoastSat | 10 m | Japan | 90% median shoreline accuracy |
| UNet [129] | Coast-Train dataset (RGB) | Manual | 0.05–15 m | USA | 85% validation accuracy, 80% IoU |
| DeepLabV3+ [62] | Landsat-8 (RGB, NIR-SWIR-Red) | Manual | 30 m | China | 99.55% accuracy |
| FPN + VGG16 [133] | Orthophotos (RGB) | Manual | 1 m | Eastern Canada | 96.06% F1-Score, 92.46% IoU |
| Various (Ensemble) [64] | Landsat-8 (Blue-Red-NIR) | OSM | 30 m | Global | 99.79% accuracy (WaterNet) |
| Various (Ensemble) [142] | ALOS-2 (SAR HH) | GPS-measured | 3 m | Japan | 11.23 m Euclidean distance |
| Various (Ensemble) [145] | Sentinel-1 SAR (pseudo-RGB) | Manual | 10 m | Arctic | 28 m deviation |
| UNet + SE [148] | Gaofen-1 (RGB) | Manual | 8 m | China | 98.55% accuracy |
| SDW-UNet [149] | Beijing II (RGB) | Manual | 0.8 m | China | 95.20% IoU |
| ACUNet [152] | MASATI, NWPU-RESISC45 | Manual | High-resolution | Global | 94.4% IoU (UNet++) |
| Unet + CBAM [155] | Sentinel-1 SAR + DEM | Morphological operations | 10 m | Taiwan | 99.02% F1-Score |
| FMPNet [156] | SLS, Gaofen-1 (RGB-NIR) | Manual | 2–8 m | China | 99.18% F1-Score |
| Attention-UNet [158] | SLS, aerial images (RGB-NIR) | NDWI, NDVI | 8 m | South Korea | 0.96 Kappa score, 98% accuracy |
| DBENet [159] | SLS, HRSC201 (RGB) | Manual | 0.4–30 m | Various | 97.348% accuracy |
| DeepSA-Net [163] | Landsat-8 (SLS, WaterNet) | Manual | 10–30 m | China | 99.37% IoU |
| ENet [166] | SLS, HRSC2016 (RGB) | Manual | Various | Asia-Pacific | 92.78% IoU |
| EMA-Net [169] | Gaofen-2 (RGB) | Manual | 4 m | China | 97.62% F1-Score |
| DANet-SWIM [171] | Landsat-8 (NDWI + RGB) | NDWI-based | 30 m | Asia-Pacific | 96.36% IoU, 99.08% pixel accuracy |
| STIRUNet [178] | Gaofen-1, BSD (RGB) | Manual | 16 m | China | 96.85% F1-Score |
| SRMA [184] | SLS, GE (RGB) | Manual | 3–5 m | China | 99.07% F1-Score |
| TCUNet [185] | Gaofen-6, Landsat-8 | Manual | 16 m, 30 m | China | 95.19% F1-Score |
9.3. Coastal Extraction
| Paper | Data | Annotation | Resolution (m/pixel) | Region | Best Results (Metric) |
|---|---|---|---|---|---|
| UNet [192] | SAR (VH polarization) | Shapefiles | 5 × 20 m | Not specified | 98.956% unweighted accuracy |
| UNet3+ [193] | Sentinel-1 (SAR VV polarization) | Shapefiles | 50 m, downsampled from 10 m | Jiangsu coast, China | 80% (precision), 90% (recall) |
| RCF-Inception [194] | RGB + BSDS500 | ArcGIS | 16 m, 50 m | Jiaozhou Bay, China | 94.8% recall, 95.4% precision |
| Transformer [198] | Landsat-5, -7, -8 (RGB) | Tidal-corrected labels | 30 m | Weitou Bay | RMSE: 0.57 px; quality: 95.24% |
| LaeNet [200] | Landsat-5, -8 (NIR + SWIR-1) | Threshold-derived labels | 30 m | Selinco Region | IoU: 98.79%; accuracy: 99.62% |
| SeNet [103] | GE RGB | Manual | 3–5 m | Not specified | F1-score (N = 1): 91.07%; precision: 99.69% |
| EWNet [204] | GF-1 (multispectral) | Manual | 8 m | China | Precision: >88%, F1-score: >83% |
| BS-Net [205] | GF-1 (RGB) | Manual | 8 m | Jiangsu Province | F1-score: 73.02% |
| HED-UNet [206] | Sentinel-1 (SAR, HH + HV) | Manual | 40 m | Antarctic | IoU: 84.9%; F1 ODS: 39.7%; accuracy: 92.0% |
| HED-UNet [215] | GE (RGB) | LabelMe | Not specified | Kaohsiung Port, Taiwan | Test accuracy: 98.3% (Adam + Focal) |
| CSAFNet [213] | SLS (RGB) | Morphological operations | 30 m | Global | 98.36% F1-Score, 96.72% IoU |
9.4. Erosion Assessment
10. Gaps and Future Directions
- 1.
- Definitions: A critical gap in this field is the inconsistent use of definitions. As mentioned earlier, terms like “coastline” and “shoreline” are often used interchangeably, despite representing distinct features in environmental contexts. This ambiguity becomes a problem with datasets containing very high resolutions where these features, which may appear similar at coarser resolutions, can and should be differentiated. Establishing clear definitions and training models to distinguish these features is crucial for accurate erosion prediction. The work by Dang et al. [113] demonstrated the ability to differentiate coastlines from shorelines.
- 2.
- Large datasets: The availability of public datasets remains a significant limitation. As seen in Section 3.4, few datasets are accessible for training DL algorithms, with most consisting of a limited number of high-resolution images. Furthermore, most datasets only offer segmentation maps rather than exact boundaries, requiring researchers to use edge detection algorithms to extract them. This field would greatly benefit from datasets dedicated to coastline and shoreline extraction, allowing direct comparison of extracted lines against GPS-tracked ground truths. Moreover, many existing datasets rely on segmentation ground truths generated using vision techniques like thresholding and morphological operations. As these methods are prone to fine-detail errors, DL models cannot effectively learn the desired behavior from the data. Datasets labeled via in situ surveys or expert annotations, such as those proposed by Blais et al. [133], would provide more reliable annotations and improve algorithm viability. Including diverse coastal regions and shoreline types in global datasets would further enhance generalization, addressing the poor performance of many models when applied to new regions.
- 3.
- Resolution: Another major gap is the lack of high-resolution data usage. Most reviewed articles rely on data with resolutions above 10 m, which are insufficient for erosion monitoring where rates are often below 1 m per year. A single-pixel deviation in these resolutions introduces errors exceeding 10 m, rendering them unrealistic for erosion monitoring. Utilizing data with finer resolutions, such as 0.10 m to 1 m, would improve precision in coastal boundary extraction and erosion prediction. Cost-effective solutions like UAVs and drones could capture such data, making high-resolution monitoring more feasible.
- 4.
- Data variability: Many of the reviewed studies overlook the impact of data variability on their results, particularly the effects of seasonal and tidal changes. Seasonal variations, such as the presence of snow, ice, or mud, can significantly change the level of detail available in the data. This can limit the ability to extract coastal boundaries during certain periods. Similarly, tidal levels are often disregarded during data collection, with some studies opting to use low-tide images for training while neglecting their potential influence on results. Although a few works have explored the impact of tidal variation, the majority fail to consider it comprehensively. A deeper analysis of how seasonal and tidal changes affect algorithm performance would provide valuable insights and enhance the robustness of future models.
- 5.
- Historical data: As mentioned, the availability of historical remote sensing data is highly valuable for coastal erosion management. Historical datasets often provide extensive coverage and are often available publicly, making them particularly interesting for research and monitoring efforts. However, these datasets typically consist of coarse-resolution or grayscale images, in contrast to the high-resolution and multispectral data used in DL approaches. To bridge this gap, advanced image processing techniques can be used to enhance these data. Super-resolution techniques, for instance, can be used to increase the resolution of images, while GANs could be used to transform grayscale images into multispectral formats (RGB, NIR, SWIR). This transformation could significantly expand the applicability of older datasets. Techniques like DeOldify [245], which specialize in cleaning and restoring old images, could further enhance the quality of historical data. By restoring image clarity and color accuracy, these techniques could make historical datasets viable for long-term coastal boundary forecasting.
- 6.
- Erosion prediction: Erosion prediction using DL and remote sensing remains an underexplored area within coastal management. Current methodologies mostly rely on traditional ML and numerical models, which often use manually extracted data from remote sensing images. Moreover, these approaches frequently integrate numerical data, limiting their applicability and availability. Historical numerical data, such as tidal levels, may not be readily available, further limiting their utility to specific regions. Leveraging remote sensing data for long-term erosion forecasting using DL would represent a significant advancement in the field. Given the extensive amount of historical remote sensing data, this approach could enable more accurate long-term erosion predictions without dependence on unavailable numerical data. By focusing exclusively on remote sensing images, DL models could address gaps in data availability, making predictions more robust and accessible. An interesting approach for future research consists of generating long-term historical coastal boundary datasets to support forecasting models. Sequential data-based models, such as RNN, LSTM and GRU are particularly promising. These architectures are well-suited for processing time-series data, enabling researchers to analyze sequential images to predict future erosion trends. Such advancements could greatly increase the predictive capabilities of DL in coastal erosion management, enabling more effective planning and mitigation strategies.
- 7.
- Real-time monitoring: There is a notable lack of real-time solutions for monitoring coastal erosion during extreme weather events such as storms and hurricanes, which can erode several meters of coastline within hours. While some studies have explored live video monitoring for coastal erosion [246,247], these efforts mostly rely on ground-fixed cameras, limiting their coverage and adaptability. Drones have been demonstrated as effective tools in coastal management [248,249]; however, these studies do not integrate DL algorithms to process the data. Developing a system that utilizes swarms of UAVs to collect and process live data for extracting coastal boundaries represents a promising research direction. Such a solution would be particularly valuable during extreme events like hurricanes and floods, enabling rapid assessment and decision-making. Future efforts could focus on creating end-to-end systems that combine live data acquisition with DL-based processing pipelines. Implementing DL models on compact platforms capable of capturing, processing and transmitting data in real time presents additional challenges. This would require advancements in lightweight model architectures, efficient processing and a robust communication system. Such developments could lead the way for scalable, real-time erosion monitoring systems, with significant applications in coastal disaster management.
- 8.
- Imaging modalities: Many imaging modalities have demonstrated their capability to extract coastal boundaries, but the majority rely on optical or SAR data, limiting the use of other data types such as LiDAR and bathymetry. LiDAR, despite its potential, remains underutilized for coastal erosion monitoring. This modality provides detailed 3D topographic information, which could significantly enhance the precision of erosion assessments. The integration of DEM with optical data has been shown to improve model performance [155]. Future studies incorporating LiDAR-derived digital models with optical data could provide valuable insights into erosion. However, the high cost of LiDAR sensors and their limited coverage result in a scarcity of publicly available data, posing challenges for large-scale applications.Bathymetry, which involves underwater LiDAR, is another promising but underexplored area. Monitoring seabed changes using bathymetric data could provide crucial insights into underwater erosion processes, which are closely linked to coastal erosion. Despite its importance, the application of DL for generating bathymetric data is still in its infancy. Notable studies, such as those by Dickens and Armstrong [104] and Al Najar et al. [234], have begun exploring this area. Expanding research efforts to use remote sensing modalities such as optical, IR and SAR data to supplement bathymetry generation could provide valuable datasets. Overall, leveraging modalities like LiDAR and bathymetry, alongside traditional optical and SAR data, has significant potential for advancing erosion monitoring.
- 9.
- Limitations: DL combined with remote sensing solutions for coastal boundary extraction and erosion monitoring face several limitations. One major challenge is the limited public and live access to high-resolution images, which hinders the development of realistic solutions. Additionally, the requirement for large and diverse datasets poses significant barriers to the training of algorithms, particularly in unique regions. The inherent “black box” nature of neural networks further complicates their application, as the results often cannot be easily explained. However, tools such as explainability techniques can provide some insights into the behavior of the model. NNs also struggle to adapt to extraordinary events or unseen scenarios, such as natural disasters. Furthermore, tidal levels and seasonal changes impose additional challenges for DL, as extensive data covering a wide range of scenarios are required to ensure robust model performance. Addressing these limitations is essential for improving the reliability and scalability of DL-based approaches in coastal monitoring.
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Panagos, P.; Standardi, G.; Borrelli, P.; Lugato, E.; Montanarella, L.; Bosello, F. Cost of agricultural productivity loss due to soil erosion in the European Union: From direct cost evaluation approaches to the use of macroeconomic models. Land Degrad. Dev. 2018, 29, 471–484. [Google Scholar] [CrossRef]
- Meena, N.K.; Gautam, R.; Tiwari, P.; Sharma, P. Nutrient losses in soil due to erosion. J. Pharmacogn. Phytochem. 2017, 6, 1009–1011. [Google Scholar]
- Prasad, D.H.; Kumar, N.D. Coastal erosion studies—A review. Int. J. Geosci. 2014, 2014, 44235. [Google Scholar] [CrossRef]
- United Nations Environment Programme (UNEP). Ocean, Seas and Coasts. Available online: https://www.unep.org/topics/ocean-seas-and-coasts#:~:text=Coastal%20regions%2C%20home%20to%2040,largest%20cities%2C%20face%20unique%20challenges (accessed on 12 July 2024).
- Chambers, M.; Liu, M. Maritime Trade and Transportation by the Numbers|Bureau of Transportation Statistics. Available online: https://www.bts.gov/archive/publications/by_the_numbers/maritime_trade_and_transportation/index (accessed on 12 July 2024).
- Angima, S.D. Erosion and Sediment Control: Vegetative Techniques. In Managing Soils and Terrestrial Systems; CRC Press: Boca Raton, FL, USA, 2020; pp. 523–528. [Google Scholar]
- Costa, G.P.; Marino, M.; Cáceres, I.; Musumeci, R.E. Effectiveness of Dune Reconstruction and Beach Nourishment to Mitigate Coastal Erosion of the Ebro Delta (Spain). J. Mar. Sci. Eng. 2023, 11, 1908. [Google Scholar] [CrossRef]
- Escudero, M.; Reguero, B.G.; Mendoza, E.; Secaira, F.; Silva, R. Coral reef geometry and hydrodynamics in beach erosion control in north quintana roo, Mexico. Front. Mar. Sci. 2021, 8, 684732. [Google Scholar] [CrossRef]
- Chaumillon, E.; Cange, V.; Gaudefroy, J.; Merle, T.; Bertin, X.; Pignon, C. Controls on shoreline changes at pluri-annual to secular timescale in mixed-energy rocky and sedimentary estuarine systems. J. Coast. Res. 2019, 88, 135–156. [Google Scholar] [CrossRef]
- Escudero, M.; Silva, R.; Mendoza, E. Beach Erosion Driven by Natural and Human Activity at Isla del Carmen Barrier Island, Mexico. J. Coast. Res. 2014, 71, 62–74. [Google Scholar] [CrossRef]
- Vaz, E.; Bowman, L. An application for regional coastal erosion processes in urban areas: A case study of the Golden Horseshoe in Canada. Land 2013, 2, 595–608. [Google Scholar] [CrossRef]
- Pinto, P.; Cabral, P.; Caetano, M.; Alves, M. Urban growth on coastal erosion vulnerable stretches. J. Coast. Res. 2009, II, 1567–1571. Available online: https://www.jstor.org/stable/25738053 (accessed on 15 January 2025).
- Mendelssohn, I.A.; Eugene Turner, R.; McKee, K.L. Louisiana’s eroding coastal zone: Management alternatives. J. Limnol. Soc. South. Afr. 1983, 9, 63–75. [Google Scholar] [CrossRef]
- Foster, N.L.; Attrill, M.J. Changes in coral reef ecosystems as an indication of climate and global change. In Climate Change; Elsevier: Amsterdam, The Netherlands, 2021; pp. 427–443. [Google Scholar]
- Stancheva, M.; Ratas, U.; Orviku, K.; Palazov, A.; Rivis, R.; Kont, A.; Peychev, V.; Tõnisson, H.; Stanchev, H. Sand dune destruction due to increased human impacts along the Bulgarian Black Sea and Estonian Baltic Sea Coasts. J. Coast. Res. 2011, 324–328. [Google Scholar]
- Masselink, G.; Russell, P. Impacts of climate change on coastal erosion. MCCIP Sci. Rev. 2013, 2013, 71–86. [Google Scholar]
- Silliman, B.R.; He, Q.; Angelini, C.; Smith, C.S.; Kirwan, M.L.; Daleo, P.; Renzi, J.J.; Butler, J.; Osborne, T.Z.; Nifong, J.C.; et al. Field experiments and meta-analysis reveal wetland vegetation as a crucial element in the coastal protection paradigm. Curr. Biol. 2019, 29, 1800–1806. [Google Scholar] [CrossRef] [PubMed]
- Feagin, R.A. Artificial dunes created to protect property on Galveston Island, Texas: The lessons learned. Ecol. Restor. 2005, 23, 89–94. [Google Scholar] [CrossRef]
- Harris, L.E. Artificial reefs for ecosystem restoration and coastal erosion protection with aquaculture and recreational amenities. Reef J. 2009, 1, 235–246. [Google Scholar]
- Laino, E.; Paranunzio, R.; Iglesias, G. Scientometric review on multiple climate-related hazards indices. Sci. Total. Environ. 2024, 945, 174004. [Google Scholar] [CrossRef] [PubMed]
- Anfuso, G.; Postacchini, M.; Di Luccio, D.; Benassai, G. Coastal sensitivity/vulnerability characterization and adaptation strategies: A review. J. Mar. Sci. Eng. 2021, 9, 72. [Google Scholar] [CrossRef]
- Cenci, L.; Disperati, L.; Persichillo, M.G.; Oliveira, E.R.; Alves, F.L.; Phillips, M. Integrating remote sensing and GIS techniques for monitoring and modeling shoreline evolution to support coastal risk management. GIScience Remote Sens. 2018, 55, 355–375. [Google Scholar] [CrossRef]
- Zhu, Z.T.; Cai, F.; Chen, S.L.; Gu, D.Q.; Feng, A.P.; Cao, C.; Qi, H.S.; Lei, G. Coastal vulnerability to erosion using a multi-criteria index: A case study of the Xiamen coast. Sustainability 2018, 11, 93. [Google Scholar] [CrossRef]
- Parthasarathy, A.; Natesan, U. Coastal vulnerability assessment: A case study on erosion and coastal change along Tuticorin, Gulf of Mannar. Nat. Hazards 2015, 75, 1713–1729. [Google Scholar] [CrossRef]
- Dada, O.A.; Almar, R.; Morand, P. Coastal vulnerability assessment of the West African coast to flooding and erosion. Sci. Rep. 2024, 14, 890. [Google Scholar] [CrossRef]
- Rocha, C.; Antunes, C.; Catita, C. Coastal indices to assess sea-level rise impacts-A brief review of the last decade. Ocean. Coast. Manag. 2023, 237, 106536. [Google Scholar] [CrossRef]
- Depountis, N.; Apostolopoulos, D.; Boumpoulis, V.; Christodoulou, D.; Dimas, A.; Fakiris, E.; Leftheriotis, G.; Menegatos, A.; Nikolakopoulos, K.; Papatheodorou, G.; et al. Coastal erosion identification and monitoring in the patras gulf (greece) using multi-discipline approaches. J. Mar. Sci. Eng. 2023, 11, 654. [Google Scholar] [CrossRef]
- Apostolopoulos, D.; Nikolakopoulos, K. A review and meta-analysis of remote sensing data, GIS methods, materials and indices used for monitoring the coastline evolution over the last twenty years. Eur. J. Remote Sens. 2021, 54, 240–265. [Google Scholar] [CrossRef]
- Parthasarathy, K.; Deka, P.C. Remote sensing and GIS application in assessment of coastal vulnerability and shoreline changes: A review. ISH J. Hydraul. Eng. 2021, 27, 588–600. [Google Scholar] [CrossRef]
- Tsiakos, C.A.D.; Chalkias, C. Use of machine learning and remote sensing techniques for shoreline monitoring: A review of recent literature. Appl. Sci. 2023, 13, 3268. [Google Scholar] [CrossRef]
- Wolf, J.; Becker, A.; Bricheno, L.; Brown, J.; Byrne, D.; De Dominicis, M.; Phillips, B. Guidance Note on the Application of Coastal Modelling for Small Island Developing States; Technical Report 73; National Oceanography Centre: Liverpool, UK, 2020. [Google Scholar] [CrossRef]
- Kerguillec, R.; Audère, M.; Baltzer, A.; Debaine, F.; Fattal, P.; Juigner, M.; Launeau, P.; Le Mauff, B.; Luquet, F.; Maanan, M.; et al. Monitoring and management of coastal hazards: Creation of a regional observatory of coastal erosion and storm surges in the pays de la Loire region (Atlantic coast, France). Ocean. Coast. Manag. 2019, 181, 104904. [Google Scholar] [CrossRef]
- Canada, N.R. The Electromagnetic Spectrum. 2015. Available online: https://natural-resources.canada.ca/maps-tools-and-publications/satellite-imagery-elevation-data-and-air-photos/tutorial-fundamentals-remote-sensing/introduction/the-electromagnetic-spectrum/14623 (accessed on 1 December 2024).
- Aggarwal, S. Principles of remote sensing. Satell. Remote Sens. GIS Appl. Agric. Meteorol. 2004, 23, 23–28. [Google Scholar]
- Kancheva, R.; Georgiev, G. Plant optical properties for chlorophyll assessment. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XIV, Edinburgh, UK, 24–26 September 2012; SPIE: San Francisco, CA, USA, 2012; Volume 8531, pp. 132–139. [Google Scholar]
- Sur, K.; Chauhan, P. Imaging spectroscopic approach for land degradation studies: A case study from the arid land of India. Geomat. Nat. Hazards Risk 2019, 10, 898–911. [Google Scholar] [CrossRef]
- Rahimzadeh-Bajgiran, P.; Berg, A.A.; Champagne, C.; Omasa, K. Estimation of soil moisture using optical/thermal infrared remote sensing in the Canadian Prairies. ISPRS J. Photogramm. Remote Sens. 2013, 83, 94–103. [Google Scholar] [CrossRef]
- Rishikeshan, C.; Ramesh, H. An automated mathematical morphology driven algorithm for water body extraction from remotely sensed images. ISPRS J. Photogramm. Remote Sens. 2018, 146, 11–21. [Google Scholar] [CrossRef]
- Benhammou, Y.; Alcaraz-Segura, D.; Guirado, E.; Khaldi, R.; Achchab, B.; Herrera, F.; Tabik, S. Sentinel2GlobalLULC: A Sentinel-2 RGB image tile dataset for global land use/cover mapping with deep learning. Sci. Data 2022, 9, 681. [Google Scholar] [CrossRef] [PubMed]
- Türker, U.; Yagci, O.; Kabdasli, M.S. Impact of nearshore vegetation on coastal dune erosion: Assessment through laboratory experiments. Environ. Earth Sci. 2019, 78, 1–14. [Google Scholar] [CrossRef]
- Jiang, W.; Ni, Y.; Pang, Z.; Li, X.; Ju, H.; He, G.; Lv, J.; Yang, K.; Fu, J.; Qin, X. An effective water body extraction method with new water index for sentinel-2 imagery. Water 2021, 13, 1647. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sensors 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Pamuji, R.; Mahardika, A.I.; Wiranda, N.; Saputra, N.A.B.; Adini, M.H.; Pramatasari, D. Utilizing Electromagnetic Radiation in Remote Sensing for Vegetation Health Analysis Using NDVI Approach with Sentinel-2 Imagery. Kasuari Phys. Educ. J. (KPEJ) 2023, 6, 127–135. [Google Scholar] [CrossRef]
- Liu, R.; Wang, S.; Zhou, Y.; Han, X.; Yao, Y. The study of the index models used in extraction of water body based on HJ-1 CCD imagery. In Proceedings of the 2011 International Conference on Multimedia Technology, Hangzhou, China, 26–28 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 904–907. [Google Scholar]
- Szabó, S.; Gácsi, Z.; Balázs, B. Specific features of NDVI, NDWI and MNDWI as reflected in land cover categories. Acta Geogr. Debrecina Landsc. Environ. Ser. 2016, 10, 194–202. [Google Scholar] [CrossRef]
- Le Hégarat-Mascle, S.; Zribi, M.; Alem, F.; Weisse, A.; Loumagne, C. Soil moisture estimation from ERS/SAR data: Toward an operational methodology. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2647–2658. [Google Scholar] [CrossRef]
- Townsend, P.A. Estimating forest structure in wetlands using multitemporal SAR. Remote Sens. Environ. 2002, 79, 288–304. [Google Scholar] [CrossRef]
- Ohkura, H. Application of SAR data to monitoring earth surface changes and displacement. Adv. Space Res. 1998, 21, 485–492. [Google Scholar] [CrossRef]
- Asiyabi, R.M.; Ghorbanian, A.; Tameh, S.N.; Amani, M.; Jin, S.; Mohammadzadeh, A. Synthetic aperture radar (SAR) for ocean: A review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9106–9138. [Google Scholar] [CrossRef]
- Hofton, M.A.; Rocchio, L.E.; Blair, J.B.; Dubayah, R. Validation of vegetation canopy lidar sub-canopy topography measurements for a dense tropical forest. J. Geodyn. 2002, 34, 491–502. [Google Scholar] [CrossRef]
- Szafarczyk, A.; Toś, C. The use of green laser in LiDAR bathymetry: State of the art and recent advancements. Sensors 2022, 23, 292. [Google Scholar] [CrossRef] [PubMed]
- Casella, E.; Rovere, A.; Pedroncini, A.; Stark, C.P.; Casella, M.; Ferrari, M.; Firpo, M. Drones as tools for monitoring beach topography changes in the Ligurian Sea (NW Mediterranean). Geo-Mar. Lett. 2016, 36, 151–163. [Google Scholar] [CrossRef]
- Jessin, J.; Heinzlef, C.; Long, N.; Serre, D. A systematic review of UAVs for island coastal environment and risk monitoring: Towards a Resilience Assessment. Drones 2023, 7, 206. [Google Scholar] [CrossRef]
- Blais, M.A.; Akhloufi, M.A. Reinforcement learning for swarm robotics: An overview of applications, algorithms and simulators. Cogn. Robot. 2023, 3, 226–256. [Google Scholar] [CrossRef]
- Sayre, R.; Noble, S.; Hamann, S.; Smith, R.; Wright, D.; Breyer, S.; Butler, K.; Van Graafeiland, K.; Frye, C.; Karagulle, D.; et al. A new 30 m resolution global shoreline vector and associated global islands database for the development of standardized ecological coastal units. J. Oper. Oceanogr. 2019, 12, S47–S56. [Google Scholar] [CrossRef]
- Sayre, R.; Martin, M.T.; Cress, J.J.; Butler, K.; Graafeiland, K.V.; Breyer, S.; Wright, D.; Frye, C.; Karagulle, D.; Allen, T.; et al. Earth’s coastlines. In GIS for Science: Maps for Saving the Planet; Esri Press: Redlands, CA, USA, 2021; Volume 3, Chapter 1; pp. 4–27. [Google Scholar]
- Wessel, P.; Smith, W.H. A global, self-consistent, hierarchical, high-resolution shoreline database. J. Geophys. Res. Solid Earth 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Patterson, T.; Kelso, N.V.; contributors. Natural Earth: Free Vector and Raster Map Data at 1:10 m, 1:50 m, and 1:110 m Scales. Public Domain. Made with Natural Earth. 2024. Available online: https://www.naturalearthdata.com (accessed on 1 November 2024).
- OpenStreetMap Contributors. Available online: https://www.openstreetmap.org (accessed on 1 November 2024).
- Seale, C.; Redfern, T.; Chatfield, P.; Luo, C.; Dempsey, K. Coastline detection in satellite imagery: A deep learning approach on new benchmark data. Remote Sens. Environ. 2022, 278, 113044. [Google Scholar] [CrossRef]
- Seale, C.; Redfern, T.; Chatfield, P.; Luo, C.; Dempsey, K. Sentinel-2 Water Edges Dataset (SWED). Available online: https://openmldata.ukho.gov.uk/ (accessed on 12 July 2024).
- Yang, T.; Jiang, S.; Hong, Z.; Zhang, Y.; Han, Y.; Zhou, R.; Wang, J.; Yang, S.; Tong, X.; Kuc, T.-y. Sea-land segmentation using deep learning techniques for landsat-8 OLI imagery. Mar. Geod. 2020, 43, 105–133. [Google Scholar] [CrossRef]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A database and web-based tool for image annotation. Int. J. Comput. Vis. 2008, 77, 157–173. [Google Scholar] [CrossRef]
- Erdem, F.; Bayram, B.; Bakirman, T.; Bayrak, O.C.; Akpinar, B. An ensemble deep learning based shoreline segmentation approach (WaterNet) from Landsat 8 OLI images. Adv. Space Res. 2021, 67, 964–974. [Google Scholar] [CrossRef]
- Scarpetta, M.; Spadavecchia, M.; D’Alessandro, V.I.; De Palma, L.; Giaquinto, N. A new dataset of satellite images for deep learning-based coastline measurement. In Proceedings of the 2022 IEEE International Conference on Metrology for Extended Reality, Artificial Intelligence and Neural Engineering (MetroXRAINE), Rome, Italy, 26–28 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 635–640. [Google Scholar]
- Andria, G.; Scarpetta, M.; Spadavecchia, M.; Affuso, P.; Giaquinto, N. SNOWED: Automatically Constructed Dataset of Satellite Imagery for Water Edge Measurements. Sensors 2023, 23, 4491. [Google Scholar] [CrossRef]
- Wernette, P.A.; Buscombe, D.D.; Favela, J.; Fitzpatrick, S.N.; Goldstein, E.; Enwright, N.M.; Dunand, E. Coast Train–Labeled Imagery for Training and Evaluation of Data-Driven Models for Image Segmentation; Data Release, Pacific Coastal and Marine Science Center, U.S. Geological Survey: Reston, VA, USA, 2022. [Google Scholar] [CrossRef]
- Pollard, J.A.; Brooks, S.M.; Spencer, T. Harmonising topographic & remotely sensed datasets, a reference dataset for shoreline and beach change analysis. Sci. Data 2019, 6, 42. [Google Scholar] [PubMed]
- Chi, M.; Plaza, A.; Benediktsson, J.A.; Sun, Z.; Shen, J.; Zhu, Y. Big data for remote sensing: Challenges and opportunities. Proc. IEEE 2016, 104, 2207–2219. [Google Scholar] [CrossRef]
- Gens, R. Remote sensing of coastlines: Detection, extraction and monitoring. Int. J. Remote Sens. 2010, 31, 1819–1836. [Google Scholar] [CrossRef]
- Krogh, A. What are artificial neural networks? Nat. Biotechnol. 2008, 26, 195–197. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Gao, S.; Zhu, Y.; Ma, C. A survey of remote sensing image classification based on CNNs. Big Earth Data 2019, 3, 232–254. [Google Scholar] [CrossRef]
- Yuan, X.; Shi, J.; Gu, L. A review of deep learning methods for semantic segmentation of remote sensing imagery. Expert Syst. Appl. 2021, 169, 114417. [Google Scholar] [CrossRef]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in vision: A survey. ACM Comput. Surv. (CSUR) 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Y.; Liu, X.; Qiu, X. A survey of transformers. AI Open 2022, 3, 111–132. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yu, X.; Zhou, Y. Lstm and gru neural network performance comparison study: Taking yelp review dataset as an example. In Proceedings of the 2020 International Workshop on Electronic Communication and Artificial Intelligence (IWECAI), Shanghai, China, 12–14 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 98–101. [Google Scholar]
- Creswell, A.; White, T.; Dumoulin, V.; Arulkumaran, K.; Sengupta, B.; Bharath, A.A. Generative adversarial networks: An overview. IEEE Signal Process. Mag. 2018, 35, 53–65. [Google Scholar] [CrossRef]
- Çelik, O.İ.; Gazioğlu, C. Coast type based accuracy assessment for coastline extraction from satellite image with machine learning classifiers. Egypt. J. Remote Sens. Space Sci. 2022, 25, 289–299. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, Q.; Xu, J. Coastline extraction using support vector machine from remote sensing image. J. Multim. 2013, 8, 175–182. [Google Scholar]
- Kalkan, K.; Bayram, B.; Maktav, D.; Sunar, F. Comparison of support vector machine and object based classification methods for coastline detection. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 125–127. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Figliomeni, F.G.; Parente, C.; Vallario, A. Machine Learning Approaches for Coastline Extraction from Sentinel-2 Images: K-Means and K-Nearest Neighbour Algorithms in Comparison. In Proceedings of the Italian Conference on Geomatics and Geospatial Technologies, Genova, Italy, 20–24 June 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 368–379. [Google Scholar]
- Guo, Z.; Wu, L.; Huang, Y.; Guo, Z.; Zhao, J.; Li, N. Water-body segmentation for SAR images: Past, current, and future. Remote Sens. 2022, 14, 1752. [Google Scholar] [CrossRef]
- Tajima, Y.; Wu, L.; Watanabe, K. Development of a shoreline detection method using an artificial neural network based on satellite SAR imagery. Remote Sens. 2021, 13, 2254. [Google Scholar] [CrossRef]
- Tajima, Y.; Wu, L.; Fuse, T.; Shimozono, T.; Sato, S. Study on shoreline monitoring system based on satellite SAR imagery. Coast. Eng. J. 2019, 61, 401–421. [Google Scholar] [CrossRef]
- De Laurentiis, L.; Latini, D.; Schiavon, G.; Del Frate, F. Multi-pol sar data fusion for coastline extraction by neural networks chaining. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 2085–2088. [Google Scholar]
- Eckhorn, R.; Reitboeck, H.J.; Arndt, M.; Dicke, P. Feature linking via synchronization among distributed assemblies: Simulations of results from cat visual cortex. Neural Comput. 1990, 2, 293–307. [Google Scholar] [CrossRef]
- Modava, M.; Akbarizadeh, G. Coastline extraction from SAR images using spatial fuzzy clustering and the active contour method. Int. J. Remote Sens. 2017, 38, 355–370. [Google Scholar] [CrossRef]
- Bengoufa, S.; Niculescu, S.; Mihoubi, M.; Belkessa, R.; Abbad, K. Rocky shoreline extraction using a deep learning model and object-based image analysis. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 43, 23–29. [Google Scholar] [CrossRef]
- Baatz, M. Multiresolution segmentation: An optimization approach for high quality multi-scale image segmentation. Angew. Geogr. Informationsverarbeitung 2000, 12–23. Available online: https://cir.nii.ac.jp/crid/1572261550679971840 (accessed on 1 December 2024).
- Boussetta, A.; Niculescu, S.; Bengoufa, S.; Zagrarni, M.F. Deep and machine learning methods for the (semi-) automatic extraction of sandy shoreline and erosion risk assessment basing on remote sensing data (case of Jerba island-Tunisia). Remote Sens. Appl. Soc. Environ. 2023, 32, 101084. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Chang, L.; Chen, Y.T.; Wu, M.C.; Alkhaleefah, M.; Chang, Y.L. U-Net for Taiwan shoreline detection from SAR images. Remote Sens. 2022, 14, 5135. [Google Scholar] [CrossRef]
- An, M.; Sun, Q.; Hu, J.; Tang, Y.; Zhu, Z. Coastline detection with Gaofen-3 SAR images using an improved FCM method. Sensors 2018, 18, 1898. [Google Scholar] [CrossRef] [PubMed]
- You, X.; Li, W. A sea-land segmentation scheme based on statistical model of sea. In Proceedings of the 2011 4th International Congress on Image and Signal Processing, Shanghai, China, 15–17 October 2011; IEEE: Piscataway, NJ, USA, 2011; Volume 3, pp. 1155–1159. [Google Scholar]
- Doan, N.T. Improving the efficiency of using deep learning model to determine shoreline position in high-resolution satellite imagery. In Proceedings of the E3S Web of Conferences, St. Petersburg, Russia, 22–23 April 2021; EDP Sciences: Les Ulis, France, 2021; Volume 310, p. 04002. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Liu, P.; Wang, C.; Ye, M.; Han, R. Coastal Zone Classification Based on U-Net and Remote Sensing. Appl. Sci. 2024, 14, 7050. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Li, R.; Liu, W.; Yang, L.; Sun, S.; Hu, W.; Zhang, F.; Li, W. DeepUNet: A deep fully convolutional network for pixel-level sea-land segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3954–3962. [Google Scholar] [CrossRef]
- Cheng, D.; Meng, G.; Cheng, G.; Pan, C. SeNet: Structured edge network for sea–land segmentation. IEEE Geosci. Remote Sens. Lett. 2016, 14, 247–251. [Google Scholar] [CrossRef]
- Dickens, K.; Armstrong, A. Application of machine learning in satellite derived bathymetry and coastline detection. SMU Data Sci. Rev. 2019, 2, 4. [Google Scholar]
- O’Sullivan, C.; Coveney, S.; Monteys, X.; Dev, S. Interpreting a semantic segmentation model for coastline detection. In Proceedings of the 2023 Photonics & Electromagnetics Research Symposium (PIERS), Prague, Czech Republic, 3–6 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 209–215. [Google Scholar]
- Sun, S.; Mu, L.; Feng, R.; Chen, Y.; Han, W. Quadtree decomposition-based Deep learning method for multiscale coastline extraction with high-resolution remote sensing imagery. Sci. Remote Sens. 2024, 9, 100112. [Google Scholar] [CrossRef]
- Howard, A.; Sandler, M.; Chu, G.; Chen, L.C.; Chen, B.; Tan, M.; Wang, W.; Zhu, Y.; Pang, R.; Vasudevan, V.; et al. Searching for mobilenetv3. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1314–1324. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-ResNet and the impact of residual connections on learning. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; AAAI Press: Washington, DC, USA, 2017. AAAI’17. pp. 4278–4284. [Google Scholar]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–11. [Google Scholar]
- Aghdami-Nia, M.; Shah-Hosseini, R.; Rostami, A.; Homayouni, S. Automatic coastline extraction through enhanced sea-land segmentation by modifying Standard U-Net. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102785. [Google Scholar] [CrossRef]
- Yang, C.; Rottensteiner, F.; Heipke, C. Investigations on skip-connections with an additional cosine similarity loss for land cover classification. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 339–346. [Google Scholar] [CrossRef]
- Jégou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The one hundred layers tiramisu: Fully convolutional densenets for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 11–19. [Google Scholar]
- Dang, K.B.; Dang, V.B.; Ngo, V.L.; Vu, K.C.; Nguyen, H.; Nguyen, D.A.; Nguyen, T.D.L.; Pham, T.P.N.; Giang, T.L.; Nguyen, H.D.; et al. Application of deep learning models to detect coastlines and shorelines. J. Environ. Manag. 2022, 320, 115732. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Zhang, Z.; Huang, C.; Dehghan, M.; Zaiane, O.; Jagersand, M. U2-Net: Going Deeper with Nested U-Structure for Salient Object Detection. Pattern Recognit. 2020, 106, 107404. [Google Scholar] [CrossRef]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.W.; Wu, J. Unet 3+: A full-scale connected unet for medical image segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1055–1059. [Google Scholar]
- Soria, X.; Sappa, A.; Humanante, P.; Akbarinia, A. Dense extreme inception network for edge detection. Pattern Recognit. 2023, 139, 109461. [Google Scholar] [CrossRef]
- Li, X.; Cao, H.; Li, J.; Li, G.; Zhao, L. A shoreline extraction method based on dual-loop network framework. Vis. Comput. 2024, 1–12. [Google Scholar] [CrossRef]
- Xie, S.; Tu, Z. Holistically-nested edge detection. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1395–1403. [Google Scholar]
- Chu, Z.; Tian, T.; Feng, R.; Wang, L. Sea-land segmentation with Res-UNet and fully connected CRF. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3840–3843. [Google Scholar]
- Shamsolmoali, P.; Zareapoor, M.; Wang, R.; Zhou, H.; Yang, J. A novel deep structure U-Net for sea-land segmentation in remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3219–3232. [Google Scholar] [CrossRef]
- Labelbox. 2025. Available online: https://labelbox.com (accessed on 1 November 2024).
- Basaeed, E.; Bhaskar, H.; Hill, P.; Al-Mualla, M.; Bull, D. A supervised hierarchical segmentation of remote-sensing images using a committee of multi-scale convolutional neural networks. Int. J. Remote Sens. 2016, 37, 1671–1691. [Google Scholar] [CrossRef]
- Quan, T.M.; Hildebrand, D.G.C.; Jeong, W.K. Fusionnet: A deep fully residual convolutional neural network for image segmentation in connectomics. Front. Comput. Sci. 2021, 3, 613981. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Nogueira, K.; Dalla Mura, M.; Chanussot, J.; Schwartz, W.R.; dos Santos, J.A. Dynamic Multicontext Segmentation of Remote Sensing Images Based on Convolutional Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7503–7520. [Google Scholar] [CrossRef]
- Wu, L.; Ishikawa, S.; Inazu, D.; Ikeya, T.; Okayasu, A. An automatic shoreline extraction method from SAR imagery using DeepLab-v3+ and its versatility. Coast. Eng. J. 2024, 1–13. [Google Scholar] [CrossRef]
- Chen, L.C. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar]
- Vos, K.; Harley, M.D.; Splinter, K.D.; Simmons, J.A.; Turner, I.L. Sub-annual to multi-decadal shoreline variability from publicly available satellite imagery. Coast. Eng. 2019, 150, 160–174. [Google Scholar] [CrossRef]
- Scala, P.; Manno, G.; Ciraolo, G. Semantic segmentation of coastal aerial/satellite images using deep learning techniques: An application to coastline detection. Comput. Geosci. 2024, 192, 105704. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2017; pp. 2881–2890. [Google Scholar]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. Refinenet: Multi-path refinement networks for high-resolution semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1925–1934. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 248–255. [Google Scholar]
- Blais, M.A.; Akhloufi, M.A. Deep learning for low altitude coastline segmentation. In Proceedings of the Ocean Sensing and Monitoring XIII, Online, 12–16 April 2021; SPIE: San Francisco, CA, USA, 2021; Volume 11752, pp. 103–111. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Chaurasia, A.; Culurciello, E. Linknet: Exploiting encoder representations for efficient semantic segmentation. In Proceedings of the 2017 IEEE Visual Communications and Image Processing (VCIP), St. Petersburg, FL, USA, 10–13 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018; pp. 7132–7141. [Google Scholar]
- Poliyapram, V.; Imamoglu, N.; Nakamura, R. Deep Learning Model for Water/Ice/Land Classification Using Large-Scale Medium Resolution Satellite Images. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 3884–3887. [Google Scholar] [CrossRef]
- Liciotti, D.; Paolanti, M.; Pietrini, R.; Frontoni, E.; Zingaretti, P. Convolutional Networks for Semantic Heads Segmentation using Top-View Depth Data in Crowded Environment. In Proceedings of the 2018 24th International Conference on Pattern Recognition (ICPR), Beijing, China, 20–24 August 2018; pp. 1384–1389. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5967–5976. [Google Scholar] [CrossRef]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Hurtik, P.; Vajgl, M. Coastline extraction from ALOS-2 satellite SAR images. Remote Sens. Lett. 2021, 12, 879–889. [Google Scholar] [CrossRef]
- Signate; JAXA. The 4th Tellus Satellite Challenge: Coastline Detection. Available online: https://signate.jp/competitions/284 (accessed on 12 July 2024).
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; PMLR: Seattle, WA, USA, 2019; pp. 6105–6114. [Google Scholar]
- Philipp, M.; Dietz, A.; Ullmann, T.; Kuenzer, C. Automated extraction of annual erosion rates for Arctic permafrost coasts using Sentinel-1, deep learning, and change vector analysis. Remote Sens. 2022, 14, 3656. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar]
- Cui, B.; Jing, W.; Huang, L.; Li, Z.; Lu, Y. SANet: A sea–land segmentation network via adaptive multiscale feature learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 116–126. [Google Scholar] [CrossRef]
- Liu, T.; Liu, P.; Jia, X.; Chen, S.; Ma, Y.; Gao, Q. Sea-Land Segmentation of Remote Sensing Images Based on SDW-UNet. Comput. Syst. Sci. Eng. 2023, 45, 1033–1045. [Google Scholar] [CrossRef]
- Oktay, O. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- Li, J.; Huang, Z.; Wang, Y.; Luo, Q. Sea and land segmentation of optical remote sensing images based on u-net optimization. Remote Sens. 2022, 14, 4163. [Google Scholar] [CrossRef]
- Gallego, A.J.; Pertusa, A.; Gil, P. Automatic ship classification from optical aerial images with convolutional neural networks. Remote Sens. 2018, 10, 511. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote sensing image scene classification: Benchmark and state of the art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Chang, L.; Chen, Y.T. Performance Evaluation and Improvement of Shoreline Detection Using Sentinel-1 SAR and DEM Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 8139–8152. [Google Scholar] [CrossRef]
- Wei, G.; Xu, J.; Chong, Q.; Huang, J. FMPNet: A fuzzy-embedded multi-scale prototype network for sea-land segmentation of remote sensing images. Eur. J. Remote Sens. 2024, 57, 2343531. [Google Scholar] [CrossRef]
- Chong, Q.; Xu, J.; Jia, F.; Liu, Z.; Yan, W.; Wang, X.; Song, Y. A multiscale fuzzy dual-domain attention network for urban remote sensing image segmentation. Int. J. Remote Sens. 2022, 43, 5480–5501. [Google Scholar] [CrossRef]
- Park, S.; Song, A. Shoreline change analysis with Deep Learning Semantic Segmentation using remote sensing and GIS data. KSCE J. Civ. Eng. 2024, 28, 928–938. [Google Scholar] [CrossRef]
- Ji, X.; Tang, L.; Lu, T.; Cai, C. DBENet: Dual-Branch Ensemble Network for Sea–Land Segmentation of Remote-Sensing Images. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, H.; Weng, L.; Yang, Y. Ship rotated bounding box space for ship extraction from high-resolution optical satellite images with complex backgrounds. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1074–1078. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Li, H.; Xiong, P.; Fan, H.; Sun, J. DFANet: Deep Feature Aggregation for Real-Time Semantic Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Lv, Q.; Wang, Q.; Song, X.; Ge, B.; Guan, H.; Lu, T.; Tao, Z. Research on coastline extraction and dynamic change from remote sensing images based on deep learning. Front. Environ. Sci. 2024, 12, 1443512. [Google Scholar] [CrossRef]
- Guo, X.; O’Neill, W.C.; Vey, B.; Yang, T.C.; Kim, T.J.; Ghassemi, M.; Pan, I.; Gichoya, J.W.; Trivedi, H.; Banerjee, I. SCU-Net: A deep learning method for segmentation and quantification of breast arterial calcifications on mammograms. Med. Phys. 2021, 48, 5851–5861. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, S.; Peng, Y.; Li, J. DenseUNet: Densely connected UNet for electron microscopy image segmentation. IET Image Process. 2020, 14, 2682–2689. [Google Scholar] [CrossRef]
- Ji, X.; Tang, L.; Chen, L.; Hao, L.Y.; Guo, H. Toward efficient and lightweight sea–land segmentation for remote sensing images. Eng. Appl. Artif. Intell. 2024, 135, 108782. [Google Scholar] [CrossRef]
- Ibtehaz, N.; Kihara, D. Acc-unet: A completely convolutional unet model for the 2020s. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Vancouver, BC, Canada, 8–12 October 2023; Springer: Berlin/Heidelberg, Germany, 2023; pp. 692–702. [Google Scholar]
- Xu, Q.; Ma, Z.; He, N.; Duan, W. DCSAU-Net: A Deeper and More Compact Split-Attention U-Net for Medical Image Segmentation. Comput. Biol. Med. 2023, 154, 106626. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.; Wen, Y.; Li, Y.; Mao, Q.; Zhai, Y. Sea-land segmentation method based on an improved MA-Net for Gaofen-2 images. Earth Sci. Inform. 2024, 17, 4115–4129. [Google Scholar] [CrossRef]
- da Costa, L.B.; de Carvalho, O.L.F.; de Albuquerque, A.O.; Gomes, R.A.T.; Guimarães, R.F.; de Carvalho Júnior, O.A. Deep semantic segmentation for detecting eucalyptus planted forests in the Brazilian territory using sentinel-2 imagery. Geocarto Int. 2022, 37, 6538–6550. [Google Scholar] [CrossRef]
- Xu, J.; Li, J.; Zhao, X.; Luan, K.; Yi, C.; Wang, Z. DANet-SMIW: An Improved Model for Island Waterline Segmentation Based on DANet. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 884–893. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3146–3154. [Google Scholar]
- Yang, M.; Yu, K.; Zhang, C.; Li, Z.; Yang, K. Denseaspp for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3684–3692. [Google Scholar]
- Zhao, H.; Zhang, Y.; Liu, S.; Shi, J.; Loy, C.C.; Lin, D.; Jia, J. Psanet: Point-wise spatial attention network for scene parsing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 267–283. [Google Scholar]
- Zhao, H.; Qi, X.; Shen, X.; Shi, J.; Jia, J. Icnet for real-time semantic segmentation on high-resolution images. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 405–420. [Google Scholar]
- Jin, Q.; Meng, Z.; Pham, T.D.; Chen, Q.; Wei, L.; Su, R. DUNet: A deformable network for retinal vessel segmentation. Knowl.-Based Syst. 2019, 178, 149–162. [Google Scholar] [CrossRef]
- Ma, T.J. Remote sensing detection enhancement. J. Big Data 2021, 8, 127. [Google Scholar] [CrossRef]
- Tong, Q.; Wu, J.; Zhu, Z.; Zhang, M.; Xing, H. STIRUnet: SwinTransformer and inverted residual convolution embedding in unet for Sea–Land segmentation. J. Environ. Manag. 2024, 357, 120773. [Google Scholar] [CrossRef]
- Yang, F.; Feng, T.; Xu, G.; Chen, Y. Applied method for water-body segmentation based on mask R-CNN. J. Appl. Remote Sens. 2020, 14, 014502. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Virtual, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 205–218. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and efficient design for semantic segmentation with transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 12077–12090. [Google Scholar]
- Zhu, Y.; Wang, B.; Liu, Q.; Tan, S.; Wang, S.; Ge, W. SRMA: A dual-branch parallel multi-scale attention network for remote sensing images sea-land segmentation. Int. J. Remote Sens. 2024, 45, 3370–3395. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, X.; Zhang, J.; Huang, B.; Du, R. TCUNet: A Lightweight Dual-Branch Parallel Network for Sea–Land Segmentation in Remote Sensing Images. Remote Sens. 2023, 15, 4413. [Google Scholar] [CrossRef]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pvt v2: Improved baselines with pyramid vision transformer. Comput. Vis. Media 2022, 8, 415–424. [Google Scholar] [CrossRef]
- He, X.; Zhou, Y.; Zhao, J.; Zhang, D.; Yao, R.; Xue, Y. Swin transformer embedding UNet for remote sensing image semantic segmentation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Wang, L.; Li, R.; Zhang, C.; Fang, S.; Duan, C.; Meng, X.; Atkinson, P.M. UNetFormer: A UNet-like transformer for efficient semantic segmentation of remote sensing urban scene imagery. ISPRS J. Photogramm. Remote Sens. 2022, 190, 196–214. [Google Scholar] [CrossRef]
- Huang, Y. ViT-r50 GAN: Vision transformers hybrid model based generative adversarial networks for image generation. In Proceedings of the 2023 3rd International Conference on Consumer Electronics and Computer Engineering (ICCECE), Guangzhou, China, 6–8 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 590–593. [Google Scholar]
- Sun, W.; Chen, C.; Liu, W.; Yang, G.; Meng, X.; Wang, L.; Ren, K. Coastline extraction using remote sensing: A review. GIScience Remote Sens. 2023, 60, 2243671. [Google Scholar] [CrossRef]
- Ciecholewski, M. Review of Segmentation Methods for Coastline Detection in SAR Images. Arch. Comput. Methods Eng. 2024, 31, 839–869. [Google Scholar] [CrossRef]
- Passarello, G.; Vitale, S.; Ferraioli, G.; Schirinzi, G.; Pascazio, V. Coastline Extraction Using SAR Images and Deep Learning. In Proceedings of the IGARSS 2024-2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 6072–6075. [Google Scholar]
- Zhang, S.; Xu, Q.; Wang, H.; Kang, Y.; Li, X. Automatic waterline extraction and topographic mapping of tidal flats from SAR images based on deep learning. Geophys. Res. Lett. 2022, 49, e2021GL096007. [Google Scholar] [CrossRef]
- Liu, X.Y.; Jia, R.S.; Liu, Q.M.; Zhao, C.Y.; Sun, H.M. Coastline extraction method based on convolutional neural networks—A case study of Jiaozhou Bay in Qingdao, China. IEEE Access 2019, 7, 180281–180291. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, M.M.; Hu, X.; Wang, K.; Bai, X. Richer Convolutional Features for Edge Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ha, Q.; Watanabe, K.; Karasawa, T.; Ushiku, Y.; Harada, T. MFNet: Towards real-time semantic segmentation for autonomous vehicles with multi-spectral scenes. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5108–5115. [Google Scholar]
- Arbeláez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 898–916. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Wang, G.; Feng, L.; Wang, Y.; Wang, G.; Liang, S. A Transformer Model for Coastline Prediction in Weitou Bay, China. Remote Sens. 2023, 15, 4771. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, X.; Ran, J.; Liu, L.; Wang, Q.; Xin, L.; Li, G. LaeNet: A novel lightweight multitask CNN for automatically extracting lake area and shoreline from remote sensing images. Remote Sens. 2020, 13, 56. [Google Scholar] [CrossRef]
- Mohajerani, S.; Saeedi, P. Cloud-Net: An end-to-end cloud detection algorithm for Landsat 8 imagery. In Proceedings of the IGARSS 2019-2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1029–1032. [Google Scholar]
- Noh, H.; Hong, S.; Han, B. Learning deconvolution network for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1520–1528. [Google Scholar]
- Liu, H.; Jezek, K. Automated extraction of coastline from satellite imagery by integrating Canny edge detection and locally adaptive thresholding methods. Int. J. Remote Sens. 2004, 25, 937–958. [Google Scholar] [CrossRef]
- Li, Z.R.; Cui, B.G.; Yang, G.; Zhang, H.Q. A coastline edge detection network based on deep learning. Comput. Eng. Sci. 2022, 44, 2220. [Google Scholar]
- Jing, W.; Cui, B.; Lu, Y.; Huang, L. BS-Net: Using joint-learning boundary and segmentation network for coastline extraction from remote sensing images. Remote Sens. Lett. 2021, 12, 1260–1268. [Google Scholar] [CrossRef]
- Heidler, K.; Mou, L.; Baumhoer, C.; Dietz, A.; Zhu, X.X. HED-UNet: Combined segmentation and edge detection for monitoring the Antarctic coastline. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–14. [Google Scholar] [CrossRef]
- Liu, H.; Jezek, K.C. A complete high-resolution coastline of Antarctica extracted from orthorectified Radarsat SAR imagery. Photogramm. Eng. Remote Sens. 2004, 70, 605–616. [Google Scholar] [CrossRef]
- Schmitt, M.; Baier, G.; Zhu, X.X. Potential of nonlocally filtered pursuit monostatic TanDEM-X data for coastline detection. ISPRS J. Photogramm. Remote Sens. 2019, 148, 130–141. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, I. Coastline detection and tracing in SAR images. IEEE Trans. Geosci. Remote Sens. 1990, 28, 662–668. [Google Scholar]
- Chan, T.; Vese, L. An active contour model without edges. In Proceedings of the International Conference on Scale-Space Theories in Computer Vision, Corfu, Greece, 26–27 September 1999; Springer: Berlin/Heidelberg, Germany, 1999; pp. 141–151. [Google Scholar]
- Yuan, Y.; Chen, X.; Wang, J. Object-contextual representations for semantic segmentation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part VI 16. Springer: Berlin/Heidelberg, Germany, 2020; pp. 173–190. [Google Scholar]
- Takikawa, T.; Acuna, D.; Jampani, V.; Fidler, S. Gated-scnn: Gated shape cnns for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 5229–5238. [Google Scholar]
- Feng, J.; Wang, S.; Gu, Z. A Novel Sea-Land Segmentation Network for Enhanced Coastline Extraction using Satellite Remote Sensing Images. Adv. Space Res. 2024, 74, 2200–2213. [Google Scholar] [CrossRef]
- Ding, L.; Tang, H.; Bruzzone, L. LANet: Local attention embedding to improve the semantic segmentation of remote sensing images. IEEE Trans. Geosci. Remote Sens. 2020, 59, 426–435. [Google Scholar] [CrossRef]
- Tseng, S.H.; Sun, W.H. Sea–Land Segmentation Using HED-UNET for Monitoring Kaohsiung Port. Mathematics 2022, 10, 4202. [Google Scholar] [CrossRef]
- Kingma, D.P. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Vos, K.; Splinter, K.D.; Harley, M.D.; Simmons, J.A.; Turner, I.L. CoastSat: A Google Earth Engine-enabled Python toolkit to extract shorelines from publicly available satellite imagery. Environ. Model. Softw. 2019, 122, 104528. [Google Scholar] [CrossRef]
- Riu, G.; Al Najar, M.; Thoumyre, G.; Almar, R.; Wilson, D.G. Global Coastline Evolution Forecasting from Satellite Imagery using Deep Learning. In Proceedings of the NeurIPS 2023 Workshop on Tackling Climate Change with Machine Learning: Blending New and Existing Knowledge Systems, New Orleans, LA, USA, 16 December 2023. [Google Scholar]
- Almar, R.; Boucharel, J.; Graffin, M.; Abessolo, G.O.; Thoumyre, G.; Papa, F.; Ranasinghe, R.; Montano, J.; Bergsma, E.W.; Baba, M.W.; et al. Influence of El Niño on the variability of global shoreline position. Nat. Commun. 2023, 14, 3133. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Li, Y.; Wang, X. Integrating a multi-variable scenario with Attention-LSTM model to forecast long-term coastal beach erosion. Sci. Total Environ. 2024, 954, 176257. [Google Scholar] [CrossRef] [PubMed]
- Koroglu, A.; Ranasinghe, R.; Jiménez, J.A.; Dastgheib, A. Comparison of coastal vulnerability index applications for Barcelona Province. Ocean. Coast. Manag. 2019, 178, 104799. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Riefolo, L.; Principato, F.; Tomasicchio, G.R. Application of a coastal vulnerability index. A case study along the Apulian Coastline, Italy. Water 2018, 10, 1218. [Google Scholar] [CrossRef]
- Pantusa, D.; D’Alessandro, F.; Frega, F.; Francone, A.; Tomasicchio, G.R. Improvement of a coastal vulnerability index and its application along the Calabria Coastline, Italy. Sci. Rep. 2022, 12, 21959. [Google Scholar] [CrossRef] [PubMed]
- Boumboulis, V.; Apostolopoulos, D.; Depountis, N.; Nikolakopoulos, K. The importance of geotechnical evaluation and shoreline evolution in coastal vulnerability index calculations. J. Mar. Sci. Eng. 2021, 9, 423. [Google Scholar] [CrossRef]
- Manno, G.; Azzara, G.; Lo Re, C.; Martinello, C.; Basile, M.; Rotigliano, E.; Ciraolo, G. An Approach for the Validation of a Coastal Erosion Vulnerability Index: An Application in Sicily. J. Mar. Sci. Eng. 2022, 11, 23. [Google Scholar] [CrossRef]
- Dike, E.C.; Amaechi, C.V.; Beddu, S.B.; Weje, I.I.; Ameme, B.G.; Efeovbokhan, O.; Oyetunji, A.K. Coastal Vulnerability Index sensitivity to shoreline position and coastal elevation parameters in the Niger Delta region, Nigeria. Sci. Total Environ. 2024, 919, 170830. [Google Scholar] [CrossRef] [PubMed]
- Maanan, M.; Maanan, M.; Rueff, H.; Adouk, N.; Zourarah, B.; Rhinane, H. Assess the human and environmental vulnerability for coastal hazard by using a multi-criteria decision analysis. Hum. Ecol. Risk Assess. Int. J. 2018, 24, 1642–1658. [Google Scholar] [CrossRef]
- Mullick, M.R.A.; Tanim, A.; Islam, S.S. Coastal vulnerability analysis of Bangladesh coast using fuzzy logic based geospatial techniques. Ocean. Coast. Manag. 2019, 174, 154–169. [Google Scholar] [CrossRef]
- de Andrade, T.S.; de Oliveira Sousa, P.H.G.; Siegle, E. Vulnerability to beach erosion based on a coastal processes approach. Appl. Geogr. 2019, 102, 12–19. [Google Scholar] [CrossRef]
- Panagiotou, E.; Chochlakis, G.; Grammatikopoulos, L.; Charou, E. Generating elevation surface from a single rgb remotely sensed image using deep learning. Remote Sens. 2020, 12, 2002. [Google Scholar] [CrossRef]
- Recla, M.; Schmitt, M. Deep Learning-based DSM Generation from Dual-Aspect SAR Data. ISPRS Ann. Photogramm Remote Sens. Spat. Inf. Sci. 2024, 10, 193–200. [Google Scholar] [CrossRef]
- Abdela, N. Deep Learning-Based Digital Surface Model (DSM) Generation Using SAR Image and Building Footprint Data. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2023. [Google Scholar]
- Zhong, J.; Sun, J.; Lai, Z.; Song, Y. Nearshore bathymetry from ICESat-2 LiDAR and Sentinel-2 imagery datasets using deep learning approach. Remote Sens. 2022, 14, 4229. [Google Scholar] [CrossRef]
- Al Najar, M.; Thoumyre, G.; Bergsma, E.W.; Almar, R.; Benshila, R.; Wilson, D.G. Satellite derived bathymetry using deep learning. Mach. Learn. 2023, 112, 1107–1130. [Google Scholar] [CrossRef]
- Zhao, S.; Tu, K.; Ye, S.; Tang, H.; Hu, Y.; Xie, C. Land use and land cover classification meets deep learning: A review. Sensors 2023, 23, 8966. [Google Scholar] [CrossRef] [PubMed]
- Alem, A.; Kumar, S. Deep learning methods for land cover and land use classification in remote sensing: A review. In Proceedings of the 2020 8th International Conference on Reliability, Infocom Technologies and Optimization (Trends and Future Directions)(ICRITO), Noida, India, 4–5 June 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 903–908. [Google Scholar]
- Moharram, M.A.; Sundaram, D.M. Land use and land cover classification with hyperspectral data: A comprehensive review of methods, challenges and future directions. Neurocomputing 2023, 536, 90–113. [Google Scholar] [CrossRef]
- Wang, J.; Bretz, M.; Dewan, M.A.A.; Delavar, M.A. Machine learning in modelling land-use and land cover-change (LULCC): Current status, challenges and prospects. Sci. Total Environ. 2022, 822, 153559. [Google Scholar] [CrossRef] [PubMed]
- Zaabar, N.; Niculescu, S.; Kamel, M.M. Application of convolutional neural networks with object-based image analysis for land cover and land use mapping in coastal areas: A case study in Ain Témouchent, Algeria. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5177–5189. [Google Scholar] [CrossRef]
- Naik, N.; Chandrasekaran, K.; Meenakshi Sundaram, V.; Panneer, P. Assessment of land use and land cover change detection and prediction using deep learning techniques for the southwestern coastal region, Goa, India. Environ. Monit. Assess. 2024, 196, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Bentivoglio, R.; Isufi, E.; Jonkman, S.N.; Taormina, R. Deep learning methods for flood mapping: A review of existing applications and future research directions. Hydrol. Earth Syst. Sci. Discuss. 2022, 2022, 1–50. [Google Scholar] [CrossRef]
- Bui, D.T.; Hoang, N.D.; Martínez-Álvarez, F.; Ngo, P.T.T.; Hoa, P.V.; Pham, T.D.; Samui, P.; Costache, R. A novel deep learning neural network approach for predicting flash flood susceptibility: A case study at a high frequency tropical storm area. Sci. Total Environ. 2020, 701, 134413. [Google Scholar]
- Toure, S.; Diop, O.; Kpalma, K.; Maiga, A.S. Shoreline detection using optical remote sensing: A review. ISPRS Int. J.-Geo-Inf. 2019, 8, 75. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.; Zheng, F.; Wang, H.; Yang, H. An Overview of Coastline Extraction from Remote Sensing Data. Remote Sens. 2023, 15, 4865. [Google Scholar] [CrossRef]
- Salmona, A.; Bouza, L.; Delon, J. Deoldify: A review and implementation of an automatic colorization method. Image Process. Line 2022, 12, 347–368. [Google Scholar] [CrossRef]
- Zhang, Y.; Wetherill, B.R.; Chen, R.F.; Peri, F.; Rosen, P.; Little, T.D. Design and implementation of a wireless video camera network for coastal erosion monitoring. Ecol. Inform. 2014, 23, 98–106. [Google Scholar] [CrossRef]
- McCarroll, R.J.; Kennedy, D.M.; Liu, J.; Allan, B.; Ierodiaconou, D. Design and application of coastal erosion indicators using satellite and drone data for a regional monitoring program. Ocean. Coast. Manag. 2024, 253, 107146. [Google Scholar] [CrossRef]
- Young, S.S.; Rao, S.; Dorey, K. Monitoring the erosion and accretion of a human-built living shoreline with drone technology. Environ. Challenges 2021, 5, 100383. [Google Scholar] [CrossRef]
- Maguire, C. Using Unmanned Aerial Vehicles and “Structure from Motion” Software to Monitor Coastal Erosion in Southeast Florida. Ph.D. Thesis, University of Miami, Coral Gables, FL, USA, 2014. [Google Scholar]
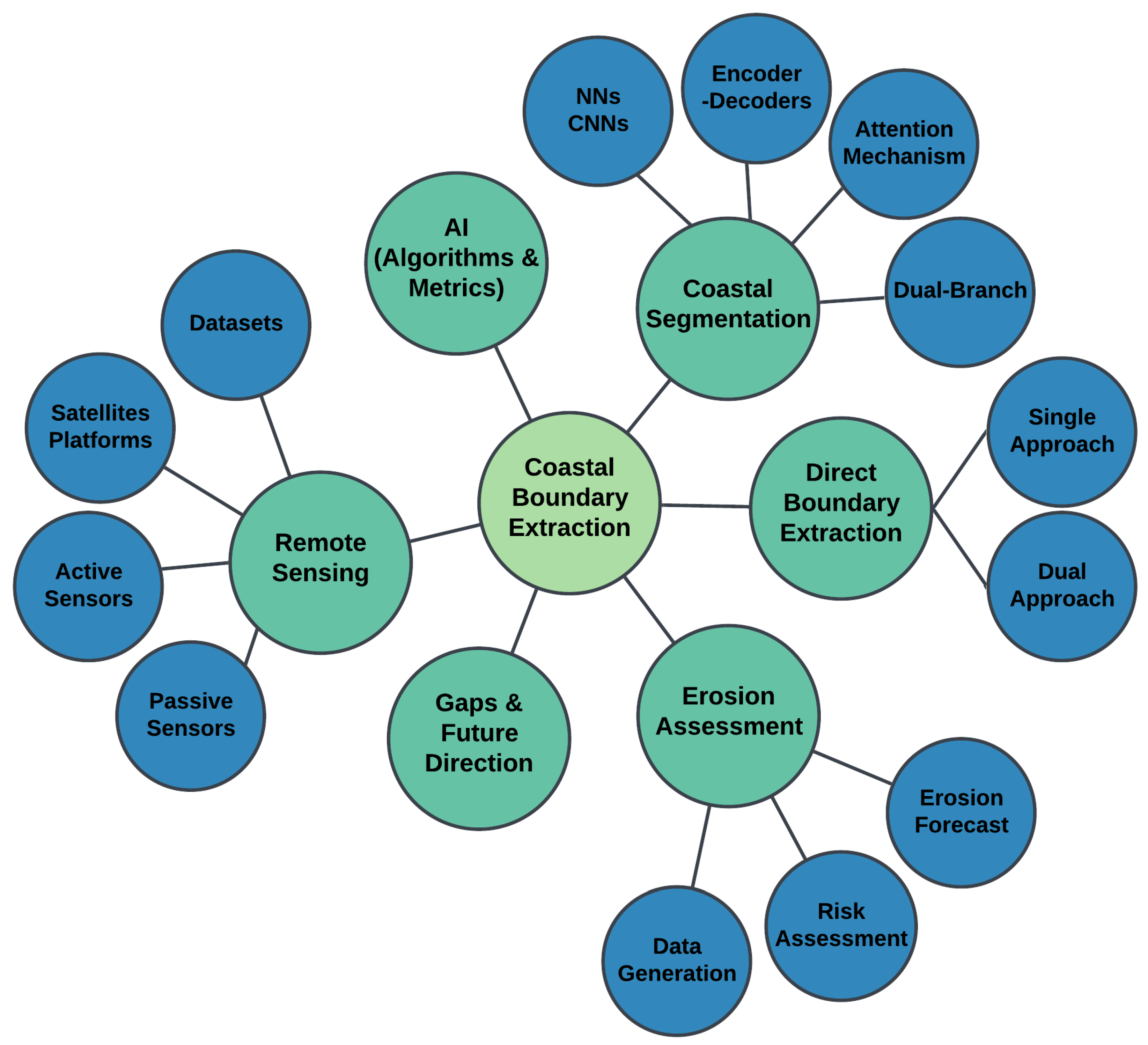
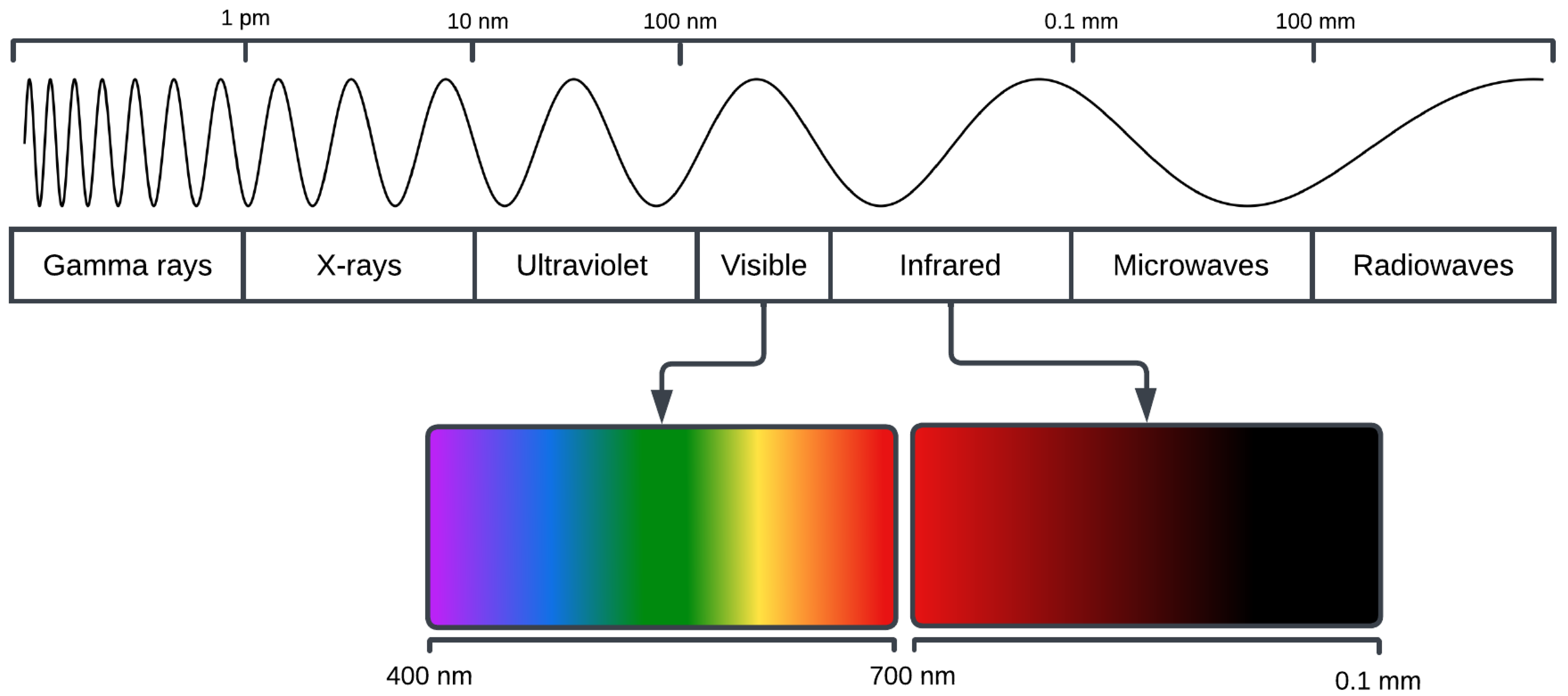




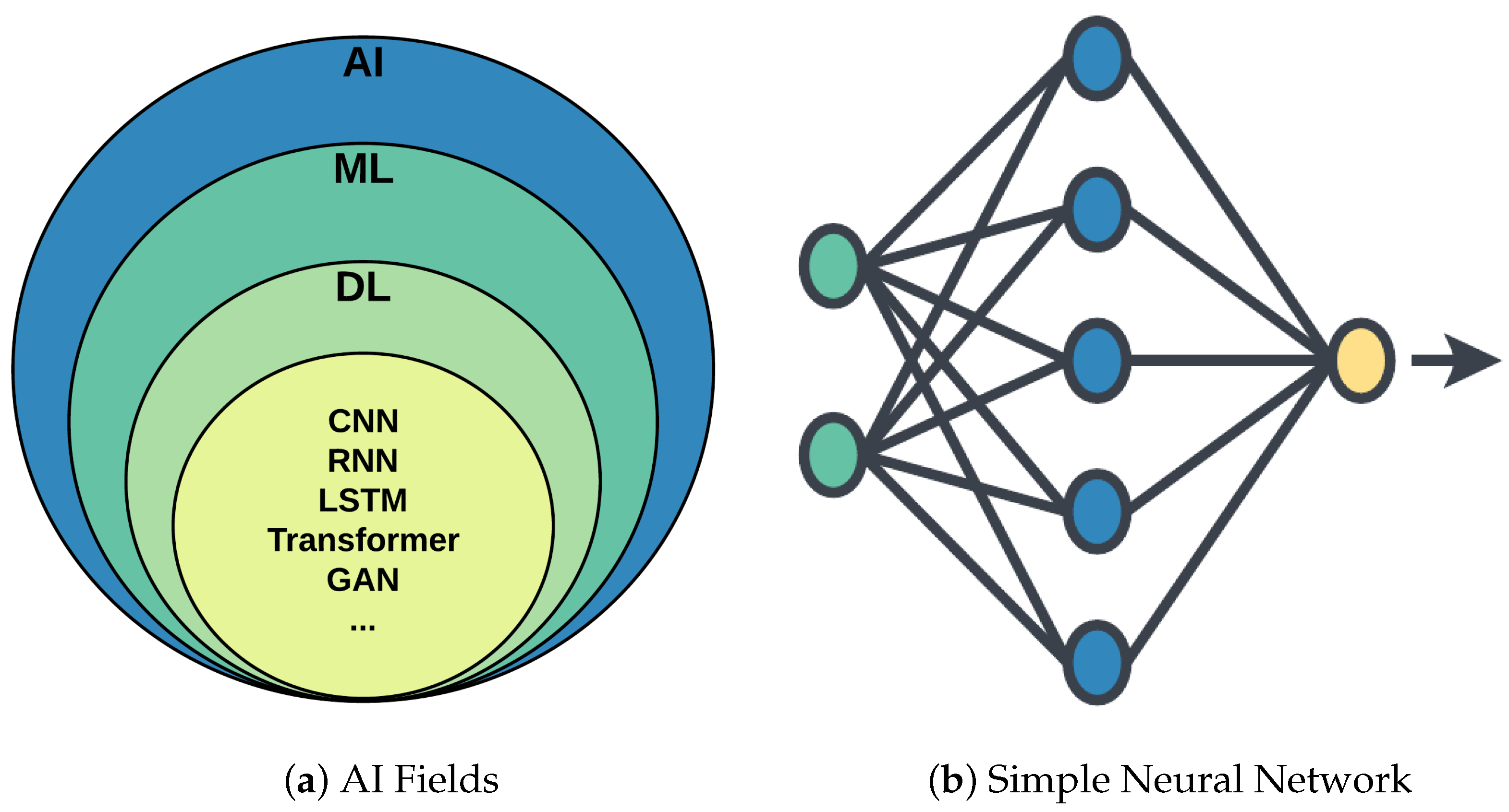
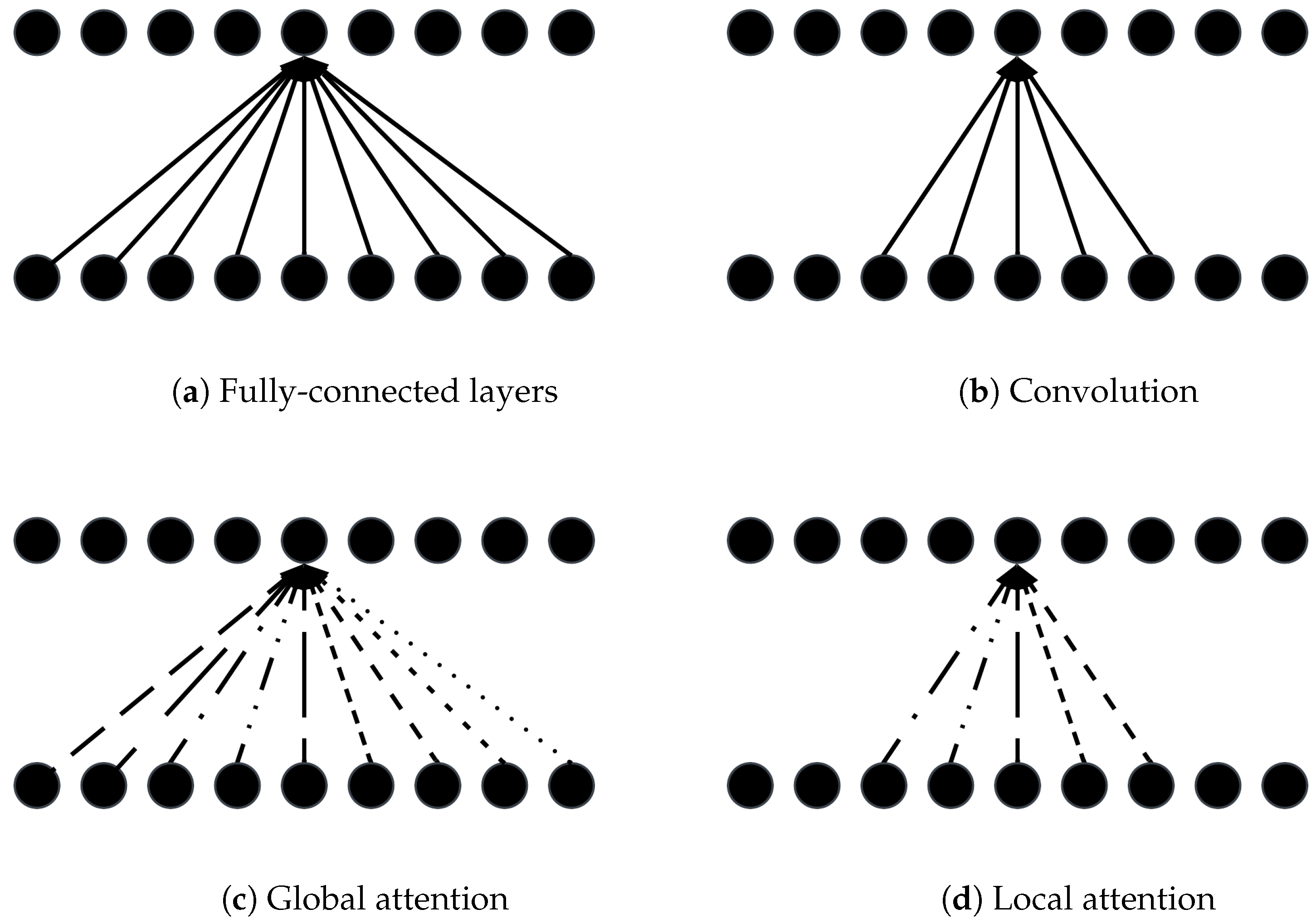
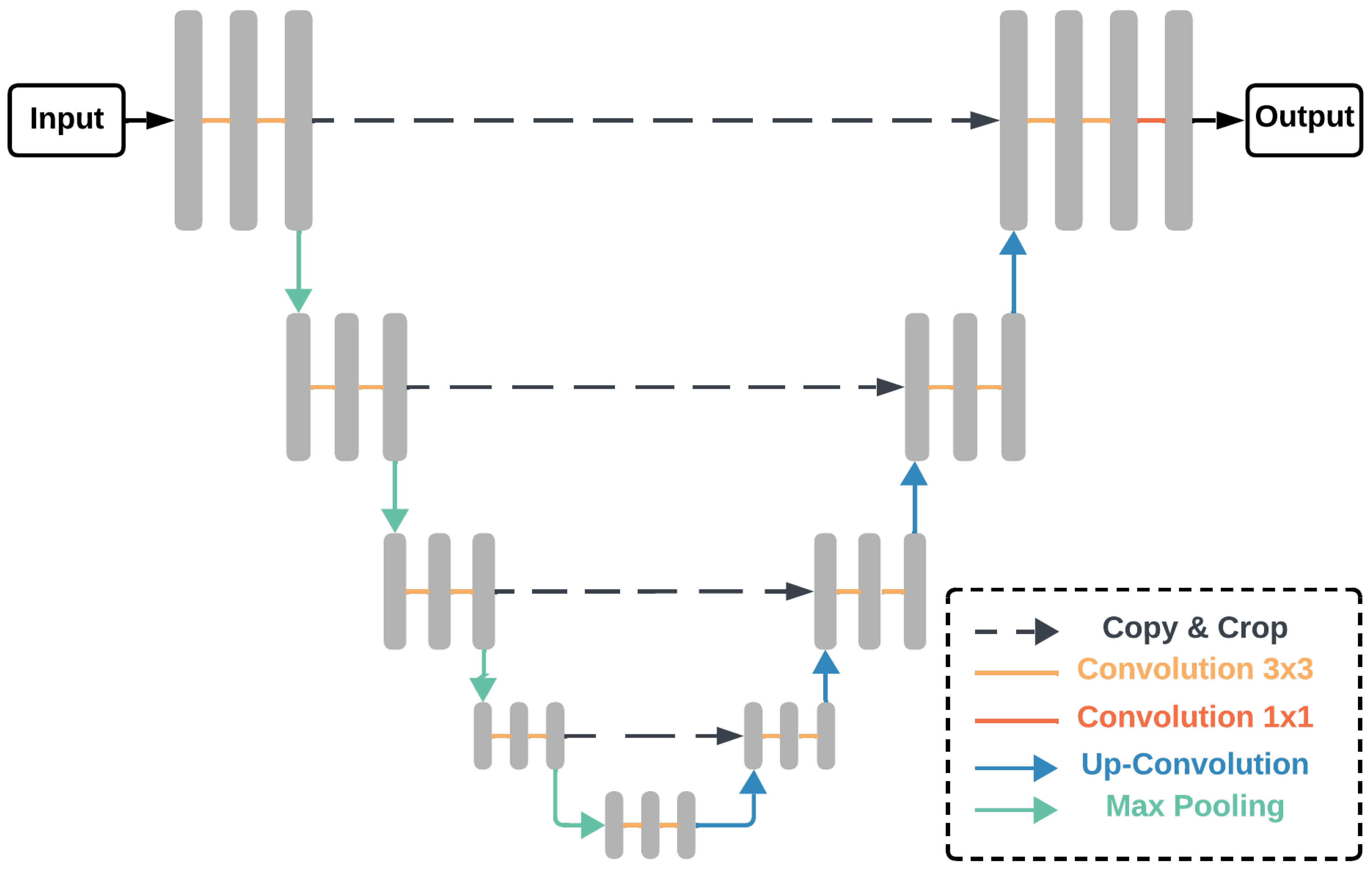
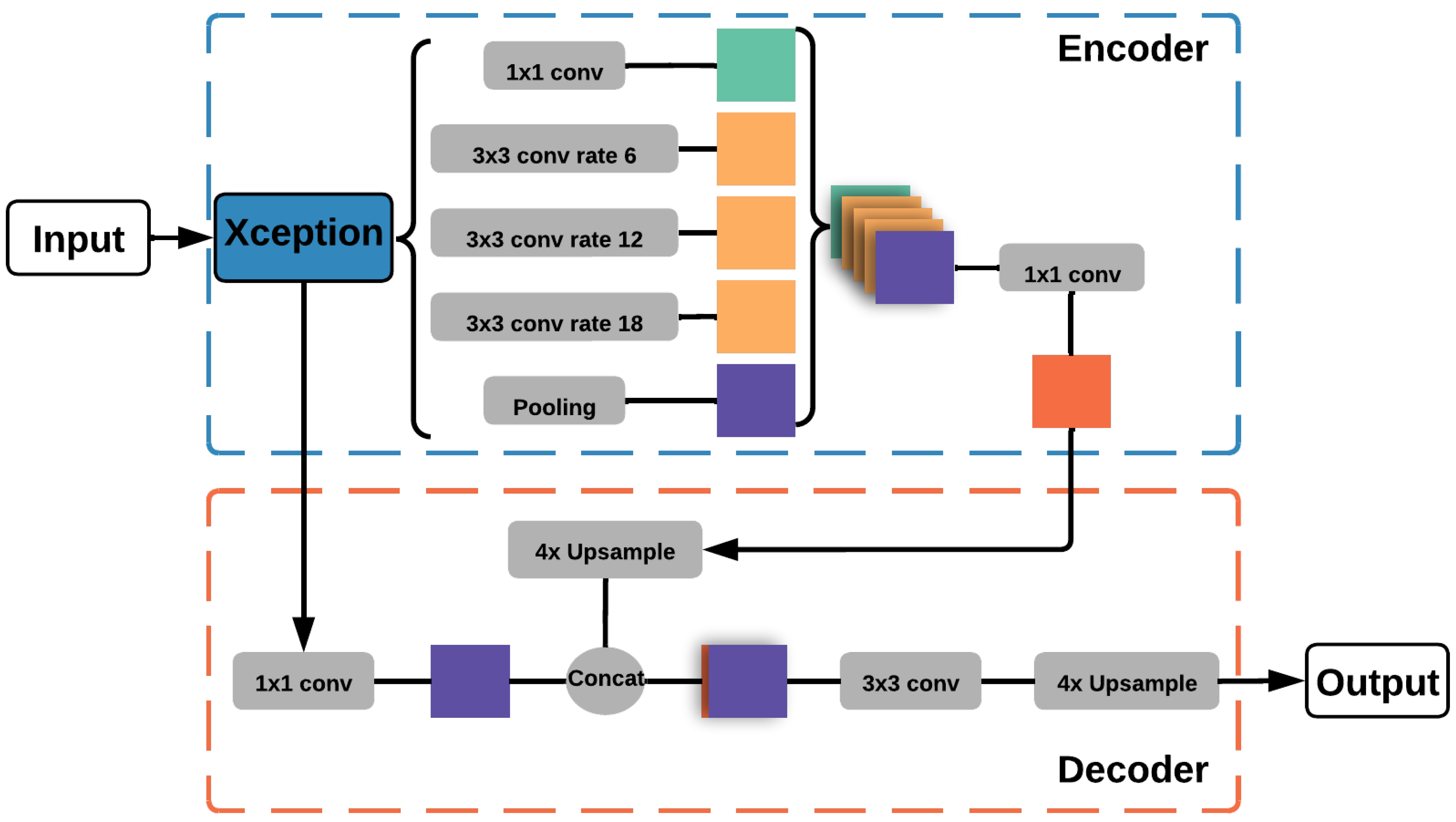

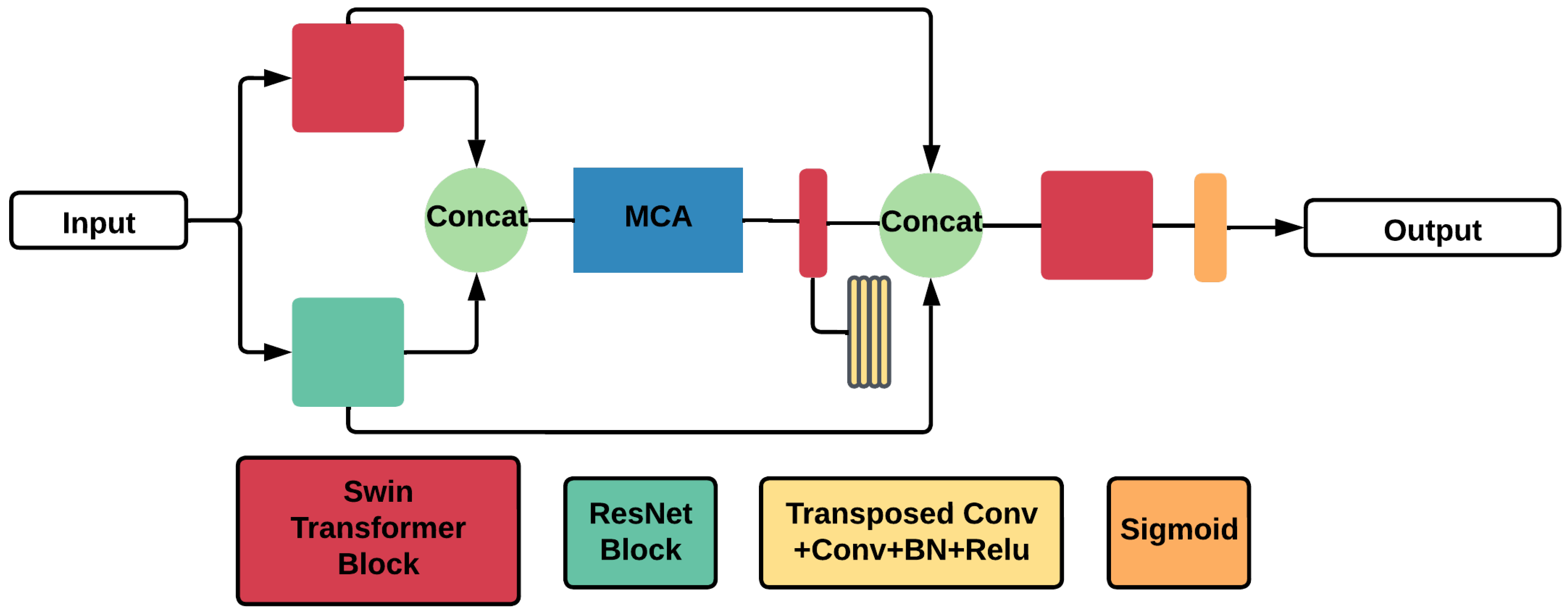

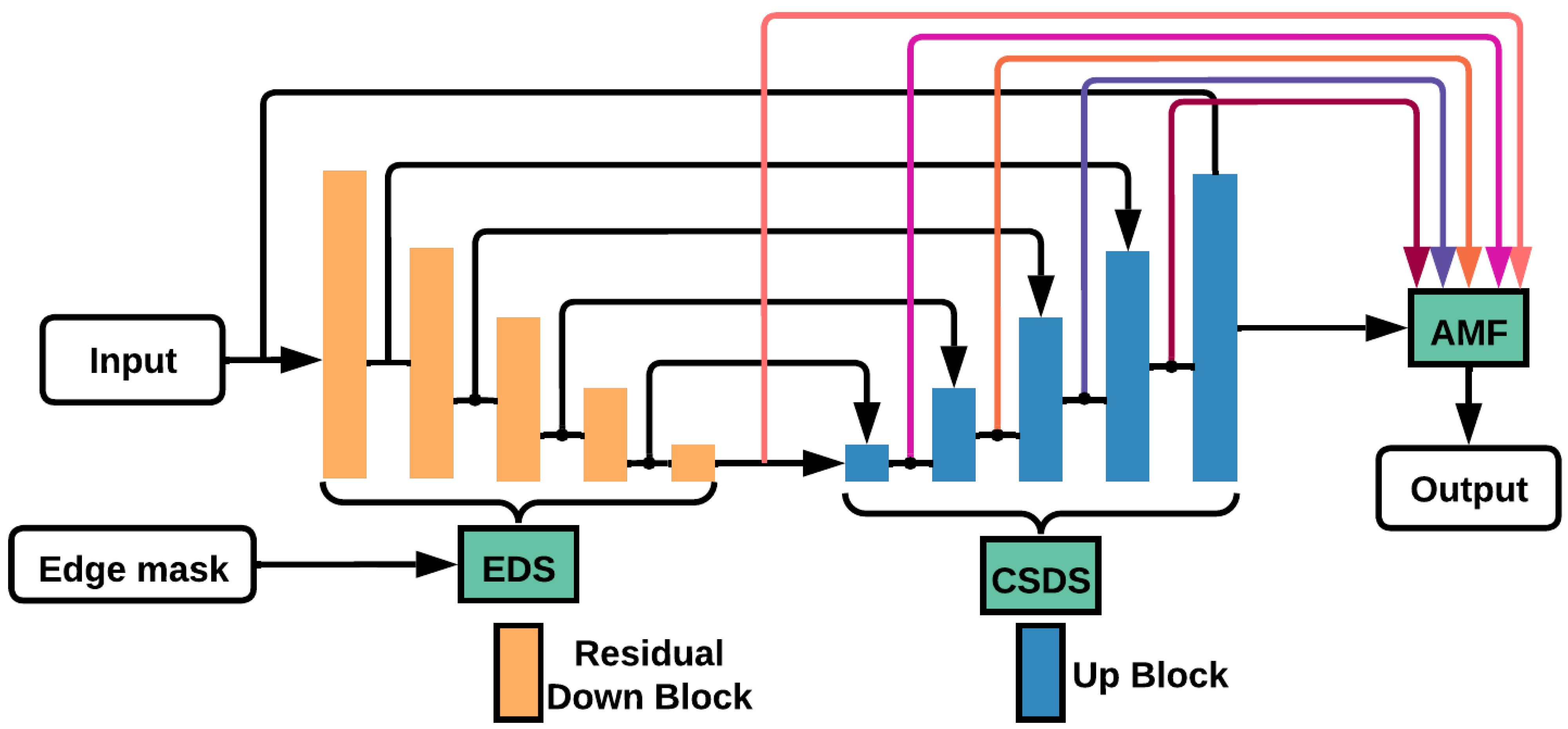
| Band | Spectral Range (nm) | Applications and Uses |
|---|---|---|
| PAN | 400–700 | High spatial resolution monochromatic images; fine details about landscapes and terrain; often used with other bands (pan-sharpening). |
| Coastal (deep blue) | 400–450 | Monitors water quality; detects shallow water features, sediment levels and chlorophyll concentrations. |
| Blue | 400–500 | Monitors water quality and turbidity; detects shallow water features and water bodies. |
| Green | 500–600 | Differentiates land from water; supports plant health and land use mapping. |
| Yellow | 580–590 | Monitors specific crops, algae and water quality. |
| Red | 600–700 | Evaluates vegetation and crop health, soil condition and vegetation indices. |
| Red edge | 680–730 | Tracks plant stress and vegetation health. |
| Near-infrared (NIR) | 700–1300 | Monitors vegetation health, detects water bodies and maps land use and vegetation indices. |
| Short-wave infrared (SWIR-1) | 1300–2000 | Measures soil and vegetation moisture, assesses drought and identifies vegetation stress. |
| Short-wave infrared (SWIR-2) | 2000–2500 | Differentiates minerals, rocks and materials; detects fires; supports geological studies. |
| Mid-infrared (MWIR) | 3000–5000 | Monitors surface temperature, thermal variations and fires; identifies clouds and moisture levels. |
| Long-wave infrared (LWIR) | 8000–14,000 | Provides thermal imaging; monitors surface temperatures, urban heat and climate studies. |
| Satellite | Bands and Resolutions | Revisit Time | Availability | Acquisition Range |
|---|---|---|---|---|
| Landsat-7 | PAN (15 m); RGB, NIR, SWIR1, SWIR2 (30 m); Thermal (30 m, resampled from 60 m) | 16 days | Free on EarthExplorer | April 1999–Present (Extended mission) |
| Landsat-8 | PAN (15 m); Coastal, RGB, NIR, SWIR1, SWIR2, Cirrus (30 m); TIRS1, TIRS2 (30 m, resampled from 100 m) | 16 days, 8 days (w/Landsat-9) | Free on EarthExplorer | March 2013–Present |
| Landsat-9 | Same as Landsat-8 | 16 days, 8 days (w/Landsat-8) | Free on EarthExplorer | October 2021–Present |
| Sentinel-2 | RGB, VNIR (10 m); VNIRs, SWIRs (20 m); Coastal, SWIRs (60 m) | 10 days, 5 days (constellation) | Free on Copernicus Hub | June 2015–Present |
| PRISMA | PAN (5 m); VNIR/SWIR (30 m) | Variable | Free access | March 2019–Present |
| Gaofen-1/6 | PAN (2 m); RGB, NIR (8 m); WFV (16 m) | 4 days | Commercial, some research access | July 2013–Present (Gaofen-1); June 2018–Present (Gaofen-6) |
| WorldView-1 | PAN (0.50 m) | 1.7 days | Commercial, some research access | September 2007–Present |
| WorldView-2 | PAN (0.48 m); Coastal, RGB, Yellow, Red-Edge, NIR1, NIR2 (1.48 m) | 1.1 days | Commercial, some research access | October 2009–Present |
| WorldView-3 | PAN (0.31 m); Coastal, RGB, Yellow, Red-Edge, NIR1, NIR2 (1.24 m); SWIR (8 bands at 3.7 m); CAVIS (12 bands at 30 m) | <1 day | Commercial, some research access | August 2014–Present |
| WorldView-4 | PAN (0.31 m); RGB, NIR (1.24 m) | <1 day | Commercial, some research access | November 2016–January 2019 |
| SPOT-6/7 | PAN (1.5 m); RGB, NIR (6 m) | 1–3 days (alone), 1 day (constellation) | Commercial, some research access | September 2012–Present (SPOT-6); June 2014–Present (SPOT-7) |
| PlanetScope | Coastal, RGB, Yellow, Red-Edge, NIR (3–5 m) | Daily | Commercial, some research access | 2014–Present |
| Pleiades-1A/1B | PAN (0.50 m); RGB, NIR (2 m) | Daily | Commercial, some research access | January 2012–Present (Pleiades-1A); December 2012–Present (Pleiades-1B) |
| Pleiades-Neo | PAN (0.30 m); Deep Blue, RGB, Red-Edge, NIR (1.2 m) | Twice per day | Commercial, some research access | April 2021–Present (Pleiades-Neo 3); December 2021–Present (Pleiades-Neo 4) |
| Terra & Aqua (MODIS) | 36-band optical-thermal range (2 bands 250 m, 5 bands 500 m, 29 bands 1 km) | 1–2 days | Free on Earthdata | February 2000–Present (Terra); July 2002–Present (Aqua) |
| Terra (ASTER) | Green/Yellow, Red, NIR1, NIR2 (15 m), 6 SWIR bands (30 m), 5 thermal bands (90 m) | 1–2 days | Free on per request | February 2000–Present |
| GeoEye-1 | PAN (0.41 m); RGB, NIR (1.65 m) | 2–8 days | Commercial, some research access | October 2008–Present |
| Beijing-3N | PAN (0.30 m); RGB-NIR (1.20 m) | 1–5 days | Commercial | August 2022–Present |
| Satellite | Sensor | Revisit Time | Availability | Data Acquisition |
|---|---|---|---|---|
| Sentinel-1 | C-SAR: SM (5 m), IWS (5 m × 20 m), EWS (20 m × 40 m), WV (5 m). | 12 days (single); 6 days (constellation) | Free via Copernicus Open Access Hub | April 2014–Present |
| RADARSAT-1 | C-SAR: single polarization (HH); resolutions: fine (8 m), standard (30 m), ScanSAR (50–100 m). | 24 days | Archived data on EODMS | November 1995–March 2013 |
| RADARSAT-2 | C-SAR: full polarization; resolutions: 1–100 m. | 24 days | Commercial; some research data | December 2007 (Approximate)–Present |
| RADARSAT Constellation | C-SAR: single, dual, full, compact polarimetry; resolutions: 3 m (spotlight) to 100 m (ScanSAR). | 12 days (single); 4 days (constellation) | Gov/research users only | June 2019–Present |
| Gaofen-3 | C-SAR: single, dual, full polarization; resolutions: spotlight (1 m), ultrafine (3 m), fine (5 m). | 29 days | Limited research access | August 2016 (Approximate)–Present |
| SAOCOM | L-SAR: single, dual, full polarization; SM (10 m), TopSAR narrow (10 m × 50 m), wide (10 m × 100 m). | 16 days (single); 8 days (constellation) | Free via CONAE | October 2018 (Approximate)–Present |
| ALOS (PALSAR) | L-SAR: single/dual polarization; resolutions: fine (10 m), polarimetric (30 m), ScanSAR (100 m). | 46 days | Archived data via JAXA | January 2006 (Approximate)–12 May 2011 |
| ALOS-2 | L-SAR: single, dual, full polarization; resolutions: spotlight (3 m × 1 m), ultrafine (3 m), fine (10 m), wide (60 m). | 14 days | Commercial/research data | June 2014–Present |
| TerraSAR-X | X-SAR: single polarization; resolutions: spotlight (1 m), SM (3 m), ScanSAR (40 m). | 11 days | Commercial | June 2007–Present |
| Capella Space | X-SAR: single polarization; resolutions: spotlight (0.5 m), SM (3 m), ScanSAR (10 m). | Hours (Constellation of 36 satellites) | Commercial | March 2019 (Approximate)–Present |
| ICEYE | X-SAR: single polarization; resolutions: spotlight (0.5 m), strip (1 m), scan (3 m). | Max 20 h (Constellation of 38 satellites) | Commercial; some free data | January 2018–Present |
| Dataset | Source | Resolution | Dates | Regions | Description | Image–Mask Pairs |
|---|---|---|---|---|---|---|
| Scarpetta et al. [65] | Sentinel-2 Level-1C | 10–60 m | Dec 2016–2022 | Hawai’i, NW/NE Continental USA, Great Lakes, Gulf of Mexico, Puerto Rico | 894 labeled tiles, 13 bands (RGB, NIR, SWIR) excluding Alaska and rivers, derived from NOAA’s CUSP. | ✓ |
| SNOWED [66] | Sentinel-2 Level-1C | 10–60 m | Jun 2015–2023 | USA coastal regions (Continental USA, Alaska, Hawaii, USA Virgin Islands, Pacific Islands, Puerto Rico) | 4334 labeled tiles, 13 bands (RGB, NIR, SWIR), derived from NOAA’s CUSP and automated labeling | ✓ |
| Seale et al. (SWED) [60] | Sentinel-2 | 10 m | 2017–2021 | Global, various high and low tide regions | 114 RGB image–mask pairs, 12 interpolated bands, semi-supervised clustering. | ✓ |
| Yang et al. (SLS) [62] | Landsat-8 OLI | 30 m | 2013–2018 | Chinese coastline | 1950 training and 1411 test patches, manually segmented using LabelMe. | ✓ |
| YTU-WaterNet [64] | Landsat-8 OLI | 10 m | 2017–2019 | Albania, Argentina, Bulgaria, England, Georgia, Greece, Ireland, Italy, Libya, Russia, South Africa, Spain, Turkey, USA | 824 training, 92 validation, 92 test images with segmentation maps from OpenStreetMap. | ✓ |
| Coast-Train [67] | Aerial, Satellite Images | 0.05–1 m (aerial), 10–15 m (satellite) | 2008–2021 | USA Pacific, Gulf of Mexico, Atlantic, Great Lakes | 502 training and 34 validation RGB images with detailed masks, up to 12 classes. | ✓ |
| Pollard et al. [68] | Environment Agency, UK | 0.10–0.25 m (aerial), 0.25–2 m (LiDAR) | 2001–2019 (aerial), 1999–2009 (LiDAR) | UK | High-resolution dataset combining aerial photography, LiDAR, field surveys; includes metadata for erosion monitoring. | ✓ |
| Global Coastline Explorer [55] | USGS | 30 m | 2014 | Global (5 continents, 21,818 large islands, 318,868 small islands) | Over 4 million segments classified into 81,000 coastal units with ecological attributes. | |
| GSHHG [57] | NOAA, University of Hawai’i | 200 m–100 km | Pre-1996 | Global | Six shoreline types, five resolution levels; integrates three data sources (shorelines, lakes, rivers). | |
| Natural Earth Data (NED) [58] | Community-maintained | 10, 30, 100 m | Unknown | Global | Physical and cultural data for cartography and visualization. | |
| OpenStreetMap (OSM) [59] | Community-maintained | Varying | Ongoing | Global | Polygons separating land and sea, widely accessible for remote sensing. |
| Model | Adam + BCE | Adam + Focal | SGD + BCE | SGD + Focal |
|---|---|---|---|---|
| Val. Acc. (%) | 93.3 | 97.2 | 72.0 | 95.6 |
| Test Acc. (%) | 91.5 | 98.3 | 59.7 | 93.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blais, M.-A.; Akhloufi, M.A. Advances in Remote Sensing and Deep Learning in Coastal Boundary Extraction for Erosion Monitoring. Geomatics 2025, 5, 9. https://doi.org/10.3390/geomatics5010009
Blais M-A, Akhloufi MA. Advances in Remote Sensing and Deep Learning in Coastal Boundary Extraction for Erosion Monitoring. Geomatics. 2025; 5(1):9. https://doi.org/10.3390/geomatics5010009
Chicago/Turabian StyleBlais, Marc-André, and Moulay A. Akhloufi. 2025. "Advances in Remote Sensing and Deep Learning in Coastal Boundary Extraction for Erosion Monitoring" Geomatics 5, no. 1: 9. https://doi.org/10.3390/geomatics5010009
APA StyleBlais, M.-A., & Akhloufi, M. A. (2025). Advances in Remote Sensing and Deep Learning in Coastal Boundary Extraction for Erosion Monitoring. Geomatics, 5(1), 9. https://doi.org/10.3390/geomatics5010009






