Medical Decision Making for Cardiac MRI with CFD “Detection of Severe Stenosis Using a 5D Model of the Descending Aorta”
Abstract
:1. Introduction
2. Mathematical Background
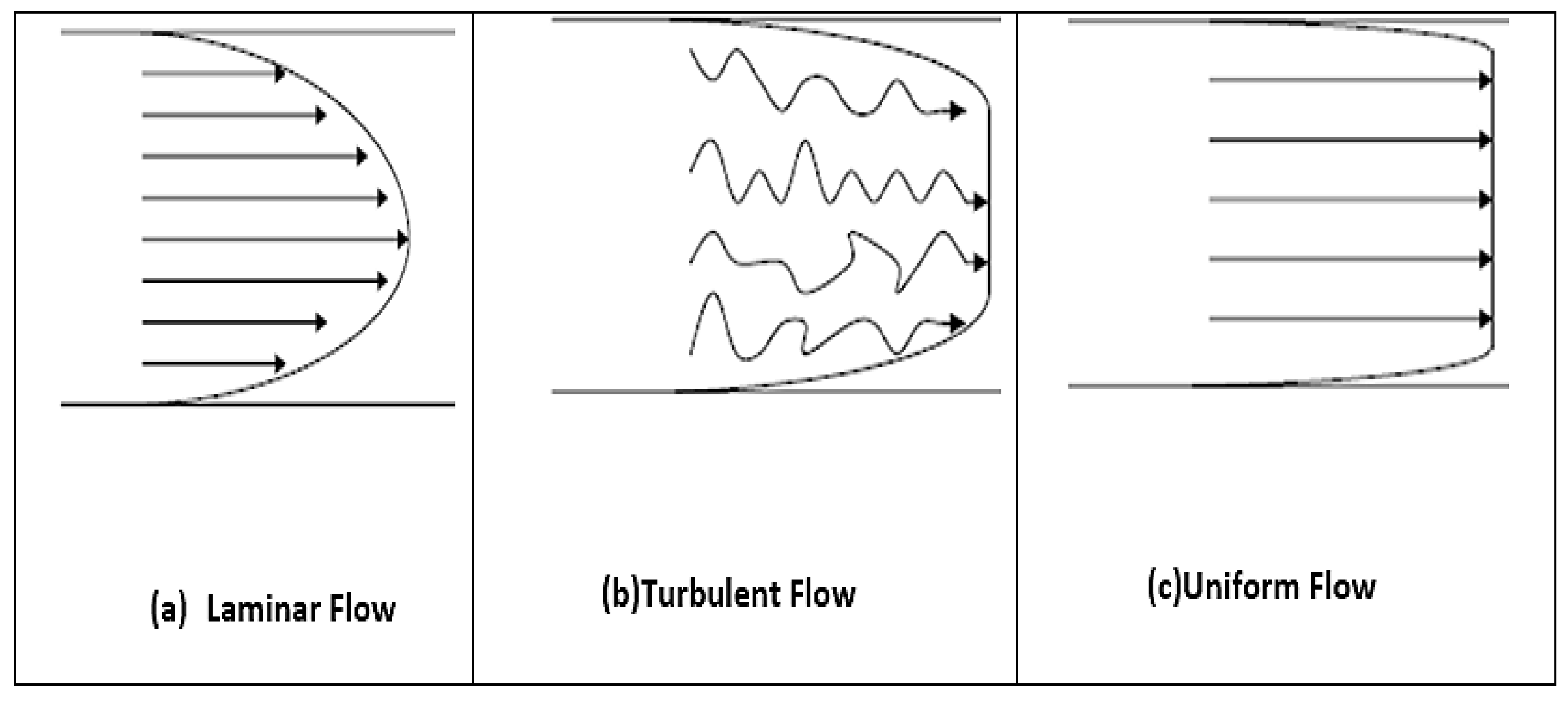
2.1. Dynamics of Laminar Viscous: Navier-Stokes Equations
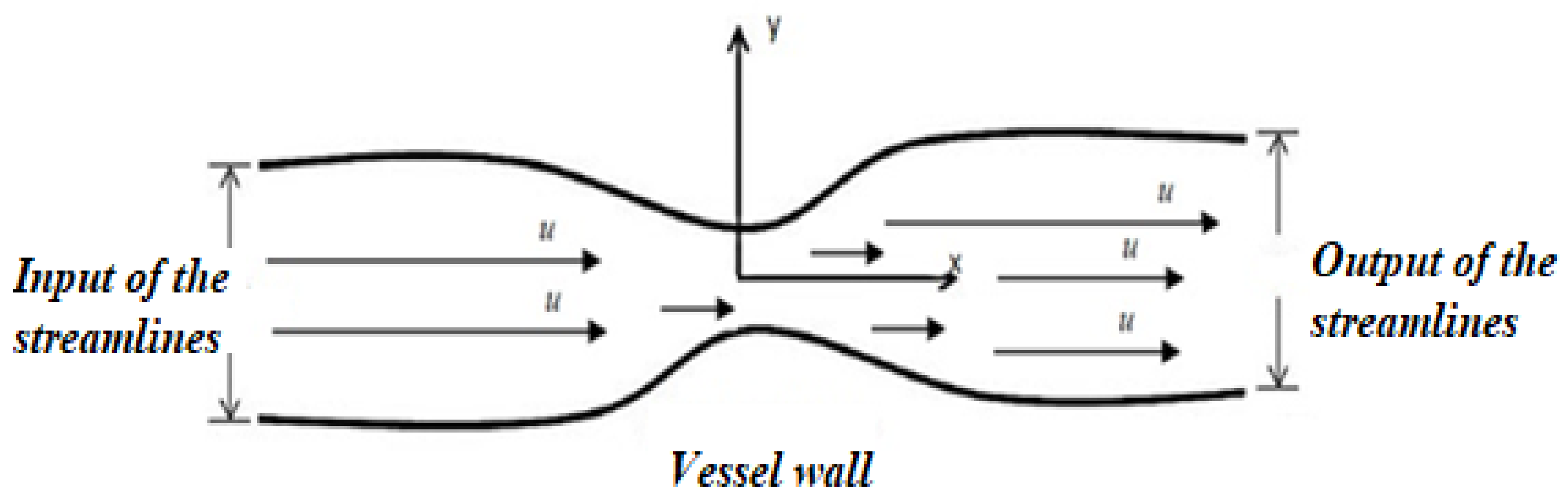
2.2. Boundary Conditions
2.3. Characteristics of Blood Flow Fluids
2.3.1. Blood Viscosity, μ
2.3.2. Geometry Design
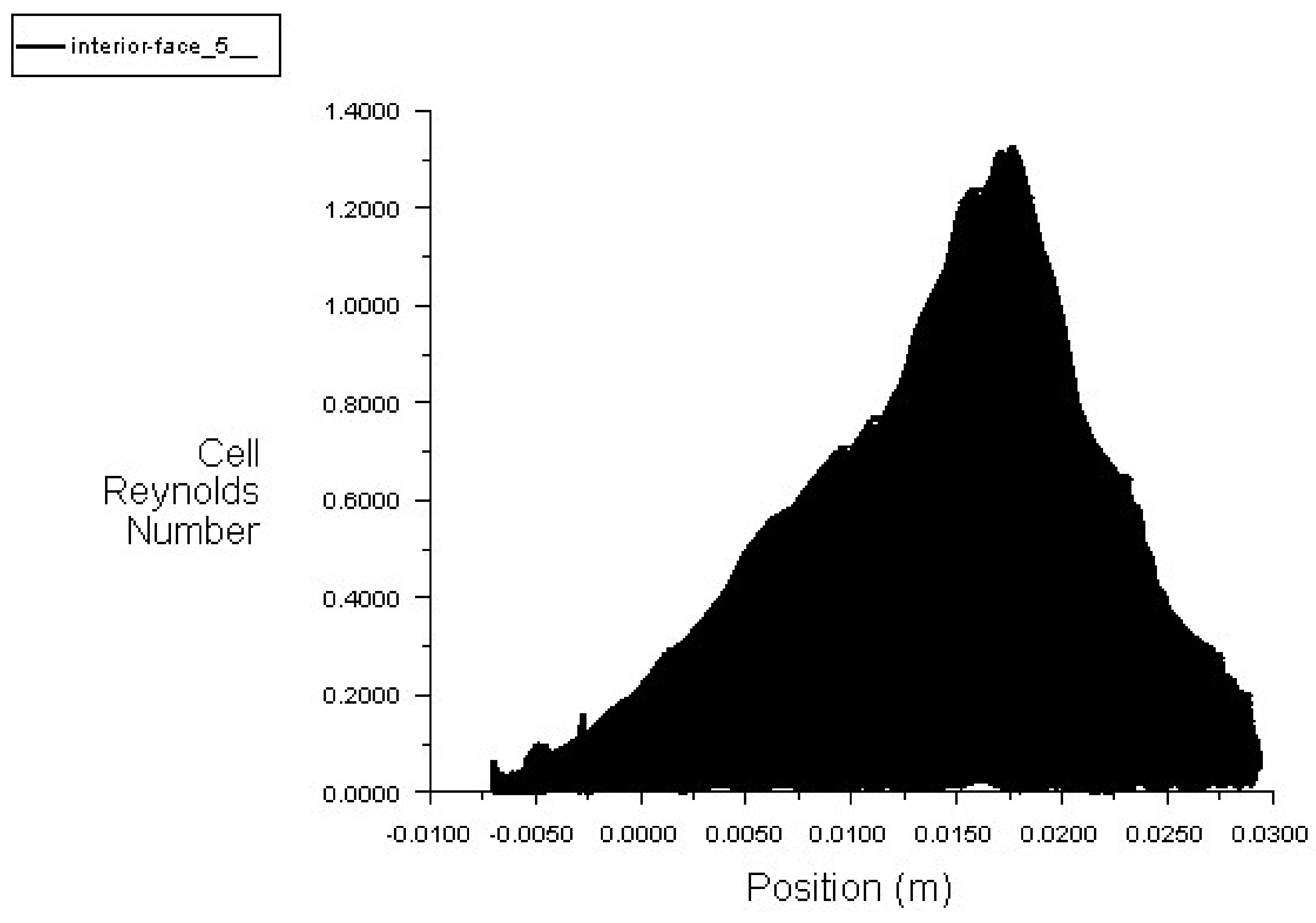
2.3.3. Reynold Number
2.3.4. Assessment of the Rate of Severe Stenosis
3. Design and Description of the Solution Methodology

4. Tools for 5D Imaging
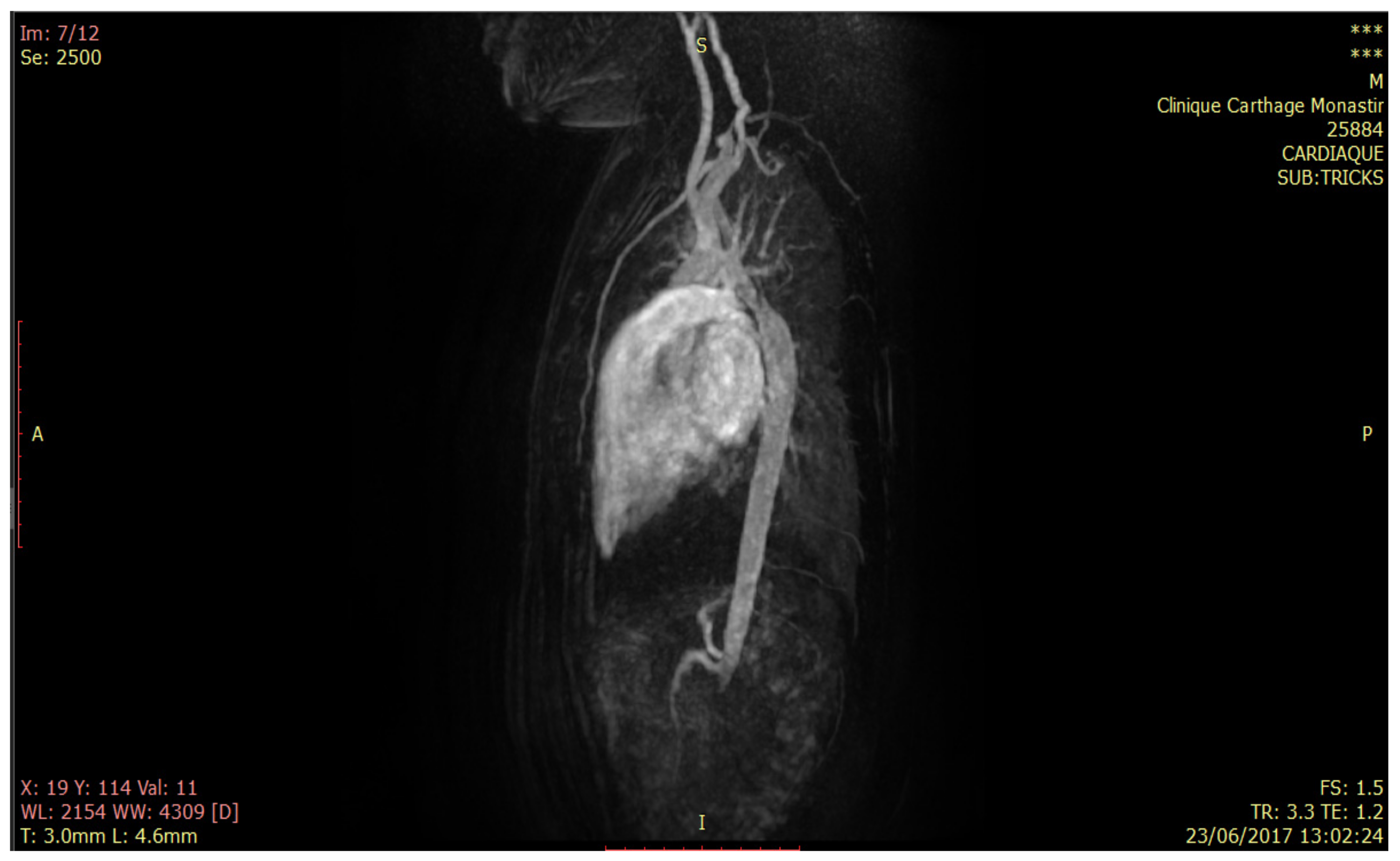
5. Methods and Materials
- ✓
- 44 TRICKS angiographic slices in dynamic acquisition on the thoracic aorta;
- ✓
- Injection perfusion sequences after injection;
- ✓
- Sequences ciné-fiesta T2 short-axis 4 cavities;
- ✓
- Subsequent infusion sequences short-axis.
- ✓
- Tricuspid valve. Aortic ring with 8.5 mm diameter;
- ✓
- Aortic stenosis at 0.42 cm2 with reduction of sigmoid opening at 5 mm;
- ✓
- At the sino-tubular junction: 25 mm;
- ✓
- 1/3 medium of the ascending aorta: 18 mm;
- ✓
- Horizontal aorta: 16 mm;
- ✓
- Size disparity with aortic stenosis at the isthmic level extended over 10 mm, reducing approximately 65% of its lumen by 6 mm in diameter;
- ✓
- Mitral valve of normal diameter 2.5–4.3 cm2;
- ✓
- The mass of VG tele-diastolic 90 g and tele-diastolic 70 g;
- ✓
- The systolic ejection function, estimated according to the 82% contour method.
- ✓
- Magnetic field: 1.5 Tesla;
- ✓
- Acquisition time: 1.2 s/Repetition time: 3.3 s;
- ✓
- Diameter of reconstruction of the cuts: 370 cm2;
- ✓
- Angle of acquisition = 30 degrees;
- ✓
- Acquisition matrix: 0/300/224/0;
- ✓
- Sections orientation matrix: −0.0393457\0.99917\−0.0105243\0.283665\0.00106985–0.958923;
- ✓
- Cutting position matrix: −1.15748\−152.042\358.794;
- ✓
- Number of time positions: 12;
- ✓
- Scanning Rentals: −43.95322037;
- ✓
- Space between pixels: 0.7227\0.7227 with allocation of 16 bits of memory.
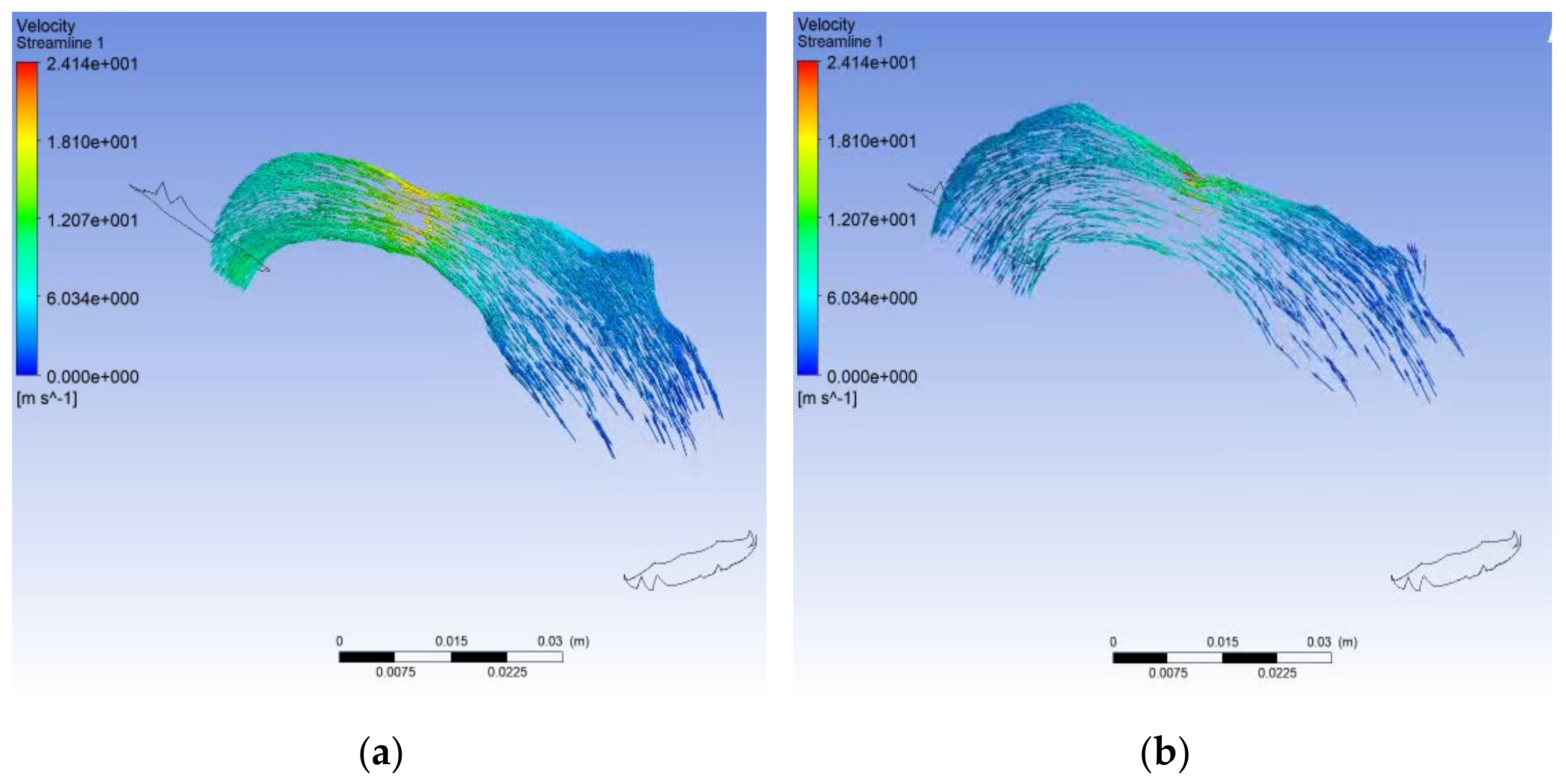
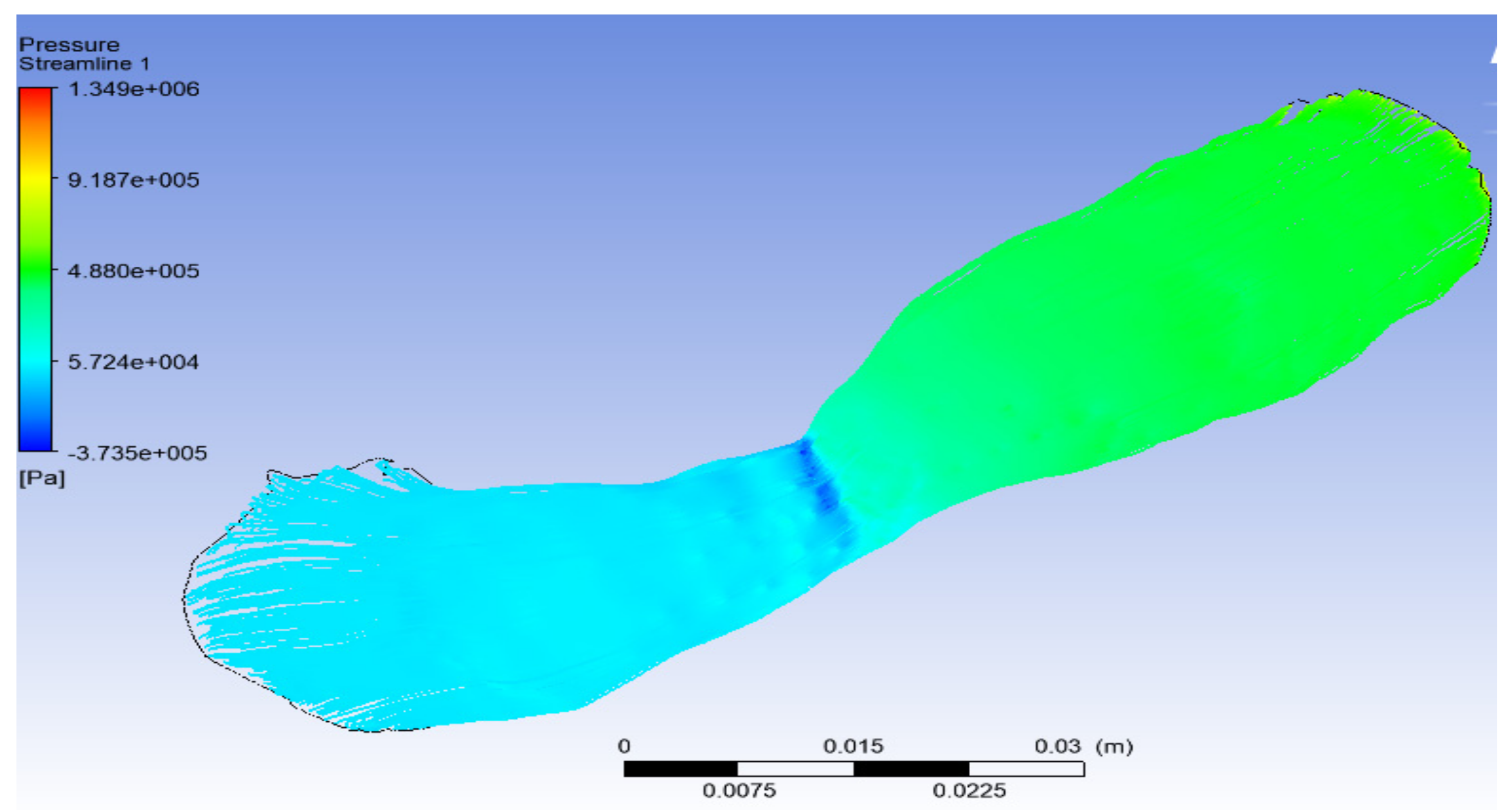
6. Results
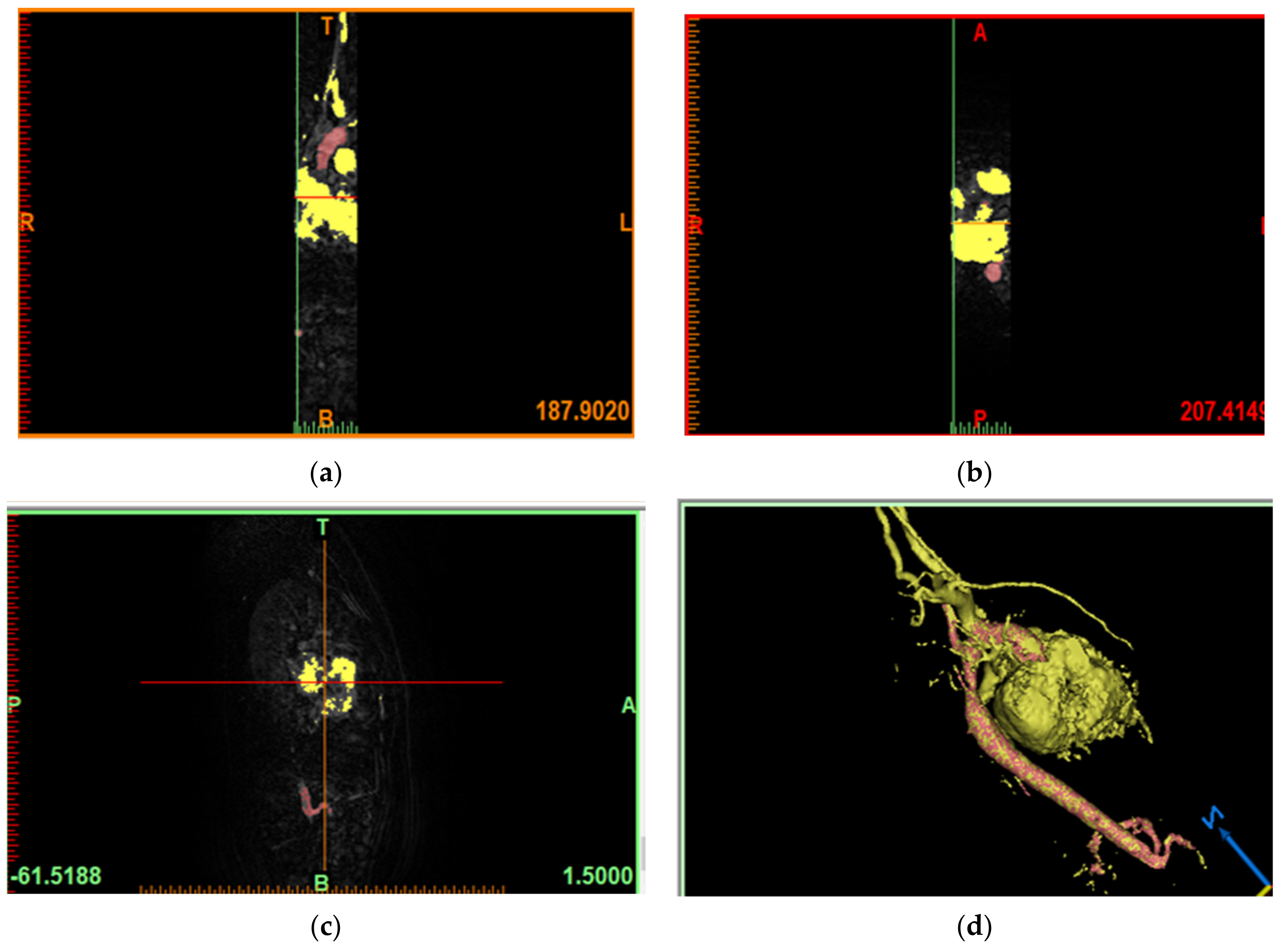
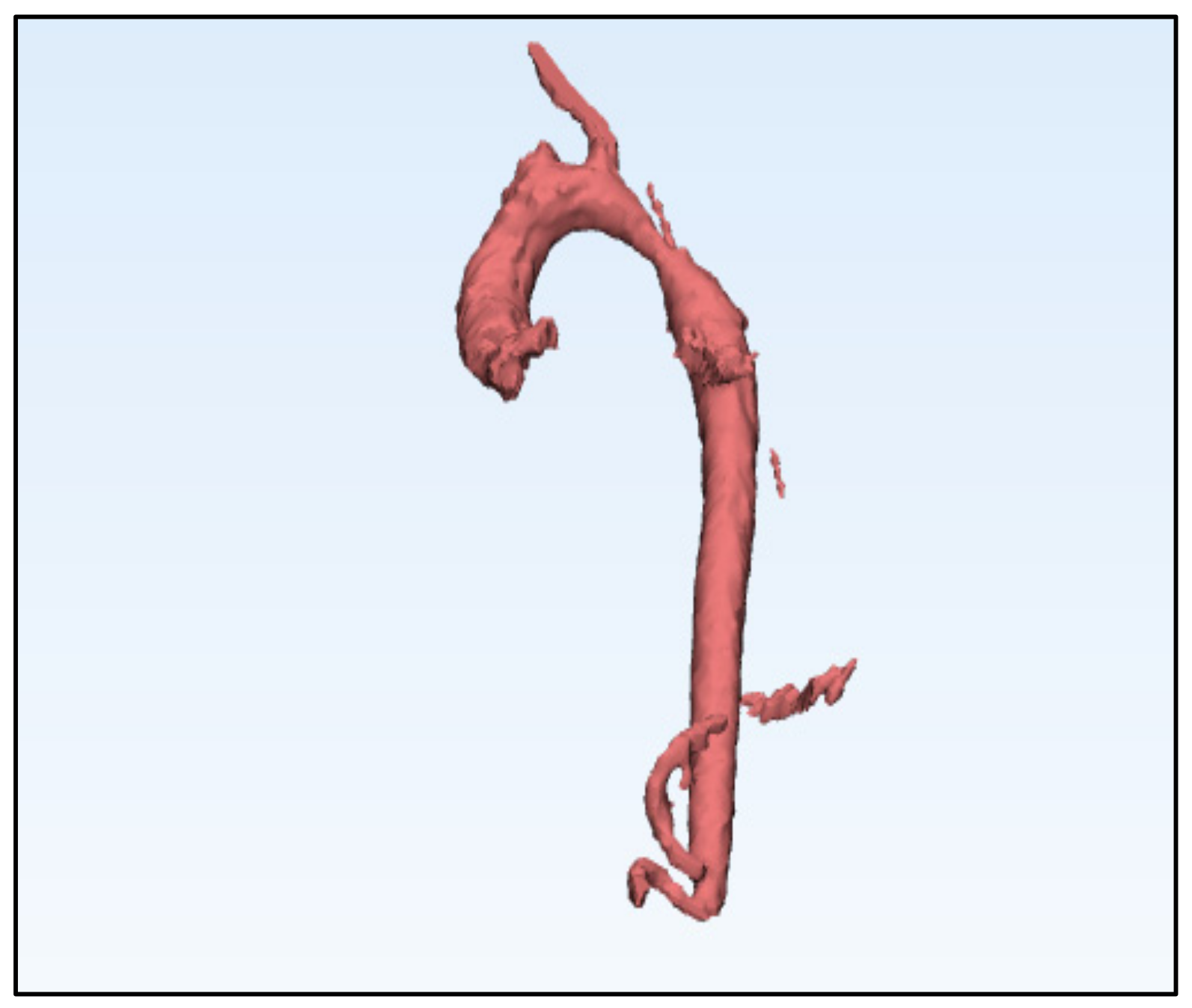
6.1. Model of the Geometry of the Descending Aorta in 3D
6.2. Generation of the Mesh Geometry
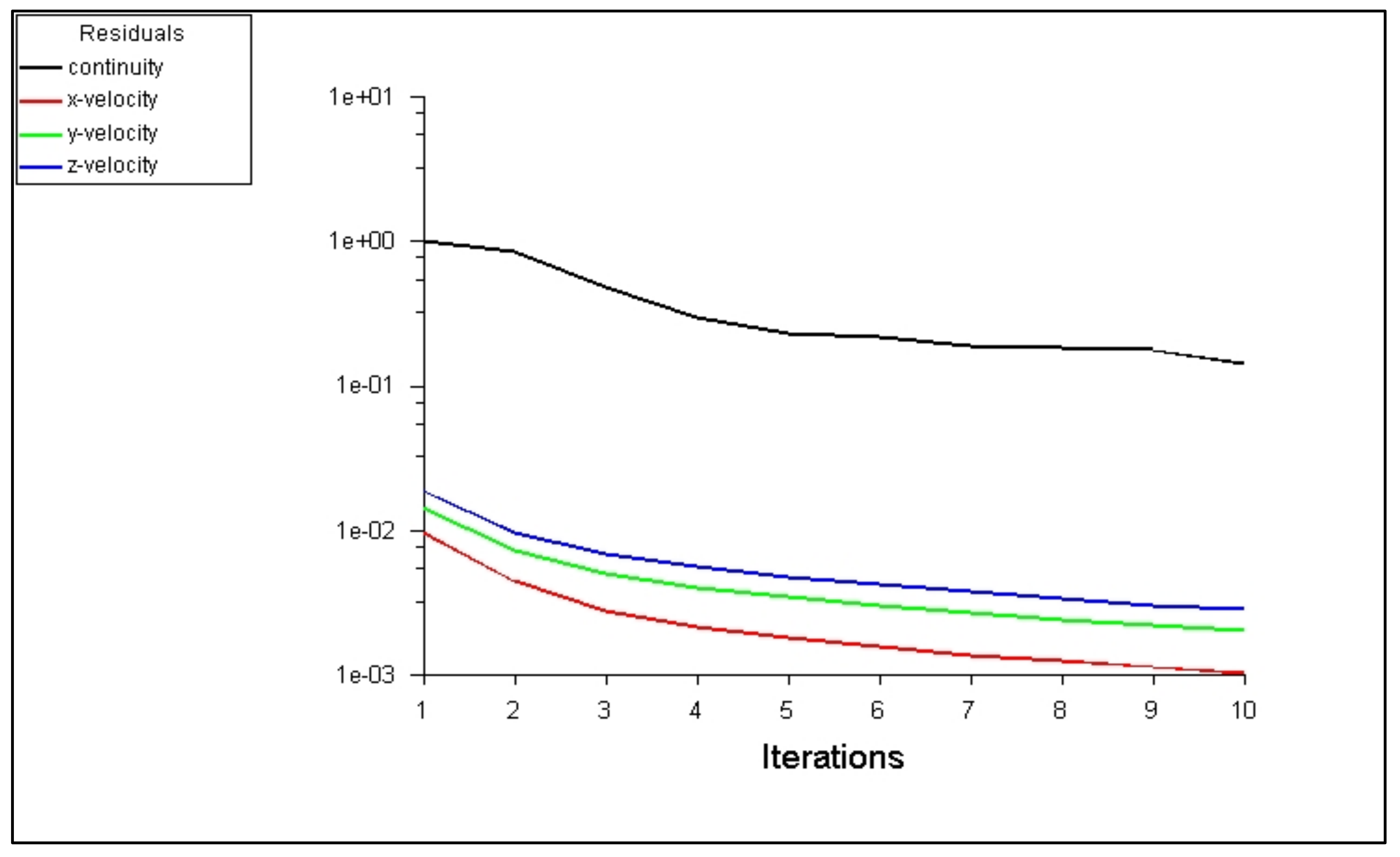
6.3. Setting of the Solution
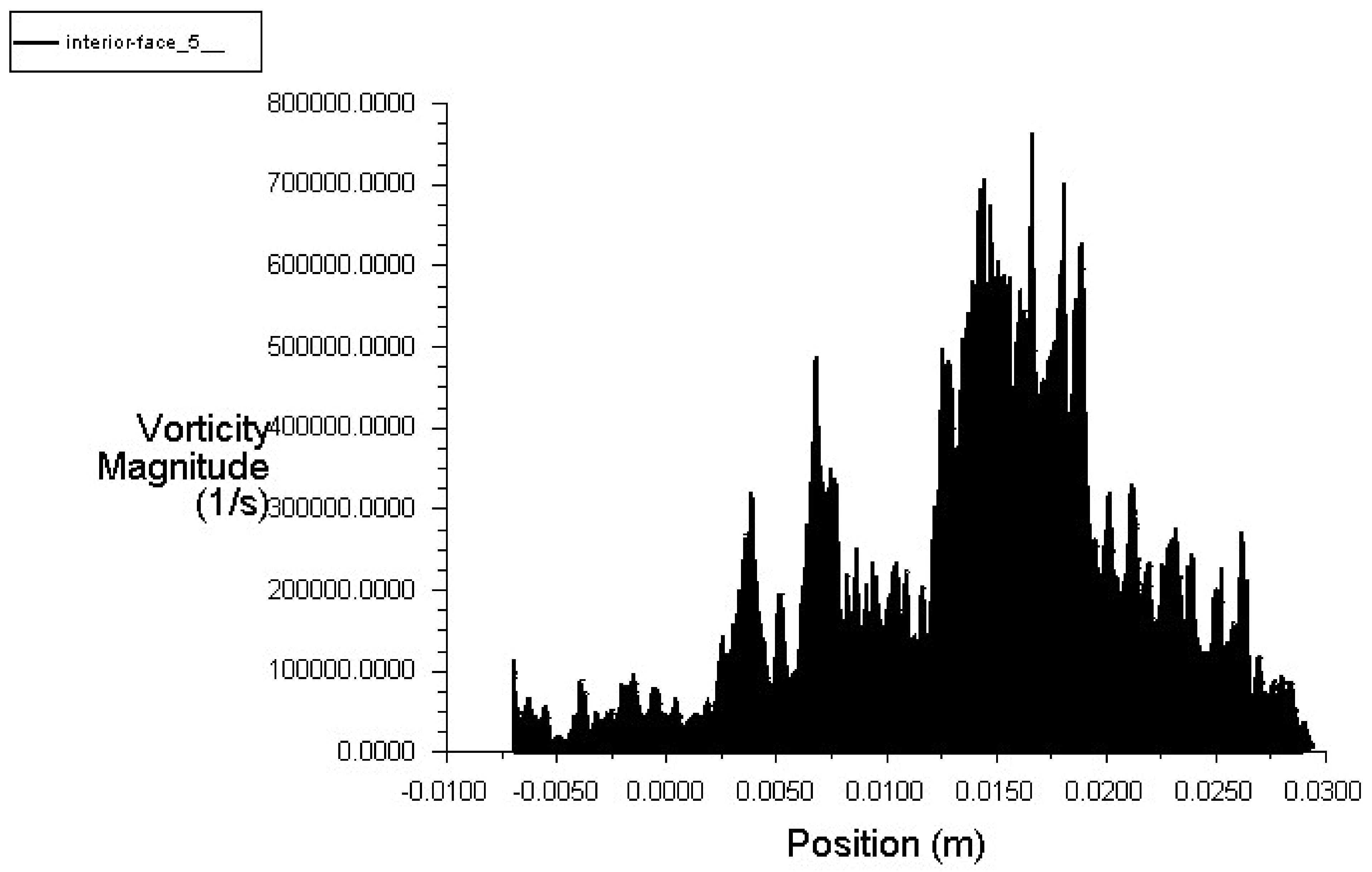
6.4. Solution with ANSYS-Fluent
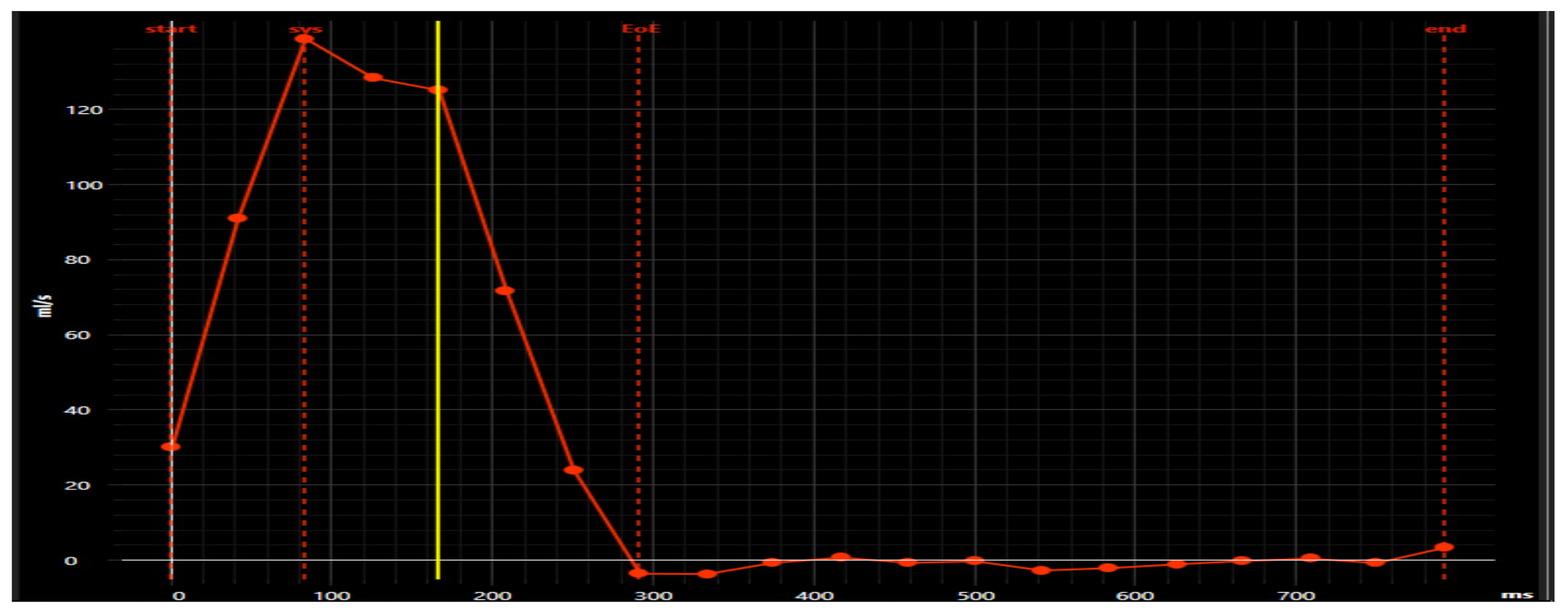
6.5. Cardiovascular Solution with Pie Medical Imaging “Caas 4D Flow”
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solaiyappan, M. Visualization pathways in biomedicine. Handb. Med. Image Process. Anal. 2009, 729–753. [Google Scholar] [CrossRef]
- Zhang, Y.; Passmore, P.; Bayford, R. Visualization and Post-processing of 5D Brain Images. In Proceedings of the 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference, Shanghai, China, 17–18 January 2006; pp. 1083–1086. [Google Scholar] [CrossRef]
- Brown, B.H.; Seagar, A.D. The Sheffield data collection system. Clin. Phys. Physiol. Meas. 1987, 8, 91–97. [Google Scholar] [CrossRef]
- Wilson, A.J.; Milnes, P.; Waterworth, A.R.; Smallwood, R.H.; Brown, B.H. Mk3.5: A modular, multi-frequency successor to the Mk3a EIS/EIT system. Physiol. Meas. 2001, 22, 49–54. [Google Scholar] [CrossRef]
- Rosset, A.; Spadola, L.; Pysher, L.; Ratib, O. Informatics in radiology (infoRAD): Navigating the fifth dimension: Innovative interface for multidimensional multimodality image navigation. Radiogr. Rev. Publ. Radiol. Soc. N. Am. Inc 2006, 26, 299–308. [Google Scholar] [CrossRef]
- Cutrale, F.; Trivedi, V.; Trinh, L.A.; Chiu, C.-L.; Choi, J.M.; Artiga, M.S.; Fraser, S.E. Hyperspectral phasor analysis enables multiplexed 5D in vivo imaging. Nat. Methods 2017, 14, 149–152. [Google Scholar] [CrossRef]
- Huang, Y.S.; Ku, H.Y.; Tsai, Y.C.; Chang, C.H.; Pao, S.H.; Sun, Y.H.; Chiou, A. 5D imaging via light sheet microscopy reveals cell dynamics during the eye-antenna disc primordium formation in Drosophila. Sci. Rep. 2017, 7, 44945. [Google Scholar] [CrossRef]
- Vamvakeros, A.; Jacques, S.D.M.; Di Michiel, M.; Matras, D.; Middelkoop, V.; Ismagilov, I.Z.; Matus, E.V.; Kuznetsov, V.V.; Drnec, J.; Senecal, P.; et al. 5D operando tomographic diffraction imaging of a catalyst bed. Nat. Commun. 2018, 9, 4751. [Google Scholar] [CrossRef] [Green Version]
- Heist, S.; Zhang, C.; Reichwald, K.; Kühmstedt, P.; Notni, G.; Tünnermann, A. 5D hyperspectral imaging: Fast and accurate measurement of surface shape and spectral characteristics using structured light. Opt. Express 2018, 26, 23366–23379. [Google Scholar] [CrossRef]
- Low, D.A.; Parikh, P.J.; Lu, W.; Dempsey, J.F.; Wahab, S.H.; Hubenschmidt, J.P.; Nystrom, M.M.; Handoko, M.; Bradley, J.D. Novel breathing motion model for radiotherapy. Int. J. Radiat. Oncol. 2005, 63, 921–929. [Google Scholar] [CrossRef]
- Sigfridsson, A.; Kvitting, J.-P.E.; Knutsson, H.; Wigström, L. Five-dimensional MRI incorporating simultaneous resolution of cardiac and respiratory phases for volumetric imaging. J. Magn. Reson. Imaging JMRI 2007, 25, 113–121. [Google Scholar] [CrossRef]
- Feng, L.; Coppo, S.; Piccini, D.; Yerly, J.; Lim, R.P.; Masci, P.G.; Stuber, M.; Sodickson, D.K.; Otazo, R. 5D whole-heart sparse MRI. Magn. Reson. Med. 2018, 79, 826–838. [Google Scholar] [CrossRef]
- Sakly, H.; Mahmoudi, R.; Akil, M.; Said, M.; Tagina, M. Moving towards a 5D cardiac model. J. Flow Vis. Image Process. 2019, 26, 19–48. [Google Scholar] [CrossRef] [Green Version]
- Sakly, H.; Said, M.; Tagina, M. Computer Methods and Programs for Medical Decision Making: 5D Cardiac Model; Eliva Press: Chisinau, Moldova, 2020. [Google Scholar]
- Sikarwar, B.S.; Roy, M.; Ranjan, P.; Goyal, A. Automatic disease screening method using image processing for dried blood microfluidic drop stain pattern recognition. J. Med. Eng. Technol. 2016, 40, 245–254. [Google Scholar] [CrossRef]
- Roy, M.; Singh Sikarwar, B.; Bhandwal, M.; Ranjan, P. Modelling of Blood Flow in Stenosed Arteries. In Proceedings of the 7th International Conference on Advances in Computing & Communications, ICACC-2017, Cochin, India, 22–24 August 2017; pp. 821–830. [Google Scholar] [CrossRef]
- Cebral, J.R.; Mut, F.; Raschi, M.; Scrivano, E.; Ceratto, R.; Lylyk, P.; Putman, C.M. Aneurysm rupture following treatment with flow-diverting stents: Computational hemodynamics analysis of treatment. AJNR Am. J. Neuroradiol. 2011, 32, 27–33. [Google Scholar] [CrossRef] [Green Version]
- Thomas, B.; Sumam, K.S. Blood Flow in Human Arterial System-A Review. Procedia Technol. Int. Conf. Emerg. Trends Eng. Sci. Technol. 2016, 24, 339–346. [Google Scholar] [CrossRef] [Green Version]
- Xiong, G.; Figueroa, C.A.; Xiao, N.; Taylor, C.A. Simulation of blood flow in deformable vessels using subject-specific geometry and spatially varying wall properties. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1000–1016. [Google Scholar] [CrossRef] [Green Version]
- Cibis, M.; Jarvis, K.; Markl, M.; Rose, M.; Rigsby, C.; Barker, A.J.; Wentzel, J.J. The effect of resolution on viscous dissipation measured with 4D flow MRI in patients with Fontan circulation: Evaluation using computational fluid dynamics. J. Biomech. 2015, 48, 2984–2989. [Google Scholar] [CrossRef] [Green Version]
- Holden, M. A review of geometric transformations for nonrigid body registration. IEEE Trans. Med. Imaging 2008, 27, 111–128. [Google Scholar] [CrossRef]
- He, X.; Hu, W.; Zhang, Y. Observer-based feedback boundary stabilization of the Navier–Stokes equations. Comput. Methods Appl. Mech. Eng. 2018, 339, 542–566. [Google Scholar] [CrossRef]
- Chan, W.Y. Simulation of Arterial Stenosis Incorporating Fluid-Structural Interaction and Non-Newtonian Blood Flow. Ph.D. Thesis, RMIT University, Melbourne, VIC, Australia, 2006. [Google Scholar]
- Bakharev, F.L.; Exner, P. Geometrically Induced Spectral Effects in Tubes with a Mixed Dirichlet—Neumann Boundary. Rep. Math. Phys. 2018, 81, 213–231. [Google Scholar] [CrossRef] [Green Version]
- Leuprecht, A.; Perktold, K. Computer simulation of non-newtonian effects on blood flow in large arteries. Comput. Methods Biomech. Biomed. Eng. 2001, 4, 149–163. [Google Scholar] [CrossRef]
- Pereira, J.M.C.; Serra e Moura, J.P.; Ervilha, A.R.; Pereira, J.C.F. On the uncertainty quantification of blood flow viscosity models. Chem. Eng. Sci. 2013, 101, 253–265. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Cimbala, J.M.; Turner, R.H. Fundamentals of Thermal Fluid Sciences 5th Edition Cengel Solutions Manual. BASIC CONCEPTS Thermodyn. 2017. Available online: https://testbanklive.com/download/fundamentals-of-thermal-fluid-sciences-5th-edition-cengel-solutions-manual/ (accessed on 1 August 2018).
- Nadeem, S.; Ali, M. Analytical solutions for pipe flow of a fourth grade fluid with Reynold and Vogel’s models of viscosities. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 2073–2090. [Google Scholar] [CrossRef]
- Disu, A.B.; Dada, M.S. Reynold’s model viscosity on radiative MHD flow in a porous medium between two vertical wavy walls. J. Taibah Univ. Sci. 2017, 11, 548–565. [Google Scholar] [CrossRef] [Green Version]
- Zaripov, T.S.; Rybdylova, O.; Sazhin, S.S. A model for heating and evaporation of a droplet cloud and its implementation into ANSYS Fluent. Int. Commun. Heat Mass Transf. 2018, 97, 85–91. [Google Scholar] [CrossRef]
- Tora, E.; Dahlquist, E. CFD Ansys—Fluent Simulation of Prevention of Dioxins Formation Via Controlling Homogeneous Mass and Heat Transfer within Circulated Fluidized Bed Combustor. Energy Procedia 2015, 75, 130–136. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, S.A.; Vahedi Tafreshi, H. Modeling particle-loaded single fiber efficiency and fiber drag using ANSYS–Fluent CFD code. Comput. Fluids 2012, 66, 157–166. [Google Scholar] [CrossRef]
- Dey, D.K.; Rao, C.R. Bayesian Thinking: Modeling and Computation; Amsterdam, The Netherlands, 2005; Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=8c0b82d85902b8be920dcaec170ffcc9&site=xueshu_se&hitarticle=1 (accessed on 20 December 2021).
- Wilhelm, M.; Dedè, L.; Sangalli, L.M.; Wilhelm, P. IGS: An IsoGeometric approach for smoothing on surfaces. Comput. Methods Appl. Mech. Eng. 2016, 302, 70–89. [Google Scholar] [CrossRef] [Green Version]
- Ray, J.; Rebischung, P.; Griffiths, J. IGS polar motion measurement accuracy. Geod. Geodyn. Geod. Astron. Geophys. Earth Rotat. 2017, 8, 413–420. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.; Gao, F.; Zhou, P.; Zhai, Z. Literature review on pressure–velocity decoupling algorithms applied to built-environment CFD simulation. Build. Environ. 2018, 143, 671–678. [Google Scholar] [CrossRef]
- Ghalichi, F.; Deng, X.; De Champlain, A.; Douville, Y.; King, M.; Guidoin, R. Low Reynolds number turbulence modeling of blood flow in arterial stenoses. Biorheology 1998, 35, 281–294. [Google Scholar] [CrossRef]
- Schlanstein, P.C.; Hesselmann, F.; Jansen, S.V.; Gemsa, J.; Kaufmann, T.A.; Klaas, M.; Roggenkamp, D.; Schröder, W.; Schmitz-Rode, T.; Steinseifer, U.; et al. Particle Image Velocimetry Used to Qualitatively Validate Computational Fluid Dynamic Simulations in an Oxygenator: A Proof of Concept. Cardiovasc. Eng. Technol. 2015, 6, 340–351. [Google Scholar] [CrossRef]
- Burris, N.S.; Sigovan, M.; Knauer, H.A.; Tseng, E.E.; Saloner, D.; Hope, M.D. Systolic flow displacement correlates with future ascending aortic growth in patients with bicuspid aortic valves undergoing magnetic resonance surveillance. Investig. Radiol. 2014, 49, 635–639. [Google Scholar] [CrossRef]
- Sigovan, M.; Hope, M.D.; Dyverfeldt, P.; Saloner, D. Comparison of four-dimensional flow parameters for quantification of flow eccentricity in the ascending aorta. J. Magn. Reson. Imaging JMRI 2011, 34, 1226–1230. [Google Scholar] [CrossRef]












| Developed-by | Cutrale et al. [6] | Huang et al. [7] | Vamvakeros et al. [8] | Heist et al. [9] | Low et al. [10] | Sigfridsson et al. [11] | Feng et al. [12] | Sakly et al. [13] |
|---|---|---|---|---|---|---|---|---|
| Field | Biomedical imaging | microscopic imaging | tomographic diffraction imaging | hyperspectral imaging | Lung Imaging | Lung and cardiac imaging | Lung and cardiac imaging | Cardiac imaging |
| 3D | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) | Coordinate (x, y, z) |
| 4D | Time (t) | Time (t) | Scattering Dimension | Time (t) | Time (t) | Respiratory time of the lungs | Time (t) | Time (t) |
| 5D | wavelength (λ) | multi-fluorescence channel | (time/imposed state) | wavelength-dependent reflectance R (λi) | Air Flow (f(tf)) | (Systole+diastole) Time for the heart | Respiratory dimension | Blood flow (f(tf)) |
| Main steps of Algorithm |
| ✓ Mask (Aorta Segment Mask)—Threshold Mask. |
| ✓ Threshold_min (int)—Minimum threshold value :226 |
| ✓ Threshold_max (int)—The maximum value of the threshold: 1634 |
| ✓ Bounding_box (Aorte.BoundingBox3d)—(optional) Bounding box including region of interest |
| Main steps of Algorithm |
| ✓ Selection (model.segment.Mask)—The original mask. |
| ✓ Region_a_mask (model.Segment.Mask)—Existing mask containing marked regions to be separated from others. Region_a_mask takes precedence over region_b_mask. |
| ✓ Region_b_mask (model.Segment.Mask)—Existing mask containing marked regions that must be separated from others. Region_a_mask takes precedence over region_b_mask. |
| ✓ Model.segment. Calculate_part (mask, quality = ‘Optimal’) |
| Features | Statistical Analysis | |
|---|---|---|
| Based on the Thickness | Based on Curvature | |
| Min-Edge | 1.76 mm | 3503.046 |
| Max Edge | 10 mm | 6265.35 |
| Median | 10 | 0.09 |
| Average | 9.78 | 2.06 |
| Standard Deviation | 0.78 | 134.66 |
| Average quadratic | 9.81 | 134.67 |
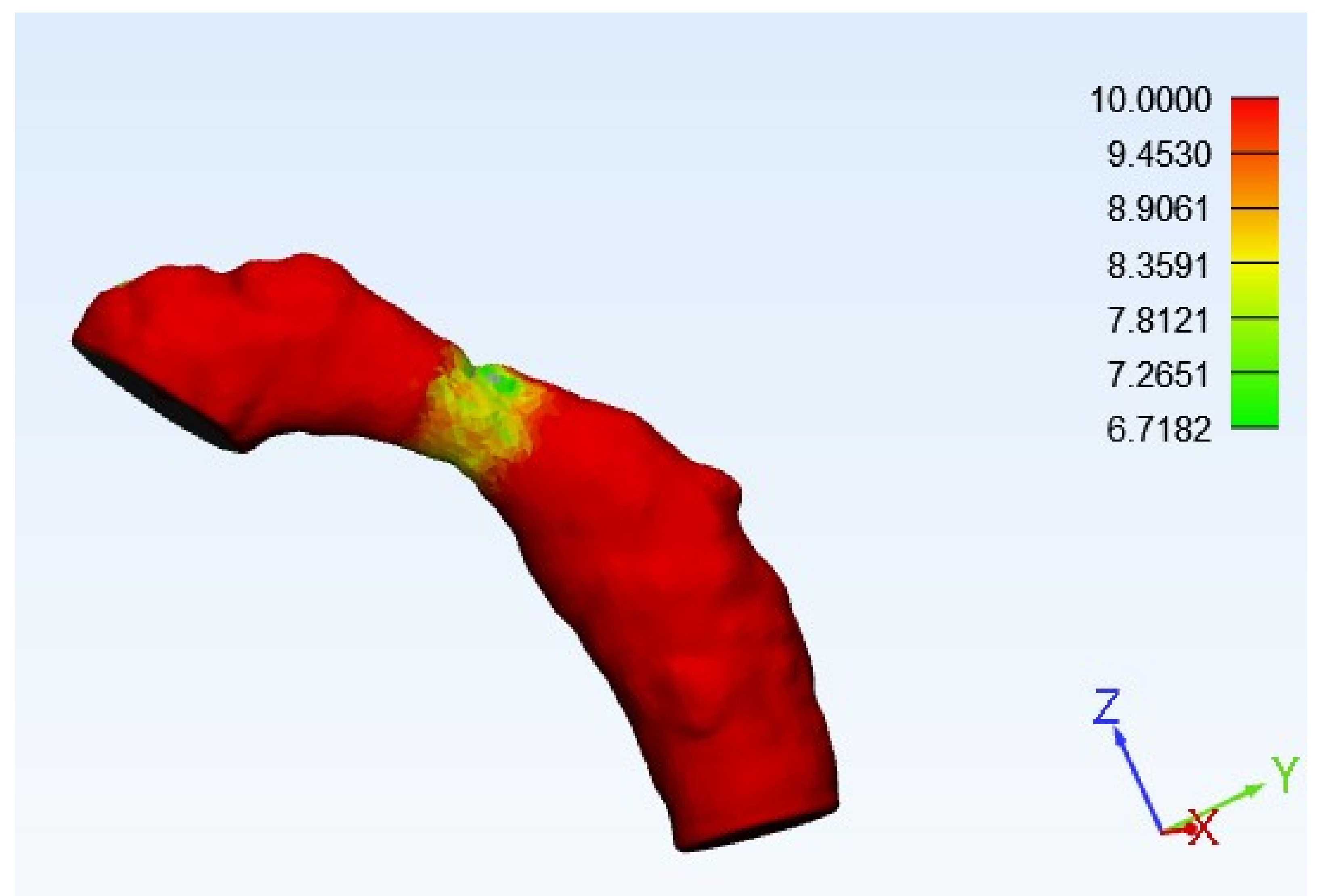
| Height (mm) | Radius (mm) | Normalized Height of the Stenosis (δ) | Rate of Stenosis (%) |
|---|---|---|---|
| 0.618 | 6.718 | 0.091991664 | 17.6% |
| 0.337 | 7.265 | 0.046386786 | 9.1% |
| 0.057 | 7.812 | 0.007296467 | 1.5% |
| 0.223 | 8.359 | 0.026677832 | 5.3% |
| 0.504 | 8.9 | 0.056629213 | 11.0% |
| 0.784 | 9.4 | 0.083404255 | 16.0% |
| 1.065 | 10 | 0.1065 | 20.2% |
| Estimated occlusion rate | 80.5% | ||
| Anterograde flow (mL/beat) | 25.56 |
| Retrograde flow (mL/beat) | 0.67 |
| pumped blood (mL/beat) | 24.89 |
| Regurgitation fraction | 0.03 |
| Difference of pressure (mmHg) | 14.96 |
| Flow movement | 0.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakly, H.; Said, M.; Tagina, M. Medical Decision Making for Cardiac MRI with CFD “Detection of Severe Stenosis Using a 5D Model of the Descending Aorta”. BioMedInformatics 2022, 2, 18-42. https://doi.org/10.3390/biomedinformatics2010002
Sakly H, Said M, Tagina M. Medical Decision Making for Cardiac MRI with CFD “Detection of Severe Stenosis Using a 5D Model of the Descending Aorta”. BioMedInformatics. 2022; 2(1):18-42. https://doi.org/10.3390/biomedinformatics2010002
Chicago/Turabian StyleSakly, Houneida, Mourad Said, and Moncef Tagina. 2022. "Medical Decision Making for Cardiac MRI with CFD “Detection of Severe Stenosis Using a 5D Model of the Descending Aorta”" BioMedInformatics 2, no. 1: 18-42. https://doi.org/10.3390/biomedinformatics2010002
APA StyleSakly, H., Said, M., & Tagina, M. (2022). Medical Decision Making for Cardiac MRI with CFD “Detection of Severe Stenosis Using a 5D Model of the Descending Aorta”. BioMedInformatics, 2(1), 18-42. https://doi.org/10.3390/biomedinformatics2010002






