Sparse-Input Neural Networks to Differentiate 32 Primary Cancer Types on the Basis of Somatic Point Mutations

Simple Summary

Cancers of unknown primary site represent ~5% of all cancer cases. Most of these cancers receive empirical chemotherapy decided by the oncologist, which typically results in poor survival rates. Identification of the primary cancer site could enable a more rational cancer treatment and even targeted therapies. Given that cancer is considered a genetic disease, one can hypothesize that somatic point mutations could be used to locate the primary cancer type. Studies have shown promising results in identifying breast and colorectal cancer, but there are cancer types/subtypes where somatic point mutations are not performing well. This could be due to somatic point mutations not significantly contributing to cancer initiation but could also be a result of other limitations such as (i) high sparsity in high dimensions, (ii) low signal-to-noise ratio, or (iii) a highly imbalanced dataset. The aim of this research was to examine the ability of somatic point mutations to classify primary cancer types/subtypes from primary tumor samples using state-of-the-art machine learning algorithms.

Abstract

Background and Objective: This paper aimed to differentiate primary cancer types from primary tumor samples on the basis of somatic point mutations (SPMs). Primary cancer site identification is necessary to perform site-specific and potentially targeted treatment. Current methods such as histopathology and lab tests cannot accurately determine cancer origin, which results in empirical patient treatment and poor survival rates. The availability of large deoxyribonucleic acid sequencing datasets has allowed scientists to examine the ability of somatic mutations to classify primary cancer sites. These datasets are highly sparse since most genes will not be mutated, have a low signal-to-noise ratio, and are often imbalanced since rare cancers have fewer samples. Methods: To overcome these limitations a sparse-input neural network (SPINN) is suggested that projects the input data in a lower-dimensional space, where the more informative genes are used for learning. To train and evaluate SPINN, an extensive dataset for SPM was collected from the cancer genome atlas containing 7624 samples spanning 32 cancer types. Different sampling strategies were performed to balance the dataset. SPINN was further validated on an independent ICGC dataset that contained 226 samples spanning four cancer types. Results and Conclusions: SPINN consistently outperformed classification algorithms such as extreme gradient boosting, deep neural networks, and support vector machines, achieving an accuracy up to 73% on independent testing data. Certain primary cancer types/subtypes (e.g., lung, brain, colon, esophagus, skin, and thyroid) were classified with an F-score > 0.80.

1. Introduction

The main disciplines used for cancer diagnosis are imaging, histopathology, and lab tests. Imaging is commonly used as a screening tool for cancer and can guide biopsy in hard-to-reach organs to extract tissue samples for histopathological examination. Histopathology can identify cancer cells but cannot always determine the primary site where the tumor originated before metastasizing to different organs. Lab tests usually examine the presence of proteins and tumor markers for signs of cancer, but the results do not indicate the cancer location and are not conclusive, as noncancerous conditions can cause similar results. Cancer cases of unknown primary site receive empirical treatments and, consequently, have poorer response and survival rate [1]. Given that cancer is a genetic disease, genome analysis could lead to the identification of primary cancer sites and more targeted treatments. Such analysis has recently become feasible due to the availability of large deoxyribonucleic acid (DNA) sequencing datasets.

Cancer type identification using genome analysis involves gene expression signatures, DNA methylation, and genetic aberrations. Gene expression might be the outcome of an altered or unaltered biological process or pathogenic medical condition, which has been used as a predictor of cancer types [2,3,4,5,6]. Abnormal DNA methylation profiles are present in all types of cancer and have also recently been used to identify cancer types [7,8]. This work focuses on a type of genetic aberration, namely, somatic point mutations (SPMs), which play an important role in tumor creation. Spontaneous mutations constantly take place, which accumulate in somatic cells. Most of these mutations are harmless, but others can affect cellular functions. Early mutations can lead to developmental disorders, and progressive accumulation of mutations can cause cancer and aging. Somatic mutations in cancer have been studied more in depth thanks to genome sequencing, providing insight into the mutational processes of genes that drive cancer. Sometimes a mutation can affect a gene or a regulatory element, leading to some cells gaining preferential growth and to clones of these cells surviving. Cancer could be considered as one end-product of somatic cell evolution, which results from the clonal expansion of a single abnormal cell. Martincorena et al. [9] explained how somatic mutations are connected to cancer, although we do not yet have full knowledge of how normal cells become cancer cells.

Somatic point mutations have been used as classifiers of the cancer site [10,11,12,13,14]. The performance of traditional classification algorithms is, however, hindered by imbalances arising from rare cancer types, small sample size, noise, and high data sparsity. Support vector machines (SVMs), classification trees, and k-nearest neighbors perform well for data with complex relations, specifically for low and moderate dimensions, but are not suitable for high-dimensional problems. Neural networks with many layers (deep) according to the circuit complexity theory can efficiently fit complex multivariate functions and perform well on high-dimensional data. Shallower neural networks could in theory perform equally well but would require many hidden units [15]. Deep neural networks (DNNs) require large training datasets and sophisticated stochastic gradient descent algorithms to alleviate the vanishing gradient problem. Most genes, however, do not contain any mutation, which would affect the learning ability of neural networks. Machine learning algorithms such as k-means clustering [14] and inter-class variations [16] have been used to find the discriminatory subset of genes to decrease the complexity of the problem. Identifying a discriminatory subset of genes will not necessarily resolve the problem of sparsity as most of the genes will still not contain a mutation.

To address the issue of sparsity and the lack of high-volume data, various methods have been proposed. Deep Gene [12] used somatic point mutations from 3122 samples and 22,834 genes from The Cancer Genome Atlas (TCGA), which were de-sparsified via two methods called ’clustered gene filtering’ (CGF) and ’indexed sparsity reduction’ (ISR) resulting in 1200 features; it achieved an average of 69% accuracy using a DNN classifier. Chen et al. [17] trained an SVM with a linear kernel on >100,000 features extracted from 22,111 genes and 6751 COSMIC samples to classify 17 cancer types. Following a 10-fold cross-validation feature extraction, averages of 62.00% accuracy, 65.24% precision, and 62.26% recall were achieved. Tumor Tracer [18] trained random forest classifiers and through a fivefold cross-validation applied to 530 features consisting of 232 mutations, 232 copy number alterations, and 96 single/trinucleotide base substitution frequencies; it achieved 85.00% accuracy, 85.83% precision, and 84.95% recall over six cancer types and 2820 COSMIC samples. However, when the copy number alterations were excluded, the achieved accuracy dropped to 69%.

This work proposes a sparse-input neural network which ‘directly’ addresses the issue of sparsity using a sparse group lasso regularization. Its performance is validated against commonly used classifiers and extreme gradient boosted trees (XGBoost) [19]. XGBoost is based on the gradient boosting machine; it can represent complex data with correlated features (genes), is robust to noise, and can manage data imbalance. Different balancing strategies were examined as a preprocessing step to examine if their application would benefit the classification accuracy. To evaluate the proposed classifiers, an extensive DNA sequencing database was collected from The Cancer Genome Atlas [20] and the ICGC [21].

2. Materials and Methods

2.1. Theory

Neural networks are not well suited for high-dimensional problems where the number of features p (e.g., p = 22,834) is high compared to the number of samples (e.g., n = 7624). The dataset formulated in this work (described later) is a set of binary features (genes) categorized into 32 cancer types. The formulated database is a case of a multiclass high-dimensional data problem as the number of features p is high compared to the number of samples. Only 1,974,759 features (genes) from the whole dataset show signs of mutation, whereby around 99% of the data is zero. Highly sparse datasets that contain many zeros (or contain incomplete data with many missing values) pose an additional problem as the learning power decreases due to a lack of informative features. To predict the response of such a complex problem, lasso (least absolute shrinkage and selection operator [22]) terms could be used in the objective function of the neural network to ensure sparsity within each group (cancer type) [23]. The L1 regularization of the neural network first layer weights θ, ${\left|\theta \right|}_1$ can result in sparse models with few weights. Consequently, when p > n, it is possible that lasso will tend to choose only one feature out of any cluster of highly correlated feature [24]. More than one gene commonly encodes a cancer type; hence, they should all be included and excluded together. This can be ensured by group lasso [25], which can result in a sparse set of groups; however, all the features in the group will be nonzero. A sparse group lasso penalty suggested by Simon et al., (2013) [26] mixes lasso and group lasso to achieve sparsity of groups and of the features within each group, which better suits the problem at hand. An extension of the sparse group lasso [27] that groups the weights of the first layer to the same input to select a subset of features and uses an additional ridge penalty applied to the weights of all layers other than the first to control their magnitude was used in this work.

$$\Psi \left(\theta ,\phi \right)={\displaystyle \sum }_{k=1}^n{\left(R_{\theta ,\phi }{x}_k-y_k\right)}^2+{\lambda }_0\Vert \phi {\Vert }_2^2+{\lambda }_1{\left|\theta \right|}_1+{\lambda }_2{\displaystyle \sum }_{j=1}^p\Vert \theta \left(j\right){\Vert }_2,$$

(1)

where R_θ,φ is the network structure with θ the weights of the first input layer and φ the weights of all layers other than the first, x is the p-dimensional feature (input) vector, y is the response variable, and λ represents the regularization parameters. x is a binary vector of length p = 22,834, where the i-th component is 0 if the i-th gene is not mutated and 1 if the i-th gene is mutated.

2.2. Classifiers

TCGA dataset described in Section 3 (22,834 genes from 7624 different samples spanning 32 cancer types) was split into two sets of samples ensuring the same proportions of class labels as the input dataset: one with 90% training and 10% testing data and the other with 80% training and 20% testing data. Samples were shuffled before splitting and split in a stratified way to ensure the same proportions of class labels between the training and testing datasets. The splitting of the training and testing datasets was repeated 10 times to avoid a misrepresentation of the actual performance of the classifiers due to the particular features of the training and testing datasets in one split. Hyperparameters and/or model parameters were optimized using a grid search approach for each classifier as part of the training. The optimal values were selected on the basis of the best mean cross-validation accuracy. Tenfold cross-validation was performed for all algorithms. Machine learning algorithms were developed in Python written in Keras [28] with a Tensorflow backend [29]. The developed algorithms were decision tree, k-nearest neighbors, support vector machines, artificial deep neural network, extreme gradient boosting (XGboost), and sparse-input neural nets (SPINNs). The k-nearest neighbors algorithm was run with k = 5. Decision trees were run with maximum depth of the tree equal to 50 and minimum number of samples required to split an internal node equal to 20. Support vector machines were run with regularization parameter C = 0.1 and kernel coefficient gamma = 100. The deep neural network was run with four hidden layers with 8000 neurons each, a total training epoch of 70, a learning rate of (0.001, 0.01, 0.1, 0.2), a weight decay of 0.0005, and a training batch of 256. The ReLu activation function was used, with softmax as the final layer. This a multiclass classification problem where the labels (cancer types) are represented as integers; hence, a sparse categorical cross-entropy objective function was used instead of a categorical cross-entropy. Given the relatively large number of classes (i.e., 32), the softmax function would be quite slow when calculating a categorical cross-entropy. Sparse categorical cross-entropy only uses a portion of all classes, thereby significantly decreasing the computational time. Training was performed by minimizing the sparse categorical cross-entropy, using adaptive learning rate optimization (ADAM [30]). XGBoost is a fast implementation of the gradient boosted decision tree.

Decision trees are regression models in the form of a tree structure. However, they are prone to bias and overfitting. Boosting is a method of sequentially training weak classifiers (decision trees) to produce a strong classifier where each classifier tries to correct its predecessor to prevent bias-related errors. Gradient boosting tries to fit the errors made in the initial fit and correct the corresponding errors in further training. XGBoost was run with a maximum tree depth of 12, boosting learning rate of 0.1, number of boosted trees to fit of 1000, subsampling parameter of 0.9, and sampling level of columns by tree of 0.8. A softmax objective function was used, and multiclass log-loss was used as an evaluation metric. SPINN (described in Section 2.1) was run with three hidden layers (with 2000, 1000, and 500 neurons), a maximum number of iterations of 1000, λ₀ = 0.0003, λ₁ = 0.001, and λ₂ = 0.1. Training was performed by minimizing the objective function in Equation (1) using ADAM [30].

2.3. Sampling Strategies

The two main strategies to deal with imbalanced datasets are either to balance the distribution of classes at the data level or to change the classifier to adapt to imbalanced data at the algorithm level. Data level balancing can be achieved by undersampling, oversampling, or a combination of both. The sampling strategies examined in this work were as follows:

• Random oversampling, where a subset from minority samples was randomly chosen; these selected samples were replicated and added to the original set.
• Synthetic minority oversampling technique (SMOTE) [31,32], where oversampling of minority class was achieved by generating synthetic samples.
• Adaptive synthetic (ADASYN) [33], where the distribution of the minority class was used to adaptively generate synthetic samples.
• Random undersampling, where data were randomly removed from the majority class to enforce balancing.
• Tomek link [34], as a modification on CNN (condensed nearest neighbor) [35], where samples were removed from the boundaries of different classes to reduce misclassification.
• One-sided selection (OSS) [36], where all majority class examples that were at the boundary or noise were removed from the dataset.
• Edited nearest neighbor (ENN) [37], where samples were removed from the class when the majority of their k nearest neighbors corresponded to a different class.
• Combination of over- and undersampling, which was performed using SMOTE with Tomek links and SMOTE with edited nearest neighbors.

3. Results

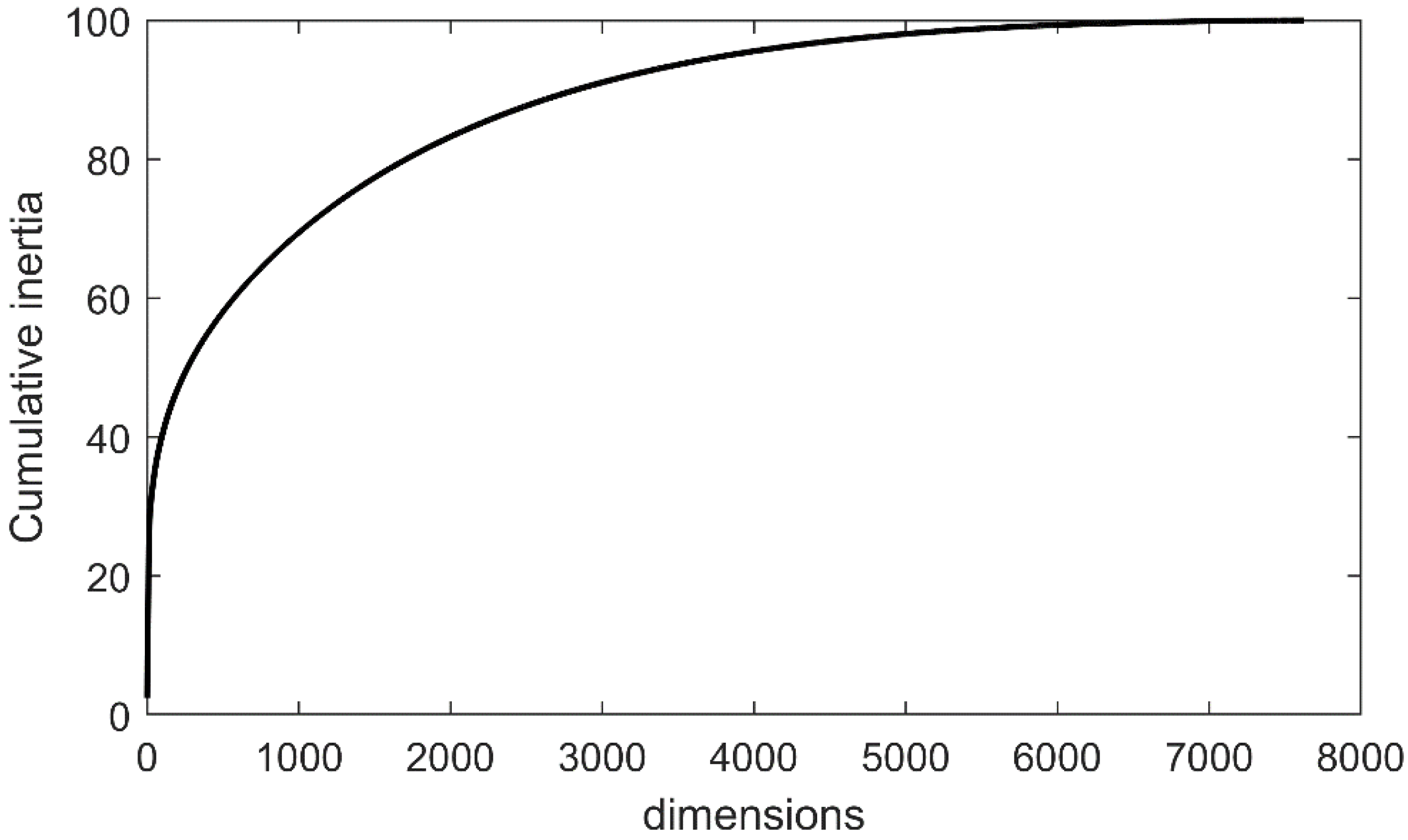
3.1. Reported Dataset

The dataset was collected from TCGA (The Cancer Genome Atlas) [20] with filter criteria IlluminaGA_DNASeq_Curated and was last updated on March 2019. All data can be found at http://tcga-data.nci.nih.gov (accessed on 30 March 2019). This dataset contains information about somatic point mutations in 22,834 genes from 7624 different samples with 32 cancer types. The inclusion of 32 tumor types and subtypes increases the number of associations between tumors and the number of convergent/divergent molecular subtypes. The cancer types are abbreviated as follows: adrenocortical carcinoma (ACC), bladder urothelial carcinoma (BLCA), breast invasive carcinoma (BRCA), cervical squamous cell carcinoma and endocervical adenocarcinoma (CESC), cholangiocarcinoma (CHOL), colon adenocarcinoma (COAD), lymphoid neoplasm diffuse large b-cell lymphoma (DLBC), esophageal carcinoma (ESCA), glioblastoma multiforme (GBM), head and neck squamous cell carcinoma (HNSC), kidney chromophobe (KICH), kidney renal papillary cell carcinoma (KIRP), acute myeloid leukemia (LAML), brain lower-grade glioma (LGG), liver hepatocellular carcinoma (LIHC), lung adenocarcinoma (LUAD), lung squamous cell carcinoma (LUSC), mesothelioma (MESO), ovarian serous cystadenocarcinoma (OV), pancreatic adenocarcinoma (PAAD), pheochromocytoma and paraganglioma (PCPG), prostate adenocarcinoma (PRAD), rectum adenocarcinoma (READ), sarcoma (SARC), skin cutaneous melanoma (SKCM), stomach adenocarcinoma (STAD), testicular germ cell tumors (TGCT), thyroid carcinoma (THCA), thymoma (THYM), uterine corpus endometrial carcinoma (UCEC), uterine carcinosarcoma (UCS), and uveal melanoma (UVM). An overview of the mutations per cancer type (Ca) is shown in

Table 1. Summary of somatic point mutations per cancer type (Ca).

Ca	Sample Number	Missense Mutations	Nonsense Mutations	Nonstop Mutations	Slice Sites	Total Mutations
ACC	91	7258	524	15	415	12,082
BLCA	130	25,108	2215	47	605	38,174
BRCA	993	55,063	4841	133	1561	83,973
CESC	194	26,606	2716	84	574	45,936
CHOL	36	3307	316	0	90	5222
COAD	423	163,454	12,146	184	9128	324,120
DLBC	48	9623	353	0	188	16,403
ESCA	183	33,179	2829	0	851	52,576
GBM	316	26,462	2230	15	813	46,899
HNSC	279	33,260	2686	44	864	49,776
KICH	66	1498	103	0	54	2341
KIRP	171	9442	515	18	697	15,007
LAML	197	1529	117	0	54	2320
LGG	286	6098	397	7	331	9256
LIHC	373	32,553	1853	0	1238	47,895
LUAD	230	47,700	3692	56	1558	69,546
LUSC	548	162,388	12,268	301	11,708	263,481
MESO	83	2780	177	8	196	5840
OV	142	7106	420	9	244	10,926
PAAD	150	19,899	1307	6	974	30,138
PCPG	184	3271	83	0	61	4212
PRAD	332	7816	433	12	496	11,846
READ	81	15,899	1724	0	306	23,862
SARC	259	15,457	785	19	332	22,185
SKCM	472	243,677	15,231	111	10,522	423,963
STAD	289	87,092	4423	93	3852	132,196
TGCT	156	2121	123	0	52	3428
THCA	406	3000	150	0	77	4489
THYM	121	15,938	1639	0	342	23,939
UCEC	248	121,440	13,472	158	1942	181,159
UCS	57	6003	612	16	275	8713
UVM	80	1665	73	0	36	2856
Total	7624	1,197,692	90,453	1336	50,436	1,974,759

. The number of samples varies heavily between different cancer types (e.g., BRCA has 993 samples whereas CHOL has only 36 samples) making the dataset highly unbalanced.

The main objectives of the formulated dataset were to compare the performance of different sampling approaches and the proposed machine learning algorithms. To gain better insight into the formulated dataset, intra- and between-class tests were performed on the original dataset before any sampling or splitting was performed. Intraclass correlations were estimated (

Table 2. Intraclass correlations for each cancer class.

ACC	BLCA	BRCA	CESC	CHOL	COAD	DLBC	ESCA
0.526	0.733	0.888	0.672	0.854	0.599	0.914	0.889
GBM	HNSC	KICH	KIRP	LAML	LGG	LIHC	LUAD
0.761	0.578	0.899	0.516	0.328	0.938	0.513	0.815
LUSC	MESO	OV	PAAD	PCPG	PRAD	READ	SARC
0.869	0.321	0.836	0.816	0.958	0.526	0.68	0.808
SKCM	STAD	TGCT	THCA	THYM	UCEC	UCS	UVM
0.689	0.648	0.968	0.548	0.928	0.623	0.87	0.769

to examine how strong samples in the same cancer class resembled each other. Other than MESO and LAML, the samples of the other cancer types were moderate, good, or excellent. Correspondence analysis was performed to determine the variables response of the gene × sample data in a low-dimensional space. Correspondence analysis can reveal the total picture of the relationship among gene–sample pairs that cannot be performed by pairwise analysis, and it was preferred over other dimension reduction methods because our data consisted of categorical variables. Cumulative inertia was calculated (Figure 1), and it was estimated that 1033 dimensions retained >70% of the total inertia. The intrinsic dimension of the data was also estimated using the maximum-likelihood estimation method [38] and was found to be equal to 811. Both these findings imply overlapping information between different samples.

To further evaluate the performance of the SPINN algorithm on an independent non-TCGA dataset, we used the ICGC (International Cancer Genome Consortium) dataset. Somatic point mutation data were collected for the BRCA, LAML, PAAD, and PRAD primary cancer sites, as shown in

Table 3. Summary of somatic point mutations per cancer type (Ca) for the ICGC dataset.

Ca.	Sample Number	Missense Mutations	Nonsense Mutations	Nonstop Mutations	Slice Sites	Total Mutations
BRCA	60	522	78	0	68	668
LAML	103	752	72	0	22	846
PAAD	98	154	16	6	7	196
PRAD	65	328	28	15	1	427

.

3.2. Overall Performance of the Classifiers on the Original Dataset

Sparse-input neural networks outperformed the other classifiers on both the 10% and the 20% testing datasets (

Table 4. Evaluation of the different classifiers on the testing TCGA dataset. The median values (25% to 75% interquartile range) of the metrics are reported over the 10 different splits of the training and testing datasets.

Learners/Classifiers	Acc	Precision	Recall	F-Score
Trained on the 90% of the samples (i.e., 6861) and tested on the 10% of the samples (i.e., 763)
Decision Tree	0.46 (0.40 to 0.51)	0.48 (0.42 to 0.51)	0.38 (0.31 to 0.43)	0.40 (0.34 to 0.44)
KNN	0.44 (0.38 to 0.49)	0.44 (0.38 to 0.47)	0.35 (0.30 to 0.39)	0.33 (0.26 to 0.39)
SVM	0.60 (0.55 to 0.64)	0.64 (0.60 to 0.68)	0.47 (0.41 to 0.51)	0.50 (0.44 to 0.53)
XGBoost	0.66 (0.42 to 0.48)	0.64 (0.59 to 0.68)	0.56 (0.51 to 0.60)	0.58 (0.53 to 0.63)
Neural Networks	0.69 (0.64 to 0.73)	0.66 (0.61 to 0.70)	0.57 (0.51 to 0.61)	0.59 (0.54 to 0.63)
SPINN	0.71 (0.67 to 0.74)	0.74 (0.70 to 0.77)	0.62 (0.57 to 0.66)	0.65 (0.61 to 0.69)
Trained on the 80% of the samples (i.e., 6099) and tested on the 20% of the samples (i.e., 1525)
Decision Tree	0.45 (0.38 to 0.51)	0.45 (0.39 to 0.51)	0.36 (0.29 to 0.41)	0.38 (0.32 to 0.43)
KNN	0.43 (0.35 to 0.49)	0.45 (0.36 to 0.48)	0.33 (0.26 to 0.38)	0.32 (0.25 to 0.38)
SVM	0.60 (0.52 to 0.65)	0.63 (0.56 to 0.68)	0.47 (0.39 to 0.52)	0.50 (0.43 to 0.55)
XGBoost	0.65 (0.59 to 0.70)	0.63 (0.56 to 0.68)	0.54 (0.49 to 0.58)	0.56 (0.50 to 0.60)
Neural Networks	0.67 (0.60 to 0.72)	0.63 (0.55 to 0.68)	0.55 (0.49 to 0.60)	0.57 (0.50 to 0.61)
SPINN	0.69 (0.63 to 0.73)	0.66 (0.61 to 0.71)	0.59 (0.54 to 0.66)	0.61 (0.56 to 0.66)

). The evaluation was performed using four different metrics, namely, accuracy, precision, recall, and F-score. Accuracy (Acc) is the most commonly used metric measuring the ratio of correctly classified samples over the total number of samples; however, it provides no insights into the ratio of true positives to true negatives. Precision relates to the true positive rate and is equal to the ratio of true positives over the sum of true and false positives. Recall, also referred to as sensitivity, relates to the ratio of correctly classified samples over all samples that have this cancer type, and it is equal to the ratio of true positives over the sum of true positives and false negatives. F-score is more complex to understand but is more reliable than accuracy in our case because the dataset was imbalanced, and the numbers of true positives and true negatives were uneven.

3.3. Sampling

Initially, the different over/undersampling strategies were applied to the training datasets. For datasets generated after applying oversampling techniques (i.e., SMOTE and ADASYN), the performance of the classifiers remained comparable to the tests on the original datasets. SMOTE gave better results than ADASYN probably due to the samples generated on the outside of the borderline of the minority class. Undersampling methods were also applied to remove many samples from the data. In the case of ENN and CNN, the created dataset contained only 1264 and 772 samples, respectively, from the original data. On the basis of this finding, one could conclude that most of the classes overlapped and had multiple covariates, as also implied by the correspondence analysis (Figure 1). This class overlapping can be considered as the main factor in a classifier’s poor performance besides class imbalance. Due to the reduced number of samples, all classifiers performed poorly on the undersampled data. The only technique that marginally benefited classification (

Table 5. Evaluation of the different classifiers on the testing TCGA dataset (after Tomek links were removed, the total number of samples was reduced to 6859 from 7624). The median values (25% to 75% interquartile range) of the metrics are reported over the 10 different splits of the training and testing datasets.

Learners/Classifiers	Acc	Precision	Recall	F-Score
Trained on the 90% of the samples (i.e., 6173) and tested on the 10% of the samples (i.e., 686)
Decision Tree	0.46 (0.40 to 0.48)	0.48 (0.42 to 0.50)	0.38 (0.33 to 0.40)	0.40 (0.36 to 0.42)
KNN	0.44 (0.39 to 0.46)	0.44 (0.40 to 0.46)	0.35 (0.30 to 0.37)	0.33 (0.29 to 0.36)
SVM	0.61 (0.57 to 0.64)	0.64 (0.60 to 0.67)	0.47 (0.41 to 0.49)	0.51 (0.47 to 0.53)
XGBoost	0.68 (0.63 to 0.71)	0.65 (0.61 to 0.67)	0.57 (0.53 to 0.60)	0.59 (0.56 to 0.61)
Neural Networks	0.70 (0.65 to 0.73)	0.65 (0.61 to 0.67)	0.59 (0.55 to 0.63)	0.60 (0.55 to 0.62)
SPINN	0.73 (0.70 to 0.76)	0.75 (0.72 to 0.78)	0.64 (0.60 to 0.67)	0.67 (0.64 to 0.71)
Trained on the 80% of the samples (i.e., 5487) and tested on the 20% of the samples (i.e., 1372)
Decision Tree	0.45 (0.39 to 0.50)	0.45 (0.40 to 0.50)	0.36 (0.30 to 0.41)	0.38 (0.33 to 0.42)
KNN	0.43 (0.39 to 0.46)	0.45 (0.40 to 0.49)	0.33 (0.27 to 0.36)	0.32 (0.27 to 0.35)
SVM	0.60 (0.55 to 0.63)	0.63 (0.59 to 0.66)	0.47 (0.42 to 0.50)	0.50 (0.45 to 0.53)
XGBoost	0.66 (0.62 to 0.69)	0.64 (0.60 to 0.67)	0.55 (0.50 to 0.59)	0.57 (0.51 to 0.60)
Neural Networks	0.68 (0.63 to 0.72)	0.66 (0.61 to 0.70)	0.57 (0.52 to 0.61)	0.58 (0.53 to 0.62)
SPINN	0.71 (0.66 to 0.73)	0.73 (0.69 to 0.76)	0.64 (0.60 to 0.67)	0.66 (0.61 to 0.70)

) was the removal of Tomek links. This approach removes samples from the boundaries of different classes to reduce misclassification.

3.4. Classifier Performance per Primary Cancer Type

In addition to the overall performance of the classifiers, it is important to examine their performance per cancer type as this varies significantly. Figure 2 and Figure 3 illustrate the performance of the sparse-input neural networks per cancer type (F-score) on the 10% and 20% TCGA testing datasets, respectively.

Table 6. Confusion matrix of multiclass classification (columns: predicted, row: true) for the sparse-input neural network on the 10% TCGA testing dataset.

	ACC	BLCA	BRCA	CESC	HNSC	KIRP	LGG	LUAD	PAAD	PRAD	STAD	UCS	CHOL	COAD	DLBC	ESCA	GBM	KICH	LAML	LIHC	LUSC	MESO	OV	PCPG	READ	SARC	SKCM	TGCT	THCA	THYM	UCEC	UVM
ACC	7	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
BLCA	0	5	0	0	2	0	0	0	0	0	3	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	0	0
BRCA	0	0	77	0	1	0	0	0	1	8	0	0	0	0	0	1	1	0	0	0	1	1	1	0	0	1	0	0	6	0	0	0
CESC	0	0	1	13	0	1	0	0	1	1	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
HNSC	0	2	2	0	16	0	0	0	0	3	2	0	0	0	0	0	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0
KIRP	1	1	0	1	1	12	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0
LGG	0	0	1	0	0	0	25	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0
LUAD	0	0	0	0	2	0	0	17	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0
PAAD	0	0	0	0	0	0	0	0	14	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
PRAD	0	0	2	0	0	0	1	0	0	25	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	1	0	2	0	0	0
STAD	0	0	1	0	5	0	0	0	1	1	15	0	0	1	0	0	0	0	0	3	0	0	0	0	0	1	0	0	0	0	1	0
UCS	0	0	0	0	0	0	0	0	1	0	0	3	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	2	0
CHOL	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0	0
COAD	0	0	0	0	0	0	0	0	0	0	0	0	0	38	0	0	0	0	0	0	2	0	0	0	2	0	0	0	0	0	0	0
DLBC	0	0	0	0	0	0	0	0	0	0	0	0	0	0	3	0	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0
ESCA	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	16	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
GBM	0	0	2	0	0	0	1	0	1	4	1	0	0	0	0	0	21	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0
KICH	0	0	0	0	0	0	0	0	0	2	0	0	0	0	0	0	0	2	0	1	0	0	1	0	0	0	0	0	1	0	0	0
LAML	0	0	0	0	0	0	1	0	0	4	0	0	0	0	0	0	0	0	15	0	0	0	0	0	0	0	0	0	0	0	0	0
LIHC	0	0	2	0	0	0	1	0	1	4	0	0	0	0	0	0	0	0	0	25	0	0	0	1	0	0	0	1	1	1	0	0
LUSC	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	53	0	0	0	0	0	0	0	0	0	0	0
MESO	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	2	0	4	0	0	0	0	0	0	0	0	0	0
OV	0	0	7	0	0	0	0	0	0	2	1	0	0	0	0	0	0	0	1	0	0	0	3	0	0	0	0	0	0	0	0	0
PCPG	0	0	2	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	12	0	1	0	1	0	0	0	0
READ	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	6	0	0	0	1	0	0	0
SARC	0	0	4	0	0	0	1	0	0	7	0	0	0	0	0	1	0	0	0	1	0	0	0	1	0	11	0	0	0	0	0	0
SKCM	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	1	0	0	0	0	42	0	1	0	0	0
TGCT	0	0	2	0	0	2	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	8	0	0	0	0
THCA	0	0	0	0	0	0	0	0	0	4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	35	0	1	0
THYM	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	3	0	0	0	0	0	0	0	0	0	6	0	1
UCEC	0	0	5	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	18	0
UVM	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	7

and

Table 7. Confusion matrix of multiclass classification (columns: predicted, row: true) for the sparse-input neural network on the 20% TCGA testing dataset.

	ACC	BLCA	BRCA	CESC	HNSC	KIRP	LGG	LUAD	PAAD	PRAD	STAD	UCS	CHOL	COAD	DLBC	ESCA	GBM	KICH	LAML	LIHC	LUSC	MESO	OV	PCPG	READ	SARC	SKCM	TGCT	THCA	THYM	UCEC	UVM
ACC	7	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
BLCA	0	4	0	0	2	0	0	0	0	0	3	0	0	0	0	0	0	0	0	1	0	0	1	1	0	0	0	0	0	0	1	0
BRCA	0	0	76	0	1	0	0	0	1	8	0	0	0	0	0	1	1	0	0	1	1	1	1	0	0	1	0	0	6	0	0	0
CESC	0	0	1	13	0	1	0	0	1	1	0	0	1	0	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
HNSC	0	2	2	0	16	0	0	0	0	3	2	0	0	0	0	0	1	0	0	1	0	0	1	0	0	0	0	0	0	0	0	0
KIRP	1	1	0	1	1	12	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0
LGG	0	0	1	0	0	0	25	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0
LUAD	0	0	0	0	2	0	0	16	0	1	2	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	0
PAAD	0	0	0	0	0	0	0	0	14	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
PRAD	0	0	2	0	0	0	1	0	0	25	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	1	0	2	0	0	0
STAD	0	0	1	0	5	0	0	0	1	1	14	0	0	1	0	0	0	0	0	3	0	0	1	0	0	1	0	0	0	0	1	0
UCS	0	0	0	0	0	0	0	0	1	1	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	2	0
CHOL	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0	0
COAD	0	0	0	0	0	0	0	0	0	0	0	0	0	37	0	0	0	0	0	0	2	0	0	0	2	0	1	0	0	0	0	0
DLBC	0	0	0	0	0	0	0	0	0	0	0	0	0	0	3	0	0	0	0	0	0	0	0	0	0	1	0	0	0	1	0	0
ESCA	0	0	1	0	0	0	0	0	0	0	0	0	0	0	0	16	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
GBM	0	0	2	0	0	0	1	0	1	4	1	0	0	0	0	0	21	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0
KICH	0	0	0	0	0	0	0	0	0	2	0	0	0	0	0	0	0	2	0	1	0	0	1	0	0	0	0	0	1	0	0	0
LAML	0	0	0	0	0	0	1	0	0	4	0	0	0	0	0	0	0	0	15	0	0	0	0	0	0	0	0	0	0	0	0	0
LIHC	0	0	2	0	0	0	1	0	1	4	0	0	0	0	0	0	0	0	0	25	0	0	0	1	0	0	0	1	1	1	0	0
LUSC	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	53	0	0	0	0	0	0	0	0	0	0	0
MESO	0	0	1	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	2	1	3	0	0	0	0	0	0	0	0	0	0
OV	0	0	7	0	0	0	0	0	0	2	1	0	0	0	0	0	0	0	1	0	0	0	3	0	0	0	0	0	0	0	0	0
PCPG	0	0	2	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	12	0	1	0	1	0	0	0	0
READ	0	0	0	0	0	0	0	0	1	0	0	0	0	1	0	0	0	0	0	0	0	0	0	0	5	0	0	0	1	0	0	0
SARC	0	0	4	0	0	0	1	0	0	7	0	0	0	0	0	1	0	0	0	1	0	0	0	1	0	11	0	0	0	0	0	0
SKCM	1	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	1	0	0	0	0	42	0	1	0	0	0
TGCT	0	0	2	0	0	2	0	0	0	2	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	1	0	8	0	0	0	0
THCA	0	0	0	0	0	0	0	0	0	4	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	35	0	1	0
THYM	0	0	1	0	0	0	0	0	1	0	0	0	0	0	0	1	0	0	0	3	0	0	0	0	0	0	0	0	0	5	0	1
UCEC	0	0	5	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	2	0	0	0	0	0	0	0	0	0	0	17	0
UVM	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	7

show the confusion matrices on the 10% and 20% TCGA testing datasets, respectively, to better understand the performance of the sparse-input neural network. SPINN consistently outperformed the other classification algorithms for all cancer types.

As expected, the classifier performance varied as a function of cancer type (e.g., 0.24 for OV and 0.94 for LUSC), but this variance should not necessarily be attributed to the sample size. Spearman’s rank correlation coefficient was used to decide whether the sample number and the F-score per cancer type were correlated without assuming them to follow a normal distribution. There was no rank correlation between sample size and F-score (r = 0.02 for the 10% testing dataset and r = 0.04 for the 20% testing dataset).

The examined classifiers were also validated on an independent non-TCGA dataset (ICGC) that consisted of four primary cancer sites (BRCA, LAML, PAAD, and PRAD). SPINN consistently outperformed the other classifiers (

Table 8. Evaluation using the F-score of the different classifiers on the independent ICGC dataset. The models validated were trained on TCGA dataset after Tomek links were removed.

	BRCA	LAML	PAAD	PRAD
Decision tree	0.40	0.45	0.41	0.19
KNN	0.39	0.44	0.39	0.18
SVM	0.53	0.55	0.54	0.25
XGBoost	0.62	0.69	0.61	0.30
Neural Networks	0.61	0.68	0.62	0.29
SPINN	0.64	0.72	0.65	0.30

).

4. Discussion

Cancers of unknown primary site represent ~5% of all cancer cases. Most of these cancers receive empirical chemotherapy decided by the oncologist, which typically results in poor survival rates. Identification of the primary cancer site could enable a more rational cancer treatment and even targeted therapies. Given that cancer is considered a genetic disease [39], one can hypothesize that somatic point mutations could be used to locate the primary cancer type. Studies have shown promising results on identifying breast and colorectal cancer [39], but there are cancer types/subtypes where somatic point mutations are not performing well. This could be due to somatic point mutations not significantly contributing to cancer initiation but could also be a result of other limitations such as (i) high sparsity in high dimensions, (ii) low signal-to-noise ratio, or (iii) a highly imbalanced dataset. With next-generation cost-effective gene sequencing, we are getting a high amount of genomics data. The aim of this research was to examine the ability of somatic point mutations to classify primary cancer types/subtypes from primary tumor samples using state-of-the-art machine learning algorithms.

TCGA open-access data were collected as described in Section 2, which consisted of 22,834 genes from 7624 different samples spanning 32 different cancer types. To the best of the author’s knowledge, this is the first time such an extensive dataset with samples from 32 cancer types has been reported. The resulting database is very imbalanced with common cancers sites such as breast having 993 samples, while rare cancer sites have as low as 36 samples. All 22,834 genes were included, resulting in a highly sparse database with 99% of the genes having no mutations. Different machine learning algorithms were trained on 90% or 80% of the original dataset and were tested on the remaining 10% or 20%, respectively. An independent validation was also performed for the BRCA, LAML, PAAD, and PRAD primary cancer sites using samples collected for the ICGC.

Neural networks perform well on high-dimensional problems and can approximate complex multivariate functions; however, given that only a small subset of the genes would be informative per cancer type, their performance was hindered. This work proposed a sparse-input neural network (described in Section 2.1) which employs a combination of lasso, group lasso, and ridge penalties to the loss function to project the input data in a lower-dimensional space where the more informative genes are used for learning. Our results show that the sparse-input neural network could achieve up to 73% accuracy on TCGA dataset without any preprocessing of features such as gene selection. The above statement shows the learning power of neural networks with regularization. XGBoost and deep neural networks also performed well compared to traditional classifiers (decision trees, KNN, and SVM). These findings were also confirmed when the trained classifiers were validated on the ICGC independent dataset.

All sampling strategies described in the literature are associated with the use of nearest neighbors to either oversample or undersample the dataset. In this work, balancing TCGA dataset using sampling strategies did not benefit the classifier performance except for removing Tomek links. This was probably due to the high amount of class overlap. Figure 2 and Figure 3 demonstrate that classification performance significantly varied as a function of cancer type. In agreement with previous studies, breast and colorectal cancer had a high classification accuracy (F-scores up to 0.73 and 0.90, respectively). This study showcased that somatic point mutations can also accurately classify other types of cancer. There were cancer types, however, where classifiers performed poorly. This is not necessarily related solely to having few training samples, as the F-score did not seem to relate to the sample size; however, for certain cancer types, it could also be related to a high amount of class overlap. This hypothesis was reinforced following ENN, CNN undersampling, correspondence analysis, and estimation of the intrinsic dimension. All analyses suggested that only ~1000 of the samples were mutually independent.

5. Conclusions

To conclude, this work determined that using only somatic point mutations can yield good performance in differentiating primary cancer types if the sparsity of the data is considered. Results, however, also indicated some similarity in the information provided by somatic point mutations for different primary cancer types. This limitation could be managed by (i) investigating preprocessing methods [40,41,42] that could cluster somatic mutations and/or learn which genes are involved in cancer initiation [43], and (ii) enriching the database especially for rare cancer types and/or introducing additional genomic information such as copy number variations, as well as DNA methylation and gene expression signatures.