Next Article in Journal
ERBB1/EGFR and JAK3 Tyrosine Kinases as Potential Therapeutic Targets in High-Risk Multiple Myeloma
Previous Article in Journal
Augmented Expression of the IL3RA/CD123 Gene in MLL/KMT2A-Rearranged Pediatric AML and Infant ALL
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Onco
Volume 2
Issue 3
10.3390/onco2030015
onco-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Dependence of Compensation Dose on Systematic and Random Interruption Treatment Time in Radiation Therapy

by
Ramin Abolfath
1,*,
Mitra Khalili
2,
Alireza G. Senejani
3,
Balachandran Kodery
1 and
Robert Ivker
1
1
Department of Radiation Oncology, New Jersey Urology, West Orange, NJ 07052, USA
2
Department of Medical Genetics and Molecular Medicine, School of Medicine, Zanjan University of Medical Sciences, Zanjan 4513956111, Iran
3
Department of Biology and Environmental Science, University of New Haven, West Haven, CT 06516, USA
*
Author to whom correspondence should be addressed.
Onco 2022, 2(3), 264-281; https://doi.org/10.3390/onco2030015
Submission received: 10 August 2022 / Revised: 31 August 2022 / Accepted: 31 August 2022 / Published: 5 September 2022
Browse Figures
Versions Notes

Abstract

:
Introduction: In this work, we develop a multi-scale model to calculate corrections to the prescription dose to predict compensation required for the DNA repair mechanism and the repopulation of the cancer cells due to the occurrence of patient scheduling variabilities and the treatment time-gap in fractionation scheme. Methods: A system of multi-scale, time-dependent birth-death Master equations is used to describe stochastic evolution of double-strand breaks (DSBs) formed on DNAs and post-irradiation intra and inter chromosomes end-joining processes in cells, including repair and mis-repair mechanisms in microscopic scale, with an extension appropriate for calculation of tumor control probability (TCP) in macroscopic scale. Variabilities in fractionation time due to systematic shifts in patient’s scheduling and randomness in inter-fractionation treatment time are modeled. For an illustration of the methodology, we focus on prostate cancer. Results: We derive analytical corrections to linear-quadratic radiobiological indices α and β as a function of variabilities in treatment time and shifts in patient’s scheduling. We illustrate the dependence of the absolute value of the compensated dose on radio-biological sensitivity, α / β , DNA repair half-time, T 1 / 2 , tumor cells repopulation rate, and the time-gaps among treatment fractions due to inter-patient variabilities. At a given tumor size, delays between fractions totaling 24 h over the entire course of treatment, in a typical prostate cancer fractionation scheme, e.g., 81 Gy, 1.8 Gy per fraction and 45 treatment days, require up to 10% compensation dose if the sublethal DNA repair half-time, T 1 / 2 , spans over 10 h. We show that the contribution of the fast DNA repair mechanisms to the total dose is negligible. Instead, any compensation to the total dose stems from the tumor cell repopulation that may go up to a significant fraction of the original dose for a time gap of up to one week. Conclusions: We recommend implementation of time irregularities in treatment scheduling in the clinic settings to be taken into account. To achieve a clinical endpoint, corrections to the prescription dose must be assessed, in particular, if modern external beam therapy techniques such as IMRT/VMAT are used for the treatment of cancer.

1. Introduction

It is now evident that increase in frequency of occurrence of natural disasters such as hurricanes, floods and large scale fires due to severe climate change and global warming, in addition to the recent pandemic, lead to temporary shut down of outpatient cancer centers. Such natural events cause unforeseen and in some cases a long interruption in patients treatments. For example, in September 2021, several radiotherapy centers were shut down due to the remnants of Hurricane Ida that resulted in severe thunderstorms and tornadoes around the North East area. It is, therefore, an emerging demand to investigate potential clinical actions that may require to adjust the prescribed doses of radiation to compensate for the patients’ anatomical changes and tumor growth that may take place during the interrupted treatment time.
In the most common modality in radiotherapy, megavoltage photons generated in clinical linear accelerators are mechanically focused to target cancerous tumors for treatment of malignancy.
In radiotherapy, radiosensitivity, repopulation, repair, reoxygenation, and redistribution also called 5R’s are known to have important impact on outcome of radiotherapy (RT) treatment [1]. Although recently, reactivation of the immune system by RT has been also proposed as 6th R [2].
Among all of these processes, damage to DNA [3,4] and tumor cell repopulation during the treatment gap play crucial roles as under treated tumors have a chance of regrowth and tumor cell repopulation, a typical condition if a delay and time-gaps among fractions occur.
In a nutshell, repair of DSBs that are caused by RT is vital for cell survival [5,6,7]. RT prompts formation of reactive oxygen species (ROS) directly or indirectly which generates apurinic/apyrimidinic (abasic) sites in the DNA, SSBs, sugar moiety modifications, and deaminated adducted bases [8]. RT stimulates the activation of DNA damage repair (DDR). The up-regulation of DDR genes (BRCA1, FANCG, RAD51) promote cell survival following irradiation in radioresistant (PC-3) prostate cancer cell line [8]. Although several mutations in these genes also increase the risk for developing breast and other neoplasias as well. Tumor cells able to efficiently repair the radiation damage would develop resistance to radiation and enable cells to survive and replicate. In addition, healthy cells surrounding the cancer cells can get damaged. They would recover by either successfully repairing their DNA or inducing cell death (apoptosis). Also, bystander effects of RT on normal cells may contribute to chromosomal aberrations and to an increase the risk for new malignancies [9].
The half-life values of DNA repair depend on cell and tissue type, physical (dose and type of radiation), chemical (oxygenation) and biological parameters (DNA repair systems). The fast repair half-life is approximately 3–22 min and the slow repair half-life is approximately 40 min–12 h. See Table 1.
To take advantage of such complex and stochastic processes and bring it under control for a therapeutic modality of cancer, various clinical trials were proposed in the last century. It is common in the current standard of practice among practitioners to follow recommendations by The Radiation Therapy Oncology Group (RTOG) and other clinical trials, in addition to in-house clinical protocols, and to prescribe a specific sequence of dose (Gy) per fraction. Synchrony between fractionation scheme, physio-chemical pathway of DNA damage and cell survival is crucial for achieving high efficacy of the treatment. It is therefore crucial to investigate and assess the sensitivities of the clinical endpoints to the clinical variations, such as the synchronization of the treatment and administration times.
The effect of time to deliver the dose has been studied extensively. For a variety of cell lines and clinically relevant scenarios the effects of dose rate and treatment interruption have been studied in Refs. [10,11,12,13,14].
A recent clinical study performed by Dong et al. [15] reported outcomes for 1728 patients. This study concluded that the treatment interruption did not lead to differences in freedom from biochemical failure or overall survival. Ohri et al. [16], reported on consequences of radiation therapy (RT) noncompliance on clinical outcomes. The authors considered patients who missed 2 or more scheduled RT appointments, excluding planned treatment breaks, noncompliant. Their model incorporated statistical analysis for patients who completed courses of external beam RT with curative intent for cancers of the head and neck, breast, lung, cervix, uterus, or rectum. The authors used a multivariable logistic regression to predict the likelihood that a given patient would be noncompliant to identify high-risk patients who require additional interventions due to noncompliance RT. Although the Ohri et al. [16] publication is an insightful analysis of consequences of non-compliance on treatment outcomes, such analysis and algorithms lack the physical, chemical and biological processes underlying the radio-biological effects as described in this study.
One of the earliest studies on the effect of the exposure time irregularities on cell survival was investigated by Elkind and Sutton [17]. In a series of in-vitro assays, they systematically exposed mammalian Chinese Hamster cells grown in culture within a range of 50 to 100 KeV X-ray energies and illustrated variabilities in cell-survival as a function of exposure time irregularities.
These experimental results demonstrated that overall cell survival tends to increase with increase in total exposure time. Hence, one can infer a compensation dose must be added to achieve a biological endpoint. The authors attributed this effect primarily to sublethal damage repair because with an increase in exposure time, subjected to constant dose, the repair mechanisms take place more effectively.
The effect of fractionation and prolonged delivery time compared with acute irradiation in intensity modulated radiotherapy was investigated by Mu et al. [18]. The study was performed in-vitro by irradiation of Chinese hamster fibroblasts (V79-379-A) to replicate clinical situations of mammalian cells, using fractionation schemes. In this experiment, each fraction was divided into different subfractions, simulating the delivery of a complicated treatment. Consistent with the earlier results reported by Elkind and Sutton [17], a prolonged delivery time was shown to cause significant reduction of radiation effects compared with acute irradiation, such that in the former tissues with a fast DNA repair may be spared, hence there would be risks for sparing tumors. Moreover, Mu et al. [18] pointed out the effect of prolonging fraction time that includes irregularities in treatment scheduling at conventional dose per fraction is underestimated by biological models.
To simulate biological effects due to irradiation with their mathematical models, Mu et al. [18] determined the radiobiological parameters α and β for the V-79 cells. α and β were obtained from a single-fraction experiment where the V-79 cells were irradiated to different dose levels with a constant dose rate (2 Gy/min). They also determined the time constant for repair of sublethal damage, τ and T 1 / 2 ( = τ / ln 2 ) , by exposing V-79 cells to two fractions with different 0–8 h time intervals between the fractions. The experiments were performed with two different doses per fraction, 2 and 4 Gy. The mathematical model used by Mu et al. [18] to plot surviving fraction against time between fractions to estimate τ and T 1 / 2 limited to several constraints. In particular, the model is a patch of different approaches and approximations. Finally, Mu et al. [18] concluded that consideration of time irregularities in treatment scheduling in the clinic must be taken into account if IMRT technique is implemented. In this work, we address this issue by presenting a unified mathematical framework and resolve various ambiguities at the mathematical and physical levels where Mu et al. [18] is dealt with.
More recently, the effect of variabilities in intra-fractionation time in carbon-ion radiotherapy were reported in Refs. [19,20,21], using microdosimetric kinetic model (MKM). Inaniwa et al. [20,21] investigated the effects of dose-delivery and unintended machine interruption time on biological effectiveness and on tumor control probability (TCP) due to patient repositioning. The authors demonstrated that the realistic biological effectiveness of therapeutic carbon-ion beam decreases with increasing interruption time. They suggested the curative dose to be increased by 20% or more compared to the planned dose if the interruption time extends to 30 min or longer. They concluded that these effects should be considered in carbon-ion radiotherapy treatment planning if a longer dose-delivery procedure time is anticipated.
In particular, it is in the current interest of cancer centers to develop a radiation therapy model to translate the fractionation variabilities to an equivalent dose that would be gained or lost because of these variations. Such investigations open up possibilities in search of solutions where subtracting or adding dose corrections to compensate the prescription dose can be introduced and incorporated to the clinical trials. This is the goal of this study.
We propose a model calculation to predict the effects of random and systematic inter-fractionation time variabilities to the prescription dose. We follow a similar line of thoughts, previously presented by Inaniwa et al. [20,21], but for photon therapy. We theoretically investigate the effect of irregularities in inter-fractionation time on biological effectiveness, cell survival and TCP. We illustrate our findings for typical fractionation schemes in prostate cancer, e.g., with 39 to 45 fractions in which the effect of intra-fractionation delivery time, as studied in Refs. [19,20,21], can be neglected. This is consistent with our institutional standard of practice and implementation of VMAT technique for a large pool of prostate cancer patients. We note that the variabilities considered in this work are due to the treatment interruption relative to the standard fractionation schedule that includes the weekends with no patient treatment.
We further engage the clinical result and conclusion drawn by Dong et al. [15] to validate the present theoretical model. Center to this validation processes is an assumption on the DNA repair rate. The numerical results presented in this work exhibit an agreement between the model prediction and the clinical data [15], if fast DNA repair mechanisms are considered as major contributors to the overall DNA repair. In contrast, if slow DNA repair mechanisms were hypothetically to contribute a dominant mechanism in DNA repair, a significant dose correction must be added to compensate for a 24 h treatment interruption.
Table
Table 1. Repair mechanisms mediated by enzymatic reactions.
Table 1. Repair mechanisms mediated by enzymatic reactions.
Fast (min)Slow (h)Totally (Not Determined)Cell TypeRef
7–41–1.5 CHO[22,23]
52.5 HF19[24]
19 minACHN Renal Cell Carcinoma[25]
≤60 minMammalian[26]
3–100.6–4 -[27]
134.5 DT40[28]
7–82.5 GM5758, GM7166, M059K, U-1810[29]
2212 human glioma cell line, M059-J and M059-K[30]

2. Materials and Methods

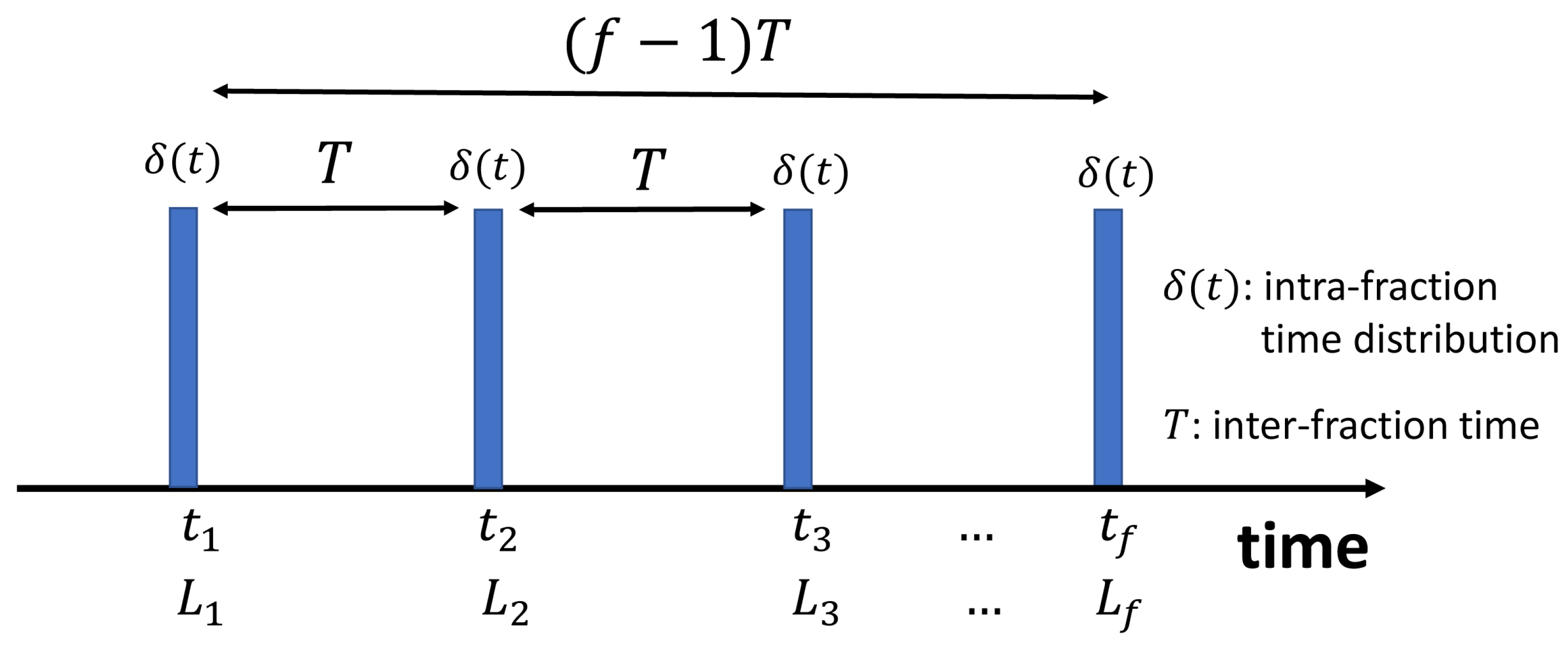
2.1. Nomenclature and Terminology

To clarify the terminology and nomenclature used in this study, we define fractionation time as well as random and systematic inter-fraction time variabilities. By fractionation time, T, we refer to the average time between two sequential fractions. The average is subjected to the entire treatment time. This is typically 24 h for a standard IMRT/VMAT fractionation plan, excluding the weekends when there is no treatment. In this work, however, we include the weekends and average based on the entire course of treatment time. As an example let us consider a total of 81 Gy prescription for a prostate cancer divided into standard fractions, f = 45 , corresponding to the dose of 1.8 Gy per fraction. Here we consider T = 32 h, including 8 weekends as depicted schematically in Figure 1.
Thus, any deviation from T = 32 h can be divided into random and systematic variations, δ T . On a cohort of patients, we refer to random variations if 〈 δ T 〉 = 0 , where 〈 δ T 〉 is mean of δ T over the entire treatment time. Note that, although, the mean-value in δ T is zero due to random fluctuations, but the the variance in the mean value, 〈 δ T 2 〉 , hence the corresponding standard deviation is non-zero. Similarly, systematic variations refer to 〈 δ T 〉 > 0 . Therefore, the total elapsed time of treatment is ( f − 1 ) T + 〈 δ T 〉 . Here f is the total number of fractions. Examples of systematic variations include frequent patient delays and machine downtime, or a temporary shut down due to natural disasters such as Hurricanes and floods that took place in 2021 when the remnants of tropical storm Ida produced severe thunderstorms and tornadoes around the North East area that led to temporary shut down of a few radiotherapy centers.

2.2. Model

In this work, we employ a system of time-dependent Master equations that describe the underlying Markov processes for the birth and death mechanisms of cancerous cells in a solid tumor. These are the processes that contribute to the growth and suppression of the tumor mass and their volume. We categorize the death process of cancerous cells into two classes of radiation and non-radiation based processes. In the former, ionization of atoms and molecules in the surrounding of the DNA in cell nuclei triggers a stochastic time-evolution of DSBs formed on DNAs that evolve into post-radiation intra and inter chromosomes end-joining processes (including repair and mis-repair enzymatic mechanisms). The latter accounts for the cellular lethal transitions and/or cell cycle termination. External non-radiation agents such as in chemo- and hormone-therapies contribute to the death rate as tumor cell repopulation also depends on adjuvant treatment such as androgen deprivation therapy. Although, the details of such mathematical model is straightforward, but some readers may find it lengthy and some readers may find it tedious. For the interested readers, we devoted an Appendix A to this paper and presented a step by step algorithmic mathematical model.

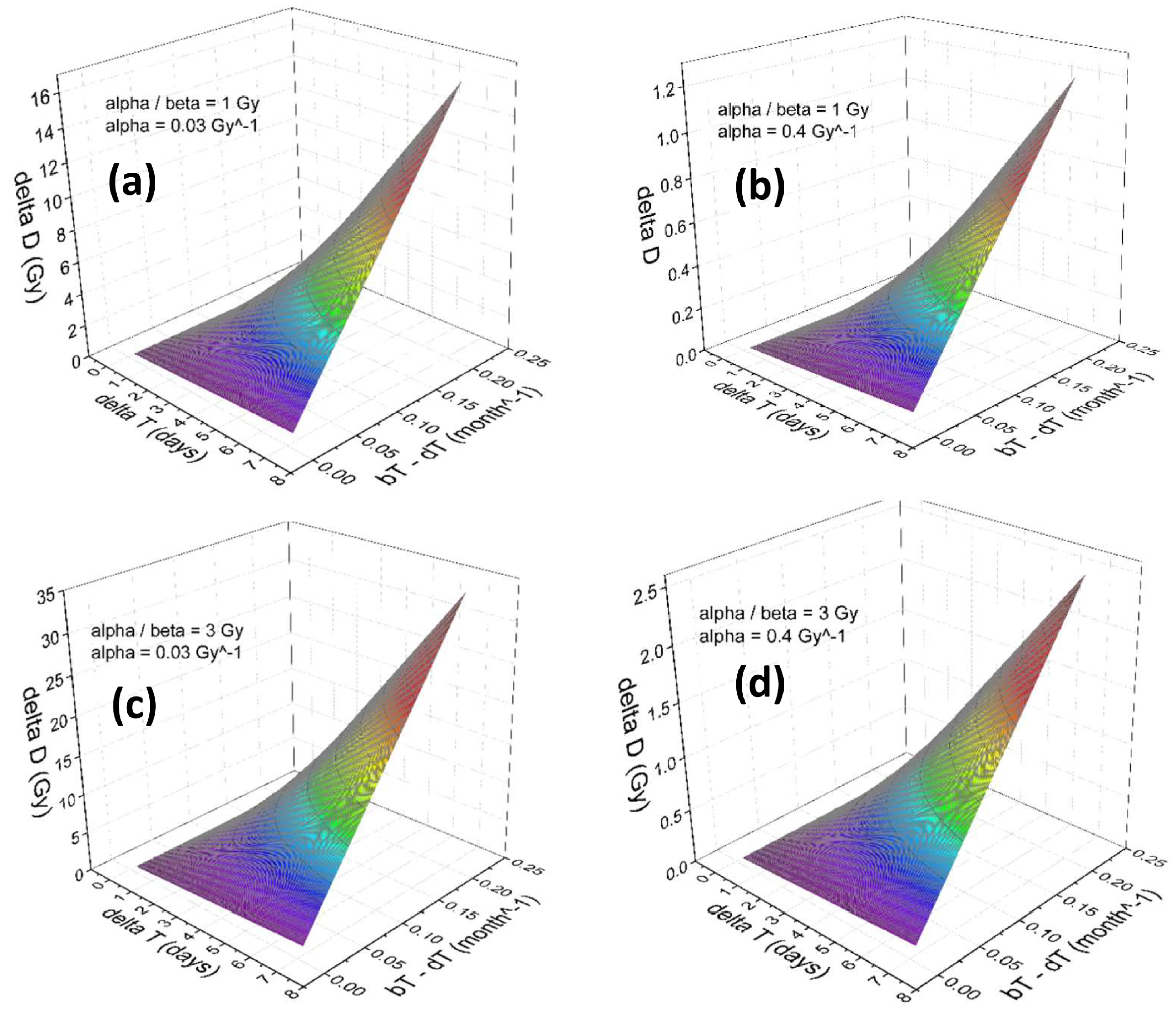
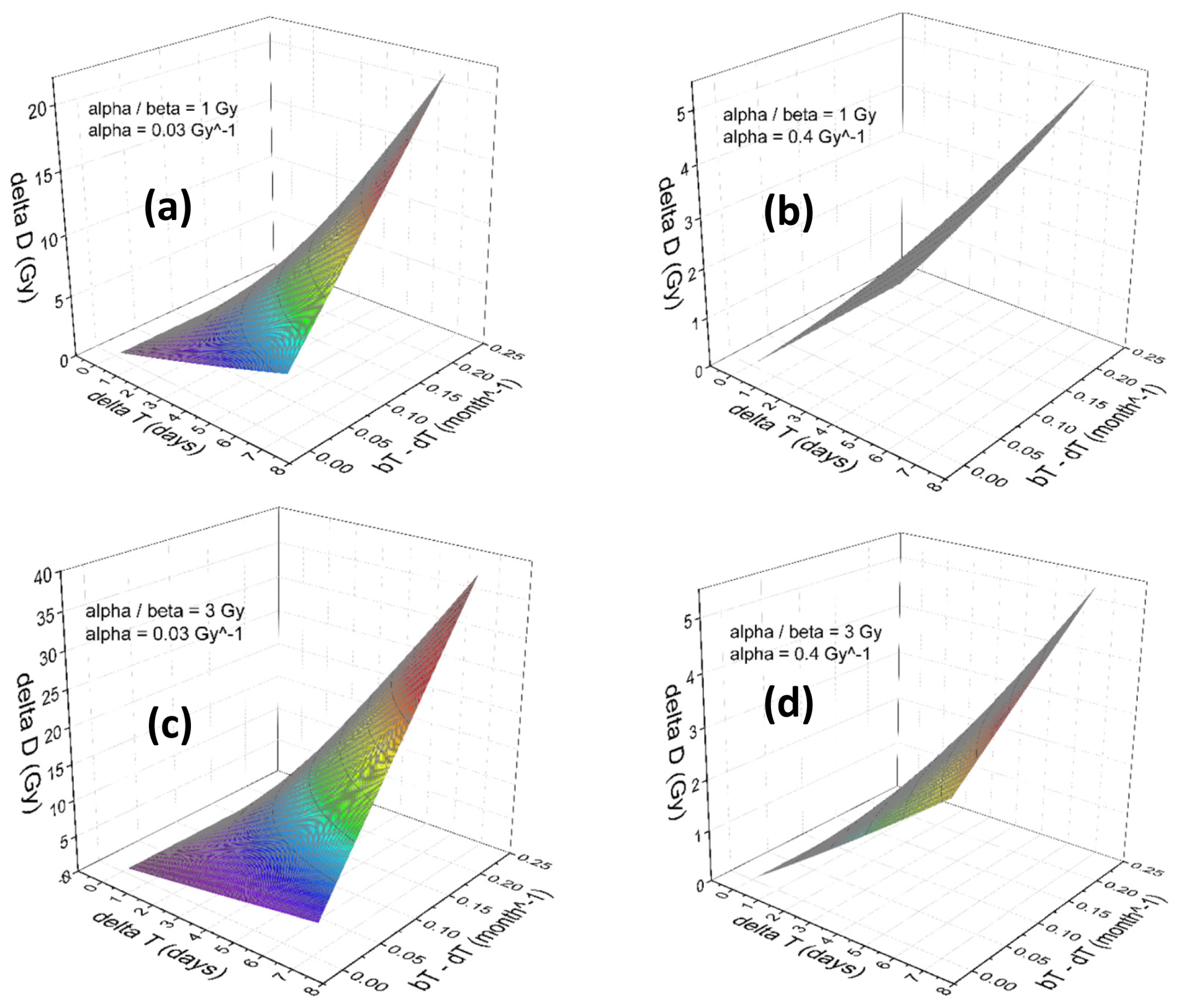
3. Results

Numerical Results

Figure 2 shows the time dependence of tumor cell population N ( t ) normalized by N 0 (the number of cells at initial time, t = 0 ) on the rates of tumor cell birth, b T , and death, d T , in the absence of radiation exposure. In our model calculation, N ( t ) depends only on the difference between b T and d T .
The time span, e.g., up to a one week, can be a representative of the time gap in the treatment. During this time, if the tumor grows, an extra radiation dose becomes necessary to compensate the effect of newly populated cancerous cells.
Considering the tumor growth factor as a free parameter, its range may vary up to a few percentage of its initial value at the beginning of the treatment gap. For example, the maximum tumor growth in a one week gap considered in the present numerical calculation is 5%. It corresponds to the birth-death rate of b T − d T = 0.25 per month.
Figure 3a–d and Figure 4a–d illustrate the results of our numerical calculation employed to calculate the absolute dose corrections, δ D , to compensate for the occurrence of the tumor cells repopulation during the treatment time disruption. The dependence of δ D on the growth rate, in addition to the tumor responses to the radiation, parameterized by the linear-quadratic α and β within a range relevant to the prostate cancer cells is shown. Note that the numerical range of δ D is due to inter-patient variabilities in prostate cancer sensitivity as a function of α / β . The range of α / β used in Figure 3 and Figure 4 were reported in literature, see for example Refs. [7,31,32]. The treatment parameters considered in this calculation are f = 45 and D = 81 Gy.
Accordingly, in the present range of parameters, to compensate a one week treatment disruption (depending upon the values of α and β ), a δ D within a wide range of 1 to 35 Gy must be applied. Note that because of the large time gap between sequential treatment fractionations, compared to T 1 / 2 , the enzymatic repair mechanism plays no role on determining the numerical values of δ D .

4. Discussion and Conclusions

The present theoretical work suggests an escalation to the prescription dose might be considerable to individuals whose tumors show significant growth during the treatment disruption time. Engaging analysis based on the personalized studies to assess the individual’s tumor growth factors that may occur due to repopulation of the cancerous cells allow for quantifying the corrections to the prescription dose. The techniques, including calculating the tumor volumes via contouring the daily based images acquired by cone-beam CT, and accessible in the clinical treatments planning systems under the setup field configurations, can be developed for these purposes. Monitoring the markers specific to cancer activities such as PSA in case of prostate cancer can be calibrated to give parameters such as b T − d T necessary to calculate δ D .
Because the individual abnormalities are not typically detectable in a large cohort of patients, the contribution of the tumor cell repopulation on the dose correction might not be identified if the clinical studies have been designed based on a cohort of patients. This includes the clinical data analysed by Dong et al. [15] where they reported unintentional treatment breaks during dose escalated external beam radiation therapy for a large cohort of patients and concluded the treatment breaks did not cause a significant difference in outcomes. It is noteworthy to mention that in our model tumor cell repopulation also depends on adjuvant treatment such as androgen deprivation therapy that was excluded in the cohort of Dong et al. [15].
In this study, we systematically correlated the dose correction, Δ D , with tumor cell repopulation and the DNA repair time, T1/2. We note that both tumor cell repopulation and T1/2 depend on several key elements, such as cell types, age of the cells, the nature of lesion, fidelity of DNA repair genes, and on the cell-cycle phase of the cells [33]. In general upon damage, the repair response can proceed for up to 24 h with the fast first phase happening during the first 15–30 min, followed by moderate second phase of up to 10 h and a very slow last phase of up to 24 h [7,28,29,34,35,36]. Furthermore, the result from previous studies on mice show that the cell death and response after acute radiation exposures was linear, whereas for the low dose rate exposures there was a variable, perhaps due to differences in time available for repair [37].
For some tumour types there is a delay of a few weeks before fast repopulation gets under way. In such cases of delayed repopulation there is no need for compensatory doses if the schedules can be completed within that delay period. Otherwise the repopulation is considered to act over a period given by ( T − T delay ), where T is the final overall treatment time.
In particular, our numerical calculations points to the sensitivity of the dose corrections to factors such as contribution of enzymatic repair processes (that is not a universal response of cells and can be individual dependent). The faster the sublethal DNA damages are repaired, the less sensitive cells are to the irregularities in the fractionation scheduling. The kinetic and swiftness of DNA repair depend on several factors such as, forms and extend of the damage, cell and tissue types, cell cycle phases, and most importantly the kind and proficiency of the recruited DNA repair system [38,39,40]. Based on types and severity of the damage, the DNA repair response kinetics can vary from few minutes to few hours long post damage. DNA single strand breaks (SSBs) are normally repaired very fast. DNA double strand breaks can also be repaired fast via nonhomologous end joining (NHEJ) slow via microhomology mediated end joining (MMEJ), or very slowly via homologous recombination (HR) [41,42,43,44]. The γ -H 2 A X is among the first markers that acts as a signaling molecule to accumulate surrounding the double strand break within minutes upon breaks [45]. Very fast and fast repair half-life is approximately 3–22 min, while the slow and very slow repair half-life is approximately 40 min–12 h (see Table 1 and Refs. [27,38,39,46]).
The NHEJ is primarily active during G0/G1 phase of the cell cycle, but it can occasionally be involved during other phases of cell cycle. MMEJ or HR on the other hand can be mostly achieved during S and G2 of the cell cycle. Simple damage such as SSBs created by base excision repair (BER) or ionization radiation are expected to be repaired very fast mechanism in presence of key enzymes such as PARP1 and XRCC1 [47,48,49]. The allele and proficiency of DNA repair enzymes can play a significant role in progression and therapy response of many human diseases such as Cancer [50]. One the other hand, complex DNA damages such as DSBs or multiple SSBs take more time to be fixed. In terms of fidelity, HR is known to be an error-free, while NHEJ and MMEJ belong to be error-prone pathways [30,38,41,42,43,51]
Finally, the present study suggests implementation of time irregularities in treatment scheduling in the clinic must be taken into account. In particular, the appropriate study should be conducted based on individuals, and not the statistics of cohort of patients that may wash out the important information on individual’s tumor growth. To achieve a clinical end point, corrections to the prescription dose must be assessed, in particular if modern external beam therapy techniques such as IMRT / VMAT are used for treatment of cancer. To achieve a curative clinical end-point, an increase in the total prescription dose delivered over the entire prescription course is suggested by adding extra fractions. This is in particular important for other types of modalities that are under investigation and development [52].

Author Contributions

R.A.: wrote the main manuscript, prepared figures, developed the algorithmic dose correction idea, performed mathematical derivations and computational steps. A.G.S., M.K.: wrote the main manuscript and performed radio-biological data analysis. B.K., R.I.: wrote the main manuscript and co-supervised the overall project. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

This study did not require the institutional ethical approval.

Informed Consent Statement

This study did not require the patient consent approval.

Data Availability Statement

There is no extra data used in this study.

Conflicts of Interest

The authors declare no competing financial interests.

Appendix A. The Mathematical Model

In a coarse-grained model such as the one described above, the transition rates are phenomenological parameters that describe the damage induction by ionizing radiation as well as enzymatic repair and mis-repair processes as described in Refs [53,54]. For illustration of the methodology, in our numerical calculation, we consider the tumor growth rate up to 5% in a week. In image-guided radiotherapy (IGRT) the information regarding the size of tumor is available in the clinical data set after acquiring daily CBCT, kV/MV and/or MRI setup fields. That information can be plugged in as an input to the model presented in this study. Thus, it can be used for estimation of the personalized prescription dose correction, independently for each individual.
Our model starts with the time evolution of DSB’s that follows a non-linear rate equation
d n ¯ ( t ) d t = μ z ˙ − λ n ¯ − γ n 2 ¯ ,
where n ¯ is the average DSBs at the time t, μ is the number of DSBs per cell induced per 1 Gy of ionizing radiation, and z ˙ is the specific energy rate in Gy per unit of time. λ and γ denote enzymatic repair and misrepair rate constants. More specifically, λ is inversely proportional to the recovery time of sub-lethal damages, λ − 1 = τ = T 1 / 2 / ln ( 2 ) where T 1 / 2 is the half time of sub-lethal repair.
Note that z ˙ is specific energy rate with identical unit to the dose rate, gray per second. The difference between z ˙ and dose rate is the scale of volumetric averaging. The dose is a macroscopic quantity thus the volume of interest is in unit of cm3. The specific energy is a micro-dosimetry quantity and has been used in this work at the level of cell volume down to DNA size, i.e., a nanoscopic scale.
Instantaneous population of broken DNAs transformed to lethally damaged chromosomes and cells can be calculated by
L ¯ [ n ( t ) ] = ∫ − ∞ t d t ′ L ( t ′ ) .
where
L ( t ) = λ L n ¯ ( t ) + γ L n 2 ¯ ( t ) .
It is straightforward to show that the linear solution of Equation (A1), n 0 , that can be derived analytically by insertion of γ = 0 is given by (see also Refs. [54,55])
n 0 t = ∫ − ∞ + ∞ d t ′ G r t − t ′ z ˙ t ′ .
Here G r t − t ′ = μ e − λ t − t ′ θ t − t ′ is the retarded Green’s function, the kernel of integral, and θ t − t ′ is the Heavyside function ( θ = 1 if t ≥ t ′ and 0 otherwise).
In a fractionation scheme where the intra-fraction variation in dose rate can be neglected in favor of inter-fractionation variations, it is appropriate to consider an acute radiation dose in each fraction
z ˙ ( t ) = ∑ i = 1 f z ˙ i ( t ) = z 1 δ ( t − T 1 ) + z 2 δ ( t − T 2 ) + z 3 δ ( t − T 3 ) + ⋯ + z f δ ( t − T f ) .
Here δ denotes Dirac delta function, hence z δ ( t ) describes the intra-fraction dose rate, and T 1 , T 2 , T 3 , … are the sequential treatment times. z 1 , z 2 , … are the radiation specific doses given in nano-meter virtual domain sizes in cell nuclei. Therefore, the physical doses calculated in treatment planning systems are the track and domain averaged over ensemble of cells, i.e., d 1 = z ¯ 1 , d 2 = z ¯ 2 , and etc.
Insertion of Equation (A5) into Equation (A4), considering standard fractionation with no interruption in treatment time, e.g., T 1 = 0 , T 2 = T , T 3 = 2 T , …, T f = ( f − 1 ) T and integration over delta function, yields the following solution
n 0 ( t ) = ∑ i = 1 f n 0 , i ( t ) = μ ( z 1 e − λ t θ ( t ) + z 2 e − λ ( t − T ) θ ( t − T ) + ⋯ + z f e − λ ( t − ( f − 1 ) T ) θ ( t − ( f − 1 ) T ) ) .
Here we replaced the actual treatment time with T, the average time between two sequential fractions. In this study, we intended to calculate the dose correction if there was any unintended delay in the patient treatment relative to an ideal fractionation.
Note that in a clinical setting where the inter-fractionation time is much larger than intra-fraction time, delta functions multiplied by the mean of specific energies can describe the intra-fractionation dose rates in a first approximation. In our institution, using VMAT for treatment of prostate cancer using Varian’s clinical linear accelerators, the intra-fractionation time of radiation is less than 5 min where T is two orders of magnitude larger. Hence, Equation (A5) is applicable to our clinical setting.

Appendix A.1. SF and TCP

Unrepaired DNA damages lead to cell lethality. Experimentally, this process can be quantified by in-vitro and/or in-vivo cell survival fraction measurements, S F = N 1 / N 0 where N 1 and N 0 are the number of survived and initial cells, respectively.
To assess the effect of scheduling time and its deviation from ideal repetition time in standard fractionation scheme and its variation to the prescription dose, appropriate calculation of TCP is needed to allow us to match the standard fractionation plan with a modified one. In particular, because a clinically optimal prescription dose on a TCP sigmoid curve intended to avoid (1) a sub-optimal radiation dose that may lead to recurrence of the tumor and (2) excessive dose radiation that lead to potential injuries and possibilities in forming tissue complications and formation of necrosis.
A relation between tumor control probability, TCP, fraction of survived cells, S F , DNA damage and the DSB mean population, n ¯ ( t ) can be calculated throughout the solutions of the system of coupled stochastic birth-death rate equations [53]. Other computational and analytical methods to investigate biological responses of the deposition dose were also investigated (see for example Refs. [56,57,58,59]). Here we adopt the method developed recently in Ref. [53] where the TCP at moment t is given by
T C P ( t ) = 1 − S F f n ¯ ( t ) N 0 .
N 0 is used to denote the number of cancerous cells that constitutes the tumor at the initial time of treatment, t = 0 , and
S F f n ¯ ( t ) = e ( b T − d T ) t − L ¯ n ¯ ( t ) 1 + b T e ( b T − d T ) t − L ¯ n ¯ ( t ) ∫ 0 t d t ′ e − ( b T − d T ) t ′ + L ¯ n ¯ ( t ′ ) .
In Equation (A8), b T and d T denote the birth and death rates of cells in absence of radiation field and L ¯ is the population of broken DNAs transformed to lethally damaged chromosomes over sufficiently long time, t → ∞ . The bar over L denotes averaging over all stochastic variables including energy deposition in an ensemble of cell nuclei.
The present TCP model exhibits interplay of sequence of events, starting from DSB induction by ionizing radiation in nanoscopic scale. Similar to the theory of dual radiation action (TDRA) [60,61,62], in this model, we consider an enzymatic mis-repair pathway starting from DSB’s, a temporary form of DNA damage that propagates to a permanent form of DNA damage, e.g., throughout occurrence of chromosome aberrations during cell cycles. Clearly, the collective deactivation of tumor cells in macroscopic scale governs the clinical outcome of radio-therapy. Thus in our coarse-grained model, the number of DSBs is linearly proportional to the specific energy (for example, see Equation (13) in Ref. [53]) and the cell lethality that determines the cell survival (see Equation (9) of the same reference) is a non-linear function of dose (see Equation (15) in Ref. [53]). Therefore, our cell deactivation model accounts for chromosome aberrations followed by induction of DSBs is a two-stage cell lethality, equivalent of TDRA, i.e., lesions followed by combinations of sublesions [62].
The TCP as given in Equation (A7) is a solution of a one-step birth-death master equation that calculates the time evolution of a tumor growth probability, T N ( t ) , with exactly N cancerous cells. A dynamical system that is based on sequence of the stochastic cell activation-disactivations in a Markov-chain is given by
d T N ( t ) d t = ( N − 1 ) b T T N − 1 + ( N + 1 ) d T + L ( t ) T N + 1 − [ b T + d T + L ( t ) ] N T N .
Because the goal in radiotherapy is to reach a point in time, t, such that no cancerous cells have a chance of survival, solutions of Equation (A9) flowing toward N ( t ) = 0 are of particular interest. Thus it is customary to define T C P = T N = 0 ( t → ∞ ) . In the absence of radiation where L ¯ = 0 , one can show T N = 0 ( t → ∞ ) = ( d / b ) N 0 . For d = b , we find T N = 0 ( t → ∞ ) = 1 . Alternatively, we may calculate N ¯ ( t ) , the average number of cancerous cells, from Equation (A9)
N ¯ ( t ) = ∑ N = 0 ∞ N T N ( t ) .
To this end, we apply a time-derivative to Equation (A10) to obtain the associated rate equation to N ¯ ( t )
d N ¯ ( t ) d t = ∑ N = 0 ∞ N d T N ( t ) d t = b T − d T − L ( t ) N ¯ ( t ) .
The solution for N ( t ) can be calculated by integration Equation (A11) over time
N ¯ [ L ( t ) ] = N 0 e ( b T − d T ) t − ∫ 0 t d t ′ L ( t ′ ) ,
where N 0 = N ¯ [ L ( t = 0 ) ] such that at L ( t = 0 ) = 0 . Under the above initial condition we assume the radiation exposure starts at t = 0 where prior to that time there is no cell lethality stemming from the radiation. Moreover, the population of cells in a colony tagged as cancer and under radiation is N 0 at t = 0 , thus T N ( t = 0 ) = δ N , N 0 .
We now turn to consider two different radio-therapy schemes that lead to two distinguishable cell lethalities L 1 and L 2 . If the cell lethality achievable by these two radio-therapies is the same, we consider these two approaches equivalent. In other words
N ¯ [ L 1 ( t 1 ) ] = N ¯ [ L 2 ( t 2 ) ] ,
where t 1 = ( f − 1 ) T 1 and t 2 = ( f − 1 ) T 2 subjected to a given dose per fraction, d. Note that the condition for Equation (A13) can be fulfilled if the total dose corresponding to t 1 and t 2 are given by D 1 and D 2 , respectively. Therefore if D 1 is the standard fractionation scheme, D 2 = D 1 + δ D where δ D is the correction dose corresponding to a change in the treatment time, i.e., δ T = T 2 − T 1 .
Inserting Equation (A13) to Equation (A12) yields
( b T − d T ) t 2 − ∫ 0 t 2 d t ′ L ( t ′ ) = ( b T − d T ) t 1 − ∫ 0 t 1 d t ′ L ( t ′ ) .
From here a condition that requires clinical equivalence for two different end times can be obtained
( b T − d T ) ( t 2 − t 1 ) = ∫ 0 t 2 d t ′ L ( t ′ ) − ∫ 0 t 1 d t ′ L ( t ′ ) = ∫ t 1 t 2 d t ′ L ( t ′ ) .
Hence
( b T − d T ) ( f − 1 ) δ T = ∫ ( f − 1 ) T ( f − 1 ) ( T + δ T ) d t ′ L ( t ′ ) .
Equation (A16) encapsulates the treatment equivalence of two radio-therapies to the cell lethality within δ T . We consider Equation (A16) to calculate the corresponding dose correction δ D subjected to a constraint that specifies the clinical endpoints.
Note that because of one-to-one correspondence between TCP and S F f , to achieve clinical end points for two cases of ideal and realistic fractionation (the latter includes time variations due to treatment interruption time), it is adequate to match S F f ’s to match T C P ’s.

Appendix A.2. Calculation of L ¯ [ ∑ i = 1 f n ¯ ( t i ) ]

By substituting n ¯ 0 for n ¯ we find
L ¯ 0 = ∫ − ∞ + ∞ d t λ L n ¯ 0 ( t ) + γ L n 0 2 ¯ ( t ) .
L ¯ 0 is used to denote population of broken DNAs transformed to lethally damaged chromosomes over sufficiently long time, t → ∞ if the DNA damage response to radiation dose is assumed to be linear.
We proceed with insertion of Equation (A6) in Equation (A17) to drive the cell lethality and survival fraction as a function of fractionation time. After performing straightforward algebraic steps, we find
L ¯ 0 = λ L λ μ z ¯ 1 + z ¯ 2 + z ¯ 3 + ⋯ + γ L 2 λ μ 2 z 1 2 ¯ + z 2 2 ¯ + z 3 2 ¯ + ⋯ + γ L λ μ 2 ( z ¯ 1 z ¯ 2 e − λ T + z ¯ 2 z ¯ 3 e − 2 λ T + z ¯ 2 z ¯ 3 e − λ T + ⋯ ) .
Here we assume uncorrelated deposited dose among fractions, e.g., z i z j ¯ = z ¯ i z ¯ j if i ≠ j .
To further proceed, we recall a known relation [60,61], z j 2 ¯ = z j ¯ z j ¯ + z D where d j = z j ¯ , z D = Δ / μ , and j is the label of jth fraction. Here Δ is the average number of DSBs per a single radiation event. We thus end up with
L ¯ 0 = λ L λ μ d 1 + d 2 + d 3 + ⋯ + γ L 2 λ μ 2 ( d 1 ( d 1 + z D ) + d 2 ( d 2 + z D ) + d 3 ( d 3 + z D ) + ⋯ ) + γ L λ μ 2 ( d 1 d 2 e − λ T + d 1 d 3 e − 2 λ T + d 2 d 3 e − λ T + ⋯ ) .
After simplifying Equation (A19), we find
L ¯ 0 = λ L λ μ + γ L 2 λ μ 2 z D d 1 + d 2 + d 3 + ⋯ + γ L 2 λ μ 2 d 1 2 + d 2 2 + d 3 2 + ⋯ + γ L λ μ 2 ( d 1 d 2 e − λ T + d 1 d 3 e − 2 λ T + d 2 d 3 e − λ T + ⋯ )
Considering d 1 = d 2 = d 3 = ⋯ = d , we find
L ¯ 0 ( d , T ) ≈ λ L λ μ + γ L 2 λ μ 2 z D f d + γ L 2 λ μ 2 f d 2 + γ L λ μ 2 ( f − 1 ) d 2 e − λ T + O ( e − λ 2 T ) .
where d and f are the dose per fraction and the number of fractions. We denote the total dose by D = f d and rewrite L ¯ 0 in terms of D
L ¯ 0 ( D , T ) ≈ λ L λ μ + γ L 2 λ μ 2 z D D + γ L 2 λ μ 2 1 f D 2 + γ L λ μ 2 f − 1 f 2 D 2 e − λ T + O ( e − λ 2 T ) .
Note that λ in the denominator of Equation (A22). Because λ is the DNA repair rate, to keep L ¯ 0 constant, the intra and inter fractions radiation doses must be adjusted according to the values of DNA repair rates that varies among different cell types. Moreover, according to Equation (A25), L ¯ 0 not only depends on the total radiation dose, D, but it is a complex non-linear function of f, d, and T.
Defining α and β in a standard single fraction ( f = 1 ) linear-quadratic cell survival model
α = λ L λ μ + γ L 2 λ μ 2 z D
and
β = γ L 2 λ μ 2 ,
Equation (A25) can be simplified to
L ¯ 0 ( D , T ) ≈ α D + 1 f + 2 f − 1 f 2 e − λ T β D 2 + O ( e − λ 2 T ) .
Considering two different treatments with inter-fractionation times, T 1 and T 2 corresponding with total doses D 1 and D 2 , and recalling Equation (A13)
N ¯ [ L 1 ( D 1 , T 1 ) ] = N ¯ [ L 2 ( D 2 , T 2 ) ] ,
in addition to Equations (A14)–(A16) and Equation (A25) we obtain a condition such that the cell lethality at very long times ( t → ∞ ) asymptotically saturates to a given value for both treatments
L ¯ 0 ( D 2 , T 2 ) − L ¯ 0 ( D 1 , T 1 ) = ( b T − d T ) ( f − 1 ) ( T 2 − T 1 )
Equation (A27) can be approximated to
L ¯ 0 ( D 2 , T 2 ) − L ¯ 0 ( D 1 , T 1 ) ≈ δ L ¯ 0 δ D δ D + δ L ¯ 0 δ T δ T + O ( δ D 2 , δ T 2 ) = ( b T − d T ) ( f − 1 ) δ T ,
where δ T = T 2 − T 1 and δ D = D 2 − D 1 and we define T ≡ T 1 and D ≡ D 1 to calculate the following differences. Up to second order of variations in time and dose we obtain
D 2 2 − D 1 2 = ( D + δ D ) 2 − D 2 = ( D 2 + δ D 2 + 2 D δ D ) − D 2 = 2 D δ D + δ D 2 ≈ 2 D δ D + O ( δ D 2 ) ,
and
D 2 2 e − λ T 2 − D 1 2 e − λ T 1 = ( D + δ D ) 2 e − λ ( T + δ T ) − D 2 e − λ T = ( D 2 + δ D 2 + 2 D δ D ) e − λ T e − λ δ T − D 2 e − λ T = ( D 2 + δ D 2 + 2 D δ D ) e − λ T ( 1 − λ δ T + λ 2 2 δ T 2 ) − D 2 e − λ T ≈ ( D 2 + 2 D δ D ) ( 1 − λ δ T ) e − λ T − D 2 e − λ T + O ( δ D 2 , δ T 2 ) = ( D 2 + 2 D δ D − D 2 λ δ T − 2 D δ D λ δ T ) e − λ T − D 2 e − λ T + O ( δ D 2 , δ T 2 ) = ( 2 D δ D − D 2 λ δ T − 2 D δ D λ δ T ) e − λ T + O ( δ D 2 , δ T 2 )
thus
D 2 2 e − λ T 2 − D 1 2 e − λ T 1 ≈ ( 2 D δ D − D 2 λ δ T − 2 D δ D λ δ T ) e − λ T + O ( δ D 2 , δ T 2 ) .
The loss of cell-killing must be compensated by a “dose correction”, δ D where the balance between the cell generation and death yields
( b T − d T ) ( f − 1 ) δ T = − 2 β f − 1 f 2 D 2 e − λ T λ δ T − 4 β f − 1 f 2 D e − λ T λ δ T δ D + α δ D + 2 β 1 f D δ D + 4 β f − 1 f 2 e − λ T D δ D + O ( δ D 2 , δ T 2 )
By knowing δ T , we can calculate the total dose correction, δ D . For T 1 / 2 = 1 / 2 h, λ = ln 2 / T 1 / 2 = 1.386 and T = 32 h, where λ T ≈ 44 > > 1 , we can simply neglect the effect of ezymatic repair in the fractionation treatments as exp ( − λ T ) ≈ 0 . Hence Equation (A32) can be simplified to
( b T − d T ) ( f − 1 ) δ T ≈ α δ D + 2 β 1 f D δ D ,
hence
δ D ≈ ( b T − d T ) ( f − 1 ) α + 2 β 1 f D δ T
In general
δ D ≈ [ ( b T − d T ) ( f − 1 ) + 2 β f − 1 f 2 D 2 e − λ T λ ] δ T α + 2 β 1 f D + 4 β f − 1 f 2 e − λ T D − 4 β f − 1 f 2 D e − λ T λ δ T .

References

  1. Herskind, C.; Ma, L.; Liu, Q.; Zhang, B.; Schneider, F.; Veldwijk, M.R.; Wenz, F. Biology of high single doses of IORT: RBE, 5 R’s, and other biological aspects. Radiat. Oncol. 2017, 12, 24. [Google Scholar] [CrossRef] [PubMed]
  2. Boustani, J.; Grapin, M.; Laurent, P.A.; Apetoh, L.; Mirjolet, C. The 6th R of Radiobiology: Reactivation of Anti-Tumor Immune Response. Cancers 2019, 11, 860. [Google Scholar] [CrossRef]
  3. Friedl, W.; Kundrat, P. A Guide to Outcome Modeling in Radiotherapy and Oncology: Listening to the Data; Naqa, I.E., Ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
  4. McMahon, S.J.; Prise, K.M. Mechanistic Modelling of Radiation Responses. Cancers 2019, 11, 205. [Google Scholar] [CrossRef] [PubMed]
  5. Brenner, D.J.; Hall, E.J.; Huang, Y.; Sachs, R.K. Evidence for formation of DNA repair centers and dose-response nonlinearity in human cells. Int. J. Radiat. Oncol. Biol. Phys. 1994, 29, 893–901. [Google Scholar] [CrossRef]
  6. Brenner, D.J. The Linear-Quadratic Model Is an Appropriate Methodology for Determining Isoeffective Doses at Large Doses per Fraction. Semin. Radiat. Oncol. 2008, 18, 234–239. [Google Scholar] [CrossRef]
  7. Carlson, D.J.; Stewart, R.D.; Li, X.A.; Jennings, K.; Wang, J.Z.; Guerrero, M. Comparison of in vitro and in vivo α/β ratios for prostate cancer. Phys. Med. Biol. 2004, 49, 4477–4491. [Google Scholar] [CrossRef] [PubMed]
  8. Aparicio, T.; Baer, R.; Gautier, J. DNA double-strand break repair pathway choice and cancer. DNA Repair 2014, 19, 169–175. [Google Scholar] [CrossRef]
  9. Borrego-Soto, G.; Ortiz-Lopez, R.; Rojas-Martínez, A. Ionizing radiation-induced DNA injury and damage detection in patients with breast cancer. Genet. Mol. Biol. 2015, 38, 420. [Google Scholar] [CrossRef]
  10. King, R.B.; Hyl, W.B.; Cole, A.J.; Butterworth, K.T.; McMahon, S.J.; Redmond, K.M.; Trainer, C.; Prise, K.M.; McGarry, C.K.; Hounsell, A.R. An in vitro study of the radiobiological effects of flattening filter free radiotherapy treatments. Phys. Med. Biol. 2013, 58, N83. [Google Scholar] [CrossRef]
  11. Butterworth, K.T.; McGarry, C.K.; Trainor, C.; O’Sullivan, J.M.; Hounsell, A.R.; Prise, K.M. A study of the biological effects of modulated 6 MV radiation fields. Phys. Med. Biol. 2010, 55, 1607–1618. [Google Scholar] [CrossRef] [Green Version]
  12. Butterworth, K.T.; McGarry, C.K.; Trainor, C.; McMahon, S.J.; O’Sullivan, J.M.; Schettino, G.; Hounsell, A.R.; Prise, K.M. Dose, dose-rate and field size effects on cell survival following exposure to non-uniform radiation fields. Phys. Med. Biol. 2012, 57, 3197–3206. [Google Scholar] [CrossRef] [PubMed]
  13. Ogino, H.; Shibamoto, Y.; Sugie, C.; Ito, M. Biological Effects of Intermittent Radiation in Cultured Tumor Cells: Influence of Fraction Number and Dose Per Fraction. J. Radiat. Res. 2005, 46, 401–406. [Google Scholar] [CrossRef] [PubMed]
  14. Bewes, J.M.; Suchowerska, N.; Jackson, M.; Zhang, M.; McKenzie, D.R. The radiobiological effect of intra-fraction dose-rate modulation in intensity modulated radiation therapy (IMRT). Phys. Med. Biol. 2008, 53, 3567–3578. [Google Scholar] [CrossRef]
  15. Dong, Y.; Zaorsky, N.G.; Li, T.; Churilla, T.M.; Viterbo, R.; Sobczak, M.L.; Smaldone, M.C.; Chen, D.Y.T.; Uzzo, R.G.; Hallman, M.A.; et al. Effects of Interruptions of External Beam Radiation Therapy on Outcomes in Patients with Prostate Cancer. J. Med. Imag. Radiat. Oncol. 2018, 62, 116–121. [Google Scholar] [CrossRef] [PubMed]
  16. Ohri, N.; Rapkin, B.D.; Guha, C.; Kalnicki, S.; Garg, M. Radiation Therapy Noncompliance and Clinical Outcomes in an Urban Academic Cancer Center. Int. J. Radiat. Oncol. Biol. Phys. 2016, 95, 563–570. [Google Scholar] [CrossRef] [PubMed]
  17. Elkind, M.M.; Sutton, H. Radiation response of mammalian cells grown in culture, 1. Repair of X-ray damage in surviving Chinese hamster cells. Radiat Res. 1960, 13, 556–593. [Google Scholar] [CrossRef]
  18. Mu, X.; Löfroth, P.O.; Karlsson, M. The effect of fraction time in intensity modulated radiotherapy: Theoretical and experimental evaluation of an optimisation problem. Radiother Oncol. 2003, 68, 181–187. [Google Scholar] [CrossRef]
  19. Nakano, H.; Kawahara, D.; Ono, K.; Akagi, Y.; Hirokawa, Y. Effect of dose-delivery time for flattened and flattening filter-free photon beams based on microdosimetric kinetic model. PLoS ONE 2018, 13, 0206673. [Google Scholar] [CrossRef]
  20. Inaniwa, T.; Kanematsu, N.; Suzuki, M. Effects of beam interruption time on tumor control probability in single-fractionated carbon-ion radiotherapy for non-small cell lung cancer. Phys. Med. Biol. 2015, 21, 4105–4121. [Google Scholar] [CrossRef]
  21. Inaniwa, T.; Suzuki, M.; Furukawa, T.; Kase, Y.; Kanematsu, N.; Shirai, T.; Hawkins, R.B. Effects of dose-delivery time structure on biological effectiveness for therapeutic carbon-355 ion beams evaluated with microdosimetric kinetic model. Radiat. Res. 2013, 180, 44–59. [Google Scholar] [CrossRef]
  22. Metzger, L.; Iliakis, G. Kinetics of DNA Double-strand Break Repair Throughout the Cell Cycle as Assayed by Pulsed Field Gel Electrophoresis in CHO Cells. Int. J. Radiat. Biol. 1991, 59, 1325–1339. [Google Scholar] [CrossRef] [PubMed]
  23. Matsuya, Y.; McMahon, S.J.; Tsutsumi, K.; Sasaki, K.; Okuyama, G.; Yoshii, Y.; Mori, R.; Oikawa, J.; Prise, K.M. Investigation of dose-rate effects and cell-cycle distribution under protracted exposure to ionizing radiation for various dose-rates. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
  24. Gastaldo, J.; Viau, M.; Bouchot, M.; Joubert, A.; Charvet, A.M.; Foray, N. Induction and repair rate of DNA damage: A unified model for describing effects of external and internal irradiation and contamination with heavy metals. J. Theor. Biol. 2008, 251, 68–81. [Google Scholar] [CrossRef]
  25. Khorramizadeh, M.; Saberi, A.; Tahmasebi-Birgani, M.; Shokrani, P.; Amouhedari, A. Impact of Prolonged Fraction Delivery Time Modelling Stereotactic Body Radiation Therapy with High Dose Hypofractionation on the Killing of Cultured ACHN Renal Cell Carcinoma Cell Line. J. Biomed. Phys. Eng. 2017, 7, 205–216. [Google Scholar]
  26. Hall, E.J.; Giaccia, A.J. Radiobiology for the Radiologist, 6th ed.; Lippincott Williams & Wilkins: Philadelphia, PA, USA, 2006. [Google Scholar]
  27. Frankenberg-Schwager, M. Review of repair kinetics for DNA damage induced in eukaryotic cells in vitro by ionizing radiation. Radiother. Oncol. 1989, 14, 307–320. [Google Scholar] [CrossRef]
  28. Wang, H.; Zeng, Z.C.; Bui, T.A.; Sonoda, E.; Takata, M.; Takeda, S.; Iliakis, G. Efficient rejoining of radiation-induced DNA double-strand breaks in vertebrate cells deficient in genes of the RAD52 epistasis group. Oncogene 2001, 20, 2212–2224. [Google Scholar] [CrossRef]
  29. Karlsson, K.H.; Radulescu, I.; Rydberg, B.; Stenerlöw, B. Repair of Radiation-Induced Heat-Labile Sites is Independent of DNA-PKcs, XRCC1 and PARP. Rad. Res. 2008, 169, 506–512. [Google Scholar] [CrossRef]
  30. DiBiase, S.J.; Zeng, Z.C.; Chen, R.; Hyslop, T.; Curran, W.J., Jr.; Iliakis, G. DNA-dependent protein kinase stimulates an independently active, nonhomologous, end-joining apparatus. Cancer Res. 2000, 60, 1245–1253. [Google Scholar] [PubMed]
  31. Oliveira, S.M.; Teixeira, N.J.; Fernandes, L. What do we know about the α/β for prostate cancer? Med. Phys. 2012, 39, 1–3. [Google Scholar] [CrossRef]
  32. Tamponi, M.; Gabriele, D.; Maggio, A.; Stasi, M.; Meloni, G.B.; Conti, M.; Gabriele, P. Prostate cancer dose–response, fractionation sensitivity and repopulation parameters evaluation from 25 international radiotherapy outcome data sets. Br. J. Radiol. 2019, 92, 20180823. [Google Scholar] [CrossRef]
  33. Chatterjee, N.; Walker, G.C. Mechanisms of DNA damage, repair, and mutagenesis. Environ. Mol. Mutagen. 2017, 58, 235–263. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  34. Neumaier, T.; Swenson, J.; Pham, C.; Polyzos, A.; Lo, A.T.; Yang, P.; Dyball, J.; Asaithamby, A.; Chen, D.J.; Bissell, M.J.; et al. Evidence for formation of DNA repair centers and dose-response nonlinearity in human cells. Proc. Natl. Acad. Sci. USA 2012, 109, 443–448. [Google Scholar] [CrossRef] [PubMed]
  35. Kosti, O.; Goldman, L.; Saha, D.T.; Orden, R.A.; Pollock, A.J.; Madej, H.L.; Hsing, A.W.; Chu, L.W.; Lynch, J.H.; Goldman, R. DNA damage phenotype and prostate cancer risk. Mutat. Res. 2011, 719, 41–46. [Google Scholar] [CrossRef]
  36. Asaithamby, A.; Uematsu, N.; Chatterjee, A.; Story, M.D.; Burma, S.; Chen, D.J. Repair of HZE-particle-induced DNA double-strand breaks in normal human fibroblasts. Radiat. Res. 2008, 169, 437–446. [Google Scholar] [CrossRef]
  37. Turner, H.C.; Shuryak, I.; Taveras, M.; Bertucci, A.; Perrier, J.R.; Chen, C.; Elliston, C.D.; Johnson, G.W.; Smilenov, L.B.; Amundson, S.A.; et al. Effect of dose rate on residual γ-H2AX levels and frequency of micronuclei in X-irradiated mouse lymphocytes. Radiat. Res. 2015, 183, 315–324. [Google Scholar] [CrossRef]
  38. Frankenburg-Schwager, M.; Harbich, R.; Beckonert, S.; Frankenberg, D. Half-life values for DNA double-strand break rejoining in yeast can vary by more than an order of magnitude depending on the irradiation conditions. Int. J. Radiat. Biol. 1994, 66, 543–547. [Google Scholar] [CrossRef] [PubMed]
  39. Olive, P.L. The role of DNA single- and double-strand breaks in cell killing by ionizing radiation. Radiat. Res. 1998, 150, S42–S51. [Google Scholar] [CrossRef] [PubMed]
  40. Friedberg, E.C. DNA damage and repair. Nature 2003, 421, 436–440. [Google Scholar] [CrossRef]
  41. Waters, C.A.; Str, N.T.; Wyatt, D.W.; Pryor, J.M.; Ramsden, D.A. Nonhomologous end joining: A good solution for bad ends. DNA Repair 2014, 17, 39–51. [Google Scholar] [CrossRef]
  42. Krejci, L.; Altmannova, V.; Spirek, M.; Zhao, X. Homologous recombination and its regulation. Nucleic Acids Res. 2012, 40, 5795–5818. [Google Scholar] [CrossRef]
  43. Deriano, L.; Roth, D.B. Modernizing the nonhomologous end-joining repertoire: Alternative and classical NHEJ share the stage. Annu. Rev. Genet. 2013, 47, 433–455. [Google Scholar] [CrossRef] [PubMed]
  44. McMahon, S.J.; Prise, K.M. A Mechanistic DNA Repair and Survival Model (Medras): Applications to Intrinsic Radiosensitivity, Relative Biological Effectiveness and Dose-Rate. Front. Oncol. 2021, 29, 689112. [Google Scholar] [CrossRef] [PubMed]
  45. Mah, L.-J.; El-Osta, A.; Karagiannis, T.C. γH2AX: A sensitive molecular marker of DNA damage and repair. Leukemia 2010, 24, 679–686. [Google Scholar] [CrossRef] [PubMed]
  46. Collins, A.R.; Ma, A.G.; Duthie, S.J. The kinetics of repair of oxidative DNA damage (strand breaks and oxidised pyrimidines) in human cells. Mutat. Res. 1995, 336, 69–77. [Google Scholar] [CrossRef]
  47. Abbotts, R.; Wilson, D.M., 3rd. Coordination of DNA single strand break repair. Free Radic. Biol. Med. 2017, 107, 228–244. [Google Scholar] [CrossRef]
  48. Caldecott, K.W. XRCC1 protein; Form and function. DNA Repair 2019, 81, 102664. [Google Scholar] [CrossRef]
  49. Pascal, J.M. The comings and goings of PARP-1 in response to DNA damage. DNA Repair 2018, 71, 177–182. [Google Scholar] [CrossRef]
  50. Knijnenburg, T.A.; Wang, L.; Zimmermann, M.T.; Chambwe, N.; Gao, G.F.; Cherniack, A.D.; Fan, H.; Shen, H.; Way, G.P.; Greene, C.S.; et al. Genomic and Molecular Landscape of DNA Damage Repair Deficiency across The Cancer Genome Atlas. Cell Rep. 2018, 3, 239–254.e6. [Google Scholar] [CrossRef]
  51. Iliakis, G.; Wang, H.; Perrault, A.R.; Boecker, W.; Rosidi, B.; Windhofer, F.; Wu, W.; Guan, J.; Terzoudi, G.; Pantelias, G. Mechanisms of DNA double strand break repair and chromosome aberration formation. Cytogenet. Genome Res. 2004, 104, 14–20. [Google Scholar] [CrossRef]
  52. Chen, X.; Liu, J.; Li, Y.; Pandey, N.K.; Chen, T.; Wang, L.; Amador, E.H.; Chen, W.; Liu, F.; Xiao, E.; et al. Study of copper-cysteamine based X-ray induced photodynamic therapy and its effects on cancer cell proliferation and migration in a clinical mimic setting. Bioact. Mater. 2022, 7, 504–514. [Google Scholar] [CrossRef]
  53. Abolfath, R.; Helo, Y.; Bronk, L.; Carabe, A.; Grosshans, D.; Mohan, R. Renormalization of radiobiological response functions by energy loss fluctuations and complexities in chromosome aberration induction: Deactivation theory for proton therapy from cells to tumor control. Eur. Phys. J. D 2019, 73, 64. [Google Scholar] [CrossRef]
  54. Sachs, R.K.; Hahnfeldt, P.; Brenner, D.J. The link between low-LET dose-response relations and the underlying kinetics of damage production/repair/misrepair. Int. J. Radiat. Biol. 1997, 72, 351. [Google Scholar] [PubMed]
  55. Hawkins, R.B. A microdosimetric-kinetic theory of the dependence of the RBE for cell death on LET. Med. Phys. 1998, 25, 1157. [Google Scholar] [CrossRef] [PubMed]
  56. Niemierko, A.; Goitein, M. Calculation of normal tissue complication probability and dose-volume histogram reduction schemes for tissues with a critical element architecture. Radiother. Oncol. 1991, 20, 166–176. [Google Scholar] [CrossRef]
  57. Young, A.; Berry, R.; Holloway, A.F.; Blackburn, N.B.; Dickinson, J.L.; Skala, M.; Phillips, J.L.; Brettingham-Moore, K.H. RNA-seq profiling of a radiation resistant and radiation sensitive prostate cancer cell line highlights opposing regulation of DNA repair and targets for radiosensitization. BMC Cancer 2014, 14, 808. [Google Scholar] [CrossRef]
  58. Thames, H.D.; Zhang, M.; Tucker, S.L.; Liu, H.H.; Dong, L.; Mohan, R. Cluster models of dose–volume effects. Int. Radiat. Oncol. Biol. Phys. 2004, 59, 1491–1504. [Google Scholar] [CrossRef]
  59. Zaider, M.; Amols, H.I. Practical considerations in using calculated healthy-tissue complication probabilities for treatment-plan optimization. Int. J. Radiat. Oncol. Biol. Phys. 1999, 44, 439–447. [Google Scholar] [CrossRef]
  60. Kellerer, A.M. Fundamentals of Microdosimetry The Dosimetry of Ionizing Radiation; Kase, K.R., Ed.; Academic: London, UK, 1985; Volume 1, pp. 77–161. [Google Scholar]
  61. Rossi, H.H.; Zaider, M. Microdosimetry and Its Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
  62. Kellerer, A.M.; Rossi, H.H. A Generalized Formulation of Dual Radiation Action. Radiat. Res. 2012, 178, AV204–AV213. [Google Scholar] [CrossRef] [Green Version]
Onco 02 00015 g001 550
Figure 1. Schematic sketch of fractionation in a typical external beam therapy. For an ideal 45 fractions including 8 weekends, T = 32 h is the mean fractionation time. L 1 , … , L f refer to lethal lesions corresponding to fractions 1 , … , f .
Figure 1. Schematic sketch of fractionation in a typical external beam therapy. For an ideal 45 fractions including 8 weekends, T = 32 h is the mean fractionation time. L 1 , … , L f refer to lethal lesions corresponding to fractions 1 , … , f .
Onco 02 00015 g001
Onco 02 00015 g002 550
Figure 2. N ( t ) / N 0 as a function of time, δ T , and tumor cell birth-death rate, b T − d T . The maximum increase in tumor volume within seven days considered in this study is 5% that corresponds to effective growth rate of b T − d T = 0.25 month−1.
Figure 2. N ( t ) / N 0 as a function of time, δ T , and tumor cell birth-death rate, b T − d T . The maximum increase in tumor volume within seven days considered in this study is 5% that corresponds to effective growth rate of b T − d T = 0.25 month−1.
Onco 02 00015 g002
Onco 02 00015 g003 550
Figure 3. Shown proposed dose prescription change δ D as a function of schedule time variation δ T , tumor cell birth-death rate, b T − d T , and linear-quadratic radiation response parameters, α and β , corresponding to the sublethal DNA repair half-time of T 1 / 2 = 0.5 h.
Figure 3. Shown proposed dose prescription change δ D as a function of schedule time variation δ T , tumor cell birth-death rate, b T − d T , and linear-quadratic radiation response parameters, α and β , corresponding to the sublethal DNA repair half-time of T 1 / 2 = 0.5 h.
Onco 02 00015 g003
Onco 02 00015 g004 550
Figure 4. Shown proposed dose prescription change δ D as a function of schedule time variation δ T , tumor cell birth-death rate, b T − d T , and linear-quadratic radiation response parameters, α and β , corresponding to the sublethal DNA repair half-time of T 1 / 2 = 2.5 h.
Figure 4. Shown proposed dose prescription change δ D as a function of schedule time variation δ T , tumor cell birth-death rate, b T − d T , and linear-quadratic radiation response parameters, α and β , corresponding to the sublethal DNA repair half-time of T 1 / 2 = 2.5 h.
Onco 02 00015 g004
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Abolfath, R.; Khalili, M.; Senejani, A.G.; Kodery, B.; Ivker, R. The Dependence of Compensation Dose on Systematic and Random Interruption Treatment Time in Radiation Therapy. Onco 2022, 2, 264-281. https://doi.org/10.3390/onco2030015

AMA Style

Abolfath R, Khalili M, Senejani AG, Kodery B, Ivker R. The Dependence of Compensation Dose on Systematic and Random Interruption Treatment Time in Radiation Therapy. Onco. 2022; 2(3):264-281. https://doi.org/10.3390/onco2030015

Chicago/Turabian Style

Abolfath, Ramin, Mitra Khalili, Alireza G. Senejani, Balachandran Kodery, and Robert Ivker. 2022. "The Dependence of Compensation Dose on Systematic and Random Interruption Treatment Time in Radiation Therapy" Onco 2, no. 3: 264-281. https://doi.org/10.3390/onco2030015

APA Style

Abolfath, R., Khalili, M., Senejani, A. G., Kodery, B., & Ivker, R. (2022). The Dependence of Compensation Dose on Systematic and Random Interruption Treatment Time in Radiation Therapy. Onco, 2(3), 264-281. https://doi.org/10.3390/onco2030015

Article Metrics

Back to TopTop