Gene Screening in High-Throughput Right-Censored Lung Cancer Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Description
2.2. Sure Independence Screening for Right-Censored Data
2.3. The Screening Index
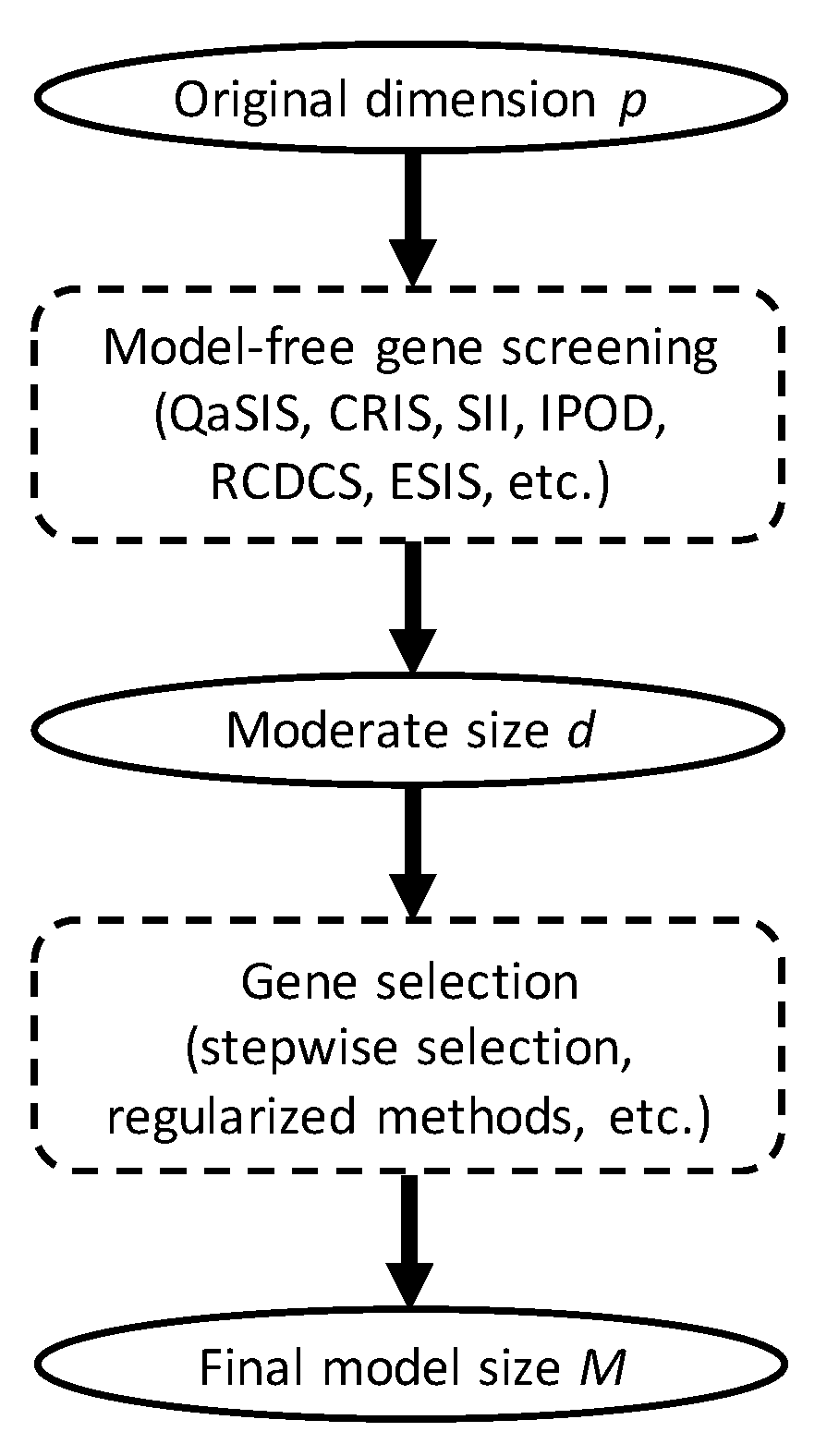
2.4. The Sreening Algorithm
- (1)
- Estimate the survival function by the Kaplan–Meier estimator asand compute the empirical CDF of as ;
- (2)
- Treat as the observed data of and compute the sample correlation for .
- (3)
- Let .
2.5. Application
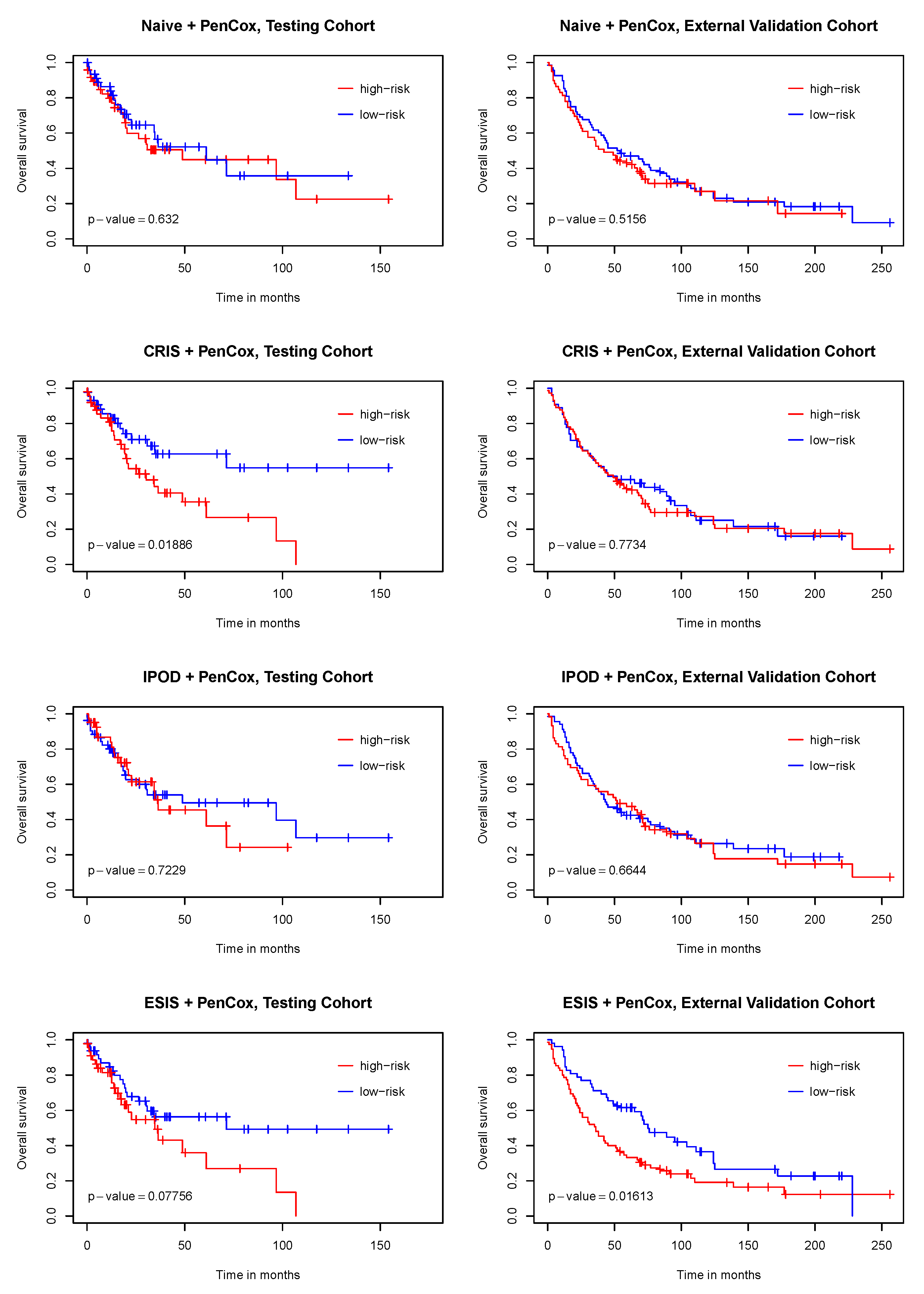
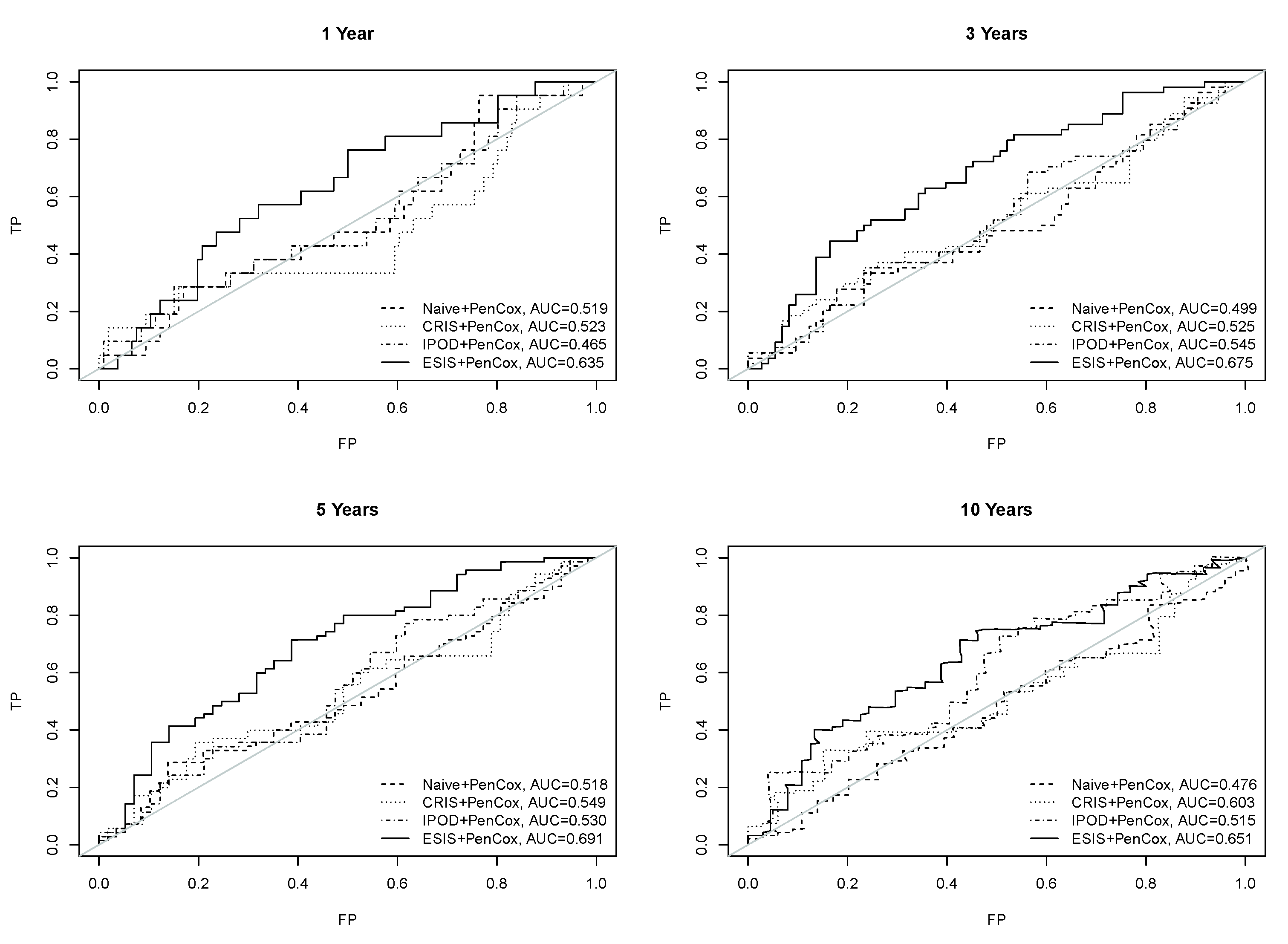
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef] [PubMed]
- Custodio, A.; Méndez, M.; Provencio, M. Targeted therapies for advanced non-small-cell lung cancer: Current status and future implications. Cancer Treat. Rev. 2012, 38, 36–53. [Google Scholar] [CrossRef]
- The Cancer Genome Atlas Research Network. Comprehensive genomic characterization of squamous cell lung cancers. Nature 2012, 489, 519–525. [Google Scholar] [CrossRef] [Green Version]
- Suda, K.; Mitsudomi, T. Successes and limitations of targeted cancer therapy in lung cancer. Successes Limitations Target. Cancer Ther. 2014, 41, 62–77. [Google Scholar]
- Lee, Y.T.; Tan, Y.J.; Oon, C.E. Molecular targeted therapy: Treating cancer with specificity. Eur. J. Pharmacol. 2018, 834, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Pi, L.; Halabi, S. Combined performance of screening and variable selection methods in ultra-high dimensional data in predicting time-to-event outcomes. Diagn. Progn. Res. 2018, 2, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Larsen, J.E.; Pavey, S.J.; Passmore, L.H.; Bowman, R.; Clarke, B.E.; Hayward, N.K.; Fong, K.M. Expression profiling defines a recurrence signature in lung squamous cell carcinoma. Carcinogenesis 2007, 28, 760–766. [Google Scholar] [CrossRef] [Green Version]
- Skrzypski, M.; Jassem, E.; Taron, M.; Sanchez, J.J.; Mendez, P.; Rzyman, W.; Gulida, G.; Raz, D.; Jablons, D.; Provencio, M.; et al. Three-gene expression signature predicts survival in early-stage squamous cell carcinoma of the lung. Clin. Cancer Res. 2008, 14, 4794–4799. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Lin, H.; He, P.; He, L.; Chen, J.; Lin, L.; Chen, Y. A TP53-associated gene signature for prediction of prognosis and therapeutic responses in lung squamous cell carcinoma. Oncoimmunology 2020, 9, 1731943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qu, H.Q.; Tien, M.; Polychronakos, C. Statistical significance in genetic association studies. Clin. Investig. Med. Med. Clin. Exp. 2010, 33, E266. [Google Scholar] [CrossRef] [PubMed]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. B (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B (Methodol.) 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Chen, J.W.; Dhahbi, J. Lung adenocarcinoma and lung squamous cell carcinoma cancer classification, biomarker identification, and gene expression analysis using overlapping feature selection methods. Sci. Rep. 2021, 11, 13323. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Lv, J. Sure independence screening for ultrahigh dimensional feature space. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2008, 70, 849–911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, R.; Zhong, W.; Zhu, L. Feature screening via distance correlation learning. J. Am. Stat. Assoc. 2012, 107, 1129–1139. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, K.; Sriperumbudur, B.; Lebanon, G. Ultrahigh Dimensional Feature Screening via RKHS Embeddings; Artificial Intelligence and Statistics: Scottsdale, AZ, USA, 2013; pp. 126–134. [Google Scholar]
- Mai, Q.; Zou, H. The fused Kolmogorov filter: A nonparametric model-free screening method. Ann. Stat. 2015, 43, 1471–1497. [Google Scholar] [CrossRef] [Green Version]
- Cui, H.; Li, R.; Zhong, W. Model-free feature screening for ultrahigh dimensional discriminant analysis. J. Am. Stat. Assoc. 2015, 110, 630–641. [Google Scholar] [CrossRef] [PubMed]
- Beyene, J.; Atenafu, E.G.; Hamid, J.S.; To, T.; Sung, L. Determining relative importance of variables in developing and validating predictive models. BMC Med. Res. Methodol. 2009, 9, 64. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heinzel, A.; Perco, P.; Mayer, G.; Oberbauer, R.; Lukas, A.; Mayer, B. From molecular signatures to predictive biomarkers: Modeling disease pathophysiology and drug mechanism of action. Front. Cell Dev. Biol. 2014, 2, 37. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, J.; Feng, Y.; Wu, Y. High-dimensional variable selection for Cox’s proportional hazards model. In Borrowing Strength: Theory Powering Applications—A Festschrift for Lawrence D. Brown; Institute of Mathematical Statistics: Hayward, CA, USA, 2010; pp. 70–86. [Google Scholar]
- Zhao, S.D.; Li, Y. Principled sure independence screening for Cox models with ultra-high-dimensional covariates. J. Multivar. Anal. 2012, 105, 397–411. [Google Scholar] [CrossRef] [PubMed]
- Gorst-Rasmussen, A.; Scheike, T. Independent screening for single-index hazard rate models with ultrahigh dimensional features. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 2013, 75, 217–245. [Google Scholar] [CrossRef] [Green Version]
- Iuliano, A.; Occhipinti, A.; Angelini, C.; De Feis, I.; Liò, P. Combining pathway identification and breast cancer survival prediction via screening-network methods. Front. Genet. 2018, 9, 206. [Google Scholar] [CrossRef]
- Tschodu, D.; Ulm, B.; Bendrat, K.; Lippoldt, J.; Gottheil, P.; Käs, J.A.; Niendorf, A. Comparative analysis of molecular signatures reveals a hybrid approach in breast cancer: Combining the Nottingham Prognostic Index with gene expressions into a hybrid signature. PLOS ONE 2022, 17, e0261035. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, C.; Dong, X.; Shen, S.; Lai, L.; He, J.; You, D.; Lin, L.; Zhu, Y.; Huang, H.; et al. Independent validation of early-stage non-small cell lung cancer prognostic scores incorporating epigenetic and transcriptional biomarkers with gene-gene interactions and main effects. Chest 2020, 158, 808–819. [Google Scholar] [CrossRef] [PubMed]
- Zhao, K.; Li, Z.; Tian, H. Twenty-gene-based prognostic model predicts lung adenocarcinoma survival. Oncotargets Ther. 2018, 11, 3415. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Wang, L.; Hong, H.G. Quantile-adaptive model-free variable screening for high-dimensional heterogeneous data. Ann. Stat. 2013, 41, 342–369. [Google Scholar] [CrossRef]
- Song, R.; Lu, W.; Ma, S.; Jessie Jeng, X. Censored rank independence screening for high-dimensional survival data. Biometrika 2014, 101, 799–814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Zheng, Q.; Peng, L.; Huang, Z. Survival impact index and ultrahigh-dimensional model-free screening with survival outcomes. Biometrics 2016, 72, 1145–1154. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.G.; Chen, X.; Christiani, D.C.; Li, Y. Integrated powered density: Screening ultrahigh dimensional covariates with survival outcomes. Biometrics 2018, 74, 421–429. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Chen, X.; Wang, H. Robust feature screening for ultra-high dimensional right censored data via distance correlation. Comput. Stat. Data Anal. 2018, 119, 118–138. [Google Scholar] [CrossRef]
- Hong, H.G.; Li, Y. Feature selection of ultrahigh-dimensional covariates with survival outcomes: A selective review. Appl. Math. 2017, 32, 379–396. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ke, C.; Yin, X. Expected Conditional Characteristic Function-based Measures for Testing Independence. J. Am. Stat. Assoc. 2020, 115, 985–996. [Google Scholar] [CrossRef]
- Botling, J.; Edlund, K.; Lohr, M.; Hellwig, B.; Holmberg, L.; Lambe, M.; Berglund, A.; Ekman, S.; Bergqvist, M.; Pontén, F.; et al. Biomarker Discovery in Non–Small Cell Lung Cancer: Integrating Gene Expression Profiling, Meta-analysis, and Tissue Microarray ValidationGene Expression–Based Biomarker Discovery in NSCLC. Clin. Cancer Res. 2013, 19, 194–204. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rousseaux, S.; Debernardi, A.; Jacquiau, B.; Vitte, A.L.; Vesin, A.; Nagy-Mignotte, H.; Moro-Sibilot, D.; Brichon, P.Y.; Lantuejoul, S.; Hainaut, P.; et al. Ectopic activation of germline and placental genes identifies aggressive metastasis-prone lung cancers. Sci. Transl. Med. 2013, 5, 186ra66. [Google Scholar] [CrossRef] [Green Version]
- Fukumizu, K.; Gretton, A.; Lanckriet, G.R.; Schölkopf, B.; Sriperumbudur, B.K. Kernel Choice and Classifiability for RKHS Embeddings of Probability Distributions. In Advances in Neural Information Processing Systems 22; Bengio, Y., Schuurmans, D., Lafferty, J.D., Williams, C.K.I., Culotta, A., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2009; pp. 1750–1758. [Google Scholar]
- Sejdinovic, D.; Sriperumbudur, B.; Gretton, A.; Fukumizu, K. Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 2013, 41, 2263–2291. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986. [Google Scholar]
- Ren, J.; Du, Y.; Li, S.; Ma, S.; Jiang, Y.; Wu, C. Robust network-based regularization and variable selection for high-dimensional genomic data in cancer prognosis. Genet. Epidemiol. 2019, 43, 276–291. [Google Scholar] [CrossRef]
- Dwight, T.; Na, U.; Kim, E.; Zhu, Y.; Richardson, A.L.; Robinson, B.G.; Tucker, K.M.; Gill, A.J.; Benn, D.E.; Clifton-Bligh, R.J.; et al. Analysis of SDHAF3 in familial and sporadic pheochromocytoma and paraganglioma. BMC Cancer 2017, 17, 497. [Google Scholar] [CrossRef] [Green Version]
- Moreno, C.; Santos, R.M.; Burns, R.; Zhang, W.C. Succinate Dehydrogenase and Ribonucleic Acid Networks in Cancer and Other Diseases. Cancers 2020, 12, 3237. [Google Scholar] [CrossRef]
- Tseng, P.L.; Wu, W.H.; Hu, T.H.; Chen, C.W.; Cheng, H.C.; Li, C.F.; Tsai, W.H.; Tsai, H.J.; Hsieh, M.C.; Chuang, J.H.; et al. Decreased succinate dehydrogenase B in human hepatocellular carcinoma accelerates tumor malignancy by inducing the Warburg effect. Sci. Rep. 2018, 8, 3081. [Google Scholar] [CrossRef] [Green Version]
- Guo, X.; Li, D.; Wu, Y.; Chen, Y.; Zhou, X.; Wang, X.; Huang, X.; Li, X.; Yang, H.; Xing, J. Genetic variants in genes of tricarboxylic acid cycle key enzymes are associated with prognosis of patients with non-small cell lung cancer. Lung Cancer 2015, 87, 162–168. [Google Scholar] [CrossRef] [PubMed]
- Campbell, R.; Chong, G.; Hawkes, E.A. Novel indications for Bruton’s tyrosine kinase inhibitors, beyond hematological malignancies. J. Clin. Med. 2018, 7, 62. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Albano, F.; Chiurazzi, F.; Mimmi, S.; Vecchio, E.; Pastore, A.; Cimmino, C.; Frieri, C.; Iaccino, E.; Pisano, A.; Golino, G.; et al. The expression of inhibitor of bruton’s tyrosine kinase gene is progressively up regulated in the clinical course of chronic lymphocytic leukaemia conferring resistance to apoptosis. Cell Death Dis. 2018, 9, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, S. Identification of monotonically differentially expressed genes for non-small cell lung cancer. BMC Bioinform. 2019, 20, 177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mardakheh, F.K.; Self, A.; Marshall, C.J. RHO binding to FAM65A regulates Golgi reorientation during cell migration. J. Cell Sci. 2016, 129, 4466–4479. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ridley, A. RhoA, RhoB and RhoC have different roles in cancer cell migration. J. Microsc. 2013, 251, 242–249. [Google Scholar] [CrossRef]
- Howrylak, J.A.; Moll, M.; Weiss, S.T.; Raby, B.A.; Wu, W.; Xing, E.P. Gene expression profiling of asthma phenotypes demonstrates molecular signatures of atopy and asthma control. J. Allergy Clin. Immunol. 2016, 137, 1390–1397. [Google Scholar] [CrossRef] [Green Version]
- Kachuri, L.; Johansson, M.; Rashkin, S.R.; Graff, R.E.; Bossé, Y.; Manem, V.; Caporaso, N.E.; Landi, M.T.; Christiani, D.C.; Vineis, P.; et al. Immune-mediated genetic pathways resulting in pulmonary function impairment increase lung cancer susceptibility. Nat. Commun. 2020, 11, 27. [Google Scholar] [CrossRef] [Green Version]
- Poteryaev, D.; Datta, S.; Ackema, K.; Zerial, M.; Spang, A. Identification of the switch in early-to-late endosome transition. Cell 2010, 141, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Liu, Y.; Yu, Q.; Ding, Z.; Qian, W.; Zhang, L.; Zhang, J.; Jiang, N.; Gui, L.; Xu, Z.; et al. Numb regulates vesicular docking for homotypic fusion of early endosomes via membrane recruitment of Mon1b. Cell Res. 2016, 26, 593–612. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Qian, J.; Yang, Y.; Fan, Y. Knockdown of MON1B Exerts Anti-Tumor Effects in Colon Cancer In Vitro. Med. Sci. Monit. Int. Med. J. Exp. Clin. Res. 2018, 24, 7710–7718. [Google Scholar] [CrossRef] [PubMed]
- Xuan, C.; Wang, Q.; Han, X.; Duan, Y.; Li, L.; Shi, L.; Wang, Y.; Shan, L.; Yao, Z.; Shang, Y. RBB, a novel transcription repressor, represses the transcription of HDM2 oncogene. Oncogene 2013, 32, 3711–3721. [Google Scholar] [CrossRef] [PubMed]
- Kheder, E.S.; Hong, D.S. Emerging Targeted Therapy for Tumors with NTRK Fusion ProteinsNovel Targeted Therapy for NTRK-Rearranged Tumors. Clin. Cancer Res. 2018, 24, 5807–5814. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, D.T.; Hutter, B.; Jäger, N.; Korshunov, A.; Kool, M.; Warnatz, H.J.; Zichner, T.; Lambert, S.R.; Ryzhova, M.; Quang, D.A.K.; et al. Recurrent somatic alterations of FGFR1 and NTRK2 in pilocytic astrocytoma. Nat. Genet. 2013, 45, 927–932. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amatu, A.; Sartore-Bianchi, A.; Siena, S. NTRK gene fusions as novel targets of cancer therapy across multiple tumour types. ESMO Open 2016, 1, e000023. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Xi, Y.; Coccimiglio, M.L.; Mennigen, J.A.; Jonz, M.G.; Ekker, M.; Trudeau, V.L. Functional prediction and physiological characterization of a novel short trans-membrane protein 1 as a subunit of mitochondrial respiratory complexes. Physiol. Genom. 2012, 44, 1133–1140. [Google Scholar] [CrossRef] [Green Version]
- Mullin, B.H.; Zhu, K.; Brown, S.J.; Mullin, S.; Tickner, J.; Pavlos, N.J.; Dudbridge, F.; Xu, J.; Walsh, J.P.; Wilson, S.G. Genetic regulatory mechanisms in human osteoclasts suggest a role for the STMP1 and DCSTAMP genes in Paget’s disease of bone. Sci. Rep. 2019, 9, 1052. [Google Scholar] [CrossRef] [Green Version]
- Feingold, E.; Pachter, L. The ENCODE (ENCyclopedia of DNA elements) project. Science 2004, 306, 636–640. [Google Scholar]
- Consortium, E.P. A user’s guide to the encyclopedia of DNA elements (ENCODE). PLoS Biol. 2011, 9, e1001046. [Google Scholar]
- Rouillard, A.D.; Gundersen, G.W.; Fernandez, N.F.; Wang, Z.; Monteiro, C.D.; McDermott, M.G.; Ma’ayan, A. The harmonizome: A collection of processed datasets gathered to serve and mine knowledge about genes and proteins. Database 2016, 2016, baw100. [Google Scholar] [CrossRef]
- Trimarchi, J.M.; Lees, J.A. Sibling rivalry in the E2F family. Nat. Rev. Mol. Cell Biol. 2002, 3, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Kar, A.; Gutierrez-Hartmann, A. Molecular mechanisms of ETS transcription factor-mediated tumorigenesis. Crit. Rev. Biochem. Mol. Biol. 2013, 48, 522–543. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanahan, D.; Weinberg, R.A. Hallmarks of cancer: The next generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [PubMed]

| Variables | Frequency (Percent) |
|---|---|
| Age | |
| Less than 50 | 15 (3.2%) |
| 50–59 | 67 (14.2%) |
| 60–69 | 178 (37.6%) |
| 70–79 | 186 (39.3%) |
| 80 or greater | 27 (5.7%) |
| Gender | |
| Female | 125 (26.4%) |
| Male | 348 (73.6%) |
| Smoking History | |
| Current reformed smoker for ≤ 15 years | 236 (49.9%) |
| Current reformed smoker for > 15 years | 81 (17.1%) |
| Current reformed smoker, duration not specified | 5 (1.1%) |
| Current smoker | 133 (28.1%) |
| Lifelong non-smoker | 18 (3.8%) |
| Lymph Node Metastasis | |
| N0 | 302 (63.8%) |
| N1, N2, N3 | 165 (34.9%) |
| NX | 6 (1.3%) |
| Distant Metastasis | |
| M0 | 386 (81.6%) |
| M1, M1a, M1b | 7 (1.5%) |
| MX | 80 (16.9%) |
| Pathological Stage | |
| I | 236 (49.9%) |
| II | 150 (31.7%) |
| III | 80 (16.9%) |
| IV | 7 (1.5%) |
| Model (No. of Genes Selected) | Gene Names |
|---|---|
| Naive + PenCox (6) | PCDHA5(+), C9ORF131(+), PM20D1(+), PCDHA3(+), FAM196B(+), PITX3(−) |
| CRIS + PenCox (10) | CCDC79(+), LCN1(+), GPR78(+), SSX1(+), CCKAR(+), SLC10A2(+), STARD6(−), GUCY2F(−), DPPA2(+), LINC00628(+) |
| IPOD + PenCox (4) | TRIM58(+), C9ORF131(+), PKNOX2(+), PCDHGA11(+) |
| ESIS + PenCox (6) | NACC2(+), FAM65A(+), LOC641845(−), MON1B(+), IBTK(+), SDHAF3(−) |
| Variable | Hazard Ratio (95% CI) | p-Value |
|---|---|---|
| 6-gene signature | 12.59 (4.11, 38.56) | <0.001 |
| Age | 1.02 (1.01, 1.04) | 0.008 |
| Gender | ||
| Male | 0.92 (0.67, 1.28) | 0.629 |
| Female | - | - |
| Tumor stage | ||
| I | 0.59 (0.42, 0.83) | 0.003 |
| II | 0.63 (0.43, 0.92) | 0.018 |
| III or IV | - | - |
| Smoking history | ||
| Lifelong non-smoker | 1.94 (0.83, 4.54) | 0.126 |
| Current smoker | 1.54 (1.14, 2.07) | 0.005 |
| Current reformed smoker | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ke, C.; Bandyopadhyay, D.; Acunzo, M.; Winn, R. Gene Screening in High-Throughput Right-Censored Lung Cancer Data. Onco 2022, 2, 305-318. https://doi.org/10.3390/onco2040017
Ke C, Bandyopadhyay D, Acunzo M, Winn R. Gene Screening in High-Throughput Right-Censored Lung Cancer Data. Onco. 2022; 2(4):305-318. https://doi.org/10.3390/onco2040017
Chicago/Turabian StyleKe, Chenlu, Dipankar Bandyopadhyay, Mario Acunzo, and Robert Winn. 2022. "Gene Screening in High-Throughput Right-Censored Lung Cancer Data" Onco 2, no. 4: 305-318. https://doi.org/10.3390/onco2040017
APA StyleKe, C., Bandyopadhyay, D., Acunzo, M., & Winn, R. (2022). Gene Screening in High-Throughput Right-Censored Lung Cancer Data. Onco, 2(4), 305-318. https://doi.org/10.3390/onco2040017







