Automated Particle Tracing & Sensitivity Analysis for Residence Time in a Saturated Subsurface Media
Abstract
1. Introduction
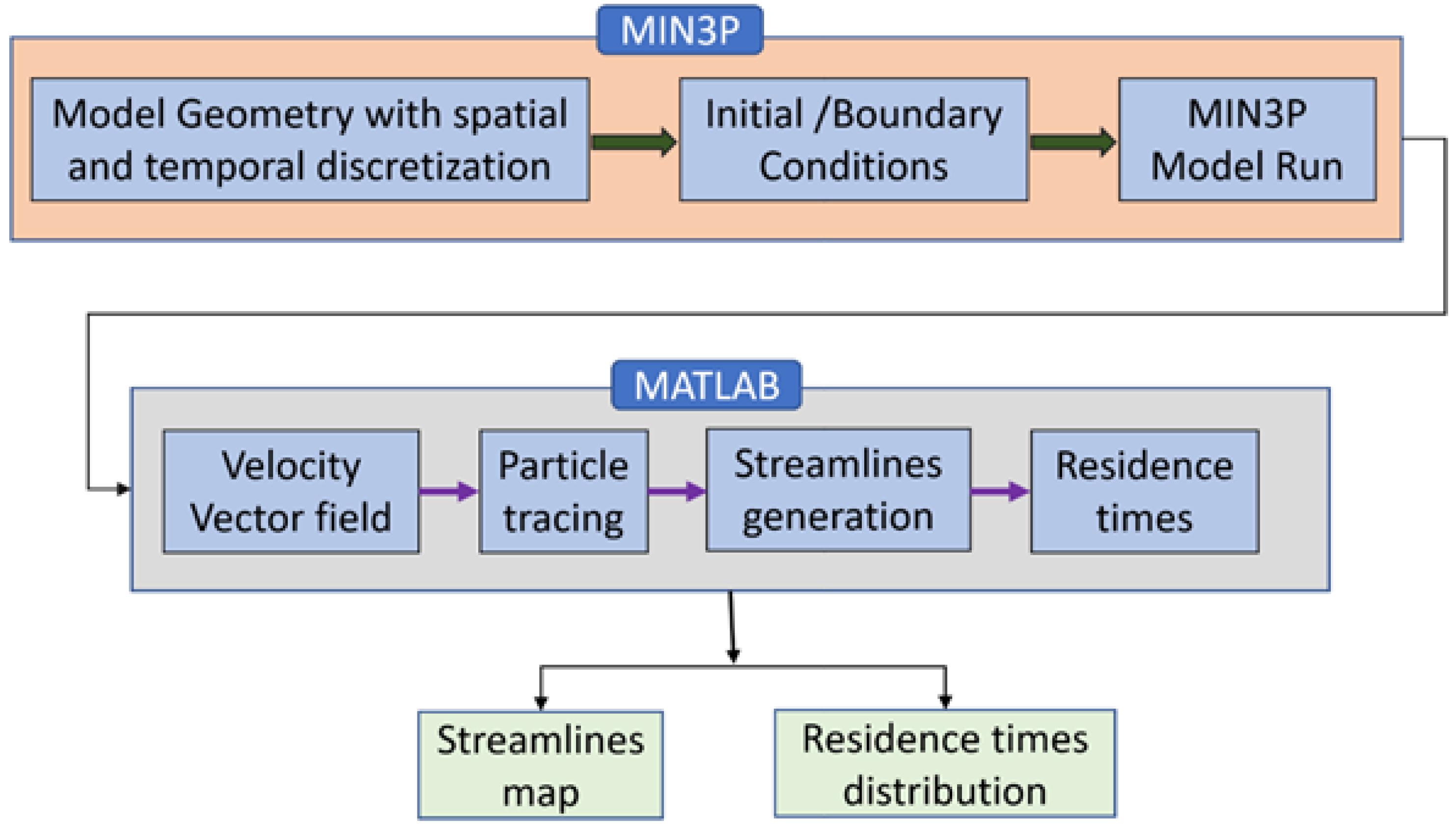
2. Materials and Methods
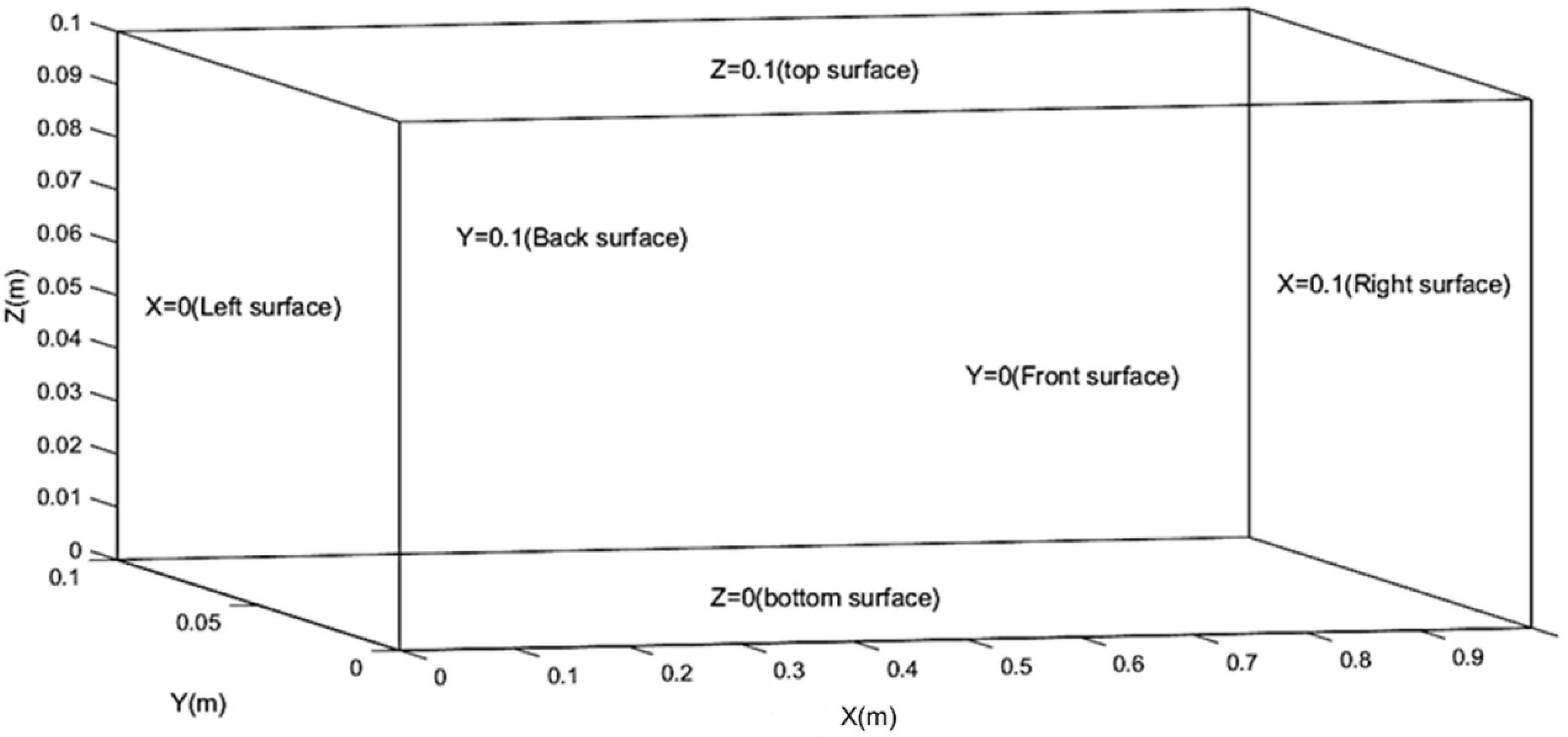
2.1. Automated Generation of Velocity Vector Field
2.2. Automated Particle Tracing Using MATLAB
2.3. Comparison with Paraview
2.4. Sensitivity Analysis of Residence Time
3. Results
3.1. Distribution of Streamlines and Residence Time
3.2. Mean Residence Time
3.3. Comparison with Paraview
3.4. Sensitivity Analysis on Spatial and Temporal Discretization
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vincenzi, V.; Piccinini, L.; Gargini, A.; Sapigni, M. Parametric and numerical modeling tools to forecast hydrogeological impacts of a tunnel. Acque Sotter.-Ital. J. Groundw. 2022, 11, 51–69. [Google Scholar] [CrossRef]
- Neukum, C.; Hötzl, H.; Himmelsbach, T. Validation of vulnerability mapping methods by field investigations and numerical modelling. Hydrogeol. J. 2008, 16, 641–658. [Google Scholar] [CrossRef]
- Yi, X. Reactive Transport Modeling of Waste Rock Weathering in Permafrost Environments. Doctoral Dissertation, University of British Columbia, Vancouver, BC, Canada, 2021. [Google Scholar] [CrossRef]
- Mehedi, M.A.A.; Yazdan, M.M.S.; Ahad, M.T.; Akatu, W.; Kumar, R.; Rahman, A. Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model. Eng 2022, 3, 276–300. [Google Scholar] [CrossRef]
- Al Hossain, B.M.T.; Ahmed, T.; Aktar, M.N.; Fida, M.; Khan, A.; Islam, A.S.; Yazdan, M.M.S.; Noor, F.; Rahaman, A.Z. Climate Change Impacts on Water Availability in the Meghna Basin. In Proceedings of the 5th International Conference on Water and Flood Management (ICWFM-2015), Dhaka, Bangladesh, 6–8 March 2015; pp. 6–8. [Google Scholar]
- Yazdan, M.M.S.; Kumar, R.; Leung, S.W. The Environmental and Health Impacts of Steroids and Hormones in Wastewater Effluent, as Well as Existing Removal Technologies: A Review. Ecologies 2022, 3, 206–224. [Google Scholar] [CrossRef]
- Crist, J.T.; McCarthy, J.F.; Zevi, Y.; Baveye, P.; Throop, J.A.; Steenhuis, T.S. Pore-scale visualization of colloid transport and retention in partly saturated porous media. Vadose Zone J. 2004, 3, 444–450. [Google Scholar] [CrossRef]
- Yazdan, M.M.S.; Ahad, T.; Jahan, I.; Mazumder, M. Review on the Evaluation of the Impacts of Wastewater Disposal in Hydraulic Fracturing Industry in the United States. Technologies 2020, 8, 67. [Google Scholar] [CrossRef]
- Yazdan, M.M.S.; Rahaman, A.Z.; Noor, F.; Duti, B.M. Establishment of co-relation between remote sensing based trmm data and ground based precipitation data in north-east region of Bangladesh. In Proceedings of the 2nd International Conference on Civil Engineering for Sustainable Development (ICCESD-2014), KUET, Khulna, Bangladesh, 14–16 February 2014. [Google Scholar]
- Xu, Z.; Niu, Z.; Pan, D.; Zhao, X.; Wei, X.; Li, X.; Wu, W. Mechanisms of bentonite colloid aggregation, retention, and release in saturated porous media: Role of counter ions and humic acid. Sci. Total Environ. 2021, 793, 148545. [Google Scholar] [CrossRef]
- Wu, R.; Chen, X.; Hammond, G.; Bisht, G.; Song, X.; Huang, M.; Niu, G.Y.; Ferre, T. Coupling surface flow with high-performance subsurface reactive flow and transport code PFLOTRAN. Environ. Model. Softw. 2021, 137, 104959. [Google Scholar] [CrossRef]
- Wang, S.; Flanagan, D.C.; Engel, B.A.; McIntosh, M.M. Impacts of subsurface hydrologic conditions on sediment selectivity and sediment transport in rills. Catena 2021, 207, 105703. [Google Scholar] [CrossRef]
- Yildirim, A.; Mader, C.A.; Martins, J.R. Accelerating parallel CFD codes on modern vector processors using blockettes. In Proceedings of the Platform for Advanced Scientific Computing Conference, Geneva, Switzerland, 5–9 July2021; pp. 1–9. [Google Scholar]
- Schwartz, S.D.; Childs, H.; Pugmire, D. Improving parallel particle advection performance with machine learning. In Proceedings of the Eurographics Symposium on Parallel Graphics and Visualization, Zurich, Switzerland, 14 June 2021; p. 12. [Google Scholar]
- Kruger, J.; Kipfer, P.; Konclratieva, P.; Westermann, R. A particle system for interactive visualization of 3D flows. IEEE Trans. Vis. Comput. Graph. 2005, 11, 744–756. [Google Scholar] [CrossRef]
- Feng, J.; Liu, D.; Liu, Y.; Li, Y.; Li, H.; Chen, L.; Xiao, J.; Liu, J.; Dong, J. Hyporheic exchange due to in-stream geomorphic structures. J. Freshw. Ecol. 2022, 37, 221–241. [Google Scholar] [CrossRef]
- Al Mehedi, M.A. Sensitivity Analysis of Hyporheic Exchange to Small Scale Changes in Gravel-Sand Flumebed Using a Coupled Groundwater-Surface Water Model. In Proceedings of the Copernicus Meetings, Online, 4–8 May 2020. [Google Scholar]
- Gropp, W.D.; Kaushik, D.K.; Keyes, D.E.; Smith, B.F. High-performance parallel implicit CFD. Parallel Comput. 2001, 27, 337–362. [Google Scholar] [CrossRef][Green Version]
- Chow, R.; Parker, B.L.; Steelman, C.M.; Thoms, A.; Nowak, W. How do fractures influence hyporheic exchange in sedimentary rock riverbeds? Water Resour. Res. 2021, 57, 7. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L.; Haggerty, R. Residence time of bedform-driven hyporheic exchange. Adv. Water Resour. 2008, 31, 1382–1386. [Google Scholar] [CrossRef]
- Bao, Z.; Beckingham, B.; Maier, U.; Haberer, C.; Grathwohl, P. Numerical modelling of soil/atmosphere exchange of POPs with MIN3P. EGU Gen. Assem. Conf. Abstr. 2014, 16, 3802. [Google Scholar]
- Brunke, M.; Gonser, T.O.M. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef]
- Bencala, K.E. Simulation of solute transport in a mountain pool-and-riffle stream with a kinetic mass transfer model for sorption. Water Resour. Res. 1983, 19, 732–738. [Google Scholar] [CrossRef]
- Laube, G.; Schmidt, C.; Fleckenstein, J.H. A systematic model-based evaluation of the influence of hydraulic conductivity, heterogeneity and domain depth on hyporheic nutrient transformation. Adv. Water Resour. 2022, 159, 104087. [Google Scholar] [CrossRef]
- ParaView. Available online: https://www.paraview.org/ (accessed on 17 May 2022).
- Weishaupt, K.; Joekar-Niasar, V.; Helmig, R. An efficient coupling of free flow and porous media flow using the pore-network modeling approach. J. Comput. Phys. X 2019, 1, 100011. [Google Scholar] [CrossRef]
- Mayer, K.; MacQuarrie, K. Solution of the MoMaS reactive transport benchmark with MIN3P—model formulation and simulation results. Comput. Geosci. 2010, 14, 405–419. [Google Scholar] [CrossRef]
- Chávez-Negrete, C.; Santana-Quinteros, D.; Domínguez-Mota, F. A Solution of Richards’ Equation by Generalized Finite Differences for Stationary Flow in a Dam. Mathematics 2021, 9, 1604. [Google Scholar] [CrossRef]
- McGuire, K.J.; DeWalle, D.R.; Gburek, W.J. Evaluation of mean residence time in subsurface waters using oxygen-18 fluctuations during drought conditions in the mid-Appalachians. J. Hydrol. 2002, 261, 132–149. [Google Scholar] [CrossRef]
- Gleason, C.L.; Frisbee, M.D.; Rademacher, L.K.; Sada, D.W.; Meyers, Z.P.; Knott, J.R.; Hedlund, B.P. Hydrogeology of desert springs in the Panamint Range, California, USA: Geologic controls on the geochemical kinetics, flowpaths, and mean residence times of springs. Hydrol. Process. 2020, 34, 2923–2948. [Google Scholar] [CrossRef]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T. MIN3P-HPC: A high-performance unstructured grid code for subsurface flow and reactive transport simulation. Math. Geosci. 2021, 53, 517–550. [Google Scholar] [CrossRef]
- Welcome to ParaView Documentation—ParaView Documentation 5.10.0 Documentation. Available online: https://docs.paraview.org/en/latest/ (accessed on 17 May 2022).
- ParaView Reference Manual—ParaView Documentation 5.10.0 Documentation. Available online: https://docs.paraview.org/en/latest/ReferenceManual/index.html (accessed on 17 May 2022).









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehedi, M.A.A.; Yazdan, M.M.S. Automated Particle Tracing & Sensitivity Analysis for Residence Time in a Saturated Subsurface Media. Liquids 2022, 2, 72-84. https://doi.org/10.3390/liquids2030006
Mehedi MAA, Yazdan MMS. Automated Particle Tracing & Sensitivity Analysis for Residence Time in a Saturated Subsurface Media. Liquids. 2022; 2(3):72-84. https://doi.org/10.3390/liquids2030006
Chicago/Turabian StyleMehedi, Md Abdullah Al, and Munshi Md. Shafwat Yazdan. 2022. "Automated Particle Tracing & Sensitivity Analysis for Residence Time in a Saturated Subsurface Media" Liquids 2, no. 3: 72-84. https://doi.org/10.3390/liquids2030006
APA StyleMehedi, M. A. A., & Yazdan, M. M. S. (2022). Automated Particle Tracing & Sensitivity Analysis for Residence Time in a Saturated Subsurface Media. Liquids, 2(3), 72-84. https://doi.org/10.3390/liquids2030006






