Solvatochromism in Solvent Mixtures: A Practical Solution for a Complex Problem
Abstract
1. Reasons for Using Mixed Solvents in Chemistry
2. A Rationale for Effects of Mixed Solvents on Chemical Phenomena
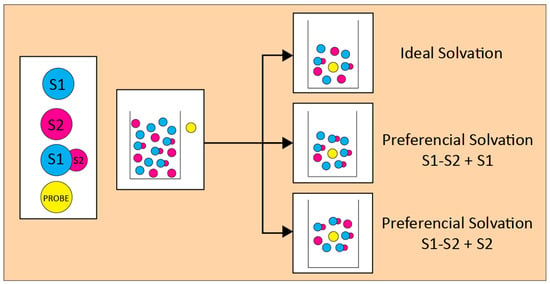
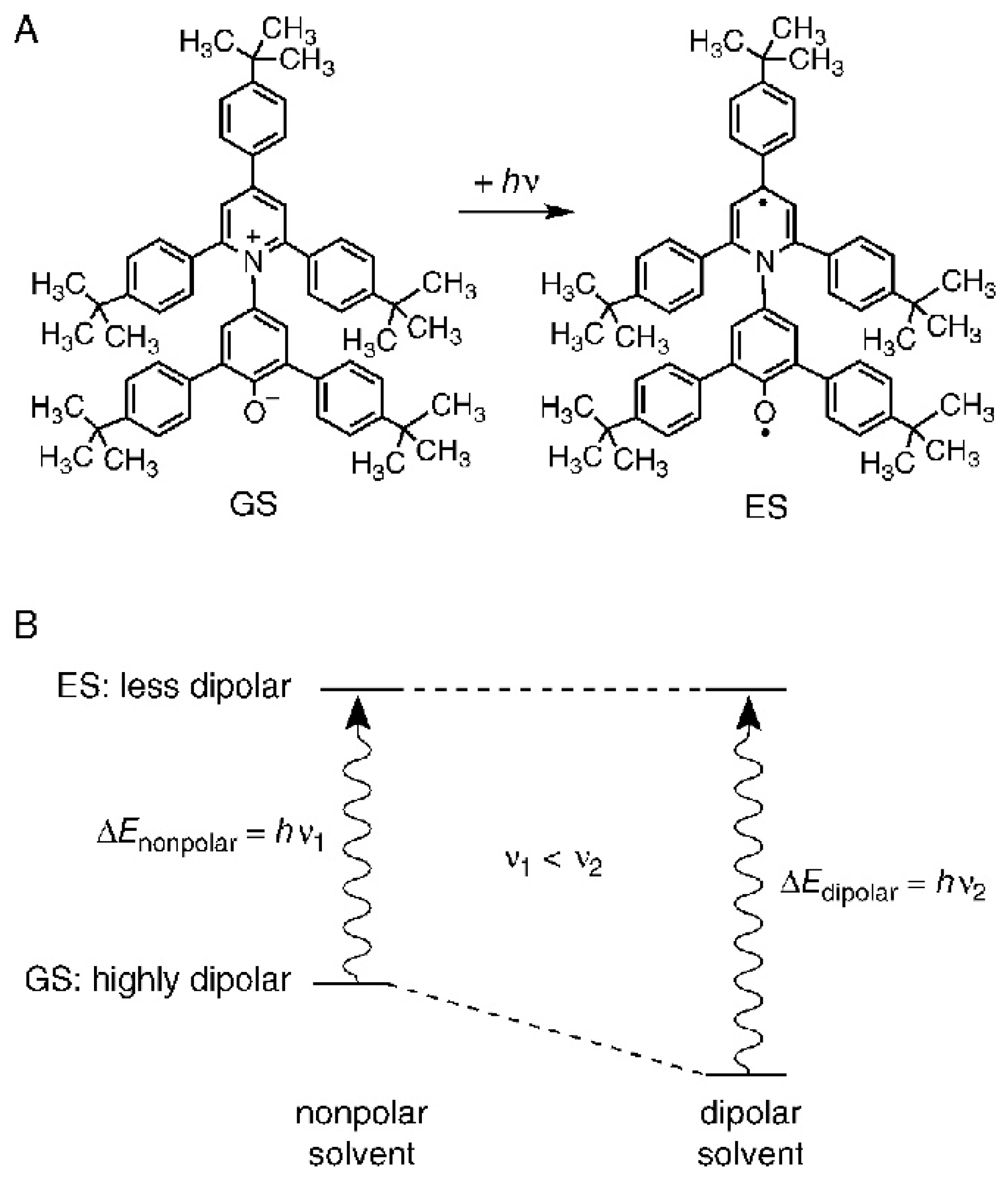
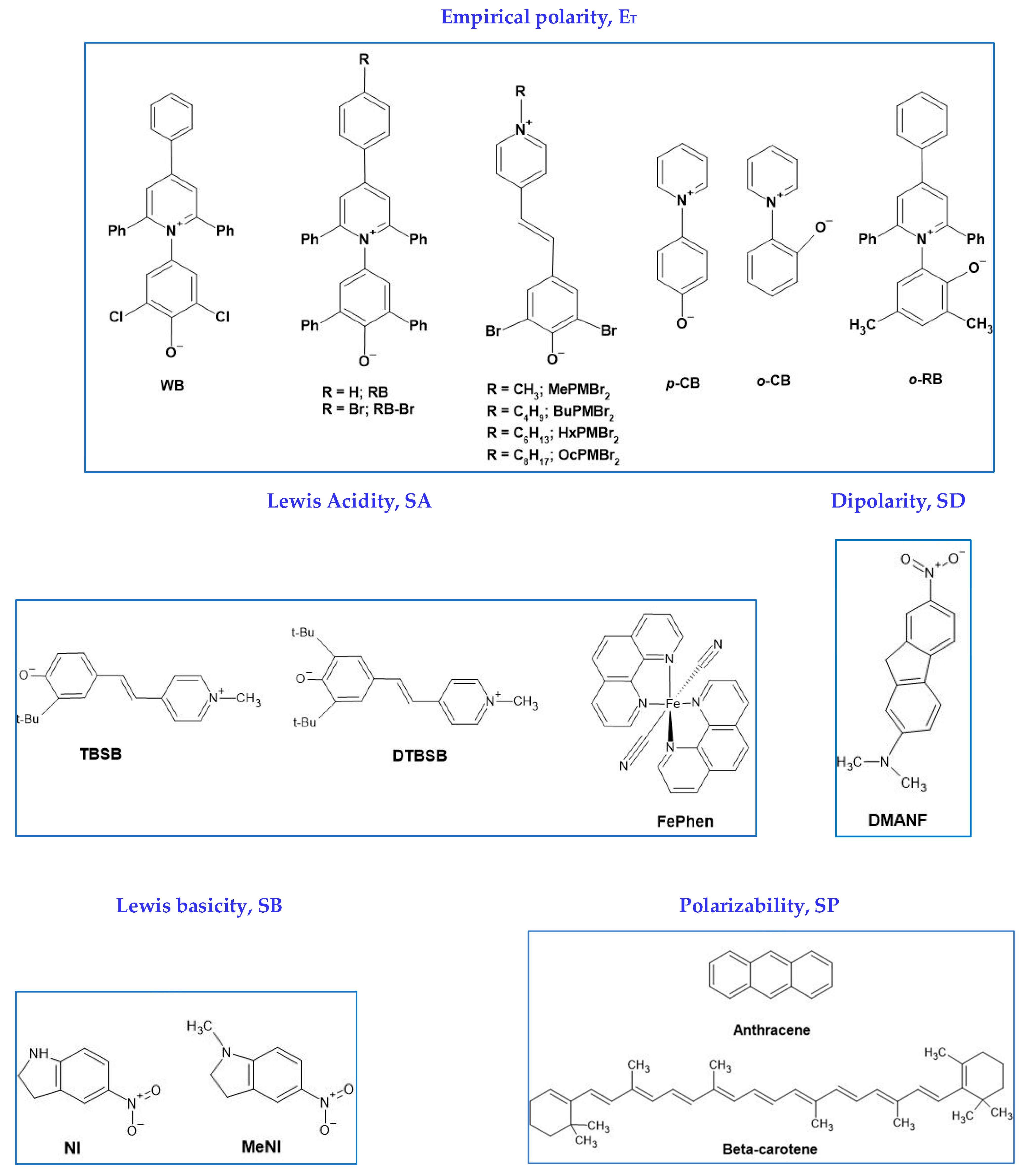
3. A Model for the Solvation of Probes
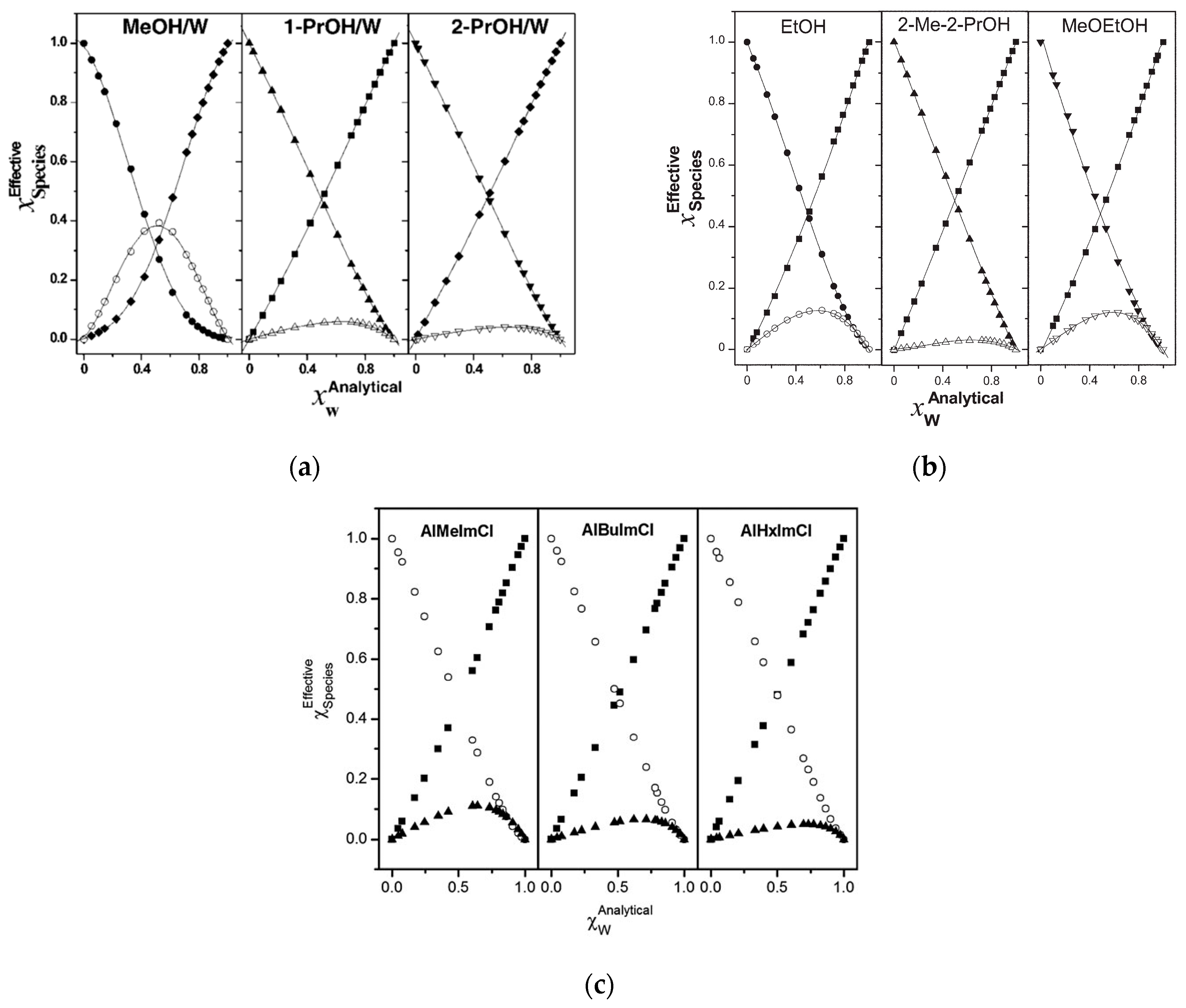
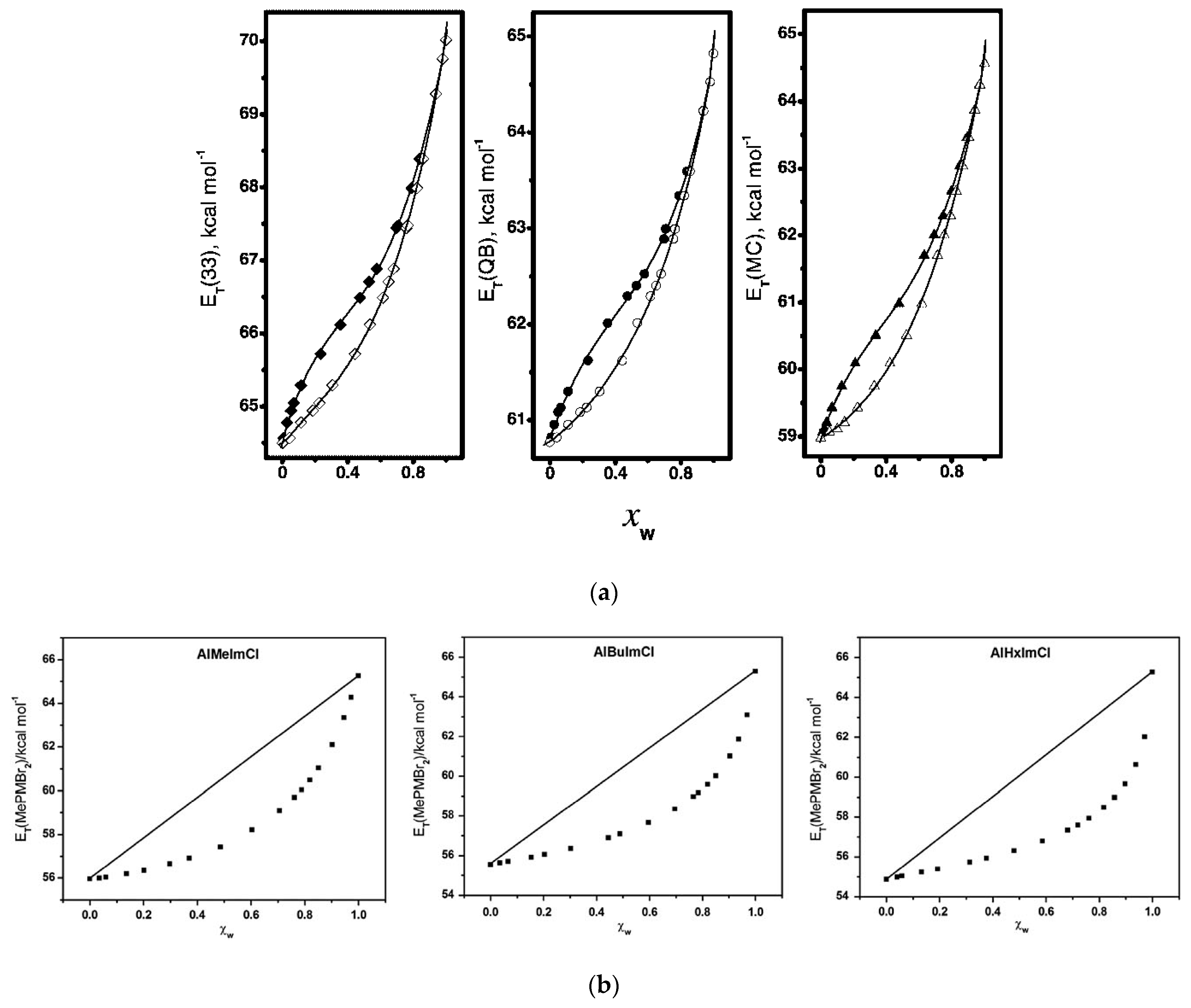
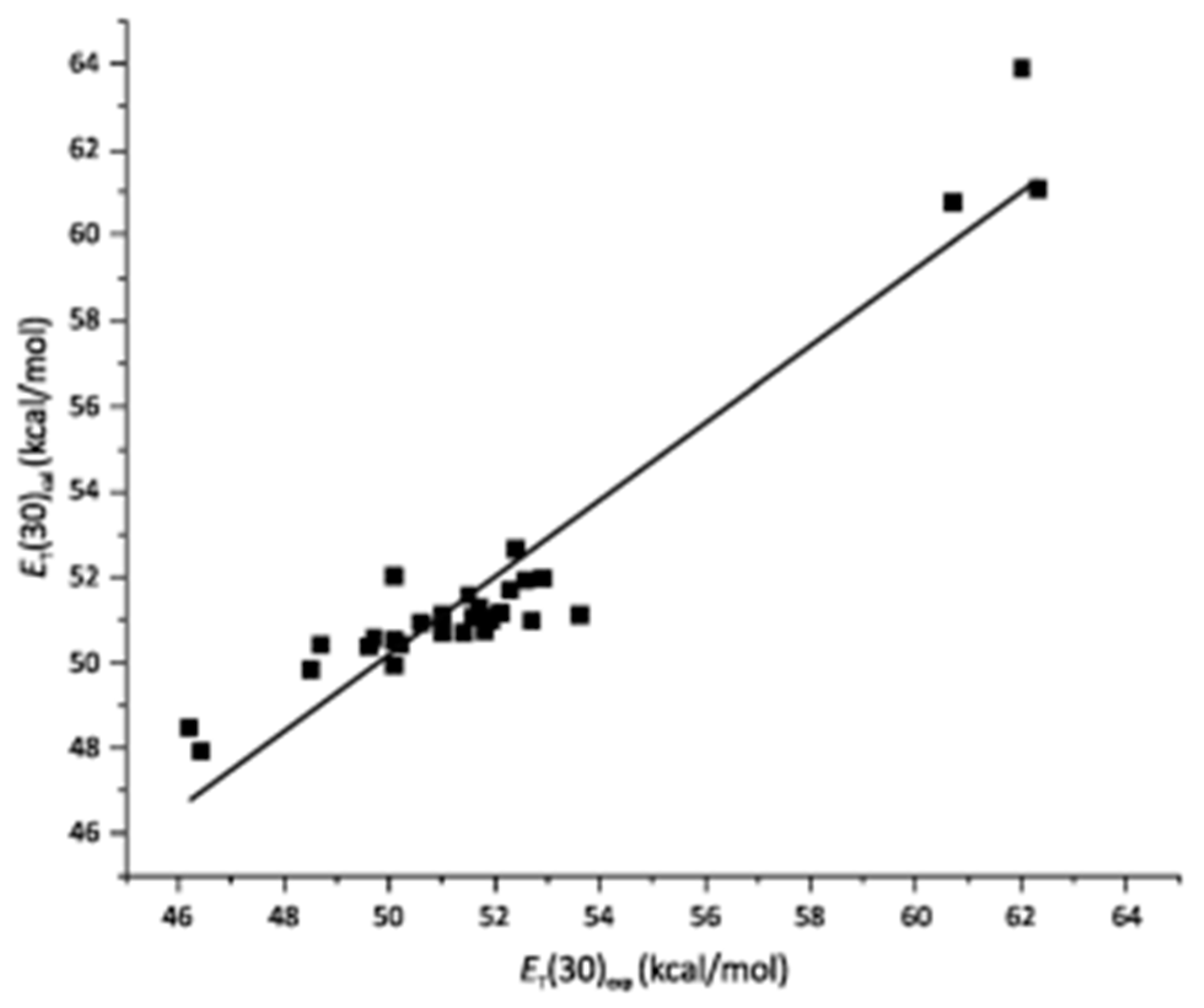
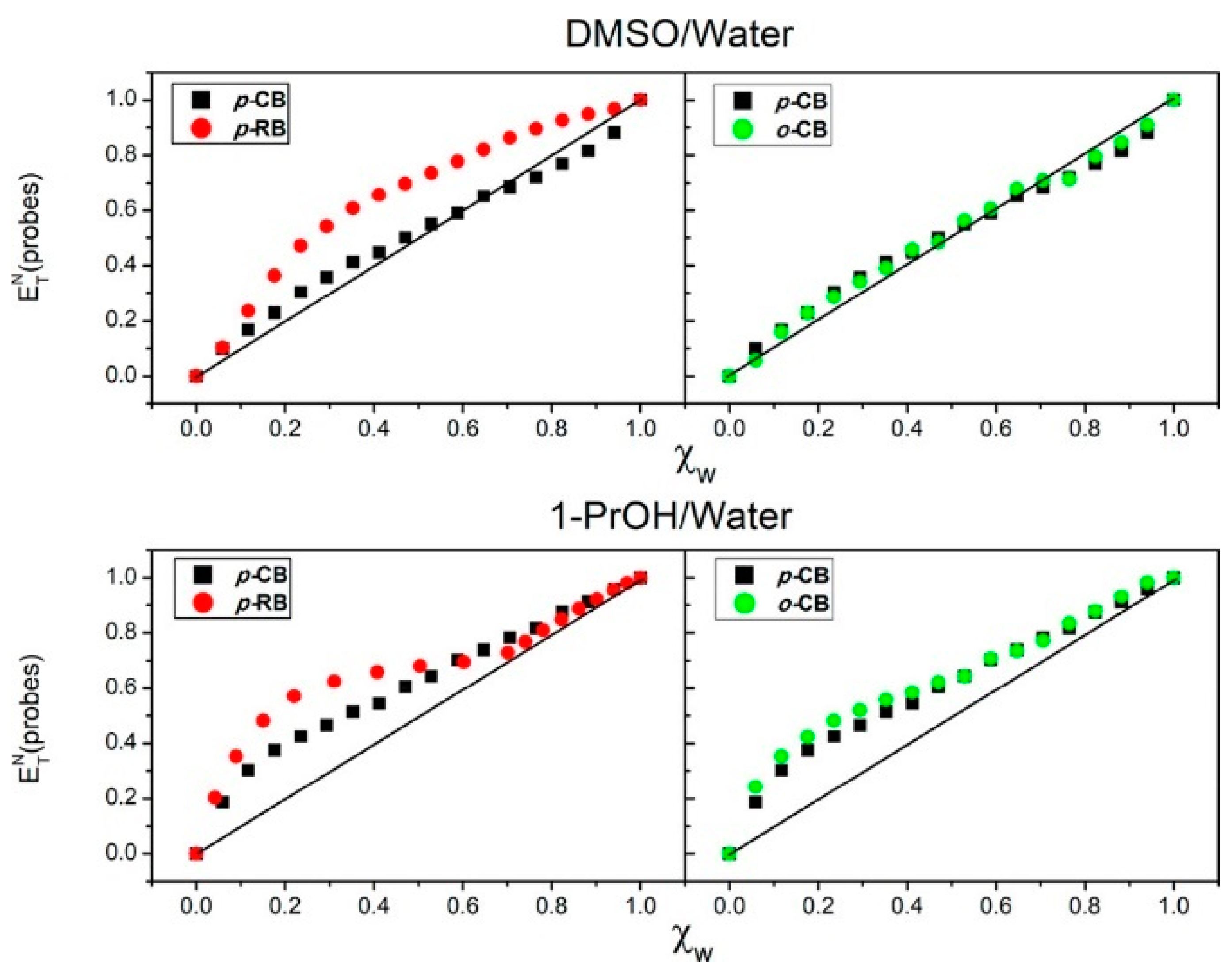
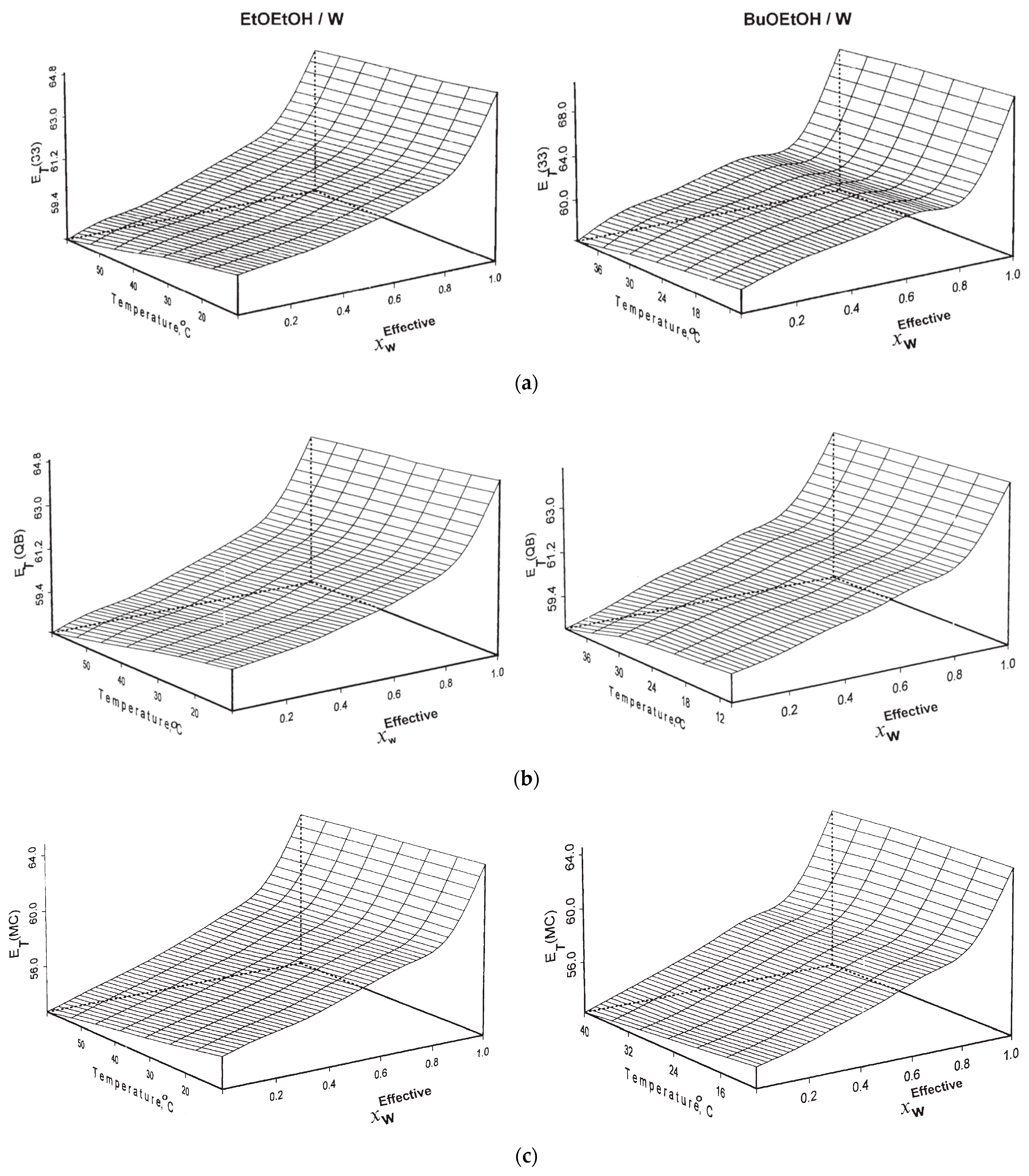
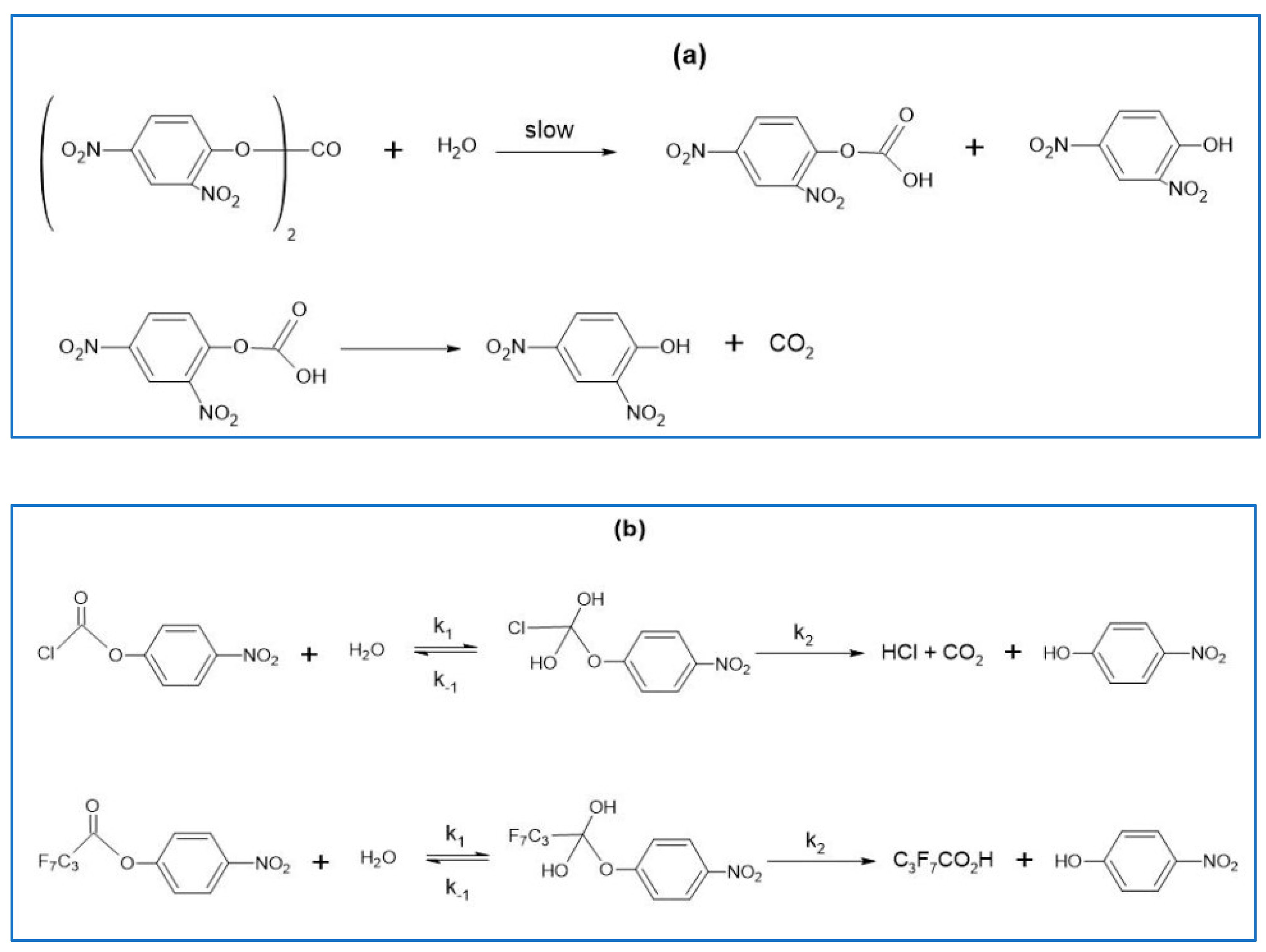
4. Selected Examples of the Application of Solvatochromism to Understand Medium Effects on Chemical Phenomena
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations and Acronyms
| AlMeImCl | 1-Allyl-3-methylimidazolium chloride |
| BuMeImCl | 1-(1-butyl)-3-methylimidazolium chloride |
| BuPMBr2 | 2,6-dibromo-4-[(E)-2-(1-butylpyridinium-4-yl)ethenyl] |
| t-Bu5RB | 2,6-bis[4-(t-butyl)phenyl]-4-{2,4,6-tris[4-(t-butyl)phenyl]pyridinium-1-yl}phenolate |
| t-BuOH | tert-Butanol |
| o-CB | 2-(pyridinium-1-yl)phenolate |
| p-CB | 4- (pyridinium-1-yl)phenolate |
| DMANF | 2-(N,N-dimethylamino)-7-nitrofluorene |
| DMF | N,N-Dimethylformamide |
| DMSO | Dimethyl sulfoxide |
| DNPC | 2,4-dinitrophenyl carbonate |
| DTBSB | o,o’-di-tert-butylstilbazolium betaine |
| ET (probe) | Empirical solvent polarity scale using a specific probe |
| EtOH | Ethanol |
| FePhen | [FeII(1,10-phenanthroline)2(CN)2] |
| HxPMBr2 | 2,6-Dibromo-4-[(E)-2-(1-hexylpyridinium-4-yl)ethenyl] |
| IL | Ionic liquid |
| Log P | Partition coefficient between two partially immiscible solvents, usually n-octanol and water |
| MCC | Microcrystalline cellulose |
| MeCN | Acetonitrile |
| MeOEtOH | 2-Methoxyethanol |
| MeOH | Methanol |
| MePMBr2 | 2,6-Dibromo-4-[(E)-2-(1-methylpyridinium-4-yl)ethenyl] |
| 2-Me-2-PrOH | 2-Methyl-2-propanol |
| MeNI | 1-Methyl-5-nitroindoline |
| MS | Molecular solvent |
| NPFB | 4-Nitrophenyl chloroformate |
| NHFB | 4-Nitrophenyl heptafluorobutyrate |
| NI | 5-Nitroindoline |
| OcPMBr2 | 2,6-Dibromo-4-[(E)-2-(1-octylpyridinium-4-yl)ethenyl] |
| PEG | Polyethylene glycol |
| 1-PrOH | 1-Propanol |
| QB | 1-Methylquinolinium-8-olate |
| RB (or p-RB) | Reichardt betaine, dye number 30 in a list of solvatochromic dyes; 2,6-diphenyl-4-(2,4,6-triphenylpyridinium-1-yl) phenolate. |
| o-RB | 2,4-dimethyl-6-(2,4,6-triphenylpyridinium-1-yl)phenolate, |
| RDA | Retro-Diels—Alder reaction |
| SA | Solvent Lewis acidity; calculated from solvatochromic data |
| SB | Solvent Lewis Basicity; calculated from solvatochromic data |
| SD | Solvent dipolarity; calculated from solvatochromic data |
| Solvatochromism Effect of the medium on the color of a solvatochromic probe | |
| SP | Solvent polarizability; calculated from solvatochromic data |
| TBSB | o-tert-butylstilbazolium betaine |
| Thermo-solvatochromism Effect of temperature on solvatochromism | |
| THF | Tetrahydrofuran |
| WB | Wolfbeis betaine; 2,6-dichloro-4-(2,4,6-triphenylpyridinium-1-yl)-phenolate |
| φ | Fractionation factor: Refers to solvent exchange equilibrium constant between bulk solvent mixture and the solvation layer of the probe |
| χ | Mole fraction |
References
- Chiavone-Filho, O.; Rasmussen, P. Solubilities of Salts in Mixed Solvents. J. Chem. Eng. Data 1993, 38, 367–369. [Google Scholar] [CrossRef]
- Pinho, S.P.; Macedo, E.A. Solubility of NaCl, NaBr, and KCl in Water, Methanol, Ethanol, and Their Mixed Solvents. J. Chem. Eng. Data 2005, 50, 29–32. [Google Scholar] [CrossRef]
- Dogan, H.; Hilmioglu, N.D. Dissolution of cellulose with NMMO by microwave heating. Carbohydr. Polym. 2009, 75, 90–94. [Google Scholar] [CrossRef]
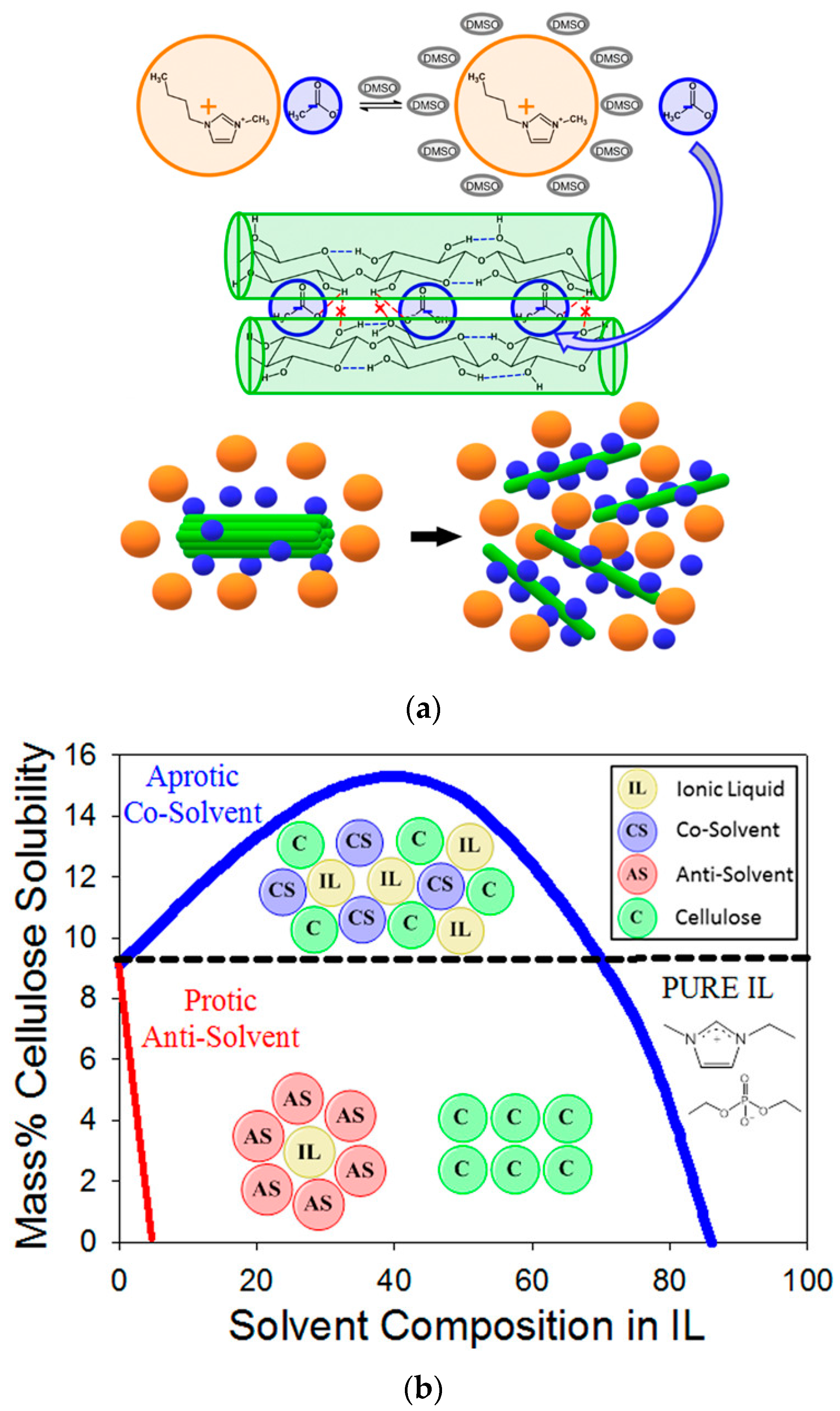
- Kostag, M.; Jedvert, K.; Achtel, C.; Heinze, T.; El Seoud, O.A. Recent advances in solvents for the dissolution, shaping and derivatization of cellulose: Quaternary ammonium electrolytes and their solutions in water and molecular solvents. Molecules 2018, 23, 511. [Google Scholar] [CrossRef] [PubMed]
- El Seoud, O.A.; Bioni, T.A.; Dignani, M.T. Understanding cellulose dissolution in ionic liquid-dimethyl sulfoxide binary mixtures: Quantification of the relative importance of hydrogen bonding and hydrophobic interactions. J. Mol. Liq. 2021, 322, 114848. [Google Scholar] [CrossRef]
- Keppeler, N.; Pires, P.A.R.; Freitas, J.L.S.; El Seoud, O.A. Cellulose dissolution in mixtures of ionic liquids and molecular solvents: The fruitful synergism of experiment and theory. J. Mol. Liq. 2023, 386, 122490. [Google Scholar] [CrossRef]
- Minnick, D.L.; Flores, R.A.; DeStefano, M.R.; Scurto, A.M. Cellulose Solubility in Ionic Liquid Mixtures: Temperature, Cosolvent, and Antisolvent Effects. J. Phys. Chem. B 2016, 120, 7906–7919. [Google Scholar] [CrossRef]
- Zhong, C.; Cheng, F.; Zhu, Y.; Gao, Z.; Jia, H.; Wei, P. Dissolution mechanism of cellulose in quaternary ammonium hydroxide: Revisiting through molecular interactions. Carbohydr. Polym. 2017, 174, 400–408. [Google Scholar] [CrossRef]
- El Seoud, O.A.; Keppeler, N. Education for Sustainable Development: An Undergraduate Chemistry Project on Cellulose Dissolution, Regeneration, and Chemical Recycling of Polycotton. J. Lab. Chem. Educ. 2020, 8, 11–17. [Google Scholar] [CrossRef]
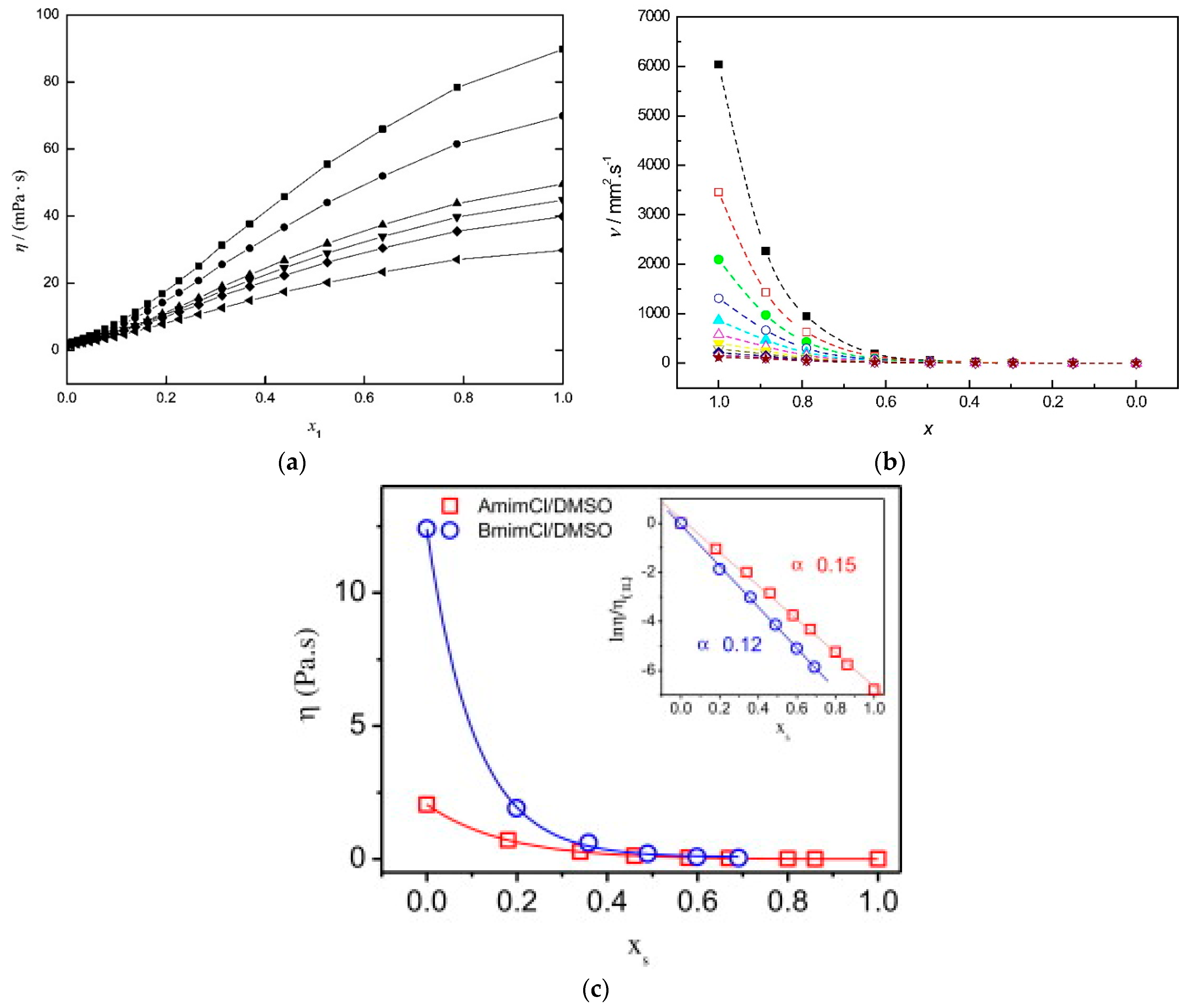
- Zhang, K.; Yang, J.; Yu, X.; Zhang, J.; Wei, X. Densities and Viscosities for Binary Mixtures of Poly(ethylene glycol) 400 + Dimethyl Sulfoxide and Poly(ethylene glycol) 600 + Water at Different Temperatures. J. Chem. Eng. Data 2011, 56, 3083–3088. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X.; Tan, H.; Liu, Z. Improvement the viscosity of imidazolium-based ionic liquid using organic solvents for biofuels. J. Mol. Liq. 2017, 248, 626–633. [Google Scholar] [CrossRef]
- Lv, Y.; Wu, J.; Zhang, J.; Niu, Y.; Liu, C.-Y.; He, J.; Zhang, J. Rheological properties of cellulose/ionic liquid/dimethylsulfoxide (DMSO) solutions. Polymer 2012, 53, 2524–2531. [Google Scholar] [CrossRef]
- Alam, M.S.; Ashokkumar, B.; Siddiq, A.M. The density, dynamic viscosity and kinematic viscosity of protic and aprotic polar solvent (pure and mixed) systems: An experimental and theoretical insight of thermophysical properties. J. Mol. Liq. 2019, 281, 584–597. [Google Scholar] [CrossRef]
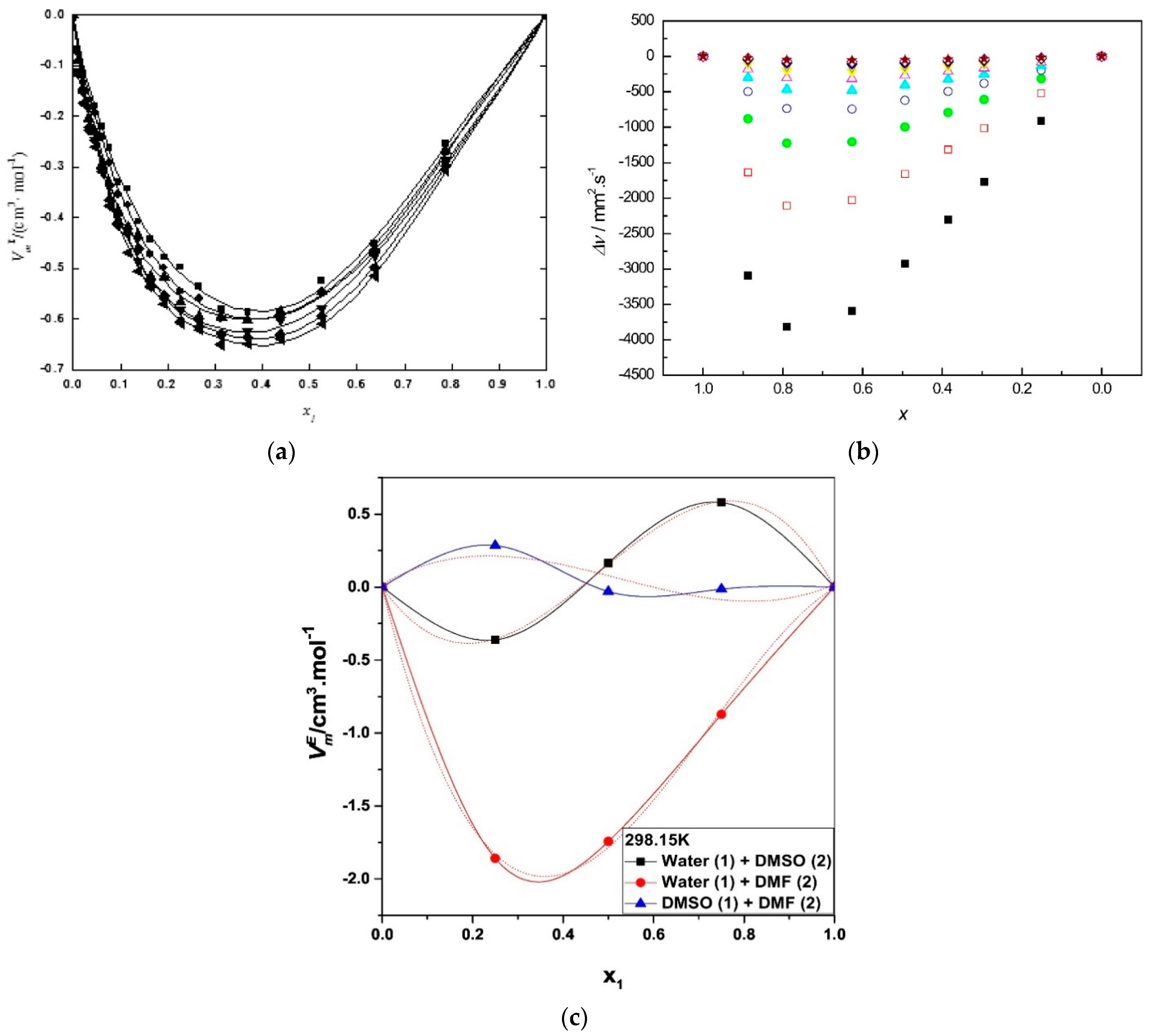
- Suppan, P. Local polarity of solvent mixtures in the field of electronically excited molecules and exciplexes. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1987, 83, 495. [Google Scholar] [CrossRef]
- Suppan, P. Time-resolved luminescence spectra of dipolar excited molecules in liquid and solid mixtures. Dynamics of dielectric enrichment and microscopic motions. Faraday Discuss. Chem. Soc. 1988, 85, 173. [Google Scholar] [CrossRef]
- LNovaki, P.; El Seoud, O.A. Solvatochromism in binary solvent mixtures: Effects of the molecular structure of the probe. Berichte Bunsenges. Phys. Chem. 1997, 101, 902–909. [Google Scholar] [CrossRef]
- Skaf, M.S. Molecular Dynamics Study of Dielectric Properties of Water−Dimethyl Sulfoxide Mixtures. J. Phys. Chem. A 1999, 103, 10719–10729. [Google Scholar] [CrossRef]
- El Seoud, O.A. Solvation in pure and mixed solvents: Some recent developments. Pure Appl. Chem. 2007, 79, 1135–1151. [Google Scholar] [CrossRef]
- Machado, V.G.; Stock, R.I.; Reichardt, C. Pyridinium N -Phenolate Betaine Dyes. Chem. Rev. 2014, 114, 10429–10475. [Google Scholar] [CrossRef]
- Bai, B.; Li, Z.; Wang, H.; Li, M.; Ozaki, Y.; Wei, J. Exploring the difference in xerogels and organogels through in situ observation. R. Soc. Open Sci. 2018, 5, 170492. [Google Scholar] [CrossRef]
- McHale, J.L. Subpicosecond Solvent Dynamics in Charge-Transfer Transitions: Challenges and Opportunities in Resonance Raman Spectroscopy. Acc. Chem. Res. 2001, 34, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Jha, K.K.; Kumar, A.; Munshi, P. Solvatochromism and Reversible Solvent Exchange Phenomena in Solvatomorphic Organic Chromophore Crystals. Cryst. Growth Des. 2023, 23, 2922–2931. [Google Scholar] [CrossRef]
- Martins, C.T.; Lima, M.S.; El Seoud, O.A. Thermosolvatochromism of merocyanine polarity indicators in pure and aqueous solvents: Relevance of solvent lipophilicity. J. Org. Chem. 2006, 71, 9068–9079. [Google Scholar] [CrossRef] [PubMed]
- El Seoud, O.A.; Loffredo, C.; Galgano, P.D.; Sato, B.M.; Reichardt, C. Have biofuel, will travel: A colorful experiment and a different approach to teach the undergraduate laboratory. J. Chem. Educ. 2011, 88, 1293–1297. [Google Scholar] [CrossRef]
- Pires, P.A.R.; El Seoud, O.A.; Machado, V.G.; de Jesus, J.C.; de Melo, C.E.A.; Buske, J.L.O.; Cardozo, A.P. Understanding Solvation: Comparison of Reichardt’s Solvatochromic Probe and Related Molecular ‘core’ Structures. J. Chem. Eng. Data 2019, 64, 2213–2220. [Google Scholar] [CrossRef]
- Dimroth, K.; Reichardt, C.; Siepmann, T.; Bohlmann, F. Über Pyridinium-N-phenol-betaine und ihre Verwendung zur Charakterisierung der Polarität von Lösungsmitteln. Justus Liebigs Ann. Chem. 1963, 661, 1–37. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- NWeiß; Schmidt, C.H.; Thielemann, G.; Heid, E.; Schröder, C.; Spange, S. The physical significance of the Kamlet–Taft π* parameter of ionic liquids. Phys. Chem. Chem. Phys. 2021, 23, 1616–1626. [Google Scholar] [CrossRef]
- El Seoud, O.A.; Kostag, M.; Jedvert, K.; Malek, N.I. Cellulose in Ionic Liquids and Alkaline Solutions: Advances in the Mechanisms of Biopolymer Dissolution and Regeneration. Polymers 2019, 11, 1917. [Google Scholar] [CrossRef]
- Tada, E.B.; Silva, P.L.; El Seoud, O.A. Thermo-solvatochromism of zwitterionic probes in aqueous alcohols: Effects of the properties of the probe and the alcohol. Phys. Chem. Chem. Phys. 2003, 5, 5378–5385. [Google Scholar] [CrossRef]
- Antonious, M.S.; Tada, E.B.; El Seoud, O.A. Thermo-solvatochromism in aqueous alcohols: Effects of the molecular structures of the alcohol and the-solvatochromic probe. J. Phys. Org. Chem. 2002, 15, 403–412. [Google Scholar] [CrossRef]
- Rosés, M.; Ràfols, C.; Ortega, J.; Bosch, E. Solute–solvent and solvent–solvent interactions in binary solvent mixtures. Part 1. A comparison of several preferential solvation models for describing ET(30) polarity of bipolar hydrogen bond acceptor-cosolvent mixtures. J. Chem. Soc. Perkin Trans. 1995, 2, 1607–1615. [Google Scholar] [CrossRef]
- Bosch, E.; Herodes, K.; Koppel, I.; Leito, I.; Koppel, I.; Taal, V.; Rosés, M. Solute-solvent and solvent-solvent interactions in binary solvent mixtures. 2. Effect of temperature on the ET(30) polarity parameter of dipolar hydrogen bond acceptor-hydrogen bond donor mixtures. J. Phys. Org. Chem. 1996, 9, 403–410. [Google Scholar] [CrossRef]
- Ortega, J.; Ràfols, C.; Bosch, E.; Rosés, M. Solute–solvent and solvent–solvent interactions in binary solvent mixtures. Part 3. The ET(30) polarity of binary mixtures of hydroxylic solvents. J. Chem. Soc. Perkin Trans. 1996, 2, 1497–1503. [Google Scholar] [CrossRef]
- Bosch, E.; Rived, F.; Rosés, M. Solute–solvent and solvent–solvent interactions in binary solvent mixtures. Part 4. Preferential solvation of solvatochromic indicators in mixtures of 2-methylpropan-2-ol with hexane, benzene, propan-2-ol, ethanol and methanol. J. Chem. Soc. Perkin Trans. 1996, 2, 2177–2184. [Google Scholar] [CrossRef]
- Ràfols, C.; Rosés, M.; Bosch, E. Solute–solvent and solvent–solvent interactions in binary solvent mixtures. Part 5. Preferential solvation of solvatochromic indicators in mixtures of propan-2-ol with hexane, benzene, ethanol and methanol. J. Chem. Soc. Perkin Trans. 1997, 2, 243–248. [Google Scholar] [CrossRef]
- Buhvestov, U.; Rived, F.; Ràfols, C.; Bosch, E.; Rosés, M. Solute-solvent and solvent-solvent interactions in binary solvent mixtures. Part 7. Comparison of the enhancement of the water structure in alcohol-water mixtures measured by solvatochromic indicators. J. Phys. Org. Chem. 1998, 11, 185–192. [Google Scholar] [CrossRef]
- Chen, J.-S.; Shiao, J.-C. Graphic method for the determination of the complex NMR shift and equilibrium constant for a hetero-association accompanying a self-association. J. Chem. Soc. Faraday Trans. 1994, 90, 429. [Google Scholar] [CrossRef]
- Eblinger, F.; Schneider, H.-J. Self-Association of Water and Water−Solute Associations in Chloroform Studied by NMR Shift Titrations. J. Phys. Chem. 1996, 100, 5533–5537. [Google Scholar] [CrossRef]
- Sacco, A.; De Cillis, F.M.; Holz, M. NMR Studies on hydrophobic interactions in solution Part 3 Salt effects on the self-association of ethanol in water at two different temperatures. J. Chem. Soc. Faraday Trans. 1998, 94, 2089–2092. [Google Scholar] [CrossRef]
- Max, J.-J.; Daneault, S.; Chapados, C. 1-Propanol hydrate by IR spectroscopy. Can. J. Chem. 2002, 80, 113–123. [Google Scholar] [CrossRef]
- Nomen, R.; Sempere, J.; Avilés, K. Detection and characterisation of water alcohol hydrates by on-line FTIR using multivariate data analysis. Chem. Eng. Sci. 2001, 56, 6577–6588. [Google Scholar] [CrossRef]
- Ghoraishi, M.S.; Hawk, J.E.; Phani, A.; Khan, M.F.; Thundat, T. Clustering mechanism of ethanol-water mixtures investigated with photothermal microfluidic cantilever deflection spectroscopy. Sci. Rep. 2016, 6, 23966. [Google Scholar] [CrossRef] [PubMed]
- Katz, E.D.; Ogan, K.; Scott, R.P.W. Distribution of a solute between two phases: The basic theory and its application to the prediction of chromatographic retention. J. Chromatogr. A 1986, 352, 67–90. [Google Scholar] [CrossRef]
- Katz, E.D.; Lochmüller, C.H.; Scott, R.P.W. Methanol-Water Association and Its Effect on Solute Retention in Liquid Chromatography. Anal. Chem. 1989, 61, 349–355. [Google Scholar] [CrossRef]
- Scott, R.P.W. The thermodynamic properties of methanol–water association and its effect on solute retention in liquid chromatography. Analyst 2000, 125, 1543–1547. [Google Scholar] [CrossRef]
- Bastos, E.L.; Silva, P.L.; El Seoud, O.A. Thermosolvatochromism of Betaine Dyes Revisited: Theoretical Calculations of the Concentrations of Alcohol−Water Hydrogen-bonded Species and Application to Solvation in Aqueous Alcohols. J. Phys. Chem. A 2006, 110, 10287–10295. [Google Scholar] [CrossRef]
- Tada, E.B.; Silva, P.L.; El Seoud, O.A. Thermo-solvatochromism of betaine dyes in aqueous alcohols: Explicit consideration of the water-alcohol complex. J. Phys. Org. Chem. 2003, 16, 691–699. [Google Scholar] [CrossRef]
- Sato, B.M.; de Oliveira, C.G.; Martins, C.T.; El Seoud, O.A. Thermo-solvatochromism in binary mixtures of water and ionic liquids: On the relative importance of solvophobic interactions. Phys. Chem. Chem. Phys. 2010, 12, 1764. [Google Scholar] [CrossRef]
- Spange, S.; Lienert, C.; Friebe, N.; Schreiter, K. Complementary interpretation of ET(30) polarity parameters of ionic liquids. Phys. Chem. Chem. Phys. 2020, 22, 9954–9966. [Google Scholar] [CrossRef]
- Sato, B.M.; Martins, C.T.; El Seoud, O.A. Solvation in aqueous binary mixtures: Consequences of the hydrophobic character of the ionic liquids and the solvatochromic probes. New J. Chem. 2012, 36, 2353. [Google Scholar] [CrossRef]
- Martins, C.T.; Lima, M.S.; El Seoud, O.A. A novel, convenient, quinoline-based merocyanine dye: Probing solvation in pure and mixed solvents and in the interfacial region of an anionic micelle. J. Phys. Org. Chem. 2005, 18, 1072–1085. [Google Scholar] [CrossRef]
- Tada, E.B.; Silva, P.L.; Tavares, C.; El Seoud, O.A. Thermo-solvatochromism of zwitterionic probes in aqueous aliphatic alcohols and in aqueous 2-alkoxyethanols: Relevance to the enthalpies of activation of chemical reactions. J. Phys. Org. Chem. 2005, 18, 398–407. [Google Scholar] [CrossRef]
- El Seoud, O.A.; El Seoud, M.I.; Farah, J.P.S. Kinetics of the pH-Independent Hydrolysis of Bis(2,4-dinitrophenyl) Carbonate in Acetonitrile−Water Mixtures: Effects of the Structure of the Solvent. J. Org. Chem. 1997, 62, 5928–5933. [Google Scholar] [CrossRef]
- El Seoud, O.A.; Siviero, F. Kinetics of the pH-independent hydrolyses of 4-nitrophenyl chloroformate and 4-nitrophenyl heptafluorobutyrate in water-acetonitrile mixtures: Consequences of solvent composition and ester hydrophobicity. J. Phys. Org. Chem. 2006, 19, 793–802. [Google Scholar] [CrossRef]
- Easteal, A. A Nuclear Magnetic Resonance Study of Water + Acetonitrile Mixtures. Aust. J. Chem. 1979, 32, 1379. [Google Scholar] [CrossRef]
- Balakrishnan, S.; Easteal, A. Intermolecular interactions in water + acetonitrile mixtures: Evidence from the composition variation of solvent polarity parameters. Aust. J. Chem. 1981, 34, 943. [Google Scholar] [CrossRef]
- Easteal, A.J.; Woolf, L.A. Measurement of (p, V, x) for (water + acetonitrile) at 298.15 K. J. Chem. Thermodyn. 1982, 14, 755–762. [Google Scholar] [CrossRef]
- Schowen, K.B.J. Solvent Hydrogen Isotope Effects. In Transition States of Biochemical Processes; Springer: Boston, MA, USA, 1978; pp. 225–283. [Google Scholar]
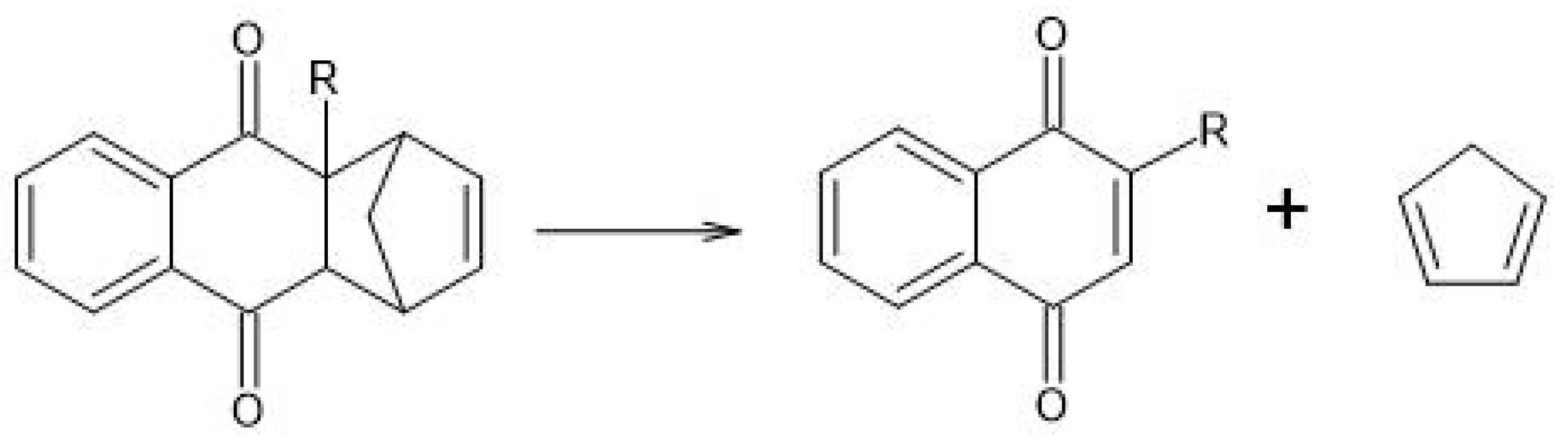
- Wijnen, J.W.; Engberts, J.B.F.N. Retro-Diels-Alder Reaction in Aqueous Solution: Toward a Better Understanding of Organic Reactivity in Water. J. Org. Chem. 1997, 62, 2039–2044. [Google Scholar] [CrossRef]
- Bioni, T.A.; de Oliveira, M.L.; Dignani, M.T.; El Seoud, O.A. Understanding the efficiency of ionic liquids-DMSO as solvents for carbohydrates: Use of solvatochromic- and related physicochemical properties. New J. Chem. 2020, 44, 14906–14914. [Google Scholar] [CrossRef]
- Lacerda, E.G.; Canuto, S.; Coutinho, K. New insights on nonlinear solvatochromism in binary mixture of solvents. In Advances in Quantum Chemistry; Oddershede, J., Brändas, E.J., Eds.; Jack Sabin, Scientist and Friend; Academic Press: Cambridge, MA, USA, 2022; pp. 57–79. [Google Scholar]
- Saini, V.; Kumar, R. A machine learning approach for predicting the empirical polarity of organic solvents. New J. Chem. 2022, 46, 16981–16989. [Google Scholar] [CrossRef]



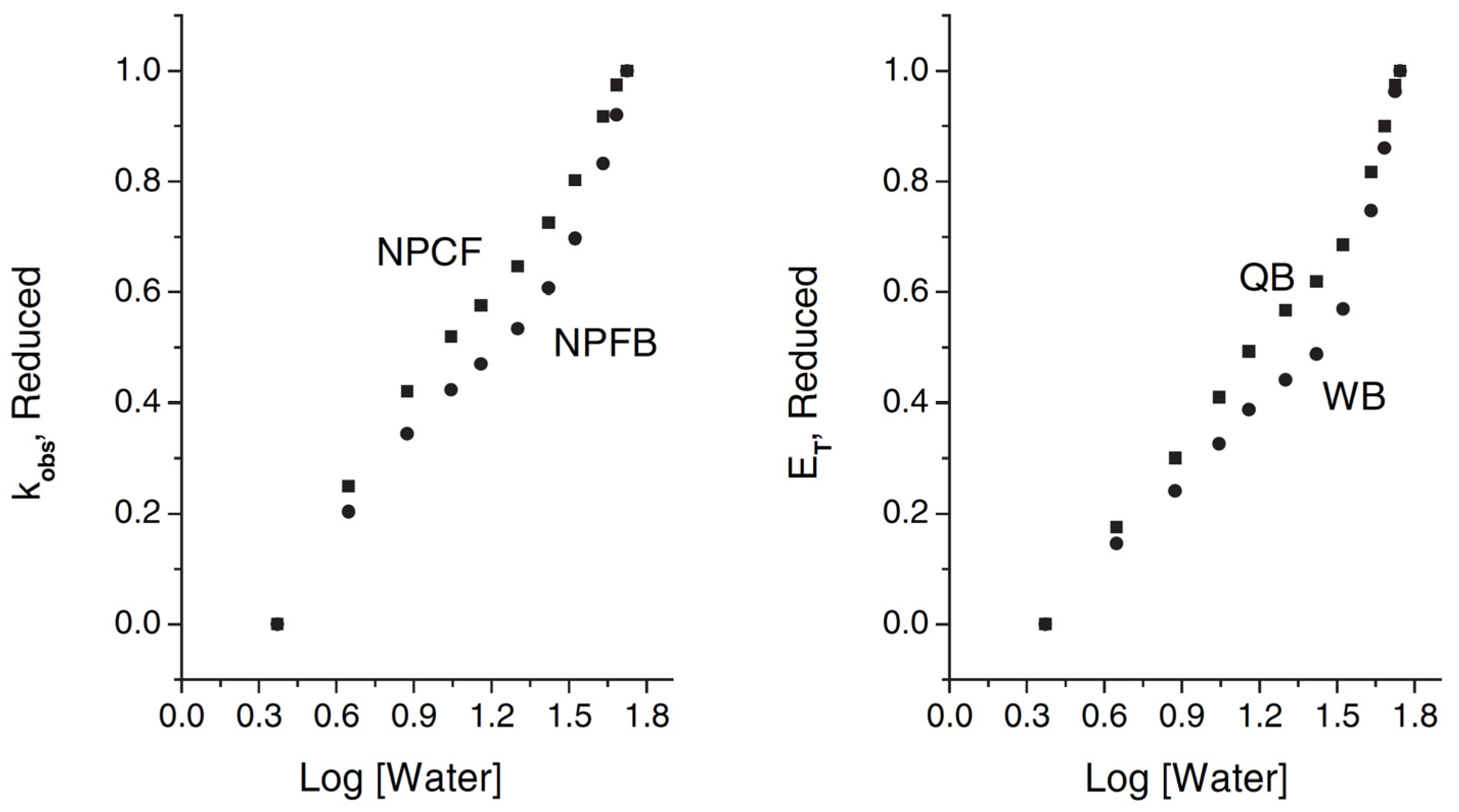
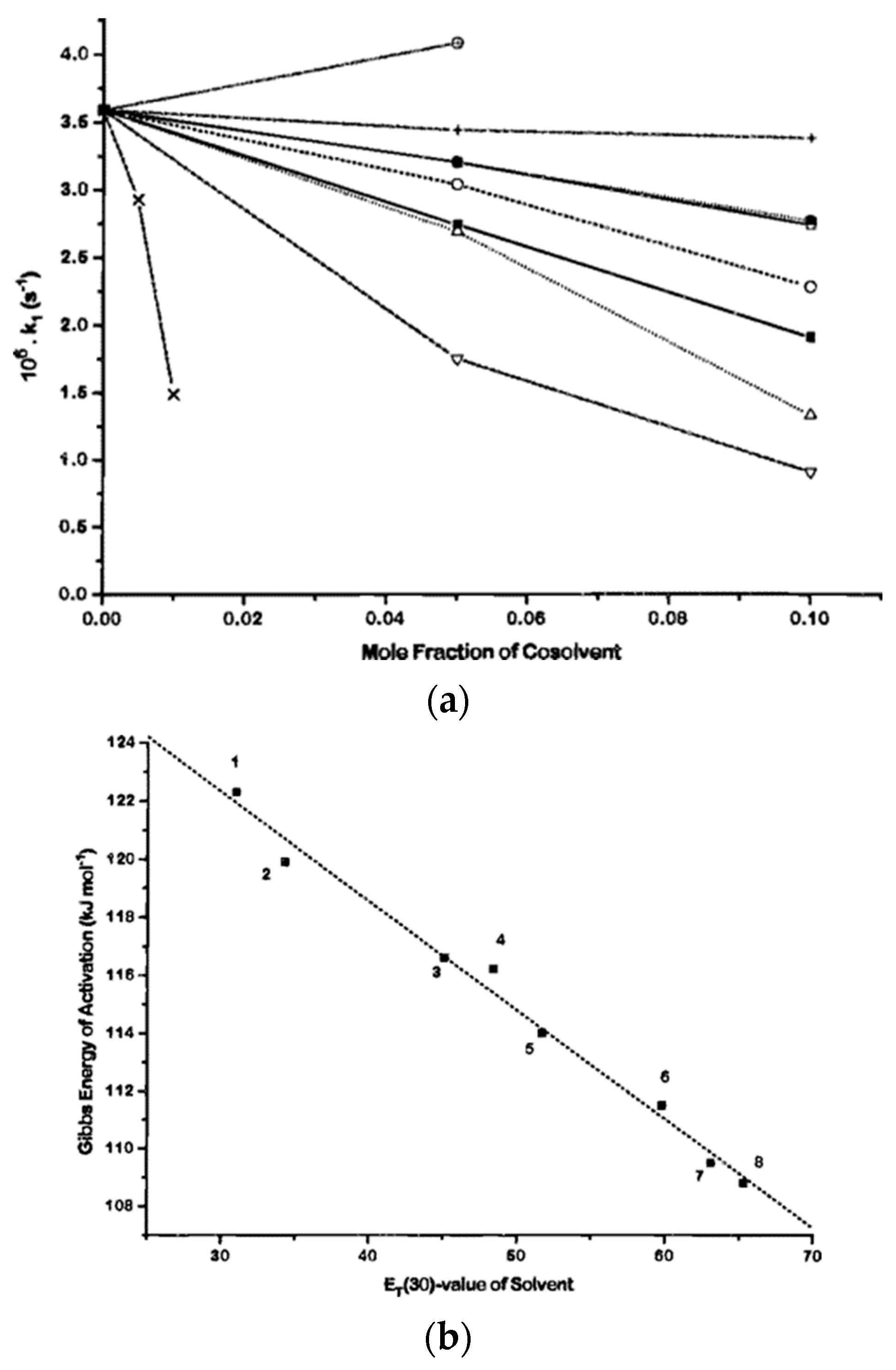
| Solvatochromism in Water/Dimethyl Sulfoxide | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| m | φ(W/DMSO) | φ(DMSO-W/DMSO) | φ(DMSO-W/W) | ET(DMSO) | ET(W) | ET(W/ DMSO) | χ2; b | R2; b | |
| p-RB | 1.32 | 0.49 | 3.29 | 6.71 | 45.3 (+0.2) a | 63.1 (0) a | 49.1 | 0.029 | 0.994 |
| p-CB | 0.80 | 0.80 | 1.70 | 2.12 | 58.4 (−0.4) a | 77.9 (+0.2) a | 67.9 | 0.034 | 0.999 |
| o-CB | 0.90 | 1.41 | 2.40 | 1.67 | 59.1 (−0.2) a | 75.8 (+0.2) a | 63.9 | 0.067 | 0.997 |
| Solvatochromism in Water/1-Propanol | |||||||||
| m | φ (W/1-PrOH) | φ (1-PrOH-W/1-PrOH) | φ (1-PrOH-W/W) | ET(1-PrOH) | ET(W) | ET(1-PrOH/W) | χ2 | R2 | |
| p-RB | 1.40 | 0.44 | 66.92 | 152.09 | 50.9 (+0.2) a | 59.1 (+0.01) a | 52.5 | 0.0023 | 0.999 |
| p-CB | 1.22 | 0.23 | 9.81 | 42.65 | 67.2 (+0.1) a | 77.7 (0) a | 74.0 | 0.006 | 0.999 |
| o-CB | 1.37 | 0.34 | 13.71 | 40.32 | 67.6 (+0.4) a | 76.1 (−0.5) a | 71.9 | 0.004 | 0.999 |
| ROH | Log P | Kassociation (L·mol−1) | φW/ROH | φROH-W/ROH | φROH-W/W |
|---|---|---|---|---|---|
| WB | |||||
| MeOH | −0.77 | 173.3 | 0.601 | 2.212 | 3.681 |
| EtOH | −0.31 | 28 | 0.554 | 11.482 | 20.727 |
| 1-PrOH | 0.25 | 12.3 | 0.265 | 149.208 | 563.049 |
| 2-PrOH | 0.05 | 8.1 | 0.551 | 192.625 | 349.592 |
| 2-Me-2-PrOH | 0.35 | 7.0 | 0.484 | 111.267 | 229.890 |
| MeO-EtOH | −0.77 | 32.1 | 0.479 | 5.659 | 11.814 |
| QB | |||||
| MeOH | −0.77 | 173.3 | 0.381 | 1.172 | 3.076 |
| EtOH | −0.31 | 28 | 0.349 | 5.053 | 14.479 |
| 1-PrOH | 0.25 | 12.3 | 0.305 | 29.599 | 97.046 |
| 2-PrOH | 0.05 | 8.1 | 0.428 | 26.418 | 61.724 |
| 2-Me-2-PrOH | 0.35 | 7.0 | 0.364 | 21.713 | 59.651 |
| MeO-EtOH | −0.77 | 32.1 | 0.341 | 4.855 | 14.238 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Seoud, O.A.; Possidonio, S.; Malek, N.I. Solvatochromism in Solvent Mixtures: A Practical Solution for a Complex Problem. Liquids 2024, 4, 73-94. https://doi.org/10.3390/liquids4010003
El Seoud OA, Possidonio S, Malek NI. Solvatochromism in Solvent Mixtures: A Practical Solution for a Complex Problem. Liquids. 2024; 4(1):73-94. https://doi.org/10.3390/liquids4010003
Chicago/Turabian StyleEl Seoud, Omar A., Shirley Possidonio, and Naved I. Malek. 2024. "Solvatochromism in Solvent Mixtures: A Practical Solution for a Complex Problem" Liquids 4, no. 1: 73-94. https://doi.org/10.3390/liquids4010003
APA StyleEl Seoud, O. A., Possidonio, S., & Malek, N. I. (2024). Solvatochromism in Solvent Mixtures: A Practical Solution for a Complex Problem. Liquids, 4(1), 73-94. https://doi.org/10.3390/liquids4010003