Water Diffusion in Additively Manufactured Polymers: Analysis of the Capillary Effect
Abstract
:1. Introduction
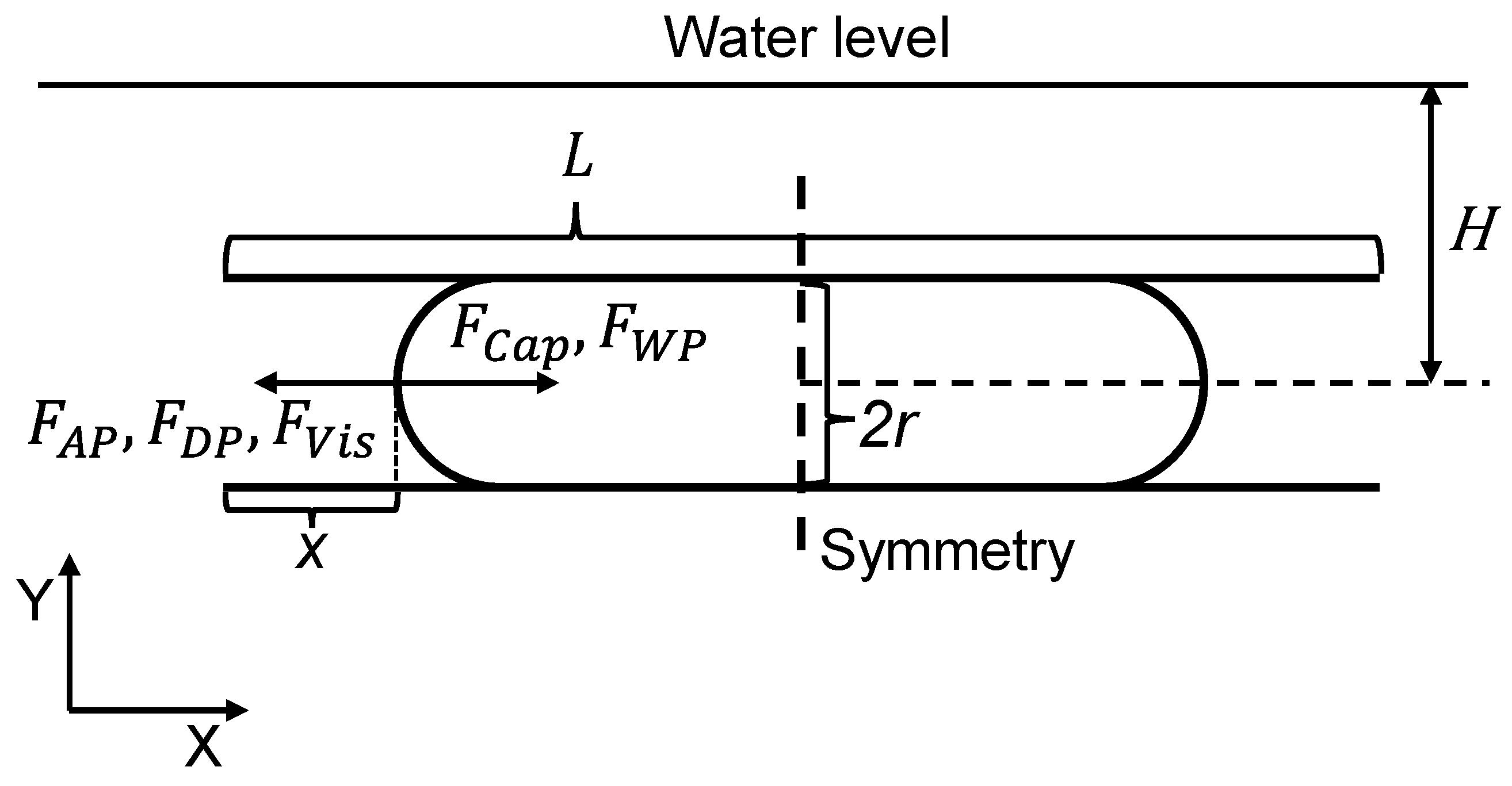
2. Capillary Effect
2.1. Fick’s Diffusion and Capillary Effect
- The capillary is a perfectly round tube that penetrates the whole specimen.
- Some part of the air in the capillary escapes immediately when the specimen is placed in the water tank.
- The residual air and water in the capillary remain at room temperature.
- The air that remains in the capillary is dry.
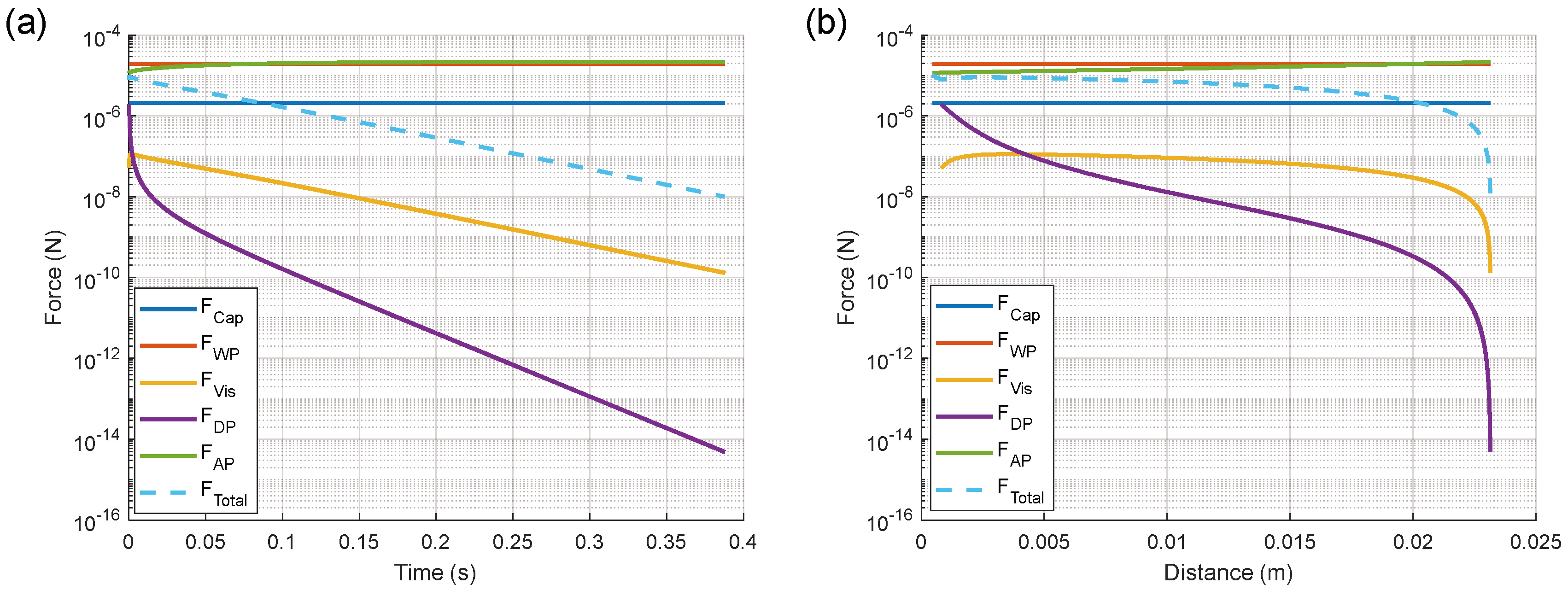
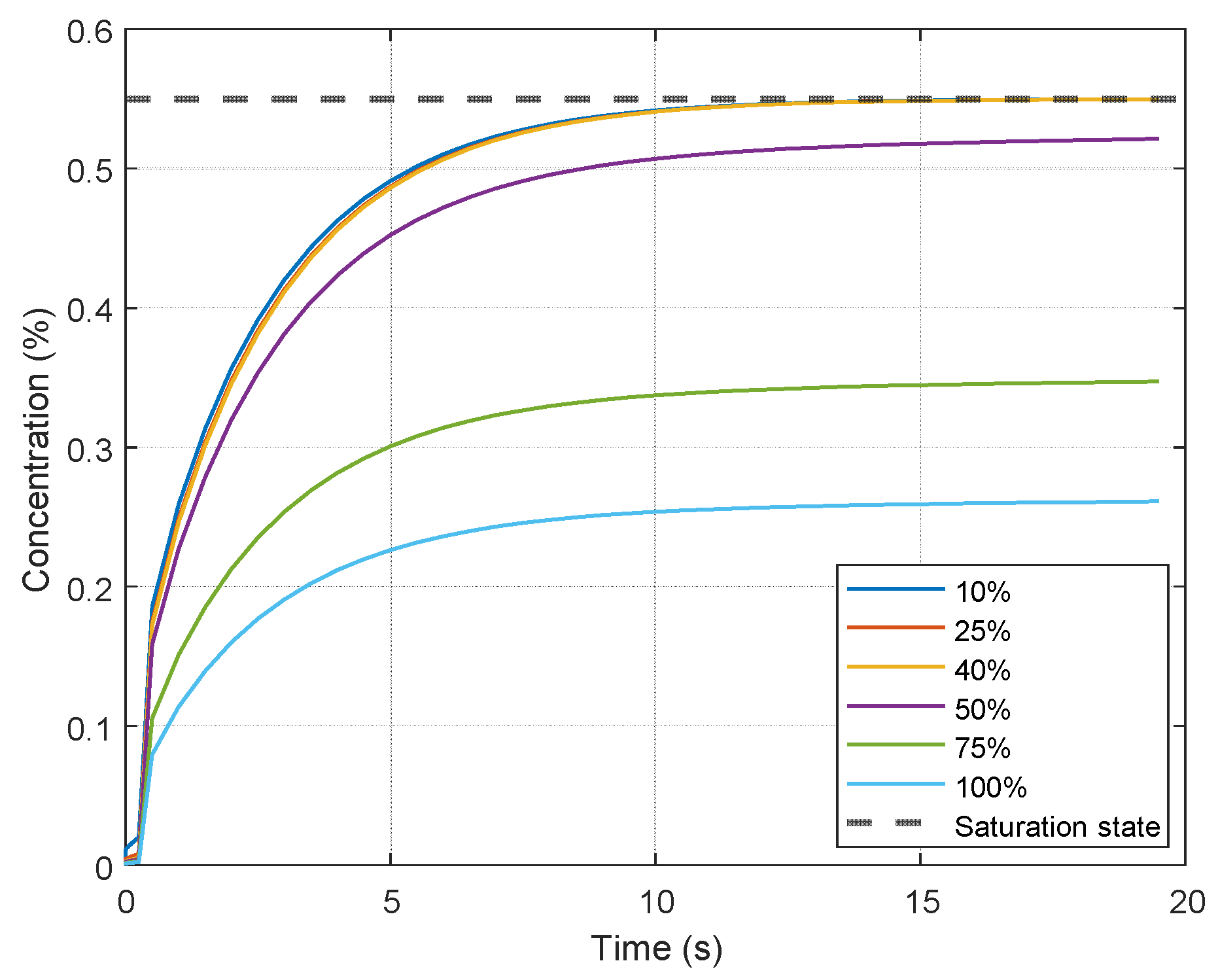
2.2. Results and Discussion
3. Finite-Element Simulations
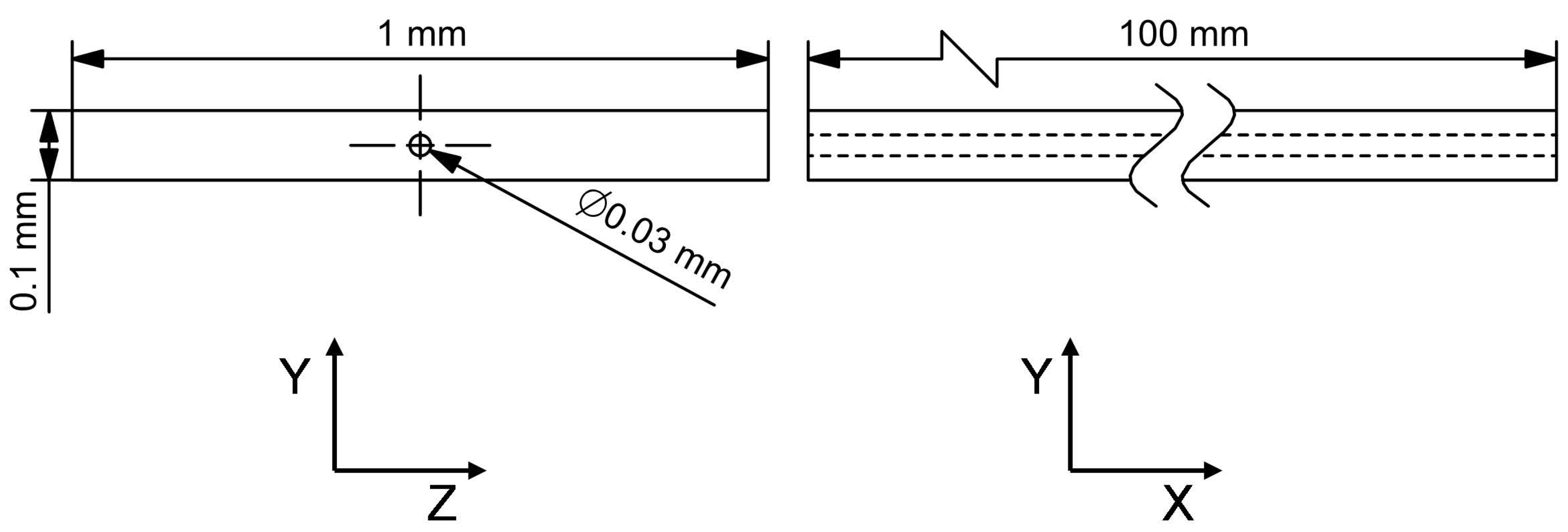
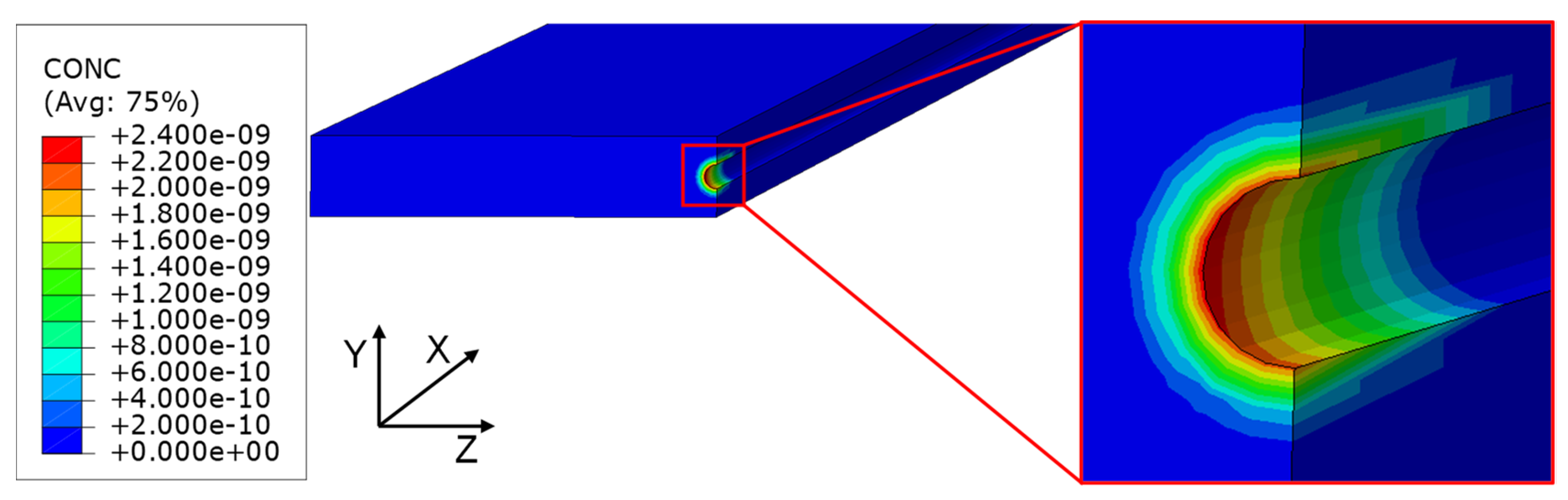
3.1. FEA Implementation
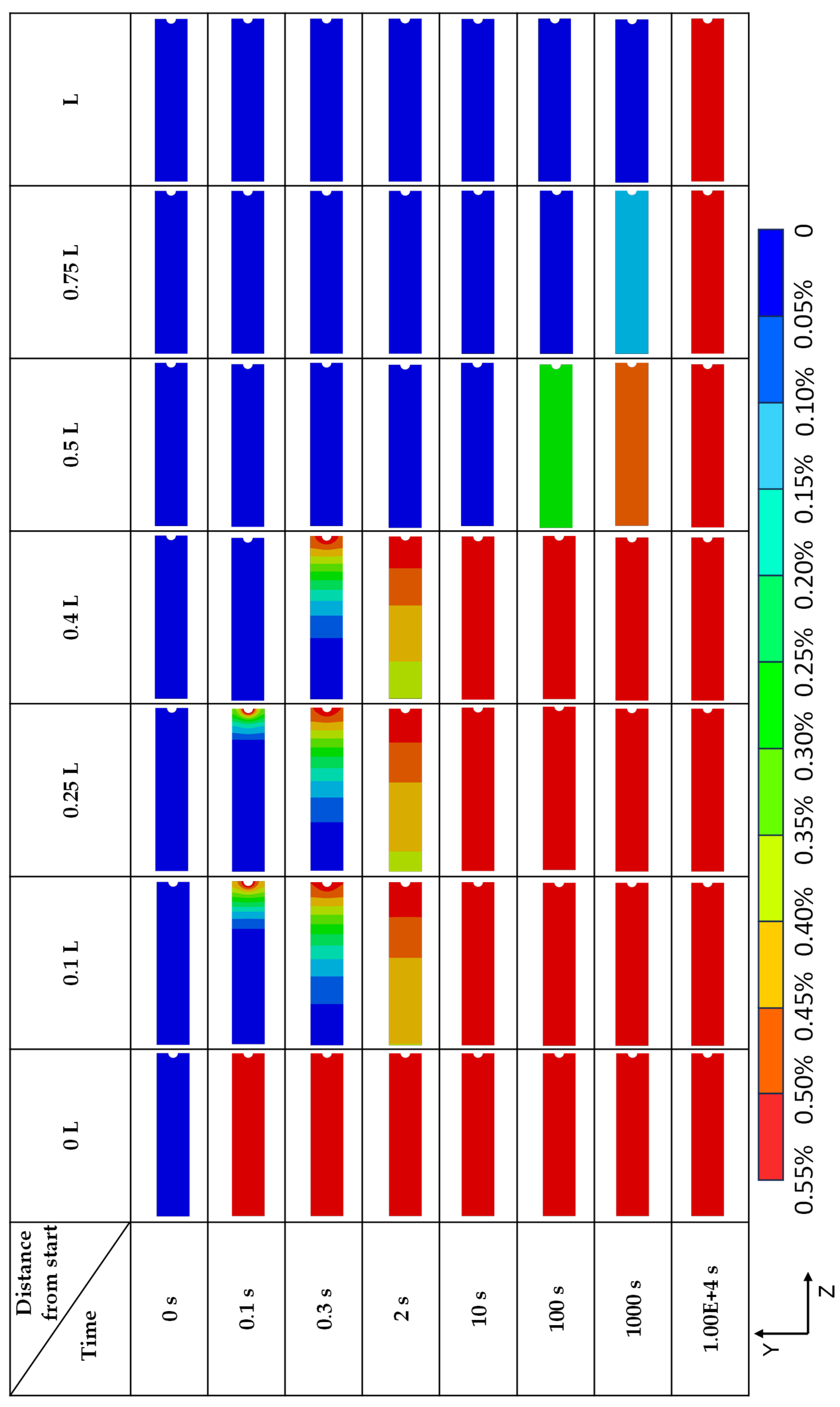
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ziółkowski, M.; Dyl, T. Possible applications of additive manufacturing technologies in shipbuilding: A review. Machines 2020, 8, 84. [Google Scholar] [CrossRef]
- Rawal, S.; Brantley, J.; Karabudak, N. Additive manufacturing of Ti-6Al-4V alloy components for spacecraft applications. In Proceedings of the RAST 2013—6th International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 12–14 June 2013; pp. 5–11. [Google Scholar] [CrossRef]
- Zhang, K.; Shi, D.; Wang, W.; Wang, Q. Mechanical characterization of hybrid lattice-to-steel joint with pyramidal CFRP truss for marine application. Compos. Struct. 2017, 160, 1198–1204. [Google Scholar] [CrossRef]
- Shuai, C.; Yang, W.; Feng, P.; Peng, S.; Pan, H. Accelerated degradation of HAP/PLLA bone scaffold by PGA blending facilitates bioactivity and osteoconductivity. Bioact. Mater. 2021, 6, 490–502. [Google Scholar] [CrossRef] [PubMed]
- Latko-Durałek, P.; Dydek, K.; Boczkowska, A. Thermal, rheological and mechanical properties of PETG/RPETG blends. J. Polym. Environ. 2019, 27, 2600–2606. [Google Scholar] [CrossRef]
- Li, W.; Zhao, X.; Liu, Y.; Ouyang, Y.; Li, W.; Chen, D.; Ye, D. Hygrothermal aging behavior and flexural property of carbon fiber-reinforced polyethylene terephthalate glycol composites. Text. Res. J. 2023, 93, 1005–1018. [Google Scholar] [CrossRef]
- Ramírez-Revilla, S.; Camacho-Valencia, D.; Gonzales-Condori, E.G.; Márquez, G. Evaluation and comparison of the degradability and compressive and tensile properties of 3D printing polymeric materials: PLA, PETG, PC, and ASA. MRS Commun. 2023, 13, 55–62. [Google Scholar] [CrossRef]
- Dhakal, H.; Zhang, Z.; Guthrie, R.; MacMullen, J.; Bennett, N. Development of flax/carbon fibre hybrid composites for enhanced properties. Carbohydr. Polym. 2013, 96, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Pérez, M.; Medina-Sánchez, G.; García-Collado, A.; Gupta, M.; Carou, D. Surface quality enhancement of fused deposition modeling (FDM) printed samples based on the selection of critical printing parameters. Materials 2018, 11, 1382. [Google Scholar] [CrossRef] [PubMed]
- Hussnain, S.; Shah, S.; Megat-Yusoff, P.; Hussain, M. Degradation and mechanical performance of fibre-reinforced polymer composites under marine environments: A review of recent advancements. Polym. Degrad. Stab. 2023, 215, 110452. [Google Scholar] [CrossRef]
- Bellini, A.; Güçeri, S. Mechanical characterization of parts fabricated using fused deposition modeling. Rapid Prototyp. J. 2003, 9, 252–264. [Google Scholar] [CrossRef]
- Tao, Y.; Kong, F.; Li, Z.; Zhang, J.; Zhao, X.; Yin, Q.; Xing, D.; Li, P. A review on voids of 3D printed parts by fused filament fabrication. J. Mater. Res. Technol. 2021, 15, 4860–4879. [Google Scholar] [CrossRef]
- Kumar, M.; Ramakrishnan, R.; Omarbekova, A. 3D printed polycarbonate reinforced acrylonitrile–butadiene–styrene composites: Composition effects on mechanical properties, micro-structure and void formation study. J. Mech. Sci. Technol. 2019, 33, 5219–5226. [Google Scholar] [CrossRef]
- Tao, Y.; Pan, L.; Liu, D.; Li, P. A case study: Mechanical modeling optimization of cellular structure fabricated using wood flour-filled polylactic acid composites with fused deposition modeling. Compos. Struct. 2019, 216, 360–365. [Google Scholar] [CrossRef]
- Goh, G.D.; Dikshit, V.; Nagalingam, A.P.; Goh, G.L.; Agarwala, S.; Sing, S.L.; Wei, J.; Yeong, W.Y. Characterization of mechanical properties and fracture mode of additively manufactured carbon fiber and glass fiber reinforced thermoplastics. Mater. Des. 2018, 137, 79–89. [Google Scholar] [CrossRef]
- Fichera, M.; Carlsson, L.A. Moisture transport in unidirectional carbon/vinylester panels with imperfect fiber/matrix interface. J. Compos. Mater. 2016, 50, 751–760. [Google Scholar] [CrossRef]
- Seppala, J.E.; Han, S.H.; Hillgartner, K.E.; Davis, C.S.; Migler, K.B. Weld formation during material extrusion additive manufacturing. Soft Matter 2017, 13, 6761–6769. [Google Scholar] [CrossRef] [PubMed]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly oriented carbon fiber–polymer composites via additive manufacturing. Compos. Sci. Technol. 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Sommacal, S.; Matschinski, A.; Drechsler, K.; Compston, P. Characterisation of void and fiber distribution in 3D printed carbon-fiber/PEEK using X-ray computed tomography. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106487. [Google Scholar] [CrossRef]
- Thomason, J.; Xypolias, G. Hydrothermal Ageing of Glass Fibre Reinforced Vinyl Ester Composites: A Review. Polymers 2023, 15, 835. [Google Scholar] [CrossRef]
- Thomason, J.L. The interface region in glass fibre-reinforced epoxy resin composites: 2. Water absorption, voids and the interface. Composites 1995, 26, 477–485. [Google Scholar] [CrossRef]
- Ayanoglu, M.O.; Carlsson, L.A.; Du, E. Effects of void content on the moisture uptake and mechanical strength of a glass/epoxy composite. J. Compos. Mater. 2023, 57, 325–336. [Google Scholar] [CrossRef]
- Caggiano, A.; Schicchi, D.S.; Mankel, C.; Ukrainczyk, N.; Koenders, E.A. A mesoscale approach for modeling capillary water absorption and transport phenomena in cementitious materials. Comput. Struct. 2018, 200, 1–10. [Google Scholar] [CrossRef]
- Galpayage Dona, K.N.U.; Du, E.; Carlsson, L.A.; Fletcher, D.M.; Boardman, R.P. Modeling of water wicking along fiber/matrix interface voids in unidirectional carbon/vinyl ester composites. Microfluid. Nanofluid. 2020, 24, 31. [Google Scholar] [CrossRef]
- Romero, P.E.; Barrios, J.M.; Molero, E.; Bustillo, A. Tuning 3D-printing parameters to produce vertical ultra-hydrophobic PETG parts with low ice adhesion: A food industry case study. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 238, 750–758. [Google Scholar] [CrossRef]
- Barrios, J.M.; Romero, P.E. Improvement of Surface Roughness and Hydrophobicity in PETG Parts Manufactured via Fused Deposition Modeling (FDM): An Application in 3D Printed Self–Cleaning Parts. Materials 2019, 12, 2499. [Google Scholar] [CrossRef]
- RS PRO 2.85 mm Black CARBON-P 3D Printer Filament, 500g|RS. Available online: https://uk.rs-online.com/web/p/3d-printing-materials/9107043/ (accessed on 10 February 2023).
- Kim, D.-H.; Seo, H.-S. Role of the Wall Layer in 3D-Printed Composites under the Salt Spray Condition. J. Mar. Sci. Eng. 2023, 11, 1416. [Google Scholar] [CrossRef]





| Property | Value |
|---|---|
| Surface tension of still water | 0.07275 N/m |
| Contact angle of PETG | 54° * |
| Density of still water | 1000 kg/m3 |
| Gravitational acceleration | 9.81 m/s2 |
| Initial pressure in the capillary | 1.013 × 105 Pa |
| Viscosity of water | 1.0016 × 10−6 Pa⋅s |
| Ageing Temperature (°C) | Diffusivity (μm2/ms) | Maximum Water Uptake (%) |
|---|---|---|
| 25 | 0.55 |
| Case | Phase 1 | Phase 2 | Phase 3 | Total Time/ms | |||
|---|---|---|---|---|---|---|---|
| Size/ ms | Number | Size/ ms | Number | Size/ ms | Number | ||
| I | 10 | 25 | 50 | 195 | 104 | ||
| II | 1 | 250 | 50 | 195 | 104 | ||
| III | 105 | 600 | 6 × 107 | ||||
| IV | 10 | 25 | 50 | 195 | 105 | 600 | 6.001 × 107 |
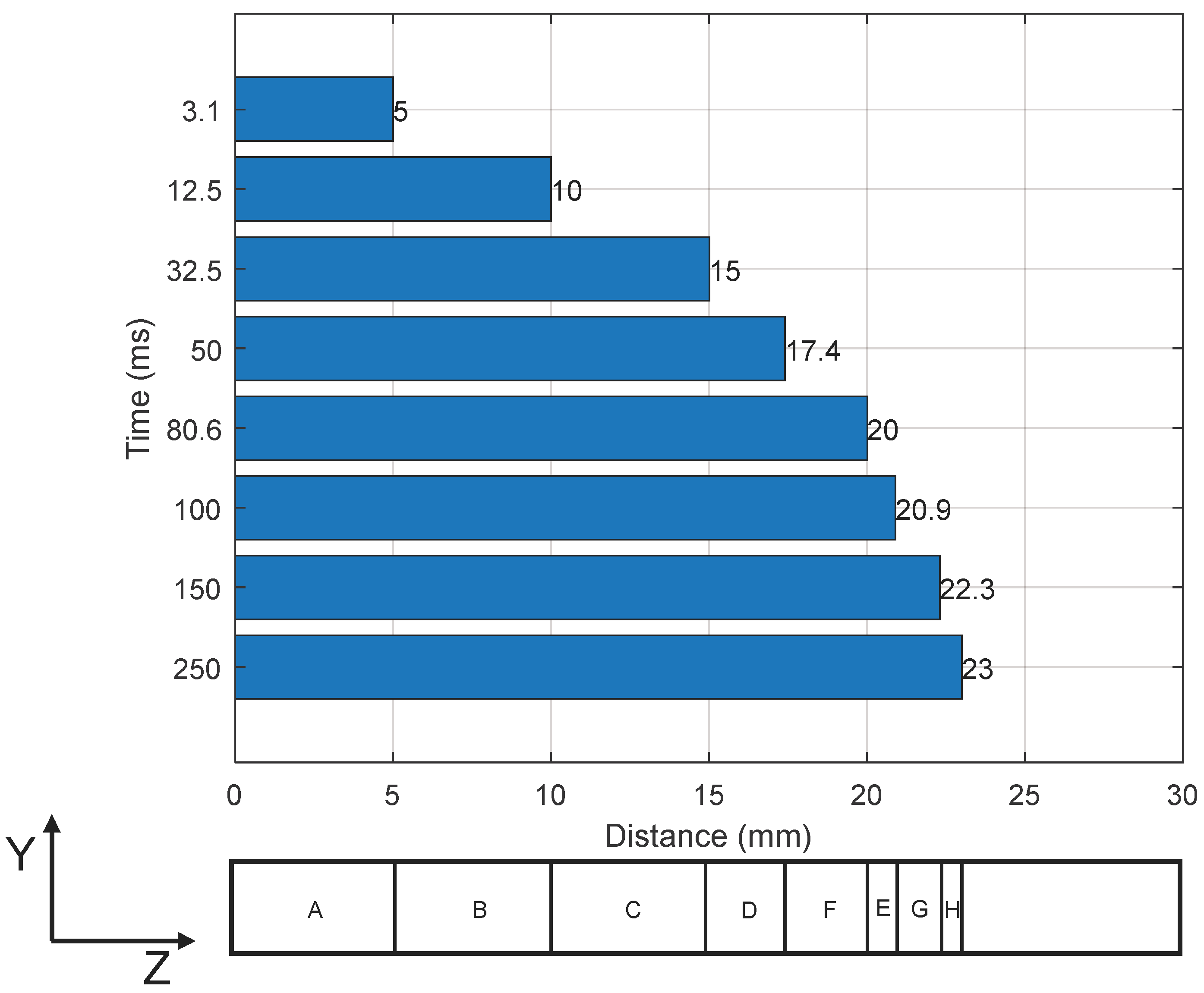
| Step Number | Capillary Flow Length/mm | Step Time/ms |
|---|---|---|
| A | 0–5 | 3.1 |
| B | 5–10 | 12.5 |
| C | 10–15 | 32.5 |
| D | 15–17.4 | 50 |
| E | 17.4–20 | 80.6 |
| F | 20–20.9 | 100 |
| G | 20.9–22.3 | 150 |
| H | 22.3–23.0 | 250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Baxevanakis, K.P.; Silberschmidt, V.V. Water Diffusion in Additively Manufactured Polymers: Analysis of the Capillary Effect. Micro 2024, 4, 281-294. https://doi.org/10.3390/micro4020017
Li B, Baxevanakis KP, Silberschmidt VV. Water Diffusion in Additively Manufactured Polymers: Analysis of the Capillary Effect. Micro. 2024; 4(2):281-294. https://doi.org/10.3390/micro4020017
Chicago/Turabian StyleLi, Boyu, Konstantinos P. Baxevanakis, and Vadim V. Silberschmidt. 2024. "Water Diffusion in Additively Manufactured Polymers: Analysis of the Capillary Effect" Micro 4, no. 2: 281-294. https://doi.org/10.3390/micro4020017
APA StyleLi, B., Baxevanakis, K. P., & Silberschmidt, V. V. (2024). Water Diffusion in Additively Manufactured Polymers: Analysis of the Capillary Effect. Micro, 4(2), 281-294. https://doi.org/10.3390/micro4020017







