Analytical Solution of the Susceptible-Infected-Recovered/Removed Model for the Not-Too-Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates
Abstract
:1. Introduction
2. SIR Model
3. Approximate Analytical Solutions
3.1. Solution in the Limit of Small
3.2. Properties of the Approximate Solution (12)
4. Special Cases
4.1. Constant Ratio
4.2. Linearly Increasing Ratio
5. Illustrative Examples
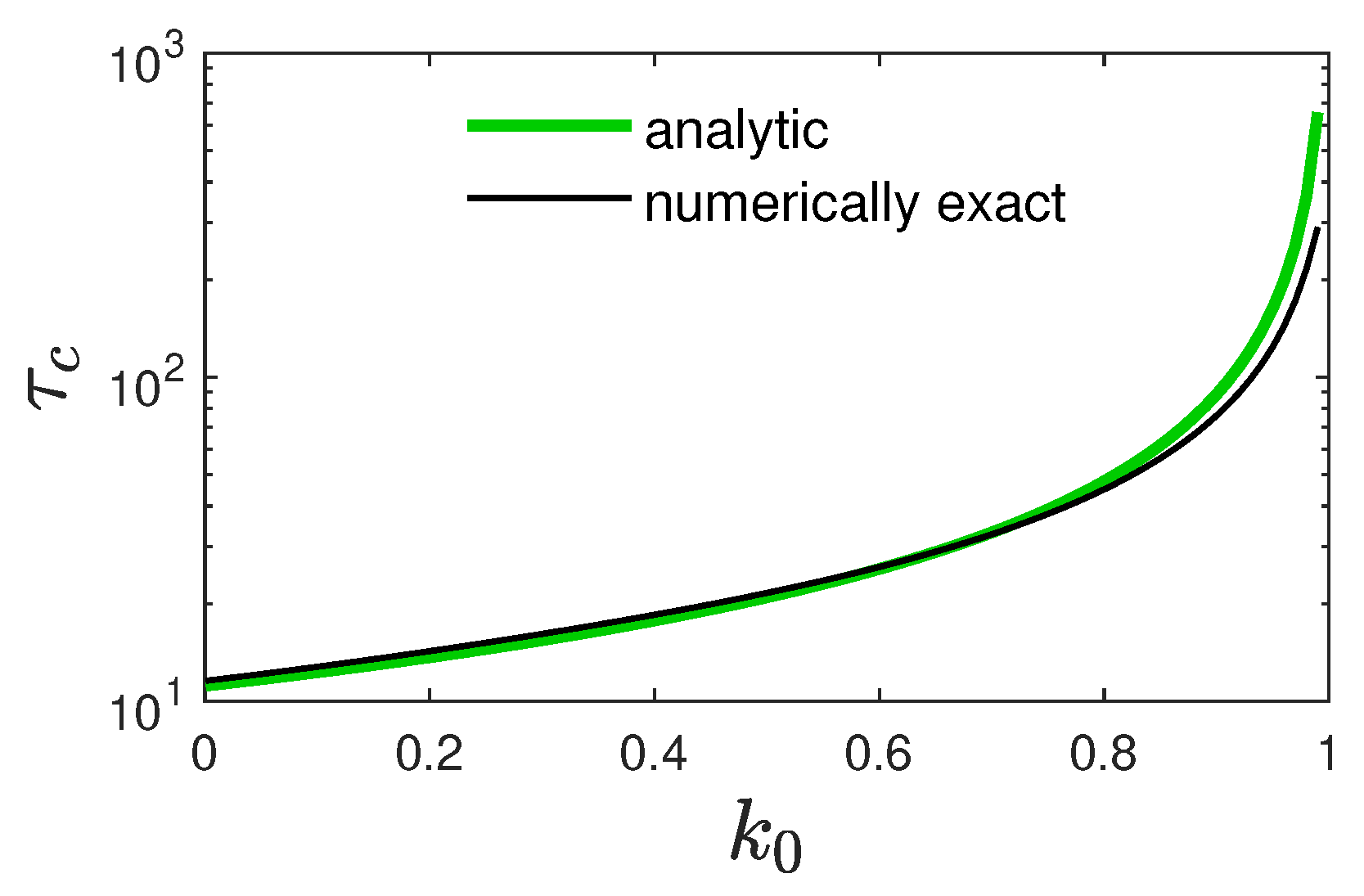
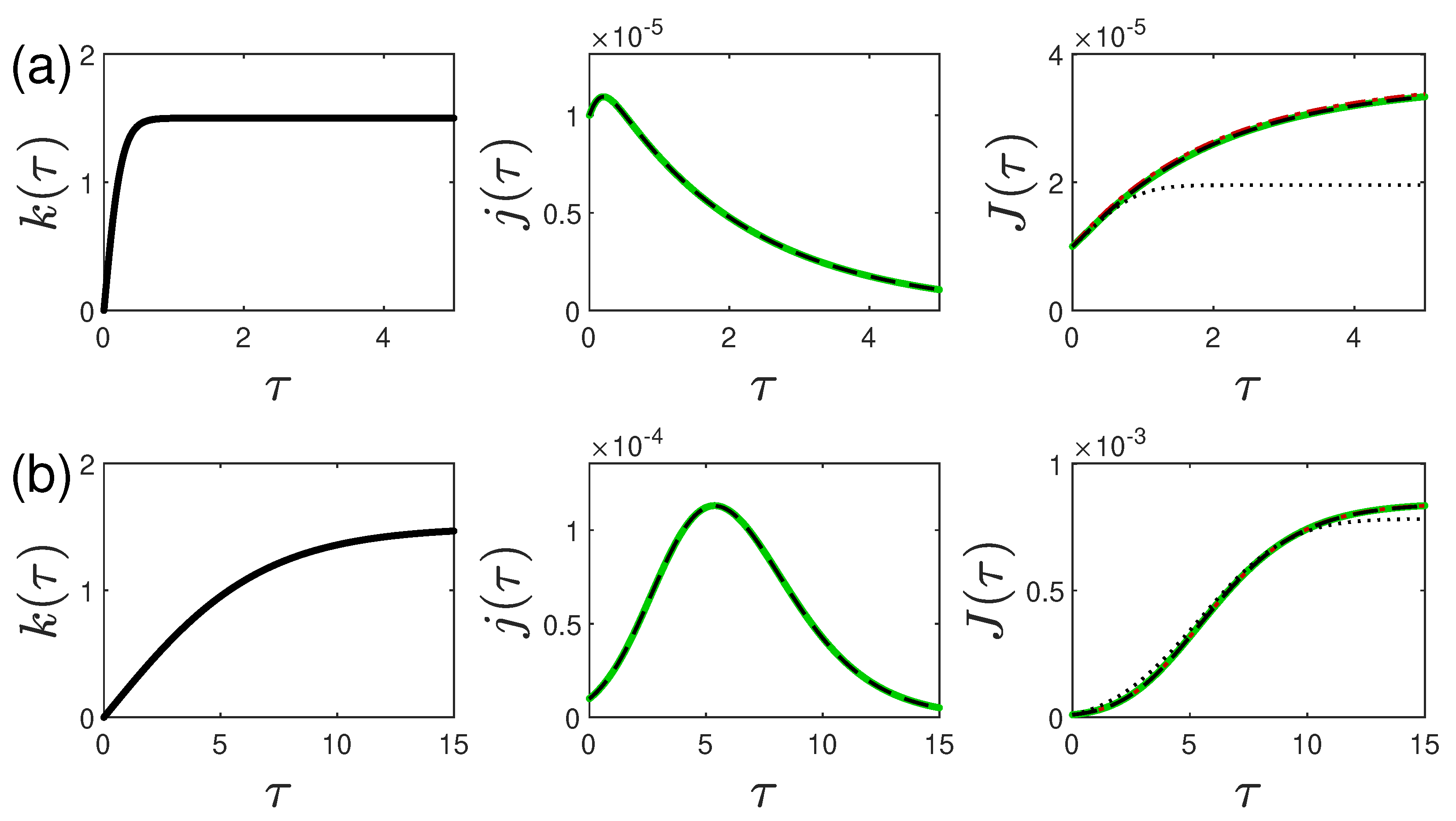
5.1. Monotonically Rising Ratio
5.2. Oscillating Ratio
6. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Cumulative Fraction for General Reduced Time Dependencies k(τ)
Appendix B. Solution at Late Times
Appendix B.1. Limit J≃J ∞ =0.7
Appendix B.2. Continuity Conditions
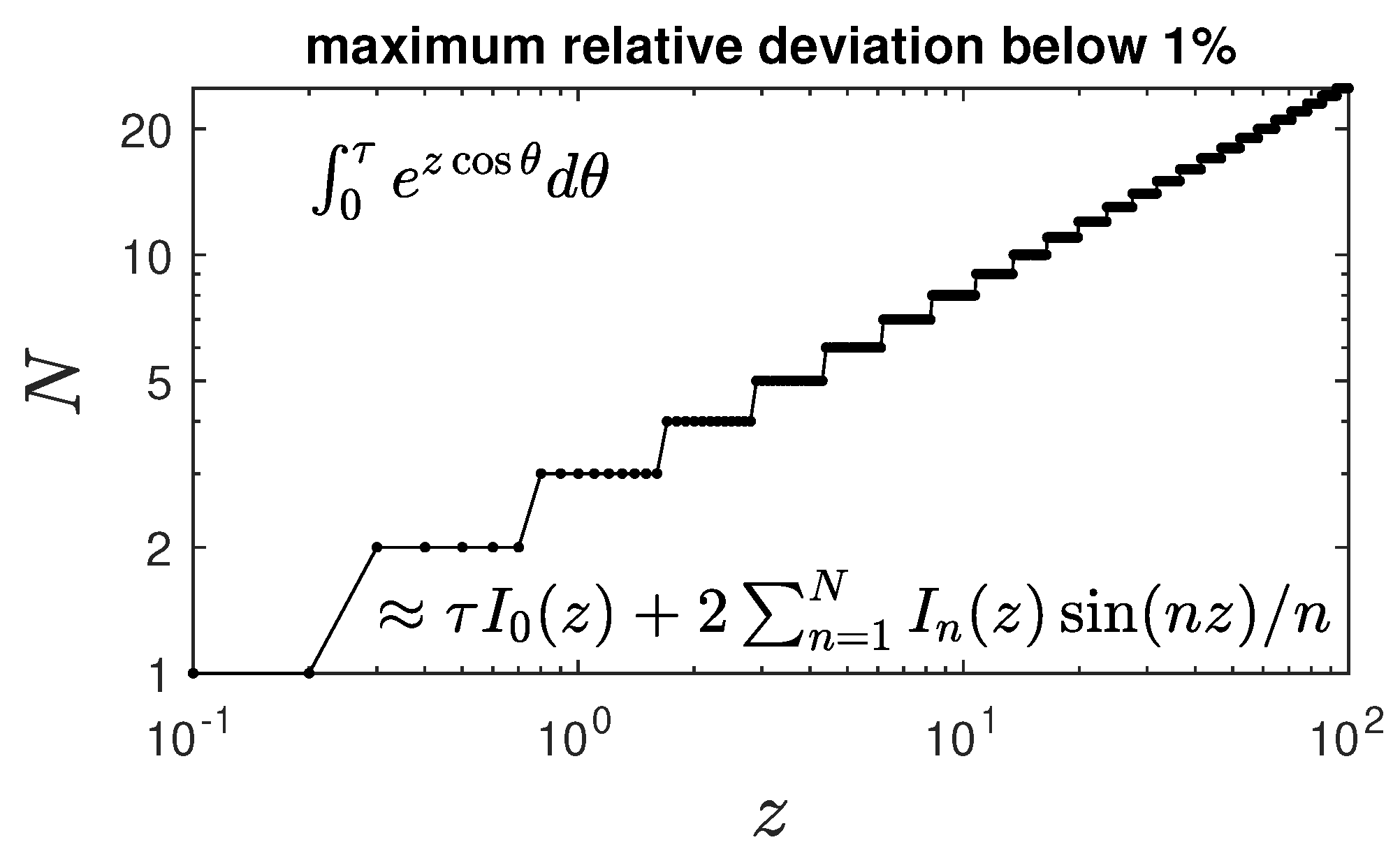
Appendix C. Expansion of H(τ) at Small Times
References
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 1927, 115, 700. [Google Scholar] [CrossRef]
- Kendall, D.G. Deterministic and stochastic epidemics in closed populations. In Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability; University of California: Berkeley, CA, USA, 1956; Volume 4, p. 149. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.N.; Mak, M.K. Exact analytical solutions of the susceptible-infected-recovered (SIR) epidemic model and of the SIR model with equal death and birth rates. Appl. Math. Comput. 2014, 236, 184–194. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. Analytical solution of the SIR-model for the temporal evolution of epidemics. Part A: Time-independent reproduction factor. J. Phys. A 2020, 53, 505601. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Analytical solution of the SIR-model for the temporal evolution of epidemics: Part B. Semi-time case. J. Phys. A 2021, 54, 175601. [Google Scholar] [CrossRef]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fract. 2020, 139, 110057. [Google Scholar] [CrossRef] [PubMed]
- Katul, G.G.; Mrad, A.; Bonetti, S.; Manoli, G.; Parolari, A.J. Global convergence of COVID-19 basic reproduction number and estimation from early-time SIR dynamics. PLoS ONE 2020, 15, e0239800. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Thomadsen, R.; Yao, S. Forecasting the spread of COVID-19 under different reopening strategies. Sci. Rep. 2020, 10, 20367. [Google Scholar] [CrossRef]
- Bagal, D.K.; Rath, A.; Barua, A.; Patnaik, D. Estimating the parameters of susceptible-infected-recovered model of COVID-19 cases in India during lockdown periods. Chaos Solitons Fract. 2020, 140, 110154. [Google Scholar] [CrossRef]
- Munoz-Fernandez, G.A.; Seoane, J.M.; Seoane-Sepulveda, J.B. A SIR-type model describing the successive waves of COVID-19. Chaos Solitons Fract. 2021, 144, 110682. [Google Scholar] [CrossRef]
- Liao, Z.; Lan, P.; Liao, Z.; Zhang, Y.; Liu, S. TW-SIR: Time-window based SIR for COVID-19 forecasts. Sci. Rep. 2020, 10, 22454. [Google Scholar] [CrossRef]
- Law, K.B.; Peariasamy, K.M.; Gill, B.S.; Singh, S.; Sundram, B.M.; Rajendran, K.; Dass, S.C.; Lee, Y.L.; Goh, P.P.; Ibrahim, H.; et al. Tracking the early depleting transmission dynamics of COVID-19 with a time-varying SIR model. Sci. Rep. 2020, 10, 21721. [Google Scholar] [CrossRef] [PubMed]
- Sharov, K.S. Creating and applying SIR modified compartmental model for calculation of COVID-19 lockdown efficiency. Chaos Solitons Fract. 2020, 141, 110295. [Google Scholar] [CrossRef] [PubMed]
- Dell’Anna, L. Solvable delay model for epidemic spreading: The case of COVID-19 in Italy. Sci. Rep. 2020, 10, 15763. [Google Scholar] [CrossRef] [PubMed]
- Quaranta, G.; Formica, G.; Machado, J.T.; Lacarbonara, W.; Masri, S.F. Understanding COVID-19 nonlinear multi-scale dynamic spreading in Italy. Nonlin. Dyn. 2020, 101, 1583–1619. [Google Scholar] [CrossRef] [PubMed]
- Nguemdjo, U.; Meno, F.; Dongfack, A.; Ventelou, B. Simulating the progression of the COVID-19 disease in Cameroon using SIR models. PLoS ONE 2020, 15, e0237832. [Google Scholar] [CrossRef] [PubMed]
- Cadoni, M. How to reduce epidemic peaks keeping under control the time-span of the epidemic. Chaos Solitons Fract. 2020, 138, 109940. [Google Scholar] [CrossRef]
- Ko, G.S.; Yoon, T. Short-Term Prediction Methodology of COVID-19 Infection in South Korea. COVID 2021, 1, 416–422. [Google Scholar] [CrossRef]
- Kaxiras, E.; Neofotistos, G.; Angelaki, E. The first 100 days: Modeling the evolution of the COVID-19 pandemic. Chaos Solitons Fract. 2020, 138, 110114. [Google Scholar] [CrossRef]
- Rao, I.J.; Brandeau, M.L. Optimal allocation of limited vaccine to control an infectious disease: Simple analytical conditions. Math. Biosci. 2021, 337, 108621. [Google Scholar] [CrossRef]
- Gatto, N.M.; Schellhorn, H. Optimal control of the SIR model in the presence of transmission and treatment uncertainty. Math. Biosci. 2021, 333, 108539. [Google Scholar] [CrossRef]
- Peng, T.; Liu, X.; Ni, H.; Cui, Z.; Du, L. City lockdown and nationwide intensive community screening are effective in controlling the COVID-19 epidemic: Analysis based on a modified SIR model. PLoS ONE 2020, 15, e0238411. [Google Scholar] [CrossRef] [PubMed]
- Shimul, S.N.; Alradie-Mohamed, A.; Kabir, R.; Al-Mohaimeed, A.; Mahmud, I. Effect of easing lockdown and restriction measures on COVID-19 epidemic projection: A case study of Saudi Arabia. PLoS ONE 2021, 16, e0256958. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, M.; Cordova-Lepe, F.; Pablo Gutierrez-Jara, J.; Vogt-Geisse, K. An SIR-type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 2021, 11, 10170. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.; Zhang, X.; Jiang, D. Asymptotic behavior of a stochastic SIR model with general incidence rate and nonlinear Levy jumps. Nonlin. Dyn. 2022, 107, 2975–2993. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, H.M.; Area, I.; Nieto, J.J. Power-series solution of compartmental epidemiological models. Math. Biosci. Eng. 2021, 18, 3274–3290. [Google Scholar] [CrossRef] [PubMed]
- Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Oussaeif, T.E.; Momani, S. A Novel Fractional-Order Discrete SIR Model for Predicting COVID-19 Behavior. Mathematics 2022, 10, 2224. [Google Scholar] [CrossRef]
- Ghosh, K.; Ghosh, A.K. Study of COVID-19 epidemiological evolution in India with a multi-wave SIR model. Nonlin. Dyn. 2022, 109, 47–55. [Google Scholar] [CrossRef]
- Marinov, T.T.; Marinova, R.S. Adaptive SIR model with vaccination: Simultaneous identification of rates and functions illustrated with COVID-19. Sci. Rep. 2022, 12, 15688. [Google Scholar] [CrossRef]
- Kuhn, M.J.; Abele, D.; Mitra, T.; Koslow, W.; Abedi, M.; Rack, K.; Siggel, M.; Khailaie, S.; Klitz, M.; Binder, S.; et al. Assessment of effective mitigation and prediction of the spread of SARS-CoV-2 in Germany using demographic information and spatial resolution. Math. Biosci. 2021, 339, 108648. [Google Scholar] [CrossRef]
- Avram, F.; Adenane, R.; Ketcheson, D.I. A Review of Matrix SIR Arino Epidemic Models. Mathematics 2021, 9, 1513. [Google Scholar] [CrossRef]
- Zanella, M.; Bardelli, C.; Azzi, M.; Deandrea, S.; Perotti, P.; Silva, S.; Cadum, E.; Figini, S.; Toscani, G. Social contacts, epidemic spreading and health system. Mathematical modeling and applications to COVID-19 infection. Math. Biosci. Eng. 2021, 18, 3384–3403. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.C.; Liu, C.T. A Stochastic Multi-Strain SIR Model with Two-Dose Vaccination Rate. Mathematics 2022, 10, 1804. [Google Scholar] [CrossRef]
- Paoluzzi, M.; Gnan, N.; Grassi, F.; Salvetti, M.; Vanacore, N.; Crisanti, A. A single-agent extension of the SIR model describes the impact of mobility restrictions on the COVID-19 epidemic. Sci. Rep. 2021, 11, 24467. [Google Scholar] [CrossRef] [PubMed]
- Sadurni, E.; Luna-Acosta, G. Exactly solvable SIR models, their extensions and their application to sensitive pandemic forecasting. Nonlin. Dyn. 2021, 103, 2955–2971. [Google Scholar] [CrossRef] [PubMed]
- Osborn, J.; Berman, S.; Bender-Bier, S.; D’Souza, G.; Myers, M. Retrospective analysis of interventions to epidemics using dynamic simulation of population behavior. Math. Biosci. 2021, 341, 108712. [Google Scholar] [CrossRef] [PubMed]
- Beneduci, R.; Bilotta, E.; Pantano, P. A unifying nonlinear probabilistic epidemic model in space and time. Sci. Rep. 2021, 11, 13860. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, G.; Grammaticos, B.; Deroulers, C.; Badoual, M. Effective epidemic model for COVID-19 using accumulated deaths. Chaos Solitons Fract. 2021, 144, 110667. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Fernandez, P.; Fernandez-Muniz, Z.; Cernea, A.; Fernandez-Martinez, J.L.; Kloczkowski, A. Three Mathematical Models for COVID-19 Prediction. Mathematics 2023, 11, 506. [Google Scholar] [CrossRef]
- Ahumada, M.; Ledesma-Araujo, A.; Gordillo, L.; Marin, J.F. Mutation and SARS-CoV-2 strain competition under vaccination in a modified SIR model. Chaos Solitons Fract. 2023, 166, 112964. [Google Scholar] [CrossRef]
- Gunaratne, C.; Reyes, R.; Hemberg, E.; O’reilly, U.M. Evaluating efficacy of indoor non-pharmaceutical interventions against COVID-19 outbreaks with a coupled spatial-SIR agent-based simulation framework. Sci. Rep. 2022, 12, 6202. [Google Scholar] [CrossRef]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G.; Mishra, A. Dynamical analysis of the infection status in diverse communities due to COVID-19 using a modified SIR model. Nonlin. Dyn. 2022, 109, 19–32. [Google Scholar] [CrossRef]
- Yuzbasi, S.; Yildirim, G. A Pell-Lucas Collocation Approach for an SIR Model on the Spread of the Novel Coronavirus (SARS CoV-2) Pandemic: The Case of Turkey. Mathematics 2023, 11, 697. [Google Scholar] [CrossRef]
- Prodanov, D. Computational aspects of the approximate analytic solutions of the SIR model: Applications to modelling of COVID-19 outbreaks. Nonlin. Dyn. 2023, 111, 15613–15631. [Google Scholar] [CrossRef]
- Liu, T.; Huang, J.; He, Z.; Zhang, Y.; Yan, N.; Zhang, C.J.P.; Ming, W.K. A real-world data validation of the value of early-stage SIR modelling to public health. Sci. Rep. 2023, 13, 9164. [Google Scholar] [CrossRef] [PubMed]
- Odagaki, T. New compartment model for COVID-19. Sci. Rep. 2023, 13, 5409. [Google Scholar] [CrossRef] [PubMed]
- Calafiore, G.C.; Novara, C.; Possieri, C. A time-varying SIRD model for the COVID-19 contagion in Italy. Annu. Rev. Control. 2020, 50, 361–372. [Google Scholar] [CrossRef] [PubMed]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2023, 35, 23671–23681. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Kröger, M. Determination of a key pandemic parameter of the SIR-epidemic model from past COVID-19 mutant waves and its variation for the validity of the Gaussian evolution. Physics 2023, 5, 205–214. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. SIR-solution for slowly time-dependent ratio between recovery and infection rates. Physics 2022, 4, 504–524. [Google Scholar] [CrossRef]
- Schlickeiser, R.; Schlickeiser, F. A gaussian model for the time development of the Sars-Cov-2 corona pandemic disease. Predictions for Germany made on March 30. Physics 2020, 2, 164–170. [Google Scholar] [CrossRef]
- Kröger, M.; Schlickeiser, R. Verification of the accuracy of the SIR model in forecasting based on the improved SIR model with a constant ratio of recovery to infection rate by comparing with monitored second wave data. R. Soc. Open Sci. 2021, 8, 211379. [Google Scholar] [CrossRef] [PubMed]
- Lixiang, L.; Yang, Z.; Deng, Z.; Meng, C.; Huang, J.; Meng, H.; Wang, D.; Chen, G.; Zhang, J.; Peng, J. Propagation analysis and prediction of the Covid-19. Infect. Dis. Model. 2020, 5, 282. [Google Scholar] [CrossRef]
- Ciufolini, I.; Paolozzi, A. Mathematical prediction of the time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur. Phys. J. Plus 2020, 135, 355. [Google Scholar] [CrossRef] [PubMed]
- Schüttler, J.; Schlickeiser, R.; Schlickeiser, F.; Kröger, M. COVID-19 predictions using a Gauss model, based on data from April 2. Physics 2020, 2, 197–212. [Google Scholar] [CrossRef]
- Singhal, A.; Singh, P.; Lall, B.; Joshi, S.D. Modeling and prediction of COVID-19 pandemic using Gaussian mixture model. Chaos Solitons Fract. 2020, 138, 110023. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Tables of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1980. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1970. [Google Scholar]
- Morse, P.M.; Feshbach, H. Methods of Theoretical Physics, Part I; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Mathews, J.; Walker, R.L. Mathematical Methods in Physics, 2nd ed.; Benjamin: Menlo Park, CA, USA, 1970. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlickeiser, R.; Kröger, M. Analytical Solution of the Susceptible-Infected-Recovered/Removed Model for the Not-Too-Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates. COVID 2023, 3, 1781-1796. https://doi.org/10.3390/covid3120123
Schlickeiser R, Kröger M. Analytical Solution of the Susceptible-Infected-Recovered/Removed Model for the Not-Too-Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates. COVID. 2023; 3(12):1781-1796. https://doi.org/10.3390/covid3120123
Chicago/Turabian StyleSchlickeiser, Reinhard, and Martin Kröger. 2023. "Analytical Solution of the Susceptible-Infected-Recovered/Removed Model for the Not-Too-Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates" COVID 3, no. 12: 1781-1796. https://doi.org/10.3390/covid3120123
APA StyleSchlickeiser, R., & Kröger, M. (2023). Analytical Solution of the Susceptible-Infected-Recovered/Removed Model for the Not-Too-Late Temporal Evolution of Epidemics for General Time-Dependent Recovery and Infection Rates. COVID, 3(12), 1781-1796. https://doi.org/10.3390/covid3120123






