Portable Magnetic Field Mapping Measurement System Based on Large-Scale Dipole Magnets in HIAF
Abstract
1. Introduction
2. Materials and Methods
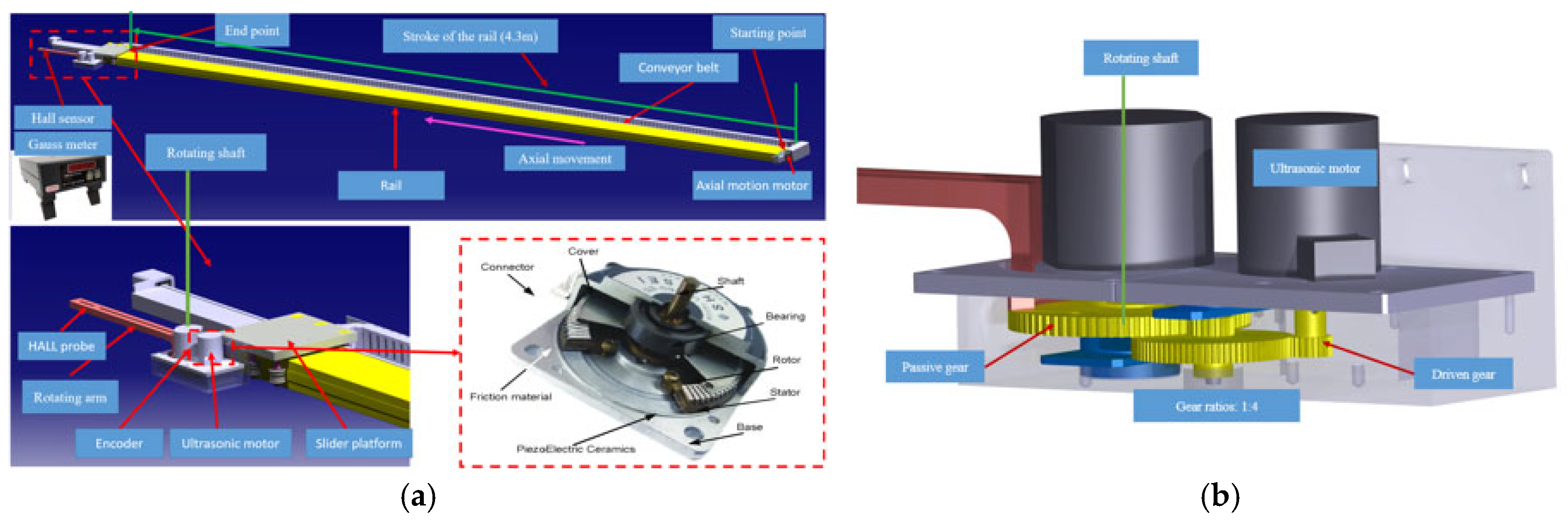
2.1. The General Design
- (1)
- The ultrasonic motor drives the rotating arm and the Hall sensor to move inside the magnet. The ultrasonic motor, which can work under strong magnetic fields, makes it possible to place the platform inside the magnet gap and drive the arm to rotate under a strong magnetic field, radically reducing the size and weight of the test system.
- (2)
- In the magnet air gap, the rotating motion mechanism is used instead of the traditional horizontal linear motion mechanism, which reduces the height of the test system and makes it possible to use in a smaller magnet gap.As shown in Figure 2a, a rotating motion mechanism was adopted inside the magnet. The ultrasonic motor and encoder can be placed on the side of the rail and only the rotating arm above the rail, thus reducing the height of the test system. If the rotating motion mechanism is not employed, an additional horizontal sliding rail must be installed above the slider platform for the horizontal linear motion mechanism. The ultrasonic motor, encoder, and measuring rod would then also be installed above the slider platform, increasing the height of the test system.At the same time, the rotating arm is installed on the slider platform, and the length only needs to cover the width of the good-field region. This reduces the length of the rotating arm so that it can be quickly stabilized after stopping (less than 1 s), which greatly reduces the settling time of the measuring rod and improves the test efficiency. In contrast, in the traditional Hall probe mapping measurement system, the length of the measuring rod often needs to exceed half the length of the magnet, and the wait time is usually more than 20 s.
- (3)
- The maximum angular resolution of the ultrasonic motor is 360°/2500. As shown in Figure 2b, the angular resolution of the rotating mechanism can be increased to 360°/10,000 by adopting the 1:4 gear set structure. The length of the rotating arm is 280 mm, the Hall sensor is mounted at the end of the rotating arm, and the circumference of the Hall sensor along the axis of rotation is 280 mm × 2π. When the Hall sensor rotates once around the rotating shaft, the circumference can be subdivided into 10,000 parts, and the calculated minimum step distance is 280 mm × 2π/10,000 ≈ 0.176 mm. As a reference point on the arc to be measured, the maximum position error of the Hall sensor from the ideal coordinate on the arc to be measured is ≈0.176 mm/2 < 0.09 mm.
2.2. The Components of the Portable Magnetic Field Mapping Measurement System
- (1)
- The rail, with a translational stroke of 4.3 m when testing the SRing dipole magnet and HFRS warm-ion superconducting dipole magnet, was lengthened to 5.3 m when testing the HFRS anti-irradiation dipole magnets.
- (2)
- The slider platform was designed to move along the rail and can be equipped with an ultrasonic motor, encoder, and rotating arm on its side.
- (3)
- The axial motion servo motor and conveyor belt are used to transfer the slider platform to the magnet air gap.
- (4)
- The ultrasonic motor and the encoder have stable operation under a strong magnetic field (≥7 T).
- (5)
- The rotating arm has an initial length of 280 mm and can be changed according to the magnet type. A Hall sensor is installed at the end. Driven by an ultrasonic motor, the measuring arm with the Hall sensor moves in an arc in the middle plane of the magnet aperture. With the axial movement of the slider table, the magnetic field distribution in the whole magnet plane can be measured.
- (6)
- The Group 3 Company’s DTM 151 Gauss meter and MPT 141 Hall probe [15].
- (7)
- A nuclear magnetic resonance instrument (NMR) [16] is used to check the magnetic field of the Gauss meter before the formal test to ensure the accuracy of the Gauss meter itself and that fixed.
2.3. The Magnetic Field Measurement Method and Coordinate Calculation
3. Results
3.1. The Magnet Parameters and Measurement Requirements for SRing and HFRS Dipole Magnets
3.2. The Measurement of SRing Dipole Magnets
3.2.1. Position Accuracy Test
3.2.2. Measurement Uncertainty
- (1)
- Position uncertainty of the Hall sensor (Lp, Yp)The position uncertainty of the Hall sensor mainly originates from the linear motion uncertainty of the slider platform along the rail and the rotation uncertainty of the rotating arm. The linear and rotational motions are independent.
- A.
- Linear motion uncertainty: Includes Type A and Type B uncertainties.
- B.
- Rotational Motion Uncertainty: Includes Type A and Type B uncertainties.
- (2)
- The uncertainty of the Gauss meter
3.2.3. The Comparison Between the Traditional and the Portable Magnetic Field Mapping Measuring System to Measure the Prototype SRing Dipole Magnet
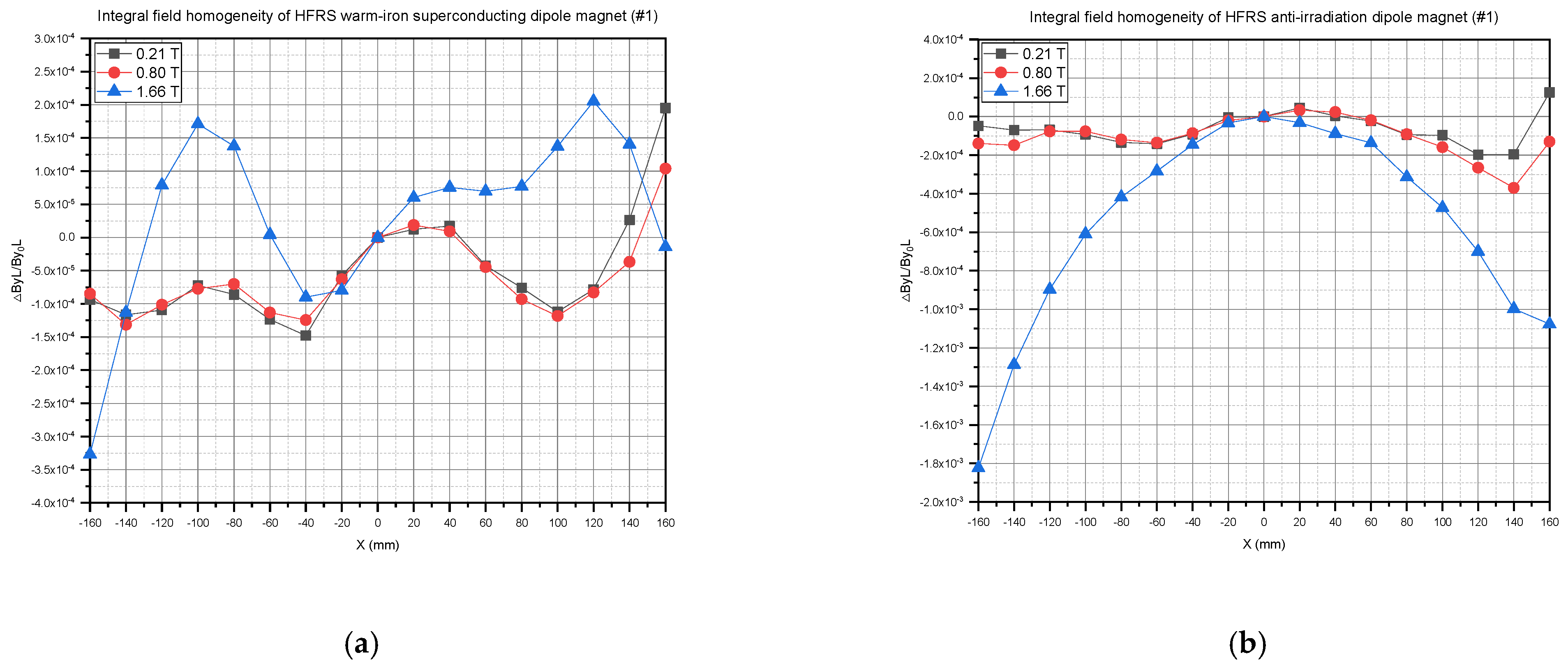
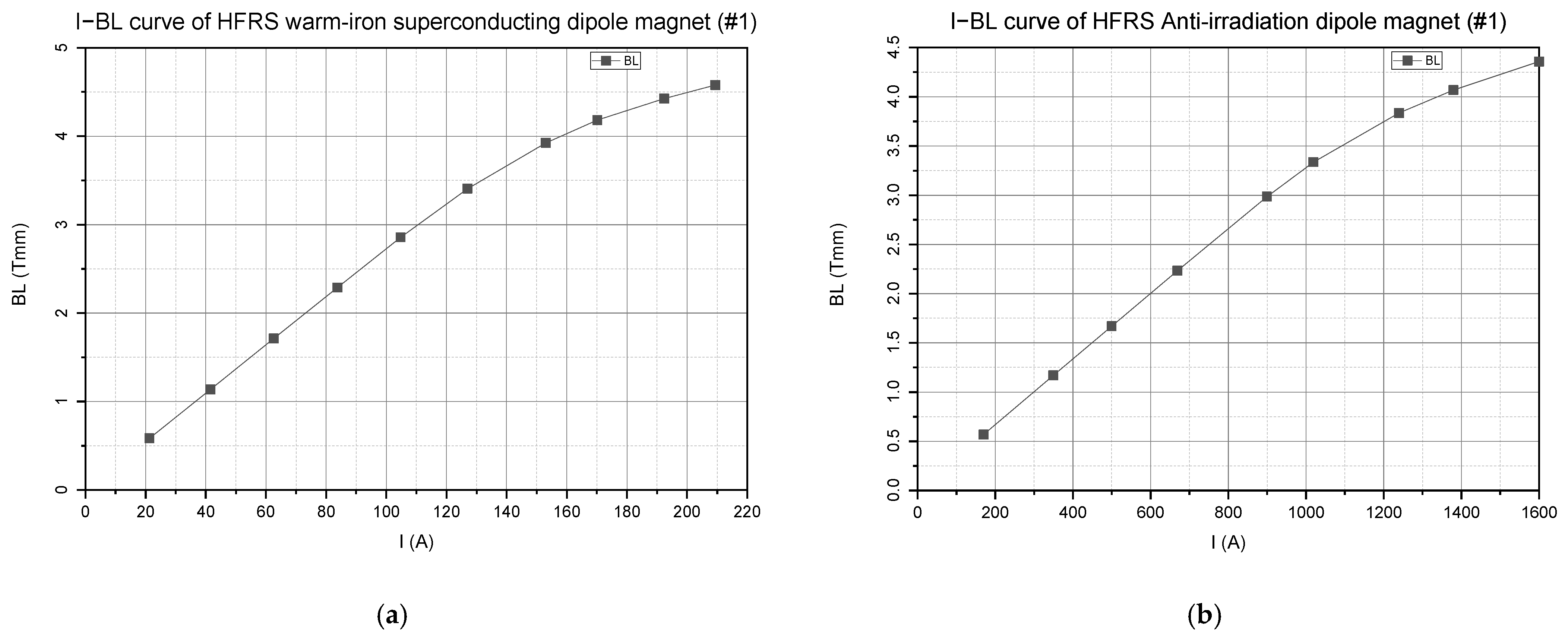
3.3. The Magnetic Field Batch Measurement of the HFRS Warm-Iron Superconducting Dipole Magnets and the HFRS Anti-Irradiation Dipole Magnets
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Ma, L.Z.; Wu, W.; Yang, W.J.; Zhao, L.X.; Yang, J.; Lv, M.B.; Mei, E.M.; Chen, Y.Q.; Zhang, J.J.; et al. Optimization design and test of the Booster Ring dipole magnet in HIAF. J. Instrum. 2022, 17, P03024. [Google Scholar] [CrossRef]
- Yang, J.C.; Xia, J.W.; Xiao, G.Q.; Xu, H.S.; Zhao, H.W.; Zhou, X.H.; Ma, X.W.; He, Y.; Ma, L.Z.; Gao, D.Q.; et al. High Intensity heavy ion Accelerator Facility (HIAF) in China. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2013, 317, 263–265. [Google Scholar] [CrossRef]
- Ma, X.; Wen, W.Q.; Zhang, S.F.; Yu, D.Y.; Cheng, R.; Yang, J.; Huang, Z.K.; Wang, H.B.; Zhu, X.L.; Cai, X.; et al. HIAF: New opportunities for atomic physics with highly charged heavy ions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2017, 408, 169–173. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, J. Status of the high-intensity heavy-ion accelerator facility in China. AAPPS Bull. 2022, 32, 35. [Google Scholar] [CrossRef]
- Wu, B.; Yang, J.C.; Xia, J.W.; Yan, X.L.; Hu, X.J.; Mao, L.J.; Sheng, L.N.; Wu, J.X.; Yin, D.Y.; Chai, W.P.; et al. The design of the Spectrometer Ring at the HIAF. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 881, 27–35. [Google Scholar] [CrossRef]
- Sheng, L.N.; Zhang, X.H.; Zhang, J.Q.; Yang, J.C.; Sun, Z.Y.; Mao, L.J.; Wu, W.; Yin, D.Y.; Ruan, S.; Shen, G.D.; et al. Ion-optical design of High energy Fragment Separator (HFRS) at HIAF. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2020, 469, 1–9. [Google Scholar] [CrossRef]
- Wu, B.; You, W.; Ou, X.; Tong, Y.; Ren, W.; Cheng, Y.; Zhang, X.; Jin, L.; Ni, D.; Mei, E.; et al. Mechanical Design, Construction and Testing of the Superferric Dipoles for the High Energy Fragment Separator of the HIAF. IEEE Trans. Appl. Supercond. 2024, 34, 5. [Google Scholar] [CrossRef]
- Moritz, G. Mechanical Equipment; CERN Accelerator School, Europa Palapa Hotel: Anacapri, Italy, 1997; pp. 251–257. [Google Scholar]
- He, Y. Magnetic Measurement System for CSR and Its Applications; University of Chinese Academy of Sciences: Beijing, China, 2003. [Google Scholar]
- Samaille, L.; Le Bec, G.; Versteegen, R. Update of the magnetic measurement benches of the ESRF. In Proceedings of the 23rd International Magnetic Measurement Workshop, Bad Zurzach, Switzerland, 6–11 October 2024. [Google Scholar]
- Zhang, X.; Jin, L. Magnetic Field Measurement System of the BRing Fast Ramping Dipole Magnet in HIAF. Nucl. Phys. Rev. 2022, 39, 470–475. [Google Scholar]
- Golluccio, G.; Giloteaux, D.; Dunkel, O.; Caltabiano, D.; Schnizer, P.; Fiscarelli, L.; Deferne, G.; Buzio, M.; Petrone, C.; Russenschuck, S. Instruments and methods for the magnetic measurement of the super-FRS magnets. In Proceedings of the IPAC2016, Busan, Republic of Korea, 8–13 May 2016. [Google Scholar]
- Hetzel, J.H.; Böker, J.; Bechstedt, U.; Quilitzsch, S.; Engin, I.; Ehrlich, C.; Bationo, B.; Tripathi, P.; Soltner, H.; Keller, P.; et al. Development of a Field Mapper for the Determination of the Multipole Components of the Curved HESR Dipole Magnets. IEEE Trans. Appl. Supercond. 2018, 28, 1–4. [Google Scholar] [CrossRef]
- CSX52S3-40. Available online: https://www.scnuaa.com/product/64.html (accessed on 12 February 2025).
- High Precision Teslameter/Gaussmeter. Available online: https://www.group3technology.com/dtm-151-product-detail (accessed on 12 February 2025).
- NMR Precision Teslameter PT2026. Available online: https://www.metrolab.com/products/nmr-precision-teslameter-pt2026 (accessed on 12 February 2025).






| Parameters | Description |
|---|---|
| The linear motion variable (the length between the rotating shaft and the origin of the stationary coordinate system) | |
| The rotational angle variable | |
| R | The deflection radius of the dipole magnet |
| r | The radius of the rotating arm (the length between the rotating shaft and the Hall sensor) |
| Lp | The length between the Hall sensor and the origin of the stationary coordinate system |
| OM | The center of the arc to be measured |
| C | The vertex of the arc to be measured |
| P | Real-time position of the Hall sensor |
| O | The origin of the stationary coordinate system (starting position of rotating shaft) |
| O′ | The origin of the moving coordinate system (real-time position of rotating shaft) |
| Parameters | SRing Dipole Magnets | HFRS Warm-Ion Superconducting Dipole Magnets | HFRS Anti-Irradiation Dipole Magnets | Unit |
|---|---|---|---|---|
| Number | 20 | 11 | 3 | / |
| Range of magnetic field | 0.21–1.66 | 0.22–1.6 | 0.21–1.6 | T |
| Reference magnetic field | 1.1 | 0.83 | 0.83 | T |
| Gap | 104 | 140 | 206 | mm |
| Good-field region (H × V) | 236 × 80 (0.21–0.84 T) 318 × 80 (0.84–1.39 T) 236 × 80 (1.39–1.66 T) | 320 × 124 | 320 × 180 | mm |
| Bending radius | 9.5 | 15.7 | 15.7 | m |
| Deflection angle | 18 | 10 | 10 | ° |
| Effective length | 2984.5 | 2740.2 | 2740.2 | mm |
| Edge angle | 0 | 0 | 0 | ° |
| Integral field homogeneity (△ByL/ByL0) | ±3 × 10−4 (318 × 80 at 1.10 T) ±5 × 10−4 (220 × 80 at 1.66 T) ±3 × 10−4 (240 × 80 at 0.21 T) | ±3 × 10−4 (0.2~1.2 T) | ±3 × 10−4 (0.83 T) ±8 × 10−4 (1.60 T) | / |
| Maximum current | 1780 | 210 | 1600 | A |
| weight | 45,000 | 52,000 | 81,000 | kg |
| Items | SRing Dipole Magnets | HFRS Warm-Ion Superconducting Dipole Magnets | HFRS Anti-Irradiation Dipole Magnets |
|---|---|---|---|
| Number | 1 | 11 | 3 |
| Reference magnetic field | 0.21 T, 1.1 T, 1.66 T | 0.22 T, 0.83 T, 1.6 T | 0.21 T, 0.83 T, 1.6 T |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, Z.; Jin, L.; Yang, J.; Ou, X.; Ni, D.; Cheng, Y.; Zhao, L.; Tong, Y.; Dong, W.; et al. Portable Magnetic Field Mapping Measurement System Based on Large-Scale Dipole Magnets in HIAF. Metrology 2025, 5, 22. https://doi.org/10.3390/metrology5020022
Zhang X, Wu Z, Jin L, Yang J, Ou X, Ni D, Cheng Y, Zhao L, Tong Y, Dong W, et al. Portable Magnetic Field Mapping Measurement System Based on Large-Scale Dipole Magnets in HIAF. Metrology. 2025; 5(2):22. https://doi.org/10.3390/metrology5020022
Chicago/Turabian StyleZhang, Xiang, Zidi Wu, Li’an Jin, Jing Yang, Xianjin Ou, Dongsheng Ni, Yue Cheng, Lixia Zhao, Yujin Tong, Weigang Dong, and et al. 2025. "Portable Magnetic Field Mapping Measurement System Based on Large-Scale Dipole Magnets in HIAF" Metrology 5, no. 2: 22. https://doi.org/10.3390/metrology5020022
APA StyleZhang, X., Wu, Z., Jin, L., Yang, J., Ou, X., Ni, D., Cheng, Y., Zhao, L., Tong, Y., Dong, W., Wu, B., Li, G., & Yao, Q. (2025). Portable Magnetic Field Mapping Measurement System Based on Large-Scale Dipole Magnets in HIAF. Metrology, 5(2), 22. https://doi.org/10.3390/metrology5020022






