Homogenization Methods of Lattice Materials
Definition
:1. Introduction
2. Homogenization Methods
2.1. Beam Theory Approach
2.2. Strain Energy Equivalence
2.3. Micropolar Theory
2.4. Solid-State Physics Approach: Bloch’s Theorem and Cauchy Born Hypothesis
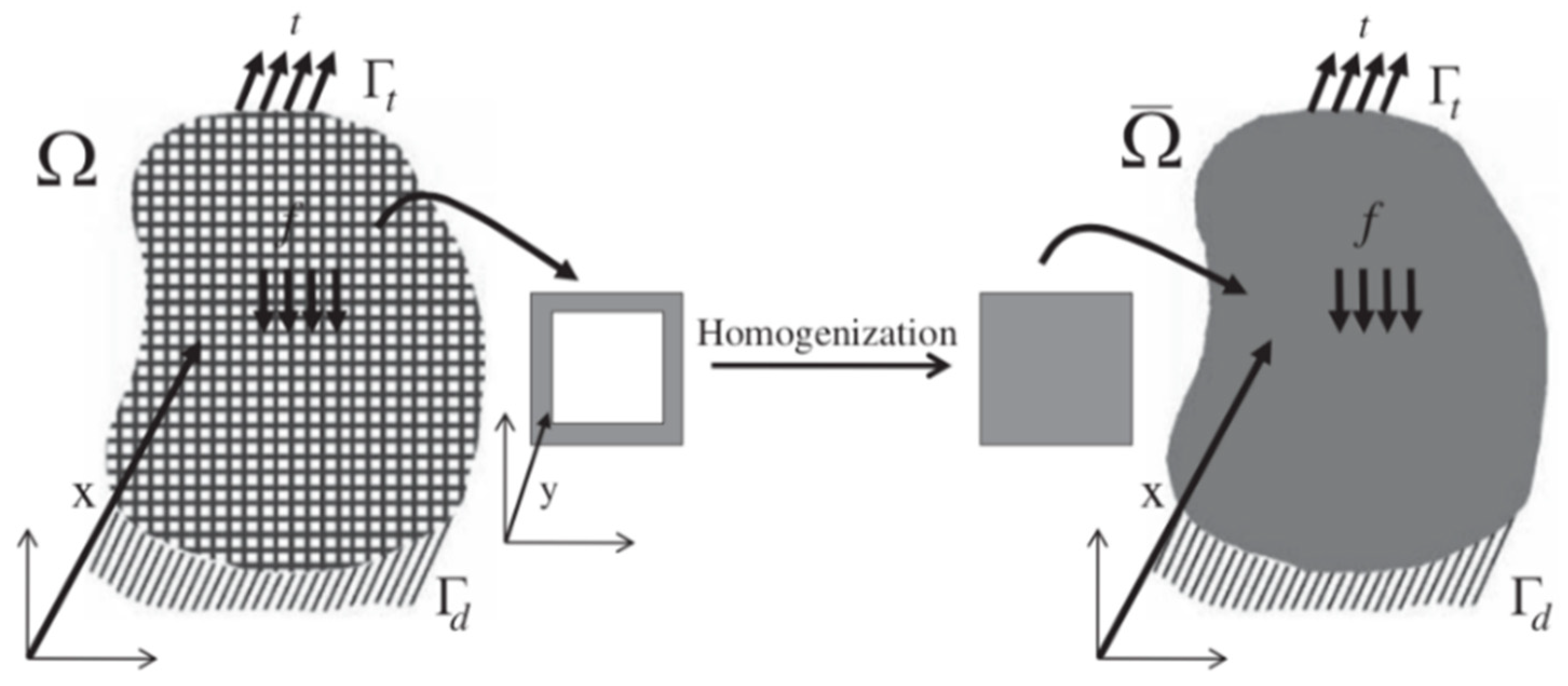
2.5. Asymptotic Homogenization Approach
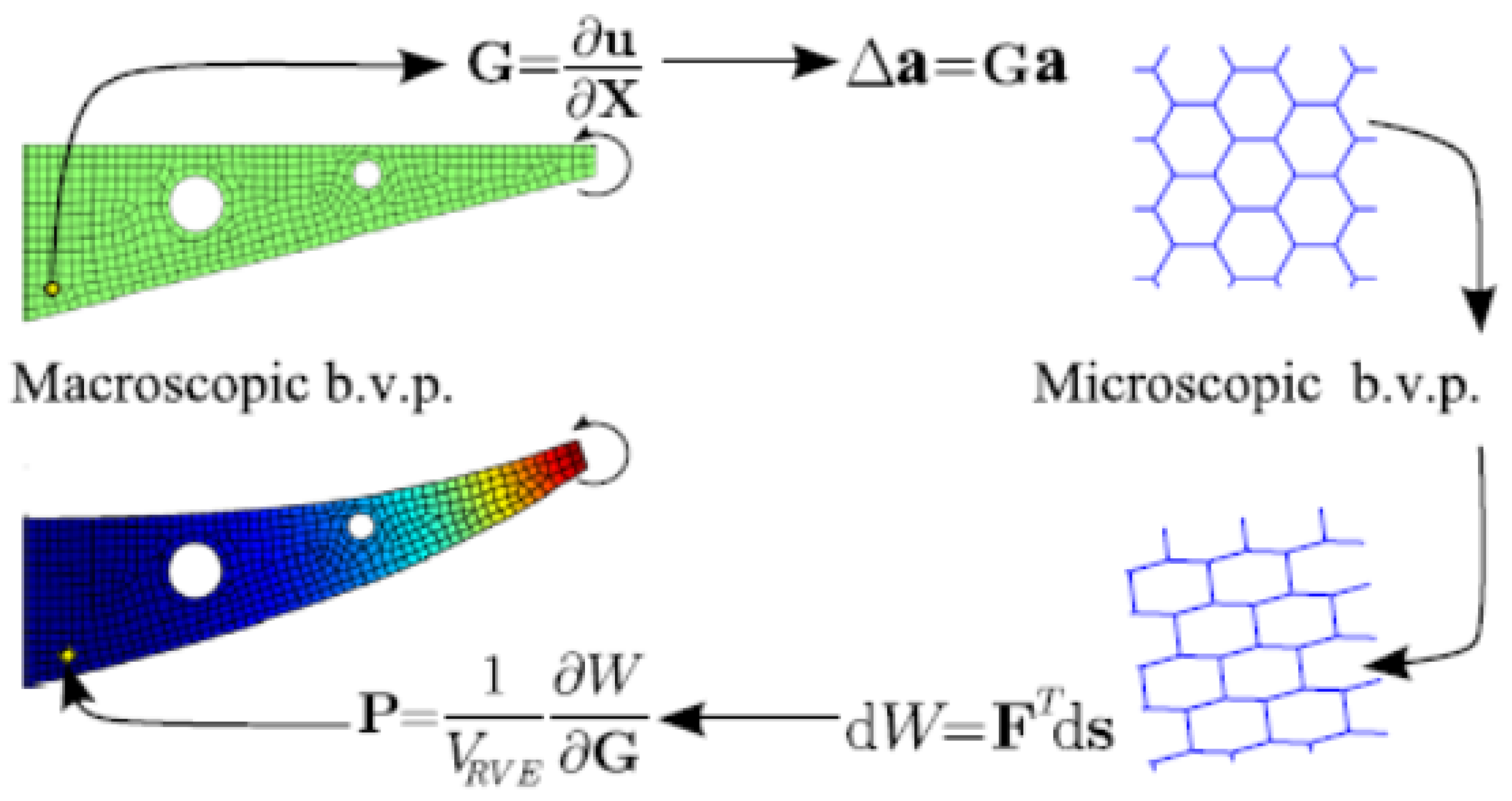
2.6. Multi-Scale Homogenization Method
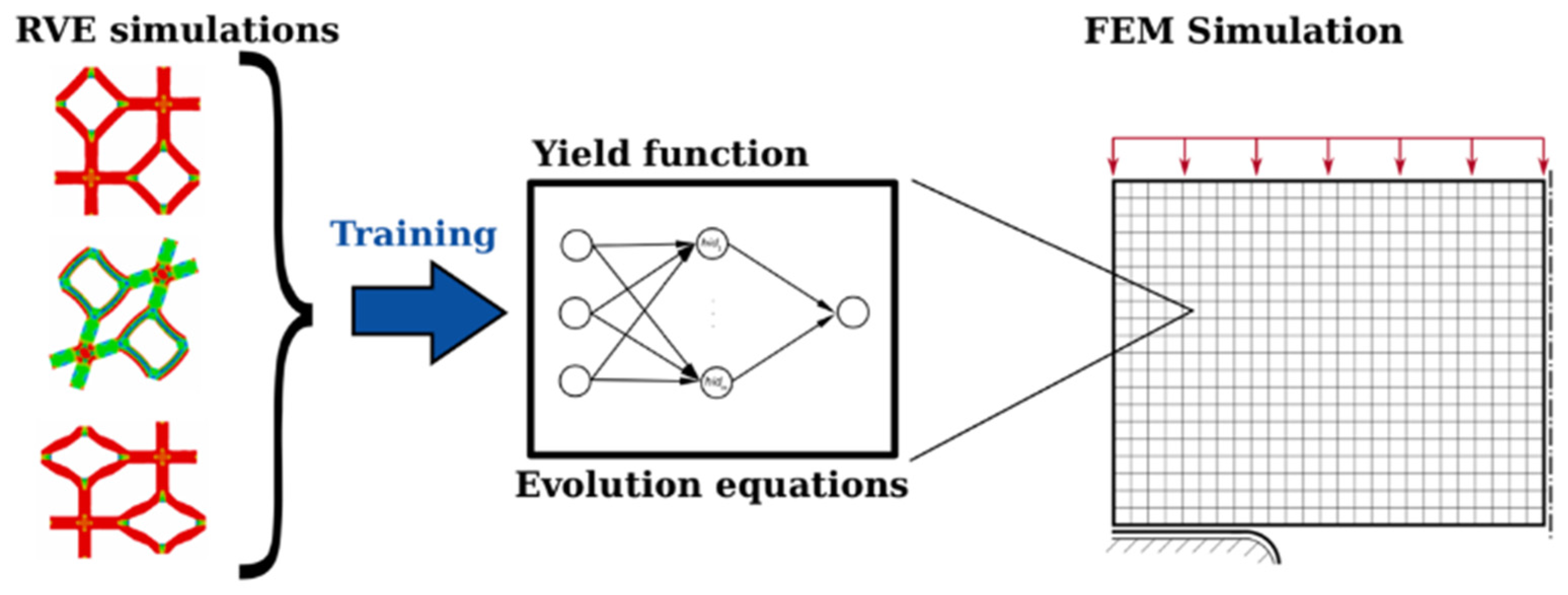
2.7. Machine Learning Approach: Data-Driven Model
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phani, A.S.; Hussein, M.I. Dynamics of Lattice Materials; Wiley Online Library: Hoboken, NJ, USA, 2017. [Google Scholar]
- Yan, J.; Cheng, G.; Liu, S.; Liu, L. Comparison of prediction on effective elastic property and shape optimization of truss material with periodic microstructure. Int. J. Mech. Sci. 2006, 48, 400–413. [Google Scholar] [CrossRef]
- Xia, Z.; Zhou, C.; Yong, Q.; Wang, X. On selection of repeated unit cell model and application of unified periodic boundary conditions in micro-mechanical analysis of composites. Int. J. Solids Struct. 2006, 43, 266–278. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Wang, A.-J.; McDowell, D.L. In-Plane Stiffness and Yield Strength of Periodic Metal Honeycombs. J. Eng. Mater. Technol. 2004, 126, 137–156. [Google Scholar] [CrossRef]
- Kelsey, S.; Gellatly, R.; Clark, B. The shear modulus of foil honeycomb cores. Aircr. Eng. Aerosp. Technol. 1958, 30, 294–302. [Google Scholar] [CrossRef]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Wang, X.L.; Stronge, W.J. Micropolar theory for two–dimensional stresses in elastic honeycomb. Proc. R. Soc. A Math. Phys. Eng. Sci. 1999, 455, 2091–2116. [Google Scholar] [CrossRef]
- Elsayed, M.S.; Pasini, D. Analysis of the elastostatic specific stiffness of 2D stretching-dominated lattice materials. Mech. Mater. 2010, 42, 709–725. [Google Scholar] [CrossRef]
- Arabnejad, S.; Pasini, D. Mechanical properties of lattice materials via asymptotic homogenization and comparison with alternative homogenization methods. Int. J. Mech. Sci. 2013, 77, 249–262. [Google Scholar] [CrossRef]
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef]
- Christensen, R. Mechanics of cellular and other low-density materials. Int. J. Solids Struct. 2000, 37, 93–104. [Google Scholar] [CrossRef]
- Hohe and, J.; Becker, W. Effective stress-strain relations for two-dimensional cellular sandwich cores: Homogenization, material models, and properties. Appl. Mech. Rev. 2002, 55, 61–87. [Google Scholar] [CrossRef]
- Buannic, N.; Cartraud, P.; Quesnel, T. Homogenization of corrugated core sandwich panels. Compos. Struct. 2003, 59, 299–312. [Google Scholar] [CrossRef]
- Hohe, J.; Becker, W. Determination of the elasticity tensor of non-orthotropic cellular sandwich cores. Tech. Mech.-Eur. J. Eng. Mech. 1999, 19, 259–268. [Google Scholar]
- Ponte Castaneda, P.; Suquet, P. On the effective mechanical behavior of weakly inhomogeneous nonlinear materials. Eur. J. Mechanics. A. Solids 1995, 14, 205–236. [Google Scholar]
- Staszak, N.; Garbowski, T.; Szymczak-Graczyk, A. Solid Truss to Shell Numerical Homogenization of Prefabricated Composite Slabs. Materials 2021, 14, 4120. [Google Scholar] [CrossRef]
- Cosserat, E.; Cosserat, F. Théorie des Corps Déformables; A. Hermann et Fils: Paris, France, 1909. [Google Scholar]
- Eringen, A.C. Linear Theory of Micropolar Elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar] [CrossRef]
- Kumar, R.S.; McDowell, D.L. Generalized continuum modeling of 2-D periodic cellular solids. Int. J. Solids Struct. 2004, 41, 7399–7422. [Google Scholar] [CrossRef]
- Phani, S.; Woodhouse, J.; Fleck, N.A. Wave propagation in two-dimensional periodic lattices. J. Acoust. Soc. Am. 2006, 119, 1995–2005. [Google Scholar] [CrossRef]
- Askar, A.; Cakmak, A. A structural model of a micropolar continuum. Int. J. Eng. Sci. 1968, 6, 583–589. [Google Scholar] [CrossRef]
- Gurtin, M. (Ed.) Phase Transformations and Material Instabilities in Solids; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Hutchinson, R.G. Mechanics of Lattice Materials; University of Cambridge: Cambridge, UK, 2005. [Google Scholar]
- Born, M.; Huang, K. Dynamical Theory of Crystal Lattices; Clarendon Press: Oxford, UK, 1954. [Google Scholar]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Takano, N.; Ohnishi, Y.; Zako, M.; Nishiyabu, K. Microstructure-based deep-drawing simulation of knitted fabric reinforced thermoplastics by homogenization theory. Int. J. Solids Struct. 2001, 38, 6333–6356. [Google Scholar] [CrossRef]
- Hollister, S.J.; Kikuchi, N. A comparison of homogenization and standard mechanics analyses for periodic porous composites. Comput. Mech. 1992, 10, 73–95. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Vigliotti, A.; Deshpande, V.S.; Pasini, D. Non linear constitutive models for lattice materials. J. Mech. Phys. Solids 2014, 64, 44–60. [Google Scholar] [CrossRef]
- Vigliotti, A.; Pasini, D. Linear multiscale analysis and finite element validation of stretching and bending dominated lattice materials. Mech. Mater. 2012, 46, 57–68. [Google Scholar] [CrossRef]
- Alwattar, T.A.; Mian, A. Development of an Elastic Material Model for BCC Lattice Cell Structures Using Finite Element Analysis and Neural Networks Approaches. J. Compos. Sci. 2019, 3, 33. [Google Scholar] [CrossRef]
- Arbabi, H.; Bunder, J.E.; Samaey, G.; Roberts, A.J.; Kevrekidis, I.G. Linking Machine Learning with Multiscale Numerics: Data-Driven Discovery of Homogenized Equations. JOM 2020, 72, 4444–4457. [Google Scholar] [CrossRef]
- Koeppe, A.; Padilla, C.A.H.; Voshage, M.; Schleifenbaum, J.H.; Markert, B. Efficient numerical modeling of 3D-printed lattice-cell structures using neural networks. Manuf. Lett. 2018, 15, 147–150. [Google Scholar] [CrossRef]
- Kollmann, H.T.; Abueidda, D.W.; Koric, S.; Guleryuz, E.; Sobh, N.A. Deep learning for topology optimization of 2D metamaterials. Mater. Des. 2020, 196, 109098. [Google Scholar] [CrossRef]
- Settgast, C.; Hütter, G.; Kuna, M.; Abendroth, M. A hybrid approach to simulate the homogenized irreversible elastic–plastic deformations and damage of foams by neural networks. Int. J. Plast. 2020, 126, 102624. [Google Scholar] [CrossRef]
- Al-Haik, M.; Hussaini, M.; Garmestani, H. Prediction of nonlinear viscoelastic behavior of polymeric composites using an artificial neural network. Int. J. Plast. 2006, 22, 1367–1392. [Google Scholar] [CrossRef]
- Fritzen, F.; Fernández, M.; Larsson, F. On-the-fly adaptivity for nonlinear twoscale simulations using artificial neural networks and reduced order modeling. Front. Mater. 2019, 6, 75. [Google Scholar] [CrossRef]
- Le, B.A.; Yvonnet, J.; He, Q. Computational homogenization of nonlinear elastic materials using neural networks. Int. J. Numer. Methods Eng. 2015, 104, 1061–1084. [Google Scholar] [CrossRef]
- Zopf, C.; Kaliske, M. Numerical characterisation of uncured elastomers by a neural network based approach. Comput. Struct. 2017, 182, 504–525. [Google Scholar] [CrossRef]
- Wojciechowski, M. Application of artificial neural network in soil parameter identification for deep excavation numerical model. Comput. Assist. Methods Eng. Sci. 2017, 18, 303–311. [Google Scholar]
- Chen, Y.; Liu, X.N.; Hu, G.K.; Sun, Q.; Zheng, Q.S. Micropolar continuum modelling of bi-dimensional tetrachiral lattices. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130734. [Google Scholar] [CrossRef]
- Fan, Z.; Yan, J.; Wallin, M.; Ristinmaa, M.; Niu, B.; Zhao, G. Multiscale eigenfrequency optimization of multimaterial lattice structures based on the asymptotic homogenization method. Struct. Multidiscip. Optim. 2019, 61, 983–998. [Google Scholar] [CrossRef]
- Vlădulescu, F.; Constantinescu, D.M. Lattice structure optimization and homogenization through finite element analyses. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1490–1502. [Google Scholar] [CrossRef]
- Xu, L.; Qian, Z. Topology optimization and de-homogenization of graded lattice structures based on asymptotic homogenization. Compos. Struct. 2021, 277, 114633. [Google Scholar] [CrossRef]
- Zhang, J.; Sato, Y.; Yanagimoto, J. Homogenization-based topology optimization integrated with elastically isotropic lattices for additive manufacturing of ultralight and ultrastiff structures. CIRP Ann. 2021, 70, 111–114. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Simplified 2D Skin Lattice Models for Multi-Axial Camber Morphing Wing Aircraft. Aerospace 2019, 6, 90. [Google Scholar] [CrossRef]
- Alsaidi, B.; Joe, W.Y.; Akbar, M. Computational Analysis of 3D Lattice Structures for Skin in Real-Scale Camber Morphing Aircraft. Aerospace 2019, 6, 79. [Google Scholar] [CrossRef]
- Alsulami, A.; Akbar, M.; Joe, W.Y. A Comparative Study: Aerodynamics of Morphed Airfoils Using CFD Techniques and Analytical Tools. In Proceedings of the ASME 2017 International Mechanical Engineering Congress and Exposition, Tampa, FL, USA, 3–9 November 2017. [Google Scholar] [CrossRef]
- La, S.; Joe, W.Y.; Akbar, M.; Alsaidi, B. Surveys on Skin Design for Morphing Wing Aircraft: Status and Challenges. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Jo, B.W.; Majid, T. Aerodynamic Analysis of Camber Morphing Airfoils in Transition via Computational Fluid Dynamics. Biomimetics 2022, 7, 52. [Google Scholar] [CrossRef]
- Majid, T.; Jo, B.W. Comparative Aerodynamic Performance Analysis of Camber Morphing and Conventional Airfoils. Appl. Sci. 2021, 11, 10663. [Google Scholar] [CrossRef]
- Majid, T.; Jo, B.W. Status and Challenges on Design and Implementation of Camber Morphing Mechanisms. Int. J. Aerosp. Eng. 2021, 2021, 6399937. [Google Scholar] [CrossRef]



| Method | Underlying Theory | Highlights | Limitation |
|---|---|---|---|
| Beam Theory [4,5,7,12] | Perform Beam Theory (BT) analysis for a single cell, considering uniform distributions over the RVE |
|
|
| Strain Energy Equivalency Approach [13,14,15,16,17] | For the equivalence condition, the averages of some mechanical properties regarding the surface or the volume must be identical. |
|
|
| Micropolar Theory Approach [8,20,22,42] | In addition to translational deformations, introduce a new variable, namely microscopic rotation, and consider that point displacement and rotations are independent kinematic quantities. |
|
|
| Bloch’s Theorem and Cauchy–Born Hypothesis Approach [9,21] |
|
|
|
| Asymptotic Homogenization Approach (AH) [10,26,27] |
|
|
|
| Multi-Scale Homogenization Method Approach [29,30,31] |
|
|
|
| Machine Learning Methodologies [32,33,34,35,36] |
|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somnic, J.; Jo, B.W. Homogenization Methods of Lattice Materials. Encyclopedia 2022, 2, 1091-1102. https://doi.org/10.3390/encyclopedia2020072
Somnic J, Jo BW. Homogenization Methods of Lattice Materials. Encyclopedia. 2022; 2(2):1091-1102. https://doi.org/10.3390/encyclopedia2020072
Chicago/Turabian StyleSomnic, Jacobs, and Bruce W. Jo. 2022. "Homogenization Methods of Lattice Materials" Encyclopedia 2, no. 2: 1091-1102. https://doi.org/10.3390/encyclopedia2020072
APA StyleSomnic, J., & Jo, B. W. (2022). Homogenization Methods of Lattice Materials. Encyclopedia, 2(2), 1091-1102. https://doi.org/10.3390/encyclopedia2020072







