The Principle of Action and Reaction According to Newton
Definition
:1. Introduction
2. The Principle of Action and Reaction in the Principia
Law 3. To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction.Whatever presses or draws something else is pressed or drawn just as much by it. If anyone presses a stone with a finger, the finger is also pressed by the stone. If a horse draws a stone tied to a rope, the horse will (so to speak) also be drawn back equally toward the stone, for the rope, stretched out at both ends, will urge the horse toward the stone and the stone toward the horse by one and the same endeavor to go slack and will impede the forward motion of the one as much as it promotes the forward motion of the other. If some body impinging upon another body changes the motion of that body in any way by its own force, then, by the force of the other body (because of the equality of their mutual pressure) [emphasis added] , it also will, in turn, undergo the same change in its own motion in the opposite direction. By means of these actions, equal changes occur in the motions, not in the velocities—that is, of course, if the bodies are not impeded by anything else. For the changes in velocities that, likewise, occur in opposite directions are inversely proportional to the bodies because the motions are changed equally. This law is valid also for attractions, as will be proved in the next scholium [13] (p. 14. Translation into English in [21]).
As much as any body acts on another so much does it experience in reaction. Whatever presses or pulls another thing by this equally is pressed or pulled (The evidenced statement can be found also in the Lucasian Lectures on algebra [22], vol. 5, Lect. 6 [1675?], p. 148). If a bladder full of air presses or carries another equal to itself both yield equally inwards. If a body impinging on another changes by its force the motion of the other then its own motion (by reason of the equality of the mutual pressure) will be changed by the same amount by the force of the other [23] (Translation into English in [24]).
8. If two quantitys (a and b) move towards one another and meete in <illeg> o. Then ye difference of theire motion shall not bee lost nor <illeg> loose its determination. For at their occursion they presse equally uppon one another [emphasis added], [and] therefore one must loose noe more motion yn ye other doth; soe yt ye difference of their motions cannot be destroyed [25] (f. 11r. Diplomatic transcription).
9. If two equall and equally swift bodys (d and c) meete one another they shall bee reflected, soe as to move as swiftly frome one another after the reflection as they did to one another before it. For first suppose the sphaericall bodys to have a springing or elastic force soe that meeting one another they will relent and be pressed into a sphaeroidicall figure, and in that moment in which there is a period put to theire motion towards one another theire figure will be most sphaeroidical and theire pression one upon the other is at the greatest, and if the endeavour to restore theire sphaericall figure bee as much vigorous and forcible as theire pressure upon one another was to destroy it they will gaine as much motion from one another after their parting as they had towards one another before theire reflection […] and there cannot bee succeede divers degrees of pressure twixt two bodys in one moment [25] (f. 11r. Critical transcription in [24]).
Now the mutual and mutually equal attraction of bodies is a branch of the third Law of motion [emphasis added] and how this branch is deduced from Phaenomena you may see in the end of the Corollaries of ye Laws of Motion, pag. 22. If a body attracts another body contiguous to it and is not mutually attracted by the other: the attracted body will drive the other before it and both will go away together wth an accelerated motion in infinitum, as it were by a self moving principle, contrary to ye first law of motion, whereas there is no such phaenomenon in all nature [28] (vol. 5. Letter To Cotes, 28 March 1713, p. 397).
3. History and Prehistory of the Principle
Since the impulsive forces of the bodies A and B are equal to each other (because their sizes and velocities are inversely proportional to each other), both bodies therefore strike with equal energy, and both suffer from the other repulses of equal energy since the strength of resistance of body B exactly equals the impulse of A itself, and therefore the direct progress of the body A toward G is altogether impeded by the force of stability [firmitudinis] or resistance of B [32] (p. 120. Translation in [33]).
- Action and reaction are always coupled, they are equal and opposite; when it comes to forces, they act on the same line of action.
- Action and reactions are equal (and opposite) not only numerically but also ontologically, in the sense that to a pressure there is always a pressure as a reaction, to a gravitational force another gravitational force, to an electric force an electric force, etc.
4. Theoretical and Experimental Justifications
Let the earth FI be cut by any plane EG into two parts EGF and EGI [Figure 1]; then their weights toward each other will be equal. For if the greater part EGI is cut into two parts, EGKH and HKI, by another plane HK parallel to the first plane EG, in such a way that HKI is equal to the part EFG that has been cut off earlier, it is manifest that the middle part EGKH will not preponderate toward either of the outer parts but will, so to speak, be suspended in equilibrium between both and will be at rest. Moreover, the outer part HKI will press upon the middle part with all its weight and will urge it toward the other outer part EGF, and, therefore, the force by which EGI, the sum of the parts HKI and EGKH, tends toward the third part EGF is equal to the weight of the part HKI, that is, equal to the weight of the third part EGF. Additionally, therefore the weights of the two parts, EGI and EGF, toward each other are equal, as I set out to demonstrate. Additionally, if these weights were not equal, the whole earth, floating in an aether free of resistance, would yield to the greater weight and in receding from it would go off indefinitely [13] (p. 25. Translation into English in [21]).
Definition 3. Inherent force of matter […]. This force is always proportional to the body and does not differ in any way from the inertia of the mass except in the manner in which it is conceived. Because of the inertia of matter, every body is only with difficulty put out of its state either of resting or of moving. Consequently, inherent force may also be called by the very significant name of force of inertia. Moreover, a body exerts this force only during a change of its state, caused by another force impressed upon it, and this exercise of force is, depending on the viewpoint, both resistance and impetus; resistance insofar as the body, in order to maintain its state, strives against the impressed force [13] (p. 2. Translation into English in [21]).
5. Reactions of Constraints
Lemma I. There is a mutual interaction between the incident ball and the plane on which it strikes, i.e., a greater or lesser opposition, in proportion as the incidence of the total motion is more or less perpendicular.
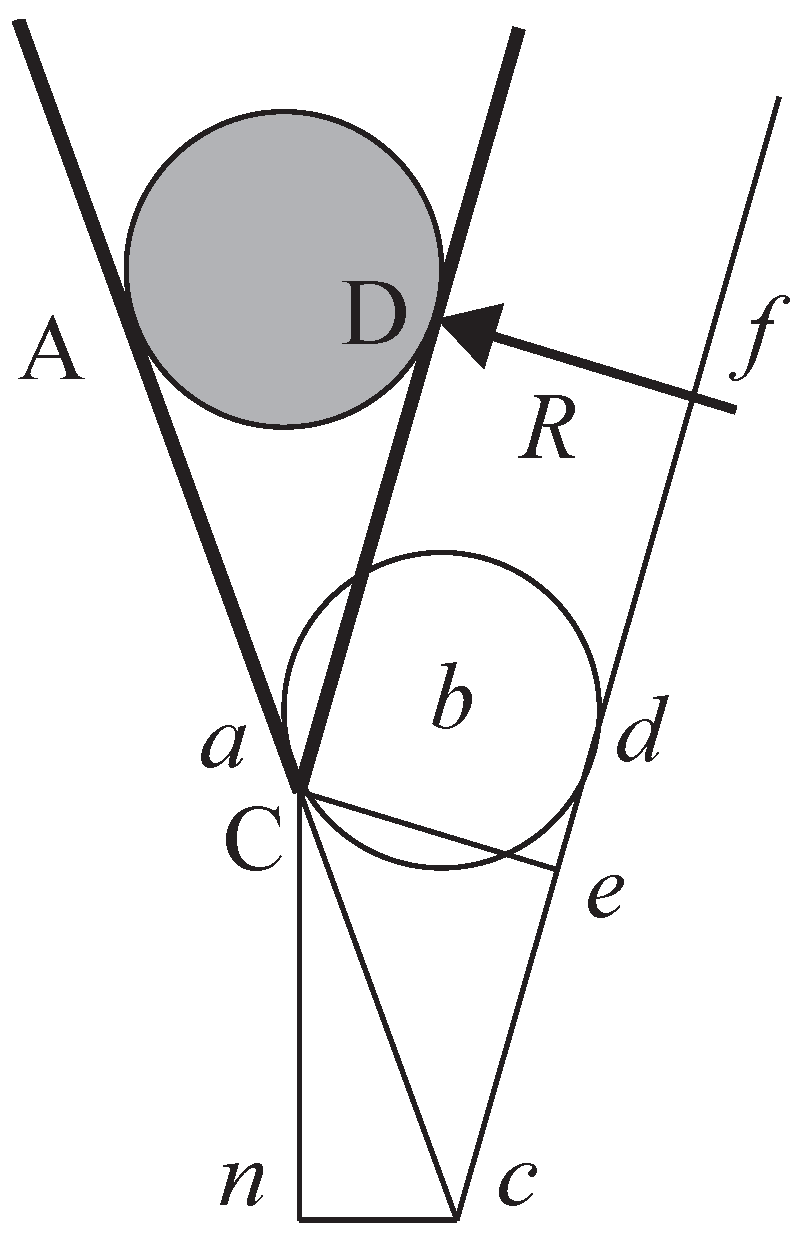
When a ball LDON falls on to a plane surface AB with some force and impact on it, there is an action of the ball on the plane, that is a percussion. Additionally, since whatever acts on another suffers from it in turn, the ball suffers something [emphasis added] from the plane; and so there is a reaction of the plane on the ball, that is a re-percussion [38] (p. 293).
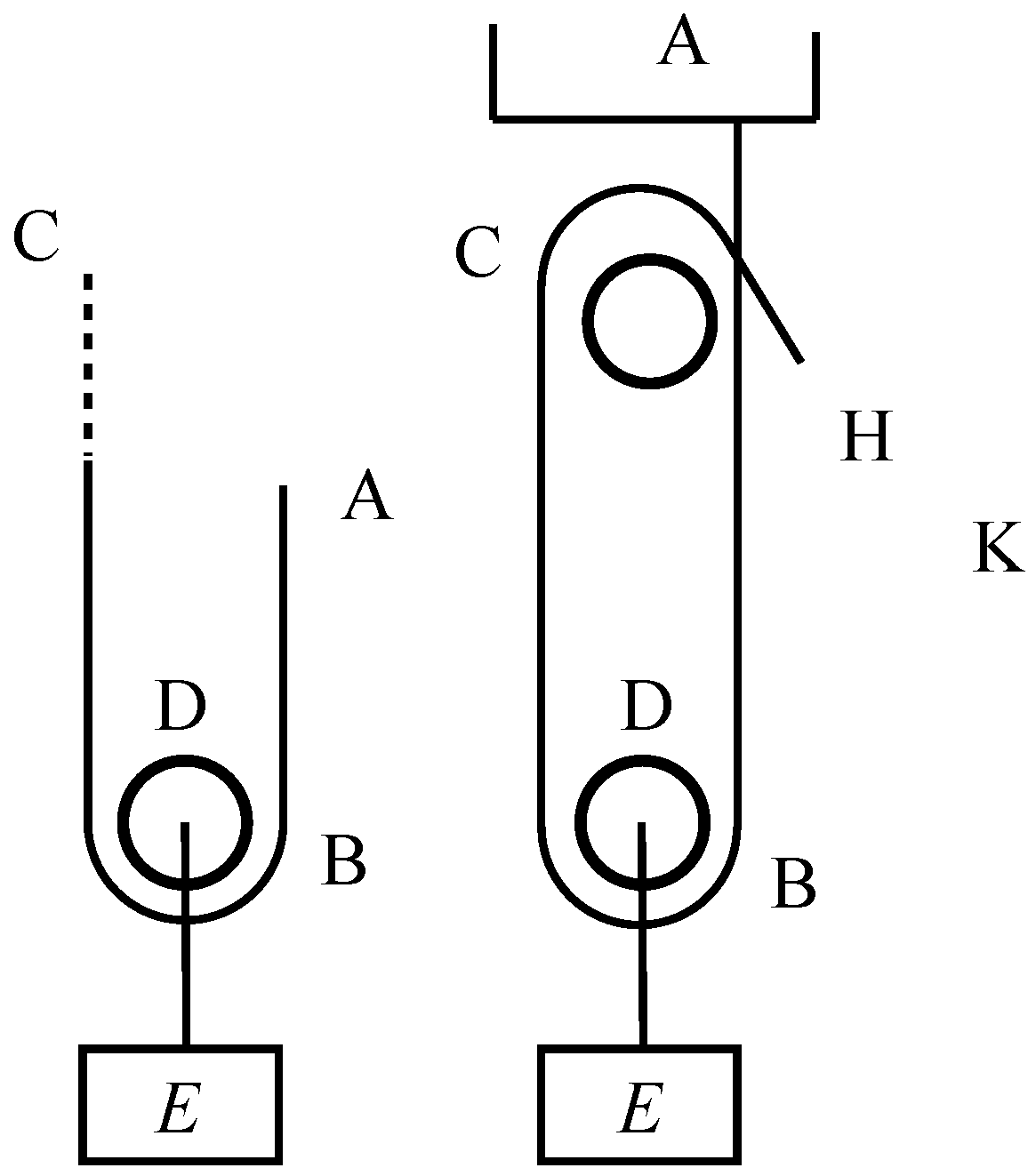
The pulley.—Let ABC be a rope passing around the pulley D [Figure 3], in which the weight E is applied and suppose first that two men support or raise equally each of the two ends of the rope, it is clear that if the weight weighs 200 pounds, each of the two men take, to support or lift, the force required to support 100 pounds, because each holds only one half. Let then that A, one end of the rope, being attached to a nail, the other C is still supported by a man, it is clear that this man in C would need, as before, only the force required to support 100 pounds, because the support is to do the same service of the man who was supposed before [40] (Letter to Constantine Huygens 5 October 1637, vol. 1, p. 437).
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Use of PA in the Principia
- p. 17
- Corollary 3 to the laws of motion. The quantity of motion, which is determined by adding the motions made in one direction and subtracting the motions made in the opposite direction, is not changed by the action of bodies on one another.For an action and the reaction opposite to it are equal by law 3, and thus by law 2, the changes which they produce in motions are equal and in opposite directions.
- p. 160
- Section XI. Book I. The motion of bodies drawn to one another by centripetal forces.Up to this point, I have been setting forth the motions of bodies attracted toward an immovable center, such as, however, hardly exists in the natural world. For attractions are always directed toward bodies, and—by the third law—the actions of attracting and attracted bodies are always mutual and equal; so that if there are two bodies, neither the attracting nor the attracted body can be at rest, but both (by corol. 4 of the laws) revolve about a common center of gravity.
- p. 187
- Proposition 69. Book I. If, in a system of several bodies A, B, C, D, …, some body A attracts all the others, B, C, D, …, by accelerative forces that are inversely as the squares of the distances from the attracting body; and if another body B also attracts the rest of the bodies A, C, D, …, by forces that are inversely as the squares of the distances from the attracting body; then the absolute forces of the attracting bodies A and B will be to each other in the same ratio as the bodies [i.e., the masses] A and B themselves to which those forces belong.For, at equal distances, the accelerative attractions of all the bodies B, C, D, … toward A are equal to one another by hypothesis; and similarly, at equal distances, the accelerative attractions of all the bodies toward B are equal to one another. Moreover, at equal distances, the absolute attractive force of body A is to the absolute attractive force of body B as the accelerative attraction of all the bodies toward A is to the accelerative attraction of all the bodies toward B at equal distances; and the accelerative attraction of body B toward A is also in the same proportion to the accelerative attraction of body A toward B. However, the accelerative attraction of body B toward A is to the accelerative attraction of body A toward B as the mass of body A is to the mass of body B, because the motive forces—which (by defs. 2, 7, and 8) are as the accelerative forces and the attracted bodies jointly—are in this case (by the third law of motion) equal to each other. Therefore the absolute attractive force of body A is to the absolute attractive force of body B as the mass of body A is to the mass of body B. Q.E.D.
- p. 194
- Proposition 75, Corollary 2. Book 1. The same is true when the attracted sphere also attracts. For its individual points will attract the individual points of the other with the same force by which they are in turn attracted by them; and thus, since in every attraction the attracting point is as much urged (by law 3) as the attracted point, the force of the mutual attraction will be duplicated, the proportions remaining the same.
- p. 239
- Section 1, Scholium. Book 2. For by the action of a swifter body, a motion that is greater in proportion to that greater velocity is communicated to a given quantity of the medium in a smaller time; and thus in an equal time, because a greater quantity of the medium is disturbed, a greater motion is communicated in proportion to the square of the velocity, and (by the second and third laws of motion) the resistance is as the motion communicated. Let us see, therefore, what kinds of motions arise from this law of resistance.
- p. 283
- Section 5, Case 3. Book 2. I say furthermore that there is equal pressure on different spherical parts. For contiguous spherical parts press one another equally in the point of contact, by the third law of motion. However, by case 2, they are also pressed on all sides by the same force. Therefore any two noncontiguous spherical parts will be pressed by the same force, since an intermediate spherical part can touch both. Q.E.D.
- p. 283
- Section 5, Case 4. Book 2. I say also that all the parts of the fluid are equally pressed on every side. For any two parts can be touched by spherical parts in any points, and there they press those spherical parts equally, by case 3, and in turn are equally pressed by them, by the third law of motion. Q.E.D.
- p. 322
- Section 7. Corollay 5. Book 2. Additionally, since similar, equal, and equally swift bodies, in mediums which have the same density and whose particles do not recede from one another, impinge upon an equal quantity of matter in equal times (whether the particles are more and smaller or fewer and larger) and impress upon it an equal quantity of motion and in turn (by the third law of motion) undergo an equal reaction from it (that is, are equally resisted), it is manifest also that in elastic fluids of the same density, when the bodies move very swiftly, the resistances they encounter are very nearly equal, whether those fluids consist of coarser particles or are made of the most subtle particles of all. The resistance to projectiles moving very quickly is not much diminished as a result of the subtlety of the medium.
- p. 341
- Section 7, Lemma 6. Book 2. With the same suppositions, these bodies are equally urged by the water flowing through the channel. This is evident by lem. 5 and the third law of motion. Of course, the water and the bodies act equally upon one another.
- p. 357
- Section 8, Corollary. Book 2. If some part of a pressure propagated through a fluid from a given point is intercepted by an obstacle, the remaining part (which is not intercepted) will spread out into the spaces behind the obstacle. This can be proved as follows. From point A let a pressure be propagated in any direction and, if possible, along straight lines; and by the obstacle NBCK, perforated in BC, let all the pressure be intercepted except the cone-shaped part APQ, which passes through the circular hole BC. By transverse planes , and , divide the cone APQ into frusta; then, while the cone ABC, by propagating the pressure, is urging the further conic frustum on the surface , and this frustum is urging the next frustum on the surface , and that frustum is urging a third frustum, and so on indefinitely, obviously (by the third law of motion) the first frustum will be as much urged and pressed on the surface by the reaction of the second frustum as it urges and presses the second frustum.
- p. 399
- Proposition 5, Corollary 1. Book 3. Therefore, there is gravity toward all planets universally. For no one doubts that Venus, Mercury, and the rest [of the planets, primary and secondary,] are bodies of the same kind as Jupiter and Saturn. Additionally, since, by the third law of motion, every attraction is mutual, Jupiter will gravitate toward all its satellites, Saturn toward its satellites, and the earth will gravitate toward the moon, and the sun toward all the primary planets.
- p. 404
- Proposition 7. Book 3. Gravity exists in all bodies universally and is proportional to the quantity of matter in each.Further, since all the parts of any planet A are heavy [or gravitate] toward any planet B, and since the gravity of each part is to the gravity of the whole as the matter of that part to the matter of the whole, and since to every action (by the third law of motion) there is an equal reaction, it follows that planet B will gravitate in turn toward all the parts of planet A, and its gravity toward any one part will be to its gravity toward the whole of the planet as the matter of that part to the matter of the whole. Q.E.D.
Appendix B. Formal Comparison between the Principle of Inertia and PA
- Axion F2.
- for any
- Axion F3.
Theorem (Noll, Gurtin, and Williams). A system of forces is pair-wise equilibrated if, and only if, the resultant forces , regarded as a function of , is additive on the separate bodies of [37] (p. 21).
In the past, instances of (6) were often inferred from a vague “axiom” called the law of “action and reaction”, which was regarded as expressing the content of Newton’s Third Law of Motion: “To an action there is always a contrary and equal reaction; or, the actions of two bodies mutually upon one another are always equal and directed toward contrary parts.” If, indeed, what NEWTON meant by “action” is what we here call “force”, which is by no means clear from their own words or the contexts in which he applied them [emphasis added], then the above argument shows that axiom to be equivalent, as far as pairs of separate bodies are concerned, to additivity of resultant forces on separate bodies. This fact is independent of whatever relations there may be among forces and motions [37] (p. 22).
- Theorem (Rizzo). In order that:
- for any
- it is necessary and sufficient that:
- for any [37] (p. 28).
References
- Lenzen, V. Newton’s third law of motion. Isis 1937, 27, 25–38. [Google Scholar] [CrossRef]
- Home, R.W. The third law in Newton’s mechanics. Br. J. Hist. Sci. 1968, 4, 39–51. [Google Scholar] [CrossRef]
- Russel, J.L. Action and reaction before Newton. Br. J. Hist. Sci. 1976, 9, 25–38. [Google Scholar] [CrossRef]
- Gauld, C. The historical context of Newton’s third law and the teaching of mechanics. Res. Sci. Educ. 1993, 23, 95–103. [Google Scholar] [CrossRef]
- Cohen, B.I. Newton’s third Law and universal gravity. J. Hist. Ideas 1987, 48, 571–593. [Google Scholar] [CrossRef]
- Fraser, D.L. The third law in Newton’s Waste book (or, the road less taken to the second law). Stud. Hist. Philos. Sci. 2005, 36, 43–60. [Google Scholar] [CrossRef]
- Stan, M. Kant’s third law of mechanics: The long shadow of Leibniz. Stud. Hist. Philos. Sci. 2013, 44, 493–504. [Google Scholar] [CrossRef]
- Antwi, V.; Addo-Wuver, F.; Sakyi-Hagan, N.A. How do our students understand Newton’s third law of motion? A study in a Ghanaian university context. Sci. Educ. Int. 2020, 31, 410–417. [Google Scholar]
- Scomparin, P.R.; Carvalho-Neto, J.T. A simple and effective magnetic dynamometer to teach Newton’s third law. Phys. Educ. 2018, 53, 1. [Google Scholar] [CrossRef]
- Montanero, M.; Suero, M.; Pardo, P. Implicit theories of static interactions between two bodies. Phys. Educ. 2002, 37, 318–323. [Google Scholar] [CrossRef]
- Gauld, C. Newton’s third law after Newton. Res. Sci. Educ. 1994, 24, 93–101. [Google Scholar] [CrossRef]
- Mach, E. The Science of Mechanics: A Critical and Historical Account of Its Development; Translated into English by McCormack TJ; Open Court: Chicago, IL, USA, 1919. [Google Scholar]
- Newton, I. Philosophia Naturalis Principia Mathematica, 3rd ed.; Innys: London, UK, 1726. [Google Scholar]
- Buenzli, P.R.; Soto, R. Violation of the action-reaction principle and self-forces induced by nonequilibrium fluctuations. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2008, 78, 020102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivlev, A.V.; Bartnick, J.; Heinen, M.; Du, C.R.; Nosenko, V.; Löwen, H. Statistical mechanics where Newton’s third law is broken. Phys. Rev. X 2015, 5, 011035. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A. Impact of recent technological advancements on newton’s third law of motion and its generalization: Part 2, questions and answers. J. Nat. Sci. Sustain. Technol. 2021, 15, 81–85. [Google Scholar]
- Epp, V.; Veselkova, A. Non-parallel currents and the Newton’s third law of motion. Eur. J. Phys. 2023, 44, 1–9. [Google Scholar] [CrossRef]
- Cavalleri, G.; Spavieri, G.; Spinelli, G. On the action and reaction principle in special relativity. Il Nuovo C. B 1988, 102, 495–509. [Google Scholar] [CrossRef]
- Canero, A.T. Newton &-vs Lorentz. J. Adv. Phys. 2018, 14, 5869–5872. [Google Scholar]
- López, C. The action reaction principle in quantum mechanics. In Quantum Foundations, Probability and Information; Khrennikov, A., Toni, B., Eds.; Springer: Cham, Switzerland, 2018; pp. 31–38. [Google Scholar]
- Newton, I. The Principia. Mathematical Principles of Natural Philosophy; Translated into English by Cohen IB, Withman A (Assisted by Budenz J); University of California Press: Oakland, CA, USA, 1999. [Google Scholar]
- Newton, I. The Mathematical Papers of Isaac Newton; Whiteside, D.T., Ed.; 8 Vols; Cambridge University Press: Cambridge, UK, 1967–1981. [Google Scholar]
- Newton, I. De Motu Corporum in Medijs Regulariter Cedentibus. MS Add. 3965.5a. Available online: https://www.newtonproject.ox.ac.uk/texts/newtons-works/scientific (accessed on 20 April 2023).
- Herivel, J. The Background to Newton’s Principia. Study of Newton’s Dynamical Researches in the Years 1664–1684; Clarendon: Oxford, UK, 1965. [Google Scholar]
- Newton, I. Newton’s Waste Book (Part 1) MS Add. 4004; Cambridge University Library: Cambridge, UK, 1664–1685; ff. cover-15. [Google Scholar]
- Capecchi, D. History of Virtual Work Laws; Birchäuser: Milan, Italy, 2012. [Google Scholar]
- Laird, E.R. The third law of motion and “inertia reaction”. Science 1917, 46, 341–342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newton, I. The Correspondence of Isaac Newton; Hall, R.A., Tilling, L., Eds.; 4 Vols; Cambridge University Press: Cambridge, UK, 1959–1978. [Google Scholar]
- Aristotle. Physica. The Internet Classical Archive. Translated into English by Hardie RP, Gaye RK. Available online: http://classics.mit.edu/Aristotle/physics.html (accessed on 15 April 2023).
- Starobinski, J. Action et Reaction. Vie et Aventures d’une Couple; Seuil: Paris, France, 2013. [Google Scholar]
- Gilbert, W. On the Loadstone and Magnetic Bodies and on the Great Magnet the Earth; Translated into English by Mottelay PF; Quaritch: London, UK, 1893. [Google Scholar]
- Borelli, A. De vi Percussionis; Monti: Bologna, Italy, 1667. [Google Scholar]
- Westfall, R. Force in Newton’s Physics. The Science of Dynamics in the Seventeenth Century; Neal Watson Academic Publications: New York, NY, USA, 1971. [Google Scholar]
- Capecchi, D. The Problem of Motion of Bodies; Springer: Cham, Switzerland; Dordrecht, The Netherlands, 2014. [Google Scholar]
- Mariotte, E. Traité de la percussion ou choc des corps; dans lequel les principales régles du mouvement sont expliqués et démontrées par leurs veritables causes. In Oeuvres de Mr Mariotte; 2 Vols; Vander, P: Leiden, The Netherlands, 1971; Volume 1, pp. 1–116. [Google Scholar]
- Nagel, E. The Structure of Science; Harcourt: New York, NY, USA, 1961. [Google Scholar]
- Truesdell, C.A. A First Course in Rational Continuum Mechanics, 2nd ed.; Academic Press: New York, NY, USA, 1991; Volume 1. [Google Scholar]
- Maignan, E. Perspectiva Horaria Sive de Horographia Gnomonica tum Theoretica, tum Practica Libri Quatuor; Rubeus: Rome, Italy, 1648. [Google Scholar]
- Varignon, P. La Nouvelle mécanique ou Statique; 2 Vols; Joubert: Paris, France, 1725. [Google Scholar]
- Descartes, R. Oeuvres de Descartes; Nouvelle édition Complétée (1896–1913); 11 Vols; Adam, C., Tannery, P., Eds.; Vrin: Paris, France, 1964. [Google Scholar]
- Bernoulli, J. Unpublished correspondence 1714–1715. Private communication by Patricia Radelet De Grave. 2011. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capecchi, D. The Principle of Action and Reaction According to Newton. Encyclopedia 2023, 3, 705-720. https://doi.org/10.3390/encyclopedia3020051
Capecchi D. The Principle of Action and Reaction According to Newton. Encyclopedia. 2023; 3(2):705-720. https://doi.org/10.3390/encyclopedia3020051
Chicago/Turabian StyleCapecchi, Danilo. 2023. "The Principle of Action and Reaction According to Newton" Encyclopedia 3, no. 2: 705-720. https://doi.org/10.3390/encyclopedia3020051
APA StyleCapecchi, D. (2023). The Principle of Action and Reaction According to Newton. Encyclopedia, 3(2), 705-720. https://doi.org/10.3390/encyclopedia3020051






