Theoretical Model of Structural Phase Transitions in Al-Cu Solid Solutions under Dynamic Loading Using Machine Learning
Abstract
1. Introduction
2. MD Study of Uniaxial Compression of Al-Cu Solid Solutions
2.1. MD Setup
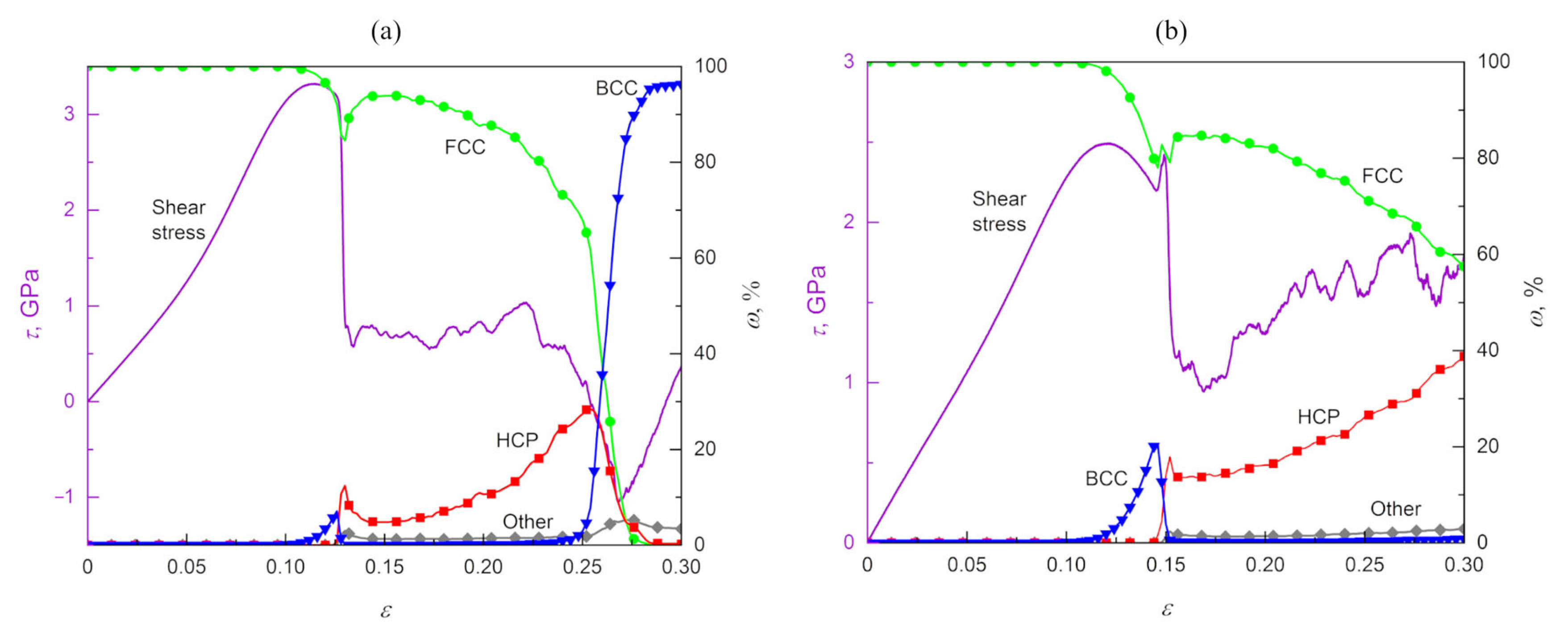
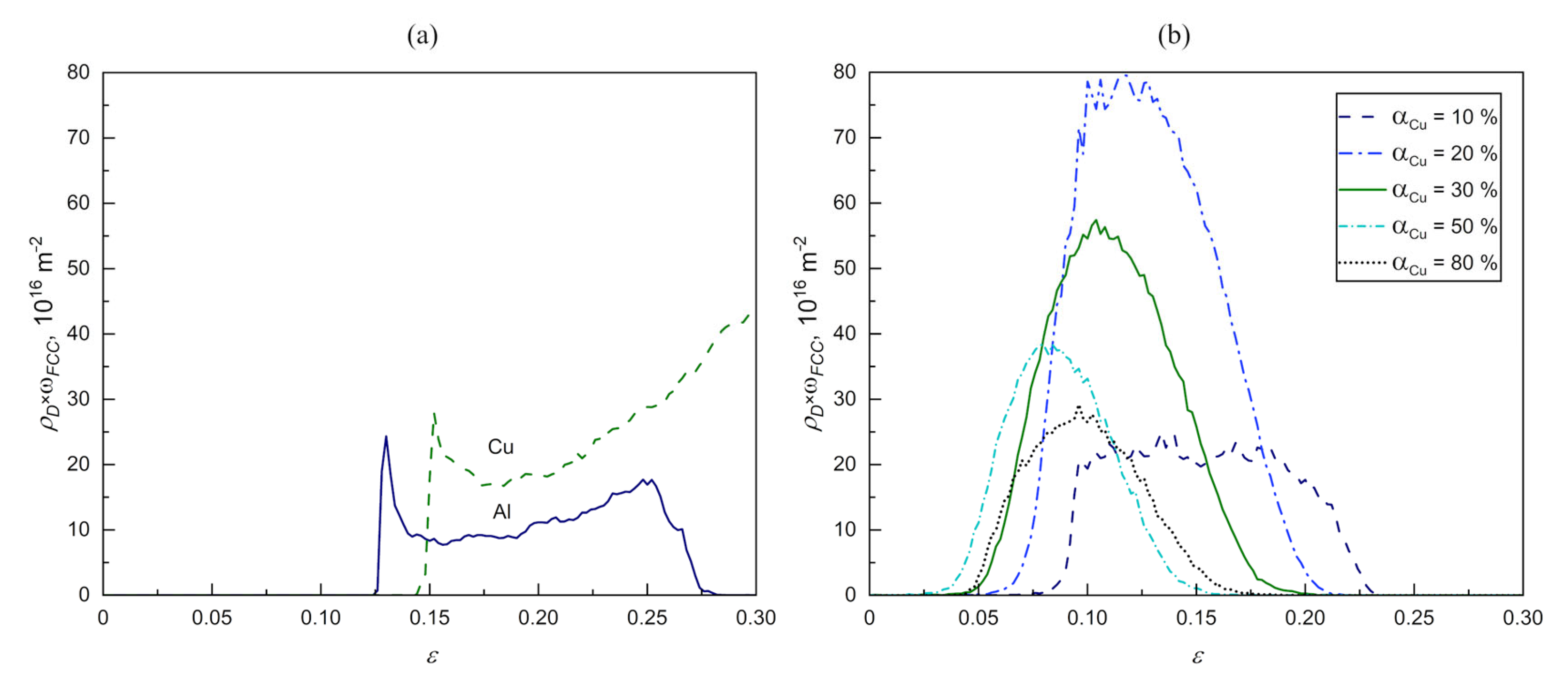
2.2. Results of MD Simulations: Dislocation Activity and Phase Transitions
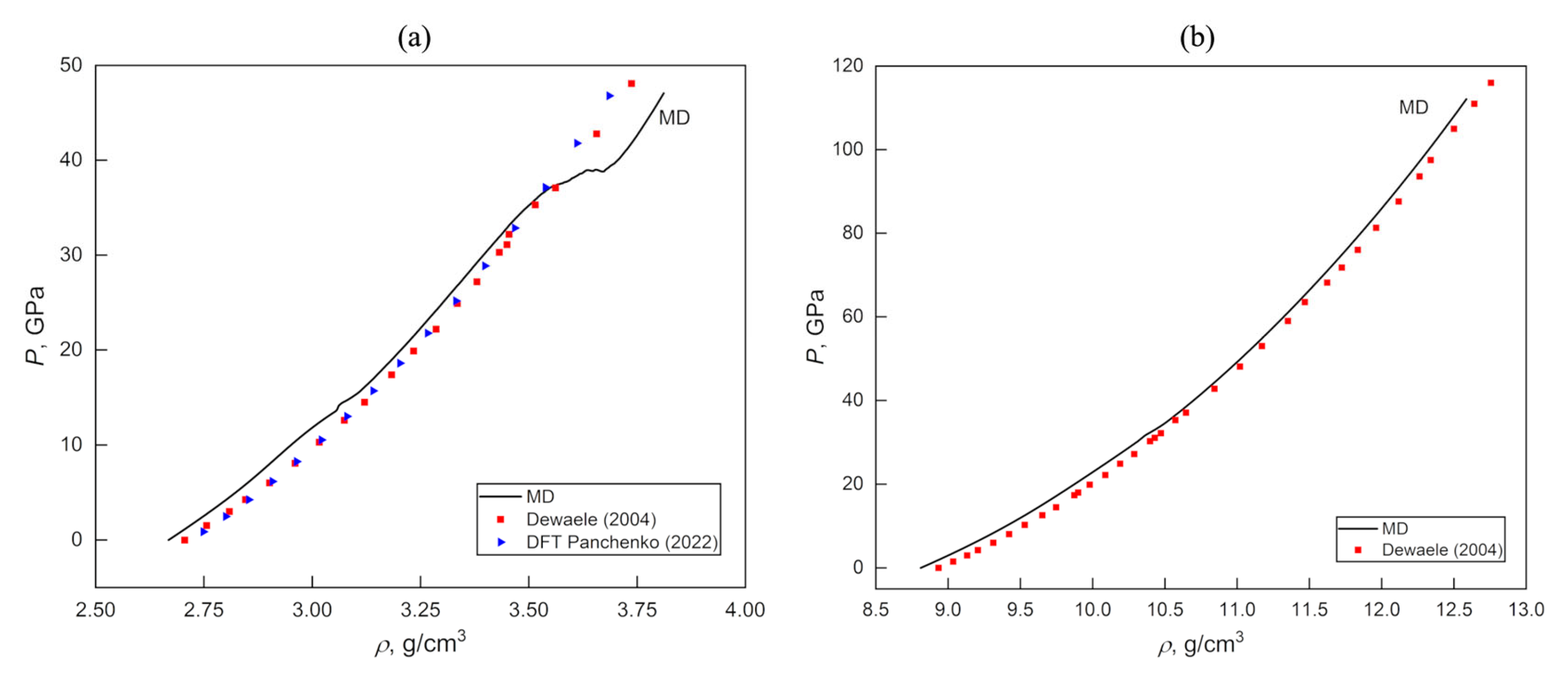
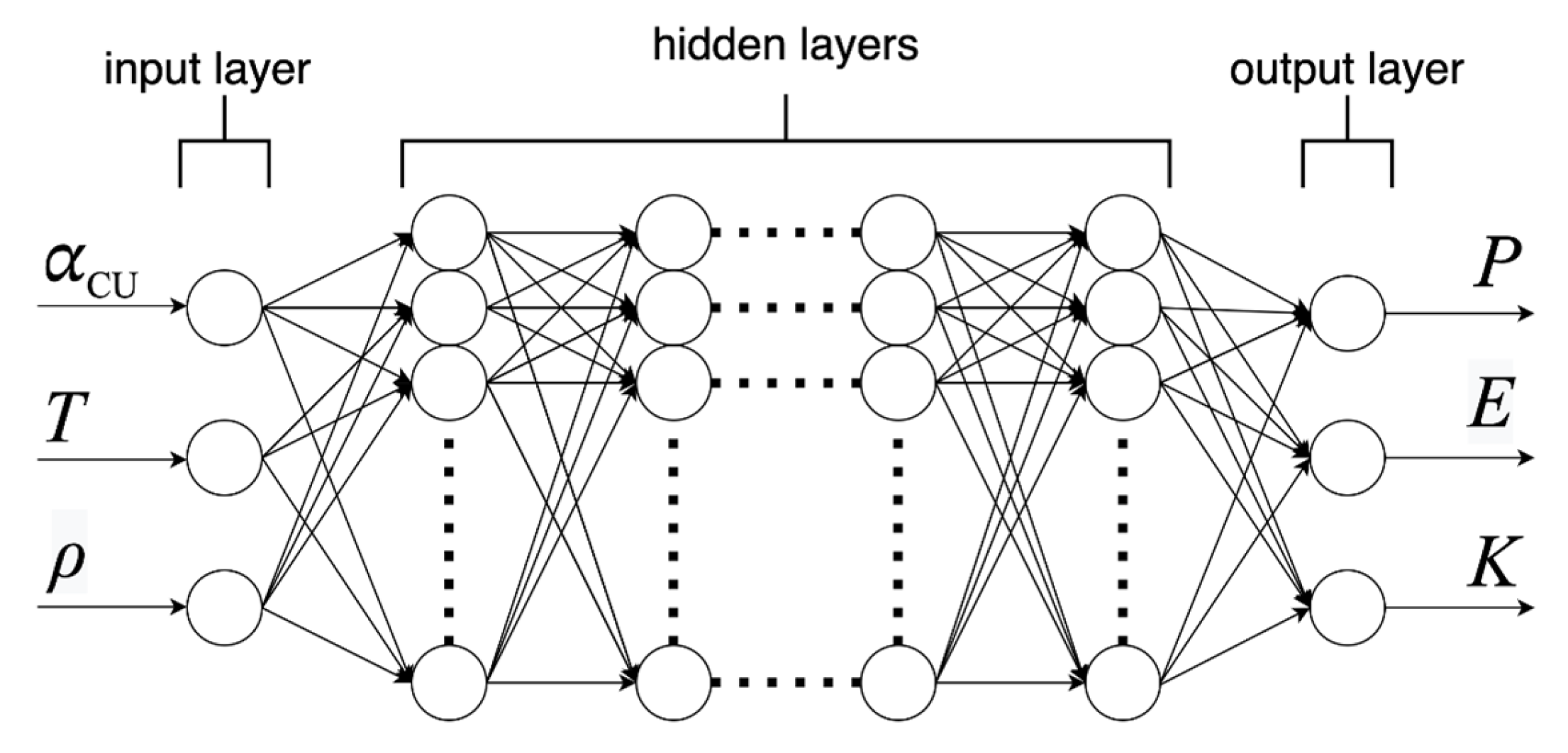
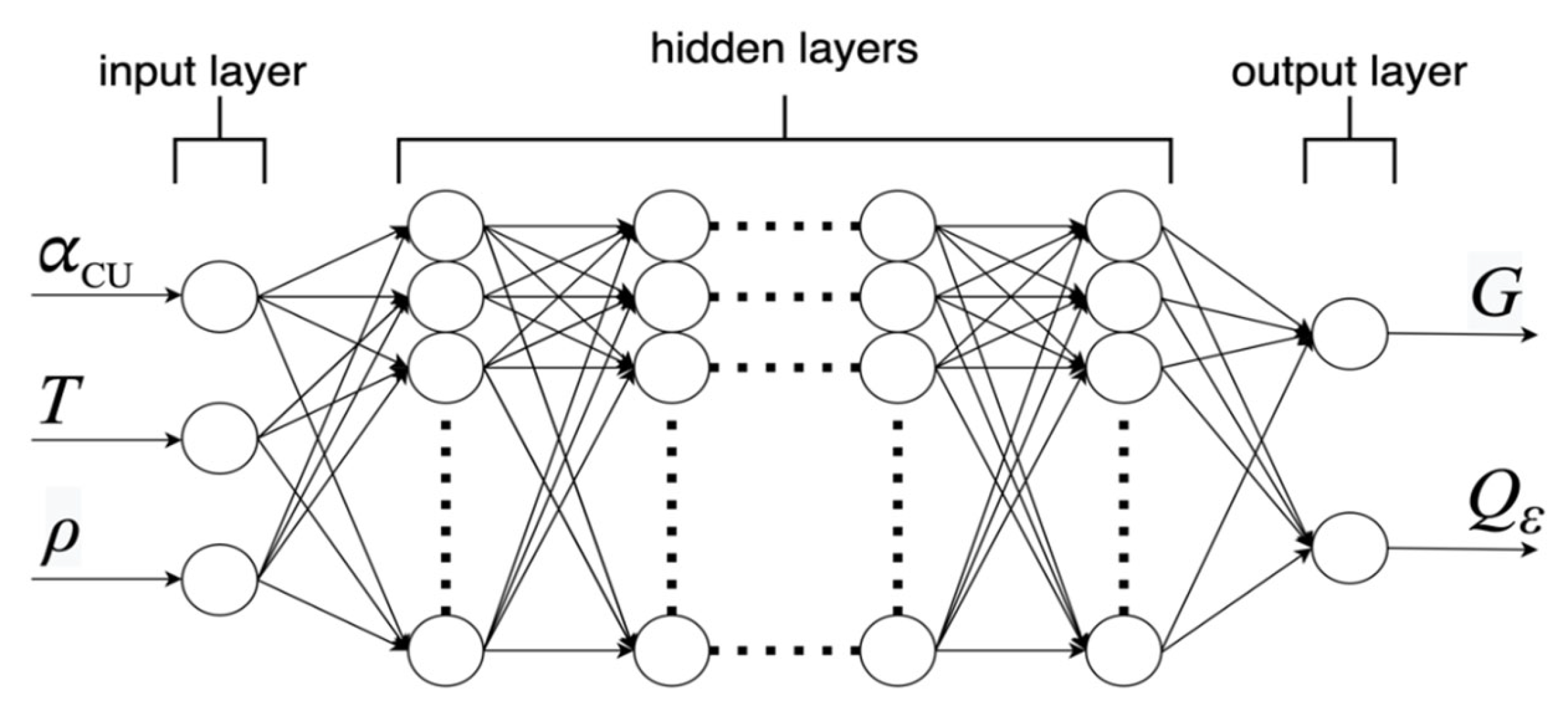
3. The Constitutive Equations in the Form of the Artificial Neural Network
4. Shear Stress Relaxations Due to Dislocation Activity and Phase Transitions
4.1. Theoretical Model of Dislocation Plasticity and Phase Transitions
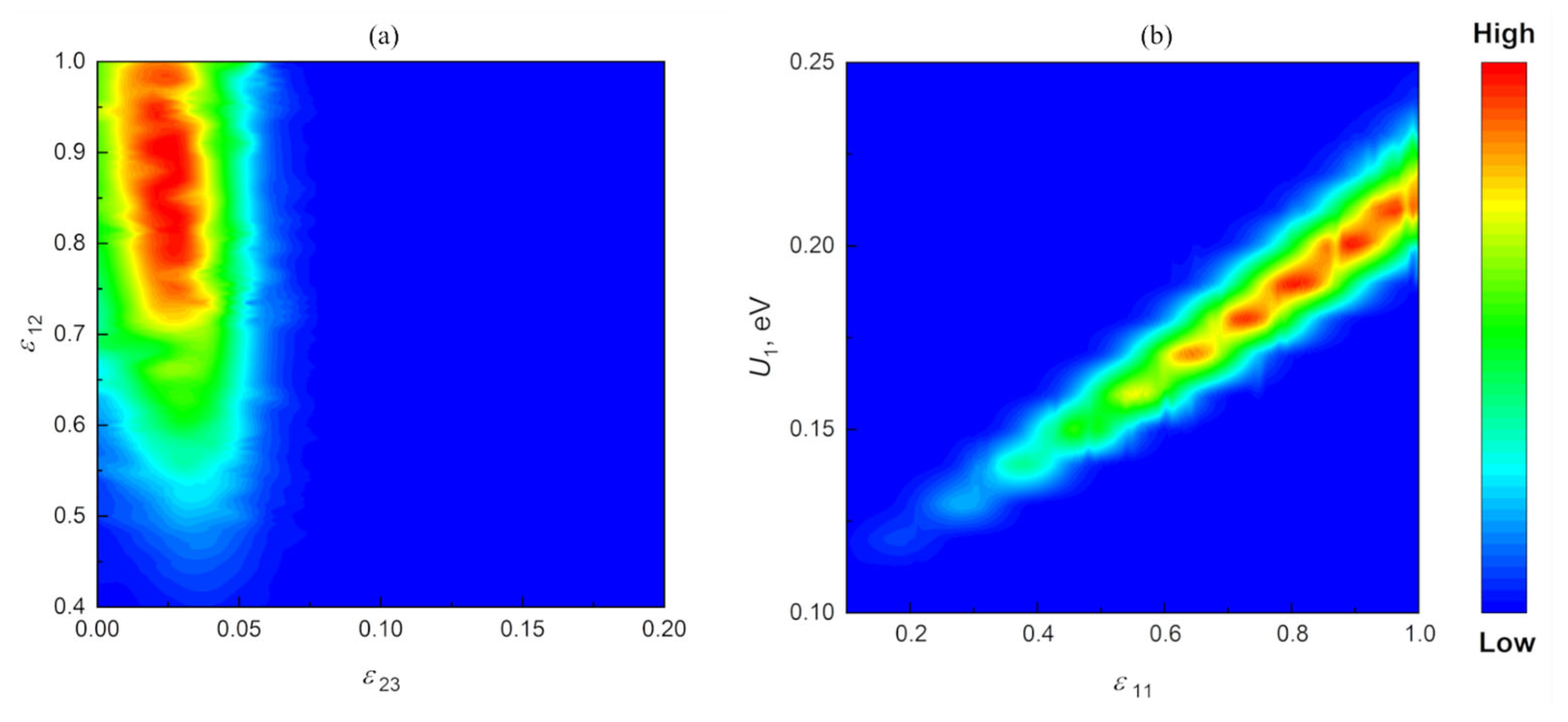
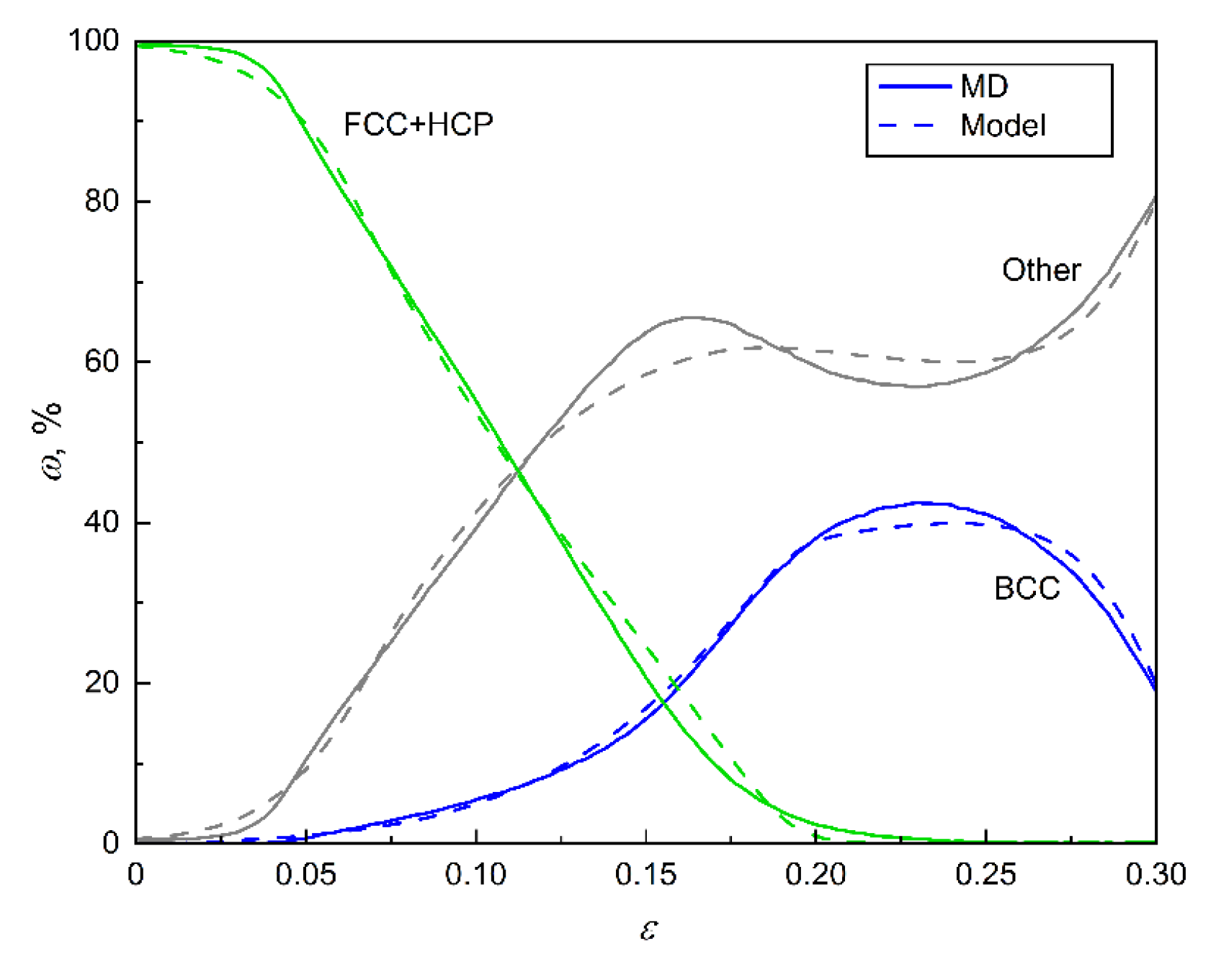
4.2. Optimization and Results of Phase Transition Model
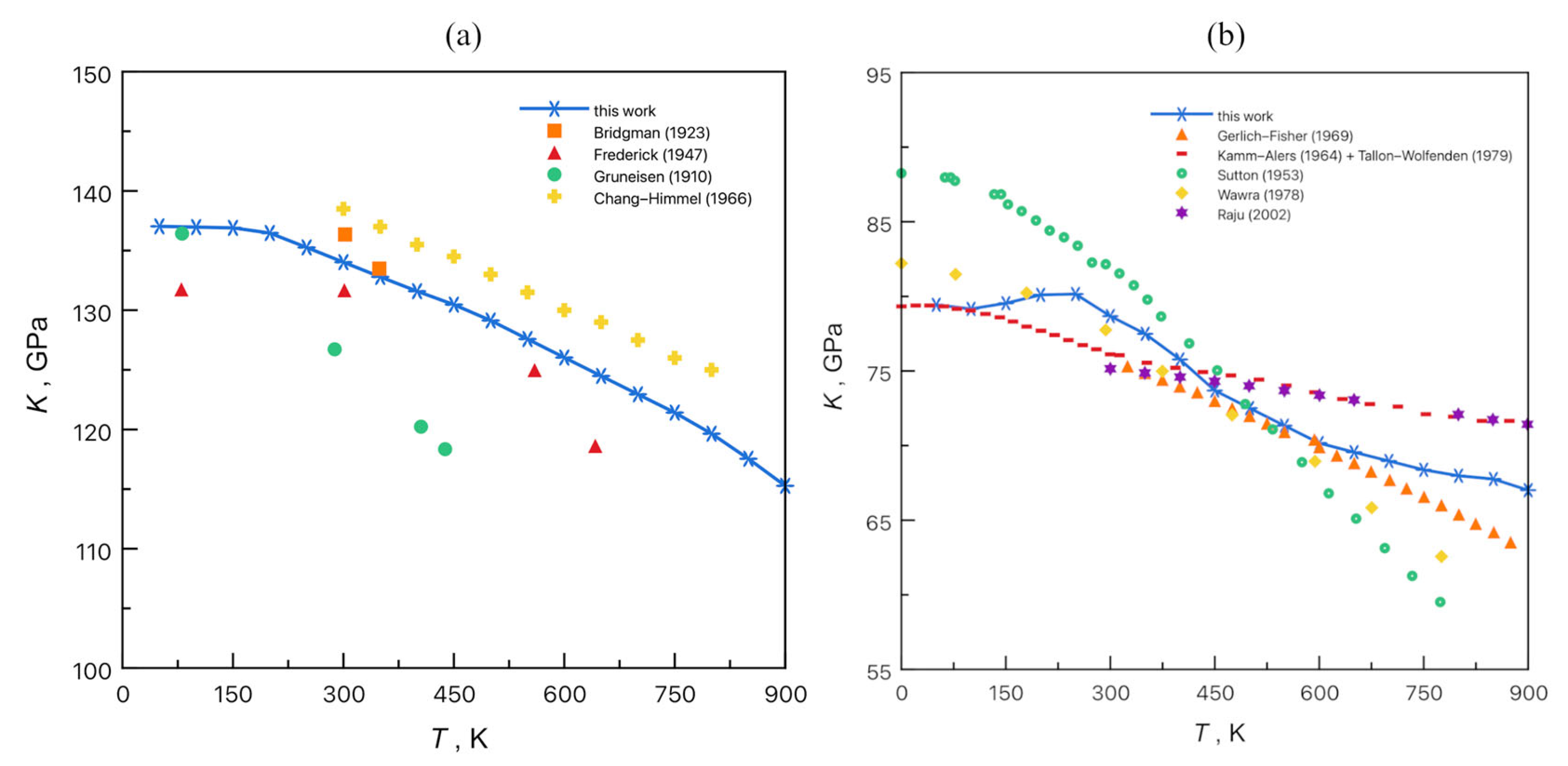
4.3. Optimization and Results of Stress Relaxation Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Steinberg, D.J.; Cochran, S.G.; Guinan, M.W. A constitutive model for metals applicable at high strain rate. J. Appl. Phys. 1980, 51, 1498–1504. [Google Scholar] [CrossRef]
- Gust, W.H. High impact deformation of metal cylinders at elevated temperatures. J. Appl. Phys. 1982, 53, 3566–3575. [Google Scholar] [CrossRef]
- Zhao, H. A constitutive model for metals over a large range of strain rates Identification for mild-steel and aluminium sheets. Mater. Sci. Eng. A 1997, 230, 95–99. [Google Scholar] [CrossRef]
- Follansbee, P.S.; Kocks, U.F. A constitutive description of the deformation of copper based on the use of the mechanical threshold stress as an internal state variable. Acta Metall. 1988, 36, 81–93. [Google Scholar] [CrossRef]
- Gourdin, W.H.; Lassila, D.H. Flow stress of OFE copper at strain rates from 10−3 to 104 s−1: Grain-size effects and comparison to the mechanical threshold stress model. Acta Metall. Mater. 1991, 39, 2337–2348. [Google Scholar] [CrossRef]
- Zerilli, F.J.; Armstrong, R.W. Dislocation mechanics-based constitutive relations for material dynamics calculations. J. Appl. Phys. 1987, 61, 1816–1825. [Google Scholar] [CrossRef]
- Bryukhanov, I.A.; Emelyanov, V.A. Shear stress relaxation through the motion of edge dislocations in Cu and Cu–Ni solid solution: A molecular dynamics and discrete dislocation study. Comput. Mater. Sci. 2022, 201, 110885. [Google Scholar] [CrossRef]
- Zhang, G.; Zhu, Z.; Ning, J.; Feng, C. Dynamic impact constitutive relation of 6008-T6 aluminum alloy based on dislocation density and second-phase particle strengthening effects. J. Alloys Compd. 2023, 932, 167718. [Google Scholar] [CrossRef]
- Khan, A.S.; Liu, J. A deformation mechanism-based crystal plasticity model of ultrafine-grained/nanocrystalline FCC polycrystals. Int. J. Plast. 2016, 86, 56–69. [Google Scholar] [CrossRef]
- Austin, R.A.; McDowell, D.L. A dislocation-based constitutive model for viscoplastic deformation of fcc metals at very high strain rates. Int. J. Plast. 2011, 27, 1–24. [Google Scholar] [CrossRef]
- Luscher, D.J.; Mayeur, J.R.; Mourad, H.M.; Hunter, A.; Kenamond, M.A. Coupling continuum dislocation transport with crystal plasticity for application to shock loading conditions. Int. J. Plast. 2016, 76, 111–129. [Google Scholar] [CrossRef]
- Yao, S.-L.; Pei, X.-Y.; Yu, J.-D.; Bai, J.-S.; Wu, Q. A dislocation-based explanation of quasi-elastic release in shock-loaded aluminum. J. Appl. Phys. 2017, 121, 035101. [Google Scholar] [CrossRef]
- Austin, R.A. Elastic precursor wave decay in shock-compressed aluminum over a wide range of temperature. J. Appl. Phys. 2018, 123, 035103. [Google Scholar] [CrossRef]
- Djordjevic, N.; Vignjevic, R.; Kiely, L.; Case, S.; De Vuyst, T.; Campbell, J.; Hughes, K. Modelling of shock waves in fcc and bcc metals using a combined continuum and dislocation kinetic approach. Int. J. Plast. 2018, 105, 211–224. [Google Scholar] [CrossRef]
- Yao, S.; Pei, X.; Liu, Z.; Yu, J.; Yu, Y.; Wu, Q. Numerical investigation of the temperature dependence of dynamic yield stress of typical BCC metals under shock loading with a dislocation-based constitutive model. Mech. Mater. 2020, 140, 103211. [Google Scholar] [CrossRef]
- Mori, T.; Huang, J.H.; Taya, M. Stress relaxation by plastic flow, interfacial sliding and diffusion in an inclusion bearing material. Acta Mater. 1997, 45, 429–438. [Google Scholar] [CrossRef]
- Borodin, E.N.; Mayer, A.E. Structural model of mechanical twinning and its application for modeling of the severe plastic deformation of copper rods in Taylor impact tests. Int. J. Plast. 2015, 74, 141–157. [Google Scholar] [CrossRef]
- Li, P.; Huang, Y.; Wang, K.; Xiao, S.; Wang, L.; Yao, S.; Zhu, W.; Hu, W. Crystallographic-orientation-dependence plasticity of niobium under shock compressions. Int. J. Plast. 2022, 150, 103195. [Google Scholar] [CrossRef]
- Feng, X.; Liu, X.; Bai, S.; Tang, Y.; Ye, Y. Investigation of dynamic tensile mechanical responses and deformation mechanism at high strain rates in a TWIP steel. J. Mater. Res. Technol. 2023, 26, 639–653. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, A.; Lorca, J. Simulation of dislocation slip and twin propagation in Mg through coupling crystal plasticity and phase field models. Mech. Mater. 2023, 180, 104608. [Google Scholar] [CrossRef]
- Fomin, E.V.; Mayer, A.E. Slip of low-angle tilt grain boundary (110) in FCC metals at perpendicular shear. Int. J. Plast. 2020, 134, 102843. [Google Scholar] [CrossRef]
- Huang, Q.; Zhao, Q.; Zhou, H.; Yang, W. Misorientation-dependent transition between grain boundary migration and sliding in FCC metals. Int. J. Plast. 2022, 159, 103466. [Google Scholar] [CrossRef]
- Verma, A.; Johnson, O.K.; Thompson, G.B.; Chesser, I.; Ogata, S.; Homer, E.R. Insights into factors that affect non-Arrhenius migration of a simulated incoherent Σ3 grain boundary. Acta Mater. 2023, 258, 119210. [Google Scholar] [CrossRef]
- Admal, N.C.; Po, G.; Marian, J. A unified framework for polycrystal plasticity with grain boundary evolution. Int. J. Plast. 2018, 106, 1–30. [Google Scholar] [CrossRef]
- Masuda, H.; Tobe, H.; Hara, T.; Sato, E. Three-dimensional characterization of superplastic grain boundary sliding inside Al–Zn–Mg–Cu alloy sheet. Scr. Mater. 2019, 164, 82–85. [Google Scholar] [CrossRef]
- Borodin, E.N.; Mayer, A.E.; Gutkin, M.Y. Coupled model for grain rotation, dislocation plasticity and grain boundary sliding in fine-grained solids. Int. J. Plast. 2020, 134, 102776. [Google Scholar] [CrossRef]
- Li, G.; Wang, Y.; Wang, K.; Xiang, M.; Chen, J. Shock induced plasticity and phase transition in single crystal lead by molecular dynamics simulations. J. Appl. Phys. 2019, 126, 075902. [Google Scholar] [CrossRef]
- Jiang, D.-D.; Shao, J.-L.; Wu, B.; Wang, P.; He, A.-M. Sudden change of spall strength induced by shock defects based on atomistic simulation of single crystal aluminum. Scr. Mater. 2022, 210, 114474. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, J.; Wei, Q.; Zhang, J.; Sun, Y.; Luo, G.; Shen, Q. Enhanced spall strength of single crystal aluminum by temperature rise mitigation and structural phase transition under shock pulse. Mech. Mater. 2023, 186, 104809. [Google Scholar] [CrossRef]
- Bolesta, A.V.; Fomin, V.M. Molecular dynamics simulation of shock-wave loading of copper and titanium. AIP Conf. Proc. 2017, 1893, 020008. [Google Scholar] [CrossRef]
- Shao, J.-L.; Guo, X.-X.; Lu, G.; He, W.; Xin, J. Influence of shear wave on the HCP nucleation in BCC iron under oblique shock conditions. Mech. Mater. 2021, 158, 103878. [Google Scholar] [CrossRef]
- Zhao, K.; Gu, Y.; Zhao, F.; Chen, Q. Revisiting the effect of shear stress on the γ→α phase transition of cerium under shock loading. Mech. Mater. 2023, 184, 104743. [Google Scholar] [CrossRef]
- Jian, Z.; Chen, Y.; Xiao, S.; Wang, L.; Li, X.; Wang, K.; Deng, H.; Hu, W. Shock-induced plasticity and phase transformation in single crystal magnesium: An interatomic potential and non-equilibrium molecular dynamics simulations. J. Phys. Condens. Matter 2022, 34, 115401. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.-C.; Shao, J.-L. FCC-BCC phase transformation induced simultaneous enhancement of tensile strength and ductility at high strain rate in high-entropy alloy. Int. J. Plast. 2023, 169, 103730. [Google Scholar] [CrossRef]
- Xie, H.; Ma, Z.; Zhang, W.; Zhao, H.; Ren, L. Phase transition in shock compressed high-entropy alloy FeNiCrCoCu. Int. J. Mech. Sci. 2023, 238, 107855. [Google Scholar] [CrossRef]
- Dewaele, A.; Loubeyre, P.; Mezouar, M. Equations of state of six metals above 94 GPa. Phys. Rev. B 2004, 70, 094112. [Google Scholar] [CrossRef]
- Sharma, S.M.; Turneaure, S.J.; Winey, J.M.; Gupta, Y.M. Transformation of shock-compressed copper to the body-centered-cubic structure at 180 GPa. Phys. Rev. B 2020, 102, 020103. [Google Scholar] [CrossRef]
- Fratanduono, D.E.; Smith, R.F.; Ali, S.J.; Braun, D.G.; Fernandez-Pañella, A.; Zhang, S.; Kraus, R.G.; Coppari, F.; McNaney, J.M.; Marshall, M.C.; et al. Probing the solid phase of noble metal copper at terapascal conditions. Phys. Rev. Lett. 2020, 124, 015701. [Google Scholar] [CrossRef]
- Javanbakht, M.; Levitas, V.I. Interaction between phase transformations and dislocations at the nanoscale. Part 2: Phase field simulation examples. J. Mech. Phys. Solids 2015, 82, 164–185. [Google Scholar] [CrossRef]
- Levitas, V.I.; Javanbakht, M. Interaction between phase transformations and dislocations at the nanoscale. Part 1. General phase field approach. J. Mech. Phys. Solids. 2015, 82, 287–319. [Google Scholar] [CrossRef]
- Yeddu, H.K.; Lookman, T. Phase-field modeling of the beta to omega phase transformation in Zr-Nb alloys. Mater. Sci. Eng. A 2015, 634, 46–54. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, G.; Wang, H.; Wu, P.; Lee, M.-G.; Li, D. Experimental and numerical study on strain path and crystal orientation dependences of phase transformation behaviors of QP1180 steel. Int. J. Plast. 2023, 160, 103499. [Google Scholar] [CrossRef]
- Binqiang, L.; Guiji, W.; Jianjun, M.; Hongpin, Z.; Fuli, T.; Jianheng, Z.; Cangli, L.; Chengwei, S. Verification of conventional equations of state for tantalum under quasi-isentropic compression. J. Appl. Phys. 2014, 116, 193506. [Google Scholar] [CrossRef]
- Shang, S.-L.; Wang, Y.; Kim, D.E.; Liu, Z.-K. First-principles thermodynamics from phonon and Debye model: Application to Ni and Ni3Al. Comput. Mater. Sci. 2010, 47, 1040–1048. [Google Scholar] [CrossRef]
- Matar, S.F.; Al Alam, A.F.; Ouaini, N. First principles account for large changes in electronic structure and bonding from LaCu to LaCuMg and LaCuMg4. Comput. Mater. Sci. 2015, 97, 231–236. [Google Scholar] [CrossRef]
- Gracheva, N.A.; Lekanov, M.V.; Mayer, A.E.; Fomin, E.V. Application of neural networks for modeling shock-wave processes in aluminum. Mech. Solids 2021, 56, 326–342. [Google Scholar] [CrossRef]
- Bonatti, C.; Berisha, B.; Mohr, D. From CP-FFT to CP-RNN: Recurrent neural network surrogate model of crystal plasticity. Int. J. Plast. 2022, 58, 103430. [Google Scholar] [CrossRef]
- Heidenreich, J.N.; Gorji, M.B.; Mohr, D. Modeling structure-property relationships with convolutional neural networks: Yield surface prediction based on microstructure images. Int. J. Plast. 2023, 163, 103506. [Google Scholar] [CrossRef]
- Casalino, G.; Minutolo, F.M.C. A model for evaluation of laser welding efficiency and quality using an artificial neural network and fuzzy logic. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2004, 218, 641–646. [Google Scholar] [CrossRef]
- Du, Y.; Mukherjee, T.; DebRoy, T. Conditions for void formation in friction stir welding from machine learning. NPJ Comput. Mater. 2019, 5, 68. [Google Scholar] [CrossRef]
- Gaja, H.; Liou, F. Defect classification of laser metal deposition using logistic regression and artificial neural networks for pattern recognition. Int. J. Adv. Manuf. Technol. 2017, 94, 315–326. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Machine-learning based temperature- and rate-dependent plasticity model: Application to analysis of fracture experiments on DP steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar] [CrossRef]
- Li, X.; Roth, C.C.; Mohr, D. Neural network based rate- and temperature-dependent Hosford–Coulomb fracture initiation model. Int. J. Mech. Sci. 2023, 260, 108643. [Google Scholar] [CrossRef]
- Nakka, R.; Harursampath, D.; Ponnusami, S.A. A generalised deep learning-based surrogate model for homogenisation utilising material property encoding and physics-based bounds. Sci. Rep. 2023, 13, 9079. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, X.; Zhong, W.; Li, M. Learning microstructure–property mapping via label-free 3D convolutional neural network. Vis. Comput. 2024. [Google Scholar] [CrossRef]
- Latypov, F.T.; Fomin, E.V.; Krasnikov, V.S.; Mayer, A.E. Dynamic compaction of aluminum with nanopores of varied shape: MD simulations and machine-learning-based approximation of deformation behavior. Int. J. Plast. 2022, 156, 103363. [Google Scholar] [CrossRef]
- Latypov, F.T.; Fomin, E.V.; Krasnikov, V.S.; Mayer, A.E. Modeling of shock wave propagation in porous magnesium based on artificial neural network. Mech. Mater. 2024, 191, 104953. [Google Scholar] [CrossRef]
- Walters, D.J.; Biswas, A.; Lawrence, E.C.; Francom, D.C.; Luscher, D.J.; Fredenburg, D.A.; Moran, K.R.; Sweeney, C.M.; Sandberg, R.L.; Ahrens, J.P.; et al. Bayesian calibration of strength parameters using hydrocode simulations of symmetric impact shock experiments of Al-5083. J. Appl. Phys. 2018, 124, 205105. [Google Scholar] [CrossRef]
- Sjue, S.; Ahrens, J.; Biswas, A.; Francom, D.; Lawrence, E.; Luscher, D.; Walters, D. Fast strength model characterization using Bayesian statistics. AIP Conf. Proc. 2020, 2272, 070043. [Google Scholar] [CrossRef]
- Nguyen, T.; Francom, D.C.; Luscher, D.J.; Wilkerson, J.W. Bayesian calibration of a physics-based crystal plasticity and damage model. J. Mech. Phys. Solids 2021, 149, 104284. [Google Scholar] [CrossRef]
- Nguyen, T.; Fensin, S.J.; Luscher, D.J. Dynamic crystal plasticity modeling of single crystal tantalum and validation using Taylor cylinder impact tests. Int. J. Plast. 2021, 139, 102940. [Google Scholar] [CrossRef]
- Rodionov, E.S.; Pogorelko, V.V.; Lupanov, V.G.; Mayer, P.N.; Mayer, A.E. Modified Taylor impact tests with profiled copper cylinders: Experiment and optimization of dislocation plasticity model. Materials 2023, 16, 5602. [Google Scholar] [CrossRef] [PubMed]
- Popova, T.V.; Mayer, A.E.; Khishchenko, K.V. Evolution of shock compression pulses in polymethacrylate and aluminum. J. Appl. Phys. 2018, 123, 235902. [Google Scholar] [CrossRef]
- Ashitkov, S.I.; Komarov, P.S.; Struleva, E.V.; Agranat, M.B.; Kanel, G.I. Mechanical and optical properties of vanadium under shock picosecond loads. JETP Lett. 2015, 101, 276–281. [Google Scholar] [CrossRef]
- Kanel, G.I.; Zaretsky, E.B.; Razorenov, S.V.; Ashitkov, S.I.; Fortov, V.E. Unusual plasticity and strength of metals at ultra-short load durations. Phys. Usp. 2017, 60, 490–508. [Google Scholar] [CrossRef]
- Zuanetti, B.; McGrane, S.D.; Bolme, C.A.; Prakash, V. Measurement of elastic precursor decay in pre-heated aluminum films under ultra-fast laser generated shocks. J. Appl. Phys. 2018, 123, 195104. [Google Scholar] [CrossRef]
- Khokhlov, V.A.; Zhakhovsky, V.V.; Inogamov, N.A.; Ashitkov, S.I.; Sitnikov, D.S.; Khishchenko, K.V.; Petrov, Y.V.; Manokhin, S.S.; Nelasov, I.V.; Shepelev, V.V.; et al. Melting of titanium by a shock wave generated by an intense femtosecond laser pulse. JETP Lett. 2022, 115, 523–530. [Google Scholar] [CrossRef]
- Jax, P.; Kratochvil, P.; Haasen, P. Solid solution hardening of gold and other f.c.c. single crystals. Acta Metall. 1970, 18, 237–245. [Google Scholar] [CrossRef]
- Monchoux, F.; Neuhäuser, H. An in situ transmission electron microscope study of dislocation glide in Cu-Ge alloys. J. Mater. Sci. 1987, 22, 1443–1449. [Google Scholar] [CrossRef]
- Roth, H.A.; Davis, C.L.; Thomson, R.C. Modeling solid solution strengthening in nickel alloys. Metall. Mater. Trans. A 1997, 28, 1329–1335. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J.L. Thermally Activated Mechanisms in Crystal Plasticity; Pergamon Press: Oxford, UK, 2003; Volume 8, pp. 3–433. [Google Scholar]
- Xu, W.; Liu, X.C.; Li, X.Y.; Lu, K. Deformation induced grain boundary segregation in nanolaminated Al–Cu alloy. Acta Mater. 2020, 182, 207–214. [Google Scholar] [CrossRef]
- Sun, W.; Zhu, Y.; Marceau, R.; Wang, L.; Zhang, Q.; Gao, X.; Hutchinson, C. Precipitation strengthening of aluminum alloys by room-temperature cyclic plasticity. Science 2019, 363, 972–975. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Apostol, F.; Mishin, Y. Interatomic potential for the Al-Cu system. Phys. Rev. B 2011, 83, 054116. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Larsen, P.M.; Schmidt, S.; Schiøtz, J. Robust structural identification via polyhedral template matching. Model. Simul. Mat. Sci. Eng. 2016, 24, 055007. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Mayer, A.E.; Mayer, P.N.; Lekanov, M.V.; Panchenko, B.A. Incipience of plastic flow in aluminum with nanopores: Molecular dynamics and machine-learning-based description. Metals 2022, 12, 2158. [Google Scholar] [CrossRef]
- Grachyova, N.A.; Fomin, E.V.; Mayer, A.E. Application of Machine Learning in the Study of Phase Transformations of Al-Cu Alloys under Deformation. Available online: https://www.researchgate.net/publication/366432358_APPLICATION_OF_MACHINE_LEARNING_IN_THE_STUDY_OF_DEFORMATION_BEHAVIOR_OF_AL-CU_ALLOYS (accessed on 10 July 2024).
- Grachyova, N.A.; Fomin, E.V.; Mayer, A.E. Theoretical description of phase transitions in Al-Cu alloys using machine learning. In XIII All-Russian Congress on Theoretical and Applied Mechanics. Collection of Abstracts: In 4 Vol.; Ministry of Science and Higher Education of the Russian Federation; Russian Academy of Sciences; Russian National Committee on Theoretical and Applied Mechanics; Peter the Great St. Petersburg Polytechnic University: St. Petersburg, Russia, 2023; pp. 358–359. [Google Scholar]
- Grachyova, N.A.; Fomin, E.V.; Mayer, A.E. Application of machine learning in the study of deformation behaviour of Al-Cu alloys, Physical Mesomechanics of Materials. In Physical Principles of Multilevel Structure Formation and Mechanisms of Nonlinear Behaviour: Proc. of Intern. Conf., Tomsk, Russia, 5–8 September 2022; Institute of Strength Physics and Materials Science SB RAS; IPC NSU: Novosibirsk, Russia, 2022; p. 556. ISBN 978-5-4437-1353-3. [Google Scholar]
- Hashiguchi, K. Elastoplasticity Theory; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Mayer, A.E.; Krasnikov, V.S.; Pogorelko, V.V. Homogeneous nucleation of dislocations in copper: Theory and approximate description based on molecular dynamics and artificial neural networks. Comput. Mater. Sci. 2022, 206, 111266. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034. [Google Scholar] [CrossRef]
- Ramachandran, P.; Zoph, B.; Le, Q.V. Searching for Activation Functions. arXiv 2017, arXiv:1710.05941. [Google Scholar] [CrossRef]
- Pogorelko, V.V.; Mayer, A.E.; Fomin, E.V.; Fedorov, E.V. Examination of machine learning method for identification of material model parameters. Int. J. Mech. Sci. 2024, 265, 108912. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Sutton, P.M. The variation of the elastic constants of crystalline aluminum with temperature between 63 °K and 773 °K. Phys. Rev. 1953, 91, 816–821. [Google Scholar] [CrossRef]
- Kamm, G.N.; Alers, G.A. Low temperature elastic moduli of aluminum. J. Appl. Phys. 1964, 35, 327–330. [Google Scholar] [CrossRef]
- Gerlich, D.; Fisher, E.S. The high temperature elastic moduli of aluminum. J. Phys. Chem. Solids 1969, 30, 1197–1205. [Google Scholar] [CrossRef]
- Tallon, J.L.; Wolfenden, A. Temperature dependence of the elastic constants of aluminum. J. Phys. Chem. Solids 1979, 40, 831–837. [Google Scholar] [CrossRef]
- Overton, W.C., Jr.; Gaffney, J. Temperature variation of the elastic constants of cubic elements. I. Copper. Phys. Rev. 1955, 98, 969–977. [Google Scholar] [CrossRef]
- Chang, Y.A.; Himmel, L. Temperature dependence of the elastic constants of Cu, Ag, and Au above room temperature. J. Appl. Phys. 1966, 37, 3567–3572. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Naimon, E.R. Elastic properties of metals and alloys. II. Copper. J. Phys. Chem. Ref. Data. 1974, 3, 897–935. [Google Scholar] [CrossRef]
- Raju, S.; Sivasubramanian, K.; Mohandas, E. The high temperature bulk modulus of aluminium: An assessment using experimental enthalpy and thermal expansion data. Solid State Commun. 2002, 122, 671–676. [Google Scholar] [CrossRef]
- Wawra, H. Die Kröner-Grenzen der Elastizitätsmoduln technisch wichtiger Werkstoffe: Teil II: Zahlenwerte zur Temperaturabhängigkeit der Moduln der Elemente. Int. J. Mater. Res. 1978, 69, 518–523. [Google Scholar] [CrossRef]
- Wen, Y.; Yunxin, W. Effects of temperature and pressure on elastic properties of single crystal aluminum in different crystal orientations. Phys. Status Solidi B 2020, 257, 2000434. [Google Scholar] [CrossRef]
- Marchand, D.; Curtin, W.A. Machine learning for metallurgy IV: A neural network potential for Al-Cu-Mg and Al-Cu-Mg-Zn. Phys. Rev. Mater. 2022, 6, 053803. [Google Scholar] [CrossRef]
- Purja Pun, G.P.; Batra, R.; Ramprasad, R.; Mishin, Y. Physically informed artificial neural networks for atomistic modeling of materials. Nat. Commun. 2019, 10, 2339. [Google Scholar] [CrossRef]
- Senoo, M.; Hayashi, T. Elastic constants of Al-Cu solid-solution alloys and their variations by aging treatments. JSME Int. J. Ser. 1 Solid Mech. Strength Mater. 1988, 31, 664–670. [Google Scholar] [CrossRef][Green Version]
- Ma, D. First-Principles Investigations of Solid Solution Strengthening in Al Alloys; Shaker Verlag GmbH: Aachen, Germany, 2012. [Google Scholar]
- Lee, E.H.; Liu, D.T. Finite–strain elastic–plastic theory with application to plane wave analysis. J. Appl. Phys. 1967, 38, 19–27. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic-plastic deformation at finite strains. J. Appl. Mech. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Nemat-Nasser, S. Decomposition of strain measures and their rates in finite deformation elastoplasticity. Int. J. Solids Struct. 1979, 15, 155–166. [Google Scholar] [CrossRef]
- Zhao, S.; Petrov, Y.V.; Volkov, G.A. The modified relaxation plasticity model and the non-monotonic stress–strain diagram. Int. J. Mech. Sci. 2023, 240, 107919. [Google Scholar] [CrossRef]
- Selyutina, N.; Borodin, E.N.; Petrov, Y.; Mayer, A.E. The definition of characteristic times of plastic relaxation by dislocation slip and grain boundary sliding in copper and nickel. Int. J. Plast. 2016, 82, 97–111. [Google Scholar] [CrossRef]
- Mayer, A.E.; Lekanov, M.V.; Grachyova, N.A.; Fomin, E.V. Machine-learning-based model of elastic—Plastic deformation of copper for application to shock wave problem. Metals 2022, 12, 402. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E. Influence of local stresses on motion of edge dislocation in aluminum. Int. J. Plast. 2018, 101, 170–187. [Google Scholar] [CrossRef]
- Kuksin, A.Y.; Yanilkin, A.V. Atomistic simulation of the motion of dislocations in metals under phonon drag conditions. Phys. Solid State 2013, 55, 1010–1019. [Google Scholar] [CrossRef]
- Krasnikov, V.S.; Mayer, A.E.; Yalovets, A.P. Dislocation based high-rate plasticity model and its application to plate-impact and ultra short electron irradiation simulations. Int. J. Plast. 2011, 27, 1294–1308. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity. In Course of Theoretical Physics; Pergamon Press: New York, NY, USA, 1986; Volume 7. [Google Scholar]
- Tohme, T.; Vanslette, K.; Youcef-Toumi, K. A generalized Bayesian approach to model calibration. Reliab. Eng. Syst. Saf. 2020, 204, 107141. [Google Scholar] [CrossRef]
- Pogorelko, V.V.; Mayer, A.E. Dynamic tensile fracture of iron: Molecular dynamics simulations and micromechanical model based on dislocation plasticity. Int. J. Plast. 2023, 167, 103678. [Google Scholar] [CrossRef]
- Meyers, M.A.; Gregori, F.; Kad, B.K.; Schneider, M.S.; Kalantar, D.H.; Remington, B.A.; Ravichandran, G.; Boehly, T.; Wark, J.S. Laser-induced shock compression of monocrystalline copper: Characterization and analysis. Acta Mater. 2003, 51, 1211–1228. [Google Scholar] [CrossRef]
- Bringa, E.M.; Rosolankova, K.; Rudd, R.E.; Remington, B.A.; Wark, J.S.; Duchaineau, M.; Kalantar, D.H.; Hawreliak, J.; Belak, J. Shock deformation of face-centred-cubic metals on subnanosecond timescales. Nat. Mater. 2006, 5, 805–809. [Google Scholar] [CrossRef]
- Hu, J.; Liu, Z.; Chen, K.; Zhuang, Z. Investigations of shock-induced deformation and dislocation mechanism by a multiscale discrete dislocation plasticity model. Comput. Mater. Sci. 2017, 131, 78–85. [Google Scholar] [CrossRef]








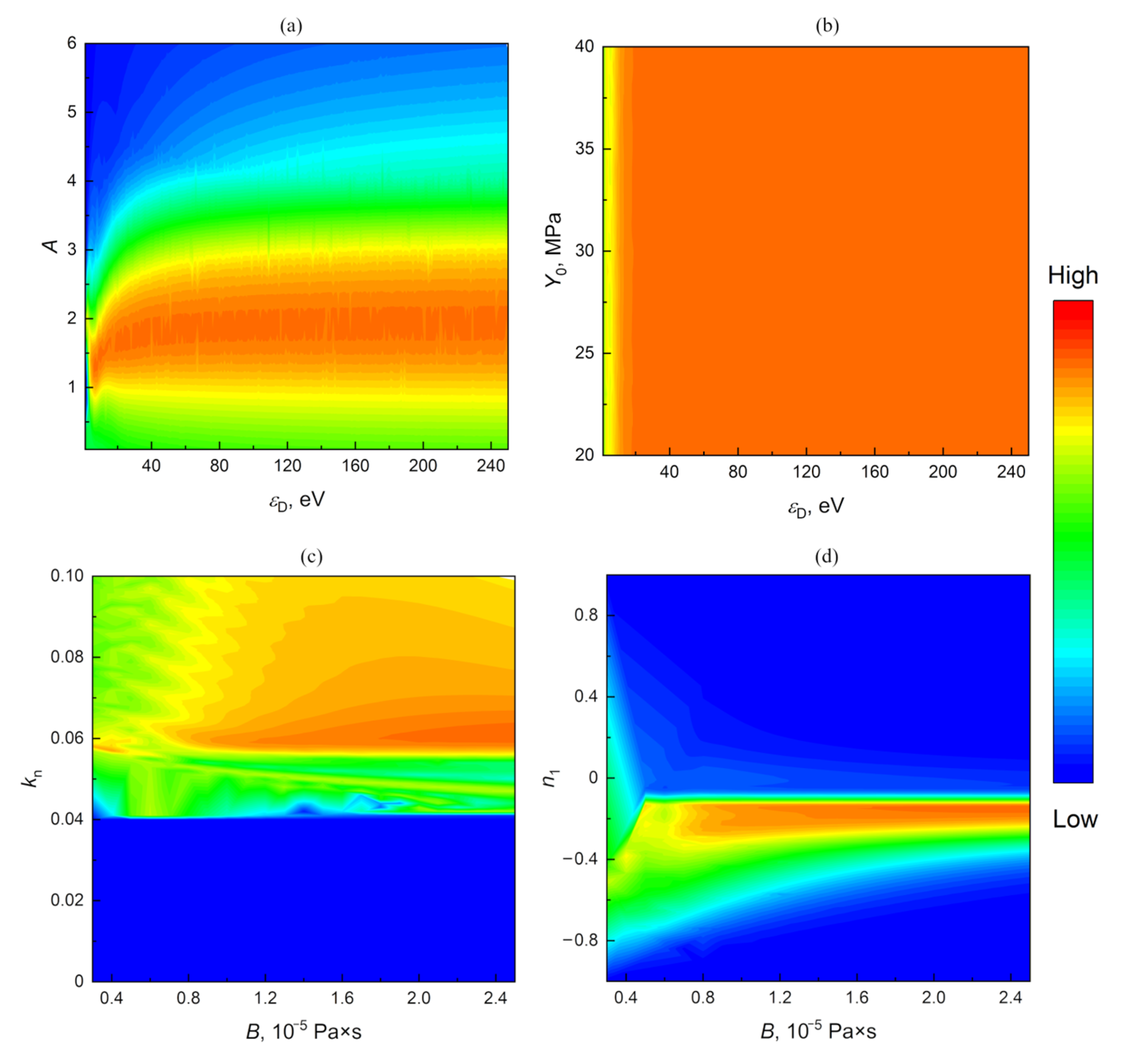

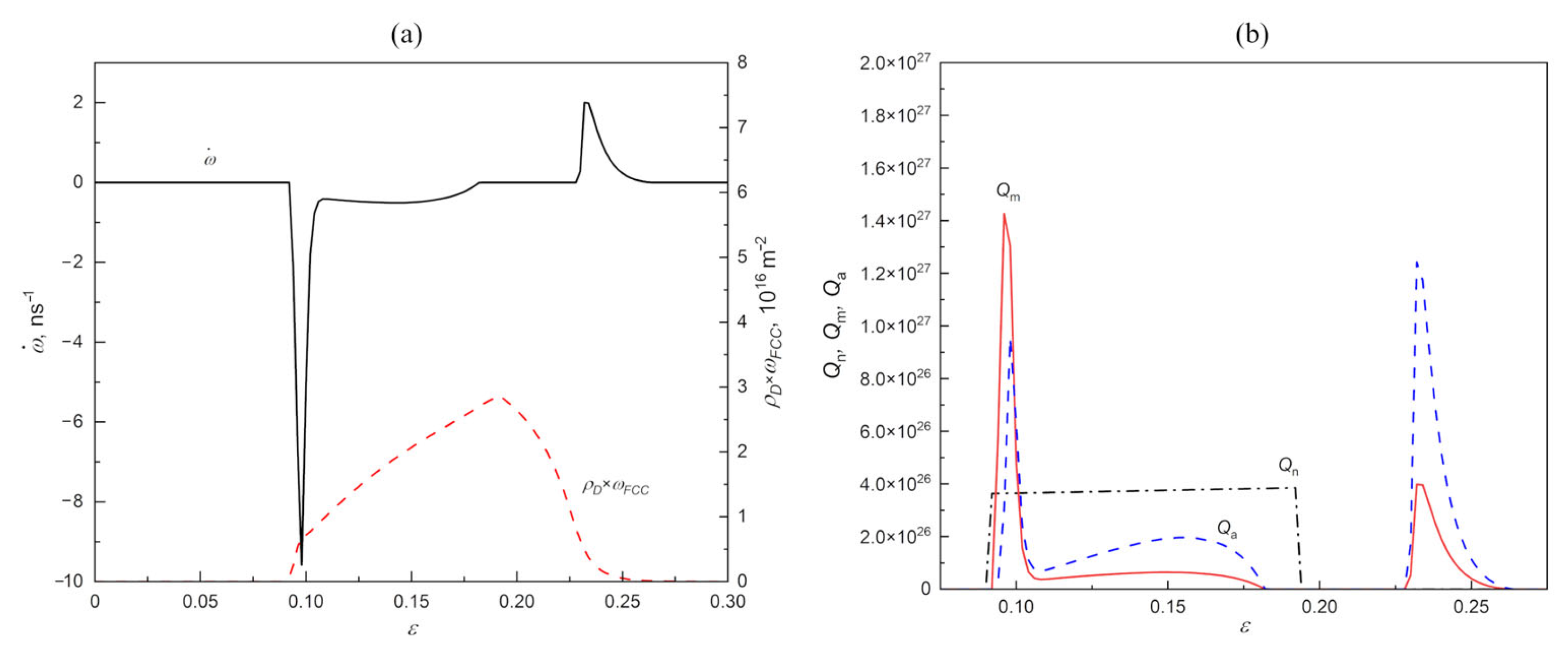
| Parameters | ANN 1 | ANN 2 |
|---|---|---|
| 0.1 | 0.6 | |
| Number of hidden layers | 5 | 6 |
| Number of neurons in each hidden layer | 20 | 20 |
| (initial step of Adam) | 0.001 | 0.001 |
| Number of epochs | 420 | 780 |
| Mini batch size | 30 | 10 |
| n (averaging parameter for calculating shear and bulk moduli) | 150 | 150 |
| Amount of training data | 230,200 (80.5%) | 109,207 (81.6%) |
| Amount of test data | 55,515 (19.5%) | 24,556 (18.4%) |
| (%) | 0/100 | |
| (kg/m3) | 2160/12,700 | |
| Tmin/Tmax (K) | 100/900 | |
| Pmin/P max (GPa) | −13.7/116 | − |
| Emin/Emax (eV/atom) | −3.60/−2.68 | − |
| Kmin/Kmax (GPa) | 10.4/320.6 | − |
| Gmin/Gmax (GPa) | − | 5.3/65.7 |
| − | 0.12/0.3 | |
| ANN Output | Type of Data Set | MAPE (%) |
|---|---|---|
| Pressure | training data | 0.21 |
| test data | 0.23 | |
| Total energy | training data | 0.26 |
| test data | 0.35 | |
| Bulk modulus | training data | 0.32 |
| test data | 0.44 | |
| Shear modulus | training data | 0.54 |
| test data | 1.0 | |
| Nucleation distance | training data | 0.52 |
| test data | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grachyova, N.; Fomin, E.; Mayer, A. Theoretical Model of Structural Phase Transitions in Al-Cu Solid Solutions under Dynamic Loading Using Machine Learning. Dynamics 2024, 4, 526-553. https://doi.org/10.3390/dynamics4030028
Grachyova N, Fomin E, Mayer A. Theoretical Model of Structural Phase Transitions in Al-Cu Solid Solutions under Dynamic Loading Using Machine Learning. Dynamics. 2024; 4(3):526-553. https://doi.org/10.3390/dynamics4030028
Chicago/Turabian StyleGrachyova, Natalya, Eugenii Fomin, and Alexander Mayer. 2024. "Theoretical Model of Structural Phase Transitions in Al-Cu Solid Solutions under Dynamic Loading Using Machine Learning" Dynamics 4, no. 3: 526-553. https://doi.org/10.3390/dynamics4030028
APA StyleGrachyova, N., Fomin, E., & Mayer, A. (2024). Theoretical Model of Structural Phase Transitions in Al-Cu Solid Solutions under Dynamic Loading Using Machine Learning. Dynamics, 4(3), 526-553. https://doi.org/10.3390/dynamics4030028






