The Adiabatic Evolution of 3D Annular Vortices with a Double-Eyewall Structure
Abstract
:1. Introduction
- Type-1 BI occurs across the secondary eyewall when the secondary eyewall is sufficiently narrow and when the circulation associated with the primary eyewall is too weak to stabilize the secondary eyewall.
- Type-2 BI occurs across the moat when the radial extent of the moat (i.e., the moat width) is narrow enough so that unstable interactions occur between the primary eyewall and the inner edge of the secondary eyewall.
2. Linear Stability Analysis
2.1. Derivation
- is the ratio of the eye to primary eyewall vorticity. Following Ref. [10], will be called the hollowness of the vortex.
- is the ratio of the primary to second eyewall vorticity. will be called the eyewall vorticity ratio.
- is the ratio of the moat vorticity to secondary eyewall vorticity. will be called the moat strength.
- is the ratio of the far-field vorticity to secondary eyewall vorticity. Since the vorticity of the outer vortex is usually denoted as the vortex skirt [43], will be called the skirt strength.
- is the ratio of the inner to outer primary eyewall radius. Notice that, as approaches 1, the primary eyewall thins. For this reason, will be called the primary eyewall thickness. It will be shown in Section 2.2 that this parameter plays an important role in the onset of BI across the primary eyewall of the vortex, which is known as Type-3 BI.
- is the ratio of the outer primary eyewall radius to the inner secondary eyewall radius. Notice that, as increases (with all other parameters held constant), decreases. Furthermore, notice that implies that . This means that is a measure of the radial extent of the moat such that values of close to 1 correspond to a vortex with a small moat and values of close to 0 correspond to a vortex with a large moat. For this reason, will be called the moat width parameter. It will be shown in Section 2.2 that this parameter plays an important role in the onset of Type-2 BI.
- is the ratio of the inner to outer secondary eyewall radius. Notice that, as approaches 1, the secondary eyewall thins. For this reason, will be called the secondary eyewall thickness. It will be shown in Section 2.2 that this parameter plays an important role in the onset of Type-1 BI.
- is the ratio of the outer secondary eyewall radius to the radius of the outer vortex. Notice that, as increases (with all other parameters held constant), decreases. Furthermore, notice that implies that . This means that is a measure of the radial extent of the skirt such that corresponds to a vortex with no skirt and corresponds to a vortex whose skirt extends through the entire far-field region of the vortex. For this reason, will be called the skirt width.
2.2. Results from Linear Stability Analysis
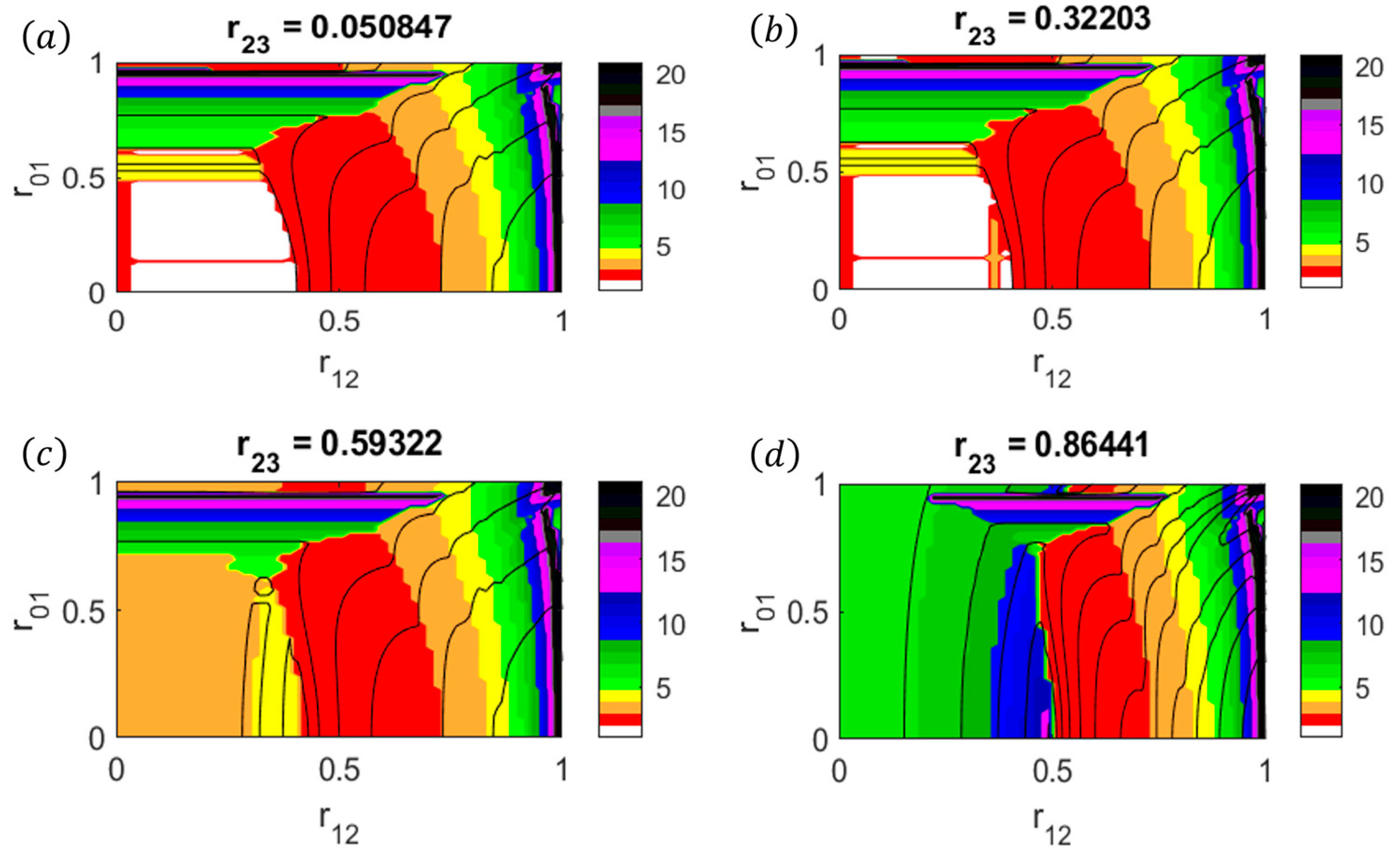
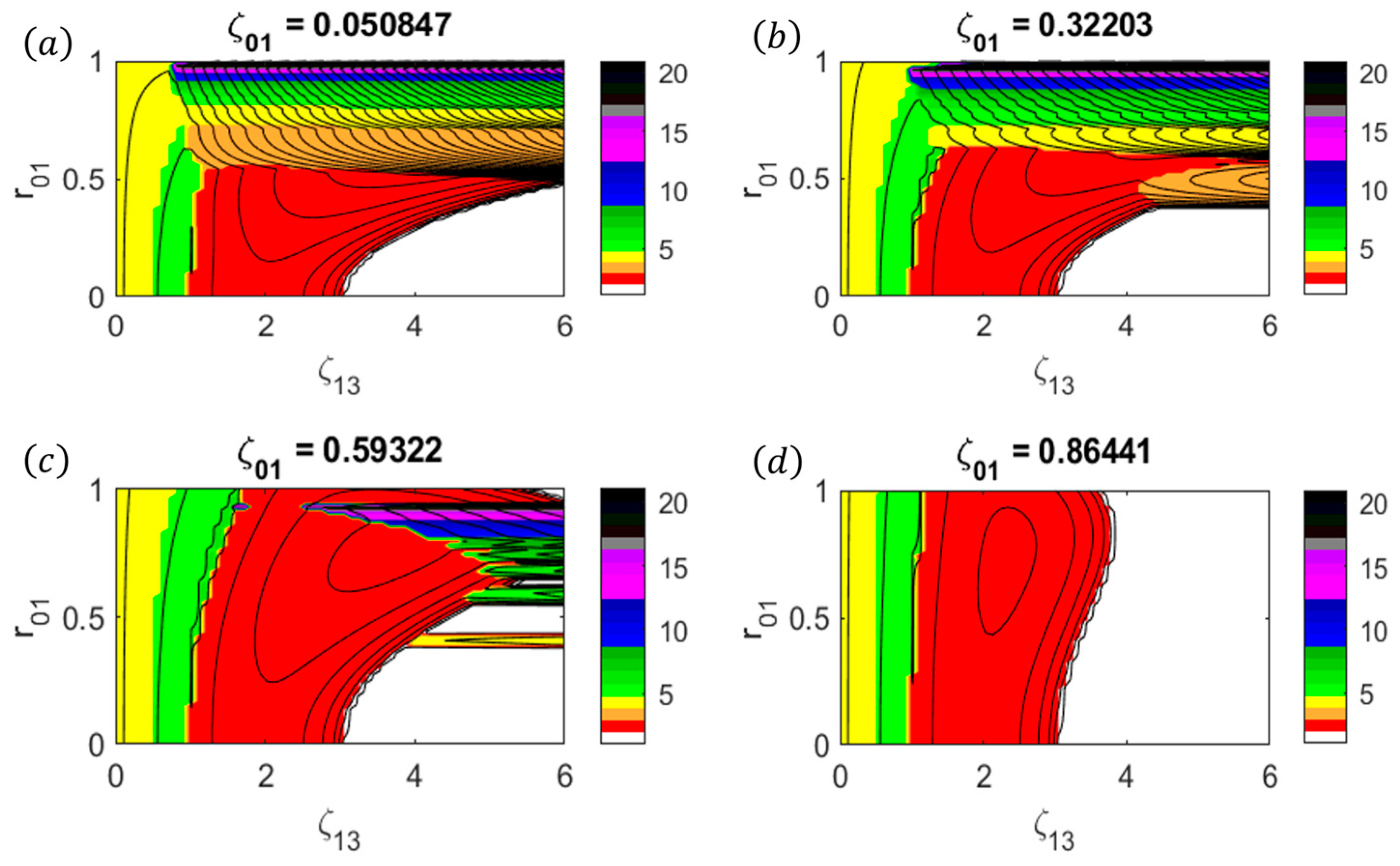
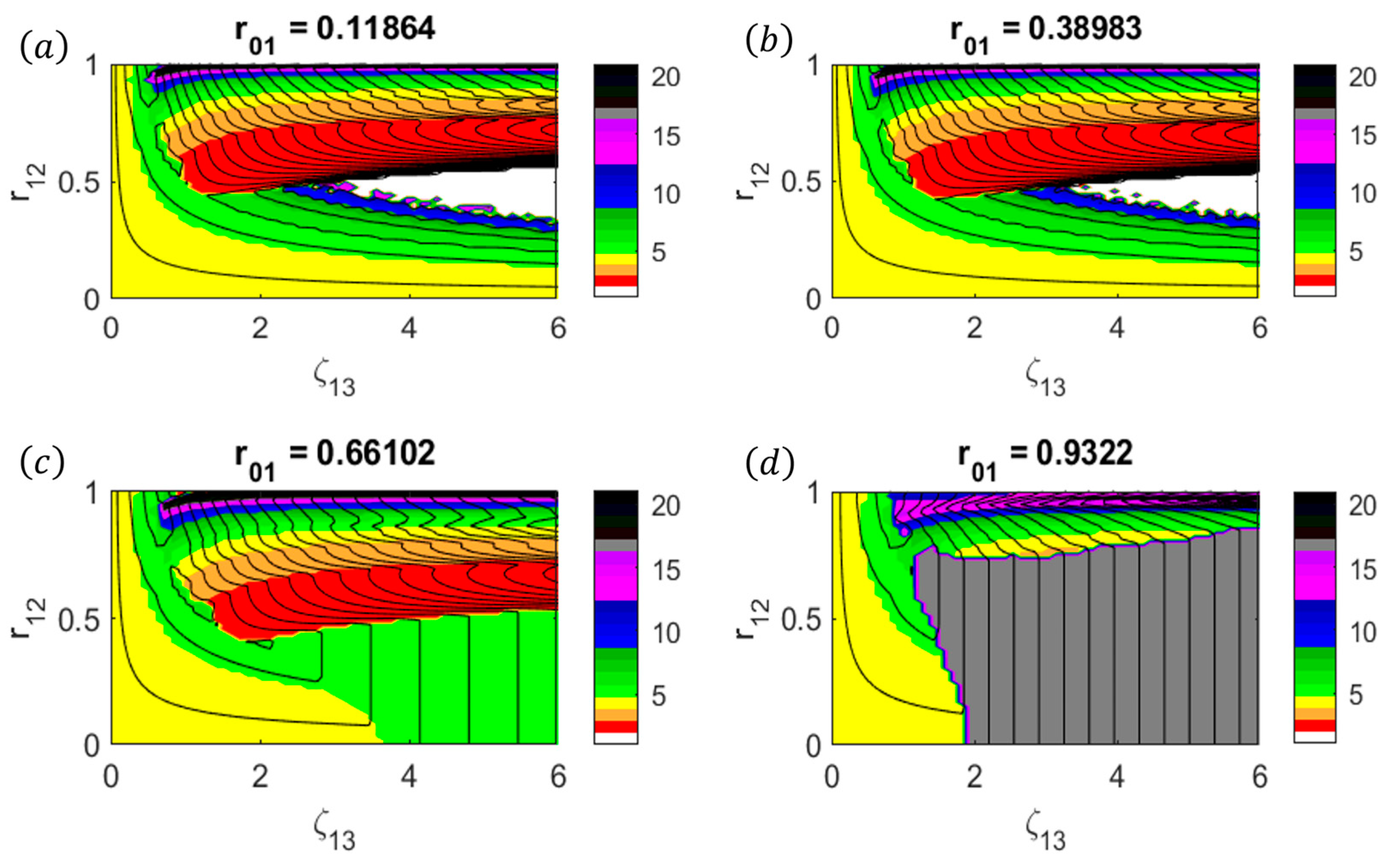
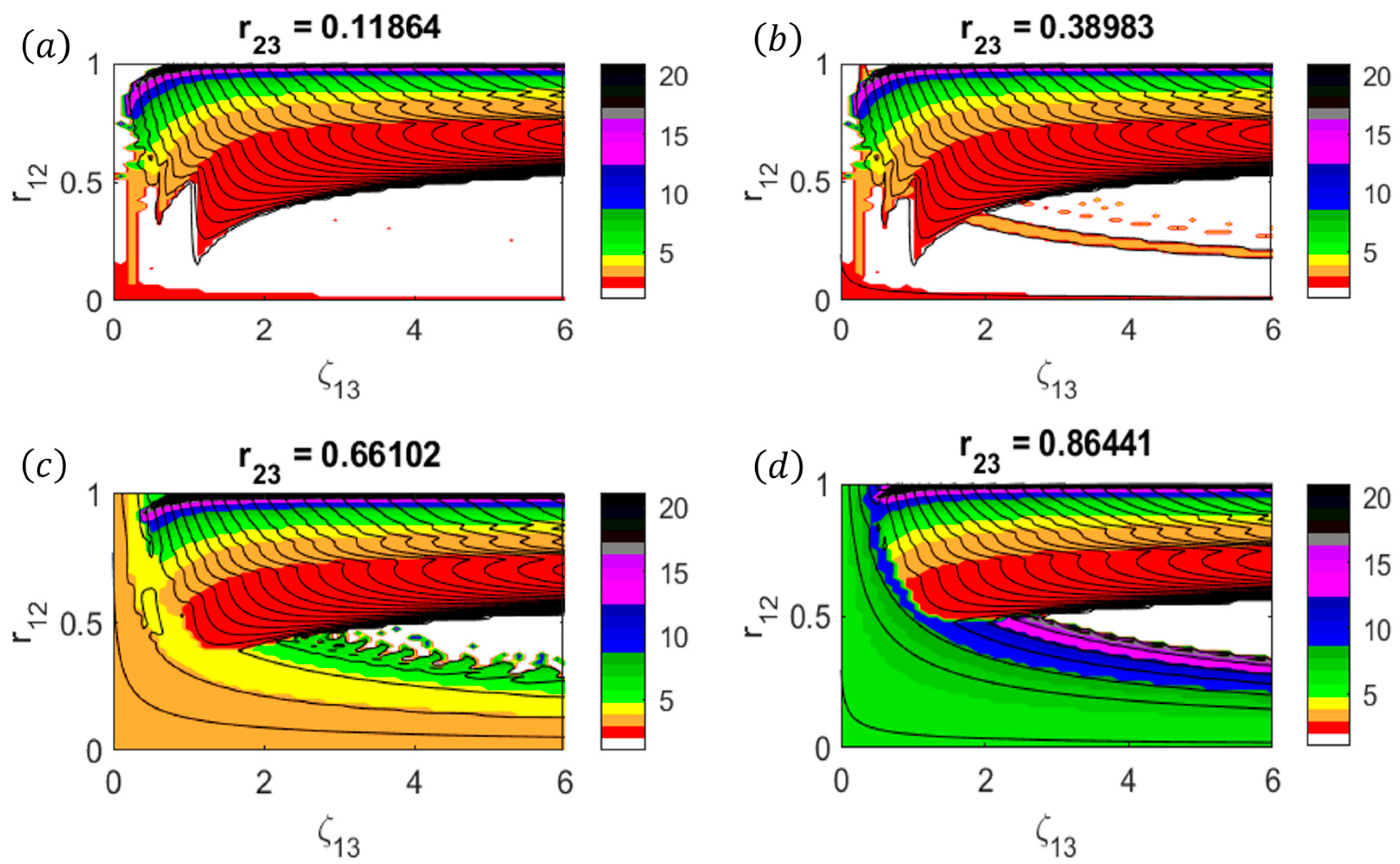
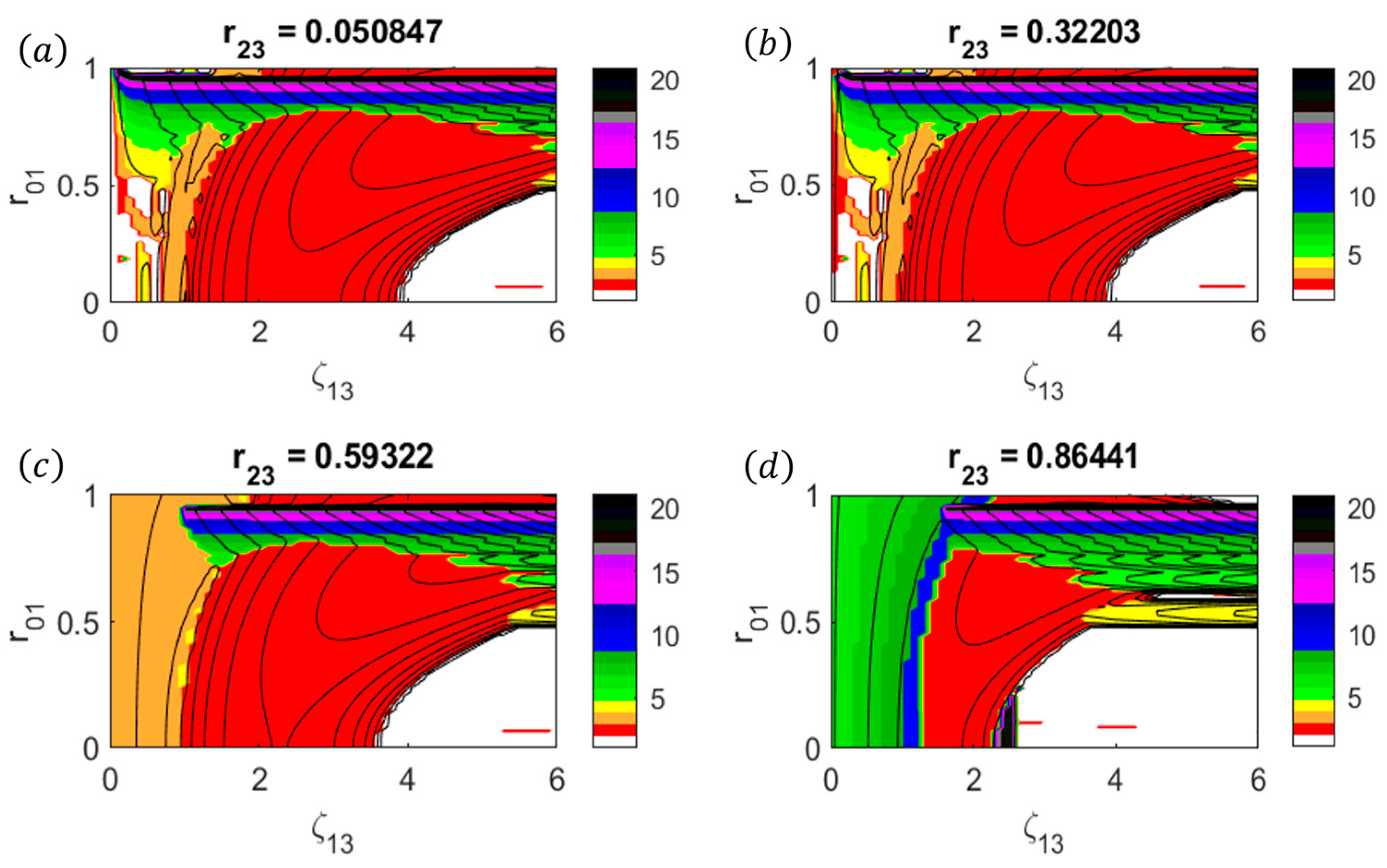
- The parameter range in which the vortex is stable is , , , and . Physically, this corresponds to a 2D annular vortex with a thick primary eyewall, a large moat, and a weak secondary eyewall.
- The parameter range in which Type-1 BI is excited across the secondary eyewall is , , , and . Physically, this corresponds to a 2D annular vortex with a thick primary eyewall, a large moat, and a strong, thin secondary eyewall. As shown in Figure 2 and Figure 5, Type-1 BI can be excited even for relatively weak secondary eyewalls if the secondary eyewall is sufficiently thin (i.e., ). In general, as increases, Type-1 BI is excited with increasingly large azimuthal wavenumbers. In contrast, Type-1 BI can be removed by increasing the circulation associated with the central vortex via and (as shown in Figure 3 and Figure 4).
- The parameter range in which Type-2 BI is excited across the moat of the vortex is , , and . Physically, this corresponds to a 2D annular vortex with a small moat and a relatively weak secondary eyewall. As shown in Figure 2, Figure 5 and Figure 6 Type-2 BI can be excited even for thin secondary eyewalls and/or thin primary eyewalls if the moat width is sufficiently small (i.e., ).
- The parameter range in which Type-3 BI is excited across the primary eyewall is , , , , and . Physically, this corresponds to a 2D annular vortex with a thin, strong primary eyewall, a large moat, and a weak secondary eyewall. As shown in Figure 5, Type-1 BI can be excited for thin secondary eyewalls only if the primary eyewall is sufficiently thin (i.e., ) and if the primary eyewall is sufficiently strong (i.e., ). In contrast, Type-1 BI can be removed by increasing the hollowness parameter, as shown in Figure 4. The transition between Type-1 and Type-3 BI is strongly governed by the eyewall vorticity ratio . Type-1 BI plays an important role in the dynamics for , whereas Type-3 BI plays an important role in the dynamics for .
3. Results
3.1. Numerical Model
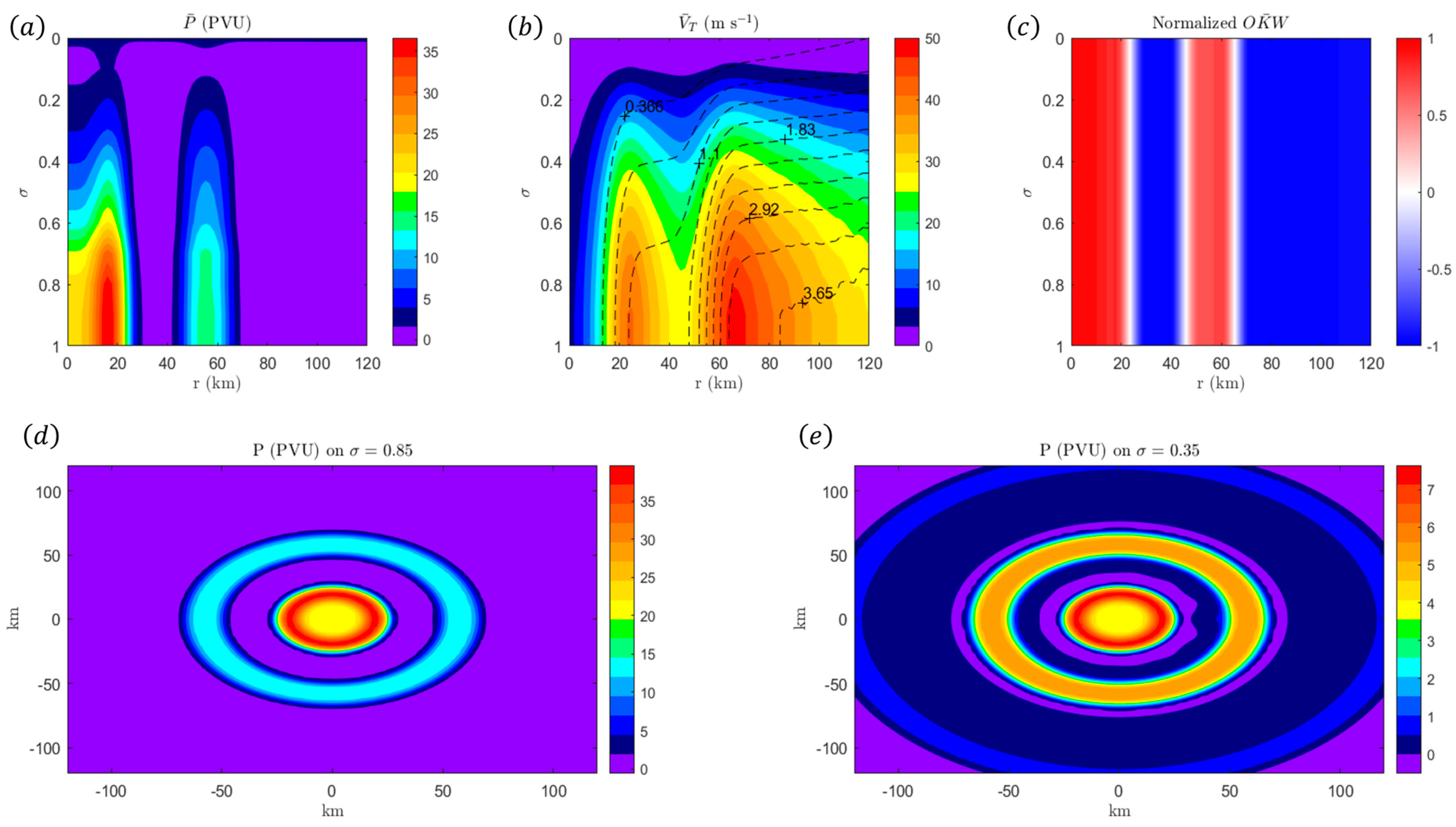
3.2. Control Experiment
4. Nonlinear Evolution of 3D Annular Vortices
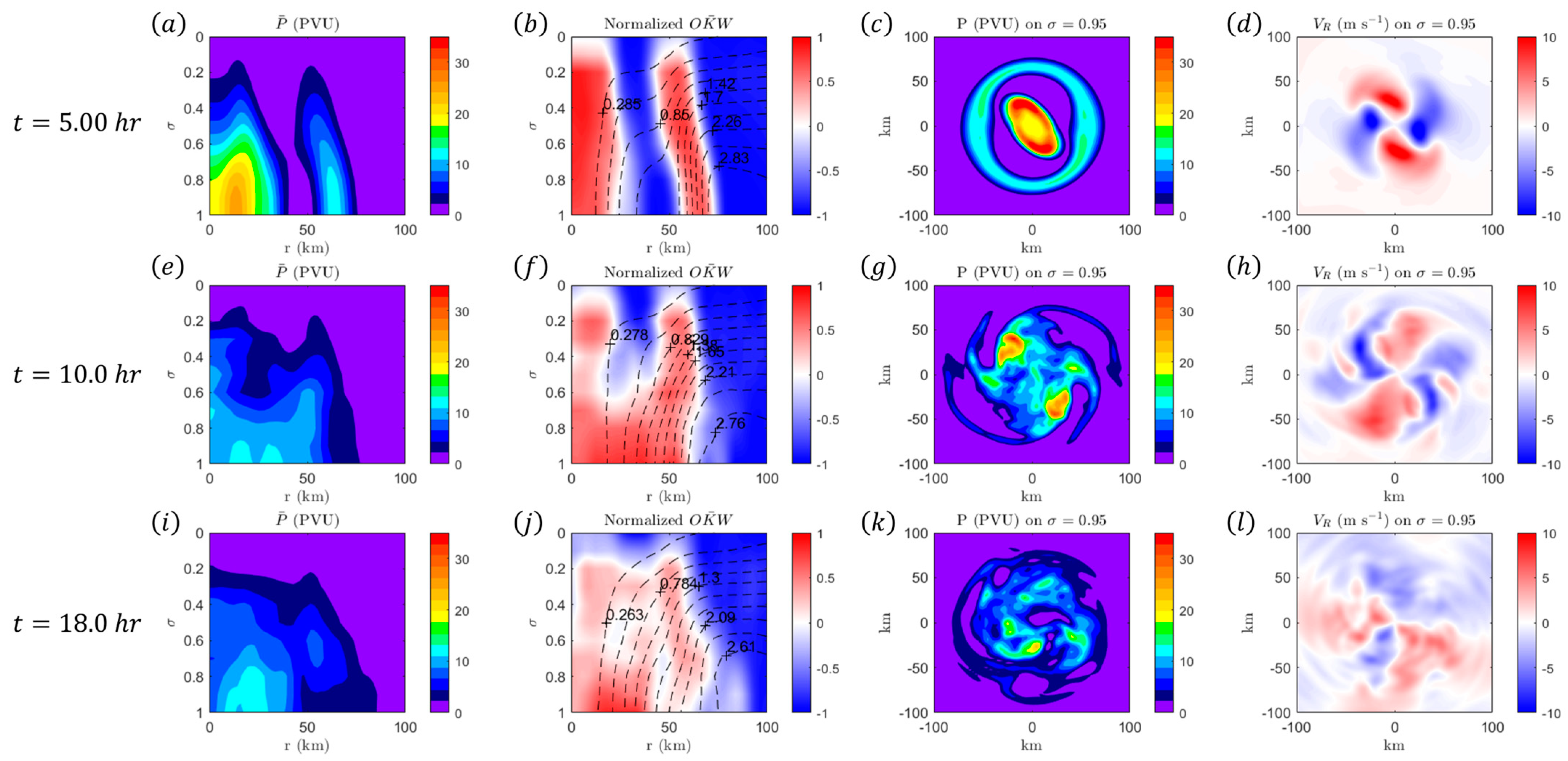
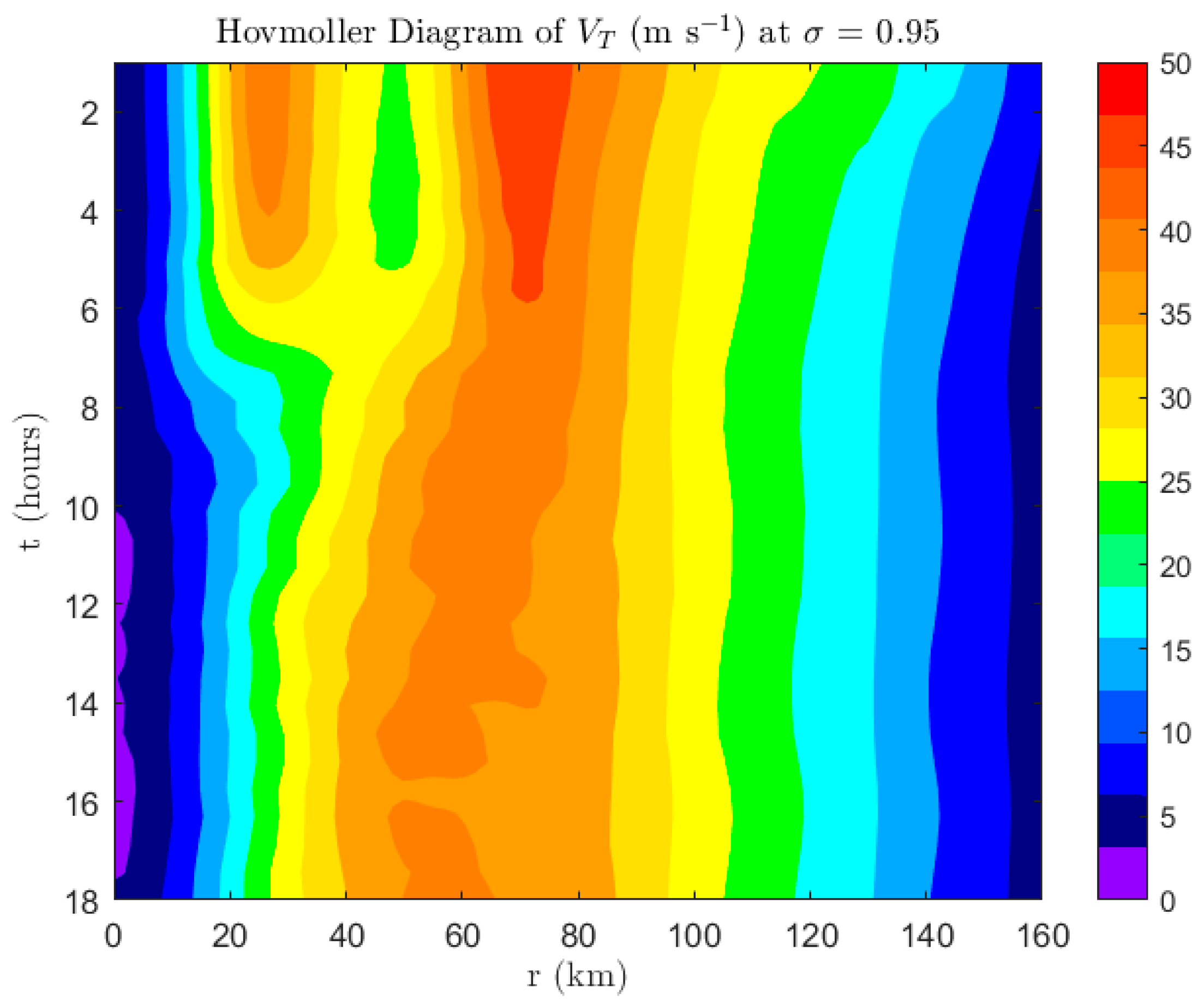
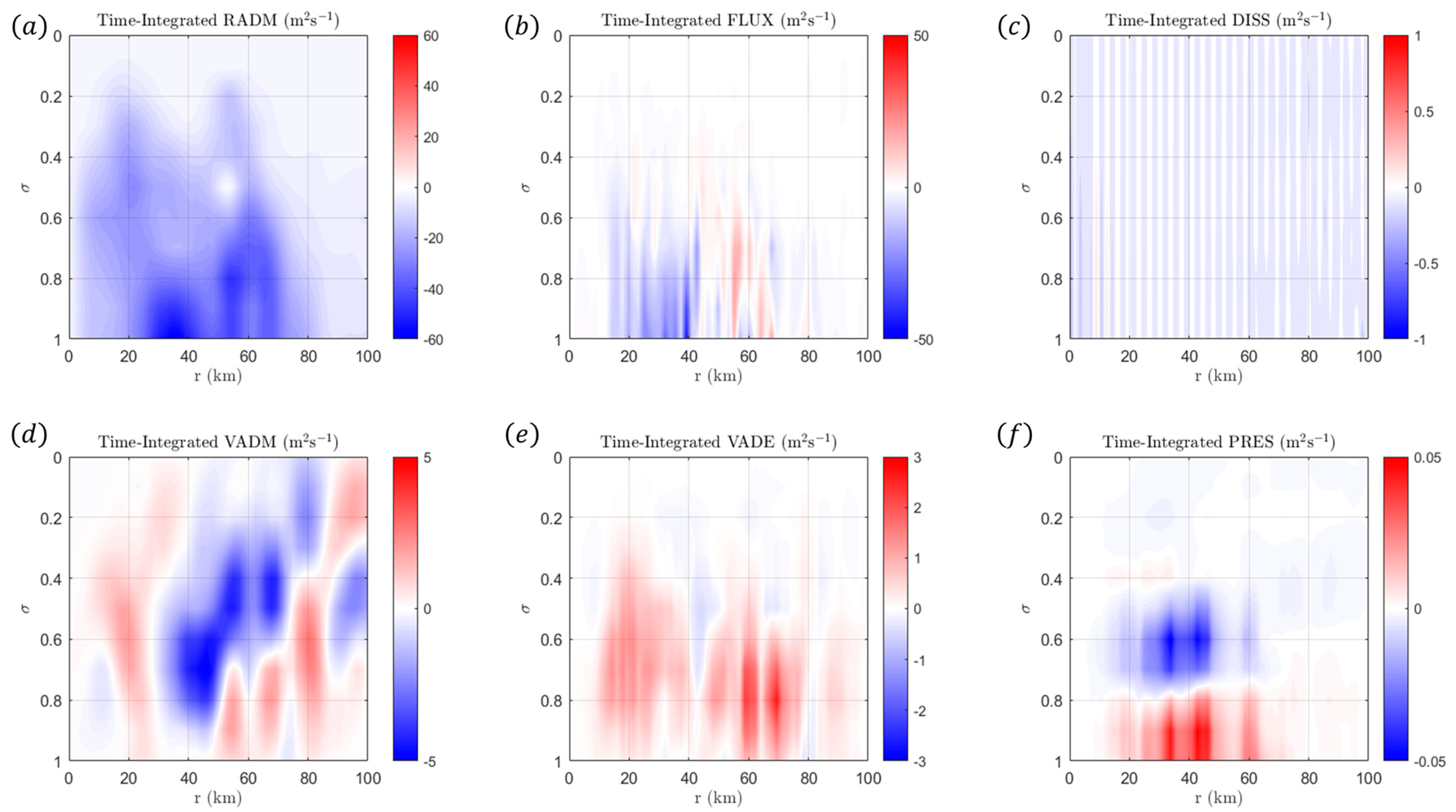
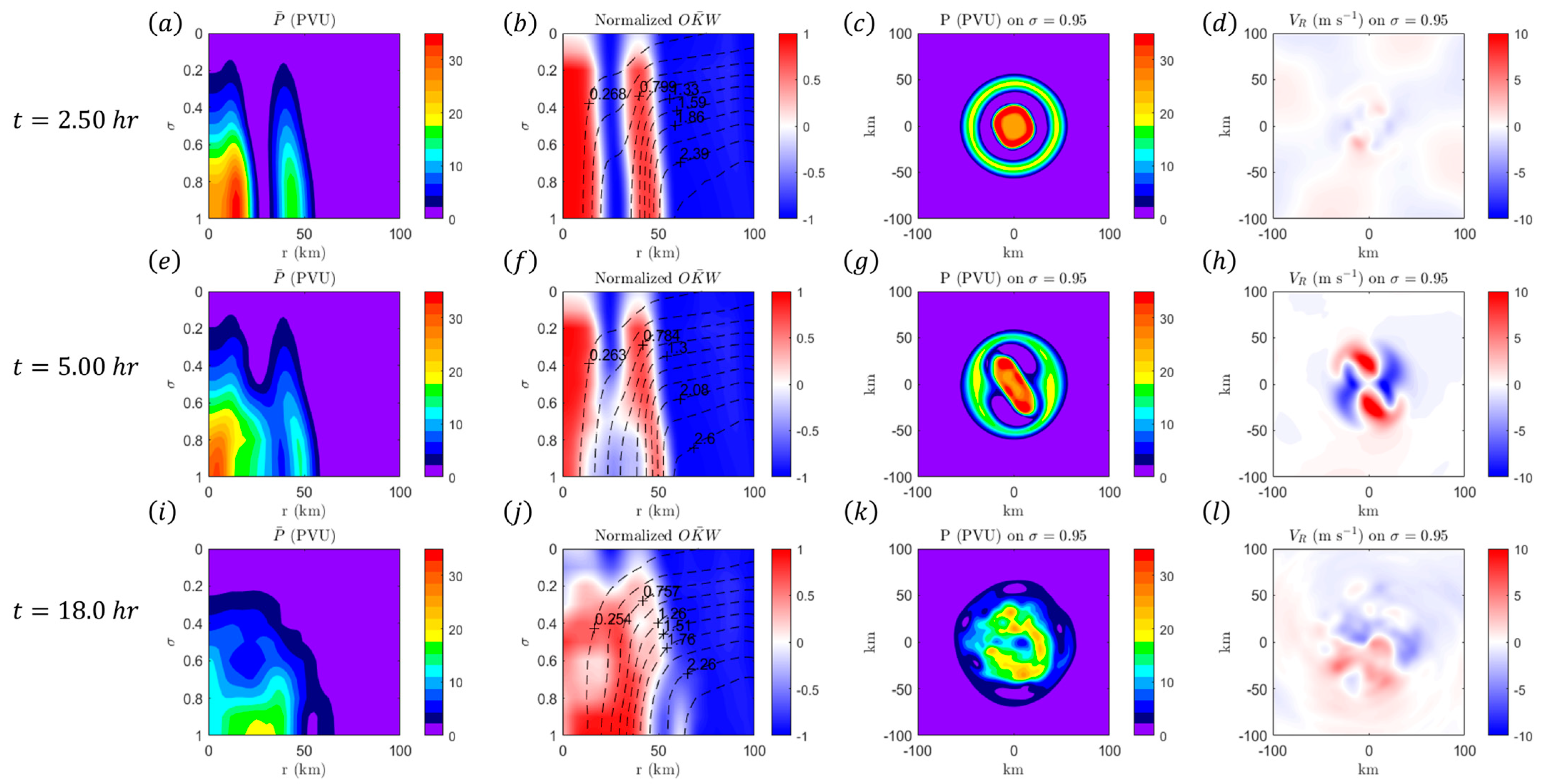
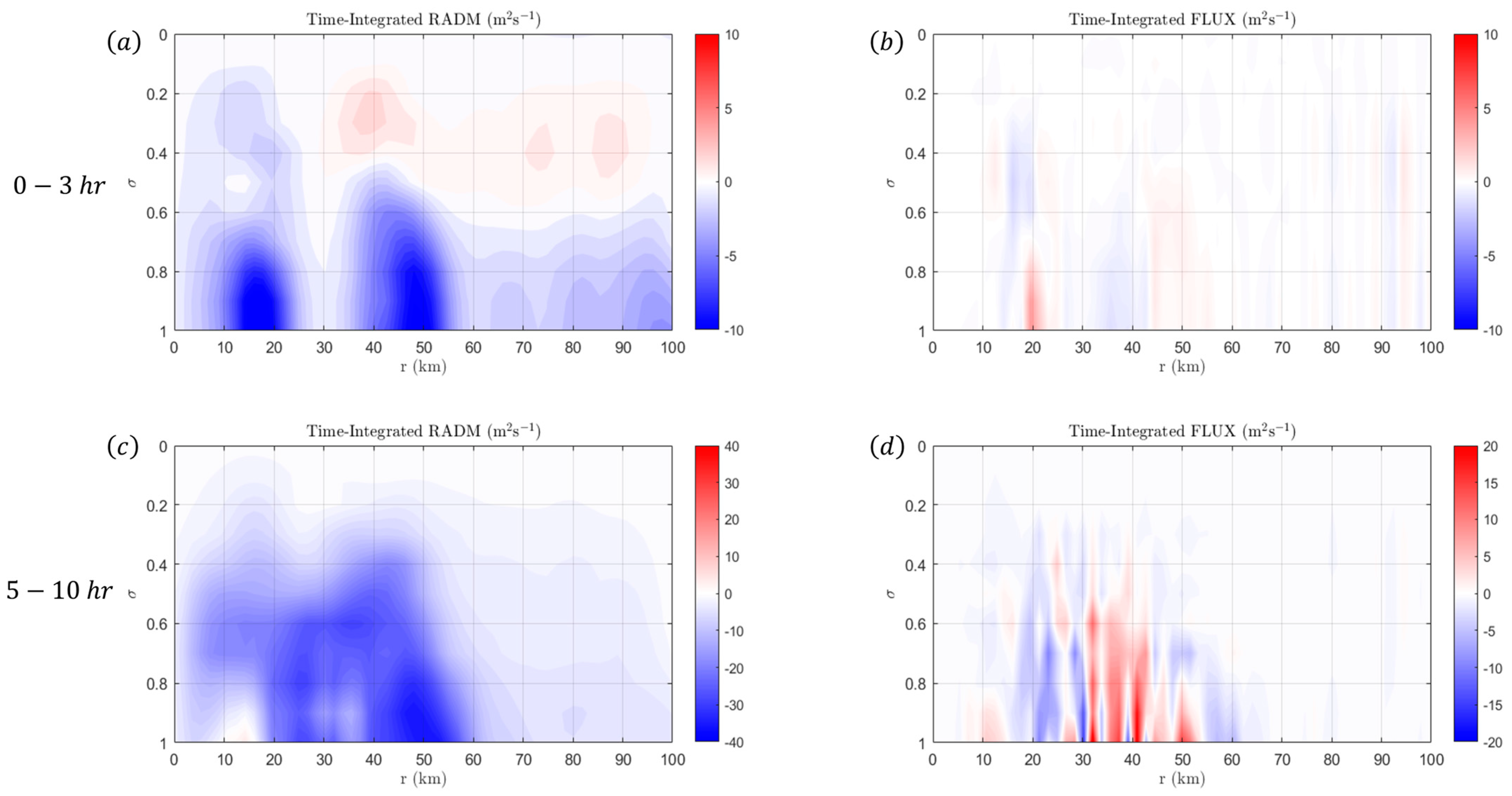
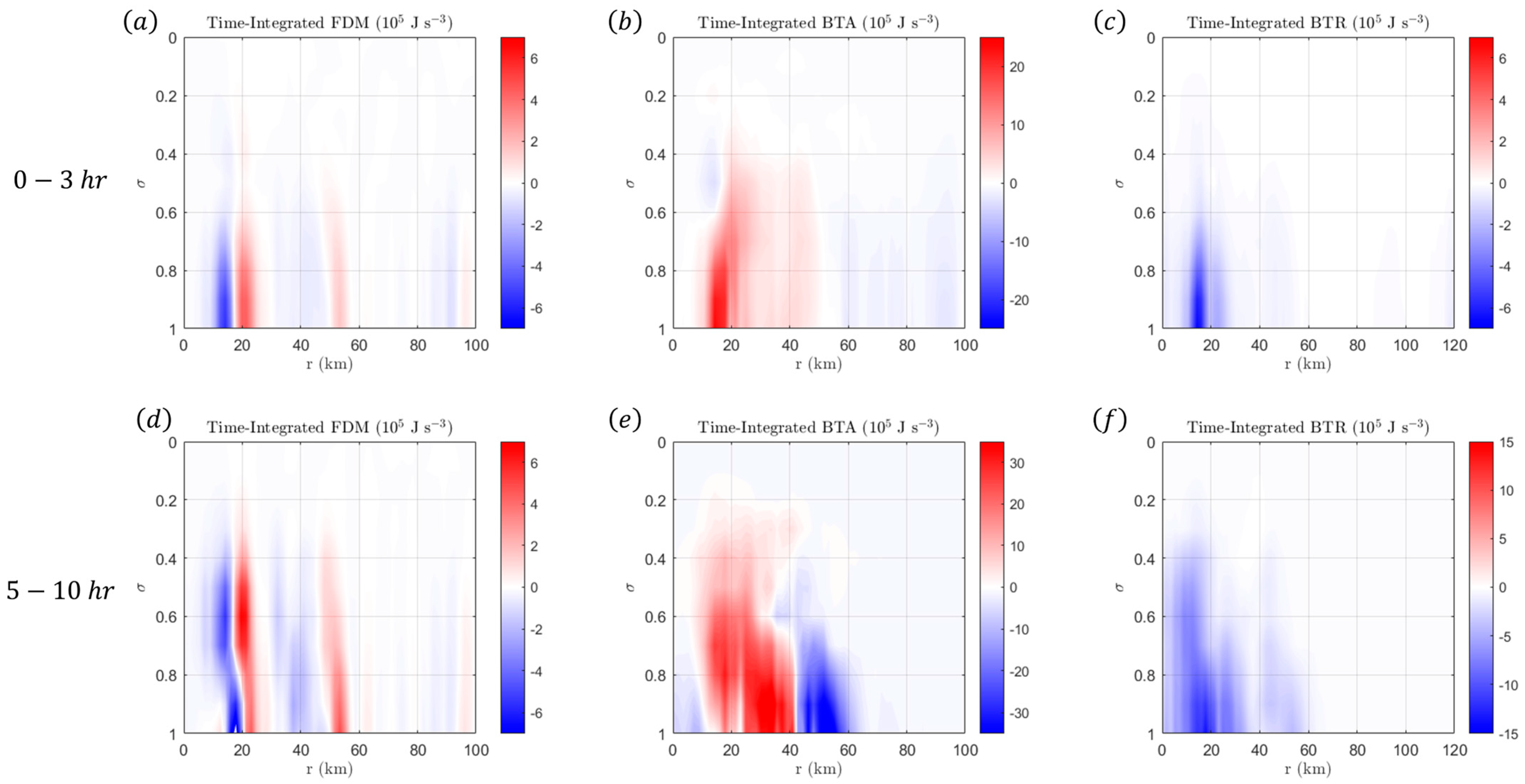
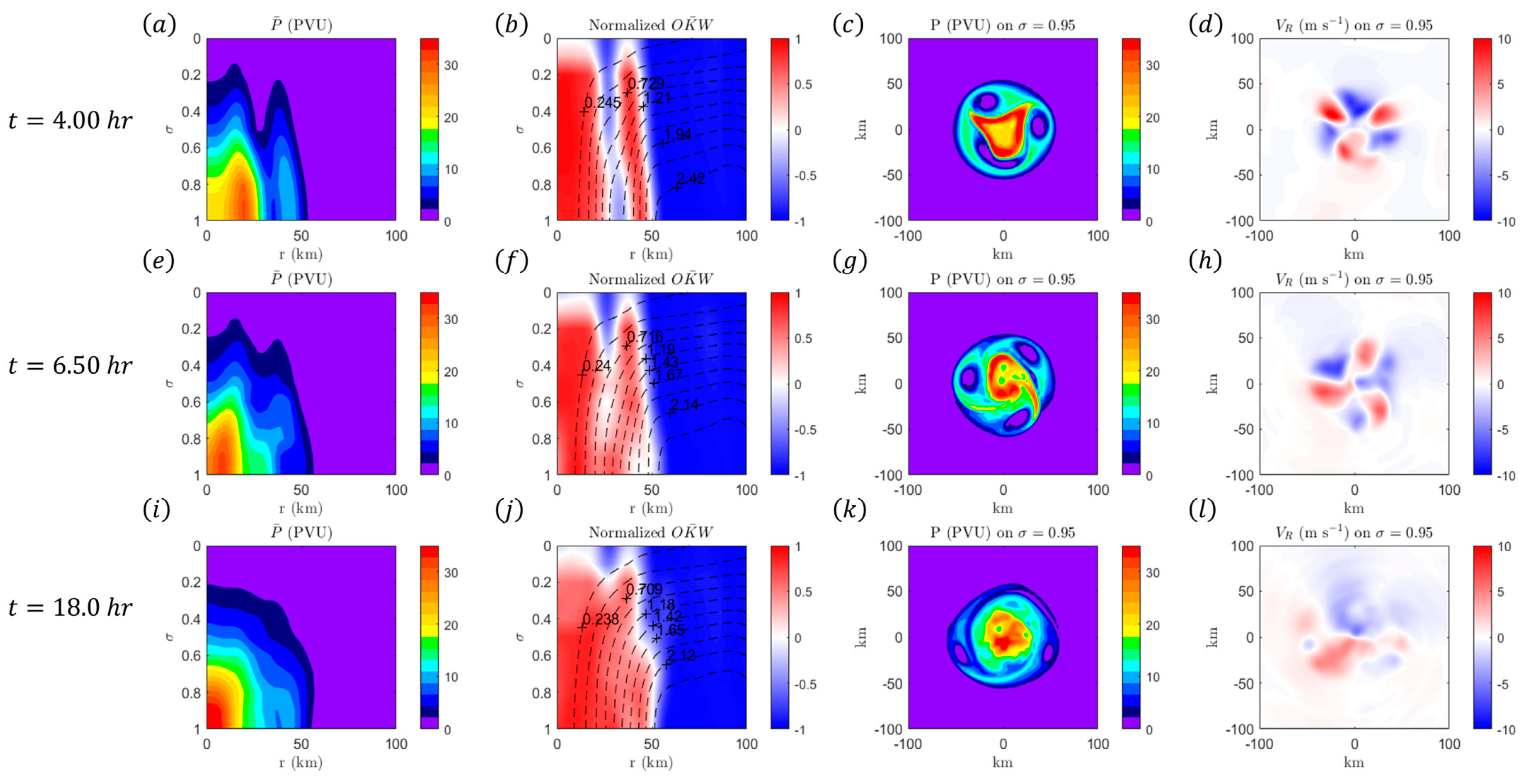
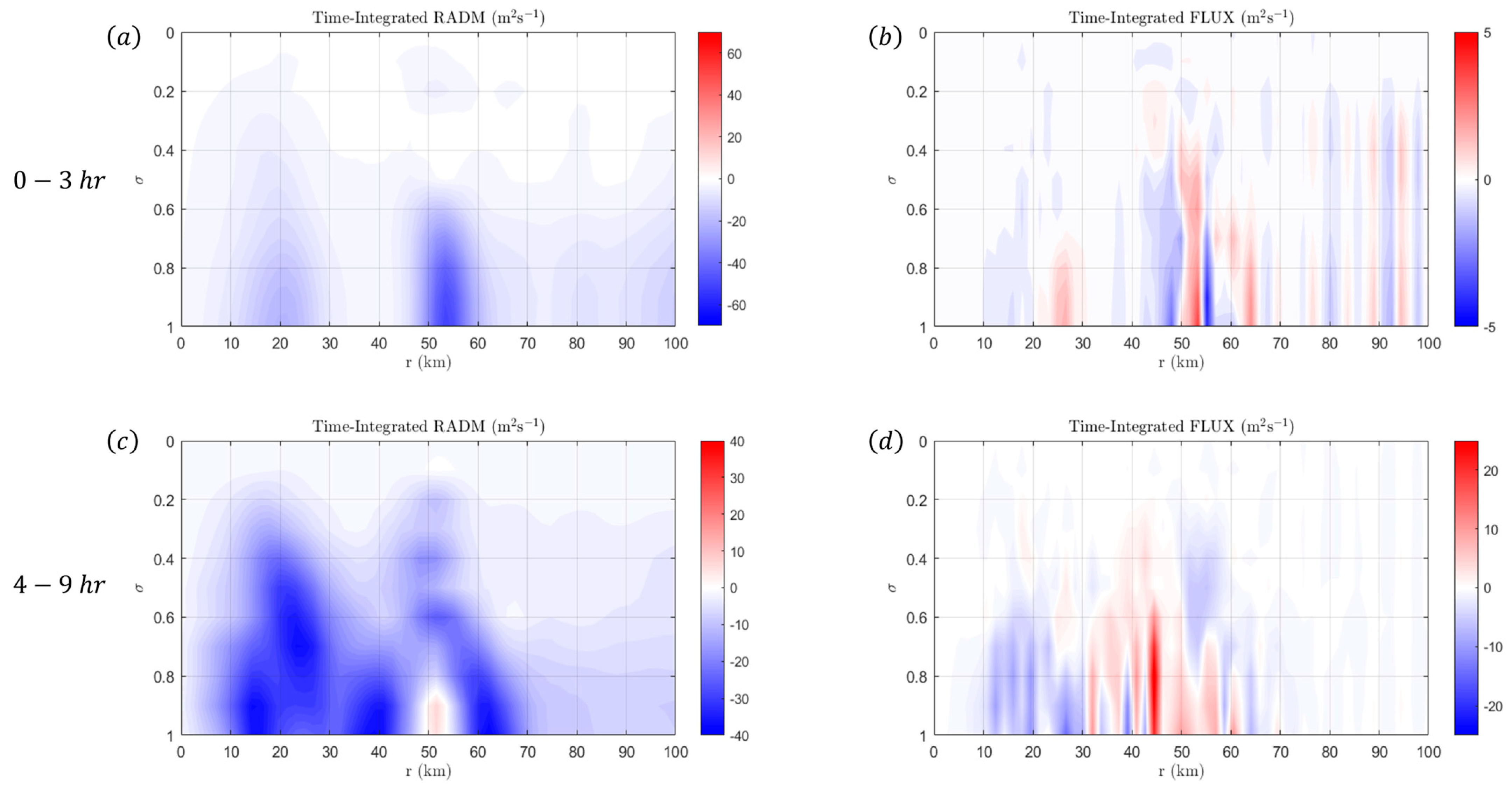
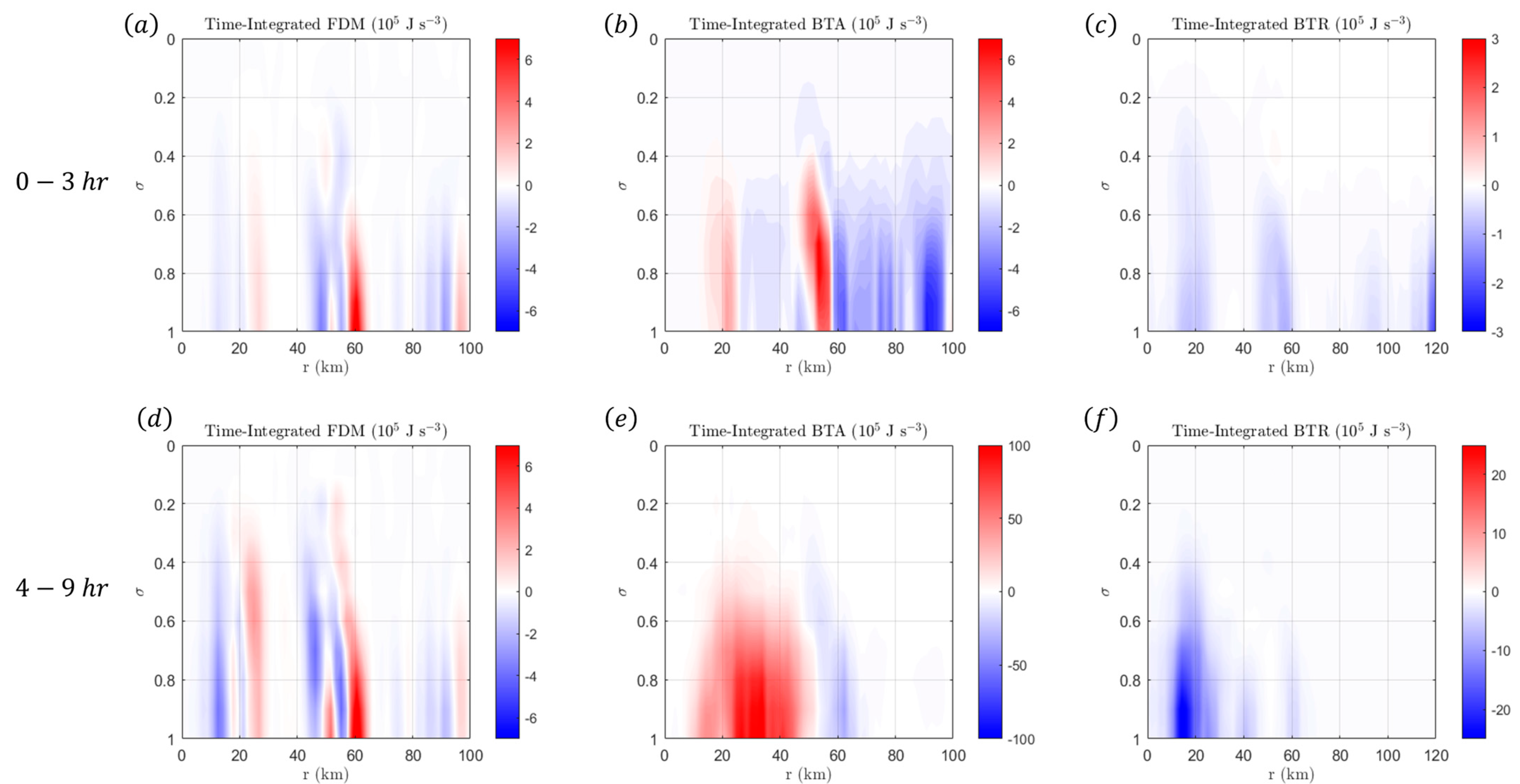
4.1. Results from Vortex I
4.2. Results from Vortex II
4.3. Results from Vortex III
5. Discussions and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Matrix
References
- Willoughby, H.E.; Clos, J.A.; Shoreibah, M.G. Concentric eyewalls, secondary wind maxima, and the evolution of the hurricane vortex. J. Atmos. Sci. 1982, 39, 395–411. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Kallenbach, R.J. A theory for vortex Rossby waves and its application to spiral bands and intensity changes in hurricanes. Q. J. R. Meteorol. Soc. 1997, 123, 435–465. [Google Scholar] [CrossRef]
- Schubert, W.H.; Montgomery, M.T.; Taft, R.K.; Guinn, T.A.; Fulton, S.R.; Kossin, J.P.; Edwards, J.P. Polygonal eyewalls, asymmetric eye contraction, and potential vorticity mixing in hurricanes. J. Atmos. Sci. 1999, 56, 1197–1223. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Montgomery, M.T.; Davis, C.A. The role of “vortical” hot towers in the formation of Tropical Cyclone Diana (1984). J. Atmos. Sci. 2004, 61, 1209–1232. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Nicholls, M.E.; Cram, T.A.; Saunders, A.B. A vortical hot tower route to tropical cyclogenesis. J. Atmos. Sci. 2006, 63, 355–386. [Google Scholar] [CrossRef]
- Hausmann, S.A.; Ooyama, K.V.; Schubert, W.H. Potential vorticity structure of simulated hurricanes. J. Atmos. Sci. 2006, 63, 87–108. [Google Scholar] [CrossRef]
- Martinez, J.; Bell, M.M.; Rogers, R.F.; Doyle, J.D. Axisymmetric potential vorticity evolution of Hurricane Patricia (2015). J. Atmos. Sci. 2019, 76, 2043–2063. [Google Scholar] [CrossRef]
- Eliassen, A. The Charney-Stern theorem on barotropic-baroclinic instability. Pure Appl. Geophys. 1983, 121, 563–572. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Shapiro, L.J. Generalized Charney-Stern and Fjortoft theorems for rapidly rotating vortices. J. Atmos. Sci. 1995, 52, 1829–1833. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Schubert, W.H.; Taft, R.K.; Wang, H.; Kossin, J.P. Lifecycles of hurricane-like vorticity rings. J. Atmos. Sci. 2009, 66, 705–722. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Schubert, W.H. Adiabatic rearrangement of hollow PV towers. J. Adv. Model. Earth Syst. 2010, 2, 1–19. [Google Scholar] [CrossRef]
- Hendricks, E.A.; Schubert, W.H.; Chen, Y.-H.; Kuo, H.-C. Hurricane eyewall evolution in a forced shallow-water model. J. Atmos. Sci. 2014, 71, 1623–1643. [Google Scholar] [CrossRef]
- Kossin, J.P.; Schubert, W.H. Mesovortices, polygonal flow patterns, and rapid pressure falls in hurricane-like vortices. J. Atmos. Sci. 2011, 58, 2196–2209. [Google Scholar] [CrossRef]
- Kwon, Y.; Frank, W.M. Dynamic instabilities of simulated hurricane-like vortices and their impacts on the core structure of hurricanes. Part I: Dry experiments. J. Atmos. Sci. 2005, 62, 3955–3973. [Google Scholar] [CrossRef]
- Menelaou, K.; Yau, M.K.; Martinez, Y. Impact of asymmetric dynamical processes on the structure and intensity change of two-dimensional hurricane-like annular vortices. J. Atmos. Sci. 2013, 70, 559–582. [Google Scholar] [CrossRef]
- Menelaou, K.; Yau, M.K.; Martinez, Y. On the origin and impact of a polygonal eyewall in the rapid intensification of Hurricane Wilma. J. Atmos. Sci. 2013, 70, 3839–3858. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T. The algebraic growth of wavenumber one disturbances in hurricane-like vortices. J. Atmos. Sci. 2000, 57, 3514–3538. [Google Scholar] [CrossRef]
- Nolan, D.S.; Montgomery, M.T. Nonhydrostatic, three-dimensional perturbations to balanced, hurricane-like vortices. Part I: Linearized formulation, stability, and evolution. J. Atmos. Sci. 2002, 59, 2989–3020. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Schubert, W.H.; McNoldy, B.D.; Kossin, J.P. Rapid filamentation zones in intense tropical cyclones. J. Atmos. Sci. 2006, 66, 133–147. [Google Scholar] [CrossRef]
- Rozoff, C.M.; Kossin, J.P.; Schubert, W.H.; Mulero, P.J. Internal control of hurricane intensity: The dual nature of potential vorticity mixing. J. Atmos. Sci. 2009, 66, 133–147. [Google Scholar] [CrossRef]
- Terway, W.D.; Montgomery, M.T. Wavenumber-2 and wavenumber-m vortex Rossby wave instabilities in a generalized three-region model. J. Atmos. Sci. 2002, 59, 2421–2427. [Google Scholar] [CrossRef]
- Williams, G.J. The generation and maintenance of hollow PV towers in a forced primitive equation model. Meteorol. Atmos. Phys. 2019, 131, 1635–1659. [Google Scholar] [CrossRef]
- Chen, Y.; Yau, M.K. Spiral bands in a simulated hurricane. Part I: Vortex Rossby wave verification. J. Atmos. Sci. 2001, 58, 2128–2145. [Google Scholar] [CrossRef]
- Kwon, Y.; Frank, W.M. Dynamical instabilities of simulated hurricane-like vortices and their impacts on the core structure of hurricanes. Part II: Moist experiments. J. Atmos. Sci. 2008, 65, 106–122. [Google Scholar] [CrossRef]
- Nguyen, C.M.; Reeder, M.J.; Davidson, N.E.; Smith, R.K.; Montgomery, M.T. Inner-core vacillation cycles during the intensification of Hurricane Katrina. Q. J. R. Meteorol. Soc. 2011, 137, 829–844. [Google Scholar] [CrossRef]
- Wu, C.-C.; Cheng, H.-J.; Wang, Y.; Chou, K.-H. A numerical investigation of the eyewall evolution of a landfalling typhoon. Mon. Weather Rev. 2009, 137, 21–40. [Google Scholar] [CrossRef]
- Wu, C.-C.; Wu, S.-N.; Wei, H.-H.; Abarca, S.F. The role of convective heating in tropical cyclone eyewall ring evolution. J. Atmos. Sci. 2016, 73, 319–330. [Google Scholar] [CrossRef]
- Yang, B.; Yang, Y.; Wang, B. The effect of internally generated inner-core asymmetries on tropical cyclone potential intensity. J. Atmos. Sci. 2007, 64, 1165–1188. [Google Scholar] [CrossRef]
- Yau, M.K.; Liu, Y.; Zhang, D.-L.; Chen, Y. A multiscale numerical study of Hurricane Andrew (1992). Part VI: Small-scale inner-core structures and wind streaks. Mon. Weather Rev. 2004, 132, 1410–1433. [Google Scholar] [CrossRef]
- Hendricks, E.A.; McNoldy, B.D.; Schubert, W.H. Observed inner-core structural variability in Hurricane Dolly (2008). Mon. Weather Rev. 2012, 140, 4066–4077. [Google Scholar] [CrossRef]
- Kossin, J.P.; Eastin, M.D. Two distinct regimes in the kinematic and thermodynamic structure of the hurricane eye and eyewall. J. Atmos. Sci. 2001, 58, 1079–1090. [Google Scholar] [CrossRef]
- Kossin, J.P.; McNoldy, B.D.; Schubert, W.H. Vortical swirls in hurricane eye clouds. Mon. Weather Rev. 2002, 130, 3144–3149. [Google Scholar] [CrossRef]
- Kossin, J.P.; Schubert, W.H. Mesovortices in Hurricane Isabel. Bull. Am. Meteorol. Soc. 2004, 85, 151–153. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Vladimirov, V.A.; Denissenko, P.V. An experimental study on hurricane mesovortices. J. Fluid Mech. 2002, 471, 1–32. [Google Scholar] [CrossRef]
- Reasor, P.D.; Montgomery, M.T.; Marks, F.D.; Gamache, J.F. Low-wavenumber structure and evolution of the hurricane inner core observed by airborne dual-Doppler radar. Mon. Weather Rev. 2000, 128, 1653–1680. [Google Scholar] [CrossRef]
- Kossin, J.P.; Sitkowski, M. An objective model for identifying secondary eyewall formation in hurricane. Mon. Weather Rev. 2009, 137, 876–892. [Google Scholar] [CrossRef]
- Samsury, C.E.; Zipser, E.J. Secondary wind maxima in hurricanes: Airflow and relationship to rainbands. Mon. Weather Rev. 1995, 123, 3502–3517. [Google Scholar] [CrossRef]
- Houze, R.A.; Chen, S.S.; Smull, B.F.; Lee, W.-C.; Bell, M.M. Hurricane intensity and eyewall replacement. Science 2007, 315, 1235–1239. [Google Scholar] [CrossRef]
- Sitkowski, M.; Kossin, J.P.; Rozoff, C.M. Intensity and structure changes during hurricane eyewall replacement cycles. Mon. Weather Rev. 2011, 139, 3829–3847. [Google Scholar] [CrossRef]
- Kossin, J.P.; Schubert, W.H.; Montgomery, M.T. Unstable interactions between a hurricane’s primary eyewall and a secondary ring of enhanced vorticity. J. Atmos. Sci. 2000, 57, 3893–3917. [Google Scholar] [CrossRef]
- Lai, T.-K.; Menelaou, K.; Yau, M.K. Barotropic instability across the moat and primary eyewall dissipation: A numerical study of Hurricane Wilma (2005). J. Atmos. Sci. 2019, 76, 989–1013. [Google Scholar] [CrossRef]
- Rostami, M.; Zeitlin, V. Evolution of double-eyewall hurricanes and emergence of complex tripolar end states in moist-convective rotating shallow water model. Phys. Fluids 2022, 34, 3–16. [Google Scholar] [CrossRef]
- Schecter, D.A.; Montgomery, M.T. On the symmetrization rate of an intense geophysical vortex. Dyn. Atmos. Ocean. 2003, 37, 55–88. [Google Scholar] [CrossRef]
- Hendricks, E.A. Tropical Cyclone Evolution via Internal Asymmetric Dynamics. Ph.D. Thesis, Colorado State University, Fort Collins, CO, USA, 2008. [Google Scholar]
- Wang, Y. An explicit simulation of tropical cyclones with a triply nested movable mesh primitive equation model: TCM3. Part I: Model description and control experiment. Mon. Weather Rev. 2001, 129, 1370–1394. [Google Scholar] [CrossRef]
- Dunion, J.P.; Marron, C.S. A reexamination of the Jordan mean tropical sounding based on awareness of the Saharan air layer: Results from 2002. J. Clim. 2008, 21, 5242–5253. [Google Scholar] [CrossRef]
- Wang, Y. Vortex Rossby waves in a numerically simulated tropical cyclone. Part I: Overall structure, potential vorticity, and kinetic energy budgets. J. Atmos. Sci. 2002, 59, 1213–1238. [Google Scholar] [CrossRef]
- Gao, C.; Zhu, P. Vortex Rossby wave propagation in baroclinic tropical cyclone-like vortices. Geophys. Res. Lett. 2016, 43, 12578–12589. [Google Scholar] [CrossRef]
- Slocum, C.J.; Taft, R.K.; Kossin, J.P.; Schubert, W.H. Barotropic instability during eyewall replacement. Meteorology 2023, 2, 191–221. [Google Scholar] [CrossRef]
- Yang, Y.-T.; Kuo, H.-C.; Hendricks, E.A.; Peng, M.S. Structural and intensity changes of concentric eyewall typhoons in the western North Pacific basin. Mon. Weather Rev. 2013, 141, 2632–2648. [Google Scholar] [CrossRef]
- Lai, T.-K.; Hendricks, E.A.; Yau, M.K.; Menelaou, K. Roles of barotropic instability across the moat in the primary eyewall decay and secondary eyewall intensification: Essential dynamics. J. Atmos. Sci. 2021, 78, 1411–1428. [Google Scholar] [CrossRef]






| Case | Instability Type | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Vortex I | 0.800 | 0.500 | 0.750 | 0.500 | 0.500 | 2.000 | 0.050 | 0.050 | |
| Vortex II | 0.600 | 0.700 | 0.750 | 0.500 | 0.500 | 2.000 | 0.050 | 0.050 | |
| Vortex III | 0.600 | 0.500 | 0.900 | 0.500 | 0.500 | 1.000 | 0.050 | 0.050 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, G.J., Jr. The Adiabatic Evolution of 3D Annular Vortices with a Double-Eyewall Structure. Dynamics 2024, 4, 698-730. https://doi.org/10.3390/dynamics4030035
Williams GJ Jr. The Adiabatic Evolution of 3D Annular Vortices with a Double-Eyewall Structure. Dynamics. 2024; 4(3):698-730. https://doi.org/10.3390/dynamics4030035
Chicago/Turabian StyleWilliams, Gabriel J., Jr. 2024. "The Adiabatic Evolution of 3D Annular Vortices with a Double-Eyewall Structure" Dynamics 4, no. 3: 698-730. https://doi.org/10.3390/dynamics4030035





