Next Article in Journal
Ab Initio Characterization of Magnetoelectric Coupling in Fe/BaTiO3, Fe/SrTiO3, Co/BaTiO3 and Co/SrTiO3 Heterostructures
Previous Article in Journal
Magnetic Field as an Important Tool in Exploring the Strongly Correlated Fermi Systems and Their Particle–Hole and Time-Reversal Asymmetries
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetism
Volume 3
Issue 3
10.3390/magnetism3030016
magnetism-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

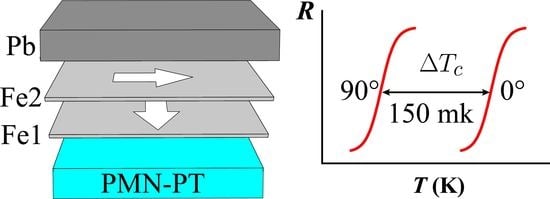
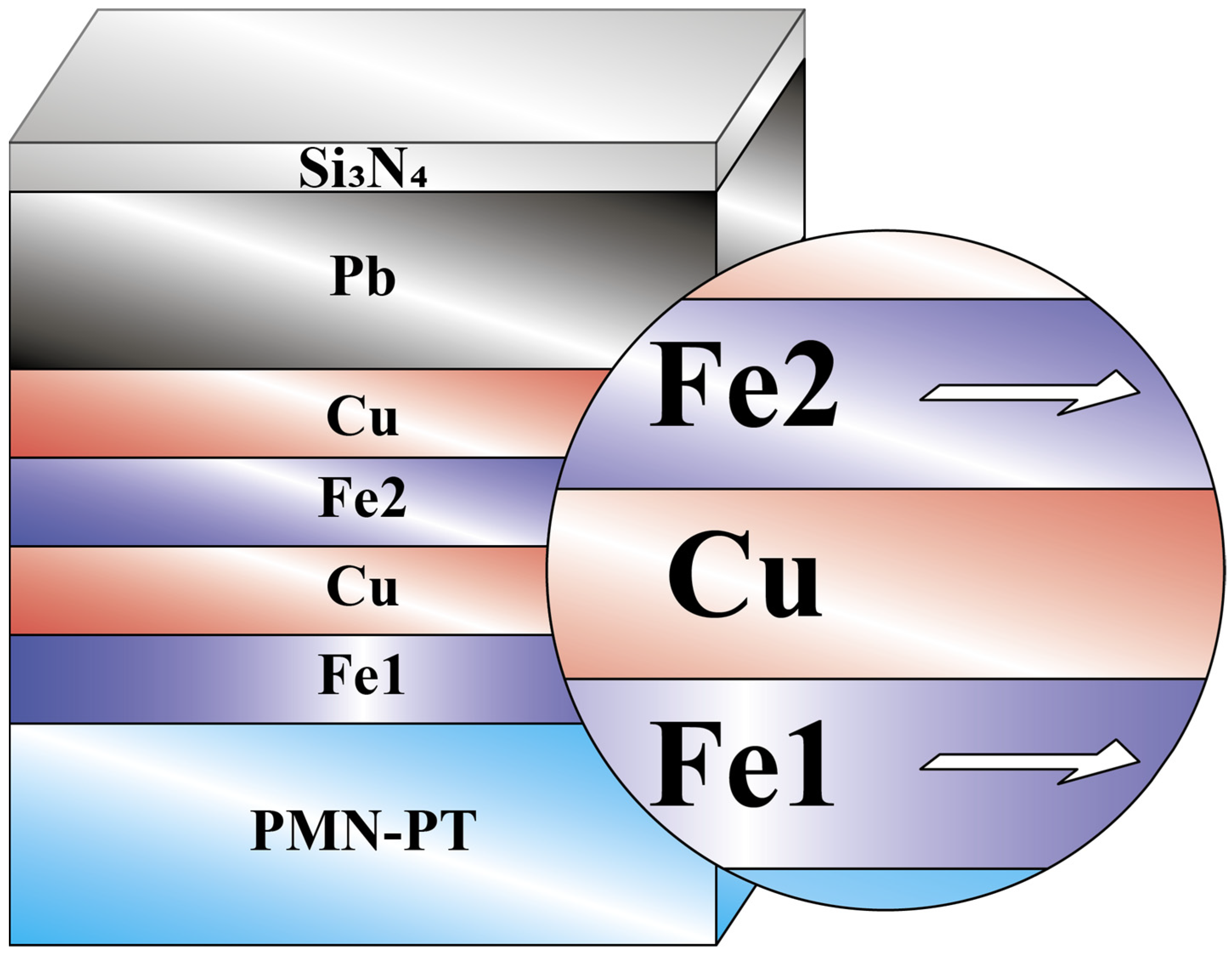
Investigation of the Features of a Superconducting Spin Valve Fe1/Cu/Fe2/Cu/Pb on a Piezoelectric PMN–PT Substrate

by
Andrey Kamashev
1,*,
Nadir Garif’yanov
1,
Aidar Validov
1,
Zvonko Jagličić
2,
Viktor Kabanov
3,
Rinat Mamin
1 and
Ilgiz Garifullin
1
1
Zavoisky Physical-Technical Institute, FRC Kazan Scientific Center of RAS, 420029 Kazan, Russia
2
Institute of Mathematics, Physics and Mechanics and Faculty of Civil and Geodetic Engineering, University of Ljubljana, 1000 Ljubljana, Slovenia
3
Department for Complex Matter, Jozef Stefan Institute, 1000 Ljubljana, Slovenia
*
Author to whom correspondence should be addressed.
Magnetism 2023, 3(3), 204-214; https://doi.org/10.3390/magnetism3030016
Submission received: 27 April 2023 / Revised: 8 June 2023 / Accepted: 4 July 2023 / Published: 13 July 2023
Browse Figures
Versions Notes

Abstract

:
The properties of a superconducting spin valve Fe1/Cu/Fe2/Cu/Pb on a piezoelectric PMN–PT substrate ([Pb(Mg1/3Nb2/3)O3]0.7–[PbTiO3]0.3) in electric and magnetic fields have been studied. The magnitude of the shift of the superconducting transition temperature in the magnetic field H = 1 kOe equal to 150 mK was detected, while the full superconducting spin valve effect was demonstrated. Abnormal behavior of the superconducting transition temperature was observed, which manifests itself in the maximum values of the superconducting transition temperature with the orthogonal orientation of the magnetization vectors of ferromagnetic layers. This may indirectly indicate the formation of the easy axis of the magnetization vector of the Fe1-layer adjacent to the piezoelectric substrate PMN–PT. It was found that with an increase in the magnitude of the applied electric field to the PMN–PT substrate, the shift in the superconducting transition temperature of the Fe1/Cu/Fe2/Cu/Pb heterostructure increases. The maximum shift was 10 mK in an electric field of 1 kV/cm. Thus, it has been shown for the first time that a piezoelectric superconducting spin valve can function.

Graphical Abstract

1. Introduction

Studies of the mutual influence of superconductivity and ferromagnetism have been carried out since the middle of the last century. These two phenomena are opposite to each other. Antagonism occurs in the fact that ferromagnetism assumes a parallel (P) orientation of the spins, and superconductivity is antiparallel (AP) since the spins of the electrons of the Cooper pair are oppositely directed. Initially, the interactions of superconductivity and ferromagnetism were studied in intermetallic compounds and alloys (see, e.g., [1,2,3]). To date, the greatest interest is associated with structures consisting of ferromagnetic and superconducting layers because in them, there is a possibility of spatial separation between superconductivity and ferromagnetism. The study of such structures has become possible due to technological progress in the preparation of high-quality thin-film layered metal multilayers (see, e.g., [4,5,6,7,8,9]).
The effect that is observed in thin-film layered metal structures based on superconductors (S) and ferromagnets (F) is called the superconductor/ferromagnet (S/F) proximity effect. Many features of this effect are described in detail in [7,9,10,11]. Two theoretical models of a superconducting spin valve (SSV) based on the S/F proximity effect were proposed at the end of 1990s by Oh et al. [12] (the F1/F2/S model) and by Tagirov [13] and Buzdin et al. [14] (the F1/S/F2 model). Both theories treat a trilayer SSV composed of one superconducting and two ferromagnetic layers where the superconducting critical temperature Tc is controlled by the reciprocal orientation of the magnetizations of the F1 and F2 layers. The effect of the superconducting spin valve consists of varying degrees of suppression of the superconductivity in SSV structures for the parallel and antiparallel mutual orientation of the magnetizations of ferromagnetic layers. This leads to a higher value of the superconducting transition temperature in the case of the antiparallel orientation of the magnetizations of the ferromagnetic layers (TcAP) than in the case of the parallel orientation (TcP), or vice versa in the case of the inverse SSV effect.
SSV structures are a promising passive element in superconducting spintronics, with which it is possible to control the superconducting current. The main condition for the possibility of such control is the realization of the full superconducting spin valve effect; that is, when ΔTc > ∂Tc (here, ΔTc is the value of superconducting spin valve effect, which is defined as the difference between TcP and TcAP; ∂Tc—width of the superconducting transition). If the full SSV effect is realized, it is possible to control the superconducting current in the system by mutually changing the direction of the magnetization vectors of the ferromagnetic layers.
Experimental works (see, e.g., [15,16,17,18]) confirmed the predicted effect of the mutual direction of the magnetization in the F/S/F structure on Tc. However, the difference between TcAP and TcP turned out to be less than the value of the width of the superconducting transitions ∂Tc. For the first time, a complete switching between the normal and superconducting states in the SSV structure (Fe1/Cu/Fe2/In) was experimentally demonstrated in 2010 by a mutual change in the direction of the magnetization vectors of the ferromagnetic layers in an external magnetic field [19] (ΔTc = 19 mK; ∂Tc ~ 7 mK were obtained). After this result, various SSV structures with different ferromagnetic and superconducting materials were studied in recent years [20,21,22,23,24,25,26,27,28,29].
The generation of long-range triplet components (LRTC) of the superconducting condensate in the F-layer was predicted in a deep analysis of the processes occurring during the penetration of a Cooper pair from the S-layer into the F-layer [30]. The total spin of such a triplet component is equal to 0 (Sz = 0) in the case of one ferromagnetic layer. Such components cannot be detected when studying the transport properties of the S/F bilayer system. The total spin of long-range triplet components is equal to 1 (Sz = ± 1) if there is some kind of magnetic inhomogeneity in the ferromagnetic layer or a second ferromagnetic layer appears with a non-collinear (for example, orthogonal) direction of the magnetization vector relative to the first one. In this case, the triplet component can penetrate anomalously deep distances from the S-layer to the F-layer. Therefore, it is often called the long-range triplet component of a superconducting condensate. The depth of its penetration is comparable to the depth of penetration of an ordinary singlet Cooper pair into a normal metal. The long-range triplet component manifests itself in systems with a noncollinear orientation of magnetizations in ferromagnetic layers [31], as well as in systems with a spatial or momentum dependence of the exchange field [32]. A series of experiments were carried out (see, e.g., reviews [10,11,33]) that show the anomalously deep penetration of the superconducting condensate into the F-layer, which is characteristic of triplet superconductivity. The gigantic magnitudes of the SSV effect caused by the triplet components of the superconducting condensate have been demonstrated in a number of papers [34,35,36]. The generation of long-range triplet components of a superconducting condensate is interesting in that an additional channel for the leakage of Cooper pairs from the S-layer to the F-layer is created. Thus, this effect can manifest itself in different ways in thin-film heterostructures.
The results of [34,35,36] show that the limiting values of the SSV effect are close to being achieved in studies in an external magnetic field. This motivates us to search for and study new SSV structures with different approaches to superconducting current control. One approach may be to investigate SSV structures on a piezoelectric substrate. This will make it possible to control the operation of the piezoelectric SSV using an electric field. It can be assumed that the mutual change in the magnetization vectors in the SSV structure will occur under the influence of an external electric field on the piezoelectric substrate due to the inverse magnetostrictive effect. The inverse magnetostrictive effect in this system arises due to the deformation of the piezoelectric substrate when an external electric field is applied. Deformations in the piezoelectric substrate induce stresses in the ferromagnetic layer which is deposited on this piezoelectric substrate. This, in turn, manifests itself in the appearance of additional magnetic anisotropy, which, with a certain construction of the system, can proceed to a change in the direction of the magnetization vector of the ferromagnetic layer.
Thus, if a superconducting spin valve F1/F2/S is prepared on a piezoelectric substrate, it may be possible to operate it using an electric field. It will be possible to demonstrate that the magnetization of the F1-layer on the piezoelectric substrate changes its direction by the action of an electric field on the substrate, and the magnetization of the F2-layer is fixed. This can be achieved using F-layers with different coercive forces.
In our previous works, we observed a change in the direction of the ferromagnetic layer magnetization vector on a ferroelectric substrate when an electric field is applied in the range from 0 to 1 kV/cm using a magneto-optical complex based on the Kerr effect (see, e.g., [37]).
In this work, we investigated the features of a superconducting spin valve Fe1/Cu/Fe2/Cu/Pb on a piezoelectric PMN–PT substrate which has one of the highest piezoelectric parameters [38,39,40]. An analysis was performed on the influence of the PMN–PT piezoelectric substrate on the magnetic and superconducting properties of SSV structure Fe1/Cu/Fe2/Cu/Pb exposed to electric and magnetic fields. The maximum shift Tc in the electric field of 1 kV/cm amounted to 10 mK. The possibility of a full SSV effect realization was demonstrated in a magnetic field. Abnormal behavior of Tc was shown, which manifests itself in the maximum values of Tc with the orthogonal orientation of the magnetization vectors of ferromagnetic layers. This may indirectly indicate the formation of the easy axis of the magnetization vector of the Fe1-layer on the piezoelectric PMN–PT substrate. The difference in Tc between parallel (TcP) and orthogonal (TcPP) orientations was about 150 mK with ∂Tc ~ 100 mK when studied in an external magnetic field.

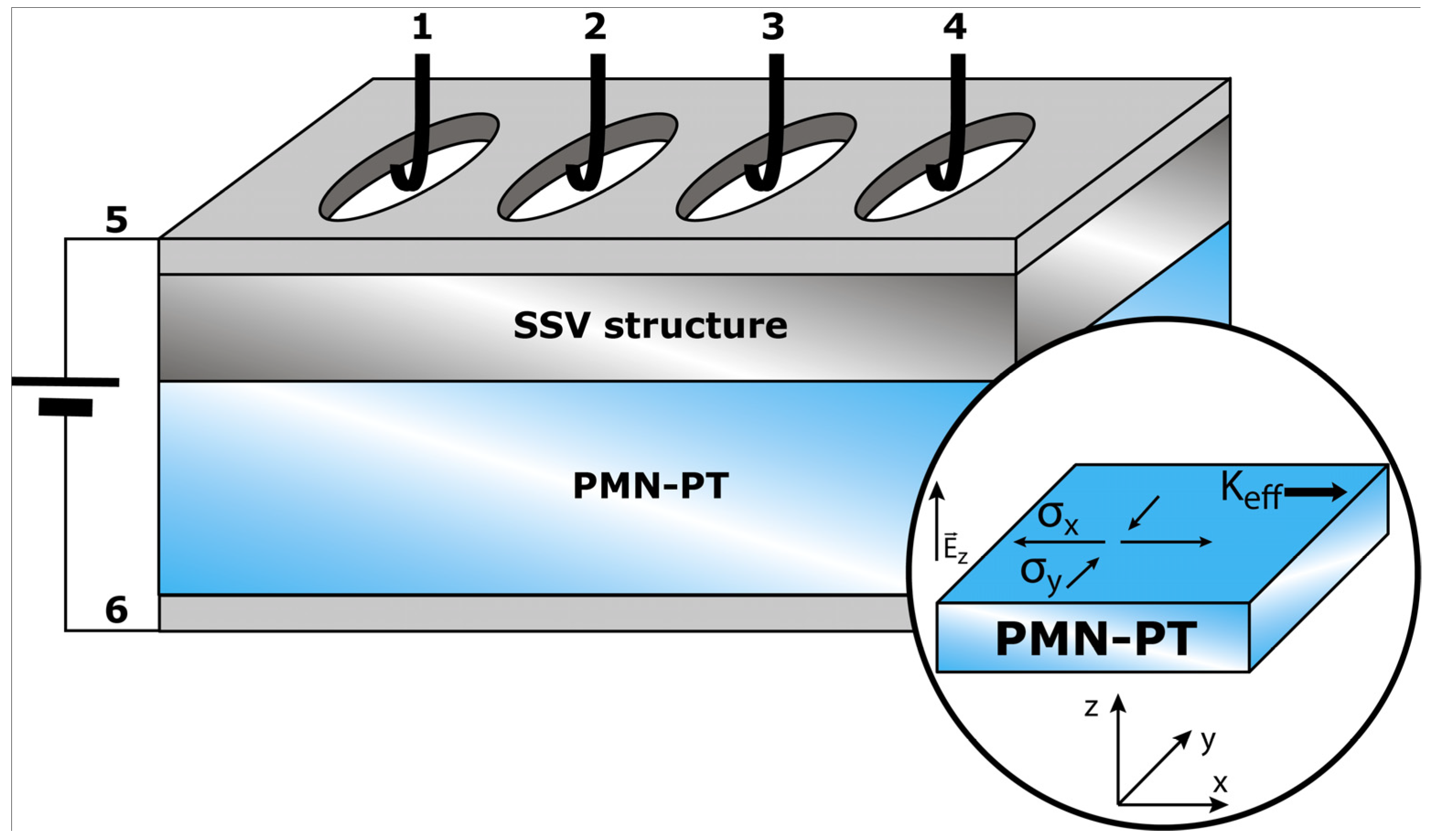
2. Materials and Methods

The samples were prepared on BESTEC equipment, which is located at the Zavoisky Physical–Technical Institute, FRC Kazan Scientific Center of RAS. The samples were produced using the method of electron beam evaporation in an ultra-high vacuum of 1 × 10−9 mbar and magnetron sputtering. The structures were deposited on piezoelectric PMN–PT substrates with dimensions of 2 × 10 × 0.5 mm3. In this work, commercial piezoelectric PMN–PT substrates ([Pb(Mg1/3Nb2/3)O3]0.7–[PbTiO3]0.3) were used with the following parameters: 0.7PMN–0.3PT with orientation [011], polished on one side with minimum roughness less than 0.5 mm. The structure of the prepared samples is shown in Figure 1. The grown heterostructures have the following composition: PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(dFe2)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 with the variable Fe2-layer thickness dFe2 in the range from 1 to 3 nm. In this construction, PMN–PT is the piezoelectric substrate, Fe1 plays the role of the ferromagnetic F1-layer, Cu(4 nm) decouples the magnetizations of the two different F-layers (Fe1 and Fe2), Fe2 plays the role of the ferromagnetic F2-layer, Cu(1.2 nm) is a buffer layer necessary for maximum smooth growth of the Pb layer, Pb (60 nm) is an S layer, and Si3N4 is a protective layer against oxidation. All materials used in the preparation of samples had a purity of better than 4N (the contamination level is below 0.01 at.%). There is no antiferromagnetic layer here, which is usually used to fix the direction of the magnetization vector of one of the ferromagnetic layers [19,27,28,29]. As a rule, we used cobalt oxide as an antiferromagnetic layer. This made it possible to fix the direction of the magnetization vector of the F1-layer up to 1.5 kOe in a given magnetic direction. Here, there is no possibility to use such a cobalt oxide layer because it is necessary to create direct contact between the piezoelectric substrate and the ferromagnetic layer (F1-layer). In this case, any additional layers between the piezoelectric substrate and the ferromagnetic layer reduce the influence of any magnetostrictive effects. The Fe1, Fe2, Cu, and Pb layers were prepared using the e-beam technique. The AC sputtering technique was used for the fabrication of the Si3N4 layer. The following deposition rates were used: 0.5 Å/s for Fe1, Fe2, and Cu layers; 12 Å/s for the Pb layer; and 1.8 Å/s for Si3N4 protective layer. The samples were prepared at a reduced substrate temperature (Tsub ~ 150 K). This critically affects the growth of the superconducting layer (Pb-layer). Earlier, we showed that the superconducting layer of lead grows smoothly at a low substrate temperature.
The electrical resistivity of samples was measured using the standard four-point method. The sample was placed in a low-temperature measuring cell in which an electric field can be applied to the sample. The electric field was applied perpendicular to the substrate plane. In this regard, the supply electrodes were located on the lower and upper faces of the sample. The scheme for measuring the Tc and applying an electric field is shown in Figure 2. In the magnetic field, measurements were carried out in a similar way, but without electric field. The temperature of the sample was controlled with the 230 Ohm Allen Bradley resistor thermometer which is particularly sensitive in the temperature range of interest. The critical temperature Tc was defined as the midpoint of the transition curve.
As a rule, the quality of a superconducting layer is determined from the residual resistivity ratio RRR = R(300 K)/R(10 K). This parameter is very important for superconducting materials. The closer this value is to 1, the worse is the quality of the superconducting material. For all our samples, RRR was in the range of 10–15, which indicates the high quality of the prepared Pb-layer.
The thickness of the S-layer is a very important parameter for the efficient operation of the SSV structure. The thickness should be sufficiently small to make the whole S-layer sensitive to the magnetic part of the system. Only in this case would the mutual orientation of the magnetizations of the F1 and F2 layers affect the Tc. According to our preliminary studies of the superconducting properties of the three-layer structures Fe(5 nm)/Cu(1.2 nm)/Pb(dPb), the optimal Pb-layer thickness was determined as dPb = 60 nm.
The procedure for measuring the Tc of samples was as follows: first, the samples were cooled to helium temperatures in an in-plane external magnetic field of the order 8 kOe (the so-called field cooling procedure); after that, the external magnetic field decreased to zero, and future studies of the samples under the influence of electric and magnetic fields were carried out.
The magnetic properties of the samples were studied using the Quantum Design SQUID MPMS-XL-5 magnetometer located in the Institute of Mathematics, Ljubljana, Slovenia. Studies of the magnetic properties of samples were also performed after the field cooling procedure.

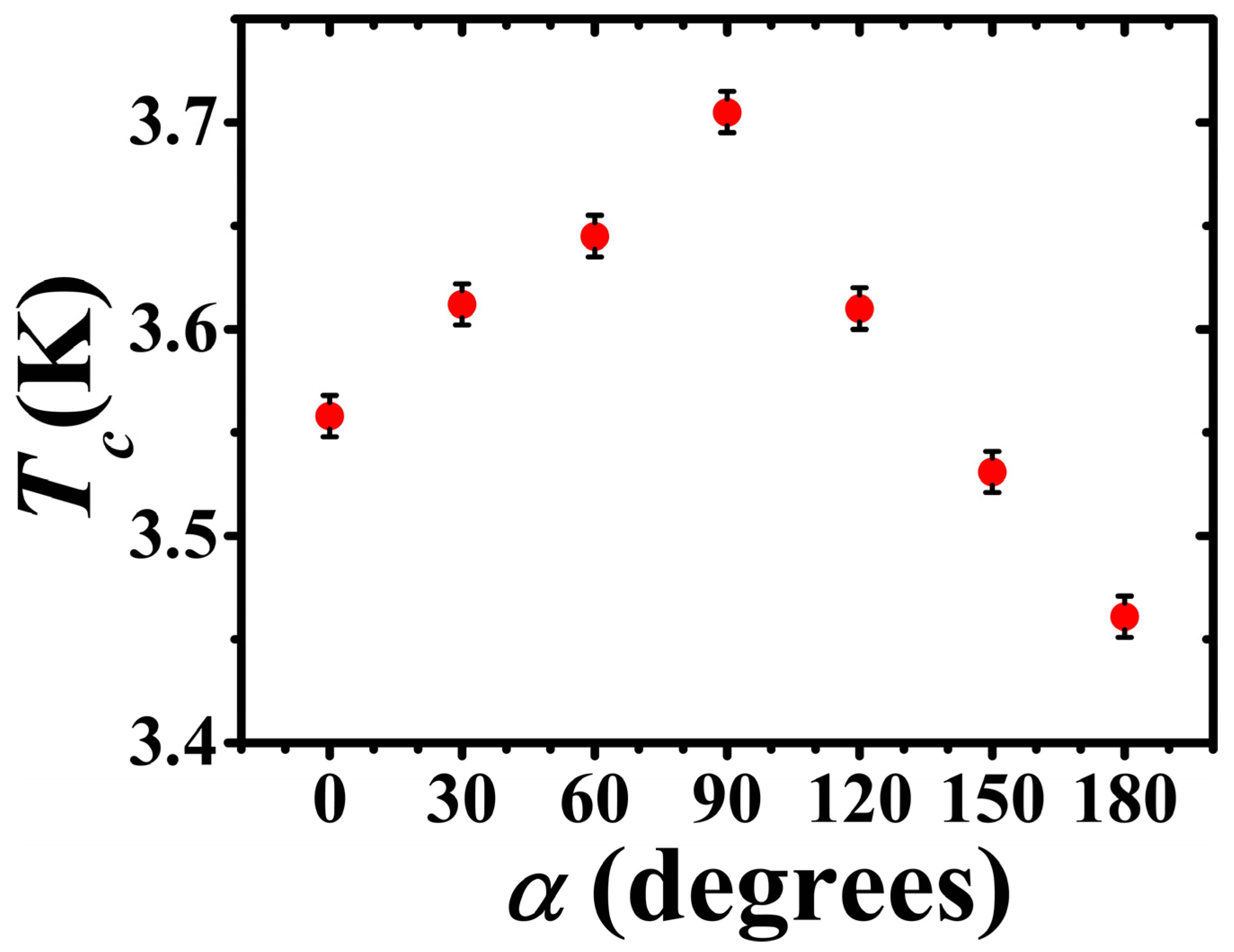
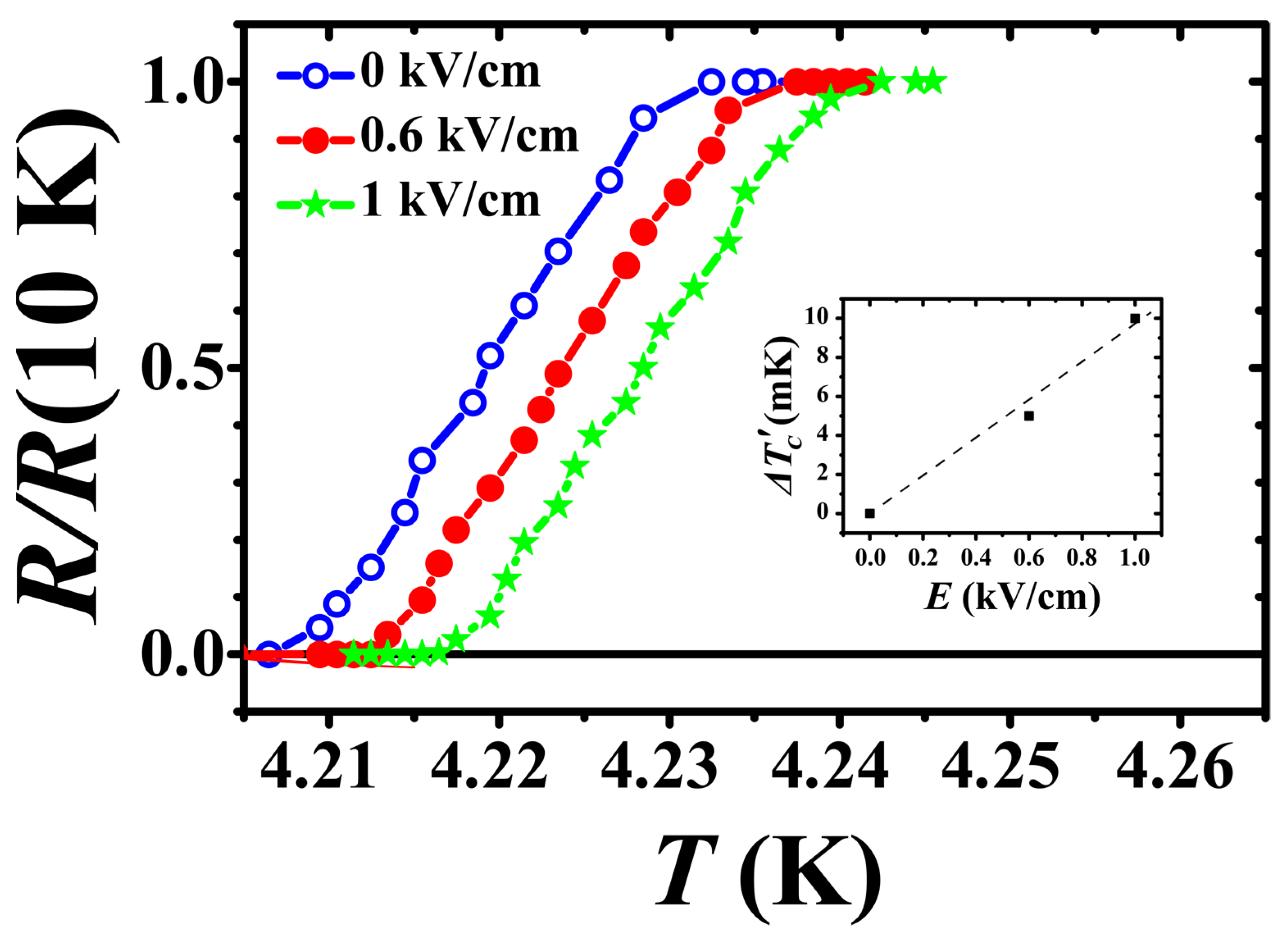
3. Results

The most interesting results were obtained for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4. Figure 3 shows the dependence of Tc on the angle α. Here, α is angle between the direction of the cooling magnetic field and the applied magnetic field H = 1 kOe. The presented dependence is typical for all sets of samples but with a smaller amplitude of effect. According to Figure 3, the difference in Tc between parallel (TcP) and orthogonal (TcPP) orientations was about 150 mK with ∂Tc ~ 100 mK. This indicates the possibility of realizing the full piezoelectric SSV effect.
Figure 4 shows magnetic hysteresis loop for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 measured at T = 30 K. The magnetic properties of ferromagnetic layers at temperatures significantly lower than the Curie temperature are practically independent from temperature. The contribution of the uncontrolled magnetic impurities of the substrate is inversely proportional to temperature. For these reasons, magnetic measurements were carried out at temperatures of 30 K, at which the contribution of uncontrolled magnetic impurities of the substrate is insignificant. The magnetic hysteresis loop in Figure 4 is typical of all sets of samples.
Figure 5 demonstrates the shifts of superconducting transitions curves for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 when applying an electric field to PMN–PT substrate.

4. Discussion

The difference in Tc between parallel (TcP) and orthogonal (TcPP) orientations was about 150 mK with ∂Tc ~ 100 mK (see Figure 3). It should be noted that in Figure 3, maximum of Tc is observed with the orthogonal orientation of the magnetizations of F-layers on the angular dependence of Tc. The angular position of this maximum is unusual. According to the theory by Fominov et al. [41], a minimum Tc should be observed near the orthogonal orientation of the magnetizations of the F-layers. This indicates the generation of long-range triplet components of a superconducting condensate [41]. This behavior has been observed in many works [29,33,34] in which the SSV effect was studied for samples prepared on conventional substrates (e.g., MgO). According to the unusual results presented in Figure 3, it can be supposed that the magnetization vector of the Fe1-layer has an easy magnetization axis. This easy magnetization axis may be due to the growth of the sample on the surface of a cooled piezoelectric substrate. Deformation of the substrate at cooling can lead to the rise of an easy magnetization axis Fe1-layer. We assume that under the influence of an external magnetic field, the magnetization vector of the Fe1-layer is more likely perpendicular (in-plane) to the magnetization vector of the Fe2-layer in the structure of the superconducting spin valve. This can explain the presence of a maximum Tc in the orthogonal orientation of the magnetization of the F-layers. Unfortunately, it was not possible to register such features of the growth of the Fe1-layer from magnetic measurements (see Figure 4). Magnetic measurements show that both F-layers’ magnetizations rotate in-plane in the magnetic field. Saturation of the magnetization of samples occurs at magnetic fields larger than 1 kOe. In the future, we will carry out a more detailed measurement of the samples on a SQUID magnetometer with the rotation of the sample in the plane of the magnetic field to determine the features of the growth of the Fe1-layer on the surface of the cooled piezoelectric substrate.
As is known, the thicker the F-layer is, the easier it is to change the direction of the magnetization vector. That is why the thickness of the Fe1-layer is larger than the thickness of the Fe2-layer in our work. The Fe1-layer has a smaller coercive force, which means that it is easier to change the direction of the magnetization vector of this layer than of the Fe2-layer by applying an electric field to the substrate.
According to the results presented in Figure 5, it was possible to observe a shift in the superconducting transition temperature when an electric field was applied to a piezoelectric substrate. This shift increased with an increase in the magnitude of the electric field applied to the sample. The superconducting transition curves in Figure 5 were measured sequentially without applying an electric field (0 kV/cm), and while applying 0.6 kV/cm and 1 kV/cm, respectively. An increase in the applied electric field from 0.6 to 1 kV/cm led to a 2-fold increase in the shift of Tc (see Figure 5). The existing construction of the low-temperature measuring cell does not allow the application of large voltage values. According to the results presented in Figure 5, it was not possible to perform a complete switching between the normal and superconducting state when an electric field was applied. The main condition for this was not achieved; here, the difference in superconducting transition temperatures is less than the width of the superconducting transition. Despite this, it was possible to demonstrate an increase in the shift of the Tc with an increase in the magnitude of the electric field applied to the sample. With an increase in the magnitude of the electric field, there is perhaps a greater mutual rotation between the directions of the magnetization vectors of the ferromagnetic layers, which leads to a greater shift of the Tc.
We can assume that without magnetic and electric fields in our SSV structures there is a certain angle between the magnetization vectors of the F-layers. This is due to the peculiarities of the growth of the F1-layer on the surface of the cooled piezoelectric substrate. The SSV structure operates on a piezoelectric substrate if it is possible to carry out a ∆Tc > ∂Tc. The result in Figure 5 demonstrates a possible change in the direction of the ferromagnetic layers vectors, but this change is not enough to realize the full piezoelectric SSV effect.
We assume the following possibility model of the piezoelectric superconducting spin valve. The mutual change of the magnetization vectors in the piezoelectric superconducting spin valve structure will occur in the external electric field. When an external electric field is applied, deformation occurs in the piezoelectric substrate; they cause mechanical stresses in the ferromagnetic layer (F1-layer) deposited on the piezoelectric substrate. As a result, due to the inverse magnetostrictive effect, magnetic anisotropy arises with the uniaxial anisotropy constant Keff. In additive, the effective magnetic field coupled with this anisotropy leads to a change in the direction of the magnetization vector of the ferromagnetic layer F1. Thus, due to the effect of magnetostriction, an anisotropy axis appears in the ferromagnetic film with a uniaxial anisotropy constant Keff = −3/2 λsϬ, where λs is the saturation magnetostriction constant and Ϭ are mechanical stresses. The mechanical stress tensor Ϭi,j arise in a piezoelectric PMN–PT substrate when an electric field Ek is applied to it along the k-axis, and at the same time, due to direct contact in a ferromagnetic film, Ϭi,j = Y dk,i,jEk, where Y—Young’s modulus, and dk,i,j—coefficient of the piezoelectric effect. Based on the uniaxial anisotropy constant Keff, one can estimate the effective field associated with this anisotropy: Heff = 2Keff/µ0Ms, where µ0—the magnetic constant, and Ms—the saturation magnetization. Taking the known constants for Fe, Co, and PMN–PT (λs ≈ −10·10−6 and ≈ −71.4·10−6, Ms ≈ 1700 kA/m and ≈ 1400 kA/m, Y ≈ 215 GPa and ≈ 206 GPa; for Fe and Co, d3.1.1 ≈ −679 pC/N, and d3.2.2 ≈ −1280 pC/N for PMN–PT), and taking into account the fact that the effective field will be directed along the axis of greatest stress, with the application of an electric field, we obtain Ez = 1 kV/cm, Heff ≈ 1.2 Oe, and Heff ≈ 10 Oe. These fields are comparable to the characteristic coercive fields for Fe and Co, which are on the order of 10–20 Oe. In addition, since the experiment takes place in the absence of an external magnetic field, the resulting anisotropy is sufficient to reverse the magnetization vector. Note that in our case, there is no shape anisotropy since we specifically made the films polycrystalline. Due to polycrystallinity, it is impossible to remove the anisotropy of the shape; however, because we have a thin film, anisotropy arises in the form of a light magnetization plane. In addition, since we have a sample of sufficiently large dimensions, there is no anisotropy of the shape in the plane.
In the future, to increase the influence of the electric field on the change in the direction of the magnetization vectors of the ferromagnetic layers, it will be possible to increase the magnitude of the applied electric field when optimizing measuring systems or to use other ferroelectric/piezoelectric substrates to increase the effect of an external electric field on the substrate due to the reverse magnetostrictive effect.
We also plan to investigate the dependence of Tc on the angle α between the magnetizations of the F1 and F2 layers when applying an electric field to the piezoelectric substrate. The results presented in Figure 5 suggest that with such a measurement, it will be possible to observe large magnitudes of the SSV effects.

5. Conclusions

In this article, a comparative analysis of the influence of the piezoelectric properties of the PMN–PT substrate on the superconducting characteristics of the superconducting spin valve Fe1/Cu/Fe2/Cu/Pb in electric and magnetic fields was carried out. According to the observed results, with an increase in the magnitude of the applied electric field to the PMN–PT substrate comes an increase in the shift of the superconducting transition temperature of the Fe1/Cu/Fe2/Cu/Pb system. The maximum value of the shift was 10 mK when an electric field of 1 kV/cm was applied. The magnitude of the shift of the superconducting transition temperature in the magnetic field equal to 150 mK was detected, while the full superconducting spin valve effect was demonstrated. Abnormal behavior of the superconducting transition temperature was shown, which, when studying the angular dependence of the superconducting transition temperature in an external magnetic field, manifests itself in the maximum values of the superconducting transition temperature with the orthogonal orientation of the magnetization vectors of the ferromagnetic layers. This may indicate the appearance of the easy axis of the magnetization vector of the Fe1-layer on the piezoelectric PMN–PT substrate. It was not possible to establish this fact from our studies of the magnetic properties of samples; it will require more detailed research in the future. The results obtained in a magnetic field indicate the possibility of realizing a working model of the superconducting spin valve on a piezoelectric substrate. The obtained results generally suggest that it is possible to demonstrate the full piezoelectric superconducting spin valve effect in the structures of a superconducting spin valve on a piezoelectric substrate.

Author Contributions

Conceptualization, A.K., R.M. and I.G.; methodology, A.K. and R.M.; validation, A.K. and I.G.; formal analysis, A.V.; investigation, A.K., N.G., Z.J., V.K. and A.V.; resources, A.K. and R.M.; data curation, A.V.; writing—original draft preparation, A.K., R.M., N.G. and I.G.; writing—review and editing, A.K. and R.M.; visualization, A.K.; supervision, I.G.; project administration, A.K.; funding acquisition, A.K. and R.M. All authors have read and agreed to the published version of the manuscript.

Funding

The work of A.K., R.M. and I.G. concerning the influence of the electric field on a piezoelectric substrate and measurements on a SQUID-magnetometer was funded by the Russian Scientific Foundation according to research project No. 21-72-10178. The work of A.K., N.G. and A.V. concerning the influence of the magnetic field on the superconducting spin valve on a piezoelectric substrate was financially supported by the government assignment for FRC Kazan Scientific Center of RAS.

Acknowledgments

Z.J. acknowledges to the Slovenian Research Agency Program No. P2-0348. V.K. acknowledges to the Slovenian Research Agency Program No. P1-0040. We are grateful to Bizyaev D.A. and Shaposhnikova T.S. for helpful discussion.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fischer, O.; Peter, M. Magnetism: Magnetic Properties of Metallic Alloys. Recent Work on Ferromagnetic Superconductors; Academic Press Inc.: New York, NY, USA, 1973. [Google Scholar]
  2. Rehmann, S.; Herrmannsdörfer, T.; Pobell, F. Interplay of Nuclear Magnetism and Superconductivity in AuIn2. Phys. Rev. Lett. 1997, 78, 1122. [Google Scholar] [CrossRef]
  3. Bulaevskii, L.N.; Buzdin, A.I.; Kulić, M.L.; Panjukov, S.V. Coexistence of superconductivity and magnetism theoretical predictions and experimental results. Adv. Phys. 1985, 34, 175–261. [Google Scholar] [CrossRef]
  4. Chien, C.L.; Jiang, J.S.; Xiao, J.Q.; Davidovic, D.; Reich, D.H. Proximity and coupling effects in superconductor/ferromagnet multilayers. J. Appl. Phys. 1997, 81, 5358–5363. [Google Scholar] [CrossRef]
  5. Chien, C.L.; Reich, D.H. Proximity effects in superconducting/magnetic multilayers. J. Mag. Mag. Mat. 1999, 200, 83–94. [Google Scholar] [CrossRef]
  6. Garifullin, I.A. Proximity effects in ferromagnet/superconductor heterostructures. J. Mag. Mag. Mat. 2002, 240, 571–576. [Google Scholar] [CrossRef] [Green Version]
  7. Izyumov, Y.; Proshin, Y.; Khusainov, M. Competition between superconductivity and magnetism in ferromagnet/superconductor heterostructures. UFN 2002, 172, 113–154. [Google Scholar] [CrossRef]
  8. Golubov, A.A.; Kupriyanov, M.Y.; Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 2004, 76, 411. [Google Scholar] [CrossRef] [Green Version]
  9. Buzdin, A.I. Proximity effects in superconductor-ferromagnet. Rev. Mod. Phys. 2005, 77, 935. [Google Scholar] [CrossRef] [Green Version]
  10. Bergeret, F.S.; Volkov, A.F.; Efetov, K.B. Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures. Rev. Mod. Phys. 2005, 77, 1321. [Google Scholar] [CrossRef] [Green Version]
  11. Efetov, K.B.; Garifullin, I.A.; Volkov, A.F.; Westerholt, K. Magnetic Heterostructures: Advances and Perspectives in Spinstructures and Spintransport; Series Springer Tracts in Modern Physics; Springer: Berlin, Germany, 2007; p. 252. [Google Scholar]
  12. Oh, S.; Youm, D.; Beasley, M.R. A superconductive magnetoresistive memory element using controlled exchange interaction. Appl. Phys. Lett. 1997, 71, 2376. [Google Scholar] [CrossRef]
  13. Tagirov, L.R. Low-field superconducting spin switch based on a superconductor/ferromagnet multilayer. Phys. Rev. Lett. 1999, 83, 2058. [Google Scholar] [CrossRef]
  14. Buzdin, A.I.; Vedyayev, A.V.; Ryzhanova, N.V. Spin-orientation–dependent superconductivity in F/S/F structures. EPL 1999, 48, 686. [Google Scholar] [CrossRef]
  15. Gu, J.Y.; You, C.Y.; Jiang, J.S.; Pearson, J.; Bazaliy, Y.a.B.; Bader, S.D. Magnetization-Orientation Dependence of the Superconducting Transition Temperature in the Ferromagnet-Superconductor-Ferromagnet System: CuNi/Nb/CuNi. Phys. Rev. Lett. 2002, 89, 267001. [Google Scholar] [CrossRef] [PubMed]
  16. Potenza, A.; Marrows, C.H. Superconductor-ferromagnet CuNi/Nb/CuNi trilayers as superconducting spin-valve core structures. Phys. Rev. B 2005, 71, 180503. [Google Scholar] [CrossRef]
  17. Moraru, I.C.; Pratt, J.r.W.P.; Birge, N.O. Magnetization-Dependent Tc Shift in Ferromagnet/Superconductor/Ferromagnet Trilayers with a Strong Ferromagnet. Phys. Rev. Lett. 2006, 96, 037004. [Google Scholar] [CrossRef] [Green Version]
  18. Miao, G.-X.; Ramos, A.V.; Moodera, J. Infinite Magnetoresistance from the Spin Dependent Proximity Effect in Symmetry Driven bcc−Fe/V/Fe Heteroepitaxial Superconducting Spin Valves. Phys. Rev. Lett. 2008, 101, 137001. [Google Scholar] [CrossRef] [PubMed]
  19. Leksin, P.V.; Garif’yanov, N.N.; Garifullin, I.A.; Schumann, J.; Vinzelberg, H.; Kataev, V.; Klingeler, R.; Schmidt, O.G.; Büchner, B. Full spin switch effect for the superconducting current in a superconductor/ferromagnet thin film heterostructure. Appl. Phys. Lett. 2010, 97, 102505. [Google Scholar] [CrossRef] [Green Version]
  20. Blamire, M.G.; Robinson, J.W.A. The interface between superconductivity and magnetism: Understanding and device prospects. J. Phys. Condens. Matter 2014, 26, 453201. [Google Scholar] [CrossRef] [PubMed]
  21. Eschrig, M. Spin-polarized supercurrents for spintronics: A review of current progress. Rep. Prog. Phys. 2015, 78, 104501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  22. Grein, R.; Löfwander, T.; Eschrig, M. Inverse proximity effect and influence of disorder on triplet supercurrents in strongly spin-polarized ferromagnets. Phys. Rev. B 2013, 88, 054502. [Google Scholar] [CrossRef] [Green Version]
  23. Flokstra, M.G.; Cunningham, T.C.; Kim, J.; Satchell, N.; Burnell, G.; Curran, P.J.; Bending, S.J.; Kinane, C.J.; Cooper, J.F.K.; Langridge, S.; et al. Controlled suppression of superconductivity by the generation of polarized Cooper pairs in spin-valve structures. Phys. Rev. B 2015, 91, 060501. [Google Scholar] [CrossRef] [Green Version]
  24. Montiel, X.; Eschrig, M. Generation of pure superconducting spin current in magnetic heterostructures via nonlocally induced magnetism due to landau fermi liquid effects. Phys. Rev. B 2018, 98, 104513. [Google Scholar] [CrossRef] [Green Version]
  25. Banerjee, N.; Ouassou, J.A.; Zhu, Y.; Stelmashenko, N.A.; Linder, J.; Blamire, M.G. Controlling the superconducting transition by spin-orbit coupling. Phys. Rev. B 2018, 97, 184521. [Google Scholar] [CrossRef] [Green Version]
  26. Pugach, N.; Safonchik, M.; Belotelov, V.; Ziman, T.; Champel, T. Superconducting Spin Valves Based on a Single Spiral Magnetic Layer. Phys. Rev. Appl. 2022, 18, 054002. [Google Scholar] [CrossRef]
  27. Leksin, P.V.; Garif’yanov, N.N.; Garifullin, I.A.; Fominov, Y.V.; Schumann, J.; Krupskaya, Y.; Kataev, V.; Schmidt, O.G.; Büchner, B. Evidence for Triplet Superconductivity in a Superconductor-Ferromagnet Spin Valve. Phys. Rev. Lett. 2012, 109, 057005. [Google Scholar] [CrossRef] [Green Version]
  28. Leksin, P.V.; Garif’Yanov, N.N.; Kamashev, A.A.; Validov, A.A.; Fominov, Y.V.; Schumann, J.; Kataev, V.; Thomas, J.; Büchner, B.; Garifullin, I.A. Isolation of proximity-induced triplet pairing channel in a superconductor/ferromagnet spin valve. Phys. Rev. B 2016, 93, 100502. [Google Scholar] [CrossRef] [Green Version]
  29. Leksin, P.V.; Garif’yanov, N.N.; Kamashev, A.A.; Fominov, Y.V.; Schumann, J.; Hess, C.; Kataev, V.; Büchner, B.; Garifullin, I.A. Superconducting spin-valve effect and triplet superconductivity in CoOx/Fe1/Cu/Fe2/Cu/Pb. Phys. Rev. B 2015, 91, 214508. [Google Scholar] [CrossRef] [Green Version]
  30. Bergeret, F.S.; Volkov, A.F.; Efetov, K.B. Long-Range Proximity Effects in Superconductor-Ferromagnet Structures. Phys. Rev. Lett. 2001, 86, 4096. [Google Scholar] [CrossRef] [Green Version]
  31. Volkov, A.F.; Bergeret, F.S.; Efetov, K.B. Odd Triplet Superconductivity in Superconductor-Ferromagnet Multilayered Structures. Phys. Rev. Lett. 2003, 90, 117006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Mel’nikov, A.S.; Samokhvalov, A.V.; Kuznetsova, S.M.; Buzdin, A.I. Interference Phenomena and Long-Range Proximity Effect in Clean Superconductor-Ferromagnet Systems. Phys. Rev. Lett. 2012, 109, 237006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  33. Efetov, K.B.; Garifullin, I.A.; Volkov, A.F.; Westerholt, K. Magnetic Nanostructures. Spin Dynamic and Spin Transport; Series Springer Tracts in Modern Physics; Springer: Berlin, Germany, 2013; pp. 85–118. [Google Scholar]
  34. Singh, A.; Voltan, S.; Lahabi, K.; Aarts, J. Colossal proximity effect in a superconducting triplet spin valve based on the half-metallic ferromagnet CrO2. Phys. Rev. X 2015, 5, 021019. [Google Scholar]
  35. Kamashev, A.A.; Garif’yanov, N.N.; Validov, A.A.; Schumann, J.; Kataev, V.; Büchner, B.; Fominov, Y.V.; Garifullin, I.A. Superconducting switching due to a triplet component in the Pb/Cu/Ni/Cu/Co2Cr1−xFexAly spin-valve structure. Beilstein J. Nanotechnol. 2019, 10, 1458. [Google Scholar] [CrossRef] [Green Version]
  36. Kamashev, A.A.; Garif’yanov, N.N.; Validov, A.A.; Schumann, J.; Kataev, V.; Büchner, B.; Fominov, Y.V.; Garifullin, I.A. Superconducting spin-valve effect in heterostructures with ferromagnetic Heusler alloy layers. Phys. Rev. B 2019, 100, 134511. [Google Scholar] [CrossRef] [Green Version]
  37. Kamashev, A.A.; Leontyev, A.V.; Mamin, R.F.; Garifullin, I.A. Features of the direction of the magnetization vector in a two-layer Fe/LiNbO3 system. Ferroelectrics 2023, 605, 54–59. [Google Scholar] [CrossRef]
  38. Zhang, W.; Wang, Z.; Yang, X.; Long, X.; He, C. Composition uniformity of Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 single crystals grown in <001> direction. J. Cryst. Growth 2021, 560–561, 126061. [Google Scholar]
  39. Zhanga, Z.; Xua, J.; Yanga, L.; Liua, S.; Xiaoa, J.; Lia, X.; Wanga, X.; Luoa, H. Design and comparison of PMN-PT single crystals and PZT ceramics based medical phased array ultrasonic transducer. Sens. Actuator A Phys. 2018, 283, 273–281. [Google Scholar] [CrossRef]
  40. Song, H.-C.; Kang, C.-Y.; Yoon, S.-Y.; Jeong, D.-Y. Engineered Domain Configuration and Piezoelectric Energy Harvesting in 0.7Pb(Mg1/3Nb2/3)O3-0.3PbTiO3 Single Crystals. Met. Mater. Int. 2012, 18, 499–503. [Google Scholar] [CrossRef]
  41. Fominov, Y.V.; Golubov, A.A.; Karminskaya, T.Y.; Kupriyanov, M.Y.; Deminov, R.G.; Tagirov, L.R. Superconducting triplet spin valve. JETP Lett. 2010, 91, 308. [Google Scholar] [CrossRef] [Green Version]
Magnetism 03 00016 g001 550
Figure 1. The structure of prepared SSV samples.
Figure 1. The structure of prepared SSV samples.
Magnetism 03 00016 g001
Magnetism 03 00016 g002 550
Figure 2. The scheme for measuring Tc by a four-probe resistivity method: 1, 4—current electrodes; 2, 3—potential electrodes; 5, 6—capacity plates for applying an electric field to a piezoelectric substrate. The inset shows the deformation of the substrate under the action of an electric field and the appearance of magnetic anisotropy with the uniaxial anisotropy constant Keff.
Figure 2. The scheme for measuring Tc by a four-probe resistivity method: 1, 4—current electrodes; 2, 3—potential electrodes; 5, 6—capacity plates for applying an electric field to a piezoelectric substrate. The inset shows the deformation of the substrate under the action of an electric field and the appearance of magnetic anisotropy with the uniaxial anisotropy constant Keff.
Magnetism 03 00016 g002
Magnetism 03 00016 g003 550
Figure 3. Dependence of Tc on the angle α between the direction of the cooling field and the applied magnetic field H = 1 kOe.
Figure 3. Dependence of Tc on the angle α between the direction of the cooling field and the applied magnetic field H = 1 kOe.
Magnetism 03 00016 g003
Magnetism 03 00016 g004 550
Figure 4. Magnetic hysteresis loop for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 measured at T = 30 K. The solid line is a guide for the eyes.
Figure 4. Magnetic hysteresis loop for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 measured at T = 30 K. The solid line is a guide for the eyes.
Magnetism 03 00016 g004
Magnetism 03 00016 g005 550
Figure 5. Superconducting transitions curves for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 when applying an electric field to PMN–PT substrate.
Figure 5. Superconducting transitions curves for the sample PMN–PT/Fe1(3 nm)/Cu(4 nm)/Fe2(1 nm)/Cu(1.2 nm)/Pb(60 nm)/Si3N4 when applying an electric field to PMN–PT substrate.
Magnetism 03 00016 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kamashev, A.; Garif’yanov, N.; Validov, A.; Jagličić, Z.; Kabanov, V.; Mamin, R.; Garifullin, I. Investigation of the Features of a Superconducting Spin Valve Fe1/Cu/Fe2/Cu/Pb on a Piezoelectric PMN–PT Substrate. Magnetism 2023, 3, 204-214. https://doi.org/10.3390/magnetism3030016

AMA Style

Kamashev A, Garif’yanov N, Validov A, Jagličić Z, Kabanov V, Mamin R, Garifullin I. Investigation of the Features of a Superconducting Spin Valve Fe1/Cu/Fe2/Cu/Pb on a Piezoelectric PMN–PT Substrate. Magnetism. 2023; 3(3):204-214. https://doi.org/10.3390/magnetism3030016

Chicago/Turabian Style

Kamashev, Andrey, Nadir Garif’yanov, Aidar Validov, Zvonko Jagličić, Viktor Kabanov, Rinat Mamin, and Ilgiz Garifullin. 2023. "Investigation of the Features of a Superconducting Spin Valve Fe1/Cu/Fe2/Cu/Pb on a Piezoelectric PMN–PT Substrate" Magnetism 3, no. 3: 204-214. https://doi.org/10.3390/magnetism3030016

APA Style

Kamashev, A., Garif’yanov, N., Validov, A., Jagličić, Z., Kabanov, V., Mamin, R., & Garifullin, I. (2023). Investigation of the Features of a Superconducting Spin Valve Fe1/Cu/Fe2/Cu/Pb on a Piezoelectric PMN–PT Substrate. Magnetism, 3(3), 204-214. https://doi.org/10.3390/magnetism3030016

Article Metrics

Back to TopTop