Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network
Abstract
:1. Introduction
- The proposed method integrates PSO and RNN to establish a comprehensive iron loss calculation model. This model accounts for high-order harmonics, rotating magnetization, and temperature factors, capturing multifaceted influences on iron loss.
- By employing multilayer RNN and PSO for training and optimization, the method overcomes issues associated with conventional polynomial fitting, offering improved accuracy in estimating iron loss even in complex scenarios beyond traditional measurement ranges.
- The developed model offers broad applicability by accurately estimating iron loss in PMSMs under diverse and complex conditions, surpassing the limitations of traditional empirical formulas.
2. Impact Factor Analysis of Iron Loss
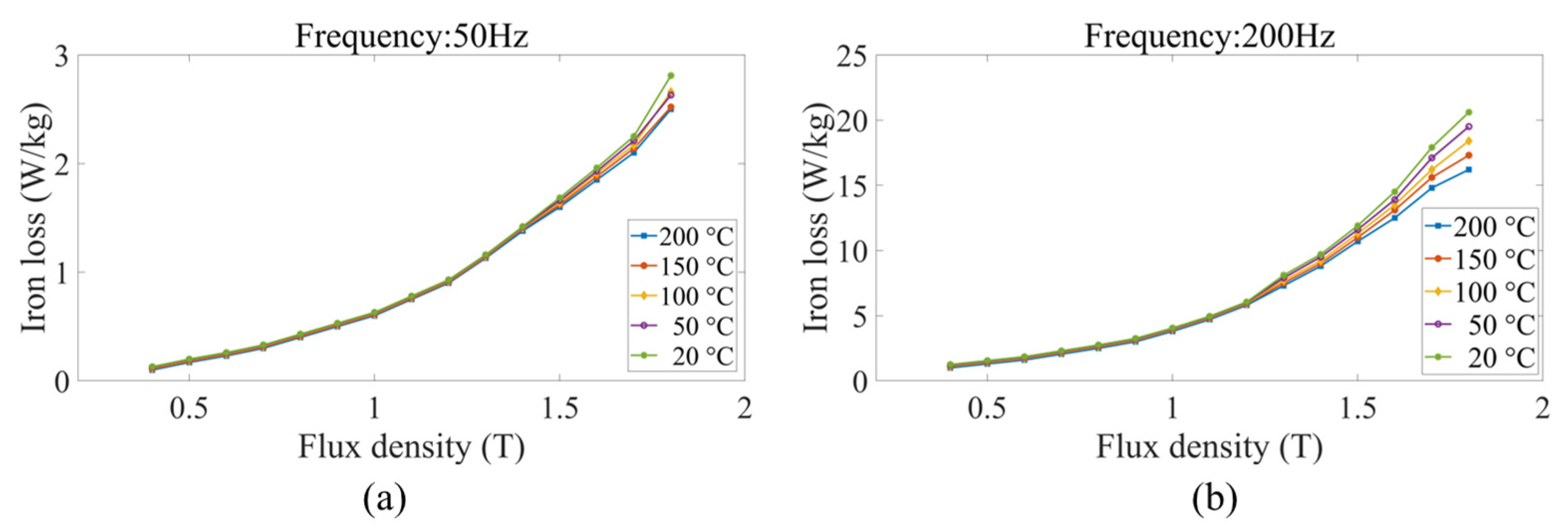
2.1. Frequencies and Temperatures
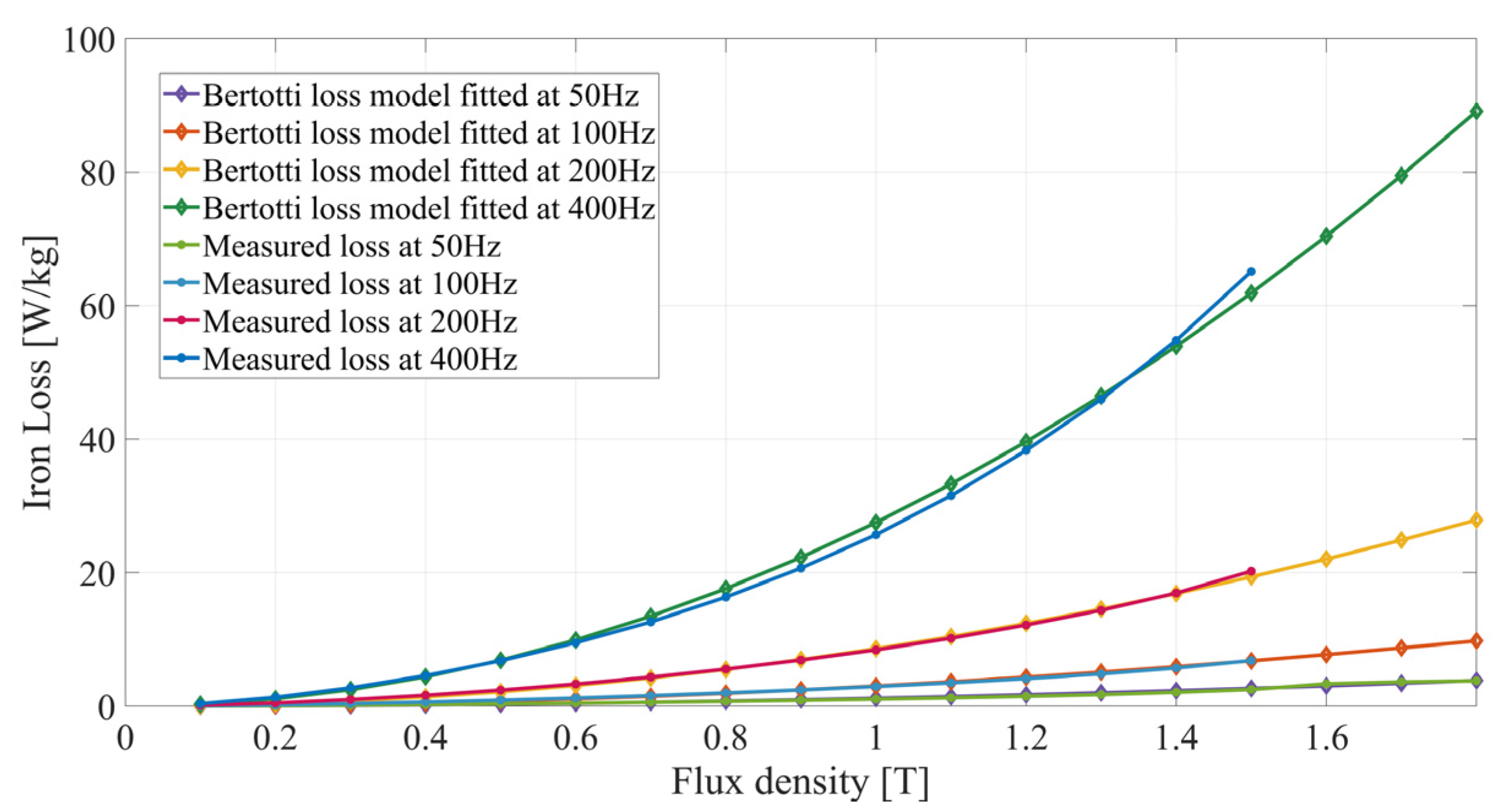
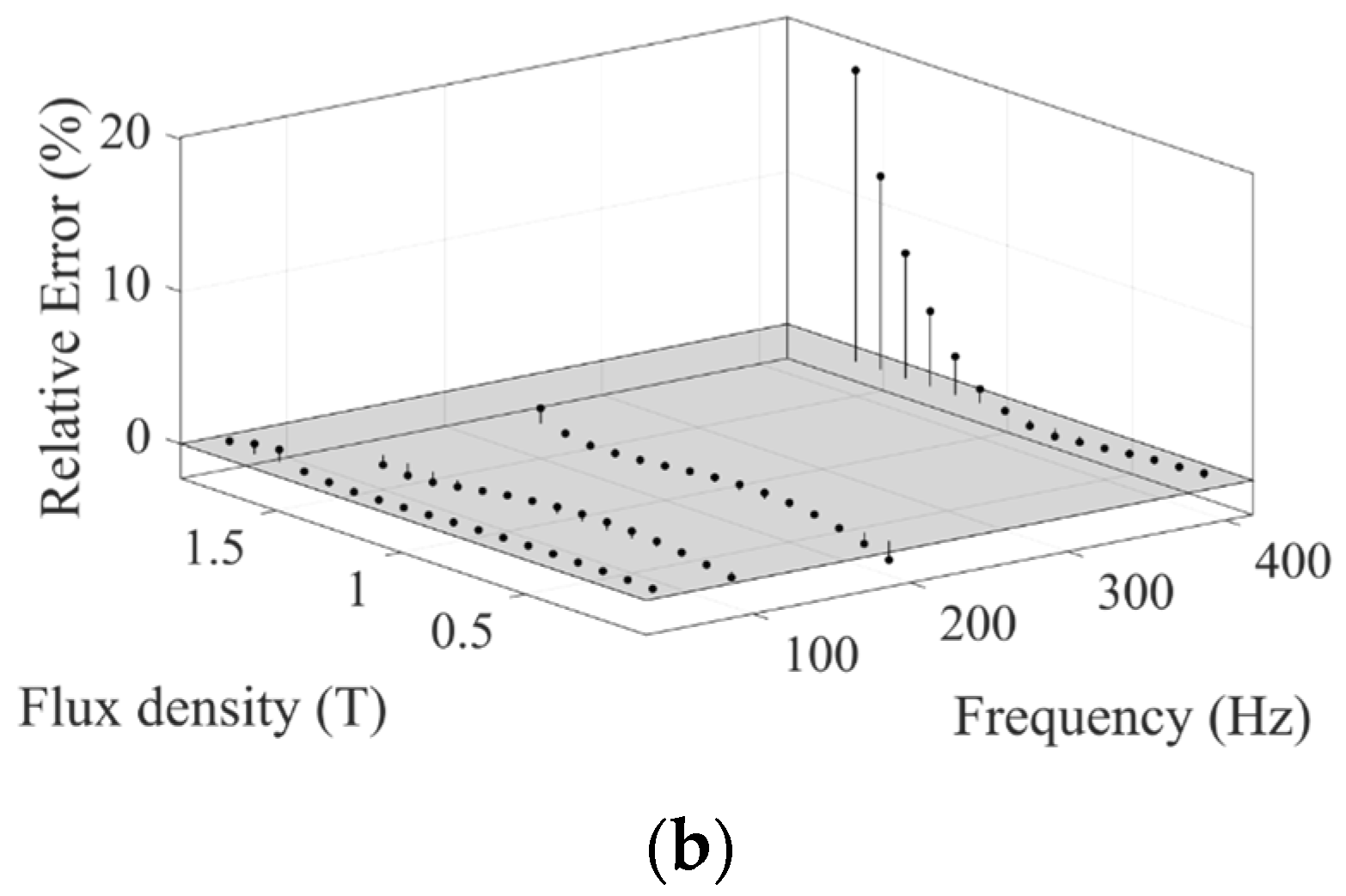
2.2. Polynomial Fitting Error
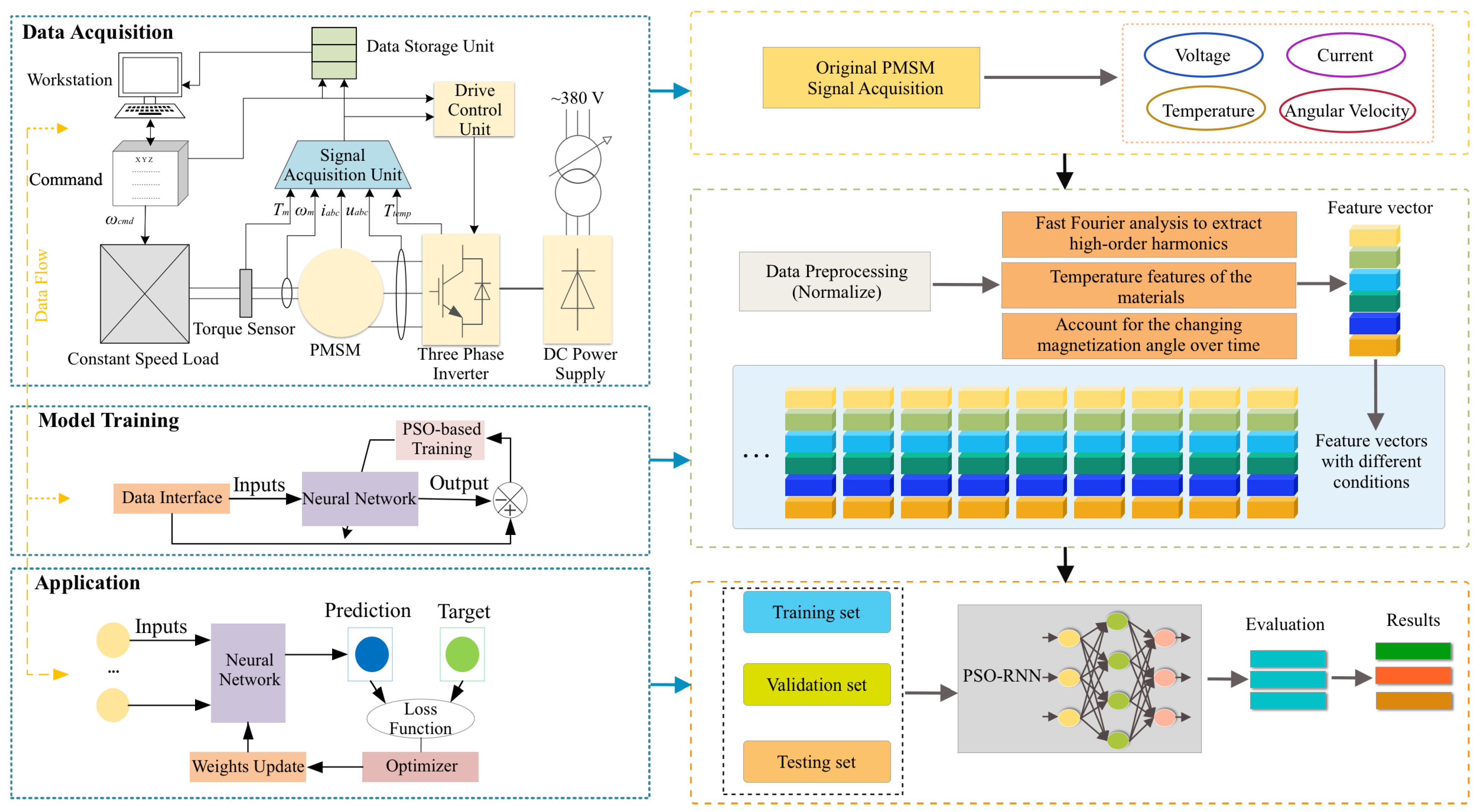
3. Iron Loss Estimation Based on the Recurrent Neural Network
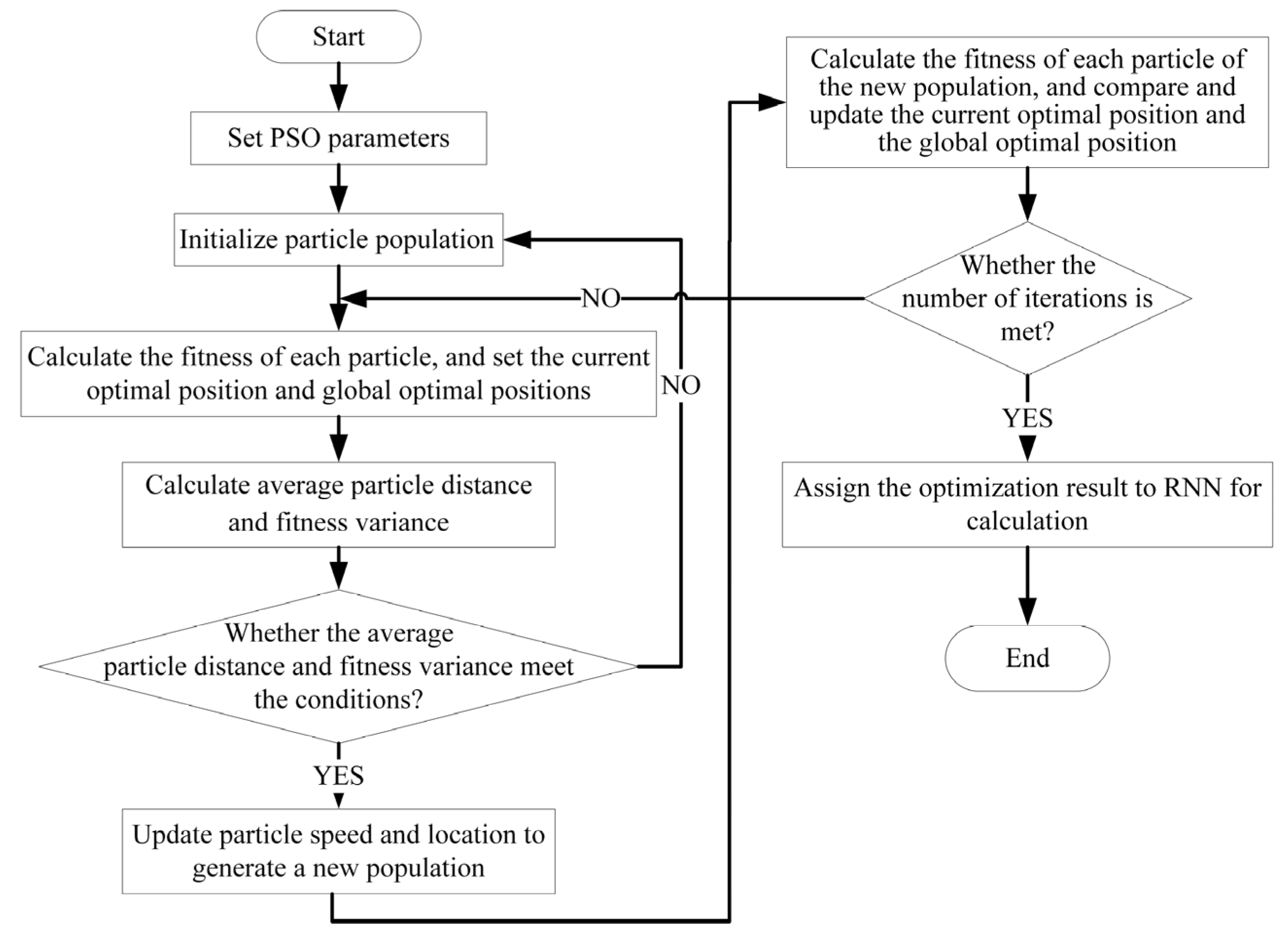
3.1. Particle Swarm Optimization and the Recurrent Neural Network
- PSO will optimize the RNN architecture, hyperparameters, or training process to enhance the accuracy and efficiency of estimating iron loss.
- RNNs will serve as the predictive model, leveraging their ability to capture sequential dependencies in data for accurate estimation.
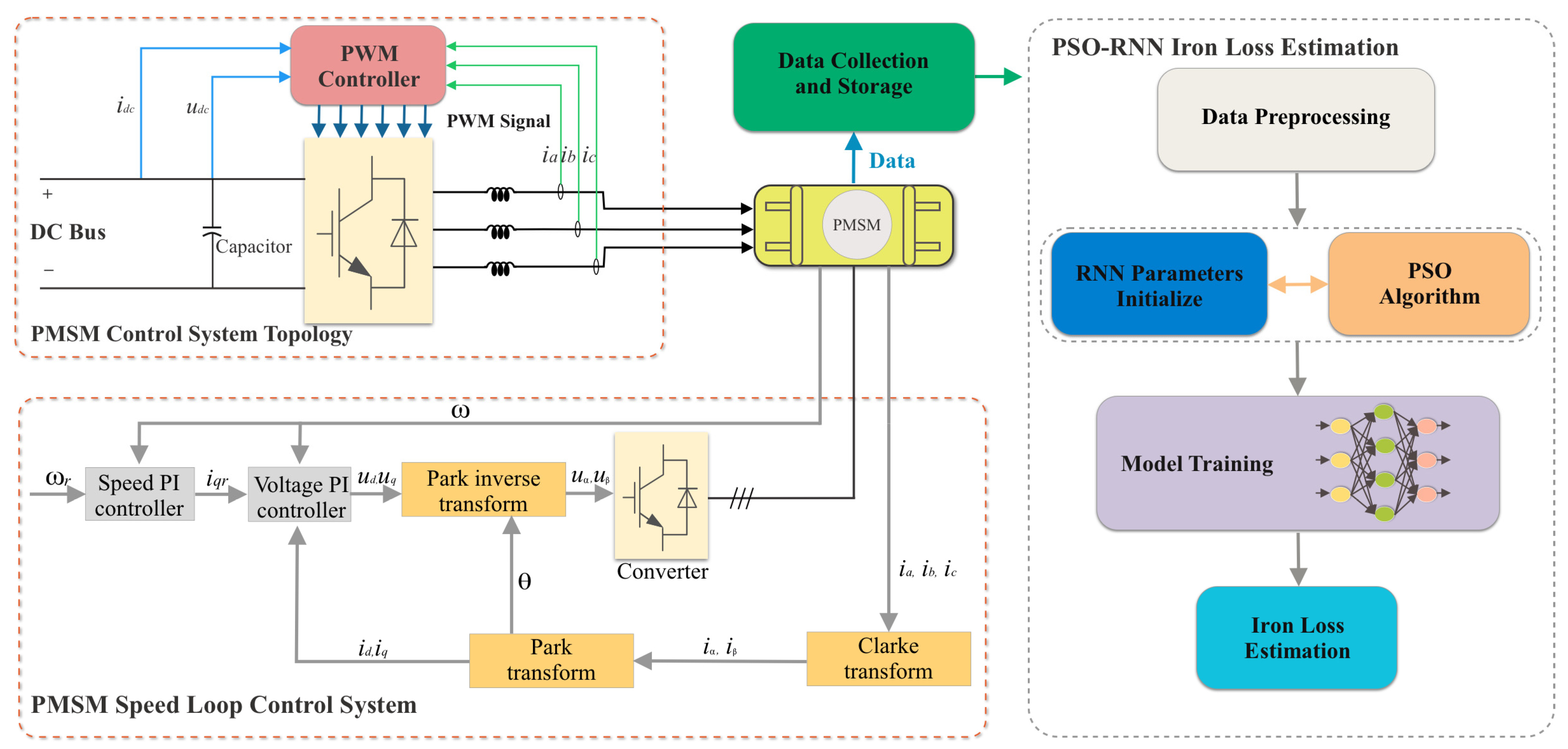
3.2. Proposed PMSM Iron Loss Method
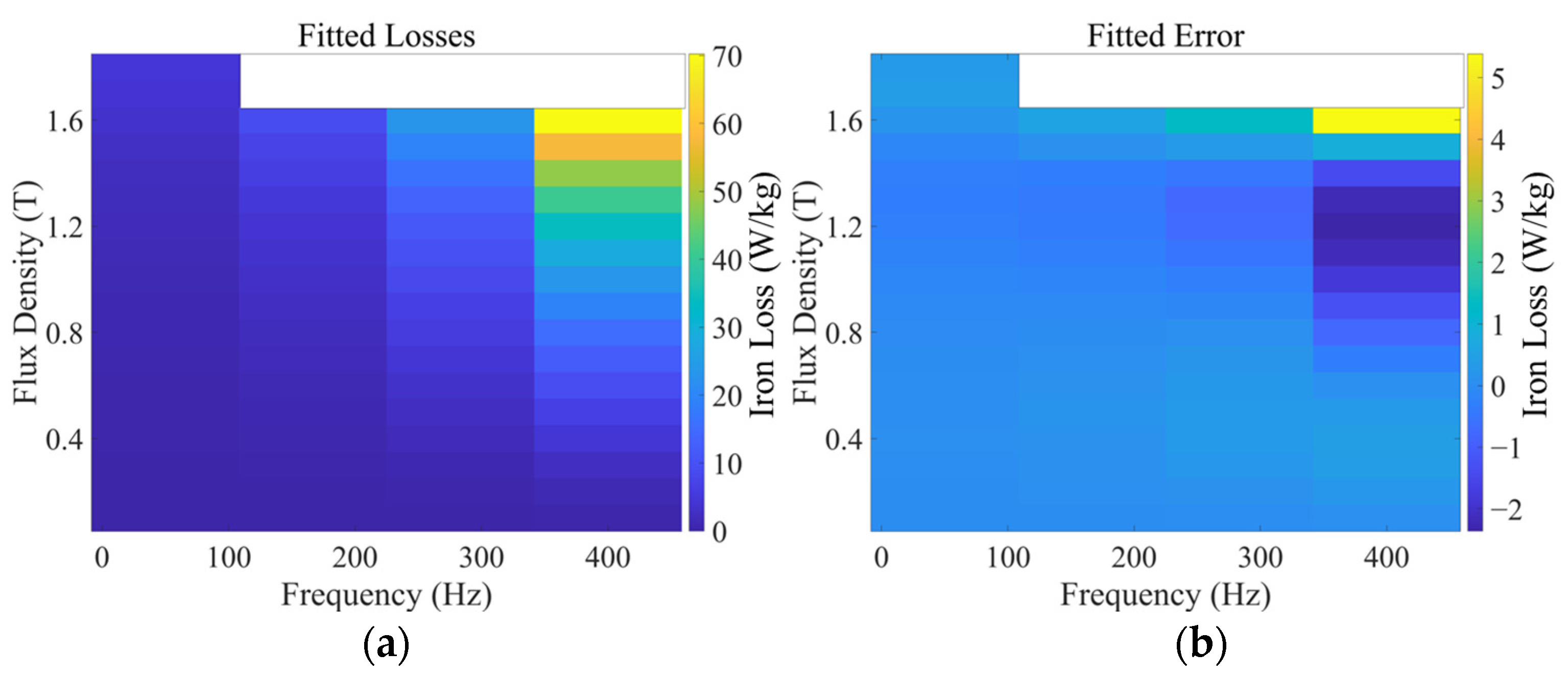
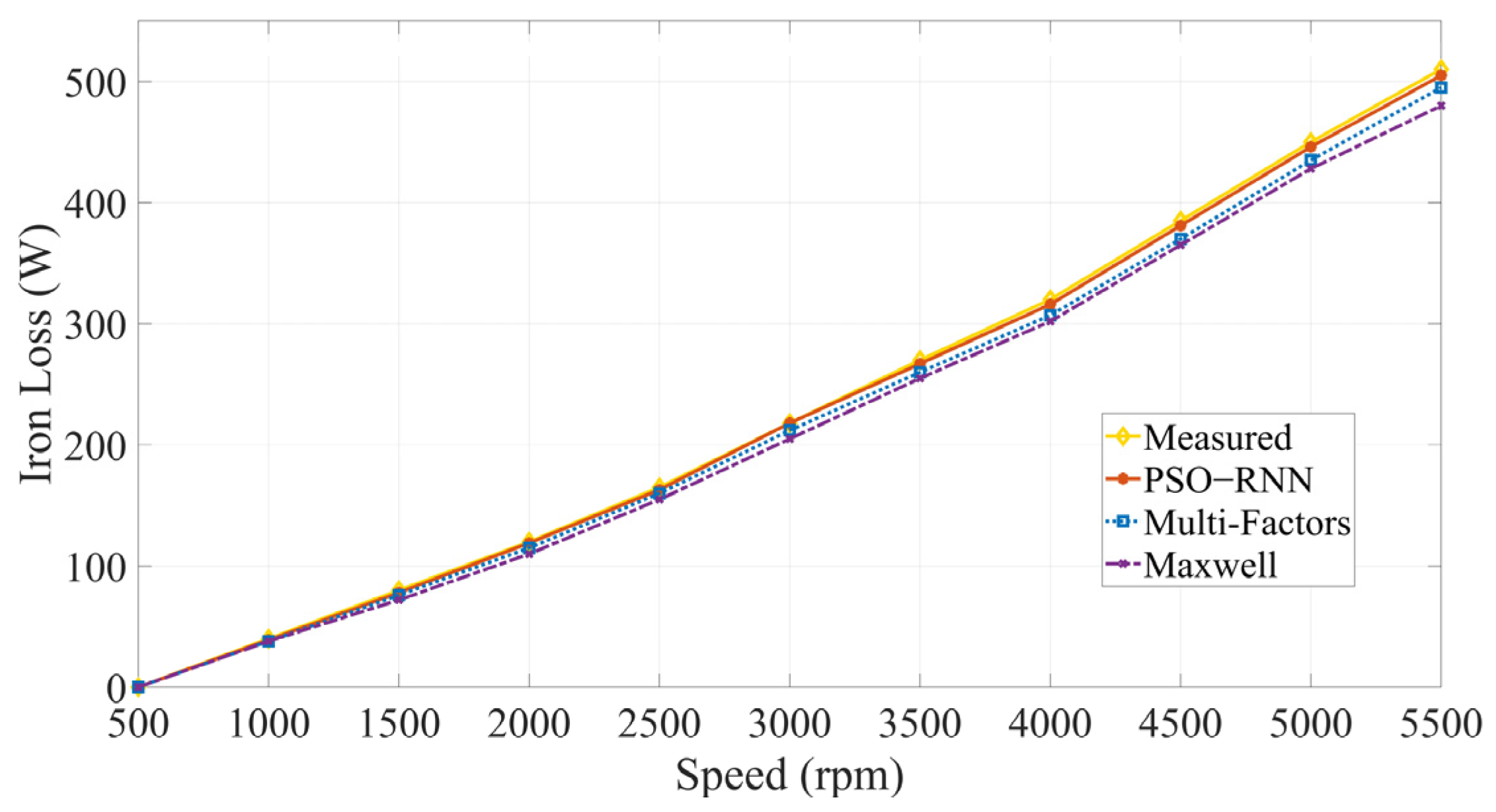
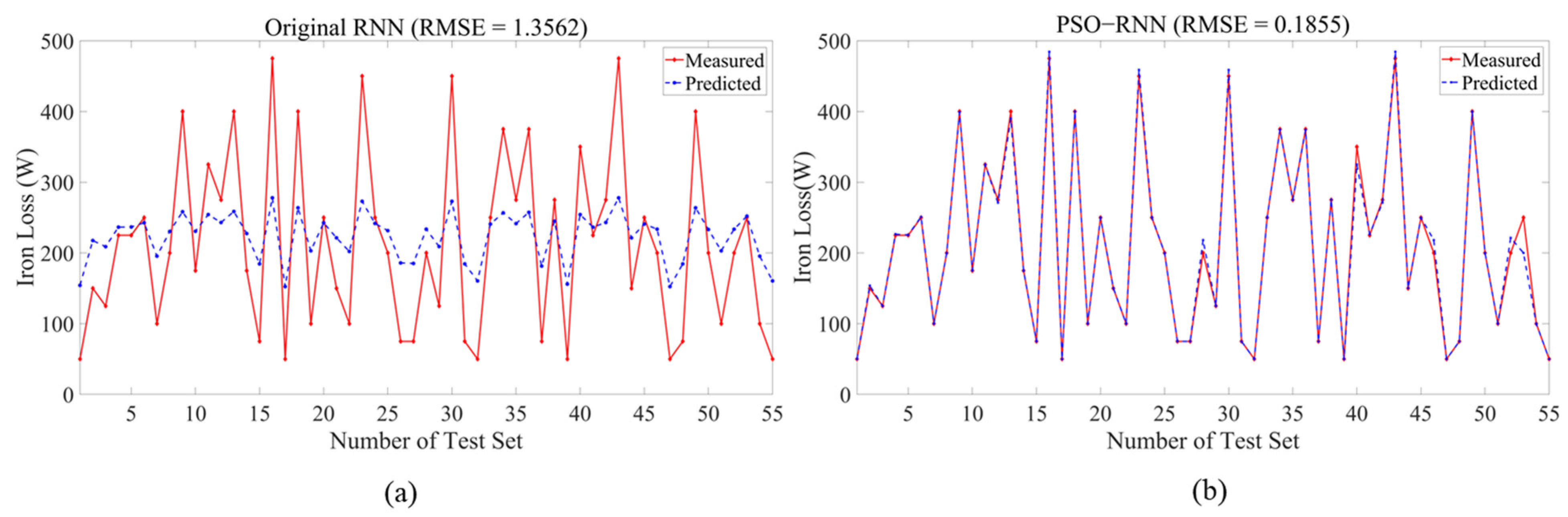
4. Result Analysis
5. Conclusions
6. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Boubaker, N.; Matt, D.; Enrici, P.; Nierlich, F.; Durand, G. Measurements of iron loss in PMSM stator cores based on CoFe and SiFe lamination sheets and stemmed from different manufacturing processes. IEEE Trans. Magn. 2018, 55, 1–9. [Google Scholar] [CrossRef]
- Tong, W.; Sun, R.; Zhang, C.; Wu, S.; Tang, R. Loss and thermal analysis of a high-speed surface-mounted PMSM with amorphous metal stator core and titanium alloy rotor sleeve. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Zhang, C.; Guo, Q.; Li, L.; Wang, M.; Wang, T. System efficiency improvement for electric vehicles adopting a permanent magnet synchronous motor direct drive system. Energies 2017, 10, 2030. [Google Scholar] [CrossRef]
- Balamurali, A.; Kundu, A.; Li, Z.; Kar, N.C. Improved harmonic iron loss and stator current vector determination for maximum efficiency control of PMSM in EV applications. IEEE Trans. Ind. Appl. 2020, 57, 363–373. [Google Scholar] [CrossRef]
- Bertotti, G.; Boglietti, A.; Chiampi, M.; Chiarabaglio, D.; Fiorillo, F.; Lazzari, M. An improved estimation of iron losses in rotating electrical machines. IEEE Trans. Magn. 1991, 27, 5007–5009. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Fu, W.; Badics, Z.; Cendes, Z. A dynamic core loss model for soft ferromagnetic and power ferrite materials in transient finite element analysis. IEEE Trans. Magn. 2004, 40, 1318–1321. [Google Scholar] [CrossRef]
- Steentjes, S.; Leßmann, M.; Hameyer, K. Advanced iron-loss calculation as a basis for efficiency improvement of electrical machines in automotive application. In Proceedings of the 2012 Electrical Systems for Aircraft, Railway and Ship Propulsion, Bologna, Italy, 16–18 October 2012; pp. 1–6. [Google Scholar]
- Fratila, M.; Benabou, A.; Tounzi, A.; Dessoude, M. Iron loss calculation in a synchronous generator using finite element analysis. IEEE Trans. Energy Convers. 2017, 32, 640–648. [Google Scholar] [CrossRef]
- Yamazaki, K.; Sato, Y.; Domenjoud, M.; Daniel, L. Iron loss analysis of permanent-magnet machines by considering hysteresis loops affected by multi-axial stress. IEEE Trans. Magn. 2019, 56, 1–4. [Google Scholar] [CrossRef]
- Abdi, S.; Abdi, E.; McMahon, R. A new iron loss model for brushless doubly-fed machines with hysteresis and field rotational losses. IEEE Trans. Energy Convers. 2021, 36, 3221–3230. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, J.; Zhu, J.; Guo, Y. Core loss modeling for permanent-magnet motor based on flux variation locus and finite-element method. IEEE Trans. Magn. 2012, 48, 1023–1026. [Google Scholar] [CrossRef]
- Al-Timimy, A.; Giangrande, P.; Degano, M.; Galea, M.; Gerada, C. Investigation of ac copper and iron losses in high-speed high-power density PMSM. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 3–6 September 2018; pp. 263–269. [Google Scholar]
- Liu, G.; Liu, M.; Zhang, Y.; Wang, H.; Gerada, C. High-speed permanent magnet synchronous motor iron loss calculation method considering multiphysics factors. IEEE Trans. Ind. Electron. 2019, 67, 5360–5368. [Google Scholar] [CrossRef]
- Liu, L.; Ba, X.; Guo, Y.; Lei, G.; Sun, X.; Zhu, J. Improved iron loss prediction models for interior PMSMs considering coupling effects of multiphysics factors. IEEE Trans. Transp. Electrif. 2022, 9, 416–427. [Google Scholar] [CrossRef]
- Yamazaki, K.; Watari, S. Loss analysis of permanent-magnet motor considering carrier harmonics of PWM inverter using combination of 2-D and 3-D finite-element method. IEEE Trans. Magn. 2005, 41, 1980–1983. [Google Scholar] [CrossRef]
- Yamazaki, K.; Abe, A. Loss analysis of interior permanent magnet motors considering carrier harmonics and magnet eddy currents using 3-D FEM. In Proceedings of the 2007 IEEE International Electric Machines & Drives Conference, Antalya, Turkey, 3–5 May 2007; Volume 2, pp. 904–909. [Google Scholar]
- Hwang, S.W.; Lim, M.S.; Hong, J.P. Hysteresis torque estimation method based on iron-loss analysis for permanent magnet synchronous motor. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Lu, H.; Li, Y.; Jin, J. Core loss computation in a permanent magnet transverse flux motor with rotating fluxes. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Denis, N.; Inoue, M.; Fujisaki, K.; Itabashi, H.; Yano, T. Iron loss reduction in permanent magnet synchronous motor by using stator core made of nanocrystalline magnetic material. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Zhu, S.; Dong, J.; Li, Y.; Hua, W. Fast calculation of carrier harmonic iron losses caused by pulse width modulation in interior permanent magnet synchronous motors. IET Electr. Power Appl. 2020, 14, 1163–1176. [Google Scholar] [CrossRef]
- Barcaro, M.; Bianchi, N.; Magnussen, F. Rotor flux-barrier geometry design to reduce stator iron losses in synchronous IPM motors under FW operations. IEEE Trans. Ind. Appl. 2010, 46, 1950–1958. [Google Scholar] [CrossRef]
- Arkadan, A.; Hijazi, T.; Masri, B. Design evaluation of conventional and toothless stator wind power axial-flux PM generator. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.G.; Lin, Z.W.; Zhong, J.J. 3D vector magnetic properties of soft magnetic composite material. J. Magn. Magn. Mater. 2006, 302, 511–516. [Google Scholar] [CrossRef]
- Huang, Z.; Fang, J.; Liu, X.; Han, B. Loss calculation and thermal analysis of rotors supported by active magnetic bearings for high-speed permanent-magnet electrical machines. IEEE Trans. Ind. Electron. 2015, 63, 2027–2035. [Google Scholar] [CrossRef]
- Popescu, M.; Ionel, D.M.; Boglietti, A.; Cavagnino, A.; Cossar, C.; McGilp, M.I. A general model for estimating the laminated steel losses under PWM voltage supply. IEEE Trans. Ind. Appl. 2010, 46, 1389–1396. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, T.; Zhao, H.; Wu, T. An analytical iron loss calculation model of inverter-fed induction motors considering supply and slot harmonics. IEEE Trans. Ind. Electron. 2019, 66, 9194–9204. [Google Scholar] [CrossRef]
- Popescu, M.; Ionel, D.M. A best-fit model of power losses in cold rolled-motor lamination steel operating in a wide range of frequency and magnetization. IEEE Trans. Magn. 2007, 43, 1753–1756. [Google Scholar] [CrossRef]
- Bi, L.; Schäfer, U.; Hu, Y. A new high-frequency iron loss model including additional iron losses due to punching and burrs’ connection. IEEE Trans. Magn. 2020, 56, 1–9. [Google Scholar] [CrossRef]
- Ionel, D.M.; Popescu, M.; Dellinger, S.J.; Miller, T.; Heideman, R.J.; McGilp, M.I. On the variation with flux and frequency of the core loss coefficients in electrical machines. IEEE Trans. Ind. Appl. 2006, 42, 658–667. [Google Scholar] [CrossRef]
- Jia, W.; Xiao, L.; Zhu, D.; Wei, J. An improved core-loss calculation method with variable coefficients based on equivalent frequency. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar]
- Chen, J.; Wang, D.; Jiang, Y.; Teng, X.; Cheng, S.; Hu, J. Examination of temperature-dependent iron loss models using a stator core. IEEE Trans. Magn. 2018, 54, 1–7. [Google Scholar] [CrossRef]
- Seo, K.S.; Kim, H.D.; Lee, K.H.; Park, I.H. Numerical and experimental characterization of thread-type magnetic core with low eddy current loss. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar] [CrossRef]
- Han, S.H.; Jahns, T.M.; Zhu, Z.Q. Analysis of rotor core eddy-current losses in interior permanent-magnet synchronous machines. IEEE Trans. Ind. Appl. 2009, 46, 196–205. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Liu, C.; Lei, G.; Guo, Y.; Zhu, J. Reduction of magnet eddy current loss in PMSM by using partial magnet segment method. IEEE Trans. Magn. 2019, 55, 1–5. [Google Scholar] [CrossRef]
- Steentjes, S.; von Pfingsten, G.; Hombitzer, M.; Hameyer, K. Iron-loss model with consideration of minor loops applied to FE-simulations of electrical machines. IEEE Trans. Magn. 2013, 49, 3945–3948. [Google Scholar] [CrossRef]
- Ruuskanen, V.; Nerg, J.; Rilla, M.; Pyrhönen, J. Iron loss analysis of the permanent-magnet synchronous machine based on finite-element analysis over the electrical vehicle drive cycle. IEEE Trans. Ind. Electron. 2016, 63, 4129–4136. [Google Scholar] [CrossRef]
- Marracci, M.; Tellini, B. Hysteresis losses of minor loops versus temperature in MnZn ferrite. IEEE Trans. Magn. 2012, 49, 2865–2869. [Google Scholar] [CrossRef]
- Shimizu, K.; Furuya, A.; Uehara, Y.; Fujisaki, J.; Kawano, H.; Tanaka, T.; Ataka, T.; Oshima, H. Loss simulation by finite-element magnetic field analysis considering dielectric effect and magnetic hysteresis in EI-Shaped Mn–Zn ferrite core. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Krings, A.; Soulard, J. Overview and comparison of iron loss models for electrical machines. J. Electr. Eng. 2010, 10, 8. [Google Scholar]
- Jing, Y.; Zhang, Y.; Zhu, J. Iron Loss Calculation of High Frequency Transformer Based on A Neural Network Dynamic Hysteresis Model. In Proceedings of the 2022 IEEE 20th Biennial Conference on Electromagnetic Field Computation (CEFC), Denver, CO, USA, 24–26 October 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Reljić, D.D.; Matić, D.Z.; Jerkan, D.G.; Oros, D.V.; Vasić, V.V. The estimation of iron losses in a non-oriented electrical steel sheet based on the artificial neural network and the genetic algorithm approaches. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 51–57. [Google Scholar] [CrossRef]
- Truong, P.H.; Flieller, D.; Nguyen, N.K.; Mercklé, J.; Dat, M.T. Optimal efficiency control of synchronous reluctance motors-based ANN considering cross magnetic saturation and iron losses. In Proceedings of the IECON 2015—41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 004690–004695. [Google Scholar] [CrossRef]
- Baosteel, B. Cold-Rolled Non-Oriented Electrical Steel. 2023. Available online: https://ecommerce.ibaosteel.com/portal/download/manual/NGO.pdf (accessed on 27 November 2023).
- Baosteel, B. Baosteel Products Electrical Steel. 2023. Available online: http://esales.baosteel.com/baosteel_products/eleSteel/en/products/products_04_2.jsp (accessed on 25 November 2023).
- Sun, X.; Shi, Z.; Lei, G.; Guo, Y.; Zhu, J. Multi-objective design optimization of an IPMSM based on multilevel strategy. IEEE Trans. Ind. Electron. 2020, 68, 139–148. [Google Scholar] [CrossRef]
- Guo, Y.; Zhu, J.; Lu, H.; Lin, Z.; Li, Y. Core loss calculation for soft magnetic composite electrical machines. IEEE Trans. Magn. 2012, 48, 3112–3115. [Google Scholar] [CrossRef]
- Lei, G.; Zhu, J.; Guo, Y. Multidisciplinary Design Optimization Methods for Electrical Machines and Drive Systems; Springer: Berlin/Heidelberg, Germany, 2016; Volume 691. [Google Scholar]
- Xu, K.; Guo, Y.; Lei, G.; Liu, L.; Zhu, J. Calculation of Iron Loss in Permanent Magnet Synchronous Motors Based on PSO-RNN. In Proceedings of the 2023 IEEE International Magnetic Conference-Short Papers (INTERMAG Short Papers), Sendai, Japan, 15–19 May 2023; pp. 1–2. [Google Scholar]
- Xu, K.; Guo, X.H.; Dai, J.Q.; Du, S.F.; Wang, Z.X.; Wang, Q.X. An Improved PSO for SHEPWM Applied to Three-Level Topology-based PMSM Driver System. J. Comput. 2019, 30, 195–206. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A study of particle swarm optimization particle trajectories. Inf. Sci. 2006, 176, 937–971. [Google Scholar] [CrossRef]
- Singh, L.; Dutta, N. Various Optimization algorithm used in CRN. In Proceedings of the 2020 International Conference on Computation, Automation and Knowledge Management (ICCAKM), Dubai, United Arab Emirates, 9–10 January 2020; pp. 95–100. [Google Scholar]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle swarm optimization: A comprehensive survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in sparrow search algorithm: A comprehensive survey. Arch. Comput. Methods Eng. 2023, 30, 427–455. [Google Scholar] [CrossRef] [PubMed]
- Rana, N.; Latiff, M.S.A.; Abdulhamid, S.M.; Chiroma, H. Whale optimization algorithm: A systematic review of contemporary applications, modifications and developments. Neural Comput. Appl. 2020, 32, 16245–16277. [Google Scholar] [CrossRef]




| Loss Model Name | Expression | No. of Parameters |
|---|---|---|
| Steinmetz [39] | 3 | |
| Steinmetz with eddy current loss | 4 | |
| Bertotti [5] | 4 | |
| ANSYS Maxwell [6] | 3 | |
| Improved loss model [7] | 5 |
| Name | Value |
|---|---|
| Population size | 100 |
| Acceleration constant C1 and C2 | 1.4 |
| Inertia weight | 0.9 |
| Inertia weight | 0.4 |
| Particle dimension | 1 |
| Maximum number of iterations | 30 |
| Name | Value |
|---|---|
| Dimension of hidden layer | 13 |
| Dimension of output layer | 1 |
| Dimension of input layer | 1 |
| Number of recurrent layers | 3 |
| Number of features in the hidden state | 6 |
| Number of input sizes | 3 |
| Name | Unit | Value |
|---|---|---|
| Stator outer radius | mm | 196 |
| Rotor outer radius | mm | 134 |
| Core length | mm | 108 |
| Airgap length | mm | 0.5 |
| Number of poles | - | 8 |
| Number of slots | - | 48 |
| Rated power | kW | 20 |
| Rated torque | Nm | 53 |
| Rated speed | rpm | 3600 |
| PM Material | - | NdFeB-35 |
| Core material | - | 35WW360 |
| Maximum speed | rpm | 5500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, K.; Guo, Y.; Lei, G.; Zhu, J. Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network. Magnetism 2023, 3, 327-342. https://doi.org/10.3390/magnetism3040025
Xu K, Guo Y, Lei G, Zhu J. Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network. Magnetism. 2023; 3(4):327-342. https://doi.org/10.3390/magnetism3040025
Chicago/Turabian StyleXu, Kai, Youguang Guo, Gang Lei, and Jianguo Zhu. 2023. "Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network" Magnetism 3, no. 4: 327-342. https://doi.org/10.3390/magnetism3040025
APA StyleXu, K., Guo, Y., Lei, G., & Zhu, J. (2023). Estimation of Iron Loss in Permanent Magnet Synchronous Motors Based on Particle Swarm Optimization and a Recurrent Neural Network. Magnetism, 3(4), 327-342. https://doi.org/10.3390/magnetism3040025









