Neutron Stars and Gravitational Waves: The Key Role of Nuclear Equation of State
Abstract
:1. Introduction
2. Cold Neutron Stars
2.1. The Momentum-Dependent Interaction Nuclear Model
2.2. Speed of Sound Formalism
2.3. Construction of the EoS
2.4. Structure Equations
2.4.1. Nonrotating Neutron Stars
2.4.2. Rotating Neutron Stars
3. Hot Neutron Stars
3.1. Thermodynamical Description of Hot Neutron Star Matter
3.2. Bulk Thermodynamic Quantities
3.3. Lepton’s Contribution
3.4. Isothermal Configuration
3.5. Isentropic Configuration and Neutrino Trapping
3.6. Construction of the Hot EoSs
3.7. Rapidly Rotating Hot Neutron Stars
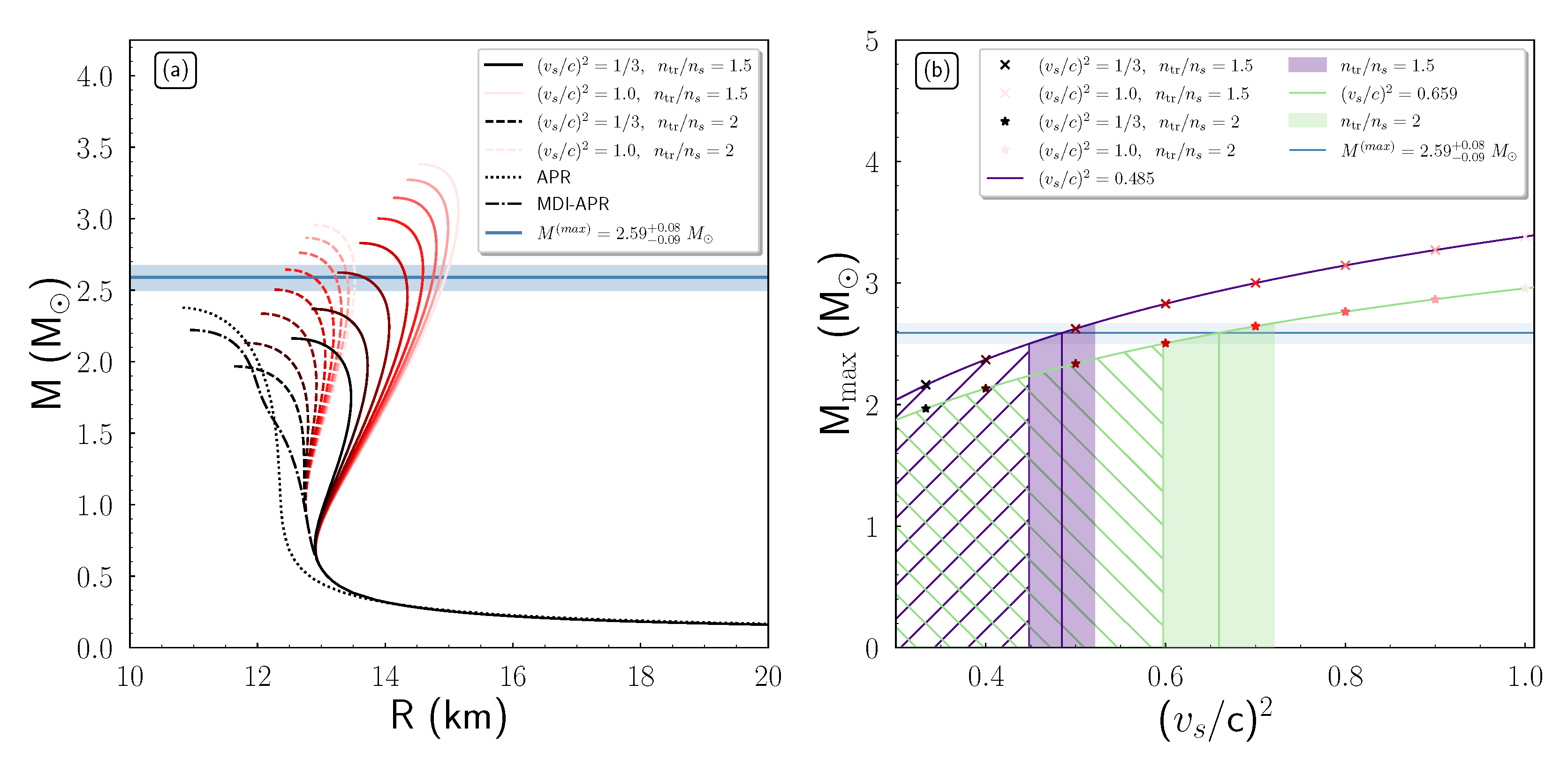
4. Results and Discussion
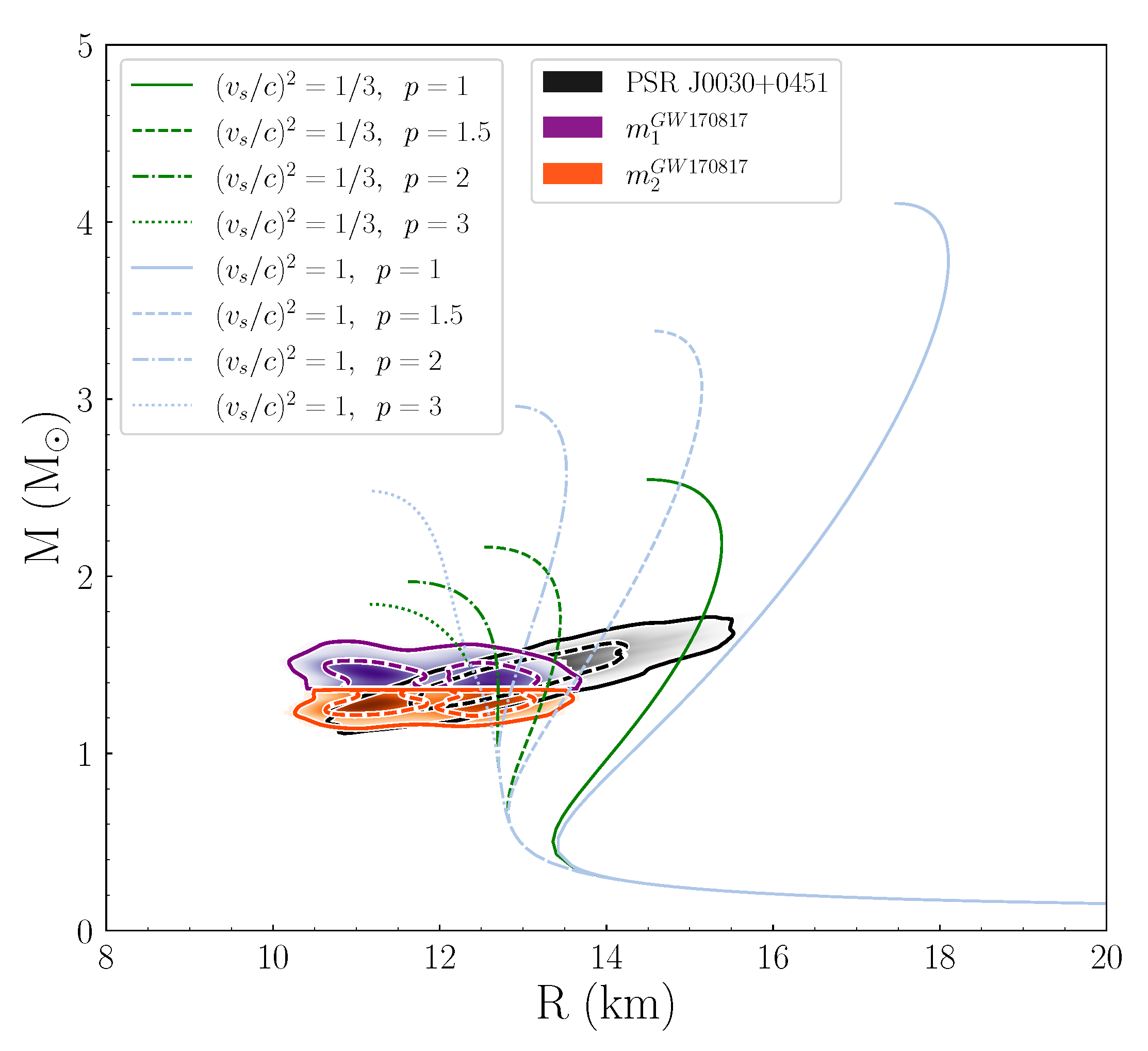
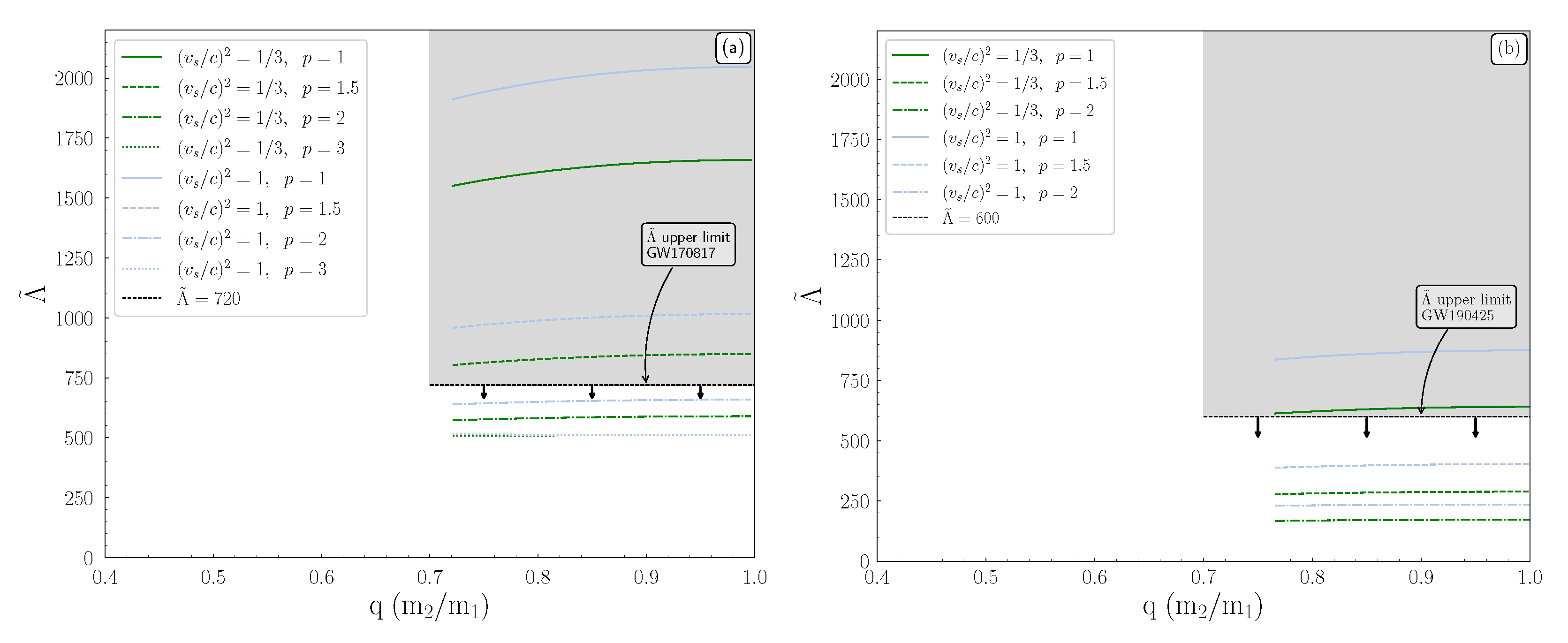
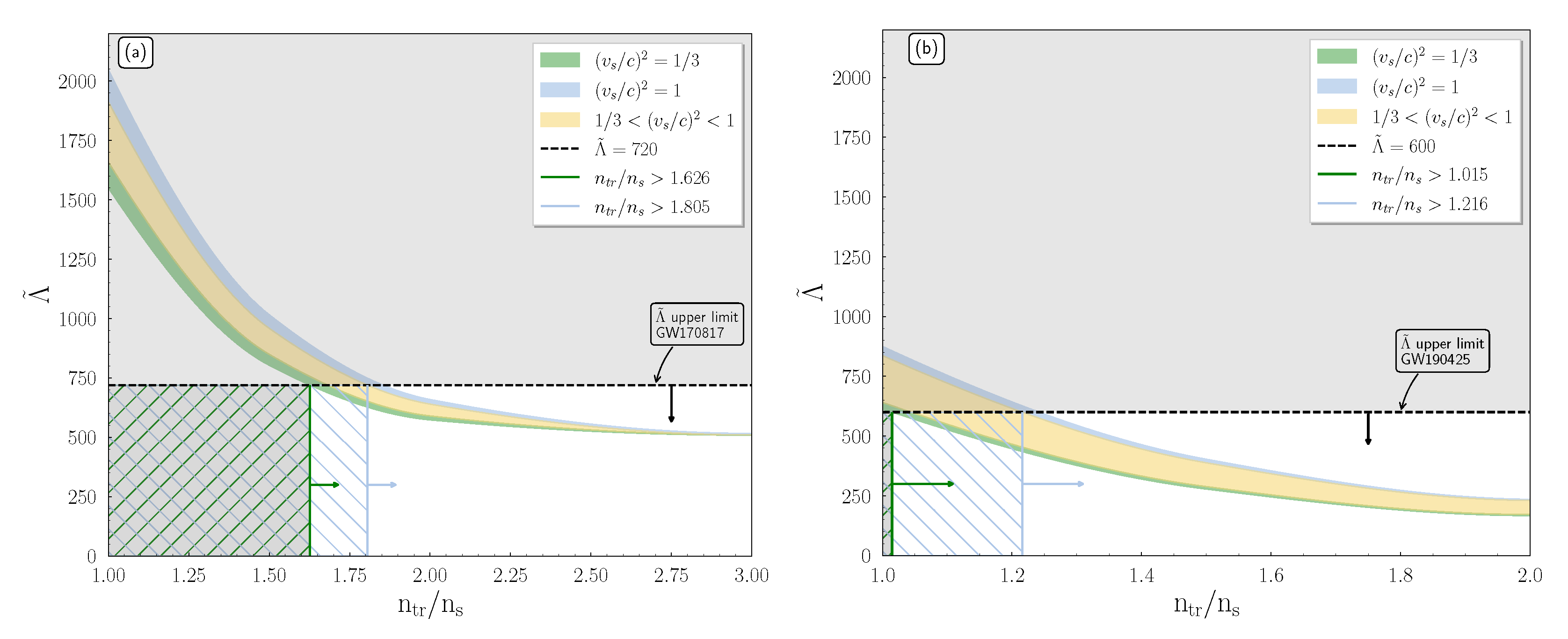
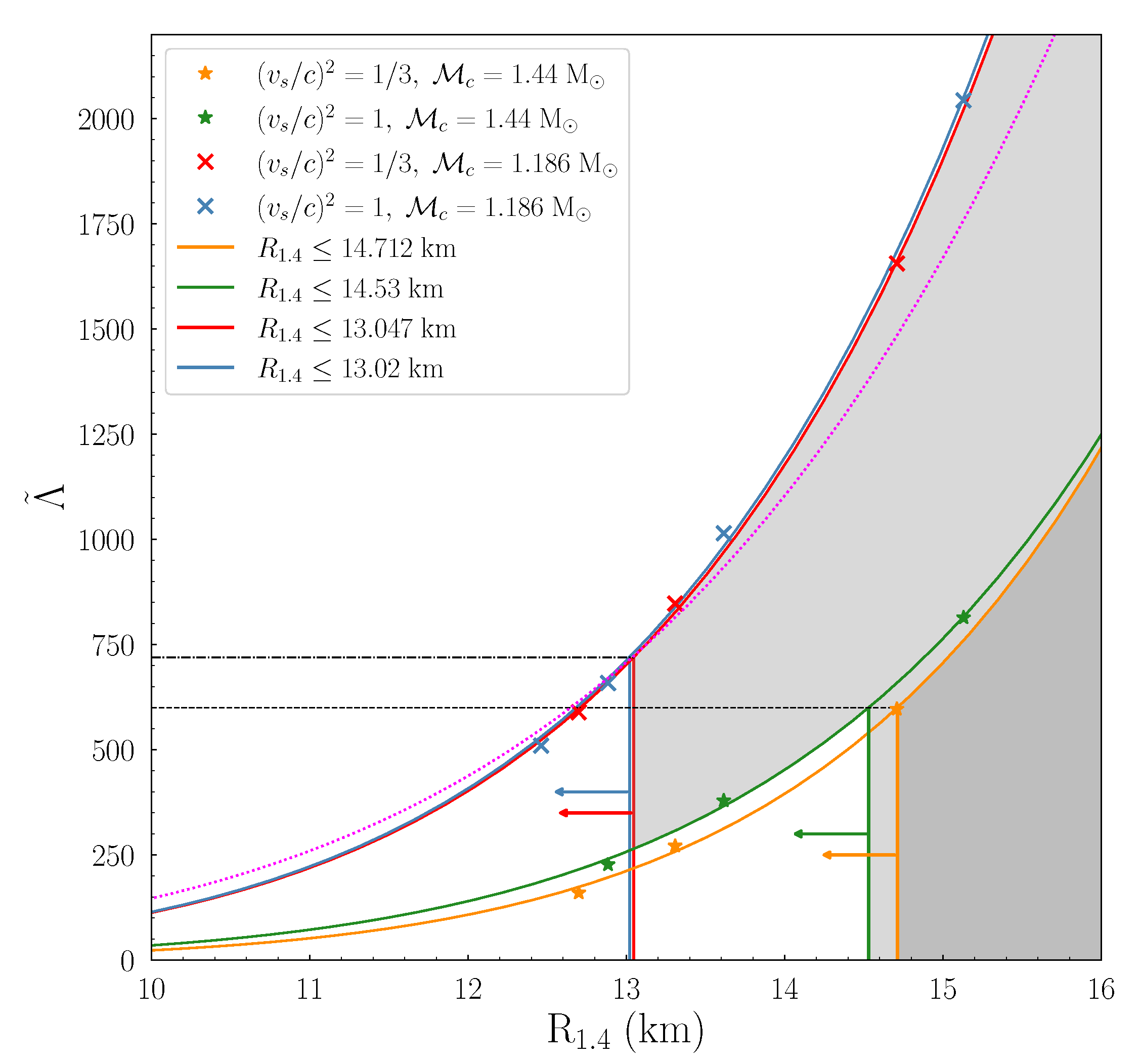
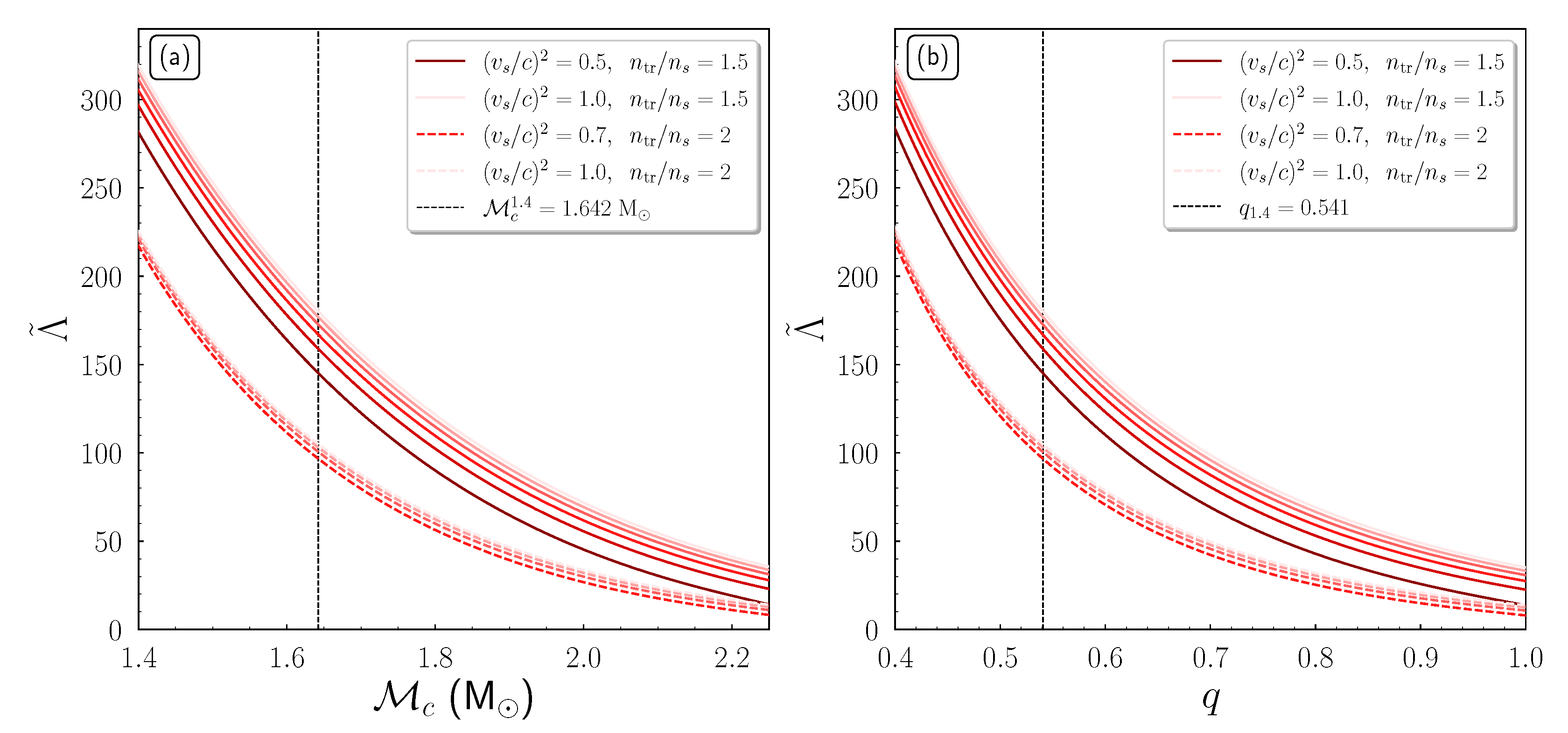
4.1. Speed of Sound and Tidal Deformability
- The overall thickness decreases as the transition density reaches higher values. This behavior can be explained by the variation of the radius presented in the M-R diagram (see Figure 2).
- The thickness of each shaded region decreases as the reaches higher values.
4.2. GW190814: A Postulation of the Most Massive Neutron Star
4.3. The Case of a Very Massive Neutron Star
4.3.1. Isolated Non-Rotating Neutron Star
4.3.2. A Very Massive Neutron Star in a Binary Neutron Stars System
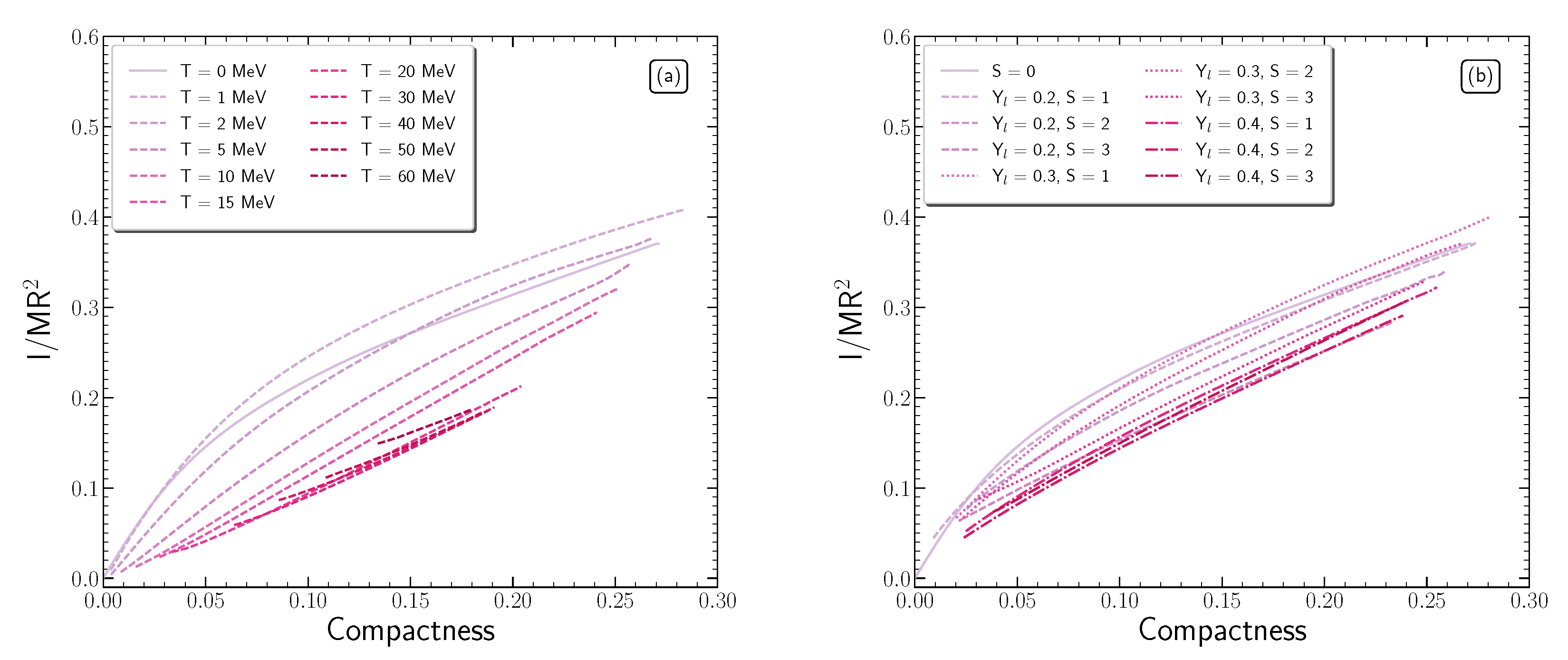
4.4. Finite Temperature Effects on Rapidly Rotating Neutron Stars
4.4.1. Sequences of Constant Baryon Mass
4.4.2. Moment of Inertia, Kerr Parameter, and Ratio
- compactness parameter: and ,
- Kerr parameter: and ,
- ratio : and ,
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EoS | Equation of state |
| MDI | Momentum dependent interaction |
| APR | Akmal, Pandharipande, and Ravenhall |
| SNM | Symmetric nuclear matter |
| ANM | Asymmetric nuclear matter |
| PNM | Pure neutron matter |
| NM | Nuclear model |
| TOV | Tolman-Oppenheimer-Volkoff |
| N.R. | Non-rotating configuration |
| M.R. | Maximally-rotating configuration |
References
- Shapiro, S.; Teukolsky, S. Black Holes, White Dwarfs, and Neutron Stars; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Glendenning, N. Compact Stars: Nuclear Physics, Particle Physics, and General Relativity; Springer: Berlin, Germany, 2000. [Google Scholar]
- Haensel, P.; Potekhin, A.; Yakovlev, D. Neutron Stars 1: Equation of State and Structure; Springer: New York, NY, USA, 2007. [Google Scholar]
- Weinberg, S. Gravitational and Cosmology: Principle and Applications of the General Theory of Relativity; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Zel’dovich, Y.B. The equation of state at ultrahigh densities and its relativistic limitations. Sov. Phys. JETP 1962, 14, 1143–1147. [Google Scholar]
- Zel’dovich, Y.; Novikov, I. Stars and Relativity; Dover Publications, Inc.: Mineapolis, MN, USA; New York, NY, USA, 1971. [Google Scholar]
- Hartle, J.B. Bounds on the mass and moment of inertia of non-rotating neutron stars. Phys. Rep. 1978, 46, 201–247. [Google Scholar] [CrossRef]
- Bedaque, P.; Steiner, A.W. Sound Velocity Bound and Neutron Stars. Phys. Rev. Lett. 2015, 114, 031103. [Google Scholar] [CrossRef]
- Moustakidis, C.C.; Gaitanos, T.; Margaritis, C.; Lalazissis, G.A. Bounds on the speed of sound in dense matter, and neutron star structure. Phys. Rev. C 2017, 95, 045801. [Google Scholar] [CrossRef]
- Reed, B.; Horowitz, C.J. Large sound speed in dense matter and the deformability of neutron stars. Phys. Rev. C 2020, 101, 045803. [Google Scholar] [CrossRef]
- Van Oeveren, E.D.; Friedman, J.L. Upper limit set by causality on the tidal deformability of a neutron star. Phys. Rev. D 2017, 95, 083014. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.L.; Rho, M. Sound velocity and tidal deformability in compact stars. Phys. Rev. D 2019, 100, 114003. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. GW190425: Observation of a Compact Binary Coalescence with Total Mass ∼ 3.4 M ⊙. Astrophys. J. 2020, 892, L3. [Google Scholar] [CrossRef]
- Arzoumanian, Z.; Brazier, A.; Burke-Spolaor, S.; Chamberlin, S.; Chatterjee, S.; Christy, B.; Cordes, J.M.; Cornish, N.J.; Crawford, F.; Cromartie, H.T.; et al. The NANOGrav 11-year Data Set: High-precision Timing of 45 Millisecond Pulsars. Astrophys. J. Suppl. Ser. 2018, 235, 37. [Google Scholar] [CrossRef] [Green Version]
- Antoniadis, J.; Freire, P.; Wex, N.; Tauris, T.; Lynch, R.; van Kerkwijk, M.H.; Kramer, M.; Bassa, C.; Dhillon, V.S.; Driebe, T.; et al. A massive pulsar in a compact relativistic binary. Science 2013, 340. [Google Scholar] [CrossRef] [Green Version]
- Cromartie, H.; Fonseca, E.; Ransom, S.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2020, 4, 72–76. [Google Scholar] [CrossRef] [Green Version]
- Linares, M.; Shahbaz, T.; Casares, J. Peering into the Dark Side: Magnesium Lines Establish a Massive Neutron Star in PSR J2215+5135. Astrophys. J. 2018, 859, 54. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. 2020, 896, L44. [Google Scholar] [CrossRef]
- Tan, H.; Noronha-Hostler, J.; Yunes, N. Neutron Star Equation of State in Light of GW190814. Phys. Rev. Lett. 2020, 125, 261104. [Google Scholar] [CrossRef]
- Datta, S.; Phukon, K.S.; Bose, S. Recognizing black holes in gravitational-wave observations: Challenges in telling apart impostors in mass-gap binaries. arXiv 2021, arXiv:gr-qc/2004.05974. [Google Scholar]
- Alsing, J.; Silva, O.H.; Berti, E. Evidence for a maximum mass cut-off in the neutron star mass distribution and constraints on the equation of state. Mon. Not. R. Astron. Soc. 2018, 478, 1377. [Google Scholar] [CrossRef] [Green Version]
- Farr, W.M.; Chatziioannou, K. A Population-Informed Mass Estimate for Pulsar J0740+6620. Res. Not. Am. Astron. Soc. 2020, 4, 65. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Measurements of Neutron Star Radii and Equation of State. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [Green Version]
- Bethe, H.; Brown, G.; Applegate, J.; Lattimer, J. Equation of state in the gravitational collapse of stars. Nucl. Phys. A 1979, 324, 487–533. [Google Scholar] [CrossRef]
- Brown, G.; Bethe, H.; Baym, G. Supernova theory. Nucl. Phys. A 1982, 375, 481–532. [Google Scholar] [CrossRef]
- Lamb, D.Q.; Lattimer, J.M.; Pethick, C.J.; Ravenhall, D.G. Hot Dense Matter and Stellar Collapse. Phys. Rev. Lett. 1978, 41, 1623–1626. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Ravenhall, D.G. Neutron star matter at high temperatures and densities. I. Bulk properties of nuclear matter. Astrophys. J. 1978, 223, 314–323. [Google Scholar] [CrossRef]
- Lattimer, J.M. The Equation of State of Hot Dense Matter and Supernovae. Ann. Rev. Nucl. Part. Sci. 1981, 31, 337–374. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A generalized equation of state for hot, dense matter. Nucl. Phys. A 1991, 535, 331–376. [Google Scholar] [CrossRef]
- Shen, H.; Toki, H.; Oyamatsu, K.; Sumiyoshi, K. Relativistic equation of state of nuclear matter for supernova and neutron star. Nucl. Phys. A 1998, 637, 435–450. [Google Scholar] [CrossRef] [Green Version]
- Shen, G.; Horowitz, C.J.; O’Connor, E. Second relativistic mean field and virial equation of state for astrophysical simulations. Phys. Rev. C 2011, 83, 065808. [Google Scholar] [CrossRef] [Green Version]
- Wellenhofer, C.; Holt, J.W.; Kaiser, N. Thermodynamics of isospin-asymmetric nuclear matter from chiral effective field theory. Phys. Rev. C 2015, 92, 015801. [Google Scholar] [CrossRef]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of supernova matter: The bulk homogeneous phase. Phys. Rev. C 2014, 89, 065802. [Google Scholar] [CrossRef] [Green Version]
- Constantinou, C.; Muccioli, B.; Prakash, M.; Lattimer, J.M. Thermal properties of hot and dense matter with finite range interactions. Phys. Rev. C 2015, 92, 025801. [Google Scholar] [CrossRef] [Green Version]
- Sammarruca, F.; Machleidt, R.; Millerson, R. Temperature effects on the neutron matter equation of state obtained from chiral effective field theory. Mod. Phys. Lett. A 2020, 35, 2050156. [Google Scholar] [CrossRef]
- Nicotra, O.E.; Baldo, M.; Burgio, G.F.; Schulze, H.-J. Protoneutron stars within the Brueckner-Bethe-Goldstone theory. Astrophys. J. 2006, 451, 213–222. [Google Scholar] [CrossRef] [Green Version]
- Burgio, G.F.; Schulze, H.-J. The maximum and minimum mass of protoneutron stars in the Brueckner theory. Astron. Astrophys. 2010, 518, A17. [Google Scholar] [CrossRef] [Green Version]
- Baldo, M.; Burgio, G. The nuclear symmetry energy. Prog. Part. Nucl. Phys. 2016, 91, 203–258. [Google Scholar] [CrossRef] [Green Version]
- Fortin, M.; Taranto, G.; Burgio, G.F.; Haensel, P.; Schulze, H.J.; Zdunik, J.L. Thermal states of neutron stars with a consistent model of interior. Mon. Not. R. Astron. Soc. 2018, 475, 5010–5022. Available online: https://academic.oup.com/mnras/article-pdf/475/4/5010/24056722/sty147.pdf (accessed on 24 September 2021). [CrossRef] [Green Version]
- Lu, J.J.; Li, Z.H.; Burgio, G.F.; Figura, A.; Schulze, H.J. Hot neutron stars with microscopic equations of state. Phys. Rev. C 2019, 100, 054335. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Lu, J.J.; Li, Z.H.; Chen, C.Y.; Burgio, G.F.; Schulze, H.J. Accurate nuclear symmetry energy at finite temperature within a Brueckner-Hartree-Fock approach. Phys. Rev. C 2021, 103, 024307. [Google Scholar] [CrossRef]
- Figura, A.; Lu, J.J.; Burgio, G.F.; Li, Z.H.; Schulze, H.J. Hybrid equation of state approach in binary neutron-star merger simulations. Phys. Rev. D 2020, 102, 043006. [Google Scholar] [CrossRef]
- Shang, X.L.; Li, A.; Miao, Z.Q.; Burgio, G.F.; Schulze, H.J. Nucleon effective mass in hot dense matter. Phys. Rev. C 2020, 101, 065801. [Google Scholar] [CrossRef]
- Wei, J.B.; Burgio, G.F.; Schulze, H.J.; Zappalà, D. Cooling of hybrid neutron stars with microscopic equations of state. Mon. Not. R. Astron. Soc. 2020, 498, 344–354. Available online: https://academic.oup.com/mnras/article-pdf/498/1/344/33710758/staa1879.pdf (accessed on 24 September 2021). [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. Finite-temperature Extension for Cold Neutron Star Equations of State. Astrophys. J. 2019, 875, 12. [Google Scholar] [CrossRef] [Green Version]
- Pons, J.A.; Reddy, S.; Prakash, M.; Lattimer, J.M.; Miralles, J.A. Evolution of Proto–Neutron Stars. Astrophys. J. 1999, 513, 780–804. [Google Scholar] [CrossRef] [Green Version]
- Prakash, M.; Lattimer, J.; Pons, J.; Steiner, A.; Reddy, S. Evolution of a Neutron Star From its Birth to Old Age. Lect. Not. Phys. 2001, 578, 364–423. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. The equation of state of hot, dense matter and neutron stars. Phys. Rep. 2016, 621, 127–164. [Google Scholar] [CrossRef] [Green Version]
- Perego, A.; Bernouzzi, S.; Radie, D. Thermodynamics conditions of matter in neutron star mergers. Eur. Phys. J. A 2019, 55, 124. [Google Scholar] [CrossRef] [Green Version]
- Bauswein, A.; Janka, H.T.; Oechslin, R. Testing approximations of thermal effects in neutron star merger simulations. Phys. Rev. D 2010, 82, 084043. [Google Scholar] [CrossRef] [Green Version]
- Kaplan, J.D.; Ott, C.D.; O’Connor, E.P.; Kiuchi, K.; Roberts, L.; Duez, M. The Influence of Thermal Pressure on Equilibrium Models of Hypermassive Neutron Star Merger Remnants. Astrophys. J. 2014, 790, 19. [Google Scholar] [CrossRef]
- Tsokaros, A.; Ruiz, M.; Shapiro, S.L.; Sun, L.; Uryū, K.b.o. Great Impostors: Extremely Compact, Merging Binary Neutron Stars in the Mass Gap Posing as Binary Black Holes. Phys. Rev. Lett. 2020, 124, 071101. [Google Scholar] [CrossRef] [Green Version]
- Yasin, H.; Schäfer, S.; Arcones, A.; Schwenk, A. Equation of State Effects in Core-Collapse Supernovae. Phys. Rev. Lett. 2020, 124, 092701. [Google Scholar] [CrossRef] [Green Version]
- Radice, D.; Bernuzzi, S.; Perego, A. The Dynamics of Binary Neutron Star Mergers and GW170817. Ann. Rev. Nucl. Part. Sci. 2020, 70, 95–119. [Google Scholar] [CrossRef]
- Sarin, N.; Lasky, P.D.; Ashton, G. Gravitational waves or deconfined quarks: What causes the premature collapse of neutron stars born in short gamma-ray bursts? Phys. Rev. D 2020, 101, 063021. [Google Scholar] [CrossRef] [Green Version]
- Soma, S.; Bandyopadhyay, D. Properties of Binary Components and Remnant in GW170817 Using Equations of State in Finite Temperature Field Theory Models. Astrophys. J. 2020, 890, 139. [Google Scholar] [CrossRef]
- Sen, D. Nuclear matter at finite temperature and static properties of proto-neutron star. J. Phys. G 2020, 48, 025201. [Google Scholar] [CrossRef]
- Gale, C.; Bertsch, G.; Das Gupta, S. Heavy-ion collision theory with momentum-dependent interactions. Phys. Rev. C 1987, 35, 1666–1671. [Google Scholar] [CrossRef]
- Prakash, M.; Bombaci, I.; Prakash, M.; Ellis, P.J.; Lattimer, J.M.; Knorren, R. Composition and structure of protoneutron stars. Phys. Rep. 1997, 280, 1–77. [Google Scholar] [CrossRef] [Green Version]
- Li, B.A.; Schröder, W.U. Isospin Physics in Heavy-Ion Collisions at Intermediate Energies; Nova Science: New York, NY, USA, 2001. [Google Scholar]
- Li, B.A.; Chen, L.W.; Ko, C.M. Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 2008, 464, 113–281. [Google Scholar] [CrossRef] [Green Version]
- Koliogiannis, P.S.; Moustakidis, C.C. Effects of the equation of state on the bulk properties of maximally rotating neutron stars. Phys. Rev. C 2020, 101, 015805. [Google Scholar] [CrossRef] [Green Version]
- Koliogiannis, P.S.; Moustakidis, C.C. Thermodynamical Description of Hot, Rapidly Rotating Neutron Stars, Protoneutron Stars, and Neutron Star Merger Remnants. Astrophys. J. 2021, 912, 69. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Speed of sound constraints from tidal deformability of neutron stars. Phys. Rev. C 2020, 102, 055801. [Google Scholar] [CrossRef]
- Kanakis-Pegios, A.; Koliogiannis, P.S.; Moustakidis, C.C. Probing the Nuclear Equation of State from the Existence of a ∼2.6 M⊙ Neutron Star: The GW190814 Puzzle. Symmetry 2021, 13, 183. [Google Scholar] [CrossRef]
- Sieniawska, M.; Bejger, M. Continuous Gravitational Waves from Neutron Stars: Current Status and Prospects. Universe 2019, 5, 217. [Google Scholar] [CrossRef] [Green Version]
- Glampedakis, K.; Gualtieri, L. Gravitational Waves from Single Neutron Stars: An Advanced Detector Era Survey. In The Physics and Astrophysics of Neutron Stars; Rezzolla, L., Pizzochero, P., Jones, D.I., Rea, N., Vidaña, I., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 673–736. [Google Scholar] [CrossRef] [Green Version]
- Andersson, N.; Kokkotas, K.D. The r-mode instability in rotating neutron stars. Int. J. Mod. Phys. D 2001, 10, 381–441. [Google Scholar] [CrossRef] [Green Version]
- Özel, F.; Freire, P. Masses, Radii, and the Equation of State of Neutron Stars. Annu. Rev. Astron. Astrophys. 2016, 54, 401–440. [Google Scholar] [CrossRef] [Green Version]
- Chatziioannou, K. Neutron-star tidal deformability and equation-of-state constraints. Gen. Relativ. Gravit. 2020, 52, 109. [Google Scholar] [CrossRef]
- Moustakidis, C.C. Effects of the nuclear equation of state on the r-mode instability and evolution of neutron stars. Phys. Rev. C 2015, 91, 035804. [Google Scholar] [CrossRef]
- Akmal, A.; Pandharipande, V.R.; Ravenhall, D.G. Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 1998, 58, 1804–1828. [Google Scholar] [CrossRef] [Green Version]
- Margaritis, C.; Koliogiannis, P.S.; Moustakidis, C.C. Speed of sound constraints on maximally rotating neutron stars. Phys. Rev. D 2020, 101, 043023. [Google Scholar] [CrossRef] [Green Version]
- Rhoades, C.E.; Ruffini, R. Maximum Mass of a Neutron Star. Phys. Rev. Lett. 1974, 32, 324–327. [Google Scholar] [CrossRef] [Green Version]
- Kalogera, V.; Baym, G. The maximum mass of a neutron star. Astrophys. J. 1996, 470, L61. [Google Scholar] [CrossRef]
- Koranda, S.; Stergioulas, N.; Friedman, J.L. Upper Limits Set by Causality on the Rotation and Mass of Uniformly Rotating Relativistic Stars. Astrophys. J. 1997, 488, 799. [Google Scholar] [CrossRef] [Green Version]
- Chamel, N.; Haensel, P.; Zdunik, J.; Fantina, A. On the Maximum Mass of Neutron Stars. Int. J. Mod. Phys. E 2013, 22, 1330018. [Google Scholar] [CrossRef] [Green Version]
- Podkowka, D.M.; Mendes, R.F.P.; Poisson, E. Trace of the energy-momentum tensor and macroscopic properties of neutron stars. Phys. Rev. D 2018, 98, 064057. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.; Zhu, Z.; Zhou, X.; Li, A. Sound velocity in dense stellar matter with strangeness and compact stars. Chin. Phys. C 2021, 45, 055104. [Google Scholar] [CrossRef]
- Tews, I.; Carlson, J.; Gandolfi, S.; Reddy, S. Constraining the Speed of Sound inside Neutron Stars with Chiral Effective Field Theory Interactions and Observations. Astrophys. J. 2018, 860, 149. [Google Scholar] [CrossRef]
- Feynman, R.; Metropolis, N.; Teller, E. Equations of State of Elements Based on the Generalized Fermi-Thomas Theory. Phys. Rev. 1949, 75, 1561. [Google Scholar] [CrossRef]
- Baym, G.; Pethik, C.; Sutherland, P. The Ground State of Matter at High Densities: Equation of State and Stellar Models. Astrophys. J. 1971, 170, 299. [Google Scholar] [CrossRef]
- Moustakidis, C.C. The stability of relativistic stars and the role of the adiabatic index. Gen. Rel. Grav. 2017, 49, 68. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Prakash, M. Neutron Star Structure and the Equation of State. Astrophys. J. 2001, 550, 426–442. [Google Scholar] [CrossRef] [Green Version]
- Postnikov, S.; Prakash, M.; Lattimer, J.M. Tidal Love numbers of neutron and self-bound quark stars. Phys. Rev. D 2010, 82, 024016. [Google Scholar] [CrossRef] [Green Version]
- Lattimer, J.M.; Prakash, M. Ultimate Energy Density of Observable Cold Baryonic Matter. Phys. Rev. Lett. 2005, 94, 111101. [Google Scholar] [CrossRef] [PubMed]
- Lattimer, J.M.; Prakash, M. Nuclear matter and its role in supernovae, neutron stars and compact object binary mergers. Phys. Rep. 2000, 333–334, 121–146. [Google Scholar] [CrossRef] [Green Version]
- Baiotti, L. Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 2019, 109, 103714. [Google Scholar] [CrossRef] [Green Version]
- Flanagan, E.E.; Hinderer, T. Constraining neutron-star tidal Love numbers with gravitational-wave detectors. Phys. Rev. D 2008, 77, 021502. [Google Scholar] [CrossRef] [Green Version]
- Hinderer, T. Tidal Love Numbers of Neutron Stars. Astrophys. J. 2008, 677, 1216–1220. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef] [Green Version]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef] [Green Version]
- Fattoyev, F.J.; Carvajal, J.; Newton, W.G.; Li, B.A. Constraining the high-density behavior of the nuclear symmetry energy with the tidal polarizability of neutron stars. Phys. Rev. C 2013, 87, 015806. [Google Scholar] [CrossRef] [Green Version]
- Lackey, B.D.; Wade, L. Reconstructing the neutron-star equation of state with gravitational-wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2015, 91, 043002. [Google Scholar] [CrossRef] [Green Version]
- Takátsy, J.; Kovács, P. Comment on “Tidal Love numbers of neutron and self-bound quark stars”. Phys. Rev. D 2020, 102, 028501. [Google Scholar] [CrossRef]
- Thorne, K.S. Tidal stabilization of rigidly rotating, fully relativistic neutron stars. Phys. Rev. D 1998, 58, 124031. [Google Scholar] [CrossRef] [Green Version]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.L.; Stergioulas, N. Rotating Relativistic Stars; Cambridge Monographs on Mathematical Physics, Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef] [Green Version]
- Takami, K.; Rezzolla, L.; Yoshida, S. A quasi-radial stability criterion for rotating relativistic stars. Mon. Not. R. Astron. Soc. Lett. 2011, 416, L1–L5. Available online: https://academic.oup.com/mnrasl/article-pdf/416/1/L1/6140636/416-1-L1.pdf (accessed on 24 September 2021). [CrossRef] [Green Version]
- Weih, L.R.; Most, E.R.; Rezzolla, L. On the stability and maximum mass of differentially rotating relativistic stars. Mon. Not. R. Astron. Soc. Lett. 2017, 473, L126–L130. Available online: https://academic.oup.com/mnrasl/article-pdf/473/1/L126/24841378/slx178.pdf (accessed on 24 September 2021). [CrossRef]
- Stergioulas, N. 1996. Available online: http://www.gravity.phys.uwm.edu/rns/ (accessed on 24 September 2021).
- Stergioulas, N.; Friedman, J.L. Comparing Models of Rapidly Rotating Relativistic Stars Constructed by Two Numerical Methods. Astrophys. J. 1995, 444, 306. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I-Numerical method and its application to uniformly rotating polytropes. Mon. Not. R. Astron. Soc. 1989, 237, 355. [Google Scholar] [CrossRef]
- Cook, G.; Shapiro, S.; Teukolsky, S. Rapidly rotating polytropes in general relativity. Astrophys. J. 1994, 422, 227. [Google Scholar] [CrossRef]
- Goodstein, D.L. States of Matter; Dove: New York, NY, USA, 1985. [Google Scholar]
- Fetter, A.L.; Walecka, J.D. Quantum Theory of Many-Particle Systems; Dover: Mineola, NY, USA, 2003. [Google Scholar]
- Prakash, M. The Equation of State and Neutron Star; unpublished; 1994. [Google Scholar]
- Burgio, G.F.; Baldo, M.; Nicotra, O.E.; Schulze, H.J. A microscopic equation of state for protoneutron stars. Astrophys. J. Suppl. 2007, 308, 387–394. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Chen, L.W.; Li, B.A.; Ma, H.R. Effects of isospin and momentum dependent interactions on liquid–gas phase transition in hot asymmetric nuclear matter. Phys. Lett. B 2007, 650, 348–353. [Google Scholar] [CrossRef] [Green Version]
- Moustakidis, C.C. Temperature and momentum dependence of single-particle properties in hot asymmetric nuclear matter. Phys. Rev. C 2008, 78, 054323. [Google Scholar] [CrossRef] [Green Version]
- Moustakidis, C.C.; Panos, C.P. Equation of state for β-stable hot nuclear matter. Phys. Rev. C 2009, 79, 045806. [Google Scholar] [CrossRef] [Green Version]
- Tan, N.H.; Loan, D.T.; Khoa, D.T.; Margueron, J. Mean-field study of hot β-stable protoneutron star matter: Impact of the symmetry energy and nucleon effective mass. Phys. Rev. C 2016, 93, 035806. [Google Scholar] [CrossRef] [Green Version]
- Takatsuka, T.; Nishizaki, S.; Hiura, J. Particular Properties of Dense Supernova Matter. Prog. Theor. Phys. 1994, 92, 779–802. Available online: https://academic.oup.com/ptp/article-pdf/92/4/779/5358408/92-4-779.pdf (accessed on 24 September 2021). [CrossRef]
- Takatsuka, T. Hot Neutron Stars at Birth and Related Problems*). Prog. Theor. Phys. 1996, 95, 901–912. Available online: https://academic.oup.com/ptp/article-pdf/95/5/901/5280763/95-5-901.pdf (accessed on 24 September 2021). [CrossRef] [Green Version]
- Friedman, J.L.; Ipser, J.R.; Sorkin, R.D. Turning Point Method for Axisymmetric Stability of Rotating Relativistic Stars. Astrophys. J. 1988, 325, 722. [Google Scholar] [CrossRef]
- Sorkin, R.D. A Stability Criterion for Many Parameter Equilibrium Families. Astrophys. J. 1982, 257, 847. [Google Scholar] [CrossRef]
- Goussard, J.O.; Haensel, P.; Zdunik, J.L. Rapid uniform rotation of protoneutron stars. Astron. Astrophys. 1997, 321, 822–834. Available online: http://aa.springer.de/papers/7321003/2300822.pdf (accessed on 24 September 2021).
- Marques, M.; Oertel, M.; Hempel, M.; Novak, J. New temperature dependent hyperonic equation of state: Application to rotating neutron star models and I–Q relations. Phys. Rev. C 2017, 96, 045806. [Google Scholar] [CrossRef] [Green Version]
- LORENE. LORENE: Langage Objet pour la RElativité NumériquE. 1998. Available online: https://lorene.obspm.fr/ (accessed on 24 September 2021).
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. 2019, 887, L24. [Google Scholar] [CrossRef] [Green Version]
- Greif, S.K.; Raaijmakers, G.; Hebeler, K.; Schwenk, A.; Watts, A.L. Equation of state sensitivities when inferring neutron star and dense matter properties. Mon. Not. R. Astron. Soc. 2019, 485, 5363–5376. Available online: https://academic.oup.com/mnras/article-pdf/485/4/5363/28262089/stz654.pdf (accessed on 24 September 2021). [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint Constraint on the Neutron Star Equation of State from Multimessenger Observations. Astrophys. J. 2018, 852, L29. [Google Scholar] [CrossRef] [Green Version]
- Tews, I.; Margueron, J.; Reddy, S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys. Rev. C 2018, 98, 045804. [Google Scholar] [CrossRef] [Green Version]
- Radice, D.; Dai, L. Multimessenger parameter estimation of GW170817. Eur. Phys. J. A 2019, 55, 50. [Google Scholar] [CrossRef] [Green Version]
- Kiuchi, K.; Kyutoku, K.; Shibata, M.; Taniguchi, K. Revisiting the Lower Bound on Tidal Deformability Derived by AT 2017gfo. Astrophys. J. 2019, 876, L31. [Google Scholar] [CrossRef] [Green Version]
- Coughlin, M.W.; Dietrich, T.; Doctor, Z.; Kasen, D.; Coughlin, S.; Jerkstrand, A.; Leloudas, G.; McBrien, O.; Metzger, B.D.; O’Shaughnessy, R.; et al. Constraints on the neutron star equation of state from AT2017gfo using radiative transfer simulations. Mon. Not. R. Astron. Soc. 2018, 480, 3871–3878. Available online: https://academic.oup.com/mnras/article-pdf/480/3/3871/33043575/sty2174.pdf (accessed on 24 September 2021). [CrossRef] [Green Version]
- Coughlin, M.W.; Dietrich, T.; Margalit, B.; Metzger, B.D. Multimessenger Bayesian parameter inference of a binary neutron star merger. Mon. Not. R. Astron. Soc. Lett. 2019, 489, L91–L96. Available online: https://academic.oup.com/mnrasl/article-pdf/489/1/L91/30032497/slz133.pdf (accessed on 24 September 2021). [CrossRef]
- Most, E.R.; Weih, L.R.; Rezzolla, L.; Schaffner-Bielich, J. New Constraints on Radii and Tidal Deformabilities of Neutron Stars from GW170817. Phys. Rev. Lett. 2018, 120, 261103. [Google Scholar] [CrossRef] [Green Version]
- Foley, R.J.; Coulter, D.A.; Kilpatrick, C.D.; Piro, A.L.; Ramirez-Ruiz, E.; Schwab, J. Updated parameter estimates for GW190425 using astrophysical arguments and implications for the electromagnetic counterpart. Mon. Not. R. Astron. Soc. 2020, 494, 190–198. Available online: https://academic.oup.com/mnras/article-pdf/494/1/190/32982848/staa725.pdf (accessed on 24 September 2021). [CrossRef] [Green Version]
- Rezzolla, L.; Most, E.R.; Weih, L.R. Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars. Astrophys. J. 2018, 852, L25. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. Tidal Deformability from GW170817 as a Direct Probe of the Neutron Star Radius. Astrophys. J. 2018, 857, L23. [Google Scholar] [CrossRef]
- Zhao, T.; Lattimer, J.M. Tidal deformabilities and neutron star mergers. Phys. Rev. D 2018, 98, 063020. [Google Scholar] [CrossRef] [Green Version]
- De, S.; Finstad, D.; Lattimer, J.M.; Brown, D.A.; Berger, E.; Biwer, C.M. Tidal Deformabilities and Radii of Neutron Stars from the Observation of GW170817. Phys. Rev. Lett. 2018, 121, 091102. [Google Scholar] [CrossRef] [Green Version]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-Wave Constraints on the Neutron-Star-Matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef] [Green Version]
- Fasano, M.; Abdelsalhin, T.; Maselli, A.; Ferrari, V. Constraining the Neutron Star Equation of State Using Multiband Independent Measurements of Radii and Tidal Deformabilities. Phys. Rev. Lett. 2019, 123, 141101. [Google Scholar] [CrossRef] [Green Version]
- Fattoyev, F.J.; Piekarewicz, J.; Horowitz, C.J. Neutron Skins and Neutron Stars in the Multimessenger Era. Phys. Rev. Lett. 2018, 120, 172702. [Google Scholar] [CrossRef] [Green Version]
- Landry, P.; Essick, R.; Chatziioannou, K. Nonparametric constraints on neutron star matter with existing and upcoming gravitational wave and pulsar observations. Phys. Rev. D 2020, 101, 123007. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. R. Astron. Soc. Lett. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Cook, G.; Shapiro, S.; Teukolsky, S. Rapidly Rotating Neutron Stars in General Relativity: Realistic Equations of State. Astrophys. J. 1994, 424, 823. [Google Scholar] [CrossRef]
- Salgado, M.; Bonazzola, S.; Gourgoulhon, E.; Haensel, P. High precision rotating neutron star models 1: Analysis of neutron star properties. Astron. Astrophys. 1994, 291, 155. [Google Scholar]
- Tsang, C.; Tsang, M.; Danielewicz, P.; Fattoyev, F.; Lynch, W. Insights on Skyrme parameters from GW170817. Phys. Lett. B 2019, 796, 1–5. [Google Scholar] [CrossRef]
- Weih, J.B.; Lu, J.J.; Burgio, G.F.; Li, Z.H.; Schulze, H.J. Are nuclear matter properties correlated to neutron star observables? Eur. Phys. J. A 2020, 56, 63. [Google Scholar] [CrossRef]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophy. J. 1974, 191, 507–520. [Google Scholar] [CrossRef]
- Morsink, S.M.; Stergioulas, N.; Blattnig, S.R. Quasi-normal Modes of Rotating Relativistic Stars: Neutral Modes for Realistic Equations of State. Astrophys. J. 1999, 510, 854–861. [Google Scholar] [CrossRef] [Green Version]









| c | ||||||||
| Event | Bounds | ||
|---|---|---|---|
| c | |||
| c | |||
| 0.448 | 0.485 | 0.52 | |||||
| 5.5754 | 0.2742 | −0.6912 | −1.9280 | 0.597 | 0.659 | 0.72 |
| Coefficients | Baryon Mass | |||
|---|---|---|---|---|
| 4.259 | 5.284 | 6.414 | 7.863 | |
| −4.787 | −3.202 | −2.099 | −1.443 | |
| 5.401 | 4.929 | 4.363 | 3.530 | |
| −1.468 | −1.443 | −1.424 | −1.636 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koliogiannis, P.S.; Kanakis-Pegios, A.; Moustakidis, C.C. Neutron Stars and Gravitational Waves: The Key Role of Nuclear Equation of State. Foundations 2021, 1, 217-255. https://doi.org/10.3390/foundations1020017
Koliogiannis PS, Kanakis-Pegios A, Moustakidis CC. Neutron Stars and Gravitational Waves: The Key Role of Nuclear Equation of State. Foundations. 2021; 1(2):217-255. https://doi.org/10.3390/foundations1020017
Chicago/Turabian StyleKoliogiannis, Polychronis S., Alkiviadis Kanakis-Pegios, and Charalampos C. Moustakidis. 2021. "Neutron Stars and Gravitational Waves: The Key Role of Nuclear Equation of State" Foundations 1, no. 2: 217-255. https://doi.org/10.3390/foundations1020017
APA StyleKoliogiannis, P. S., Kanakis-Pegios, A., & Moustakidis, C. C. (2021). Neutron Stars and Gravitational Waves: The Key Role of Nuclear Equation of State. Foundations, 1(2), 217-255. https://doi.org/10.3390/foundations1020017







