Divergence in the Relativistic Mean Field Formalism: A Case Study of the Ground State Properties of the Decay Chain of 214,216,218U Isotopes
Abstract
:1. Introduction
2. Theoretical Framework
Preformed Cluster-Decay Model (PCM)
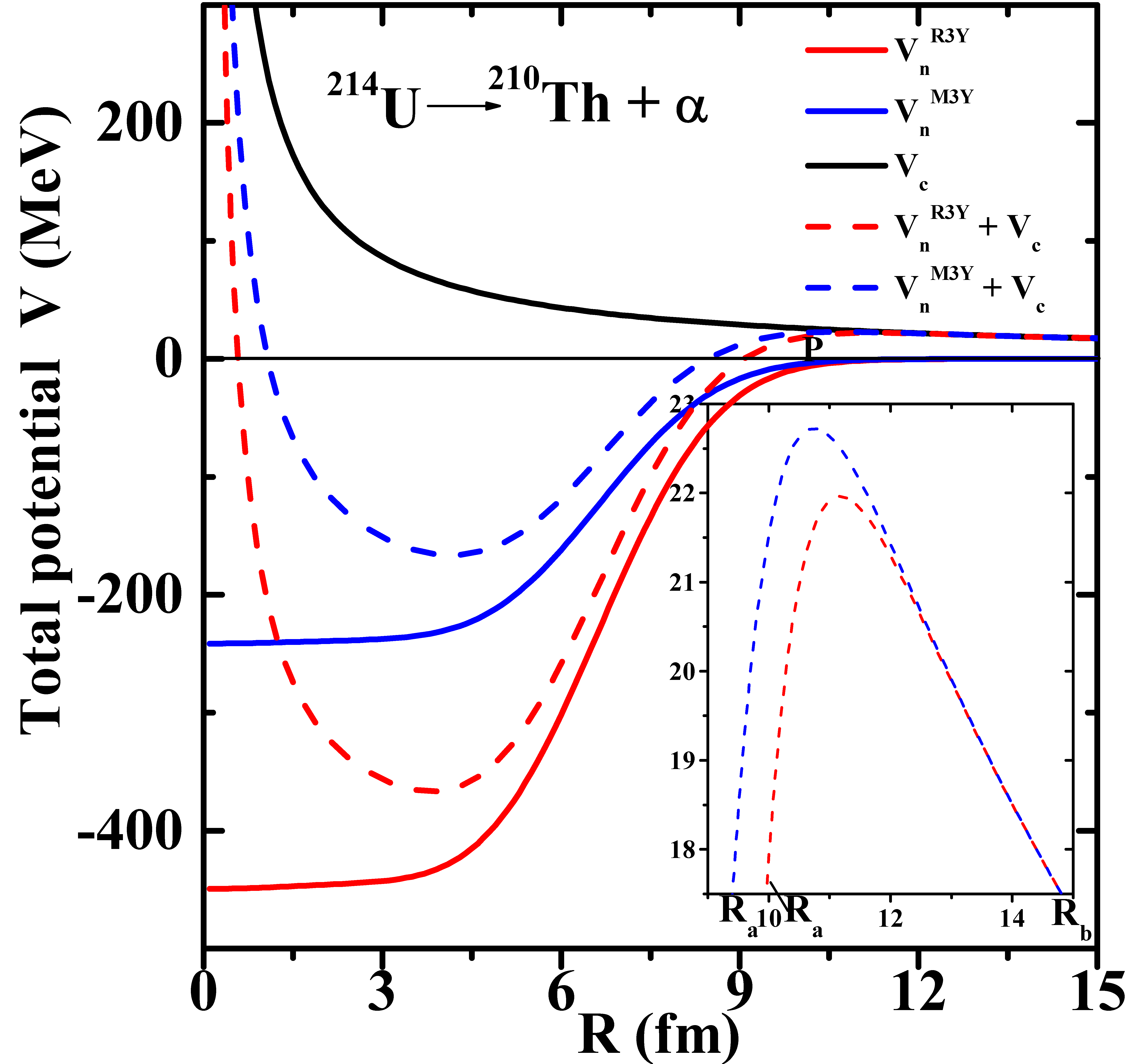
3. Calculations and Discussions
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CSF | Common Scaling Factor |
| PCM | Preformed Cluster-decay Model |
| WKB | Wentzel–Kramers–Brillouin |
| FRDM | Finite-Range-Droplet Model |
| RMF | Relativistic Mean-Field |
| M3Y | Michigan-3-Yukawa |
| R3Y | Relativistic (Mean-Field)-3-Yukawa |
| OPEP | One-Pion Exchange Potential |
| NN | Nucleon–Nucleon |
References
- Geiger, H.; Nuttall, J.M. The ranges of the α particles from various radioactive substances and a relation between range and period of transformation. Philos. Mag. 1911, 22, 613. [Google Scholar] [CrossRef] [Green Version]
- Geiger, H. Reichweitemessungen an α-Strahlen. Z. Phys. 1922, 8, 45. [Google Scholar] [CrossRef]
- Van Duppen, P.; Andreyev, A.N. Alpha decay and beta-delayed fission: Tools for nuclear physics studies. In The Euroschool on Exotic Beams; Scheidenberger, C., Pfutzner, M., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 5, pp. 65–116. [Google Scholar]
- Qi, C.; Liotta, R.; Wyss, R. The single-particle unit for alpha decay. Prog. Part. Nucl. Phys. 2019, 105, 214. [Google Scholar] [CrossRef] [Green Version]
- Gupta, M.; Heinz, S.; Munzenberg, G. Half lives and Q values of nuclei appearing in the α-decay chains of recently reported new isotopes. Rom. J. Phys. 2018, 63, 304. [Google Scholar]
- Bhuyan, M.; Patra, S.K.; Gupta, R.K. Relativistic mean-field study of the properties of Z = 117 nuclei and the decay chains of the 293,294117 isotopes. Phys. Rev. C 2011, 84, 014317. [Google Scholar] [CrossRef] [Green Version]
- Fynbo, H.O.; Diget, C.A.; Bergmann, U.C.; Borge, M.J.; Cederkäll, J.; Dendooven, P.; Fraile, L.M.; Franchoo, S.; Fedosseev, V.N.; Fulton, B.R.; et al. Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances. Nat. Lond. 2005, 433, 136. [Google Scholar] [CrossRef]
- Delion, D.S.; Sandulescu, A.; Greiner, W. Evidence for α clustering in heavy and superheavy nuclei. Phys. Rev. C 2004, 69, 044318. [Google Scholar] [CrossRef]
- Lovas, R.G.; Liotta, R.J.; Insolia, A.; Varga, K.; Delion, D.S. Microscopic theory of cluster radioactivity. Phys. Rep. 1998, 294, 265. [Google Scholar] [CrossRef]
- Seweryniak, D.; Starosta, K.; Davids, C.N.; Gros, S.; Hecht, A.A.; Hoteling, N.; Khoo, T.L.; Lagergren, K.; Lotay, G.; Peterson, D.; et al. α decay of 105Te. Phys. Rev. C 2006, 73, 061301(R). [Google Scholar] [CrossRef]
- Andreyev, A.N.; Huyse, M.; Van Duppen, P.; Weissman, L.; Ackermann, D.; Gerl, J.; Hessberger, F.P.; Hofmann, S.; Kleinböhl, A.; Münzenberg, G.; et al. A triplet of differently shaped spin-zero states in the atomic nucleus 186Pb. Nat. Lond. 2000, 405, 430. [Google Scholar] [CrossRef]
- Andreyev, A.N.; Huyse, M.; Van Duppen, P.; Qi, C.; Liotta, R.J.; Antalic, S.; Ackermann, D.; Franchoo, S.; Hessberger, F.P.; Hofmann, S.; et al. Signatures of the Z = 82 shell closure in α-decay process. Phys. Rev. Lett. 2013, 110, 242502. [Google Scholar] [CrossRef]
- Auranen, K.; Seweryniak, D.; Albers, M.; Ayangeakaa, A.D.; Bottoni, S.; Carpenter, M.P.; Chiara, C.J.; Copp, P.; David, H.M.; Doherty, D.T.; et al. Superallowed α Decay to Doubly Magic 100Sn. Phys. Rev. Lett. 2018, 121, 182501. [Google Scholar] [CrossRef] [Green Version]
- Wauters, J.; Bijnens, N.; Dendooven, P.; Huyse, M.; Hwang, H.Y.; Reusen, G.; von Schwarzenberg, J.; Van Duppen, P.; Kirchner, R.; Roeckl, E. Fine structure in the alpha decay of even-even nuclei as an experimental proof for the stability of the Z = 82 magic shell at the very neutron-deficient side. Phys. Rev. Lett. 1994, 72, 1329. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.Y.; Yang, H.B.; Huang, M.H.; Gan, Z.G.; Yuan, C.X.; Qi, C.; Andreyev, A.N.; Liu, M.L.; Ma, L.; Zhang, M.M.; et al. New α-Emitting Isotope 214U and Abnormal Enhancement of α-Particle Clustering in Lightest Uranium Isotopes. Phys. Rev. Lett. 2021, 126, 152502. [Google Scholar] [CrossRef]
- Sorlin, O.; Porquet, M.G. Nuclear magic numbers: New features far from stability. Prog. Part. Nucl. Phys. 2008, 61, 602. [Google Scholar] [CrossRef] [Green Version]
- Zong-Qiang, S.; Jian-You, G. Study of the Alpha-Decay Chain for 194Rn with Relativistic Mean-Field Theory. Commun. Theor. Phys. 2008, 49, 1583. [Google Scholar] [CrossRef]
- Santhosh, K.P.; Sukumaran, I. Alpha decay studies on Po isotopes using different versions of nuclear potentials. Eur. Phys. J. A 2017, 53, 1. [Google Scholar] [CrossRef]
- Poenaru, D.N.; Ivascu, M.; Greiner, W. Half lives for spontaneous emission of heavy ions from atomic nuclei. International Journal of Radiation Applications and Instrumentation. Part D Nucl. Tracks Radiat. Meas. 1986, 12, 313. [Google Scholar] [CrossRef]
- Cui, J.P.; Xiao, Y.; Gao, Y.H.; Wang, Y.Z. α-decay half-lives of neutron-deficient nuclei. Nucl. Phys. A 2019, 987, 99–111. [Google Scholar] [CrossRef]
- Adel, A.; Abdulghany, A.R. Proton radioactivity and α-decay of neutron-deficient nuclei. Phys. Scr. 2021, 96, 125314. [Google Scholar] [CrossRef]
- Phookan, C.K. α-particle preformation of heavy nuclei using proximity potential. Chin. J. Phys. 2017, 55, 176. [Google Scholar] [CrossRef]
- He, Y.; Yu, X.; Zhang, H.F. Improved empirical formula for α particle preformation factor. Chin. Phys. C 2021, 45, 014110. [Google Scholar] [CrossRef]
- Seif, W.M. The α decay spectroscopic factor of heavy and superheavy nuclei. J. Phys. G Nucl. Part. Phys. 2013, 40, 105102. [Google Scholar] [CrossRef]
- Seif, W.M.; Botros, M.M.; Refaie, A.I. Preformation probability inside α emitters having different ground state spin-parity than their daughters. Phys. Rev. C 2015, 92, 044302. [Google Scholar] [CrossRef] [Green Version]
- Gamow, G. Zur quantentheorie des atomkernes. Z. Phys. 1928, 51, 204. [Google Scholar] [CrossRef]
- Gurney, R.W.; Condon, E.U. Wave mechanics and radioactive disintegration. Nature 1928, 122, 439. [Google Scholar] [CrossRef]
- Niyti, G.; Sawhney, M.K.; Sharma, R.K. Gupta, α-decay chains of recoiled superheavy nuclei: A theoretical study. Phys. Rev. C 2015, 91, 054606. [Google Scholar] [CrossRef]
- Quentin, P.; Flocard, H. Self-consistent calculations of nuclear properties with phenomenological effective forces. Annu. Rev. Nucl. Part. Sci. 1978, 28, 523. [Google Scholar] [CrossRef]
- Hornyak, W. Nuclear Structure; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Schunck, N.; Robledo, L.M. Microscopic theory of nuclear fission: A review. Rep. Prog. Phys. 2016, 79, 116301. [Google Scholar] [CrossRef] [Green Version]
- Vautherin, D.; Brink, D.T. Hartree-Fock calculations with Skyrme’s interaction. I. Spherical nuclei. Phys. Rev. C 1972, 5, 626. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.W.; Meiner, U.G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773. [Google Scholar] [CrossRef]
- Ekström, A.; Baardsen, G.; Forssén, C.; Hagen, G.; Hjorth-Jensen, M.; Jansen, G.R.; Machleidt, R.; Nazarewicz, W.; Papenbrock, T.; Sarich, J.; et al. Optimized chiral nucleon-nucleon interaction at next-to-next-to-leading order. Phys. Rev. Lett. 2013, 110, 192502. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Bhuyan, M.; Patra, S.K.; Gupta, R.K. Optical potential obtained from relativistic-mean-field theory-based microscopic nucleon–nucleon interaction: Applied to cluster radioactive decays. J. Phys. G Nucl. Part. Phys. 2012, 39, 069501. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Bhuyan, M.; Patra, S.K.; Gupta, R.K. A new microscopic nucleon-nucleon interaction derived from relativistic mean field theory. arXiv 2010, arXiv:1011.5732. [Google Scholar]
- Satchler, G.R.; Love, W.G. Folding model potentials from realistic interactions for heavy-ion scattering. Phys. Rep. 1979, 55, 183. [Google Scholar] [CrossRef] [Green Version]
- Biswal, S.K.; El Sheikh, M.A.; Biswal, N.; Yusof, N.; Kassim, H.A.; Patra, S.K.; Bhuyan, M. Nuclear matter properties of finite nuclei using relativistic mean field formalism. Nucl. Phys. A 2020, 1004, 122042. [Google Scholar] [CrossRef]
- Itagaki, N.; Afanasjev, A.V.; Ray, D. Possibility of 14C cluster as a building block of medium-mass nuclei. Phys. Rev. C 2020, 101, 034304. [Google Scholar] [CrossRef] [Green Version]
- Taninah, A.; Agbemava, S.E.; Afanasjev, A.V. Covariant density functional theory: An estimation of systematic uncertainties. Bull. Am. Phys. Soc. 2020, 65, 19. [Google Scholar]
- Horowitz, C.J.; Serot, B.D. Self-consistent hartree description of finite nuclei in a relativistic quantum field theory. Nucl. Phys. A 1981, 368, 503. [Google Scholar] [CrossRef]
- Serot, B.D.; Walecka, J.D. Relativistic nuclear many-body theory. Recent Prog. Many-Body Theor. 1992, 49, 49–92. [Google Scholar]
- Reinhard, P.G. The relativistic mean-field description of nuclei and nuclear dynamics. Rep. Prog. Phys. 1989, 52, 439. [Google Scholar] [CrossRef]
- Ebran, J.P.; Khan, E.; Lasseri, R.; Marevic, P.; Niksic, T.; Sandulescu, N.; Vretenar, D. Investigation of nuclear cluster phenomenology with the relativistic EDF approach. II Nuovo C. C-Colloq. Phys. 2019, 42, 2–3. [Google Scholar]
- Kumar, R.; Sandhu, K.; Sharma, M.K.; Gupta, R.K. Fusion-evaporation residues and α-decay chains of the superheavy element Z = 115 formed in the 243Am+ 48Ca reaction using the dynamical cluster-decay model. Phys. Rev. C 2013, 87, 054610. [Google Scholar] [CrossRef]
- Sharma, K.; Sawhney, G.; Sharma, M.K.; Gupta, R.K. Decay of Plutonium isotopes via spontaneous and heavy-ion induced fission paths. Nucl. Phys. A 2018, 972, 1. [Google Scholar] [CrossRef]
- Deng, J.G.; Zhang, H.F. Analytic formula for estimating the α-particle preformation factor. Phys. Rev. C 2020, 102, 044314. [Google Scholar] [CrossRef]
- Deng, J.G.; Zhang, H.F. Systematic study of α decay half-lives within the Generalized Liquid Drop Model with various versions of proximity energies. Chin. Phys. C 2021, 45, 024104. [Google Scholar] [CrossRef]
- Wentzel, G. Eine verallgemeinerung der quantenbedingungen für die zwecke der wellenmechanik. Z. Physik 1926, 38, 518. [Google Scholar] [CrossRef]
- Kramers, H.A. Wellenmechanik und halbzahlige Quantisierung. Z. Physik 1926, 39, 828. [Google Scholar] [CrossRef]
- Brillouin, L. Schr "o dinger’s undulatory method; a general method of r ’e solution by successive approximations. C. R. Acad. Sci. 1926, 183, 24. [Google Scholar]
- Möller, P.; Sierk, A.J.; Ichikawa, T.; Sagawa, H. Nuclear ground-state masses and deformations: FRDM. At. Data Nucl. Data Tables 2016, 109, 1. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Wang, N.; Deng, Y.; Wu, X. Further improvements on a global nuclear mass model. Phys. Rev. C 2011, 84, 014333. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Patra, S.K.; Gupta, R.K. Cluster radioactive decay within the preformed cluster model using relativistic mean-field theory densities. Phys. Rev. C 2010, 82, 014607. [Google Scholar] [CrossRef]
- Sahu, B.B.; Singh, S.K.; Bhuyan, M.; Biswal, S.K.; Patra, S.K. Importance of nonlinearity in the NN potential. Phys. Rev. C 2014, 89, 034614. [Google Scholar] [CrossRef]
- Bhuyan, M.; Patra, S.K.; Arumugam, P.; Gupta, R.K. Nuclear sub-structure in 112–122Ba nuclei within relativistic mean field theory. Int. J. Mod. Phys. E 2011, 20, 1227. [Google Scholar] [CrossRef] [Green Version]
- Ring, P. Relativistic mean field theory in finite nuclei. Prog. Part. Nucl. Phys. 1996, 37, 193. [Google Scholar] [CrossRef]
- Bhuyan, M. Structural evolution in transitional nuclei of mass 82 ≤ A ≤ 132. Phys. Rev. C 2015, 92, 034323. [Google Scholar] [CrossRef] [Green Version]
- Lalazissis, G.A.; Karatzikos, S.; Fossion, R.; Arteaga, D.P.; Afanasjev, A.V.; Ring, P. The effective force NL3 revisited. Phys. Lett. B 2009, 671, 36. [Google Scholar] [CrossRef] [Green Version]
- Gupta, R.K. Collective clusterization in nuclei and excited compound systems: The dynamical cluster-decay model. In Clusters in Nuclei; Springer: Berlin/Heidelberg, Germany, 2010; pp. 223–265. [Google Scholar]
- Basu, D.N. Folding model analysis of alpha radioactivity. J. Phys. G Nucl. Part. Phys. 2003, 29, 2079. [Google Scholar] [CrossRef] [Green Version]
- Malik, S.S.; Gupta, R.K. Theory of cluster radioactive decay and of cluster formation in nuclei. Phys. Rev. C 1989, 39, 1992. [Google Scholar] [CrossRef]
- Gupta, R.K.; Greiner, W. Cluster radioactivity. Int. J. Mod. Phys. E 1994, 3, 335. [Google Scholar] [CrossRef]
- Matsuse, T.; Beck, C.; Nouicer, R.; Mahboub, D. Extended Hauser-Feshbach method for statistical binary decay of light-mass systems. Phys. Rev. C 1997, 55, 1380. [Google Scholar] [CrossRef] [Green Version]
- Sanders, S.J.; Kovar, D.G.; Back, B.B.; Beck, C.; Henderson, D.J.; Janssens, R.V.F.; Wang, T.F.; Wilkins, B.D. Binary decay of 56Ni formed in the 32+24Mg reaction. Phys. Rev. C 1989, 40, 2091. [Google Scholar] [CrossRef]
- Sanders, S.J. Fusion-fission in nuclear systems with 40 ≤ ACN ≤ 80. Phys. Rev. C 1991, 44, 2676. [Google Scholar] [CrossRef]
- Royer, G.; Normand, C.; Druet, E. Analytic description of the fusion and fission processes through compact quasi-molecular shapes. Nucl. Phys. A 1998, 634, 267. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.; Bao, X.; Zhang, H.; Li, J.; Zhang, H. New numerical method for fission half-lives of heavy and superheavy nuclei at ground and excited states. Nucl. Phys. A 2014, 929, 246. [Google Scholar] [CrossRef]
- Poenaru, D.N. Particle Emission From Nuclei: Volume I: Nuclear Deformation Energy; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Greiner, M.; Scheid, W. Radioactive decay into excited states via heavy ion emission. J. Phys. G Nucl. Part. Phys. 1986, 12, L229. [Google Scholar] [CrossRef]
- Khoa, D.T.; Von Oertzen, W. Refractive alpha-nucleus scattering: A probe for the incompressibility of cold nuclear matter. Phys. Lett. B 1995, 342, 6. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.W.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495. [Google Scholar] [CrossRef]
- Sahoo, T.; Patra, S.K. Search for the stable isotopes for Z = 119 and 121 superheavy elements using relativistic mean field model. Phys. Scr. 2020, 95, 085302. [Google Scholar] [CrossRef]
- Pattnaik, J.A.; Panda, R.N.; Bhuyan, M.; Patra, S.K. Isotopic shift and search of magic number in the superheavy region. Phys. Scr. 2021, 96, 125319. [Google Scholar]
- Hong-Fei, Z.; Jun-Qing, L.; Wei, Z.; Xiao-Hong, Z.; Zai-Guo, G. Systematic study on alpha decay half-lives of superheavy nuclei. Commun. Theor. Phys. 2007, 48, 545. [Google Scholar] [CrossRef]
- Patyk, Z.; Baran, A.; Berger, J.F.; Dechargé, J.; Dobaczewski, J.; Ring, P.; Sobiczewski, A. Masses and radii of spherical nuclei calculated in various microscopic approaches. Phys. Rev. C 1999, 59, 704. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Zhang, Z.Y.; Gan, Z.G.; Yang, H.B.; Yu, L.; Jiang, J.; Wang, J.G.; Tian, Y.L.; Wang, Y.S.; Guo, S.; et al. α-decay properties of the new isotope 216U. Phys. Rev. C 2015, 91, 051302. [Google Scholar] [CrossRef]
- NNDC. National Nuclear Data Center, Chart of Nuclides; Brookhaven National Lab. (BNL): Upton, NY, USA, 2020.
- Niu, Z.M.; Zhu, Z.L.; Niu, Y.F.; Sun, B.H.; Heng, T.H.; Guo, J.Y. Radial basis function approach in nuclear mass predictions. Phys. Rev. C 2013, 88, 024325. [Google Scholar] [CrossRef] [Green Version]
- Leppänen, A.P.; Uusitalo, J.; Leino, M.; Eeckhaudt, S.; Grahn, T.; Greenlees, P.T.; Jones, P.; Julin, R.; Juutinen, S.; Kettunen, H.; et al. α decay studies of the nuclides 218U and 219U. Phys. Rev. C 2007, 75, 054307. [Google Scholar]
- Kumar, S.; Balasubramaniam, M.; Gupta, R.K.; Münzenberg, G.; Scheid, W. The formation and decay of superheavy nuclei produced in 48Ca-induced reactions. J. Phys. G Nucl. Part. Phys. 2003, 29, 625. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Thakur, S.; Kumar, R. Decay studies of 288-287115 alpha-decay chains. J. Phys. G Nucl. Part. Phys. 2009, 36, 105104. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S. α decay chains study for the recently observed superheavy element Z = 117 within the isospin cluster model. Phys. Rev. C 2012, 85, 024320. [Google Scholar] [CrossRef] [Green Version]
- Manjunatha, H.C.; Sowmya, N. Competition between spontaneous fission ternary fission cluster decay and alpha decay in the super heavy nuclei of Z = 126. Nucl. Phys. A 2018, 969, 68. [Google Scholar] [CrossRef]
- Van de Vel, K. Shape Coexistence in Neutron-Deficient Polonium and Lead Nuclei. Ph.D. Thesis, Katholieke Universiteit Leuven, Leuven, Belgium, 2003. [Google Scholar]
- Bender, M.; Cornelius, T.; Lalazissis, G.A.; Maruhn, J.A.; Nazarewicz, W.; Reinhard, P.G. The Z = 82 shell closure in neutron-deficient Pb isotopes. Eur. Phys. J. A-Hadron. Nucl. 2002, 14, 23. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.D.; Zhang, H.F. α decay preformation probabilities across the N = 126 shell closure based on the single particle energy spectra. J. Phys. G Nucl. Part. Phys. 2018, 45, 075106. [Google Scholar] [CrossRef]
- Van Duppen, P.; Huyse, M. Shape coexistence around the Z = 82 closed shell probed by α-decay. Hyperfine Interact. 2000, 129, 149. [Google Scholar] [CrossRef]
- Swain, R.; Patra, S.K.; Sahu, B.B. Nuclear structure and decay modes of Ra isotopes within an axially deformed relativistic mean field model. Chin. Phys. C 2018, 42, 084102. [Google Scholar] [CrossRef]
- Julin, R.; Helariutta, K.; Muikku, M. Intruder states in very neutron-deficient Hg, Pb and Po nuclei. J. Phys. G Nucl. Part. Phys. 2001, 27, R109. [Google Scholar] [CrossRef]
- Sahu, B.; Agarwalla, S.K.; Patra, S.K. Half-lives of proton emitters using relativistic mean field theory. Phys. Rev. C 2011, 84, 054604. [Google Scholar] [CrossRef]
- Leino, M.; Uusitalo, J.; Allatt, R.G.; Armbruster, P.; Enqvist, T.; Eskola, K.; Hofmann, S.; Hurskanen, S.; Jokinen, A.; Ninov, V.; et al. Alpha decay studies of neutron-deficient radium isotopes. Phys. A Hadron. Nucl. 1996, 355, 157. [Google Scholar] [CrossRef]





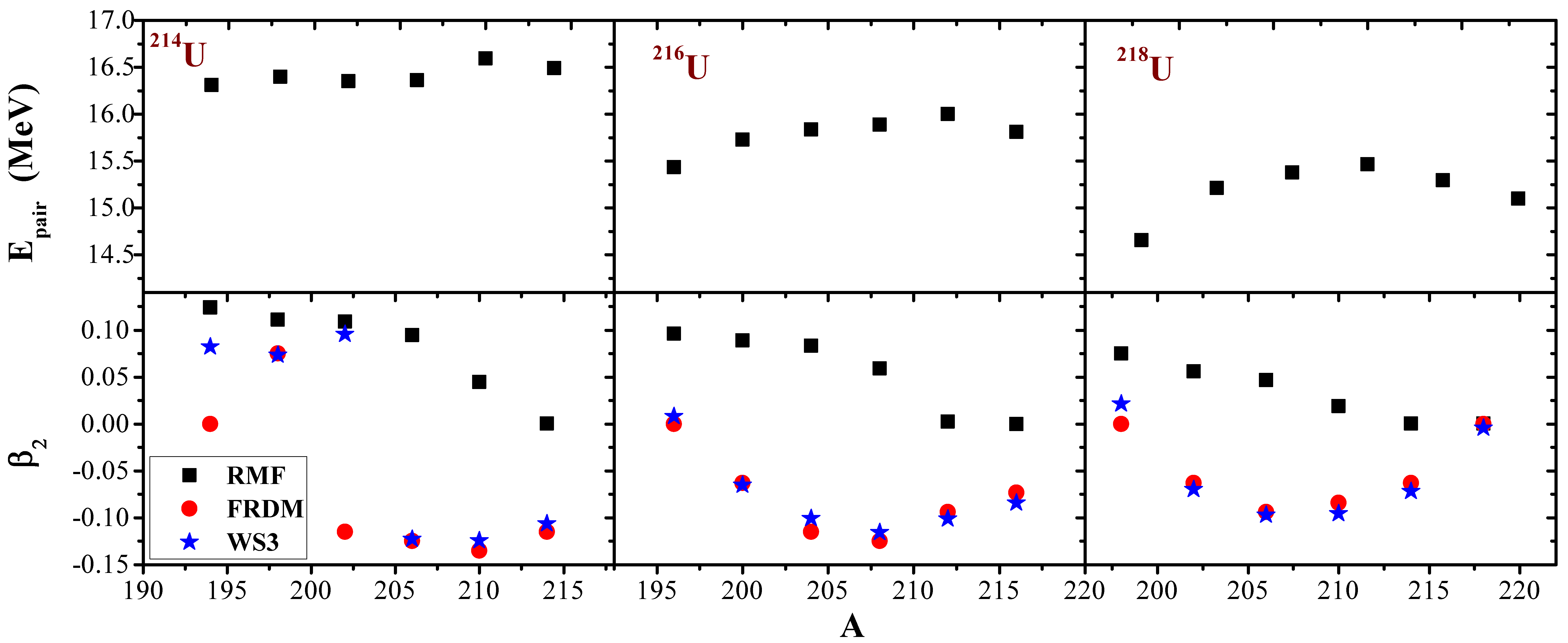

| Nuclei | RMF | FRDM | WS3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B.E | B.E/A | rms | B.E | B.E/A | B.E | B.E/A | |||||||||
| 16.49 | −5.141 | 1640.51 | 7.67 | 5.66 | 5.73 | 5.60 | 5.68 | 0.001 | 1630.22 | 7.62 | −0.115 | 1629.70 | 7.62 | −0.106 | |
| 16.59 | −5.173 | 1618.15 | 7.71 | 5.62 | 5.70 | 5.56 | 5.64 | 0.045 | 1610.37 | 7.67 | −0.135 | 1610.53 | 7.67 | −0.124 | |
| 16.36 | −5.207 | 1596.11 | 7.75 | 5.58 | 5.67 | 5.52 | 5.61 | 0.095 | 1589.89 | 7.72 | −0.125 | 1590.06 | 7.72 | −0.123 | |
| 16.35 | −5.241 | 1573.09 | 7.79 | 5.54 | 5.64 | 5.49 | 5.58 | 0.109 | 1568.87 | 7.77 | −0.115 | 1569.16 | 7.77 | 0.096 | |
| 16.40 | −5.276 | 1549.31 | 7.83 | 5.50 | 5.61 | 5.44 | 5.54 | 0.111 | 1547.43 | 7.82 | 0.075 | 1547.97 | 7.82 | 0.074 | |
| 16.31 | −5.312 | 1524.98 | 7.86 | 5.47 | 5.58 | 5.41 | 5.51 | 0.124 | 1526.18 | 7.87 | 0.000 | 1526.38 | 7.87 | 0.083 | |
| 15.81 | −5.125 | 1659.59 | 7.68 | 5.66 | 5.76 | 5.61 | 5.69 | 0.000 | 1648.69 | 7.63 | −0.073 | 1648.16 | 7.63 | −0.084 | |
| 16.00 | −5.157 | 1637.16 | 7.72 | 5.62 | 5.72 | 5.57 | 5.66 | 0.003 | 1628.74 | 7.68 | −0.094 | 1628.38 | 7.68 | −0.101 | |
| 15.89 | −5.190 | 1614.15 | 7.76 | 5.59 | 5.69 | 5.53 | 5.62 | 0.059 | 1608.11 | 7.73 | −0.125 | 1608.51 | 7.73 | −0.116 | |
| 15.84 | −5.224 | 1590.80 | 7.80 | 5.55 | 5.66 | 5.489 | 5.59 | 0.083 | 1586.94 | 7.78 | −0.115 | 1587.23 | 7.78 | −0.101 | |
| 15.73 | −5.258 | 1566.81 | 7.83 | 5.51 | 5.63 | 5.45 | 5.55 | 0.089 | 1565.52 | 7.83 | −0.063 | 1565.66 | 7.83 | −0.065 | |
| 15.43 | −5.294 | 1542.13 | 7.87 | 5.47 | 5.60 | 5.41 | 5.52 | 0.096 | 1543.48 | 7.88 | 0.000 | 1543.96 | 7.88 | 0.008 | |
| 15.10 | −5.109 | 1677.21 | 7.69 | 5.67 | 5.78 | 5.62 | 5.71 | 0.001 | 1666.17 | 7.64 | 0.000 | 1665.89 | 7.64 | −0.004 | |
| 15.29 | −5.141 | 1655.61 | 7.74 | 5.63 | 5.75 | 5.58 | 5.68 | 0.000 | 1646.39 | 7.69 | −0.063 | 1645.97 | 7.69 | −0.072 | |
| 15.46 | −5.173 | 1632.02 | 7.77 | 5.59 | 5.71 | 5.56 | 5.64 | 0.019 | 1625.80 | 7.74 | −0.084 | 1625.57 | 7.74 | −0.096 | |
| 15.38 | −5.207 | 1608.23 | 7.81 | 5.55 | 5.68 | 5.49 | 5.60 | 0.047 | 1604.44 | 7.79 | −0.094 | 1604.86 | 7.79 | −0.097 | |
| 15.22 | −5.241 | 1583.85 | 7.84 | 5.51 | 5.65 | 5.45 | 5.57 | 0.056 | 1582.71 | 7.84 | −0.063 | 1582.92 | 7.84 | −0.070 | |
| 14.66 | −5.276 | 1558.98 | 7.87 | 5.47 | 5.62 | 5.42 | 5.54 | 0.075 | 1560.26 | 7.88 | 0.000 | 1560.75 | 7.88 | 0.022 | |
| R3Y | M3Y | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| -Transition | Experiment | Q Values (MeV) | Scaling Factor | Scaling Factor | ||||||||||||
| Parent | Daughter | RMF | FRDM | WS3 | RMF | FRDM | WS3 | RMF | FRDM | WS3 | ||||||
| 8.533 | −3.284 | 5.942 | 8.446 | 9.126 | 1.270 | 5.672 | −3.285 | −4.950 | 0.540 | 5.291 | −3.197 | −4.721 | ||||
| 8.069 | −1.790 | 6.247 | 7.816 | 7.831 | 1.537 | 3.913 | −1.789 | −1.835 | 0.590 | 3.654 | −1.846 | −1.889 | ||||
| 7.415 | −0.620 | 5.280 | 7.276 | 7.394 | 1.737 | 8.001 | −0.633 | −1.020 | 0.836 | 7.622 | −0.833 | −1.209 | ||||
| 6.774 | 1.093 | 4.518 | 6.856 | 7.099 | 0.728 | 9.098 | 1.094 | 0.717 | 1.487 | 12.858 | 1.088 | 0.230 | ||||
| 6.309 | 2.270 | 3.966 | 7.046 | 6.710 | 1.469 | 18.299 | 2.269 | 3.404 | 1.302 | 18.525 | 2.271 | 3.433 | ||||
| 8.384 | −2.326 | 5.863 | 8.346 | 8.513 | 1.810 | 7.004 | −2.319 | −2.779 | 0.914 | 6.796 | −2.387 | −2.837 | ||||
| 7.958 | −1.499 | 5.287 | 7.666 | 8.424 | 1.393 | 8.513 | −1.496 | −3.643 | 0.610 | 8.219 | −1.505 | −3.553 | ||||
| 7.273 | 0.137 | 4.951 | 7.126 | 7.019 | 1.913 | 10.236 | 0.119 | 0.492 | 1.110 | 10.291 | 0.214 | 0.584 | ||||
| 6.546 | 2.013 | 4.303 | 6.876 | 6.727 | 0.700 | 10.568 | 2.014 | 2.205 | 0.956 | 15.236 | 2.014 | 2.543 | ||||
| 5.981 | 3.794 | 3.614 | 6.256 | 6.589 | 0.797 | 16.290 | 3.795 | 3.123 | 1.103 | 20.254 | 3.794 | 2.513 | ||||
| 8.775 | −3.292 | 6.692 | 8.516 | 8.366 | 1.318 | 2.609 | −3.293 | −2.896 | 0.592 | 2.316 | −3.293 | −2.920 | ||||
| 7.827 | −1.060 | 4.708 | 7.706 | 7.896 | 1.812 | 12.896 | −1.060 | −1.641 | 0.872 | −9.977 | −1.060 | −1.631 | ||||
| 7.151 | 0.585 | 4.500 | 6.936 | 7.591 | 1.622 | 13.039 | 0.585 | −1.599 | 0.828 | 12.905 | 0.585 | −1.558 | ||||
| 6.384 | 2.740 | 3.924 | 6.566 | 6.353 | 0.964 | 16.978 | 2.741 | 3.486 | 1.188 | 18.083 | 2.740 | 2.735 | ||||
| 5.701 | 5.143 | 3.422 | 5.846 | 6.130 | 1.655 | 21.800 | 5.142 | 3.913 | 0.840 | 21.656 | 5.144 | 3.934 | ||||
| Parent Nuclei | Expt. | R3Y | M3Y | ||||
|---|---|---|---|---|---|---|---|
| R (fm) | Scaling Factor | R (fm) | Scaling Factor | ||||
| −3.284 | 1.249 | −3.285 | 0.544 | −3.200 | |||
| −1.790 | 1.208 | −1.791 | 1.390 | −1.850 | |||
| −0.620 | 1.070 | −0.636 | 0.560 | −0.833 | |||
| 1.093 | 0.728 | 1.098 | 1.010 | 1.104 | |||
| 2.270 | 1.480 | 2.276 | 1.050 | 2.267 | |||
| −2.326 | 1.156 | −2.319 | 0.492 | −2.326 | |||
| −1.499 | 1.399 | −1.499 | 0.730 | −1.501 | |||
| 0.137 | 1.911 | 0.189 | 0.980 | 0.127 | |||
| 2.013 | 1.030 | 2.008 | 0.961 | 2.225 | |||
| 3.794 | 1.710 | 3.816 | 1.400 | 3.796 | |||
| −3.292 | 0.793 | −3.280 | 0.625 | −3.296 | |||
| −1.060 | 0.591 | −1.061 | 1.020 | −1.129 | |||
| 0.585 | 1.090 | 0.549 | 0.730 | 0.581 | |||
| 2.740 | 1.364 | 2.734 | 1.200 | 2.742 | |||
| 5.143 | 0.690 | 5.144 | 0.780 | 5.194 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joshua, T.M.; Jain, N.; Kumar, R.; Anwar, K.; Abdullah, N.; Bhuyan, M. Divergence in the Relativistic Mean Field Formalism: A Case Study of the Ground State Properties of the Decay Chain of 214,216,218U Isotopes. Foundations 2022, 2, 85-104. https://doi.org/10.3390/foundations2010004
Joshua TM, Jain N, Kumar R, Anwar K, Abdullah N, Bhuyan M. Divergence in the Relativistic Mean Field Formalism: A Case Study of the Ground State Properties of the Decay Chain of 214,216,218U Isotopes. Foundations. 2022; 2(1):85-104. https://doi.org/10.3390/foundations2010004
Chicago/Turabian StyleJoshua, Tolulope Majekodunmi, Nishu Jain, Raj Kumar, Khairul Anwar, Nooraihan Abdullah, and Mrutunjaya Bhuyan. 2022. "Divergence in the Relativistic Mean Field Formalism: A Case Study of the Ground State Properties of the Decay Chain of 214,216,218U Isotopes" Foundations 2, no. 1: 85-104. https://doi.org/10.3390/foundations2010004
APA StyleJoshua, T. M., Jain, N., Kumar, R., Anwar, K., Abdullah, N., & Bhuyan, M. (2022). Divergence in the Relativistic Mean Field Formalism: A Case Study of the Ground State Properties of the Decay Chain of 214,216,218U Isotopes. Foundations, 2(1), 85-104. https://doi.org/10.3390/foundations2010004








