Isotopic Shift in Hg-Isotopes within Brückner versus Relativistic Energy Density Functional

Abstract

The present study is focused on revealing a characteristic kink of the neutron shell closure N = 126 across the Hg-isotopic chain within the relativistic mean-field (RMF) approach with the IOPB-I, DD-ME2, DD-PC1 and NL3 parameter sets. The RMF densities are converted to their spherical equivalence via the Wood–Saxon approximation and used as input within the parametrization procedure of the coherent density fluctuation model (CDFM). The nuclear matter symmetry energy is calculated using the Brückner energy density functional, and its surface, as well as volume components, are evaluated within Danielwicz’s liquid drop prescription. In addition, a comparison between Brückner and relativistic energy density functionals using the NL3 parameter set is shown as a representative case. The binding energy, charge distribution radius and symmetry energy are used as indicators of the isotopic shift in both ground and isomeric states. We have found the presence of a kink at the shell/sub-shell closure at N = 126 for neutron-rich ${}^{206}$Hg. The formation of the kink is traceable to the early filling of the 1$i_{11/2}$ orbitals rather than 2$g_{9/2}$, due to the large spin-orbit splitting. As such, the link between the occupational probability and the magicity of nuclei over the Hg-isotopic chain is established.

1. Introduction

One of the prevailing interests in nuclear physics is to unravel the nuclear structure to explore the collective properties in the neighbourhood of magic numbers as well as the atomic transitions of rare-earth nuclei [1,2,3,4]. The nuclear isotopic shift emerges as one of the viable tools which serve as a premise for testing nuclear theories [5,6,7]. An earlier study has revealed that the measurement of isotopic shift can provide helpful information on the charge radius difference between isomeric states of various nuclei [8]. The isotopic shift which relates to the changes in charge radius, $\Delta \langle R_{ch}^2\rangle$, can also be expressed with reference to a change of the deformation squared, $\Delta \langle {\beta }^2\rangle$. In addition to the root-mean-square radius, several comprehensive experimental details on the nuclear charge distribution are limited to stable isotopes from the electron scattering experiment. Until now, renewed experimental effort with sophisticated facilities such as high-precision laser at ISOLDE (CERN) [9], Intensity Heavy ion Accelerator Facility (HIAF) [10] and Gamow–Teller giant resonance (GTR) at RIKEN [11] are still being directed towards the measurement of nuclear charge radii.

On the theoretical front, nuclear models are usually employed for the treatment of isotopic shifts in heavy systems [12]. The primitive non-relativistic energy density functionals (NR-EDFs) were found to be incapable of producing isotopic shift with experimental exactitude for certain nuclei [13]. Alternatively, the description of NR-EDFs can be improved either by incorporating gradient terms in pairing interactions or by adding a density-dependent term in spin-orbit interactions. On the other hand, the relativistic mean-field (RMF) theories have been used in Refs. [14,15,16] to predict isotopic shift in charge radii near experimentally measured values. The charge distribution and finite mass of the nucleus has a considerable influence on the atomic spectra. As such, the spectra lines associated with different isotopes manifest a little shift in energy [17]. In other words, the isotopic shift is usually occasioned by certain deviations (from systematic trend) resulting from the domination of the quantum shell effect over the charge radius [15,18]. Moreover, the charge radius, single-particle energies and occupation are other benchmarks for the isotopic shifts.

The newly measured ${}^{207,208}\mathrm{Hg}$ isotopes from ISOLDE (CERN) [9] which reveal that isotopic shift can be observed below the shell closure $Z=82$ motivate us and open the direction into the present study. In comparison with the mean-field approaches, the authors demonstrated that isotopic shift in the neighbourhood of the neutron shell closure $N=126$ can find a good description in the mean-field level. Recently, the emergence of single-particle energy levels at shell and sub-shell closures (in the vicinity of magic numbers) has been traced to the presence of isotopic shift [15,19]. Hence, the Shell Model [20] which underscores the concept of magicity is adopted for the treatment of nuclear isotopic shift [15]. The analysis is carried out within the relativistic mean-field framework (for DD-PC1 [21], DD-ME2 [22], IOPB-I [23] and NL3 [24] parameter sets) which is generally appropriate for heavy spherical-deformed nuclei [25]. The spherical shape results from the closed-shell configuration, while the deformed shape emerges from the breaking of the magic shell. Nonetheless, the energy spacing of the positive parity states of some Hg-isotopes are marked with certain irregularities, especially at high spin states [26,27].

In the present study, it is of interest to examine the emergence of isotopic shift over the Hg-isotopic chain and to relate such to the single-particle energy levels at or around the neutron magic number N = 126 within the relativistic mean-field (RMF) approach using the DD-PC1 [21], DD-ME2 [22], IOPB-I [23] and NL3 [24] parameter sets. The ground-state features such as binding energy (BE), root mean square (rms) charge radius ($R_{ch}$), single-particle energies and the shell occupation probability are used as shift indicators for the considered Hg isotopes within neutron number $95\le N\le 134$ at both ground and isomeric states. The surface property such as symmetry energy is estimated using the Brückner energy density functional, and its volume and surface contributions are deduced by employing Danielwicz’s liquid drop prescription. A detailed description of the RMF model, as well as the procedures, are taken to fit the energy density functional $\mathcal{E}\left(\rho \right)$ to obtain an analytical expression in coordinate space using the Brückner energy density functionals are outlined in Section 2. The subsequent part of this section is devoted to the coherent density fluctuation model (CDFM) which is employed to study the surface properties. The discussions on the obtained results are given in Section 3, and Section 4 summarises the inferences drawn from the study.

2. Relativistic Mean Field Approach

The conventional non-linear relativistic mean-field Lagrangian density is constructed from the interacting nucleons with the interchange of the $\sigma$, $\omega$ and $\rho$ mesons. As an extension of the previous version, the self-and cross-couplings of the $\sigma$, $\omega$ and $\rho$ mesons are introduced into the Lagrangian, called “the effective field theory motivated relativistic mean-field formalism” [23,28,29,30,31]. As a result of the cross-coupling within the participating mesons, the variation of the neutron-skin thickness in heavy-mass nuclei such as ${}^{208}$Pb becomes feasible. It is worth noting that the self-coupling of the $\sigma$ mesons sways a minimizing effect on the nuclear matter incompressibility [28,32,33]. The energy density functional used here describes the interactions between the nucleon and various mesons like $\sigma$, $\omega$, $\rho$ and $\delta$. Various self and cross-couplings terms are also taken into account. Further details can be found in Ref. [23].

The parameters DD-PC1 [21], DD-ME2 [22], IOPB-I [23] and NL3 [24] are obtained by assuming that a uniform field is created by the exchange of mesons, in which the oscillations of nucleons in a periodic motion are considered as simple harmonic. The equations of motion for the fields are obtained using the classical variational principle resulting in a closed set of equations which are deduced self-consistently [23] and whose scalar and vector densities are simplified as,

$$\begin{array}{ccc}\hfill {\rho }_s\left(r\right)& =& \sum _{\alpha }{\phi }_{\alpha }^{†}\left(r\right)\beta {\phi }_{\alpha }\left(r\right),\hfill \end{array}$$

(1)

$$\begin{array}{ccc}\hfill {\rho }_v\left(r\right)& =& \sum _{\alpha }{\phi }_{\alpha }^{†}\left(r\right){\phi }_{\alpha }\left(r\right),\hfill \end{array}$$

(2)

respectively, are extrapolated from the converged solutions within the spherical harmonics. The energy density is improvised to investigate the bulk properties of close-shell nuclei in the super-heavy region. As such, ground state observables binding energy (B.E), charge radii and rms radii, etc., are estimated. The spherical densities are used as inputs within the CDFM to obtain the weight function ${\left|F\left(x\right)\right|}^2$, which is a crucial quantity for calculating the symmetry energy of a finite nucleus ($S^A$).

2.1. Spherical Equivalent Density Using Wood–Saxon Fitting

The geometrical relation $r^2=x^2+y^2+z^2$ is employed for the calculation of the spherical equivalent density as a function of the radial coordinate r. However, the acquired densities remain unaltered during this procedure. Instead, the $r_{\perp }$ and z values combine and yield an average r for each density. The Wood–Saxon expression for the fitting of such densities is given as

$$\rho \left(r\right)={\rho }_0/(1+exp[(r-R)/a)],$$

(3)

where $r_{\perp }$ and z represent the cylindrical co-ordinates of the radial vector R [34].

2.2. Brückner’s Prescription and Symmetry Energy

Consider an isotropic and infinite nuclear matter whose energy density expression for the Brückner functional is given as [35,36]:

$$\begin{array}{ccc}\hfill \mathcal{E}{\left(\rho \right)}_{nucl.}& =& A{V}_0\left(x\right)+V_C-V_{Cx},\hfill \end{array}$$

(4)

where

$$\begin{array}{ccc}\hfill V_0\left(x\right)& =& 37.53[{(1+\alpha )}^{5/3}+{(1-\alpha )}^{5/3}]{\rho }_0{\left(x\right)}^{2/3}\hfill \\ & & +b_1{\rho }_0\left(x\right)+b_2{\rho }_0{\left(x\right)}^{4/3}+b_3{\rho }_0{\left(x\right)}^{5/3}\hfill \\ & & +{\alpha }^2[b_4{\rho }_0\left(x\right)+b_5{\rho }_0{\left(x\right)}^{4/3}+b_6{\rho }_0{\left(x\right)}^{5/3}].\hfill \end{array}$$

(5)

Here, $b_1=-741.28$, $b_2=1179.89$, $b_3=-467.54$, $b_4=148.26$, $b_5=372.84$, $b_6=-769.57$ and $\alpha =\frac{{\rho }_n-{\rho }_p}{\rho }$ are the asymmetry parameters where, $\rho ={\rho }_n+{\rho }_p$ in Ref. [19] and therein. The protons possess Coulomb energy $V_C=\frac{3}{5}\frac{Z^2{e}^2}{x}$ and Coulomb exchange energy $V_{Cx}=0.7386Z{e}^2{(3Z/4\pi x^3)}^{1/3}$ in each flucton. The conversion from the NM quantities, Equation (4), from momentum ($\rho -$) to coordinate ($r-$) space in local density approximation (LDA) is a central part of our calculation. The NM symmetry energy parameter $S^{NM}$ is estimated from the standard expression [23,35,37]:

$$\begin{array}{ccc}\hfill S^{NM}& =& \frac{1}{2}\frac{{\partial }^2(\mathcal{E}/\rho )}{\partial {\alpha }^2}{|}_{\alpha =0}\hfill \\ & =& 41.7{\rho }_0{\left(x\right)}^{2/3}+b_4{\rho }_0\left(x\right)+b_5{\rho }_0{\left(x\right)}^{4/3}+b_6{\rho }_0{\left(x\right)}^{5/3},\hfill \end{array}$$

(6)

at local density. The calculated nuclear densities of Hg nuclei from RMF are used as input in the CDFM approach as discussed in the subsequent sub-section.

2.3. The Coherent Density Fluctuations Model

The Coherent Density Fluctuations Model (CDFM) [38] deals with the variations in momentum and density distribution. This model provides a simple approach to investigating the surface property such as symmetry energy of finite nuclei. Within the CDFM formalism, the NM tool $S^{NM}$ from Equation (8) is utilized to calculate its value for the finite nucleus [38,39,40,41]. More comprehensive derivations can be found in Refs. [39,41,42,43,44]. The ${\left|F\left(x\right)\right|}^2$ for a given density $\rho$ (r) is expressed as,

$${\left|F\left(x\right)\right|}^2=-{\left(\frac{1}{{\rho }_0\left(x\right)}\frac{d\rho \left(r\right)}{dr}\right)}_{r=x},$$

(7)

with ${\int }_0^{\infty }dx{\left|F\left(x\right)\right|}^2=1$. The finite nuclear symmetry energy $S^A$ is computed by weighting the respective infinite nuclear matter quantity using the CDFM, which yields [41,42,44,45,46]

$$\begin{array}{c}\hfill S^A={\int }_0^{\infty }dx{\left|F\left(x\right)\right|}^2{S}^{NM}\left(\rho \left(x\right)\right),\end{array}$$

(8)

Equation (8) denotes the surface weighted average of the respective NM quantity at local density for finite nuclei.

The volume and surface components of symmetry energy $S^A$ for finite nuclei in Danielewicz’s prescription are written as [16],

$$\begin{array}{c}\hfill S^A=\frac{S_V}{1+\frac{S_S}{S_V}{A}^{-1/3}}=\frac{S_V}{1+A^{-1/3}/\kappa }.\end{array}$$

(9)

where the ratio $\kappa \equiv \frac{S^V}{S^S}$ is defined as [16,47]:

$$\begin{array}{c}\hfill \kappa =\frac{3}{R{\rho }_0}{\int }_0^{\infty }dx{\left|F\left(x\right)\right|}^{2}x{\rho }_0\left(x\right)\left({\left(\frac{{\rho }_0}{\rho \left(x\right)}\right)}^{\gamma }-1\right).\end{array}$$

(10)

In Equation (10), the value of $\gamma =0.3$ follows Ref. [48]. A new approach was recently employed by Gaidarov et al. to calculate the $S^V$ and $S^S$ which entails the use of the non-relativistic densities within the weight function [49].

3. Results and Discussions

The ground state (GS) and isomeric state (IS) properties are calculated and used as indicators/indexes to determine the isotopic shift in the present study. The available experimental data are compared with the ground state properties such as the binding energy and nuclear charge radius $R_{ch}$ while those of the isomeric states are analysed separately. The Wood–Saxon fitting (Section 2.1) is used to obtain the spherical equivalent densities of the Hg-isotopes. The obtained spherical equivalent densities are further used to calculate the weight function ${\left|F\left(x\right)\right|}^2$ [Equation (7)] which is a key input for the estimation of the NM parameter symmetry energy. The symmetry energy is estimated by using the Brückner functional as well as Danielwicz’s prescription within the framework of CDFM formalism. The results are presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. The well-known three-point method [16] and a standard deviation method are employed for the calculation of the shift over the isotope chain for each of the investigated quantities. It is given as [16],

$$\begin{array}{c}\hfill {▵}_{kn}\mathcal{O}(Z,N)\equiv \frac{1}{2}[\mathcal{O}(Z,N+k)-2\mathcal{O}(Z,N)+\mathcal{O}(Z,N-k)].\end{array}$$

(11)

Here, $\mathcal{O}$ represents the estimated value of the quantity, and k = 2 refers to the curvature/kink parameter. The standard deviation method at a certain neutron number N is explained as [15],

$$\begin{array}{c}\hfill {\langle \Delta R_{ch}^2\rangle }^A={\langle R_{ch}^2\rangle }^A-{\langle R_{ch}^2\rangle }^i,\end{array}$$

(12)

where i symbolizes the mass of each Hg-nucleus having neutron number $N=126$. Using the estimated R${}_{ch}$ values, the isotopic shift ${\langle \Delta R_{ch}^2\rangle }^A$ is obtained from Equations (11) and (12) for IOPB-I, NL3, DD-ME2 and DD-PC1 parameter sets.

3.1. Shift in Binding Energy and Charge Radius

The binding energies (BE) and nuclear charge distribution radius ($R_{ch}$) are determined for both the intrinsic ground and intrinsic isomeric states using the RMF (IOPB-I, NL3) as well as the density-dependent DD-ME2 and DD-PC1 parameter sets in the considered Hg-isotopic chain. The BE and $R_{ch}$ help in providing valuable information about the shell/sub-shell closures in the isotopic chain. In Figure 1, nearly all the theoretically predicted results are very consistent with the experimental data. In the first and second panels, the ground state BE and $R_{ch}$ are presented. Both quantities (BE and $R_{ch}$) are increasing with neutron numbers along the isotopic chain. The abrupt rise in $R_{ch}$ between N = 100 and 110 is consistent with the experimental measurement with a slight difference in their values. This rise can be attributed to a shape transition of the corresponding nucleus [50]. The upper panel of Figure 2, shows the deviation of the calculated binding energies from the experimental data as a function of neutron number. The deviations of the considered forces are found within the range of −3.8 to 5.2 MeV, and the least deviation indicates the credibility of the parameters. Relatively, the NL3 (purple triangles) appears to be more reliable and consistent. A similar trend is noticed with some fluctuations in magnitude. The shift in the binding energies and charge distribution radii are given in the middle and lower panels, respectively. Each of the parameter sets predicts a conspicuous downward kink at neutron number N = 126. The shift for BE is calculated by the three-point method, Equation (11), and the shift for $R_{ch}$ is determined by the standard deviation method, Equation (12). In addition, the extracted experimental data of isotopic shift at N = 126 from the work of Goodacre et al. [9] is given for comparison. The experimental data by Goodacre et al. are in good agreement with all the force parameters. In both shifts, one can observe the kinks at neutron number N = 126. In addition, there are certain discrepancies in the isotopic trend because of the effect of magic shell neutron number N = 126, which is common in mean-field calculations.

Similarly, the BE and $R_{ch}$ of the isomeric states are displayed in Figure 3. In this study, we performed the deformed calculations with different initial deformations having fixed the harmonic oscillator shell as $N_F$ = 12 & $N_B$ = 20. The maximum energy state corresponds to the ground state, and the second-highest state next to the ground state is called the isomeric configuration. These isomeric states are different from the excited states employing their lifetime and configurations. From the figure, an obvious difference is noticed in all predictions compared with those of the ground state in Figure 1. Here, BE marginal deviates from the normal uniform trend at N = 118. Likewise, certain discrepancies (more pronounced than those of the ground state) are visible for $R_{ch}$, accompanied by a relatively large variation in IOPB-I predictions at higher N (=118–135). The shifts in the third and fourth panels also show that the IOPB-I and DD-PC1 predictions are characterised by anomalous kinks and large variation, respectively. The NL3 set maintains the same trend as the IOPB-I parameter although with a small difference in magnitude.

Figure 1. (Color online) The binding energy (BE) in MeV and charge distribution radius ($R_{ch}$) in fm are shown for the ground state of Hg-isotopes along with the available experimental data [51,52].

Figure 1. (Color online) The binding energy (BE) in MeV and charge distribution radius ($R_{ch}$) in fm are shown for the ground state of Hg-isotopes along with the available experimental data [51,52].

Figure 2. (Color online) The binding energy deviation ($B{E}_{Expt.}$-$B{E}_{Cal.}$), the isotopic shifts of binding energy (BE) and charge distribution radius ($R_{ch}$) in fm are shown in the upper, middle and lower panels respectively for the ground state of Hg-isotopes. The available experimental data are given for comparison [51,52]. The predictions by Goodacre et al. [9] for the isotopic shift at N = 126 are also given for comparison. The energies are in MeV and radius in fm.

Figure 2. (Color online) The binding energy deviation ($B{E}_{Expt.}$-$B{E}_{Cal.}$), the isotopic shifts of binding energy (BE) and charge distribution radius ($R_{ch}$) in fm are shown in the upper, middle and lower panels respectively for the ground state of Hg-isotopes. The available experimental data are given for comparison [51,52]. The predictions by Goodacre et al. [9] for the isotopic shift at N = 126 are also given for comparison. The energies are in MeV and radius in fm.

Figure 3. (Color online) The binding energy (BE) and charge distribution radius ($R_{ch}$) are shown along with their respective shifts ($\Delta BE$, $\Delta R_{ch}^2$) for the isomeric state of Hg-isotopes. The energies in MeV and radius in fm.

Figure 3. (Color online) The binding energy (BE) and charge distribution radius ($R_{ch}$) are shown along with their respective shifts ($\Delta BE$, $\Delta R_{ch}^2$) for the isomeric state of Hg-isotopes. The energies in MeV and radius in fm.

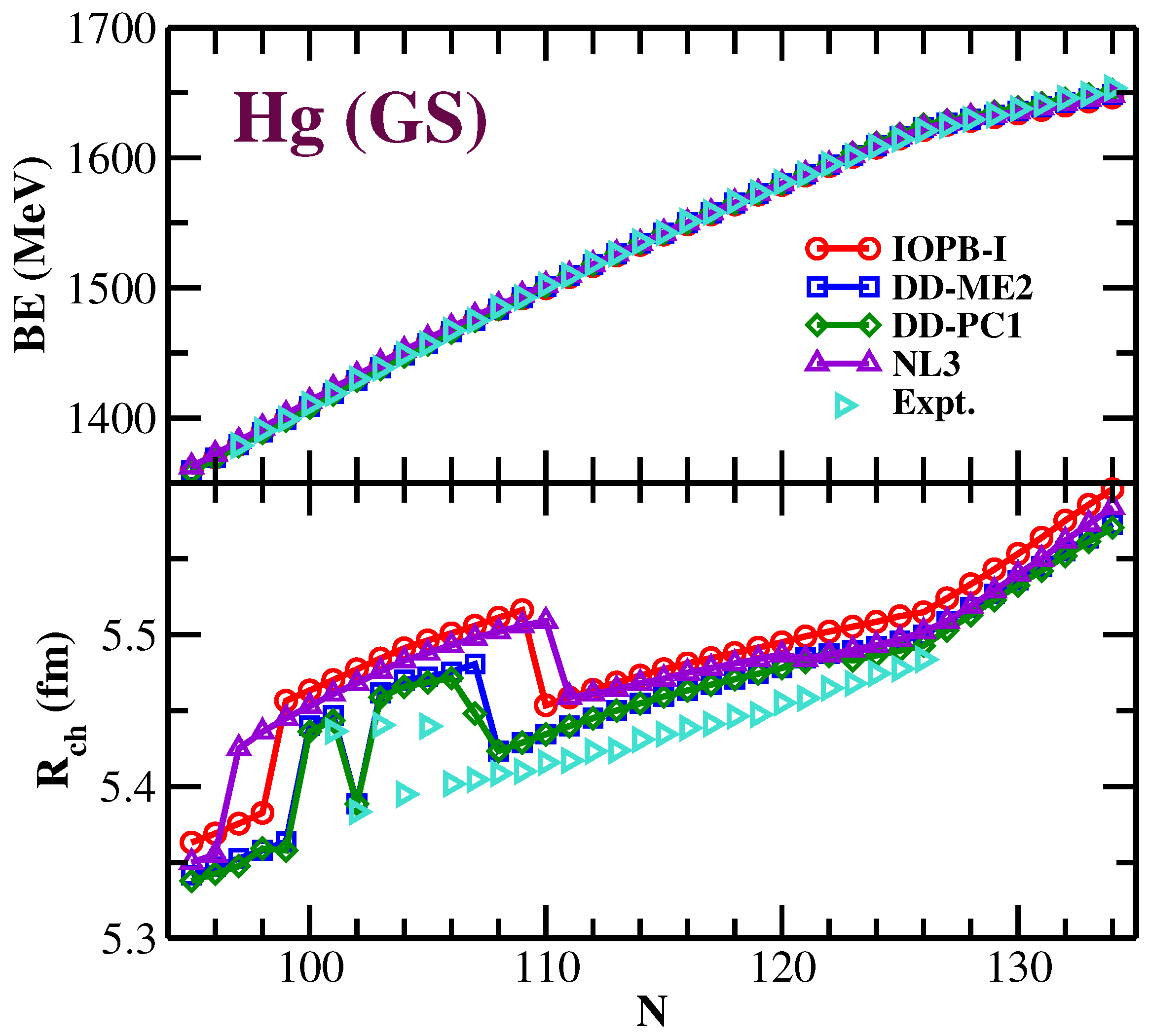
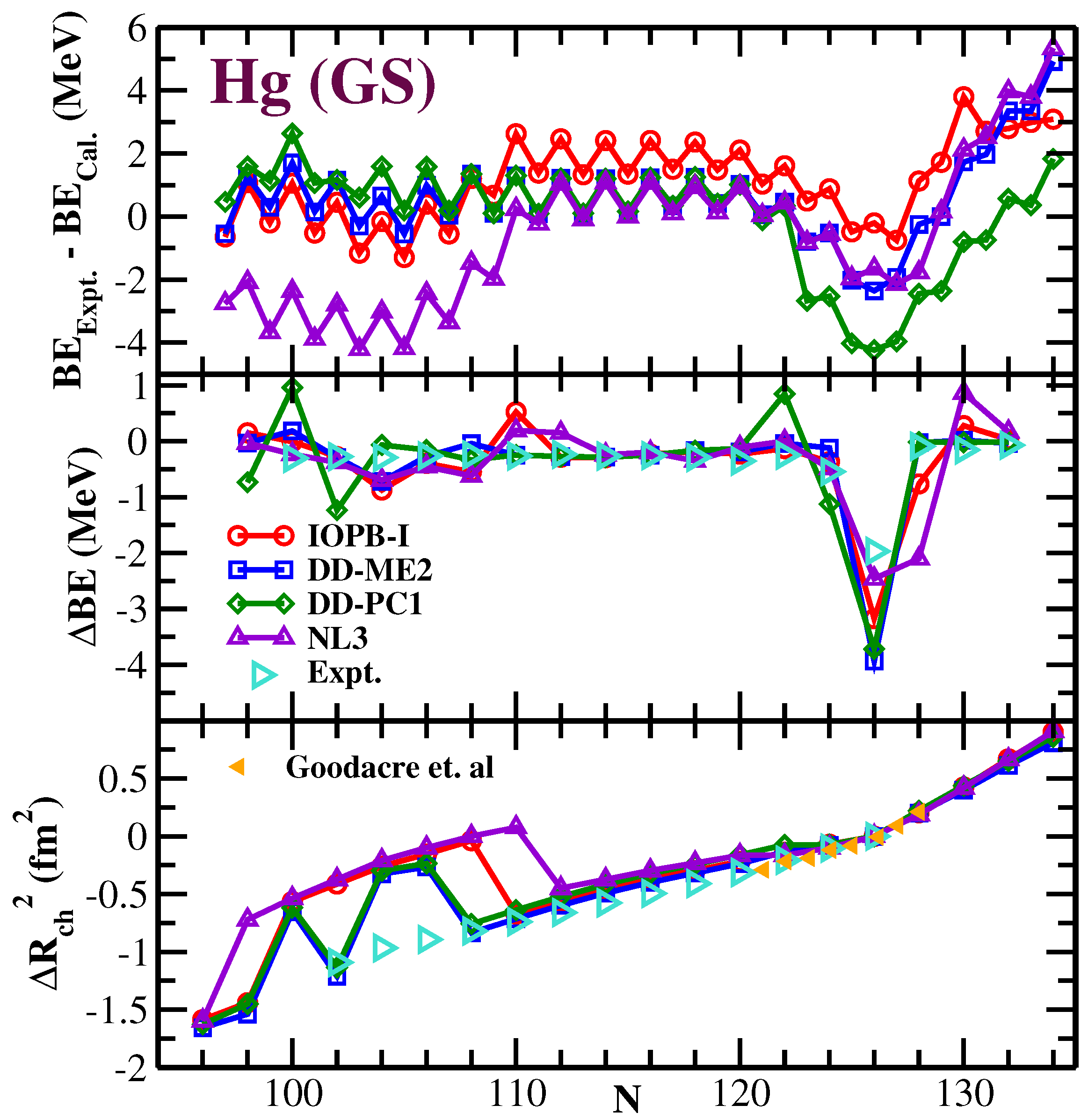
3.2. Symmetry Energy and Its Shift

Several ways are available to examine the characteristics of finite nuclei as they relate to their iso-spin and density-dependent NM quantities which include the symmetry energy and other derivatives. Here, the CDFM approach as well as the Brückner’s energy density functional in Section 2.2 are employed along with the volume and surface contributions to the symmetry energy. The symmetry energy $S^A$ of a finite nucleus is obtained from the NM symmetry energy by taking Brückner’s energy density functional Equation (6) approach. Elaborate details are given in Refs. [19,53] which involve the folding of the density and weight function. In other words, the symmetry energy of infinite nuclear matter $S^{NM}$ is combined with the weight function ${\left|F\left(x\right)\right|}^2$ to determine the symmetry energy of the finite nucleus in Equation (8). The notable values of ${\left|F\left(x\right)\right|}^2$ (its peak value) are found in the range corresponding to the surface region of the density. As such, these quantities are referred to as surface properties.

The estimated finite nuclei surface $S_S$ and volume $S_V$ components of the symmetry energy, the total symmetry energy $S^A$ itself as well as its shift $\Delta S^A$ for both ground state (GS) and isomeric state (IS) are shown in Figure 4 and Figure 5, respectively, as a function of the neutron number using the IOPB-I, DD-ME2 and DD-PC1 parameter sets over the Hg-isotopic chain. In Figure 4, we observed the change in magnitude of the above-described quantities for Hg-isotopic series with neutron number N. In other words, a similar variation is noticed in all the observables $S_S$, $S_V$, $S^A$ and $\Delta S^A$, manifesting high undulations/fluctuations at $80\le N\le 110$ which become lesser with the increase in N. Using Brückner’s prescription, no clear peak in $S^A$ is found at the magic closed-shell N = 126. In Figure 4, we have also presented the volume and surface contribution of symmetry energy ($S_V,S_S$) as a function of neutron number N. $S_V$ and $S_S$ follow the trend with some fluctuations, accompanied by the symmetry energy $S^A$ which exhibits some difference in magnitude. The volume contributions of symmetry energy $S_V$ have a higher magnitude as compared to the surface contribution symmetry energy $S_S$. However, when the three-point method (Equation (11)) is used to obtain the isotopic shift of Hg-isotopes, no peak is found at N = 126, as illustrated in Figure 4. A similar procedure is repeated for the isomeric states as shown in Figure 5 and we find the same observation.

Figure 4. (Color online) The symmetry energy ($S^A$) and its volume $S_V$ and surface $S_S$ components for IOPB-I, DD-ME2 and DD-PC1 parameter sets are shown along with the shift corresponding to the total symmetry energy ($\Delta S^A$) for the ground state of Hg-isotopes.

Figure 4. (Color online) The symmetry energy ($S^A$) and its volume $S_V$ and surface $S_S$ components for IOPB-I, DD-ME2 and DD-PC1 parameter sets are shown along with the shift corresponding to the total symmetry energy ($\Delta S^A$) for the ground state of Hg-isotopes.

Figure 5. (Color online) Same as Figure 4, but for the existing isomeric states of Hg-isotopes.

Figure 5. (Color online) Same as Figure 4, but for the existing isomeric states of Hg-isotopes.

Since the conventional Brückner energy density functional (B-EDF) fails in Figure 4 to reveal a conspicuous peak in the symmetry energy at $N=126$, indicating the presence of a closed shell/sub-shell as presented in Ref. [9]. We therefore employ the effective theory motivated relativistic energy density functional (E-RMF) which has been recently shown [54] to resolve the Coester band problem [55,56,57]. Here, we have shown the calculations of symmetry energy $S^A$ for the ground states of Hg-isotopic series with NL3 set [24] as a representative case. Figure 6 shows a relative comparison between the prediction of the B-EDF and E-RMF using the NL3 parameter set. Unlike the B-EDF, a notable peak is formed along with the symmetry energy $S^A$ Hg-isotopic chain at $N=126$ as well as its isotopic shift $\Delta S^A$. In addition to the fluctuations, the component $S_V$ and $S_S$ combines to give $S^A$ as explained earlier. The same is obtained in Figure 7 for the isomeric states of the Hg-isotopic series. Here also, the conventional Brückner energy density functional fails to produce the peak at N = 126, which is smoothly obtained by the newly developed relativistic energy density functional. In addition to these, we noticed a conspicuous peak at N = 111 for the B-EDF, which is very little in magnitude in the case of thenE-RMF energy density functional. In addition, the same scenario (observed earlier for the ground state) comes into play in the study of isotopic shift. Thus, these results further assert the experimental findings of Goodacre et al. [9,58], where it was demonstrated that the aforementioned observables are predominantly governed by the relative energies as well as the orbital occupation.

Figure 6. (Color online) The total symmetry energy ($S^A$) and its shift within the Brückner functional and the Relativistic energy density functional used to obtain the volume $S_V$ and surface $S_S$ symmetry energies with Danielwiz’s prescription are shown for the ground state of Hg-isotopes using RMF (NL3) parameter set.

Figure 6. (Color online) The total symmetry energy ($S^A$) and its shift within the Brückner functional and the Relativistic energy density functional used to obtain the volume $S_V$ and surface $S_S$ symmetry energies with Danielwiz’s prescription are shown for the ground state of Hg-isotopes using RMF (NL3) parameter set.

Figure 7. (Color online) Same as Figure 6, but for isomeric states of Hg-isotopes.

Figure 7. (Color online) Same as Figure 6, but for isomeric states of Hg-isotopes.

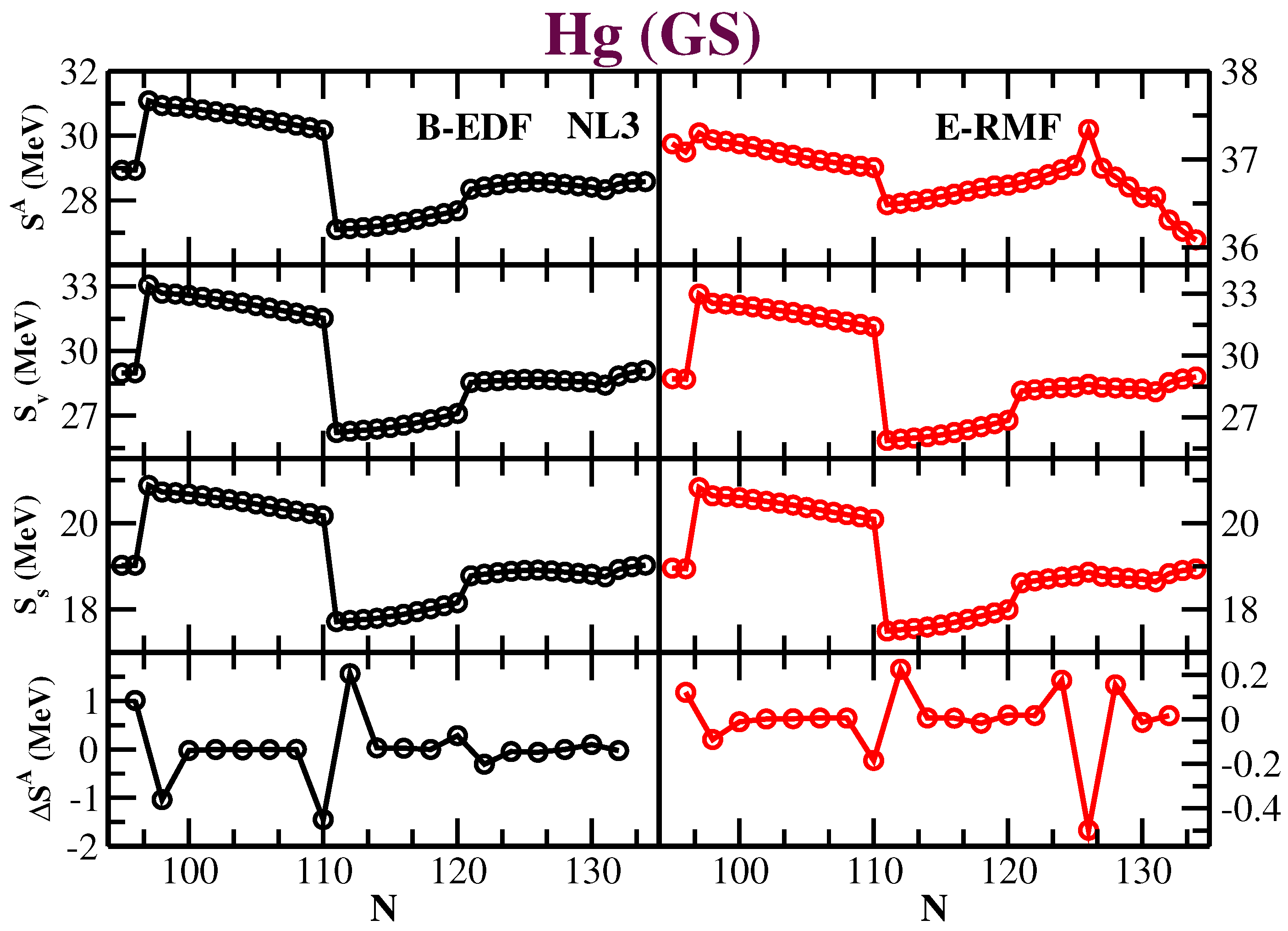
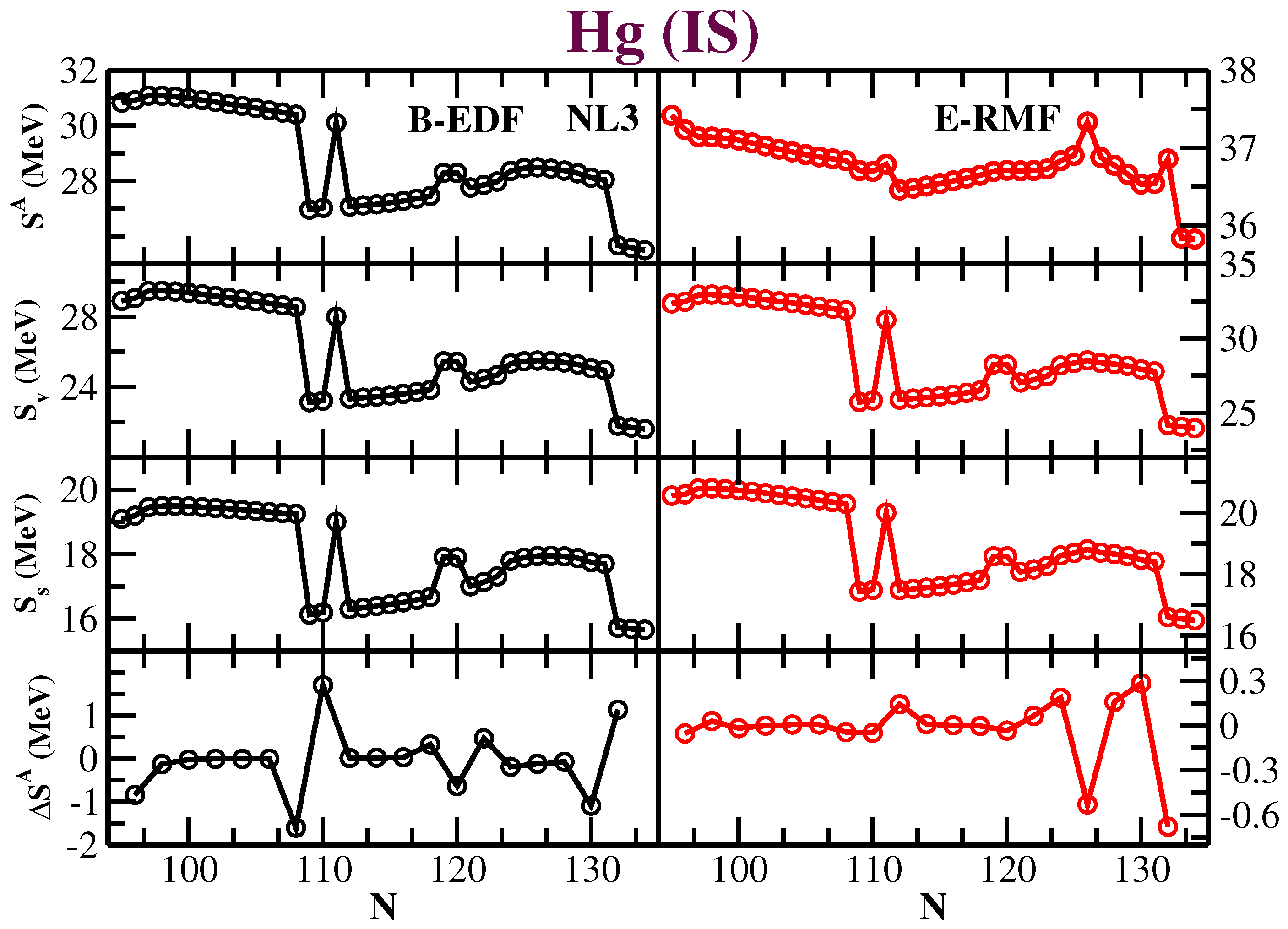
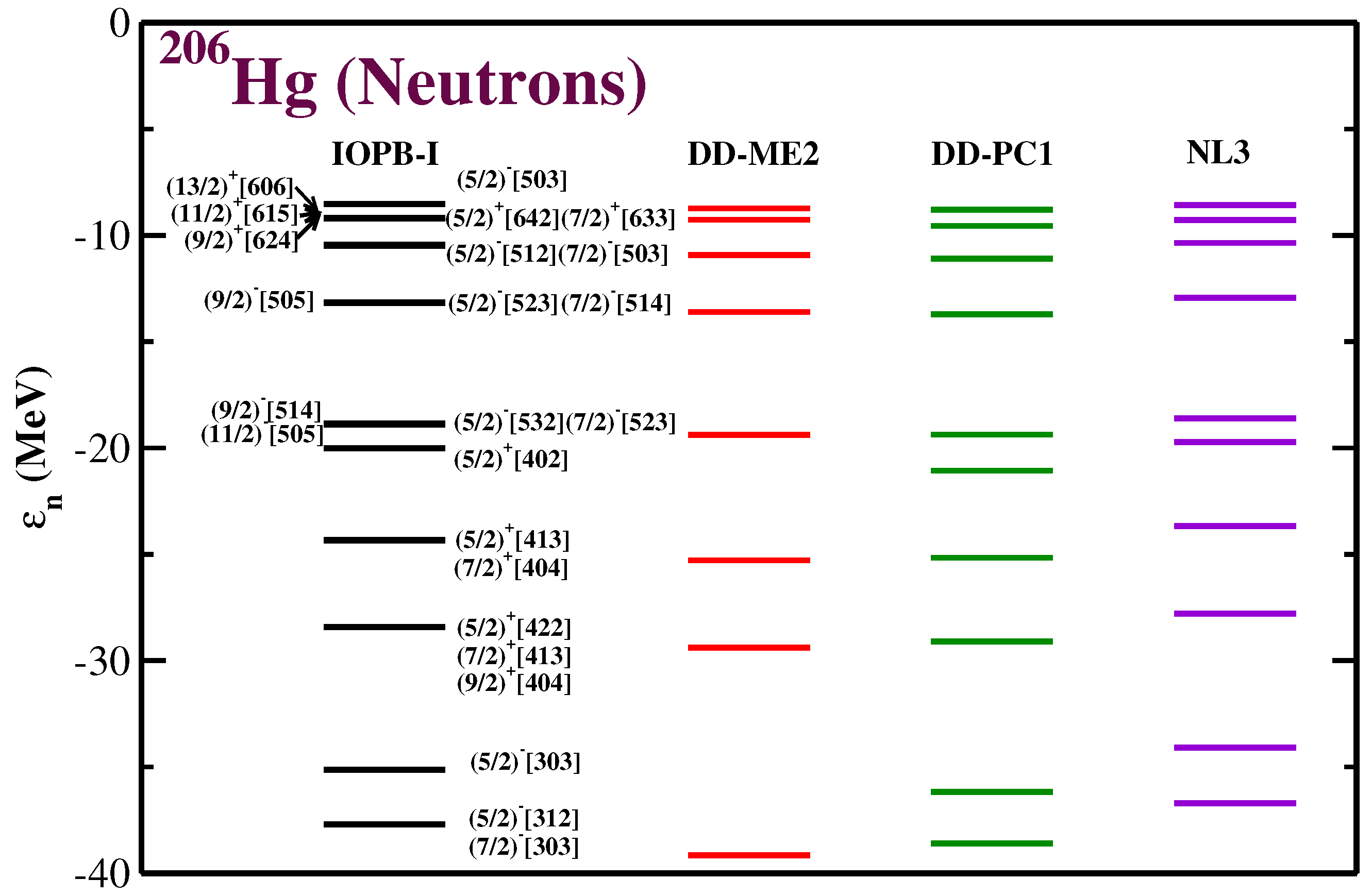
3.3. Single Particle Energy and Its Occupancy

The neutron single-particle energy spectra (${ϵ}_n$) are calculated for the newly developed IOPB-I, widely used NL3 and the density-dependent DD-ME2 and DD-PC1 sets for ${}^{206}$Hg nuclei. The neutron Nilson orbitals $\left[N{n}_3\Lambda \right]{\Omega }^{\pi }$[59] are presented near the Fermi surface for ${}^{206}$Hg and displayed in Figure 8. In Figure 9, the neutron orbital occupation probabilities obtained from the IOPB-I, NL3, DD-ME2 and DD-PC1 parameter sets, corresponding to the neutron number N = 126, are presented for some selected Hg-isotopes. In addition, the filling of the valence orbital in the neutron magic, N = 126 for Hg is noticed. For instance, the 2$g_{9/2}$ & 1$i_{11/2}$ orbitals are taken as the reference orbitals of the ${}^{206}$Hg isotope for observation. All the parameter sets predict a relatively large occupation of the 1$i_{11/2}$ for the isotopes beyond ${}^{206}$Hg. This fact suggests the cause for the emergence of an isotopic shift.

It has been recently demonstrated (in Refs. [9,15,16] and references therein) that the isotopic shift in the nuclear charge radii has a propensity to be strongly influenced by the orbital-filling/occupation probability. In contrast with the traditional electronic configuration, the occurrence of an isotopic shift at N = 126 arises due to the early occupation of 1$i_{11/2}$ orbital than 2$g_{9/2}$. In the nuclear system, it has been observed that large spin-orbit splitting is responsible for the earlier filling of the higher spin orbitals. In the case of the atomic system, an opposite trend in the filling of the electrons which arises from the small spin-orbit interaction among the electronic orbitals is noticed. From the nuclear matter viewpoint, it is obvious that nuclear symmetry energy tends to increase the overlap between neighbouring orbitals and the overall density. Such an effect will be increased if the overlap between those wave functions is maximum [15,60]. Thus, this investigation reveals the correlation between the occupation probability and magicity as well as the isotopic shift of different observables in terms of the magic neutron number.

Figure 8. (Color online) The ground state neutron single particle energies ${ϵ}_n$ of ${}^{206}$Hg near the Fermi level with IOPB-I, DD-ME2, DD-PC1 and NL3 parameter sets.

Figure 8. (Color online) The ground state neutron single particle energies ${ϵ}_n$ of ${}^{206}$Hg near the Fermi level with IOPB-I, DD-ME2, DD-PC1 and NL3 parameter sets.

Figure 9. (Color online) The ground state neutron occupation probabilities of 2$g_{9/2}$ & 1$i_{11/2}$ orbitals as a function of their respective single particle energies ${ϵ}_n$ for the considered IOPB-I, DD-ME2, DD-PC1 and NL3 parameter sets.

Figure 9. (Color online) The ground state neutron occupation probabilities of 2$g_{9/2}$ & 1$i_{11/2}$ orbitals as a function of their respective single particle energies ${ϵ}_n$ for the considered IOPB-I, DD-ME2, DD-PC1 and NL3 parameter sets.

4. Conclusions

In this study, the systematic theoretical analysis of the Hg-isotopic chain is presented. The peaks in several observables over the isotope chain of Hg-nuclei are observed. The emergence of kink along the isotope chain of a nucleus has a keen correlation with the presence of a closed shell/sub-shell. The ground-state properties such as the BE, $rms$ radius and single-particle energies are computed for the isotope chain of Hg-nuclei using relativistic mean-field formalism. Then, the RMF densities are converted to their respective spherical equivalent densities by Wood–Saxon approximations. These converted densities which are also clear indicators of the magicity of nuclei that lie away from the $\beta$-stability line [42,43,44,53], are used within the Coherent Density Fluctuation Model (CDFM) to determine the symmetry energy [43]. Again, the shift in symmetry energy for Hg-isotopes are determined for all the parameter sets. In addition, the surface and volume contributions of symmetry energy by Danielwicz’s liquid drop prescription are estimated. This procedure is repeated for the isomeric states of Hg-isotopes.

We have established the shell/sub-shell closure at N = 126 for neutron-rich ${}^{206}$Hg using the newly derived relativistic energy density functional. The pronounced peaks at N = 126 in the shift of binding energy and charge distribution radius of Hg-isotopes indicate the shell closures property. Again, the early filling of the higher spin orbitals due to the large spin-orbit splitting is the primary basis for the appearance of kinks at the magic numbers. Here, in ${}^{206}$Hg, the 1$i_{11/2}$ orbital is filled earlier than the 2$g_{9/2}$ orbital. Hence, this establishes a connection between occupation probability and the magic numbers in the isotope chain for an atomic nucleus. We therefore conclude that to reveal the shell/sub-shell closures across the whole isotope chain, the shift of various structural observables is a crucial quantity that cannot be undermined. The relativistic energy density functional for IOPB-I, DD-ME2, and DD-PC1 sets are not developed yet; nonetheless, we have performed a systematic study for symmetry energy with the relativistic energy density functional of the NL3 set, which is already derived in Ref. [54]. Again, we have observed a notable peak at N = 126, in the case of symmetry energy as well as in its shift for the newly developed E-RMF energy density functional instead of tghe conventional Brückner’s energy density functional for the NL3 set. One of the drawbacks may be the use of Brückner’s EDF in the conversion of the energy density functional from the momentum space to the coordinate space in the local density approximation. In a recent study, Kumar et al. [54] pointed out that the present Brückner’s energy density functional is unable to resolve the Coester band problem [55,56] and could be a reason for the failure of the prediction of the proper peak at magic number [54]. Furthermore, the construction of the relativistic energy density functional for IOPB-I, and the density-dependant DD-ME2 and DD-PC1 parameter sets are in progress. This could be the reason behind the non-appearance of peaks. Careful consideration of relativistic energy density functional [54] over Brückner’s EDF could produce an appropriate magnitude in symmetry energy and with the peak in the isotopic shift. To avoid unnecessary repetition, uncertainties in binding energies arising from the polarization effects in the pairing channel are not included in this work. Such effects can be found in Refs. [9,58].