Interaction Parameters for the Formation of Mixed Micelles and Partitioning of Solutes in Them: A Review
Abstract
:1. Introduction
2. Theories for the Formation and Partitioning of the Mixed Micelle
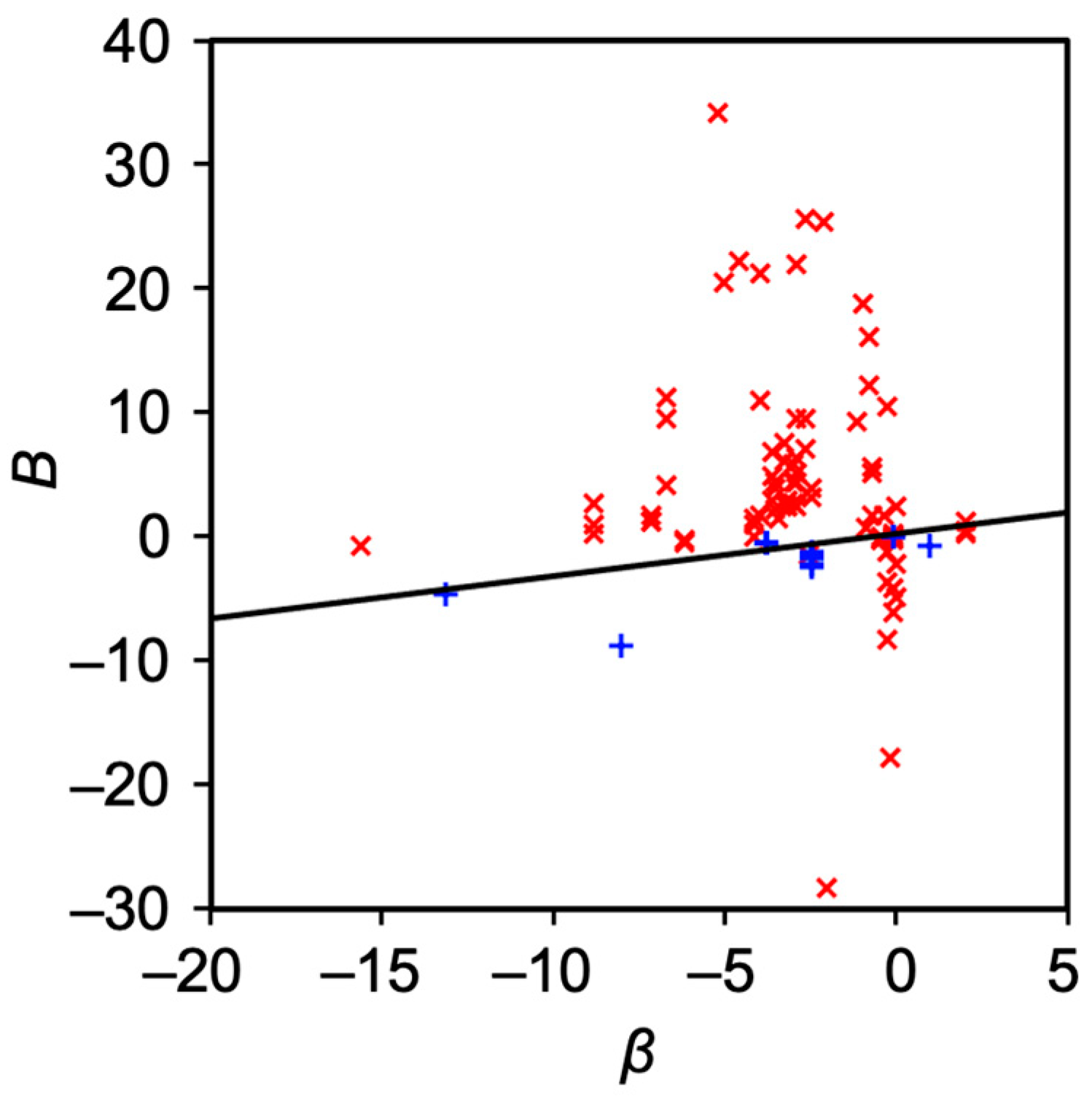
3. Results
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Molina, M.; Silva, M. Micellar Electrokinetic Chromatography: Current Developments and Future. Electrophoresis 2002, 23, 3907–3921. [Google Scholar] [CrossRef] [PubMed]
- Ulbrich, K.; Holá, K.; Šubr, V.; Bakandritsos, A.; Tuček, J.; Zbořil, R. Targeted Drug Delivery with Polymers and Magnetic Nanoparticles: Covalent and Noncovalent Approaches, Release Control, and Clinical Studies. Chem. Rev. 2016, 116, 5338–5431. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Huang, G.; Gao, J. Cooperativity Principles in Self-Assembled Nanomedicine. Chem. Rev. 2018, 118, 5359–5391. [Google Scholar] [CrossRef] [PubMed]
- Bernardo-Bermejo, S.; Sánchez-López, E.; Castro-Puyana, M.; Marina, M.L. Chiral Capillary Electrophoresis. Trends Anal. Chem. 2020, 124, 115807. [Google Scholar] [CrossRef]
- Rubingh, D.N. Mixed Micelle Solutions. In Solution Chemistry of Surfactants; L. Mittal, K., Ed.; Springer: Boston, MA, USA, 1979; pp. 337–354. [Google Scholar] [CrossRef]
- Holland, P.M.; Rubingh, D.N. Nonideal Multicomponent Mixed Micelle Model. J. Phys. Chem. 1983, 87, 1984–1990. [Google Scholar] [CrossRef]
- Paria, S. Surfactant-Enhanced Remediation of Organic Contaminated Soil and Water. Adv. Colloid Interface Sci. 2008, 138, 24–58. [Google Scholar] [CrossRef]
- Lamichhane, S.; Bal Krishna, K.C.; Sarukkalige, R. Surfactant-Enhanced Remediation of Polycyclic Aromatic Hydrocarbons: A Review. J. Environ. Manage. 2017, 199, 46–61. [Google Scholar] [CrossRef]
- Schacht, V.J.; Grant, S.C.; Haftka, J.J.H.; Gaus, C.; Hawker, D.W. Transport potential of super-hydrophobic organic contaminants in anionic-nonionic surfactant mixture micelles. Chemosphere 2019, 230, 173–181. [Google Scholar] [CrossRef]
- Slavchov, R.I.; Georgiev, G.S. Markov Chain Model for the Critical Micelle Concentration of Surfactant Mixtures. Colloid Polym. Sci. 2014, 292, 2927–2937. [Google Scholar] [CrossRef]
- Rosen, M.J. Molecular Interactions and Synergism in Mixtures of Two Surfactants. In Surfactants and Interfacial Phenomena; Rosen, M.J., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; pp. 379–414. [Google Scholar] [CrossRef]
- O’Connell, J.P.; Prausnitz, J.M. Thermodynamics of Gas Solubility in Mixed Solvents. Ind. Eng. Chem. 1964, 3, 347–351. [Google Scholar] [CrossRef]
- O’Connell, J.P. Molecular Thermodynamics of Gases in Mixed Solvents. AIChE J. 1971, 17, 658–663. [Google Scholar] [CrossRef]
- Treiner, C.; Bocquet, J.F.; Pommier, C. The Case of a Synergistic Solubilization Effect: The Partitioning of 1-Pentanol in Aqueous Solutions of Mixed Ionic Hydrocarbon and Fluorocarbon Surfactants. J. Phys. Chem. 1986, 90, 3052–3054. [Google Scholar] [CrossRef]
- Treiner, C.; Nortz, M.; Vaution, C.; Puisieux, F. Micellar Solubilization in Aqueous Binary Surfactant Systems: Barbituric Acids in Mixed Anionic + Nonionic or Cationic + Nonionic Mixtures. J. Colloid Interface Sci. 1988, 125, 261–270. [Google Scholar] [CrossRef]
- Treiner, C. The Thermodynamics of Micellar Solubilization of Neutral Solutes in Aqueous Binary Surfactant Systems. Chem. Soc. Rev. 1994, 23, 349–356. [Google Scholar] [CrossRef]
- Zhu, B.Y.; Rosen, M.J. Synergism in binary mixtures of surfactants. J. Colloid Interface Sci. 1984, 99, 435–442. [Google Scholar] [CrossRef]
- Treiner, C.; Vaution, C.; Miralles, E.; Puisieux, F. Influence of Sodium Dodecylsulfate and of Inorganic Electrolytes on the Micellar Solubilization of Butobarbitone in Aqueous Polyoxyethylene Lauryl Ether Solutions at 298.15 K. Colloids Surf. 1985, 14, 285–292. [Google Scholar] [CrossRef]
- Asakawa, T.; Miyagishi, S.; Nishida, M. Fluorine Nuclear Magnetic Resonance of Fluorocarbon and Hydrocarbon Surfactant Mixtures. J. Colloid Interface Sci. 1985, 104, 279–281. [Google Scholar] [CrossRef]
- Treiner, C.; Khodja, A.A.; Fromon, M. Micellar Solubilization of 1-Pentanol in Binary Surfactant Solutions: A Regular Solution Approach. Langmuir 1987, 3, 729–735. [Google Scholar] [CrossRef]
- Treiner, C.; Nortz, M.; Vaution, C. Micellar Solubilization in Strongly Interacting Binary Surfactant Systems. Langmuir 1990, 6, 1211–1216. [Google Scholar] [CrossRef]
- Sharma, K.S.; Patil, S.R.; Rakshit, A.K.; Glenn, K.; Doiron, M.; Palepu, R.M.; Hassan, P.A. Self-Aggregation of a Cationic−Nonionic Surfactant Mixture in Aqueous Media: Tensiometric, Conductometric, Sensity, Light Scattering, Potentiometric, and Fluorometric Studies. J. Phys. Chem. B 2004, 108, 12804–12812. [Google Scholar] [CrossRef]
- Mir, M.A.; Chat, O.A.; Najar, M.H.; Younis, M.; Dar, A.A.; Rather, G.M. Solubilization of Triphenylamine, Triphenylphosphine, Triphenylphosphineoxide and Triphenylmethanol in Single and Binary Surfactant Systems. J. Colloid Interface Sci. 2011, 364, 163–169. [Google Scholar] [CrossRef]
- Wei, J.; Huang, G.; An, C.; Yu, H. Investigation on the Solubilization of Polycyclic Aromatic Hydrocarbons in the Presence of Single and Mixed Gemini Surfactants. J. Hazard. Mater. 2011, 190, 840–847. [Google Scholar] [CrossRef] [PubMed]
- Georgiev, G.S. Markov Chain Model of Mixed Surfactant Systems. Colloid Polym Sci. 1996, 274, 49–58. [Google Scholar] [CrossRef]
- Suzuki, N. Understanding Nonlinear Composition Dependency of Enantioselectivity in Chiral Separation Using Mixed Micelle. J. Colloid Interface Sci. 2022, 627, 578–586. [Google Scholar] [CrossRef]
- Suzuki, N. Regular Solution Theory for Nonlinear Composition Dependency of Enantioselectivity by Mixed Micelle. J. Mol. Liq. 2022, 367, 120597. [Google Scholar] [CrossRef]
- Suzuki, N.; Taura, D.; Komichi, Y. Critical Micelle Concentration and Partition Coefficient of Mixed Micelles: Analysis of Ternary Systems Based on Markov Chain Model and Simple Mixture Model. J. Mol. Liq. 2023, 376, 121383. [Google Scholar] [CrossRef]
- Jouyban, A. Review of the Cosolvency Models for Predicting Solubility of Drugs in Water-Cosolvent Mixtures. J. Pharm. Pharm. Sci. 2008, 11, 32–58. [Google Scholar] [CrossRef]
- Jouyban, A. Review of the Cosolvency Models for Predicting Drug Solubility in Solvent Mixtures: An Update. J. Pharm. Pharm. Sci. 2019, 22, 466–485. [Google Scholar] [CrossRef]
- Osborne-Lee, I.W.; Schechter, R.S.; Wade, W.H. Monomer—Micellar equilibrium of aqueous surfactant solutions by the use of ultrafiltration. J. Colloid Interface Sci. 1983, 94, 179–186. [Google Scholar] [CrossRef]
- Warr, G.G.; Grieser, F.; Healy, T.W. Composition of mixed micelles of polydisperse nonionic surfactants. J. Phys. Chem. 1983, 87, 1220–1223. [Google Scholar] [CrossRef]
- Makayssi, A.; Lemordant, D.; Treiner, C. Structural change and micellar composition in aqueous solutions of binary cationic surfactant mixtures as deduced from cross-flow ultrafiltration experiments. Langmuir 1993, 9, 2808–2813. [Google Scholar] [CrossRef]
- Huang, L.; Somasundaran, P. Changes in Micelle Compositions and Monomer Concentrations in Mixed Surfactant Solutions. Langmuir 1996, 12, 5790–5795. [Google Scholar] [CrossRef]
- Pedone, L.; Chillura Martino, D.; Caponetti, E.; Floriano, M.A.; Triolo, R. Determination of the Composition of Mixed Hydrogenated and Fluorinated Micelles by Small Angle Neutron Scattering. J. Phys. Chem. B 1997, 101, 9525–9531. [Google Scholar] [CrossRef]
- Almgren, M.; Garamus, V.M.; Asakawa, T.; Jiang, N. Contrast Variation SANS Investigation of Composition Distributions in Mixed Surfactant Micelles. J. Phys. Chem. B 2007, 111, 7133–7141. [Google Scholar] [CrossRef]
- Rodríguez, J.L.; Minardi, R.M.; Schulz, E.P.; Pieroni, O.; Schulz, P.C. The Composition of Mixed Micelles Formed by Dodecyl Trimethyl Ammonium Bromide and Benzethonium Chloride in Water. J. Surfactants Deterg. 2011, 15, 147–155. [Google Scholar] [CrossRef]
- Hua, X.Y.; Rosen, M.J. Synergism in Binary Mixtures of Surfactants. J. Colloid Interface Sci. 1982, 90, 212–219. [Google Scholar] [CrossRef]
- Naqvi, A.Z.; Kabir-ud-Din; Panda, M. Mixed micellization: Improved physicochemical behavior of different amphiphiles in presence of gemini surfactants. J. Mol. Liq. 2021, 343, 116876. [Google Scholar] [CrossRef]
- Malik, N.A. Solubilization and Interaction Studies of Bile Salts with Surfactants and Drugs: A Review. Appl. Biochem. Biotechnol. 2016, 179, 179–201. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, H.; Srivastava, A.; Fujimori, M.; Tomoo, K.; Nakanishi, A.; Tandia, M.; Kadota, K.; Tozuka, Y. Investigation of Physiological Properties of Transglycosylated Stevia with Cationic Surfactant and Its Application To Enhance the Solubility of Rebamipide. J. Phys. Chem. B 2018, 122, 10051–10061. [Google Scholar] [CrossRef]
- Terabe, S. Capillary separation: Micellar electrokinetic chromatography. Annu. Rev. Anal. Chem. 2009, 2, 99–120. [Google Scholar] [CrossRef]
- Rizvi, S.A.A.; Do, D.P.; Saleh, A.M. Fundamentals of micellar electrokinetic chromatography (MEKC). European Journal of Chemistry 2011, 2, 276–281. [Google Scholar] [CrossRef]
- Miyabe, K.; Suzuki, N. Kinetic Study of Solute Permeation across Surfactant Micelle/Bulk Solvent Interface by Moment Analysis—Chromatographic Capillary Electrophoresis (MA-CCE). Bull. Chem. Soc. Jpn. 2016, 89, 1212–1218. [Google Scholar] [CrossRef]
- Miyabe, K.; Inaba, S.; Umeda, M. A study on attempt for determination of permeation kinetics of coumarin at lipid bilayer of liposomes by using capillary electrophoresis with moment analysis theory. J. Chromatogr. A 2023, 1687, 463691. [Google Scholar] [CrossRef] [PubMed]
- Yoda, K.; Tamori, K.; Esumi, K.; Meguro, K. Solubilization of Alcohols in Single and Mixed Surfactant Aqueous Solutions Containing Fluorocarbon Surfactant. Colloids Surf. 1991, 58, 87–98. [Google Scholar] [CrossRef]
- Kabir-ud-Din; Shafi, M.; Bhat, P.A.; Dar, A.A. Solubilization Capabilities of Mixtures of Cationic Gemini Surfactant with Conventional Cationic, Nonionic and Anionic Surfactants Towards Polycyclic Aromatic Hydrocarbons. J. Hazard. Mater. 2009, 167, 575–581. [Google Scholar] [CrossRef]
- Wei, J.; Huang, G.; Zhu, L.; Zhao, S.; An, C.; Fan, Y. Enhanced Aqueous Solubility of Naphthalene and Pyrene by Binary and Ternary Gemini Cationic and Conventional Nonionic Surfactants. Chemosphere 2012, 89, 1347–1353. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Huang, G.; Yu, H.; An, C. Efficiency of Single and Mixed Gemini/Conventional Micelles on Solubilization of Phenanthrene. Chem. Eng. J. 2011, 168, 201–207. [Google Scholar] [CrossRef]
- Panda, M.; Kabir-ud-Din. Solubilization of Polycyclic Aromatic Hydrocarbons by Gemini-Conventional Mixed Surfactant Systems. J. Mol. Liq. 2013, 187, 106–113. [Google Scholar] [CrossRef]
- Dar, A.A.; Rather, G.M.; Das, A.R. Mixed Micelle Formation and Solubilization Behavior Toward Polycyclic Aromatic Hydrocarbons of Binary and Ternary Cationic–Nonionic Surfactant Mixtures. J. Phys. Chem. B 2007, 111, 3122–3132. [Google Scholar] [CrossRef]
- Maswal, M.; Chat, O.A.; Jabeen, S.; Ashraf, U.; Masrat, R.; Shah, R.A.; Dar, A.A. Solubilization and Co-Solubilization of Carbamazepine and Nifedipine in Mixed Micellar Systems: Insights From Surface Tension, Electronic Absorption, Fluorescence and HPLC Measurements. RSC Adv. 2015, 5, 7697–7712. [Google Scholar] [CrossRef]
- Bhat, P.A.; Rather, G.M.; Dar, A.A. Effect of Surfactant Mixing on Partitioning of Model Hydrophobic Drug, Naproxen, between Aqueous and Micellar Phases. J. Phys. Chem. B 2009, 113, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Mehling, T.; Kloss, L.; Ingram, T.; Smirnova, I. Partition Coefficients of Ionizable Solutes in Mixed Nonionic/Ionic Micellar Systems. Langmuir 2013, 29, 1035–1044. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Zhu, L. Solubilization of Pyrene by Anionic-Nonionic Mixed Surfactants. J. Hazard. Mater. 2004, 109, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Feng, S. Synergistic Solubilization of Polycyclic Aromatic Hydrocarbons by Mixed Anionic-Nonionic Surfactants. Chemosphere 2003, 53, 459–467. [Google Scholar] [CrossRef]
- Al-Hadabi, B.A.; Aoudia, M. Surfactant–Surfactant and Surfactant–Solute Interactions in SLES–Brij35 Mixed Micelles: Effect of the Degree of Ethoxylation on Pyrene Solubilization Enhancement in Water. Colloids Surf. A Physicochem. Eng. Asp. 2014, 459, 82–89. [Google Scholar] [CrossRef]
- Ogino, K.; Kakihara, T.; Uchiyama, H.; Abe, M. Solution Properties of Mixed Surfactant System Sodium Dodecyl Sulfate and Alkyl Polyoxyethylene Ether System. J. Am. Oil Chem. Soc. 1988, 65, 405–411. [Google Scholar] [CrossRef]
- Tokuoka, Y.; Uchiyama, H.; Abe, M. Solubilization of Some Synthetic Perfumes by Anionic-Nonionic Mixed Surfactant Systems. 2. J. Phys. Chem. 1994, 98, 6167–6171. [Google Scholar] [CrossRef]
- Cabana Saavedra, L.C.; Pachon Gomez, E.M.; Oliveira, R.G.; Fernandez, M.A. Aggregation Behaviour and Solubilization Capability of Mixed Micellar Systems Formed by a Gemini Lipoamino Acid and a Non-Ionic Surfactant. Colloids Surf., A 2017, 533, 41–47. [Google Scholar] [CrossRef]
- Shannigrahi, M.; Bagchi, S. Novel Fluorescent Probe as Aggregation Predictor and Micro-Polarity Reporter for Micelles and Mixed Micelles. Spectrochim. Acta A 2005, 61, 2131–2138. [Google Scholar] [CrossRef]
- Vashishat, R.; Sanan, R.; Mahajan, R.K. Bile Salt-Surface Active Ionic Liquid Mixtures: Mixed Micellization and Solubilization of Phenothiazine. RSC Adv. 2015, 5, 72132–72141. [Google Scholar] [CrossRef]
- Srivastava, A.; Uchiyama, H.; Wada, Y.; Hatanaka, Y.; Shirakawa, Y.; Kadota, K.; Tozuka, Y. Mixed Micelles of the Antihistaminic Cationic Drug Diphenhydramine Hydrochloride with Anionic and Non-Ionic Surfactants Show Improved Solubility, Drug Release and Cytotoxicity of Ethenzamide. J. Mol. Liq. 2019, 277, 349–359. [Google Scholar] [CrossRef]
- Mahbub, S.; Rub, M.A.; Hoque, M.A.; Khan, M.A. Influence of NaCl/Urea on the Aggregation Behavior of Dodecyltrimethylammonium Chloride and Sodium Dodecyl Sulfate at Varying Temperatures and Compositions: Experimental and Theoretical Approach. J. Phys. Org. Chem. 2018, 32, e3917. [Google Scholar] [CrossRef]
- Cui, Z.G.; Canselier, J.P. Interfacial and Aggregation Properties of Some Anionic/Cationic Surfactant Binary Systems II. Mixed Micelle Formation and Surface Tension Reduction Effectiveness. Colloid Polym Sci. 2001, 279, 259–267. [Google Scholar] [CrossRef]
- Cui, Z.; Canselier, J.P. Solubilization in Some Anionic/Cationic Surfactant Binary Systems. Polym. Int. 2003, 52, 548–552. [Google Scholar] [CrossRef]
- Ellegaard, M.D.; Abildskov, J.; O’Connell, J.P. Molecular Thermodynamic Modeling of Mixed Solvent Solubility. Ind. Eng. Chem. Res. 2010, 49, 11620–11632. [Google Scholar] [CrossRef]
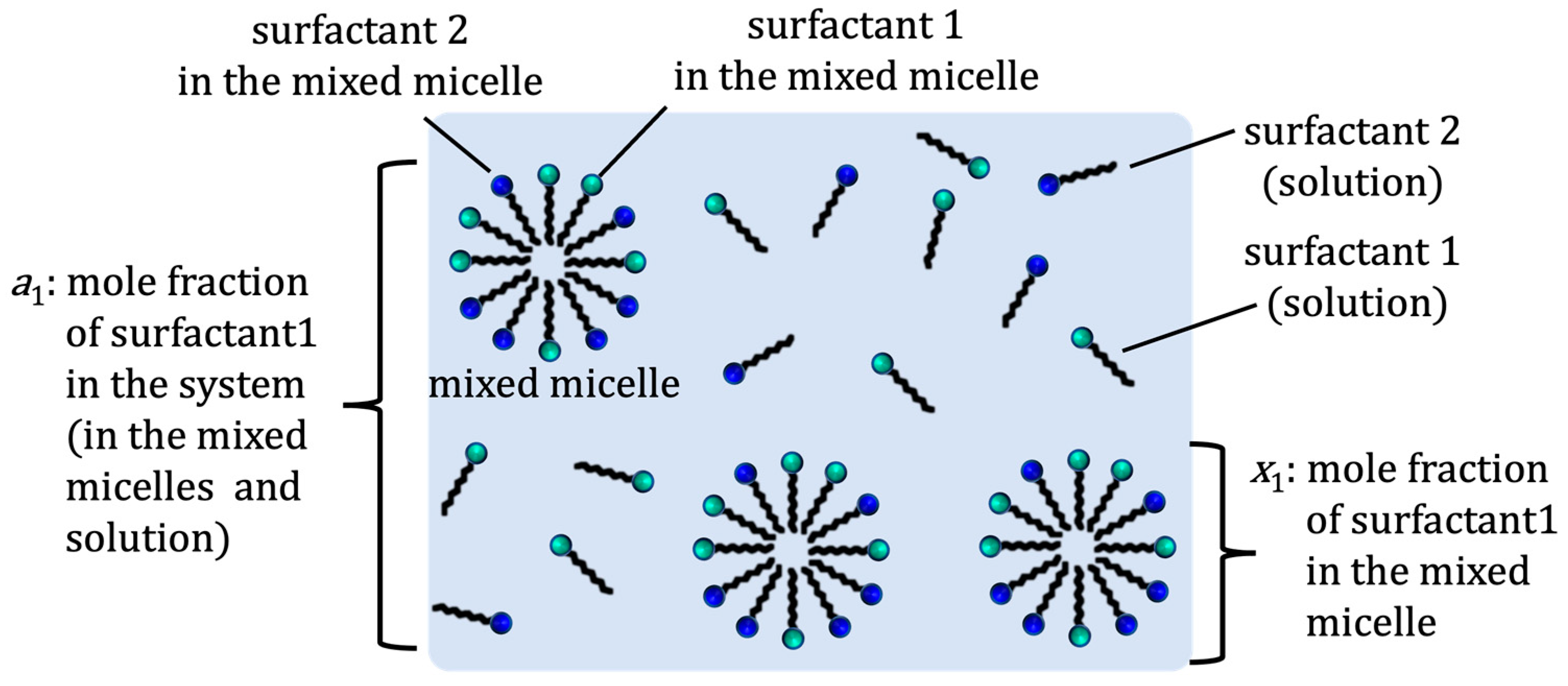
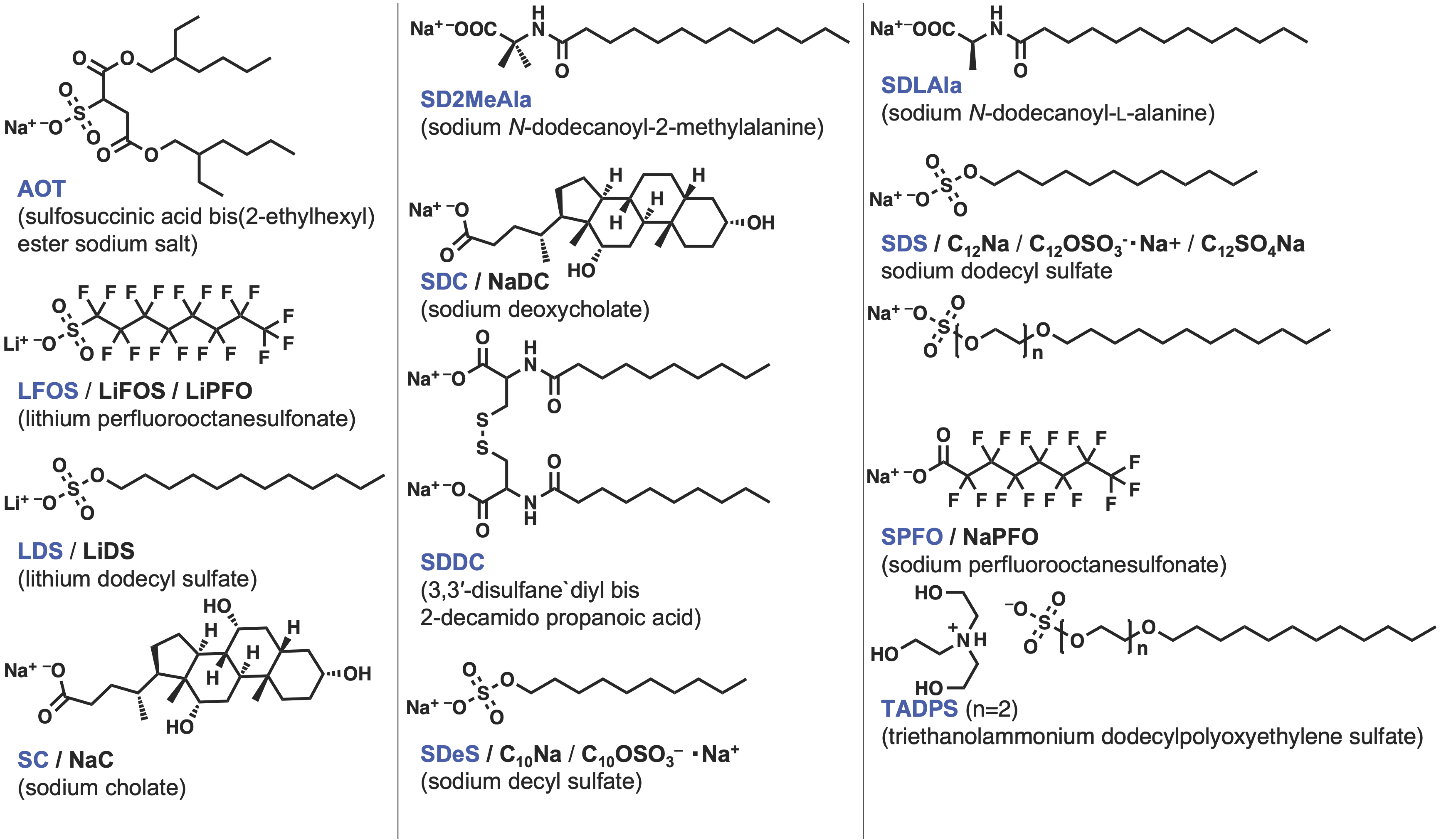

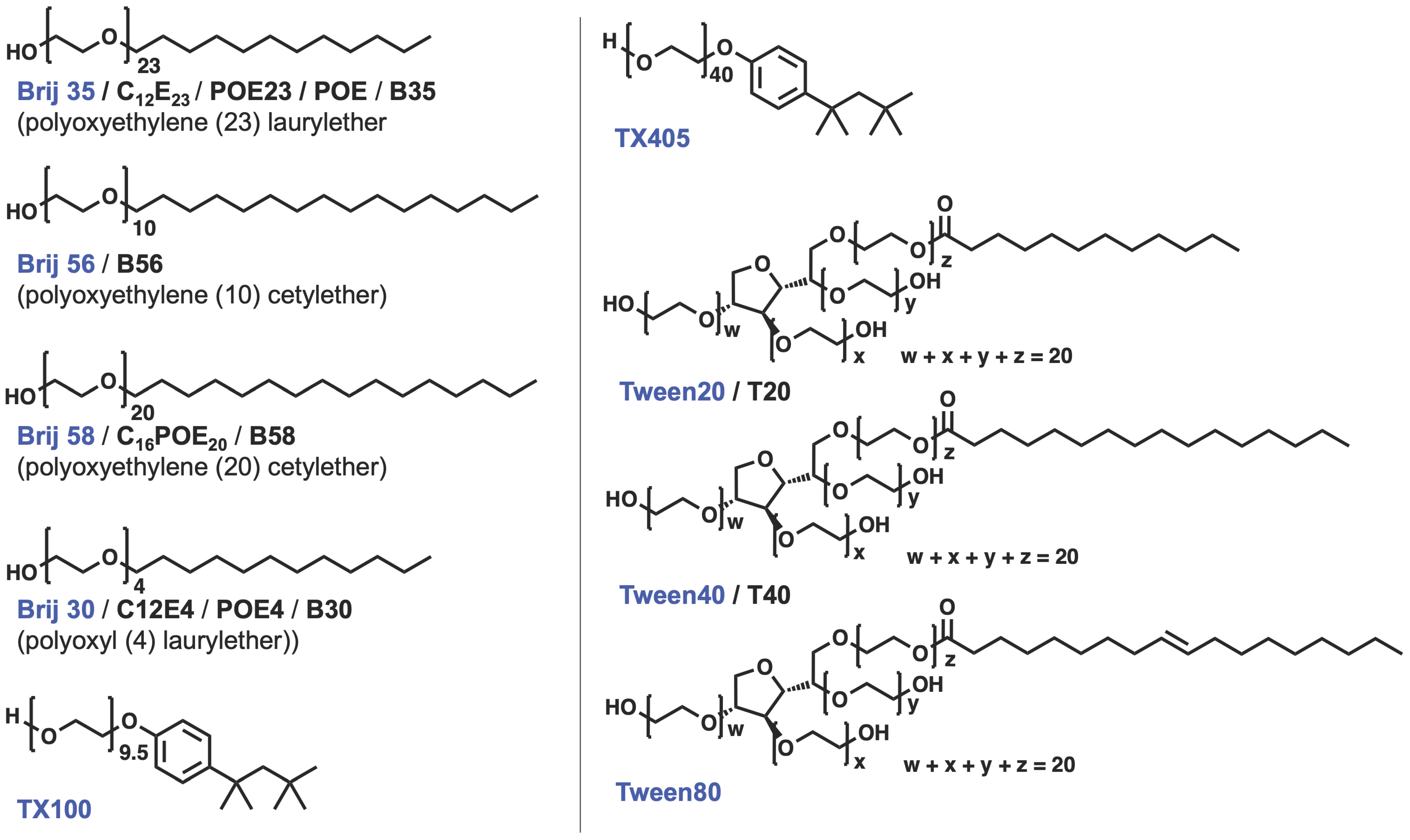
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| AA01 | LFOS/LDS | 2.2 | 23 | NMR | [19] | 1-pentanol | – | 25 | GC | [20] |
| AA02 | LFOS/LDS | 2.2 | 23 | ST | [46] | 1-hexanol | – | – | GC | [46] |
| AA03 | LFOS/LDS | 2.2 | 23 | ST | [46] | 2,2,3,3,4,4,4-heptafluorobutanol | – | – | GC | [46] |
| AA04 | SPFO/SDeS | 1.8 | 23 | NMR | [19] | 1-pentanol | – | 25 | GC | [14] |
| AA05 | SPFO/SDS | 2.1 | 23 | NMR | [19] | 1-pentanol | – | 25 | GC | [14] |
| AA06 | SD2MeAla/SDLAla | −0.090 | 25 | ST | [27] | norphenylephrine | 0.20 | 25 | MEKC | [27] |
| AA07 | SD3MeAla/SDLAla | −0.090 | 25 | ST | [27] | homatropine | 0.16 | 25 | MEKC | [27] |
| AA08 | SD4MeAla/SDLAla | −0.090 | 25 | ST | [27] | bupivacaine | 0.21 | 25 | MEKC | [27] |
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| CC01 | CG1/CPC | −0.8 | 25 | ST | [47] | anthracene | 12.25 | 25 | UV–Vis | [47] |
| CC02 | CG1/CPC | −0.8 | 25 | ST | [47] | pyrene | 16.28 | 25 | UV–Vis | [47] |
| CC03 | CG4/CG2 | −0.08 | 25 | ST | [24] | naphthalene | −4.71 | 25 | UV–Vis | [24] |
| CC04 | CG4/CG2 | −0.08 | 25 | ST | [24] | naphthalene | 2.58 | 25 | UV–Vis | [24] |
| CC05 | CG4/CG2 | −0.08 | 25 | ST | [24] | naphthalene | −2.13 | 25 | UV–Vis | [24] |
| CC06 | CG4/CG3 | −0.14 | 25 | ST | [24] | phenanthrene | −5.92 | 25 | UV–Vis | [24] |
| CC07 | CG4/CG3 | −0.14 | 25 | ST | [24] | phenanthrene | 0.25 | 25 | UV–Vis | [24] |
| CC08 | CG4/CG3 | −0.14 | 25 | ST | [24] | phenanthrene | −4.01 | 25 | UV–Vis | [24] |
| CC09 | CG4/CG5 | −0.29 | 25 | ST | [24] | pyrene | −3.67 | 25 | UV–Vis | [24] |
| CC10 | CG4/CG5 | −0.29 | 25 | ST | [24] | pyrene | −8.22 | 25 | UV–Vis | [24] |
| CC11 | CG4/CG5 | −0.29 | 25 | ST | [24] | pyrene | 10.5 | 25 | UV–Vis | [24] |
| CC12 | CG4/CG5 | −0.38 | 25 | ST | [48] | naphthalene | – | 25 | UV–Vis | [48] |
| CC13 | CG4/CG5 | −0.38 | 25 | ST | [48] | pyrene | – | 25 | UV–Vis | [48] |
| CC14 | CG4/CPC | −0.32 | 25 | ST | [47] | phenanthrene | −1.06 | 25 | UV–Vis | [49] |
| CC15 | CG4/DTAB | −0.22 | 25 | ST | [47] | phenanthrene | −17.6 | 25 | UV–Vis | [49] |
| CC16 | CG6/CTAB | −8.91 | 30 | ST | [50] | naphthalene | 1.04 | 30 | UV–Vis | [50] |
| CC17 | CG6/CTAB | −8.91 | 30 | ST | [50] | anthracene | 0.45 | 30 | UV–Vis | [50] |
| CC18 | CG6/CTAB | −8.91 | 30 | ST | [50] | pyrene | 2.73 | 30 | UV–Vis | [50] |
| CC19 | CG7/CTAB | −7.2 | 30 | ST | [50] | naphthalene | 1.26 | 30 | UV–Vis | [50] |
| CC20 | CG7/CTAB | −7.2 | 30 | ST | [50] | anthracene | 1.92 | 30 | UV–Vis | [50] |
| CC21 | CG7/CTAB | −7.2 | 30 | ST | [50] | pyrene | 1.39 | 30 | UV–Vis | [50] |
| CC22 | CG1/CTAB | −6.76 | 30 | ST | [50] | naphthalene | 4.17 | 30 | UV–Vis | [50] |
| CC23 | CG1/CTAB | −6.76 | 30 | ST | [50] | anthracene | 9.73 | 30 | UV–Vis | [50] |
| CC24 | CG1/CTAB | −6.76 | 30 | ST | [50] | pyrene | 11.21 | 30 | UV–Vis | [50] |
| CC25 | CTAB/HBzC | −0.47 | 25 | ST | [51] | naphthalene | −0.03 | 25 | UV–Vis | [51] |
| CC26 | CTAB/HBzC | −0.47 | 25 | ST | [51] | anthracene | 0.01 | 25 | UV–Vis | [51] |
| CC27 | CTAB/HBzC | −0.47 | 25 | ST | [51] | pyrene | −0.1 | 25 | UV–Vis | [51] |
| CC28 | DTAB/DEB | −0.14 | 25 | ST | [51] | naphthalene | 0.04 | 25 | UV–Vis | [51] |
| CC29 | DTAB/DEB | −0.14 | 25 | ST | [51] | anthracene | −0.25 | 25 | UV–Vis | [51] |
| CC30 | DTAB/DEB | −0.14 | 25 | ST | [51] | pyrene | −0.2 | 25 | UV–Vis | [51] |
| CC31 | TTAC/TBzC | 0.92 | – | CD | [21] | butobarbital | −0.60 | 25 | UV–Vis | [21] |
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| NN01 | Brij30/Tween20 | −0.59 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NN02 | Brij30/Tween20 | −0.59 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NN03 | Brij35/Tween20 | −2.67 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NN04 | Brij35/Tween20 | −2.67 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NN05 | Brij56/Tween40 | −1.36 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NN06 | Brij56/Tween40 | −1.36 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NN07 | Brij58/Brij35 | −1.23 | 25 | ST | [53] | naproxen | 9.39 | 25 | UV–Vis | [53] |
| NN08 | Brij58/Tween40 | −2.67 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NN09 | Brij58/Tween40 | −2.67 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| NA01 | Brij30/SC | −8.77 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA02 | Brij30/SC | −8.77 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA03 | Brij35/SC | −7.97 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA04 | Brij35/SC | −7.97 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA05 | Brij35/SDS | −2.5 | 25 | ST | [18] | 1-pentanol | – | 25 | GC | [20] |
| NA06 | Brij35/SDS | −2.5 | 25 | ST | [18] | heptabarbital | −2.1 | 25 | UV–Vis | [21] |
| NA07 | Brij35/SDS | −2.5 | 25 | ST | [18] | reposal | −2.3 | – | UV–Vis | [15] |
| NA08 | Brij35/SDS | −2.5 | 25 | ST | [18] | pentobarbital | −1.4 | – | UV–Vis | [15] |
| NA09 | Brij35/SDS | −2.5 | 25 | ST | [18] | butobarbital | −1.7 | – | UV–Vis | [15] |
| NA10 | Brij35/SDS | −2.5 | 25 | ST | [18] | barbital | −1.1 | – | UV–Vis | [15] |
| NA11 | Brij35/SDS | −2.5 | 25 | ST | [18] | reposal (0.2 M NaCl) | −1.7 | – | UV–Vis | [15] |
| NA12 | Brij35/SDS | −2.71 | 25 | ST | [53] | naproxen | 25.8 | 25 | UV–Vis | [53] |
| NA13 | Brij35/SDS | −2.71 | 25 | ST | [53] | propranolol | – | 25 | MEUF | [54] |
| NA14 | Brij35/SDS | −2.71 | 25 | ST | [53] | lidocaine | – | 25 | MEUF | [54] |
| NA15 | Brij35/SDS | −2.71 | 25 | ST | [53] | ephedrine | – | 25 | MEUF | [54] |
| NA16 | Brij35/SDS | −2.71 | 25 | ST | [53] | syringic acid | – | 25 | MEUF | [54] |
| NA17 | Brij35/SDS | −2.71 | 25 | ST | [53] | acetone | – | 25 | MEUF | [54] |
| NA18 | Brij35/SDS | −2.71 | 25 | ST | [53] | toluene | – | 25 | MEUF | [54] |
| NA19 | Brij35/SDS | −2.71 | 25 | ST | [53] | phenol | – | 25 | MEUF | [54] |
| NA20 | Brij35/SDS | −2.71 | 25 | ST | [53] | triphenylamine | 7.09 | 25 | UV–Vis | [23] |
| NA21 | Brij35/SDS | −2.71 | 25 | ST | [53] | triphenylphosphine | 30.1 | 25 | UV–Vis | [23] |
| NA22 | Brij35/SDS | −2.71 | 25 | ST | [53] | triphenyl phosphine oxide | 9.69 | 25 | UV–Vis | [23] |
| NA23 | Brij35/SDS | −2.6 | 25 | ST | [55] | pyrene | −1.34 | 25 | UV–Vis | [55] |
| NA24 | Brij35/SDS | −2.71 | 25 | ST | [53] | naphthalene | – | 25 | UV–Vis | [56] |
| NA25 | Brij35/SDS | −2.71 | 25 | ST | [53] | anthracene | – | 25 | UV–Vis | [56] |
| NA26 | Brij35/SDS | −2.71 | 25 | ST | [53] | phenanthrene | – | 25 | UV–Vis | [56] |
| NA27 | Brij35/SDS | −2.71 | 25 | ST | [53] | pyrene | – | 25 | UV–Vis | [56] |
| NA28 | Brij35/SDS | −2.71 | 25 | ST | [53] | linalool | – | 25 | UV–Vis | [56] |
| NA29 | Brij35/SDS | −2.71 | 25 | ST | [53] | benzyl acetate | – | 25 | UV–Vis | [56] |
| NA30 | Brij35/SDS | −2.71 | 25 | ST | [53] | α-ionone | – | 25 | UV–Vis | [56] |
| NA31 | Brij35/SDS | −2.71 | 25 | ST | [53] | α-hexylcinnamaldehyde | – | 25 | UV–Vis | [56] |
| NA32 | Brij35/SLE1S | 2.01 | – | FL | [57] | pyrene | 1.33 | – | UV–Vis | [57] |
| NA33 | Brij35/SLE2S | 2.01 | – | FL | [57] | pyrene | 0.68 | – | UV–Vis | [57] |
| NA34 | Brij35/SLE3S | 2.01 | – | FL | [57] | pyrene | 0.40 | – | UV–Vis | [57] |
| NA35 | Brij56/SC | −10.42 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA36 | Brij56/SC | −10.42 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA37 | Brij58/SC | −9.11 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA38 | Brij58/SC | −9.11 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA39 | Brij58/SDS | −5.07 | 25 | ST | [53] | naproxen | 20.6 | 25 | UV–Vis | [53] |
| NA40 | Brij58/SDS | −2.1 | 25 | ST | [55,58] | pyrene | −28.3 | 25 | UV–Vis | [55] |
| NA41 | Brij58/SDS | −6.18 | 30 | ST | [55,58] | limonene | −0.02 | 30 | UV–Vis | [59] |
| NA42 | Brij58/SDS | −6.18 | 30 | ST | [55,58] | eugenol | −0.40 | 30 | UV–Vis | [59] |
| NA43 | Tween20/SC | −8.08 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA44 | Tween20/SC | −8.08 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA45 | Tween40/SC | −8.9 | 25 | ST | [52] | nifedipine | – | 25 | UV–Vis | [52] |
| NA46 | Tween40/SC | −8.9 | 25 | ST | [52] | carbamazepine | – | 25 | UV–Vis | [52] |
| NA47 | Tween80/SDDC | −4.2 | 30 | ST | [60] | naphthalene | – | 30 | UV–Vis | [60] |
| NA48 | Tween80/SDDC | −4.2 | 30 | ST | [60] | phenanthrene | – | 30 | UV–Vis | [60] |
| NA49 | Tween80/SDDC | −4.2 | 30 | ST | [60] | pyrene | – | 30 | UV–Vis | [60] |
| NA50 | TX100/SDS | −1.5 | 25 | ST | [55] | pyrene | −2.81 | 25 | UV–Vis | [55] |
| NA51 | TX100/SDS | −1.5 | 25 | ST | [55] | naphthalene | – | 25 | UV–Vis | [56] |
| NA52 | TX100/SDS | −1.5 | 25 | ST | [55] | acenaphthylene | – | 25 | UV–Vis | [56] |
| NA53 | TX100/SDS | −1.5 | 25 | ST | [55] | anthracene | – | 25 | UV–Vis | [56] |
| NA54 | TX100/SDS | −1.5 | 25 | ST | [55] | phenanthrene | – | 25 | UV–Vis | [56] |
| NA55 | TX100/SDS | −1.5 | 25 | ST | [55] | pyrene | – | 25 | UV–Vis | [56] |
| NA56 | TX100/SDS | −4.02 | 30 | FL | [61] | 2-[3-(N-methyl- N-phenylamino)- 2-propenylidene] indanone | – | 30 | UV–Vis | [61] |
| NA57 | TX405/SDS | −3.5 | 25 | ST | [55] | pyrene | 1.54 | 25 | UV–Vis | [55] |
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| NC01 | Brij30/DEB | −3.66 | 25 | ST | [51] | naphthalene | 3.15 | 25 | UV–Vis | [51] |
| NC02 | Brij30/DEB | −3.66 | 25 | ST | [51] | anthracene | 6.96 | 25 | UV–Vis | [51] |
| NC03 | Brij30/DEB | −3.66 | 25 | ST | [51] | pyrene | 5.03 | 25 | UV–Vis | [51] |
| NC04 | Brij30/DTAB | −3.53 | 25 | ST | [51] | naphthalene | 2.34 | 25 | UV–Vis | [51] |
| NC05 | Brij30/DTAB | −3.53 | 25 | ST | [51] | anthracene | 4.11 | 25 | UV–Vis | [51] |
| NC06 | Brij30/DTAB | −3.53 | 25 | ST | [51] | pyrene | 4.58 | 25 | UV–Vis | [51] |
| NC07 | Brij35/CG4 | −0.38 | 25 | ST | [47] | phenanthrene | 1.8 | 25 | UV–Vis | [49] |
| NC08 | Brij35/CG4 | −1.27 | 25 | ST | [48] | naphthalene | – | 25 | UV–Vis | [48] |
| NC09 | Brij35/CG4 | −1.27 | 25 | ST | [48] | pyrene | – | 25 | UV–Vis | [48] |
| NC10 | Brij35/CG5 | −1.42 | 25 | ST | [48] | naphthalene | – | 25 | UV–Vis | [48] |
| NC11 | Brij35/CG5 | −1.42 | 25 | ST | [48] | pyrene | – | 25 | UV–Vis | [48] |
| NC12 | Brij35/CTAB | −1.03 | 25 | ST | [53] | naproxen | 18.9 | 25 | UV–Vis | [53] |
| NC13 | Brij35/CTAB | −1.03 | 25 | ST | [53] | lidocaine | – | 25 | MLC | [54] |
| NC14 | Brij35/CTAB | −1.03 | 25 | ST | [53] | coumarin | – | 25 | MLC | [54] |
| NC15 | Brij35/CTAB | −1.03 | 25 | ST | [53] | isovanillin | – | 25 | MLC | [54] |
| NC16 | Brij35/CTAB | −1.03 | 25 | ST | [53] | phenol | – | 25 | MLC | [54] |
| NC17 | Brij35/CTAB | −1.03 | 25 | ST | [53] | syringic acid | – | 25 | MLC | [54] |
| NC18 | Brij35/CTAB | −1.03 | 25 | ST | [53] | ferulic acid | – | 25 | MLC | [54] |
| NC19 | Brij35/CTAB | −1.03 | 25 | ST | [53] | vanillic acid | – | 25 | MLC | [54] |
| NC20 | Brij35/DTAB | −3.98 | 25 | ST | [53] | naproxen | 21.4 | 25 | UV–Vis | [53] |
| NC21 | Brij35/DTAB | −3.98 | 25 | ST | [53] | triphenylamine | 11 | 25 | UV–Vis | [23] |
| NC22 | Brij35/DTAB | −3.98 | 25 | ST | [53] | triphenylphosphine | 22.9 | 25 | UV–Vis | [23] |
| NC23 | Brij35/DTAB | −3.98 | 25 | ST | [53] | triphenylphosphine oxide | 1.87 | 25 | UV–Vis | [23] |
| NC24 | Brij35/TTAB | −3.8 | 25 | FL | [22] | reposal | −0.3 | – | UV–Vis | [15] |
| NC25 | Brij35/TTAB | −3.8 | 25 | FL | [22] | pentobarbital | −0.4 | – | UV–Vis | [15] |
| NC26 | Brij35/TTAB | −3.8 | 25 | FL | [22] | butobarbital | −0.4 | – | UV–Vis | [15] |
| NC27 | Brij35/TTAB | −3.8 | 25 | FL | [22] | barbital | −0.3 | – | UV–Vis | [15] |
| NC28 | Brij35/TTAB | −2.17 | 25 | ST | [53] | naproxen | 25.6 | 25 | UV–Vis | [53] |
| NC29 | Brij56/CG1 | −2.55 | 25 | ST | [47] | anthracene | 3.33 | 25 | UV–Vis | [47] |
| NC30 | Brij56/CG1 | −2.55 | 25 | ST | [47] | pyrene | 4.06 | 25 | UV–Vis | [47] |
| NC31 | Brij58/CG6 | −3.24 | 30 | ST | [50] | naphthalene | 2.97 | 30 | UV–Vis | [50] |
| NC32 | Brij58/CG6 | −3.24 | 30 | ST | [50] | anthracene | 2.65 | 30 | UV–Vis | [50] |
| NC33 | Brij58/CG6 | −3.24 | 30 | ST | [50] | pyrene | 2.57 | 30 | UV–Vis | [50] |
| NC34 | Brij58/CG7 | −4.16 | 30 | ST | [50] | naphthalene | 1.05 | 30 | UV–Vis | [50] |
| NC35 | Brij58/CG7 | −4.16 | 30 | ST | [50] | anthracene | 1.51 | 30 | UV–Vis | [50] |
| NC36 | Brij58/CG7 | −4.16 | 30 | ST | [50] | pyrene | 0.2 | 30 | UV–Vis | [50] |
| NC37 | Brij58/CG1 | −0.75 | 30 | ST | [50] | naphthalene | 1.9 | 30 | UV–Vis | [50] |
| NC38 | Brij58/CG1 | −0.75 | 30 | ST | [50] | anthracene | 5.69 | 30 | UV–Vis | [50] |
| NC39 | Brij58/CG1 | −0.75 | 30 | ST | [50] | pyrene | 5.31 | 30 | UV–Vis | [50] |
| NC40 | Brij58/CTAB | −2.99 | 25 | ST | [53] | naproxen | 22 | 25 | UV–Vis | [53] |
| NC41 | Brij58/CTAB | −3.05 | 25 | ST | [51] | naphthalene | 2.86 | 25 | UV–Vis | [51] |
| NC42 | Brij58/CTAB | −3.05 | 25 | ST | [51] | anthracene | 4.56 | 25 | UV–Vis | [51] |
| NC43 | Brij58/CTAB | −3.05 | 25 | ST | [51] | pyrene | 5.96 | 25 | UV–Vis | [51] |
| NC44 | Brij58/CTAB | −2.99 | 25 | ST | [53] | triphenylamine | 6.44 | 25 | UV–Vis | [23] |
| NC45 | Brij58/CTAB | −2.99 | 25 | ST | [53] | triphenylphosphine | 23.6 | 25 | UV–Vis | [23] |
| NC46 | Brij58/CTAB | −2.99 | 25 | ST | [53] | triphenylphosphine oxide | 9.62 | 25 | UV–Vis | [23] |
| NC47 | Brij58/DTAB | −5.25 | 25 | ST | [53] | naproxen | 34.3 | 25 | UV–Vis | [53] |
| NC48 | Brij58/HBzC | −2.98 | 25 | ST | [51] | naphthalene | 2.46 | 25 | UV–Vis | [51] |
| NC49 | Brij58/HBzC | −2.98 | 25 | ST | [51] | anthracene | 4.57 | 25 | UV–Vis | [51] |
| NC50 | Brij58/HBzC | −2.98 | 25 | ST | [51] | pyrene | 5.26 | 25 | UV–Vis | [51] |
| NC51 | Brij58/TTAB | −4.61 | 25 | ST | [53] | naproxen | 22.4 | 25 | UV–Vis | [53] |
| NC52 | TX100/CG4 | −0.94 | 25 | ST | [47] | phenanthrene | 0.76 | 25 | UV–Vis | [49] |
| Measurement of β | Measurement of B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sys. ID | Surfactants | β | T [°C] | Method | Ref. | Solute | B | T [°C] | Method | Ref. |
| AC01 | AOT/CG1 | −3.33 | 25 | ST | [47] | anthracene | 6.25 | 25 | UV–Vis | [47] |
| AC02 | AOT/CG1 | −3.33 | 25 | ST | [47] | pyrene | 7.69 | 25 | UV–Vis | [47] |
| AC03 | SC/DMIMB | −9.03 | 25 | FL | [62] | phenothiazine | – | – | UV–Vis | [62] |
| AC04 | SDC/DCP | −3.69 | 25 | ST | [63] | ethenzamide | – | 37 | HPLC | [63] |
| AC05 | SDC/DMIMB | −9.95 | 25 | FL | [62] | phenothiazine | – | – | UV–Vis | [62] |
| AC06 | SDeS/DeTAB | −13.2 | 23 | ST | [6] | butobarbital | −4.5 | 25 | UV–Vis | [21] |
| AC07 | SDeS/DeTAB | −13.2 | 23 | ST | [6] | 1-pentanol | – | 25 | GC | [20] |
| AC08 | SDS/DTAC | −8.09 | 25 | CD | [64] | heptabarbital | −8.8 | 25 | UV–Vis | [21] |
| AC09 | TADPS/CPC | −18.3 | 25 | ST | [65] | toluene | – | 25 | UV–Vis | [66] |
| AC10 | TADPS/CTAB | −15.7 | 25 | ST | [65] | 1-octanol | −0.61 | 25 | UV–Vis | [66] |
| AC11 | TADPS/CTAB | −15.7 | 25 | ST | [65] | n-heptane | – | 25 | UV–Vis | [66] |
| AC12 | TADPS/CTAB | −15.7 | 25 | ST | [65] | toluene | – | 25 | UV–Vis | [66] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suzuki, N. Interaction Parameters for the Formation of Mixed Micelles and Partitioning of Solutes in Them: A Review. AppliedChem 2024, 4, 1-14. https://doi.org/10.3390/appliedchem4010001
Suzuki N. Interaction Parameters for the Formation of Mixed Micelles and Partitioning of Solutes in Them: A Review. AppliedChem. 2024; 4(1):1-14. https://doi.org/10.3390/appliedchem4010001
Chicago/Turabian StyleSuzuki, Nozomu. 2024. "Interaction Parameters for the Formation of Mixed Micelles and Partitioning of Solutes in Them: A Review" AppliedChem 4, no. 1: 1-14. https://doi.org/10.3390/appliedchem4010001
APA StyleSuzuki, N. (2024). Interaction Parameters for the Formation of Mixed Micelles and Partitioning of Solutes in Them: A Review. AppliedChem, 4(1), 1-14. https://doi.org/10.3390/appliedchem4010001





