Variability of the Spreading of the Patos Lagoon Plume Using Numerical Drifters
Abstract
:1. Introduction
Study Area
2. Material and Methods
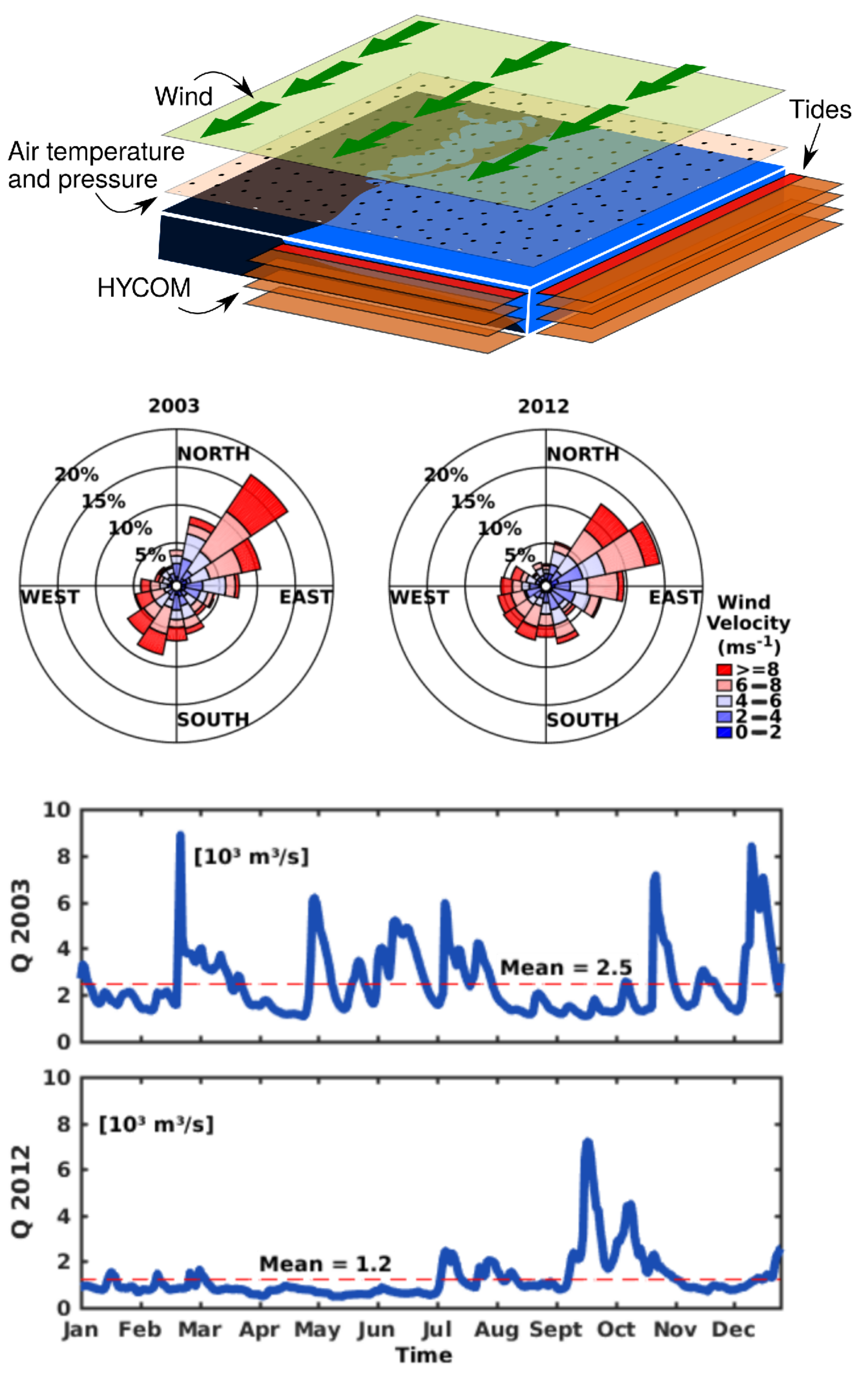
2.1. Hydrodynamic Model and Lagrangian Module
2.2. Boundary Conditions
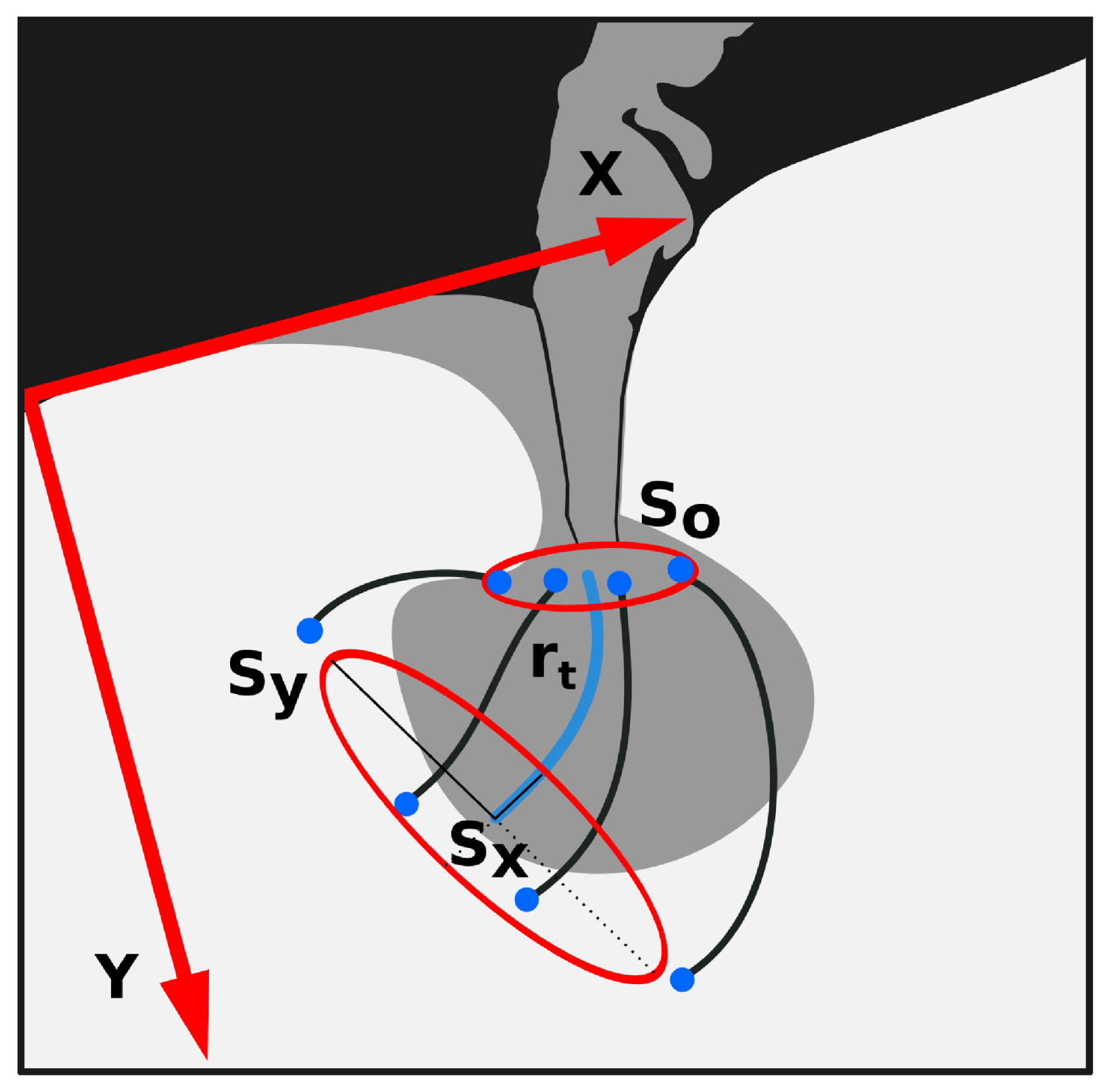
2.3. Drifters’ Spreading Metrics
2.4. Scale Parameters
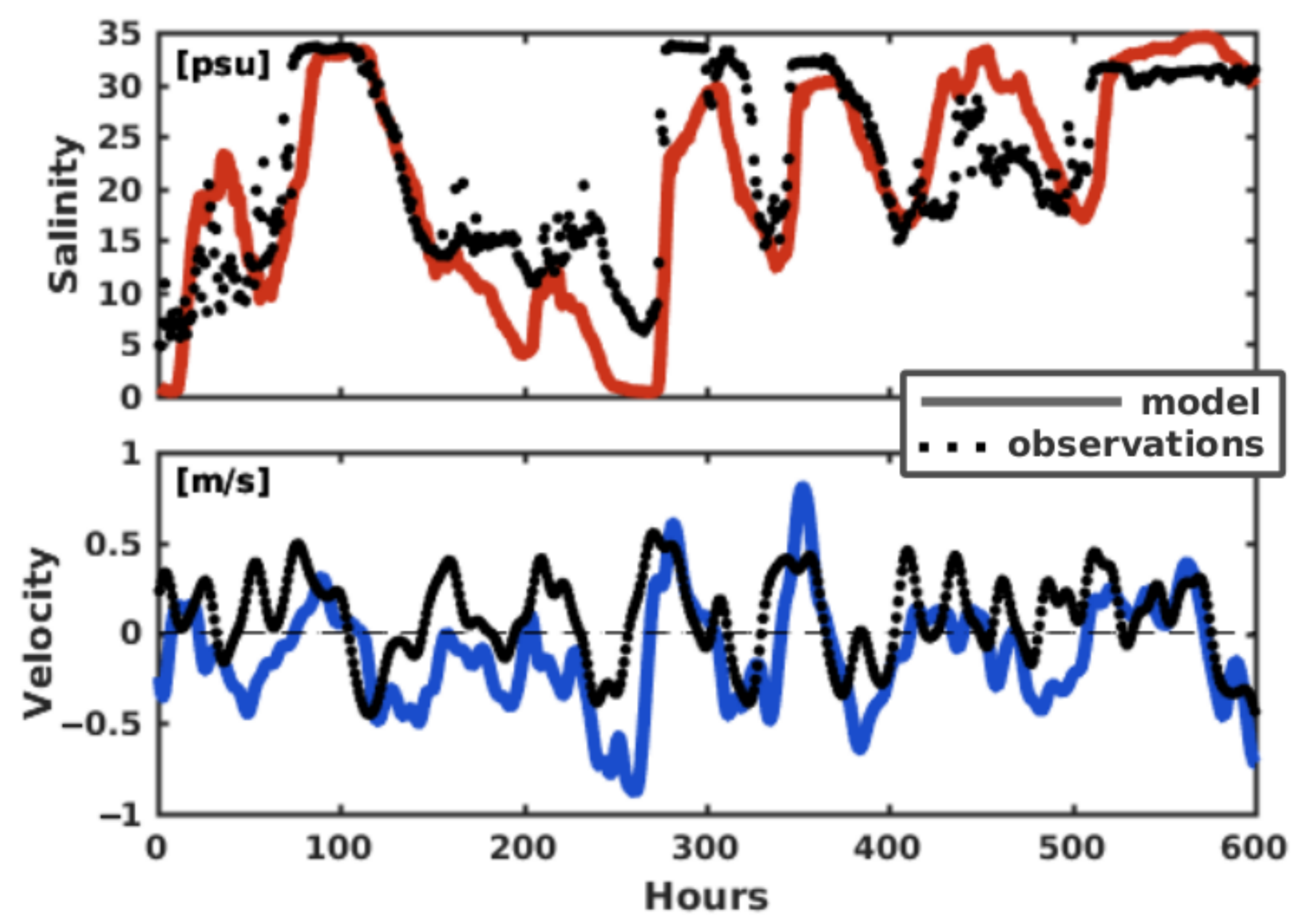
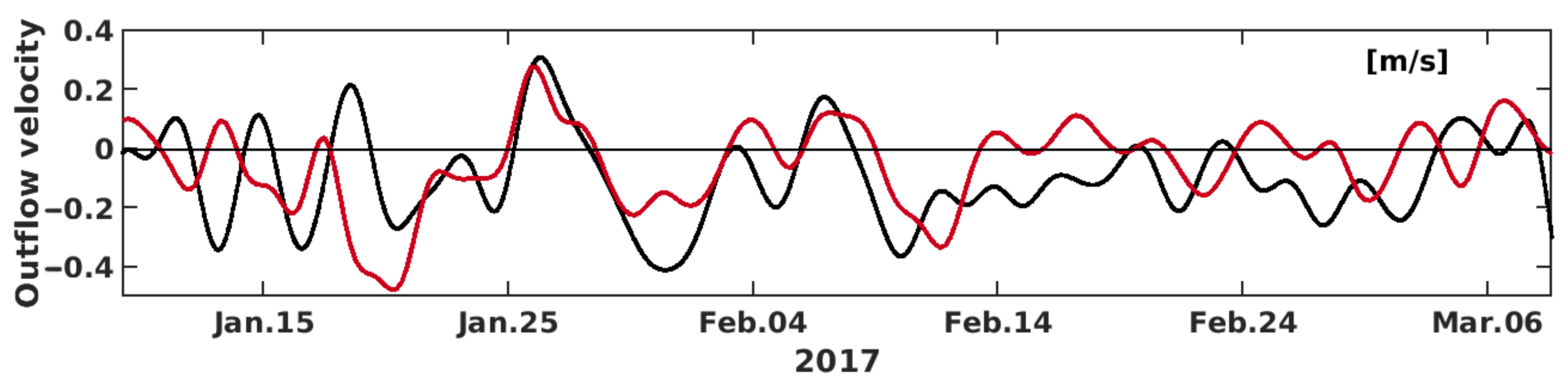
2.5. Validation of the Hydrodynamic Model
3. Results and Discussion
3.1. Plume Circulation Pattern
3.2. Dynamical Classification
3.3. Trajectories of the Drifters
3.4. Drifter’s Spreading
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Trenberth, K.E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the global water budget and its annual cycle using observational and model data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Sharples, J.; Middelburg, J.J.; Fennel, K.; Jickells, T.D. What proportion of riverine nutrients reaches the open ocean? In Global Biogeochemical Cycles; Wiley: New York, NY, USA, 2016. [Google Scholar]
- Vizy, E.K.; Cook, K.H. Influence of the Amazon/Orinoco Plume on the summertime Atlantic climate. J. Geophys. Res. Atmos. 2010, 115, D21112. [Google Scholar] [CrossRef]
- Milliman, J.D.; Syvitski, J.P. Geomorphic/tectonic control of sediment discharge to the ocean: The importance of small mountainous rivers. J. Geol. 1992, 100, 525–544. [Google Scholar] [CrossRef]
- Wheatcroft, R.A.; Hatten, J.A.; Pasternack, G.B.; Warrick, J.A.; Goni, M.A. The role of effective discharge in the ocean delivery of particulate organic carbon by small, mountainous river systems. Limnol. Oceanogr. 2010, 55, 161–171. [Google Scholar] [CrossRef] [Green Version]
- Marques, W.C.; Fernandes, E.H.; Moller, O.O. Straining and advection contributions to the mixing process of the Patos Lagoon coastal plume, Brazil. J. Geophys. Res. Ocean. 2010, 115, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Garvine, R.W. A dynamical system for classifying buoyant coastal discharges. Cont. Shelf Res. 1995, 15, 1585–1596. [Google Scholar] [CrossRef]
- Horner-Devine, A.R.; Hetland, R.D.; MacDonald, D.G. Mixing and transport in coastal river plumes. Annu. Rev. Fluid Mech. 2015, 47, 569–594. [Google Scholar] [CrossRef]
- O’Donnell, J.; Ackleson, S.G.; Levine, E.R. On the spatial scales of a river plume. J. Geophys. Res. Ocean. 2008, 113, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Marques, W.; Fernandes, E.; Monteiro, I.; Möller, O. Numerical modeling of the Patos Lagoon coastal plume, Brazil. Cont. Shelf Res. 2009, 29, 556–571. [Google Scholar] [CrossRef]
- Hetland, R.D. Relating river plume structure to vertical mixing. J. Phys. Oceanogr. 2005, 35, 1667–1688. [Google Scholar] [CrossRef]
- Yankovsky, A.E.; Chapman, D.C. A simple theory for the fate of buoyant coastal discharges. J. Phys. Oceanogr. 1997, 27, 1386–1401. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Horner-Devine, A.R. Laboratory investigation of the impact of lateral spreading on buoyancy flux in a river plume. J. Phys. Oceanogr. 2013, 43, 2588–2610. [Google Scholar] [CrossRef]
- Jurisa, J.T.; Nash, J.D.; Moum, J.N.; Kilcher, L.F. Controls on Turbulent Mixing in a Strongly Stratified and Sheared Tidal River Plume. J. Phys. Oceanogr. 2016, 46, 2373–2388. [Google Scholar] [CrossRef]
- Warrick, J.A.; DiGiacomo, P.M.; Weisberg, S.B.; Nezlin, N.P.; Mengel, M.; Jones, B.H.; Ohlmann, J.C.; Washburn, L.; Terrill, E.J.; Farnsworth, K.L. River plume patterns and dynamics within the Southern California Bight. Cont. Shelf Res. 2007, 27, 2427–2448. [Google Scholar] [CrossRef]
- Bao, H.; Lee, T.Y.; Huang, J.C.; Feng, X.; Dai, M.; Kao, S.J. Importance of Oceanian small mountainous rivers (SMRs) in global land-to-ocean output of lignin and modern biospheric carbon. Sci. Rep. 2015, 5, 16217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Osadchiev, A.; Korotenko, K.; Zavialov, P.; Chiang, W.S.; Liu, C.C. Transport and bottom accumulation of fine river sediments under typhoon conditions and associated submarine landslides: Case study of the Peinan River, Taiwan. Nat. Hazards Earth Syst. Sci. 2016, 16, 41–54. [Google Scholar] [CrossRef]
- Ostrander, C.E.; McManus, M.A.; DeCarlo, E.H.; Mackenzie, F.T. Temporal and spatial variability of freshwater plumes in a semienclosed estuarine-bay system. Estuaries Coasts 2008, 31, 192. [Google Scholar] [CrossRef]
- Pimenta, F.M.; Kirwan, A., Jr. The response of large outflows to wind forcing. Cont. Shelf Res. 2014, 89, 24–37. [Google Scholar] [CrossRef]
- Suanda, S.H.; Kumar, N.; Miller, A.J.; Di Lorenzo, E.; Haas, K.; Cai, D.; Edwards, C.A.; Washburn, L.; Fewings, M.R.; Torres, R.; et al. Wind relaxation and a coastal buoyant plume north of Pt. Conception, CA: Observations, simulations, and scalings. J. Geophys. Res. Ocean. 2016, 121, 7455–7475. [Google Scholar] [CrossRef]
- Zhao, J.; Gong, W.; Shen, J. The effect of wind on the dispersal of a tropical small river plume. Front. Earth Sci. 2018, 12, 170–190. [Google Scholar] [CrossRef]
- Huang, W.; Li, C.; White, J.R.; Bargu, S.; Milan, B.; Bentley, S. Numerical experiments on variation of freshwater plume and leakage effect from Mississippi River Diversion in the Lake Pontchartrain Estuary. J. Geophys. Res. Ocean. 2020, 125, e2019JC015282. [Google Scholar] [CrossRef]
- Orton, P.M.; Jay, D.A. Observations at the tidal plume front of a high-volume river outflow. Geophys. Res. Lett. 2005, 32, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Kilcher, L.F.; Nash, J.D.; Moum, J.N. The role of turbulence stress divergence in decelerating a river plume. J. Geophys. Res. Ocean. 2012, 117, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Rong, Z.; Hetland, R.D.; Zhang, W.; Zhang, X. Current–wave interaction in the Mississippi–Atchafalaya river plume on the Texas–Louisiana shelf. Ocean. Model. 2014, 84, 67–83. [Google Scholar] [CrossRef] [Green Version]
- Zavialov, P.; Möller, O.; Campos, E. First direct measurements of currents on the continental shelf of southern Brazil. Cont. Shelf Res. 2002, 22, 1975–1986. [Google Scholar] [CrossRef]
- Burrage, D.; Wesson, J.; Martinez, C.; Pérez, T.; Möller, O.; Piola, A. Patos Lagoon outflow within the Río de la Plata plume using an airborne salinity mapper: Observing an embedded plume. Cont. Shelf Res. 2008, 28, 1625–1638. [Google Scholar] [CrossRef]
- Möller, O.O.; Castaing, P.; Salomon, J.C.; Lazure, P. The influence of local and non-local forcing effects on the subtidal circulation of Patos Lagoon. Estuaries Coasts 2001, 24, 297–311. [Google Scholar] [CrossRef]
- Möller, O.O.; Castaing, P.; Fernandes, E.H.L.; Lazure, P. Tidal frequency dynamics of a southern Brazil coastal lagoon: Choking and short period forced oscillations. Estuaries Coasts 2007, 30, 311–320. [Google Scholar] [CrossRef]
- Zavialov, P.; Kostianoy, A.; Möller, O. SAFARI cruise: Mapping river discharge effects on Southern Brazilian shelf. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Zavialov, P.; Pelevin, V.; Belyaev, N.; Izhitskiy, A.; Konovalov, B.; Krementskiy, V.; Goncharenko, I.; Osadchiev, A.; Soloviev, D.; Garcia, C.; et al. High resolution LiDAR measurements reveal fine internal structure and variability of sediment-carrying coastal plume. Estuar. Coast. Shelf Sci. 2018, 205, 40–45. [Google Scholar] [CrossRef]
- Fernandes, E.; Dyer, K.; Moller, O.; Niencheski, L. The Patos Lagoon hydrodynamics during an El Niño event (1998). Cont. Shelf Res. 2002, 22, 1699–1713. [Google Scholar] [CrossRef]
- Fernandes, E.H.L.; Dyer, K.R.; Moller, O.O. Spatial gradients in the flow of southern Patos Lagoon. J. Coast. Res. 2005, 20, 759–769. [Google Scholar] [CrossRef]
- Marques, W.C.; Fernandes, E.H.; Moraes, B.C.; Möller, O.O.; Malcherek, A. Dynamics of the Patos Lagoon coastal plume and its contribution to the deposition pattern of the southern Brazilian inner shelf. J. Geophys. Res. Ocean. 2010, 115, 1–22. [Google Scholar] [CrossRef]
- Hervouet, J.M. Free Surface Flows: Modelling with Finite Element Methods; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Marques, W.; Stringari, C.; Kirinus, E.; Möller, O., Jr.; Toldo, E., Jr.; Andrade, M. Numerical modeling of the Tramandaí beach oil spill, Brazil—Case study for January 2012 event. Appl. Ocean. Res. 2017, 65, 178–191. [Google Scholar] [CrossRef]
- Cucco, A.; Umgiesser, G. Modeling the Venice Lagoon residence time. Ecol. Model. 2006, 193, 34–51. [Google Scholar] [CrossRef]
- Chassignet, E.P.; Hurlburt, H.E.; Smedstad, O.M.; Halliwell, G.R.; Hogan, P.J.; Wallcraft, A.J.; Baraille, R.; Bleck, R. The HYCOM (hybrid coordinate ocean model) data assimilative system. J. Mar. Syst. 2007, 65, 60–83. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef] [Green Version]
- Pham, C.T.; Joly, A. Telemac Modelling System: Telemac-3D Software—Operating Manual; Technical Report; EDF: Chateau, France, 2016. [Google Scholar]
- Simmons, A.; Uppala, S.; Dee, D.; Kobayashi, S. ERA-Interim: New ECMWF reanalysis products from 1989 onwards. Ecmwf Newsl. 2007, 110, 25–35. [Google Scholar]
- Chen, F.; MacDonald, D.G.; Hetland, R.D. Lateral spreading of a near-field river plume: Observations and numerical simulations. J. Geophys. Res. Ocean. 2009, 114, 1–12. [Google Scholar] [CrossRef]
- Fontoura, J.A.; Almeida, L.E.; Calliari, L.J.; Cavalcanti, A.M.; Möller, O., Jr.; Romeu, M.A.R.; Christófaro, B.R. Coastal Hydrodynamics and Longshore Transport of Sand on Cassino Beach and on Mar Grosso Beach, Southern Brazil. J. Coast. Res. 2012, 29, 855–869. [Google Scholar] [CrossRef]
- Bennett, A. Relative dispersion: Local and nonlocal dynamics. J. Atmos. Sci. 1984, 41, 1881–1886. [Google Scholar] [CrossRef] [Green Version]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Cambridge, MA, USA, 2011; Volume 101. [Google Scholar]
- Tilburg, C.E.; Gill, S.M.; Zeeman, S.I.; Carlson, A.E.; Arienti, T.W.; Eickhorst, J.A.; Yund, P.O. Characteristics of a shallow river plume: Observations from the Saco River Coastal Observing System. Estuaries Coasts 2011, 34, 785–799. [Google Scholar] [CrossRef]
- Chao, S.Y. Wind-driven motion of estuarine plumes. J. Phys. Oceanogr. 1988, 18, 1144–1166. [Google Scholar] [CrossRef] [Green Version]
- Sanders, T.M.; Garvine, R.W. Fresh water delivery to the continental shelf and subsequent mixing: An observational study. J. Geophys. Res. Ocean. 2001, 106, 27087–27101. [Google Scholar] [CrossRef]
- Thomson, R.E.; Emery, W.J. Data Analysis Methods in Physical Oceanography; Newnes: London, UK, 2014. [Google Scholar]
- Qu, L.; Hetland, R.D. Temporal resolution of wind forcing required for river plume simulations. J. Geophys. Res. Ocean. 2019, 124, 1459–1473. [Google Scholar] [CrossRef]
- Silva, D.V.D.; Oleinik, P.H.; Costi, J.; de Paula Kirinus, E.; Marques, W.C. Residence time patterns of Mirim Lagoon (Brazil) derived from two-dimensional hydrodynamic simulations. Environ. Earth Sci. 2019, 78, 163. [Google Scholar] [CrossRef]
- Vieira, H.M.; Weschenfelder, J.; Fernandes, E.H.; Oliveira, H.A.; Möller, O.O.; García-Rodríguez, F. Links between surface sediment composition, morphometry and hydrodynamics in a large shallow coastal lagoon. Sediment. Geol. 2020, 398, 105591. [Google Scholar] [CrossRef]
- Marques, W.C.; Monteiro, I.O.; Möller, O.O. The Exchange Processes in the Patos Lagoon Estuarine Channel, Brazil. Int. J. Geosci. 2011, 2, 248. [Google Scholar] [CrossRef] [Green Version]
- Castelao, R.M.; Moller, O.O., Jr. A modeling study of Patos Lagoon (Brazil) flow response to idealized wind and river discharge: Dynamical analysis. Braz. J. Oceanogr. 2006, 54, 1–17. [Google Scholar] [CrossRef]
- Barros, G.; Marques, W. Long-Term Temporal Variability of the Freshwater Discharge and Water Levels at Patos Lagoon, Rio Grande do Sul, Brazil. Int. J. Geophys. 2012, 2012, 459497. [Google Scholar] [CrossRef]
- Barros, G.P.; Marques, W.C.; Kirinus, E.D.P. Influence of the freshwater discharge on the hydrodynamics of Patos Lagoon, Brazil. Int. J. Geosci. 2014, 2014, 925–942. [Google Scholar] [CrossRef] [Green Version]
- Mendes, R.; Sousa, M.C.; Gómez-Gesteira, M.; Dias, J.M.; de Castro, M. New insights into the Western Iberian Buoyant Plume: Interaction between the Douro and Minho River plumes under winter conditions. Prog. Oceanogr. 2016, 141, 30–43. [Google Scholar] [CrossRef]
- Lentz, S.J.; Largier, J. The influence of wind forcing on the Chesapeake Bay buoyant coastal current. J. Phys. Oceanogr. 2006, 36, 1305–1316. [Google Scholar] [CrossRef]
- Yankovsky, A.E.; Hickey, B.M.; Münchow, A.K. Impact of variable inflow on the dynamics of a coastal buoyant plume. J. Geophys. Res. Ocean. 2001, 106, 19809–19824. [Google Scholar] [CrossRef] [Green Version]
- Hodapp, M.J.; Kirinus, E.d.P.; Marques, W.C.; Oleinik, P.H.; Moller, O.O. Investigation of persistent coherent structures along the Southern Brazilian Shelf. Braz. J. Oceanogr. 2018, 66, 199–209. [Google Scholar] [CrossRef] [Green Version]
- Warrick, J.A.; Stevens, A.W. A buoyant plume adjacent to a headland—Observations of the Elwha River plume. Cont. Shelf Res. 2011, 31, 85–97. [Google Scholar] [CrossRef]
- McCabe, R.M.; MacCready, P.; Hickey, B.M. Ebb-Tide Dynamics and Spreading of a Large River Plume*. J. Phys. Oceanogr. 2009, 39, 2839–2856. [Google Scholar] [CrossRef]
- Feddersen, F.; Olabarrieta, M.; Guza, R.; Winters, D.; Raubenheimer, B.; Elgar, S. Observations and modeling of a tidal inlet dye tracer plume. J. Geophys. Res. Ocean. 2016, 121, 7819–7844. [Google Scholar] [CrossRef]
- Osadchiev, A.; Sedakov, R.; Barymova, A. Response of a small river plume on wind forcing. Front. Mar. Sci. 2021, 8, 1–9. [Google Scholar] [CrossRef]
- Spydell, M.S.; Feddersen, F.; Olabarrieta, M.; Chen, J.; Guza, R.; Raubenheimer, B.; Elgar, S. Observed and modeled drifters at a tidal inlet. J. Geophys. Res. Ocean. 2015, 120, 4825–4844. [Google Scholar] [CrossRef]
- Blanken, H.; Hannah, C.; Klymak, J.M.; Juhász, T. Surface Drift and Dispersion in a Multiply Connected Fjord System. J. Geophys. Res. Ocean. 2020, 125, 1–20. [Google Scholar] [CrossRef]


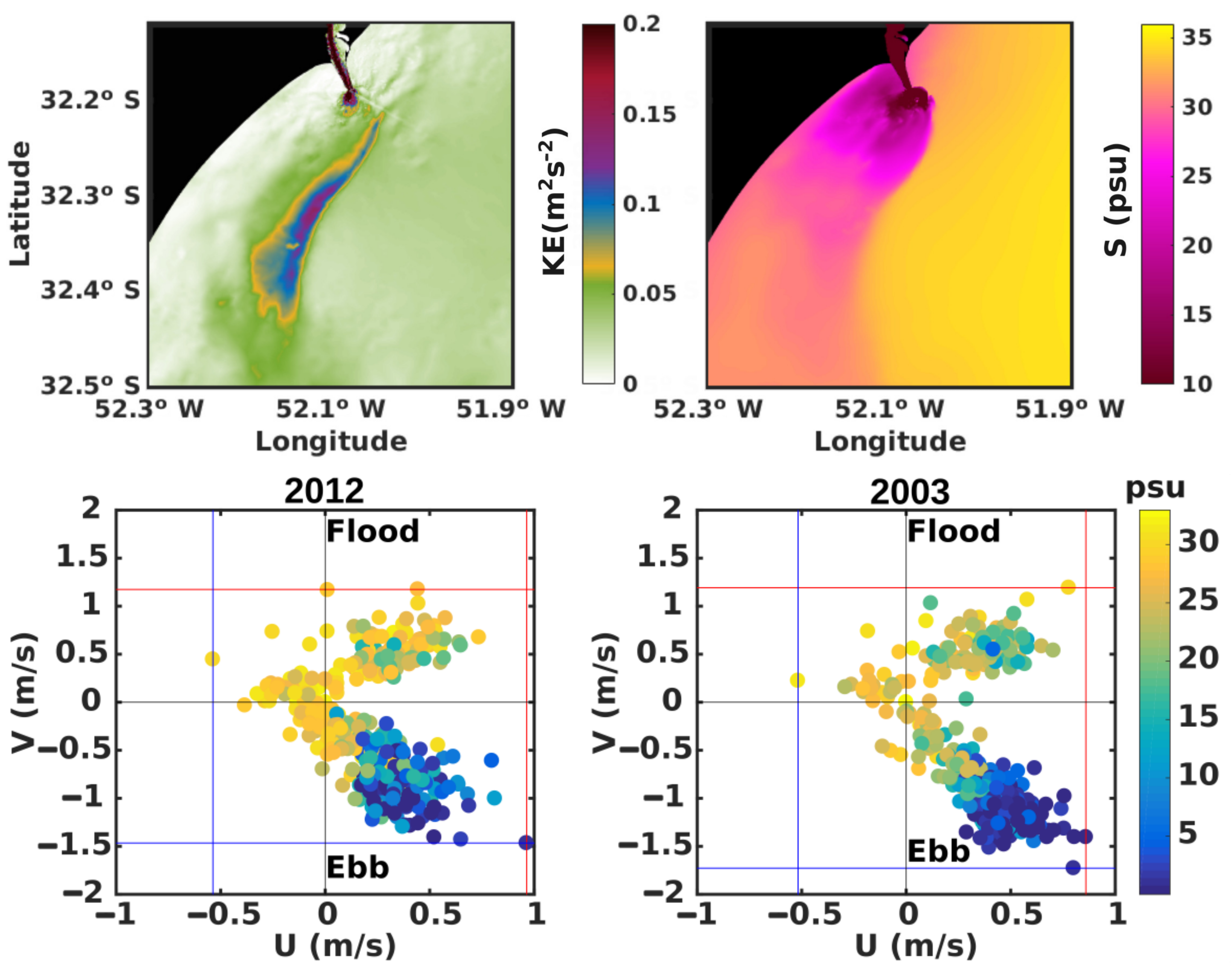

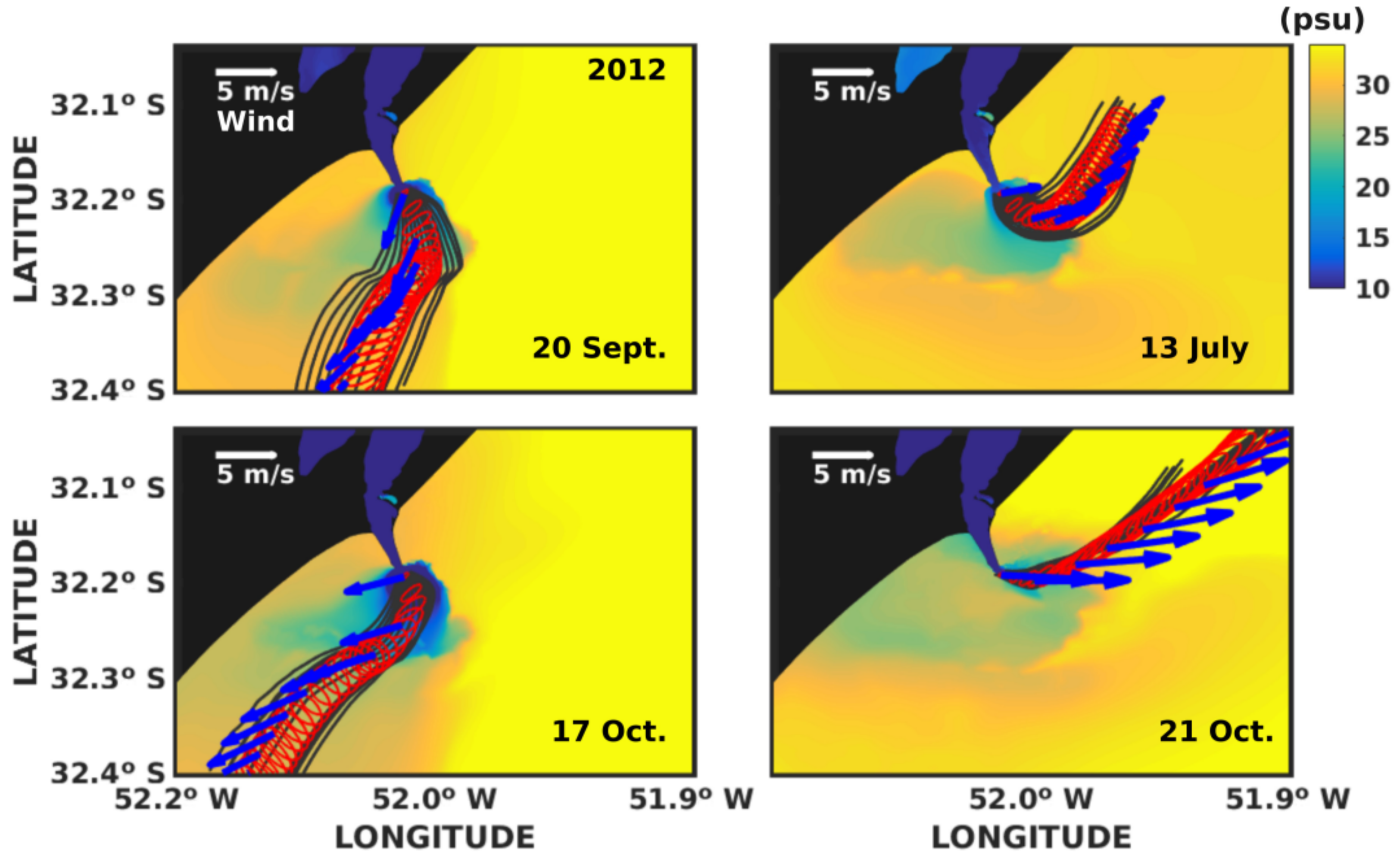
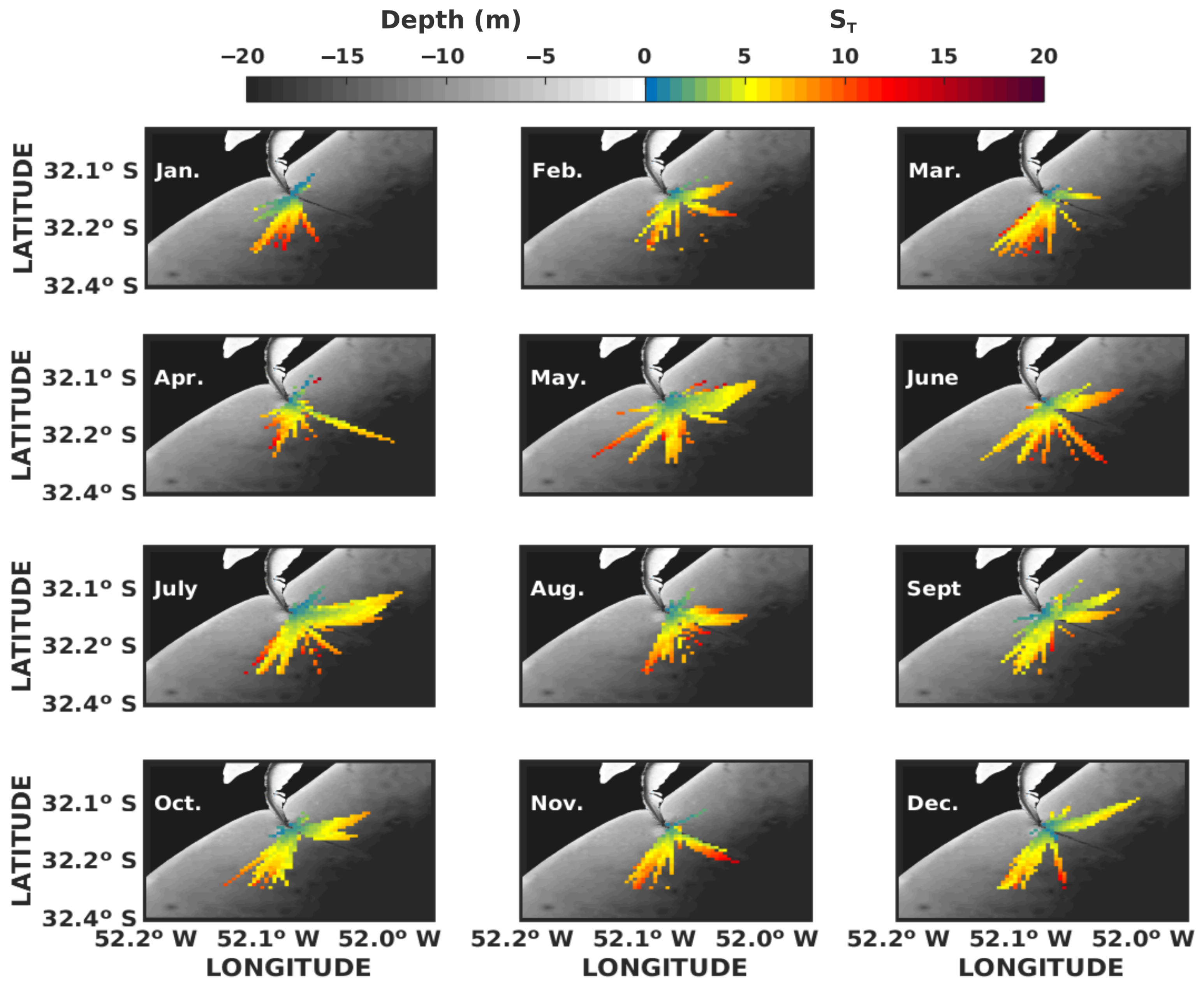
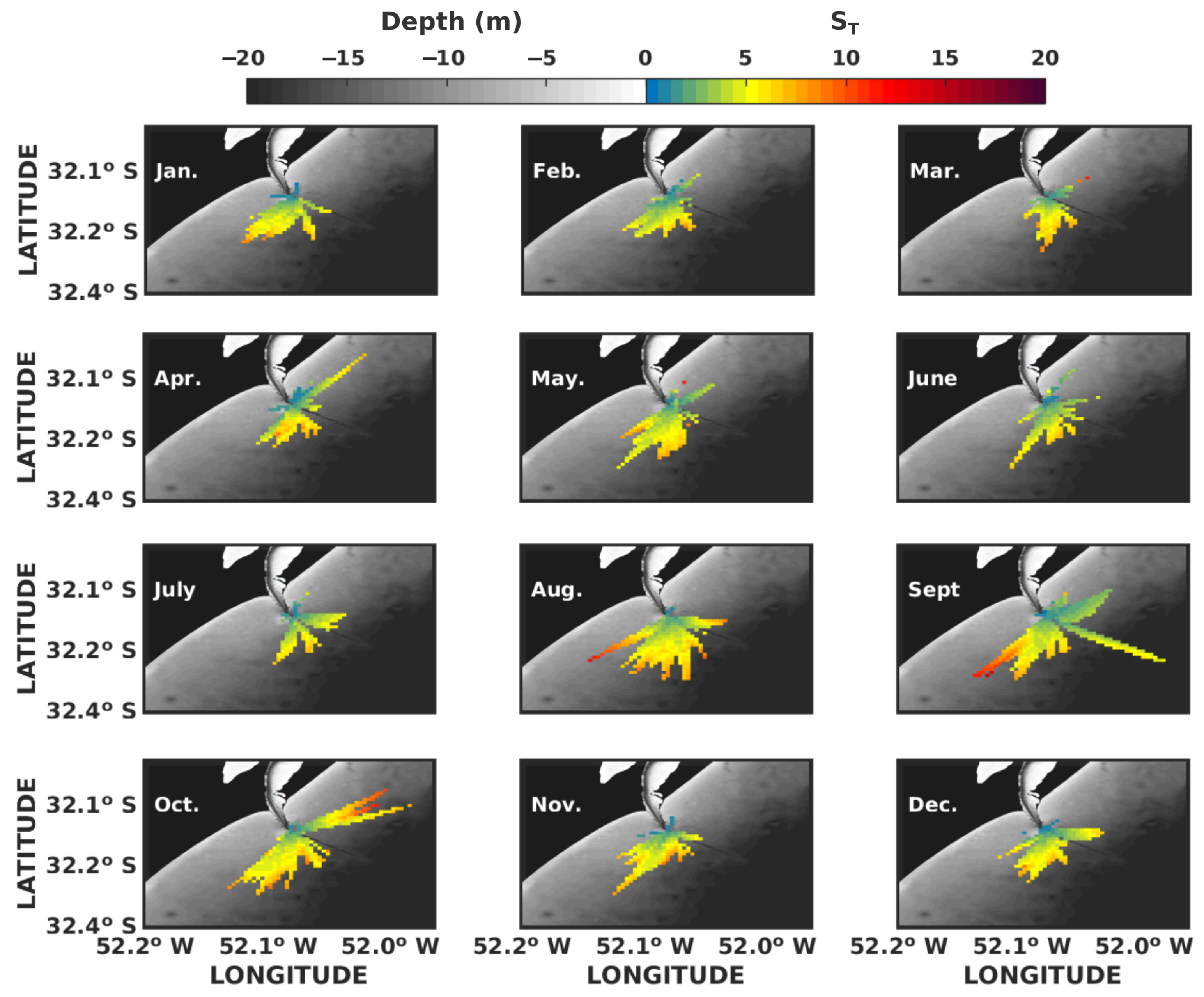
| Scale Parameters | 2003 | 2012 |
|---|---|---|
| (km) | 11.42 | 10.39 |
| 0.10 | 0.26 | |
| R | 0.85 | 1.28 |
| 0.20 | 0.81 | |
| 0.85 | 1.28 | |
| 0.06 | 0.06 | |
| 4.22 | 1.58 | |
| 1.34 | 0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Silva, D.V.; Oleinik, P.H.; Costi, J.; de Paula Kirinus, E.; Marques, W.C.; Moller, O.O. Variability of the Spreading of the Patos Lagoon Plume Using Numerical Drifters. Coasts 2022, 2, 51-69. https://doi.org/10.3390/coasts2020004
da Silva DV, Oleinik PH, Costi J, de Paula Kirinus E, Marques WC, Moller OO. Variability of the Spreading of the Patos Lagoon Plume Using Numerical Drifters. Coasts. 2022; 2(2):51-69. https://doi.org/10.3390/coasts2020004
Chicago/Turabian Styleda Silva, Douglas Vieira, Phelype Haron Oleinik, Juliana Costi, Eduardo de Paula Kirinus, Wiliam Correa Marques, and Osmar Olinto Moller. 2022. "Variability of the Spreading of the Patos Lagoon Plume Using Numerical Drifters" Coasts 2, no. 2: 51-69. https://doi.org/10.3390/coasts2020004






