Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
3.1. Shoreline Change Analysis
- End Point Rate (EPR). This is defined as the ratio of the distance between the oldest and the most recent coastline, over the period (in years) between both lines [17]; it is defined in distance over a unit of time (m/year).
3.2. Spatial Autocorrelation
3.2.1. Geospatial Approach
3.2.2. Global Moran’s Index
3.2.3. Local Moran’s Index and Local Getis–Ord
4. Results
4.1. Variation in the Colombian Coastline 1986–2016 (Regional Characteristics of Caribbean and Pacific Coasts)
4.2. Spatial Autocorrelation of the Rates of Change in the Coastline
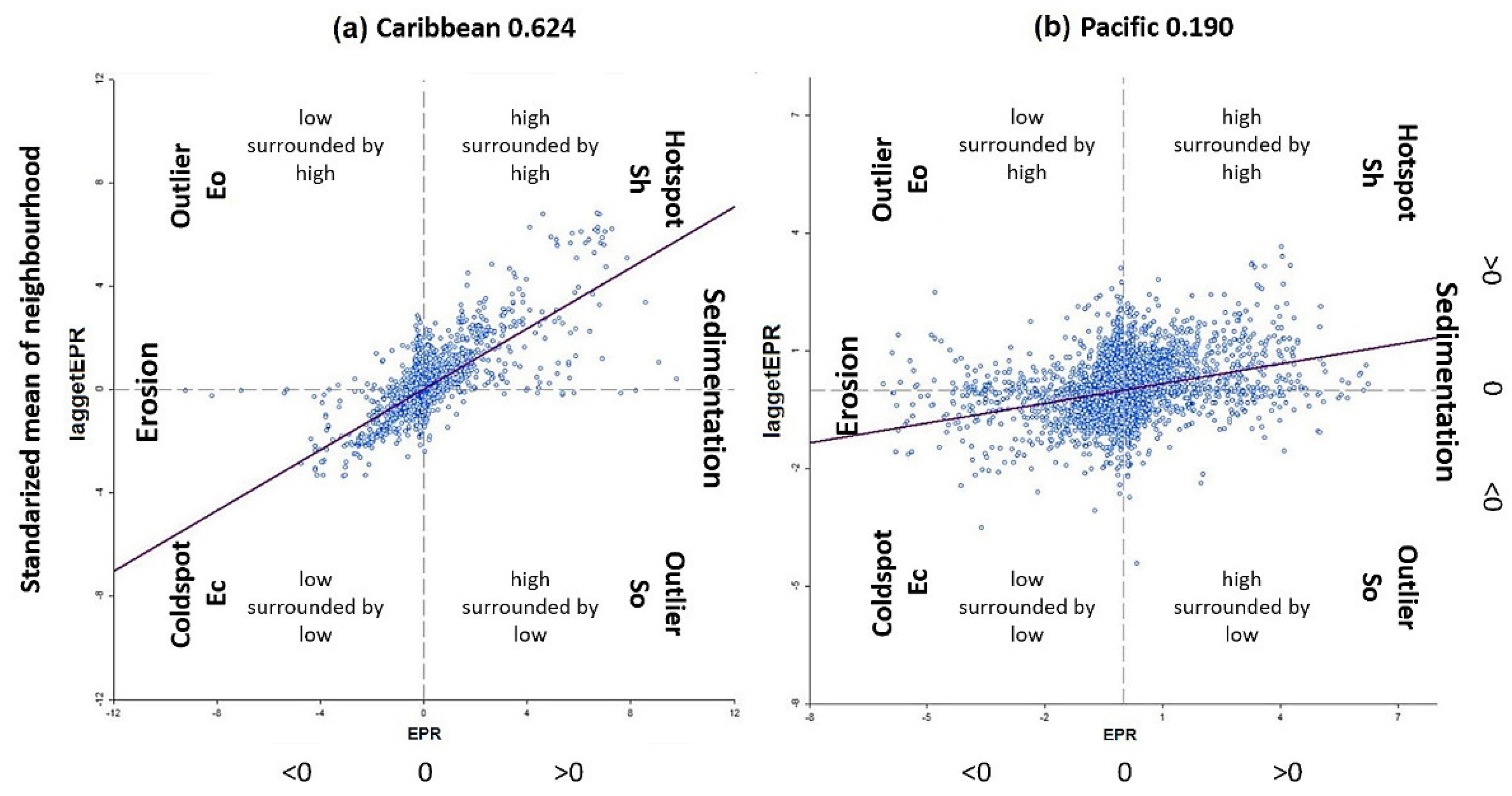
4.2.1. Global Moran’s Index
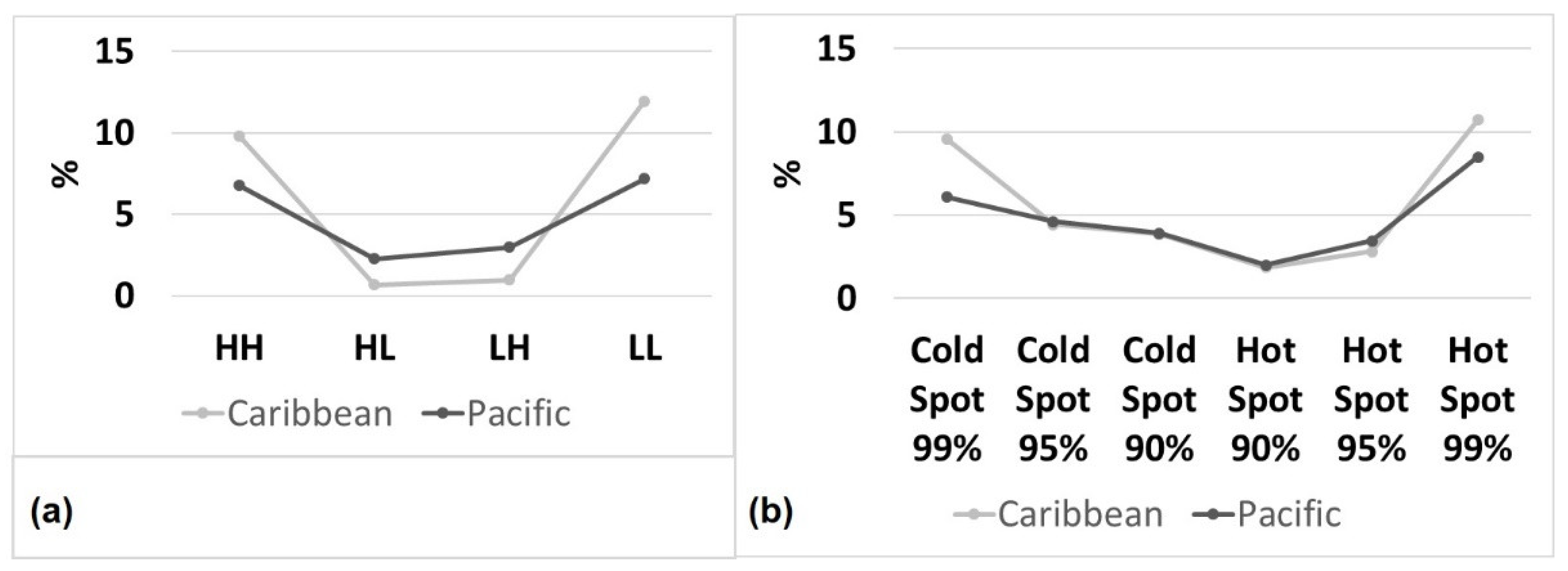
4.2.2. Local Getas–Ord
4.2.3. Local Moran’s Index
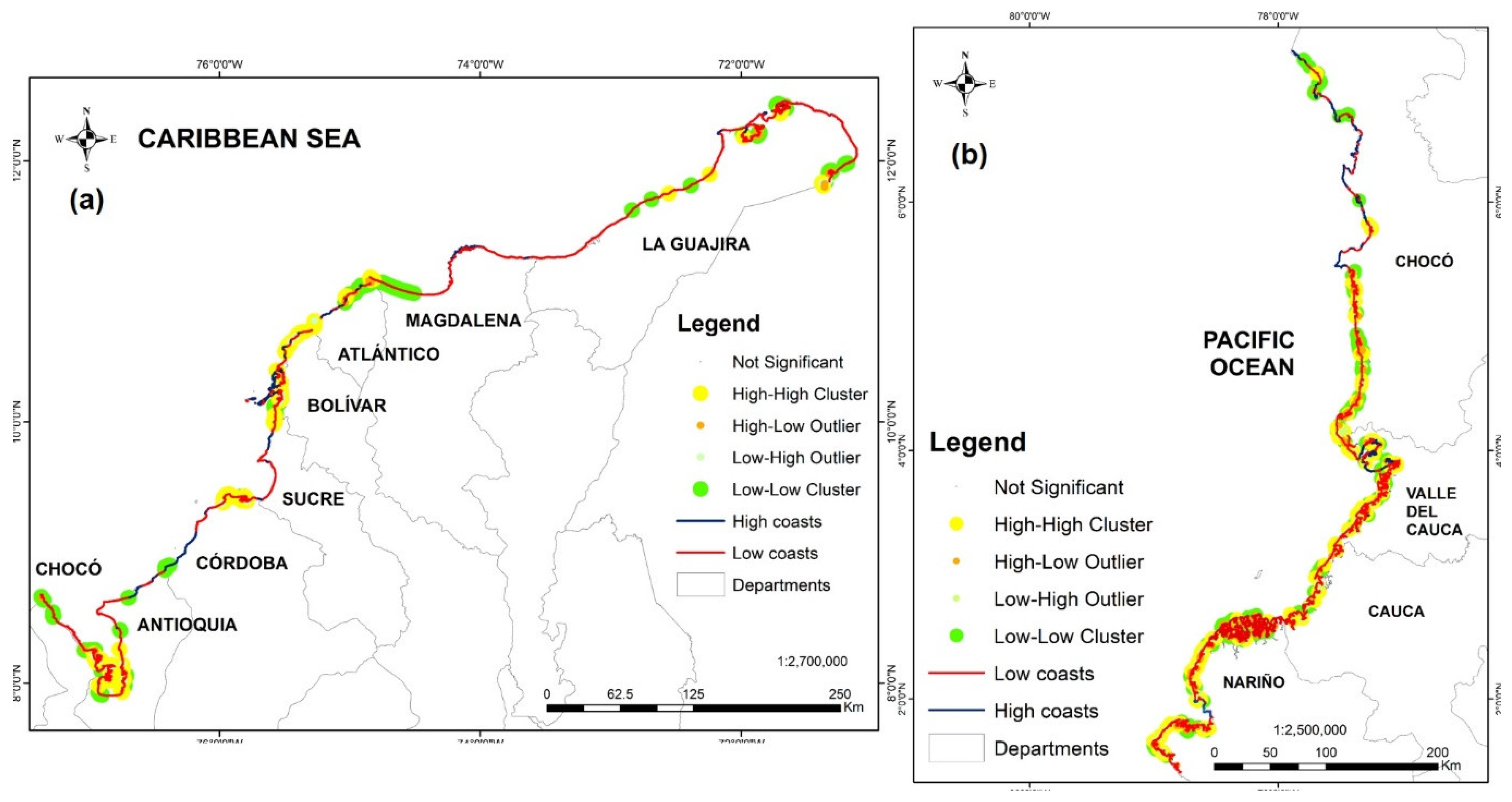
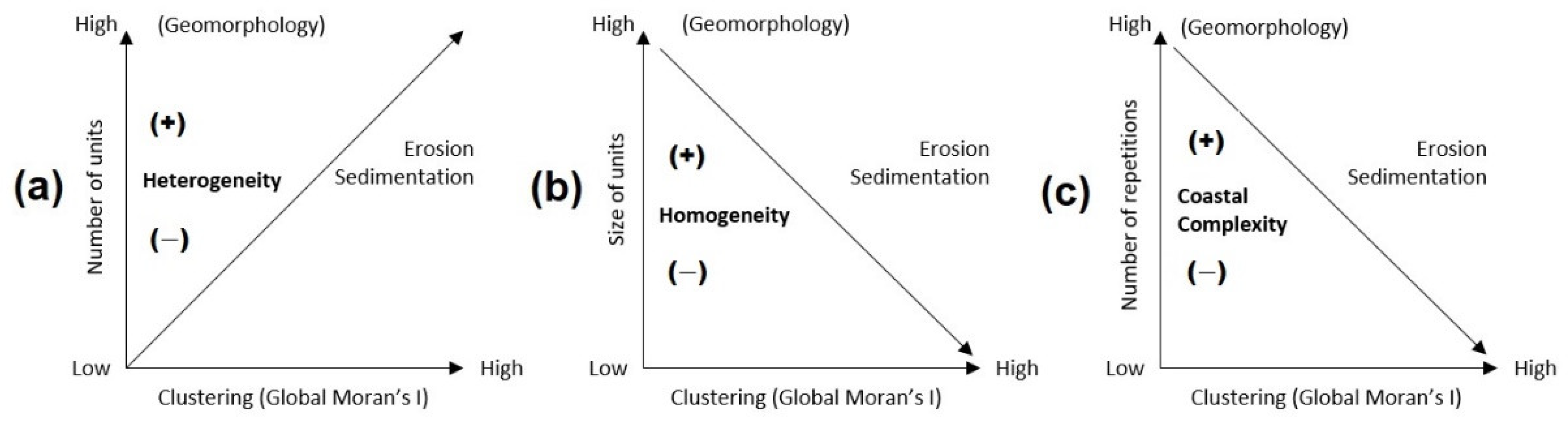
4.2.4. Spatial Clustering by Coastal Erosion and Sedimentation
5. Discussion
6. Conclusions
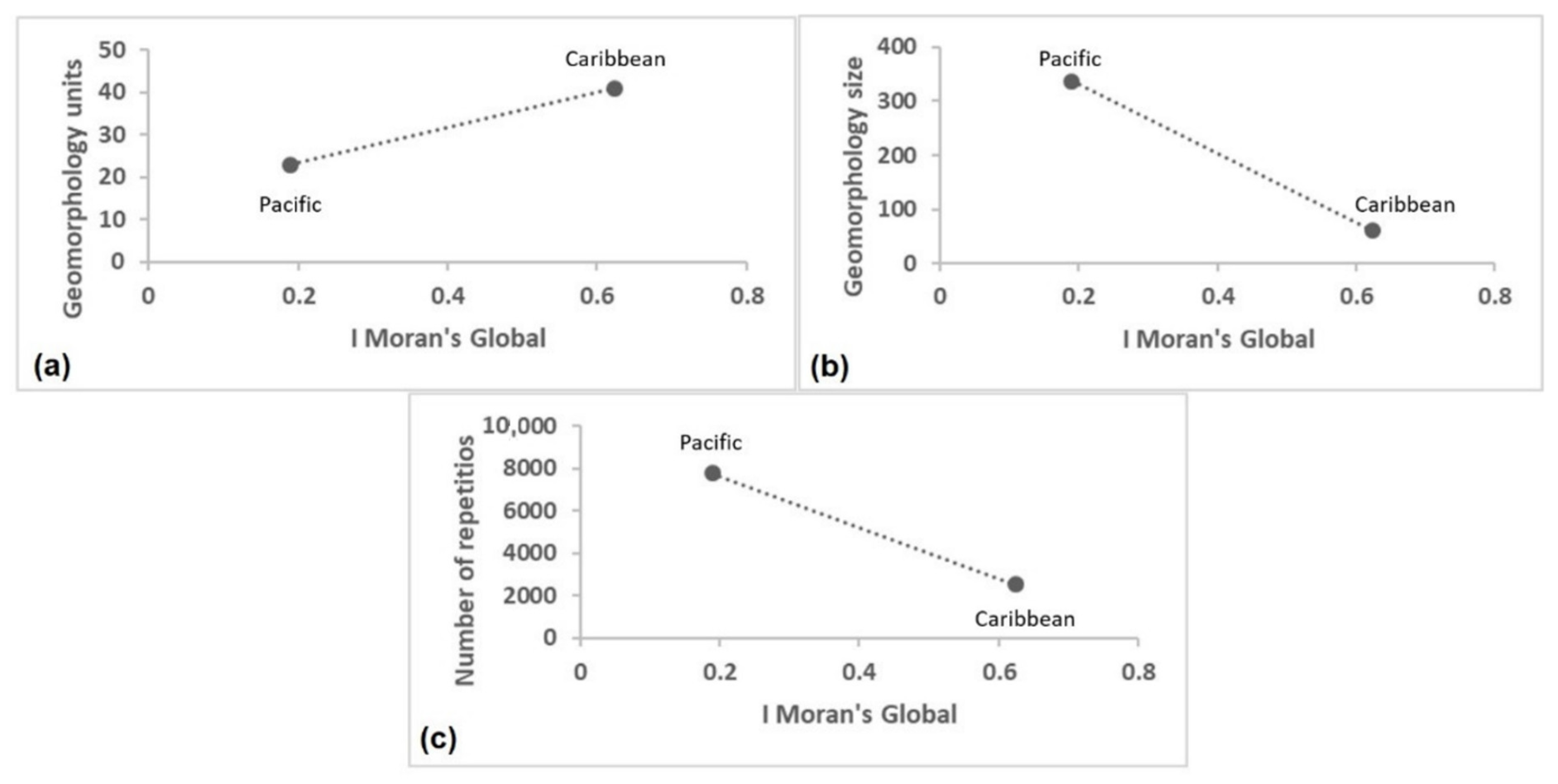
- Caribbean: Significant areas here display low complexity, extensive spaces, and geomorphological unification (Local Index). This area has greater regional significance (Global Index). It has a greater slope of lagged EPR values.
- Pacific: In areas with greater significance, larger sizes are attained. However, in terms of scale (Local Index), coastal complexity (mouth, islands, bars, beach, mouth, etc.) is indicated by larger geoforms (e.g., mangrove swamps), which generates significance in confined or ungrouped areas. This region has less significance (Global Index). The area is ungrouped and dispersed, with lower slopes of the EPR lagged-value curve, and HH and LL predominate, but HL and LH show more significant values here than in the Caribbean, which aids in differentiation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bracs, M.A.; Turner, I.L.; Splinter, K.D.; Short, A.D.; Mortlock, T.R. Synchronised patterns of erosion and deposition observed at two beaches. Mar. Geol. 2016, 380, 196–204. [Google Scholar] [CrossRef]
- Ricaurte-Villota, C.; Coca, O.; González, M.; Bejarano-Espinosa, M.; Morales, D.F.; Correa-Rojas, C.; Briceño-Zuluaga, F.; Legarda, G.; Arteaga, M. Amenaza y Vulnerabilidad Por Erosión Costera en Colombia: Enfoque Regional Para La Gestión Del Riesgo; Invemar: Santa Marta, Colombia, 2018; ISBN 9789588935423. [Google Scholar]
- Coca, O.; Ricaurte-Villota, C. Validation of the hazard and vulnerability analysis of coastal erosion in the Caribbean and pacific coast of Colombia. J. Mar. Sci. Eng. 2019, 7, 260. [Google Scholar] [CrossRef] [Green Version]
- Ferrer-Valero, N.; Hernández-Calvento, L.; Hernández-Cordero, A.I. Human impacts quantification on the coastal landforms of Gran Canaria Island (Canary Islands). Geomorphology 2017, 286, 58–67. [Google Scholar] [CrossRef]
- European Commission Living with Coastal Erosion in Europe: Sediment and Space for Sustainability; Eurosion: Brussels, Belgium, 2004; ISBN 92-9167-186-X.
- Posada, B.O.; Henao Pineda, W. Diagnóstico de la Erosión En La Zona Costera del Caribe Colombiano; Invemar: Santa Marta, Colombia, 2008; ISBN 9789589810491. [Google Scholar]
- Posada, B.O.; Henao Pineda, W.; Guzmán Ospitia, G. Diagnóstico de la Erosión Y Sedimentación En La Zona Costera del Pacífico Colombiano; Invemar: Santa Marta, Colombia, 2009; ISBN 9789588448244. [Google Scholar]
- Posada, B.O.; Henao Pineda, W.; Morales, D.F. Diagnóstico de la Erosión Costera Del Territorio Insular Colombiano; Invemar: Santa Marta, Colombia, 2011; ISBN 978-958-8448-44-2. [Google Scholar]
- Cifuentes, M.A.; Rosero, L.V.; Selvaraj, J. Detección de cambios de la línea costera al norte del distrito de Buenaventura mediante el uso de sensores remotos. Bol. Invest. Mar. Cost. 2017, 46, 137–152. [Google Scholar] [CrossRef]
- Coca, O.; Ricaurte-Villota, C. Análisis de la evolución litoral y respuesta de las comunidades afro-descendientes asentadas en la zona costera: Caso de estudio La Barra, Buenaventura, Pacífico Colombiano. Entorno Geográfico 2019, 7–26. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.G.; Anfuso, G.; Williams, A.T. Coastal erosion along the Caribbean coast of Colombia: Magnitudes, causes and management. Ocean Coast. Manag. 2015, 114, 129–144. [Google Scholar] [CrossRef]
- Gutierrez-Valderrama, J.E.; Carvajal, A.F.; Pabón, J.D.; Ruiz, F.; Cusva Verdugo, A.; Nieto, V.; Lecanda, X.; Rodríguez, J.; Mendoza, J.; Álvarez, J.C.; et al. Tercera comunicación nacional de Colombia; Unidas, N., Ideam, P., Eds.; IDEAM: Bogotá, Colombia, 2017; p. 122. [Google Scholar]
- Castelle, B.; Masselink, G.; Scott, T.; Stokes, C.; Konstantinou, A.; Marieu, V.; Bujan, S. Satellite-derived shoreline detection at a high-energy meso-macrotidal beach. Geomorphology 2021, 383, 107707. [Google Scholar] [CrossRef]
- Luijendijk, A.; Hagenaars, G.; Ranasinghe, R.; Baart, F.; Donchyts, G.; Aarninkhof, S. The State of the World’s Beaches. Sci. Rep. 2018, 8, 6641. [Google Scholar] [CrossRef]
- Mentaschi, L.; Vousdoukas, M.I.; Pekel, J.F.; Voukouvalas, E.; Feyen, L. Global long-term observations of coastal erosion and accretion. Sci. Rep. 2018, 8, 12876. [Google Scholar] [CrossRef] [Green Version]
- Vousdoukas, M.I.; Ranasinghe, R.; Mentaschi, L.; Plomaritis, T.A.; Athanasiou, P.; Luijendijk, A.; Feyen, L. Sandy coastlines under threat of erosion. Nat. Clim. Chang. 2020, 10, 260–263. [Google Scholar] [CrossRef]
- Himmelstoss, E.A.; Henderson, R.E.; Kratzmann, M.G.; Farris, A.S. Digital Shoreline Analysis System (DSAS) Version 5.0 User Guide. Open-File Rep. 2018, 1179, 126. [Google Scholar]
- Natesan, U.; Parthasarathy, A.; Vishnunath, R.; Kumar, G.E.J.; Ferrer, V.A. Monitoring Longterm Shoreline Changes along Tamil Nadu, India Using Geospatial Techniques. Aquat. Procedia 2015, 4, 325–332. [Google Scholar] [CrossRef]
- Thieler, E.R.; Himmelstoss, E.A.; Zichichi, J.L.; Ergul, A. The Digital Shoreline Analysis System (DSAS) Version 4.0—An ArcGIS Extension for Calculating Shoreline Change; US Geological Survey: Reston, VA, USA, 2009; ISBN 2008-1278. [Google Scholar]
- Coca, O.; Ricaurte-villota, C.; Morales, D.F. Modelo de gestión y análisis del riesgo por erosión costera. Caso de estudio departamento de Córdoba. In Investigaciones en Gestión del Riesgo de desastres para Colombia. Avances, perspectivas y casos de estudio; Comisión Nacional Asesora para la Investigación en Gestión del Riesgo de Desastres (CNAIGRD): Bogotá, Colombia, 2021; pp. 326–356. ISBN 9789585509191. [Google Scholar]
- Kuleli, T.; Guneroglu, A.; Karsli, F.; Dihkan, M. Automatic detection of shoreline change on coastal Ramsar wetlands of Turkey. Ocean Eng. 2011, 38, 1141–1149. [Google Scholar] [CrossRef]
- Radosavljevic, B.; Lantuit, H.; Pollard, W.; Overduin, P.; Couture, N.; Sachs, T.; Helm, V.; Fritz, M. Erosion and Flooding—Threats to Coastal Infrastructure in the Arctic: A Case Study from Herschel Island, Yukon Territory, Canada. Estuaries and Coasts 2016, 39, 900–915. [Google Scholar] [CrossRef] [Green Version]
- Cliff, A.; Ord, K. The Problem of Spatial Autocorrelation. In Studies in Regional Science; Scott, A., Ed.; Pion: London, UK, 1969; pp. 25–55. [Google Scholar]
- Goodchild, M.F. Spatial autocorrelation; Geo Books: Norwich, UK, 1986; ISBN 0860942236. [Google Scholar]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Pérez-Rubio, I.; Mende, A. Análisis espacial de susceptibilidad de erosión en una cuenca hidrográfica del trópico húmedo de Costa Rica. Rev. Ciencias Ambient. (Trop. J. Environ. Sci.) 2018, 52, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Javari, M. Spatial-temporal Variability of Seasonal Precipitation in Iran. Open Atmos. Sci. J. 2016, 10, 84–102. [Google Scholar] [CrossRef] [Green Version]
- Nelson, T.A.; Boots, B. Detecting spatial hot spots in landscape ecology. Ecography 2008, 31, 556–566. [Google Scholar] [CrossRef]
- Borrás Ramos, V. Análisis exploratorio de datos espaciales de pobreza: Aplicación 1996-2011 a tres ciudades de Uruguay (Montevideo, Maldonado y Salto). Geogr. y Sist. Inf. Geográfica 2019, 11. Sección I: 12–30. [Google Scholar]
- Gordziejczuk, M.A.; Lucero, P.I. Turismo y calidad de vida: Un estudio de autocorrelación espacial aplicado a la ciudad de Mar del Plata, provincia de Buenos Aires, Argentina. Cuad. Geogr. Rev. Colomb. Geogr. 2019, 28, 23–42. [Google Scholar] [CrossRef]
- Celemín, J.P. Autocorrelación espacial e indicadores locales de asociación espacial. Importancia, estructura y aplicación Spatial Autocorrelation and Local Indicators of Spatial Association: Importance, Structure and Application. Rev. Univ. Geogr. 2009, 18, 11–31. [Google Scholar]
- Siabato, W.; Guzmán-Manrique, J. La autocorrelación espacial y el desarrollo de la geografía cuantitativa. Cuad. Geogr. Rev. Colomb. Geogr. 2019, 28, 1–22. [Google Scholar] [CrossRef]
- Vilalta, C.J. Cómo enseñar autocorrelación espacial. Econ. Soc. Territ. 2005. [Google Scholar] [CrossRef] [Green Version]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Shoreline Change Rate Analysis: Long Term Versus Short Term Data. Shore and Beach 1993, 61, 13–20. [Google Scholar]
- Douglas, B.C.; Crowell, M. Long-term shoreline position prediction and error propagation. J. Coast. Res. 2000, 16, 145–152. [Google Scholar]
- Moore, L.J. Shoreline mapping techniques. J. Coast. Res. 2000, 16, 111–124. [Google Scholar]
- Thieler, E.R.; Danforth, W.W. Historical shoreline mapping (I): Improving techniques and reducing positioning errors. J. Coast. Res. 1994, 10, 549–563. [Google Scholar]
- Crowell, M.; Leatherman, S.P.; Buckley, M.K. Historical shoreline change: Error analysis and mapping accuracy. J. Coast. Res. 1991, 7, 839–852. [Google Scholar]
- Ojeda Zújar, J.; Díaz Cuevas, M.D.P.; Prieto Campos, A.; Álvarez Francoso, J.I. Línea de costa y sistemas de información geográfica: Modelo de datos para la caracterización y cálculo de indicadores en la costa andaluza. Investig. Geográficas 2013, 37–52. [Google Scholar] [CrossRef] [Green Version]
- Genz, A.S.; Fletcher, C.H.; Dunn, R.A.; Frazer, L.N.; Rooney, J.J. The predictive accuracy of shoreline change rate methods and alongshore beach variation on Maui, Hawaii. J. Coast. Res. 2007, 23, 87–105. [Google Scholar] [CrossRef] [Green Version]
- Hughey, S.M.; Kaczynski, A.T.; Porter, D.E.; Hibbert, J.; Turner-McGrievy, G.; Liu, J. Spatial clustering patterns of child weight status in a southeastern US county. Appl. Geogr. 2018, 99, 12–21. [Google Scholar] [CrossRef]
- Romine, B.M.; Fletcher, C.H.; Frazer, L.N.; Genz, A.S.; Barbee, M.M.; Lim, S.C. Historical shoreline change, southeast oahu, Hawaii; Applying polynomial models to calculate shoreline change rates. J. Coast. Res. 2009, 25, 1236–1253. [Google Scholar] [CrossRef]
- Ranasinghe, R. Assessing climate change impacts on open sandy coasts: A review. Earth-Science Rev. 2016, 160, 320–332. [Google Scholar] [CrossRef] [Green Version]
- Bayram, B.; Acar, U.; Seker, D.; Ari, A. A novel algorithm for coastline fitting through a case study over the bosphorus. J. Coast. Res. 2008, 24, 983–991. [Google Scholar] [CrossRef]
- García-Rubio, G.; Huntley, D.; Russell, P. Evaluating shoreline identification using optical satellite images. Mar. Geol. 2015, 359, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Trinder, J.; Turner, I.L. Automatic super-resolution shoreline change monitoring using Landsat archival data: A case study at Narrabeen–Collaroy Beach, Australia. J. Appl. Remote Sens. 2017, 11, 016036. [Google Scholar] [CrossRef]
- Pardo-Pascual, J.E.; Almonacid-Caballer, J.; Ruiz, L.A.; Palomar-Vázquez, J. Automatic extraction of shorelines from Landsat TM and ETM+ multi-temporal images with subpixel precision. Remote Sens. Environ. 2012, 123, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hagenaars, G.; de Vries, S.; Luijendijk, A.P.; de Boer, W.P.; Reniers, A.J.H.M. On the accuracy of automated shoreline detection derived from satellite imagery: A case study of the sand motor mega-scale nourishment. Coast. Eng. 2018, 133, 113–125. [Google Scholar] [CrossRef]
- Eamer, J.B.R.; Walker, I.J. Quantifying spatial and temporal trends in beach-dune volumetric changes using spatial statistics. Geomorphology 2013, 191, 94–108. [Google Scholar] [CrossRef]
- Walker, I.J.; Eamer, J.B.R.; Darke, I.B. Assessing significant geomorphic changes and effectiveness of dynamic restoration in a coastal dune ecosystem. Geomorphology 2013, 199, 192–204. [Google Scholar] [CrossRef]
- Flint, C.; Harrower, M.; Edsall, R. But How Does Place Matter? Using Bayesian Networks to Explore a Structural Definition of Place. In Proceedings of the The New Methodologies for the Social Sciences Conference; University of Colorado: Boulder, CO, USA, 2000. [Google Scholar]
- LeSage, J. Spatial Econometrics Toolbox; Universidad de Toledo: Toledo, Spain, 1999. [Google Scholar]
- O’Loughlin, J.; Anselin, L. Geography of International Conflict and Cooperation: Theory and Methods. In The New Geopolitics; Don Ward, M., Ed.; Routledge: Philadelphia, PA, USA, 1992; pp. 11–38. ISBN 9781315075242. [Google Scholar]
- Buzai, G.D. Mapas Sociales; Lugar Editorial: Luján, Argentina, 2007; ISBN 9789508924513. [Google Scholar]
- Burt, J.; Barber, G.; Rigby, D. Elementary Statistics for Geographers; The Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Laraia, B.A.; Blanchard, S.D.; Karter, A.J.; Jones-Smith, J.C.; Warton, M.; Kersten, E.; Jerrett, M.; Moffet, H.H.; Adler, N.; Schillinger, D.; et al. Spatial pattern of body mass index among adults in the diabetes study of Northern California (DISTANCE). Int. J. Health Geogr. 2014, 13, 48. [Google Scholar] [CrossRef] [Green Version]
- Auchincloss, A.H.; Gebreab, S.Y.; Mair, C.; Diez Roux, A.V. A review of spatial methods in epidemiology, 2000-2010. Annu. Rev. Public Health 2012, 33, 107–122. [Google Scholar] [CrossRef] [Green Version]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24, 189–206. [Google Scholar] [CrossRef]
- Keith Ord, J.; Getis, A. Testing for local spatial autocorrelation in the presence of global autocorrelation. J. Reg. Sci. 2001, 41, 411–432. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Anselin, L. Exploring Spatial Data with GeoDa: A Workbook. Geography 2005, 244. [Google Scholar]
- Moran, P.A.P. The spectral theory of discrete stochastic processes. Biometrika 1949, 36, 63–70. [Google Scholar] [CrossRef]
- Moran, P.A.P. Notes on continuous stochastic phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef]
- Martínez, J.O.; González, J.L. Evolución Histórica De Las Islas Barrera Del Sector de Buenaventura y El Naya; Invemar: Santa Marta, Colombia, 1997; ISBN 9589595049. [Google Scholar]
- Restrepo-López, J.C.; Ortíz -Royero, J.C.; Otero-Díaz, L.; Ospino-Ortiz, S.R. Transporte de sedimentos en suspensión en los principales ríos del Caribe colombiano: Magnitud, tendencias y variabilidad. Rev. la Acad. Colomb. Ciencias Exactas, Físicas y Nat. 2015, 39, 527. [Google Scholar] [CrossRef]
- Restrepo, J.D.; López, S.A. Morphodynamics of the Pacific and Caribbean deltas of Colombia, South America. J. South Am. Earth Sci. 2008, 25, 1–21. [Google Scholar] [CrossRef]
- Bernal, G.; Betancur, J. Sedimentología de Lagunas Costeras: Ciénaga Grande de Santa Marta y Ciénaga de Pajarales. Boletín Investig. Mar. Costeras1 1996, 49–76. [Google Scholar] [CrossRef]
- Restrepo, J.C.; Orejarena-Rondón, A.; Consuegra, C.; Pérez, J.; Llinas, H.; Otero, L.; Álvarez, O. Siltation on a highly regulated estuarine system: The Magdalena River mouth case (Northwestern South America). Estuar. Coast. Shelf Sci. 2020, 245, 107020. [Google Scholar] [CrossRef]
- Fuentes Delgado, J.E. Desaparición de las islas: Cambios ambientales en el delta del río Magdalena desde la cartografía histórica. Hist. y Espac. 2022, 18, 159–192. [Google Scholar] [CrossRef]
- Bastidas-Salamanca, M.; Ricaute-Villota, C. Regionalización Oceanográfica, Una Visión Dinámica Del Caribe; Invemar: Santa Marta, Colombia, 2017; ISBN 9789588935249. [Google Scholar]
- Otero, L.J.; Ortiz-Royero, J.C.; Ruiz-Merchan, J.K.; Higgins, A.E.; Henriquez, S.A. Storms or cold fronts: What is really responsible for the extreme waves regime in the Colombian Caribbean coastal region? Nat. Hazards Earth Syst. Sci. 2016, 16, 391–401. [Google Scholar] [CrossRef] [Green Version]
- Correa, I.; Morton, R. Pacific Coast of Colombia BT—Encyclopedia of the World’s Coastal Landforms; Bird, E.C.F., Ed.; Springer: Dordrecht, The Netherlands, 2010; pp. 193–198. ISBN 978-1-4020-8639-7. [Google Scholar]
- Martínez-Ardila, N.J. Amenazas naturales en el litoral Pacífico colombiano asociadas al ascenso del nivel del mar. Cuad. Geogr. Rev. Colomb. Geogr. 2005, 83–96. [Google Scholar]
- Castelle, B.; Guillot, B.; Marieu, V.; Chaumillon, E.; Hanquiez, V.; Bujan, S.; Poppeschi, C. Spatial and temporal patterns of shoreline change of a 280-km high-energy disrupted sandy coast from 1950 to 2014: SW France. Estuar. Coast. Shelf Sci. 2018, 200, 212–223. [Google Scholar] [CrossRef]
- Wang, X.-Z.; Zhang, H.-G.; Fu, B.; Shi, A. Analysis on the coastline change and erosion-accretion evolution of the Pearl River Estuary, China, based on remote-sensing images and nautical charts. J. Appl. Remote Sens. 2013, 7, 073519. [Google Scholar] [CrossRef] [Green Version]
- Currin, C.; Davis, J.; Baron, L.C.; Malhotra, A.; Fonseca, M. Shoreline change in the New River Estuary, North Carolina: Rates and consequences. J. Coast. Res. 2015, 31, 1069–1077. [Google Scholar] [CrossRef]
- Cowart, L.; Walsh, J.P.; Corbett, D.R. Analyzing Estuarine Shoreline Change: A Case Study of Cedar Island, North Carolina. J. Coast. Res. 2010, 265, 817–830. [Google Scholar] [CrossRef]
- Restrepo, J.D.; Kjerfve, B.; Correa, I.D.; González, J. Morphodynamics of a high discharge tropical delta, San Juan River, Pacific coast of Colombia. Mar. Geol. 2002, 192, 355–381. [Google Scholar] [CrossRef]
- Karin, P.; Álvarez, S. Clasificación fisiográfica del terreno a partir de la inclusión de nuevos elementos conceptuales. Perspect. Geográfica 2009, 1, 181–218. [Google Scholar] [CrossRef]
- Villota, H. Nuevos elementos conceptuales para la clasificación fisiográfica del terreno. Rev. CIAF -St. Fe Bogotá 1997, 15, 83–117. [Google Scholar]
- Masselink, G.; Russell, P.; Rennie, A.; Brooks, S.; Spencer, T. The impacts of climate change on coastal geomorphology and coastal erosion relevant to the coastal and marine environment around the UK. Mar. Clim. Chang. Impacts Partnersh. Sci. Rev. 2020, 2020, 456–481. [Google Scholar] [CrossRef]
- Galgano, F.A., Jr. Shoreline behavior along the Atlantic coast of Delaware. Middle States Geogr. 2008, 41, 74–81. [Google Scholar]
- Galal, E.M.; Takewaka, S. The influence of alongshore and cross-shore wave energy flux on large- and small-scale coastal erosion patterns. Earth Surf. Process. Landforms 2011, 36, 953–966. [Google Scholar] [CrossRef]
- Awad, M.; El-Sayed, H.M. The analysis of shoreline change dynamics and future predictions using automated spatial techniques: Case of El-Omayed on the Mediterranean coast of Egypt. Ocean Coast. Manag. 2021, 205, 105568. [Google Scholar] [CrossRef]
- Molina, R.; Manno, G.; Re, C.L.; Anfuso, G.; Ciraolo, G. A methodological approach to determine sound response modalities to coastal erosion processes in mediterranean Andalusia (Spain). J. Mar. Sci. Eng. 2020, 8, 154. [Google Scholar] [CrossRef] [Green Version]
- Borzì, L.; Anfuso, G.; Manno, G.; Distefano, S.; Urso, S.; Chiarella, D.; Di Stefano, A. Shoreline Evolution and Environmental Changes at the NW Area. Land 2021, 10, 1034. [Google Scholar] [CrossRef]
- Molina, R.; Anfuso, G.; Manno, G.; Prieto, F.J.G. The Mediterranean coast of Andalusia (Spain): Medium-term evolution and impacts of coastal structures. Sustainability 2019, 11, 3539. [Google Scholar] [CrossRef] [Green Version]
- Duan, P.; Li, J.; Wang, M.; Wu, J. Spatial-Temporal Analysis of the Coastline Changes in Fujian Province, China from 1995 to 2015. J. Environ. Sci. Manag. 2021, 24, 1–9. [Google Scholar] [CrossRef]
- Martínez, C.; Grez, P.W.; Martín, R.A.; Acuña, C.E.; Torres, I.; Contreras-López, M. Coastal erosion in sandy beaches along a tectonically active coast: The Chile study case. Prog. Phys. Geogr. 2022, 46, 250–271. [Google Scholar] [CrossRef]
- Godwyn-Paulson, P.; Jonathan, M.P.; Hernandez, F.R.; Muthusankar, G.; Lakshumanan, C. Coastline variability of several Latin American cities alongside Pacific Ocean due to the unusual “Sea Swell” events of 2015. Environ. Monit. Assess. 2020, 192, 1–12. [Google Scholar] [CrossRef]
- Godwyn-Paulson, P.; Jonathan, M.P.; Roy, P.D.; Rodríguez-Espinosa, P.F.; Muthusankar, G.; Muñoz-Sevilla, N.P.; Lakshumanan, C. Evolution of southern Mexican Pacific coastline: Responses to meteo-oceanographic and physiographic conditions. Reg. Stud. Mar. Sci. 2021, 47, 101914. [Google Scholar] [CrossRef]
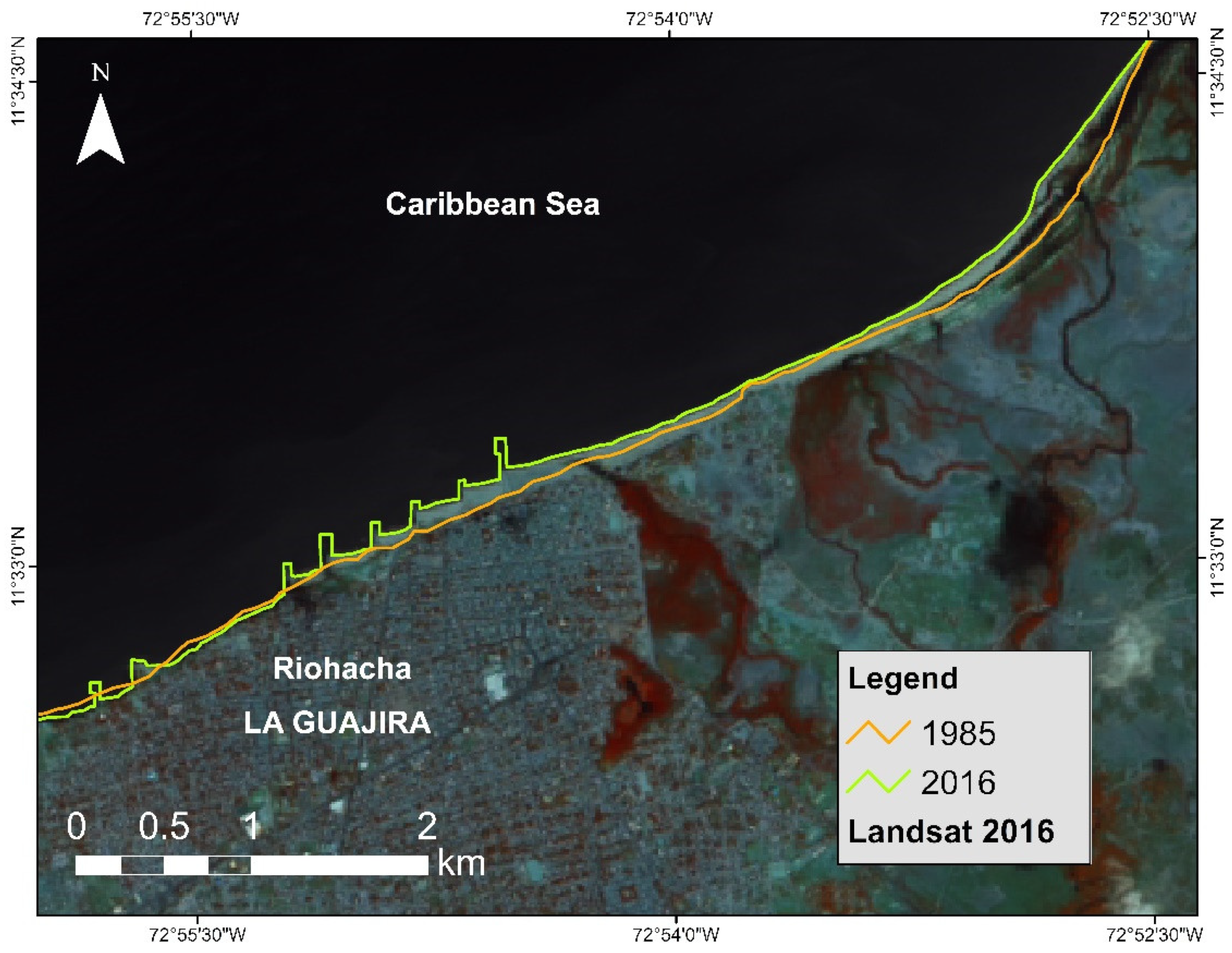

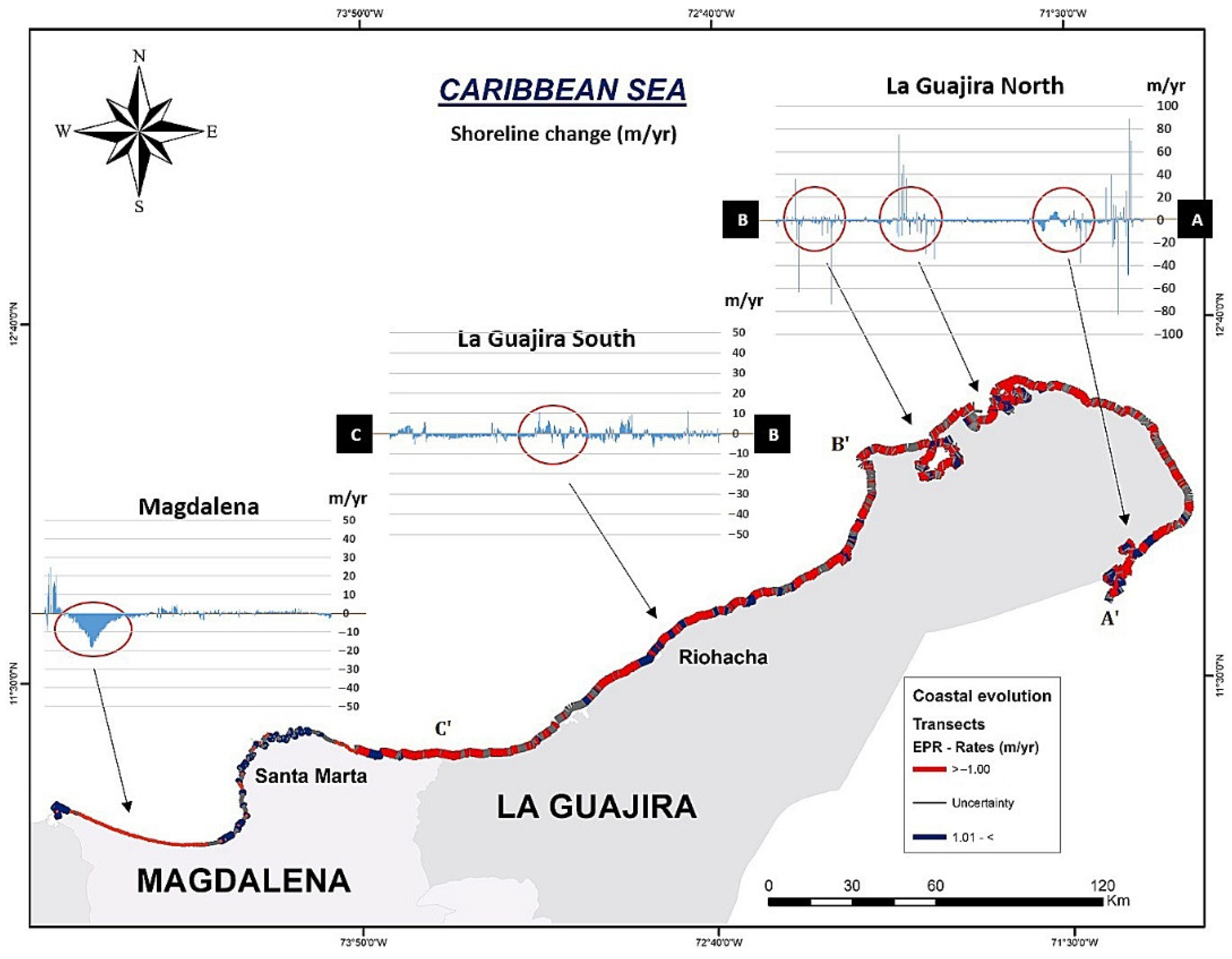
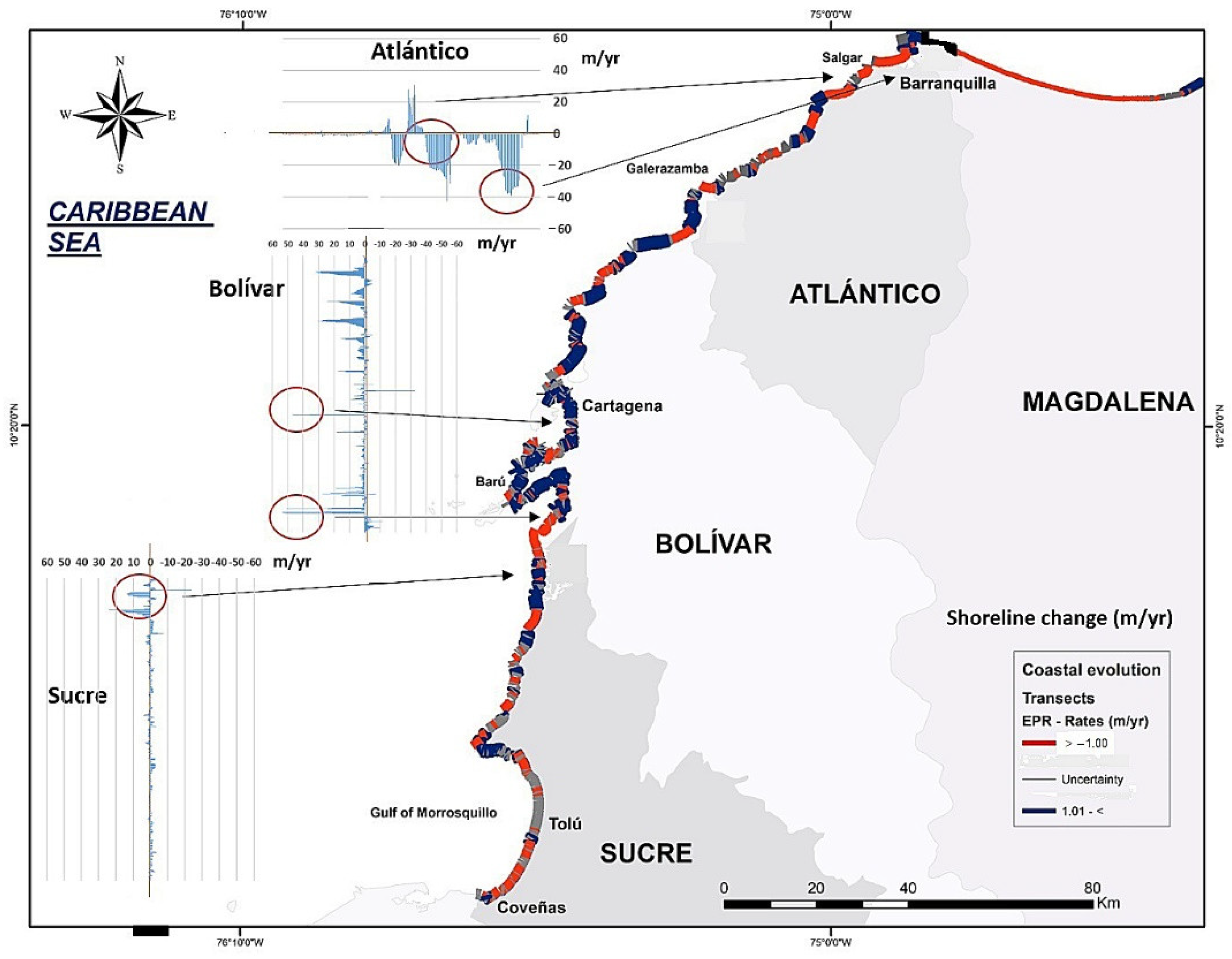
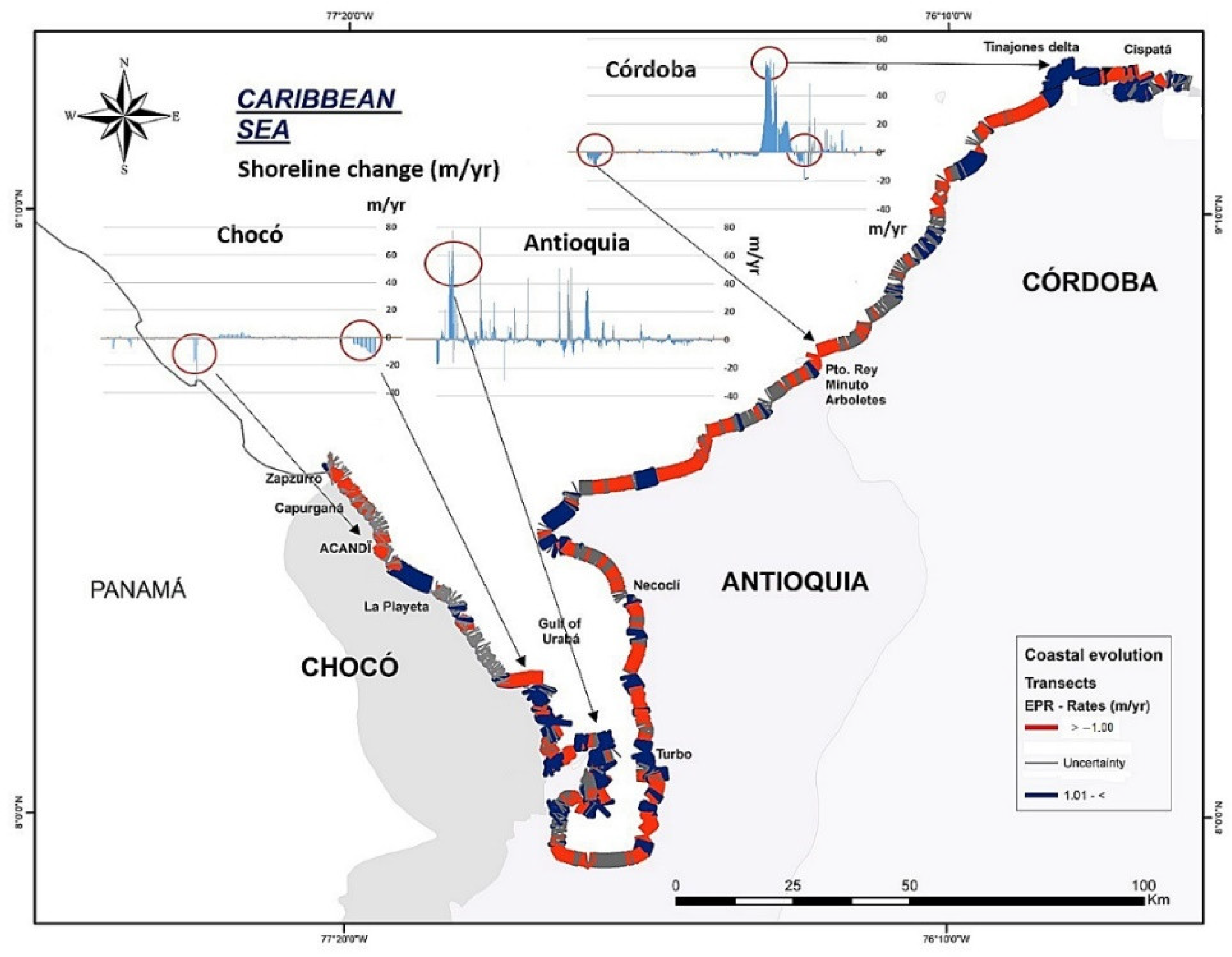
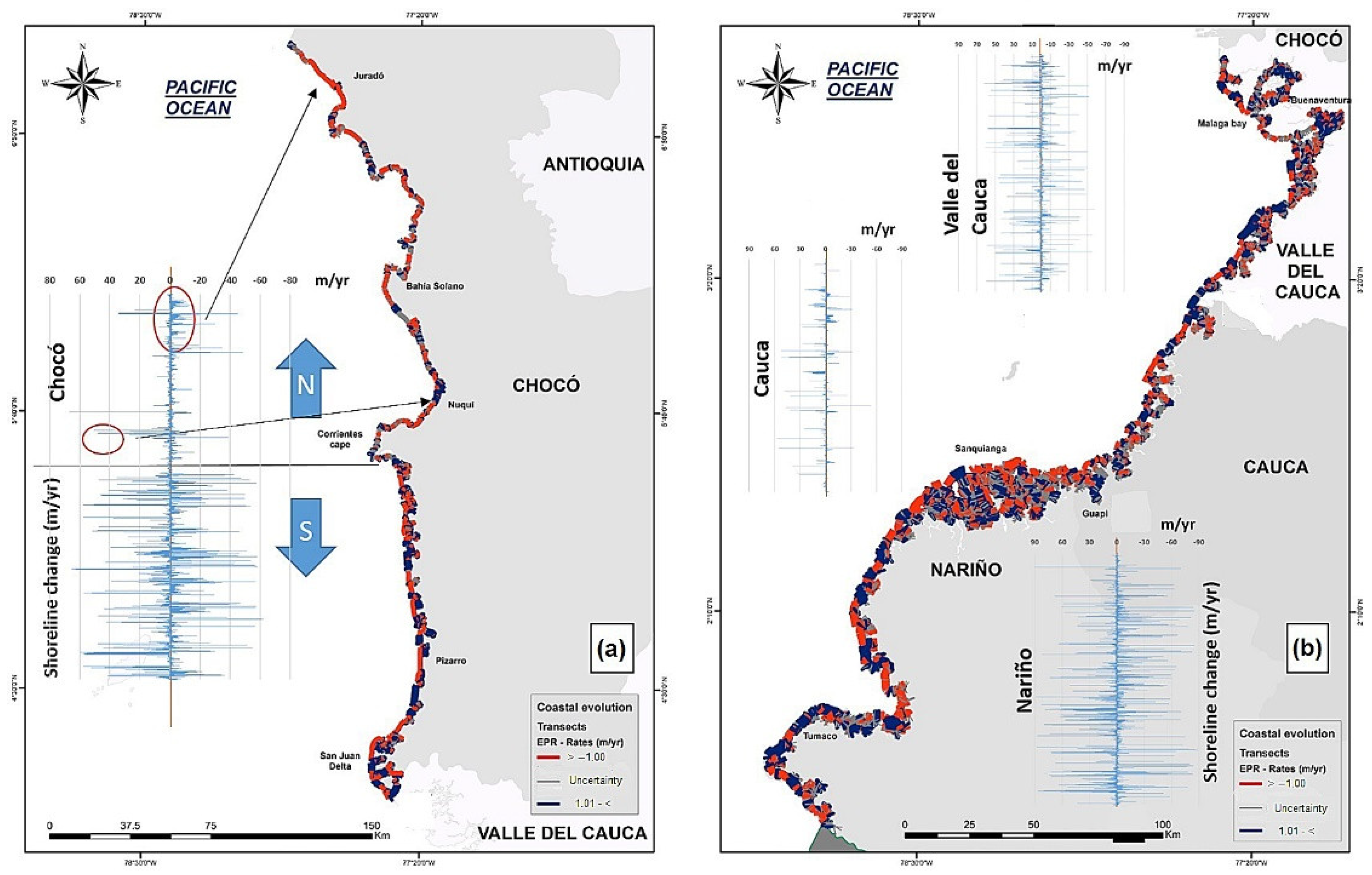
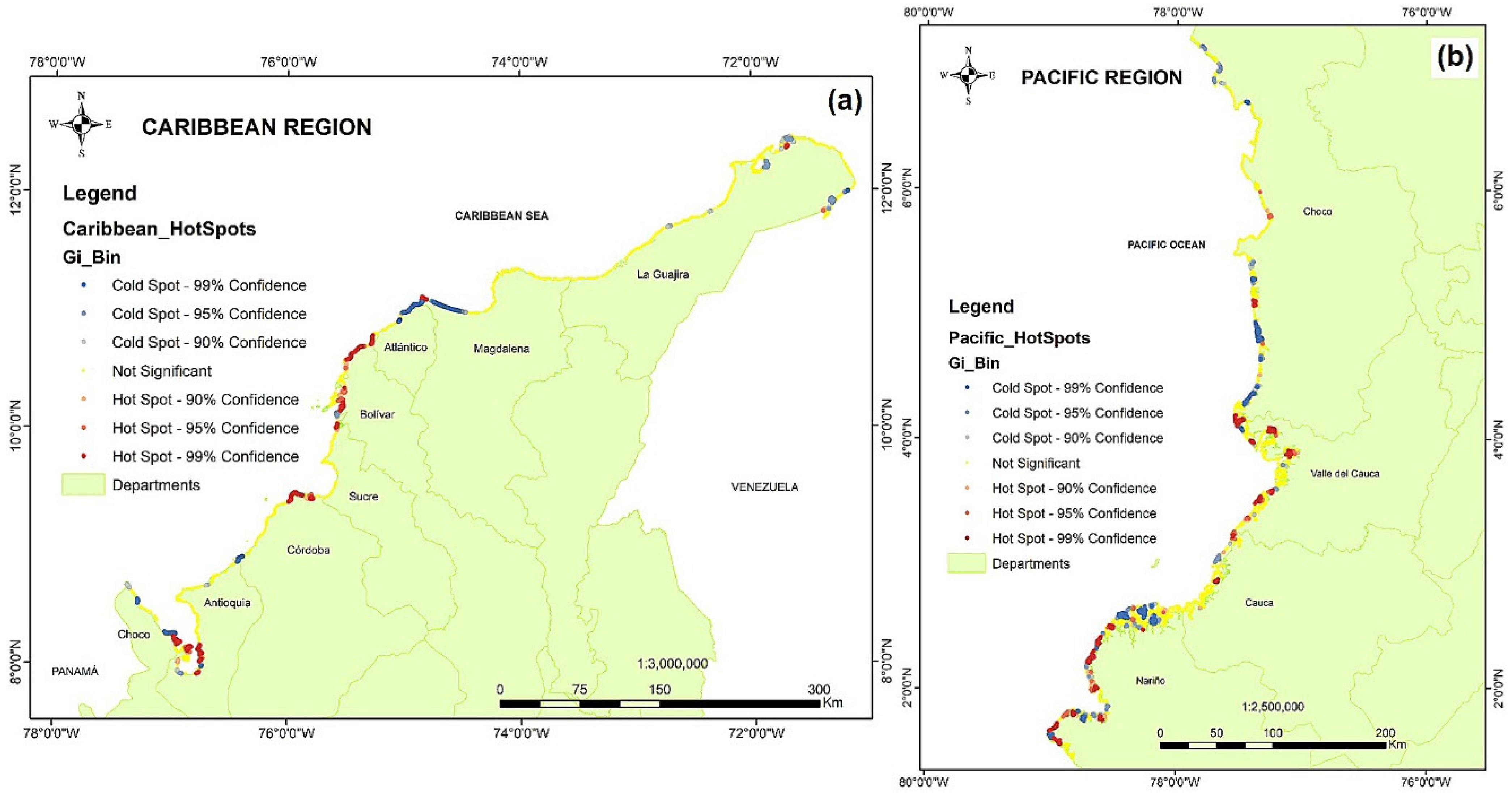
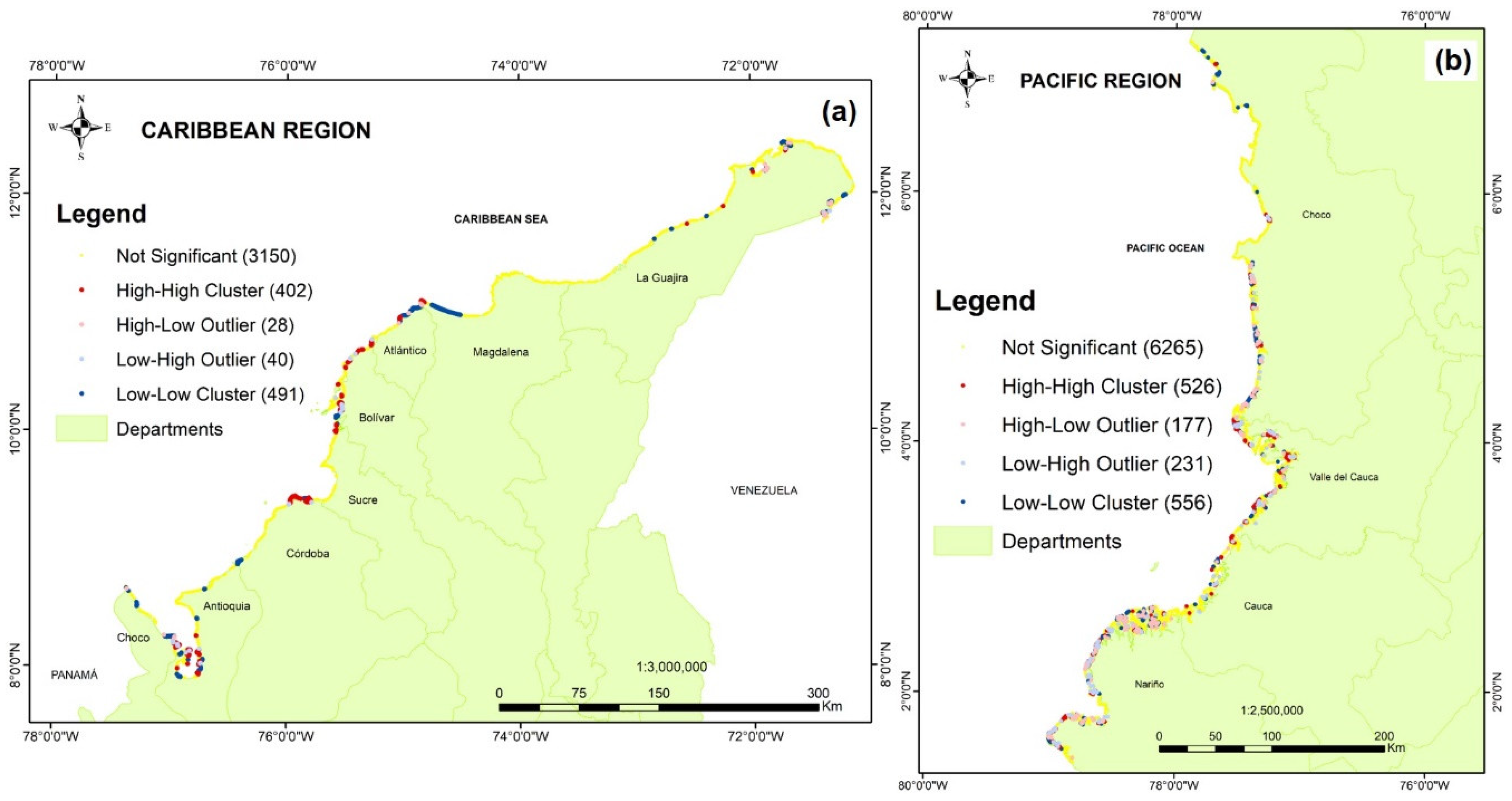
| Region | Number of Feature | Percentage of Spatial Connectivity | Average Number of Neighbors | Minimum Number of Neighbors | Maximum Number of Neighbors |
|---|---|---|---|---|---|
| Pacific | 7755 | 0.43 | 33.04 | 1 | 84 |
| Caribbean | 4111 | 0.85 | 35.09 | 1 | 79 |
| Region | Global Moran’s I | Local Moran’s I | ||
|---|---|---|---|---|
| Index Value | z-Score | High-High Cluster Observations 1 (#,*,%) | Low-Low Cluster Observations 1 (#,*,%) | |
| Caribbean | 0.587 | 25.33 | 313, 6 | 350, 6.7 |
| Pacific | 0.275 | 8.61 | 402, 5.1 | 366, 4.7 |
| Pacific | Caribbean | |||
|---|---|---|---|---|
| Gi | Number | % | Number | % |
| Cold spot 99% | 473 | 6.09% | 393 | 9.55% |
| Cold spot 95% | 358 | 4.61% | 183 | 4.45% |
| Cold spot 90% | 304 | 3.92% | 159 | 3.86% |
| Not significant | 5539 | 71.4% | 2742 | 66.6% |
| Hot spot 90% | 156 | 2.01% | 77 | 1.87% |
| Hot spot 95% | 267 | 3.44% | 116 | 2.82% |
| Hot spot 99% | 658 | 8.48% | 441 | 10.7% |
| Total | 7755 | 100% | 4111 | 100% |
| Total hot + cold spot (99, 95, and 90%) | 2216 | 28.5% | 1369 | 33.3% |
| Total hot + cold spot (99%) | 14.58% | 20.28% | ||
| LISA | Pacific | Caribbean | ||
|---|---|---|---|---|
| Number Observations | % | Number Observations | % | |
| HH | 526 | 6.78% | 402 | 9.78% |
| LL | 556 | 7.17% | 491 | 11.94% |
| LH | 231 | 2.98% | 40 | 0.97% |
| HL | 177 | 2.28% | 28 | 0.68% |
| Not significant | 6265 | 80.79% | 3150 | 76.62% |
| Total | 7755 | 100% | 4111 | 100% |
| Region | Moran’s I | Geomorphology Units | Number of Repetitions | Size Units (Geomorphology Units/# Repetitions) |
|---|---|---|---|---|
| Caribbean | 0.624 | 41 | 2511 | 61 |
| Pacific | 0.190 | 23 | 7755 | 337 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coca, O.; Ricaurte-Villota, C. Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean. Coasts 2022, 2, 125-151. https://doi.org/10.3390/coasts2030008
Coca O, Ricaurte-Villota C. Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean. Coasts. 2022; 2(3):125-151. https://doi.org/10.3390/coasts2030008
Chicago/Turabian StyleCoca, Oswaldo, and Constanza Ricaurte-Villota. 2022. "Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean" Coasts 2, no. 3: 125-151. https://doi.org/10.3390/coasts2030008
APA StyleCoca, O., & Ricaurte-Villota, C. (2022). Regional Patterns of Coastal Erosion and Sedimentation Derived from Spatial Autocorrelation Analysis: Pacific and Colombian Caribbean. Coasts, 2(3), 125-151. https://doi.org/10.3390/coasts2030008







