Solid and Liquid Oxygen under Ultrahigh Magnetic Fields
Abstract
:1. Introduction
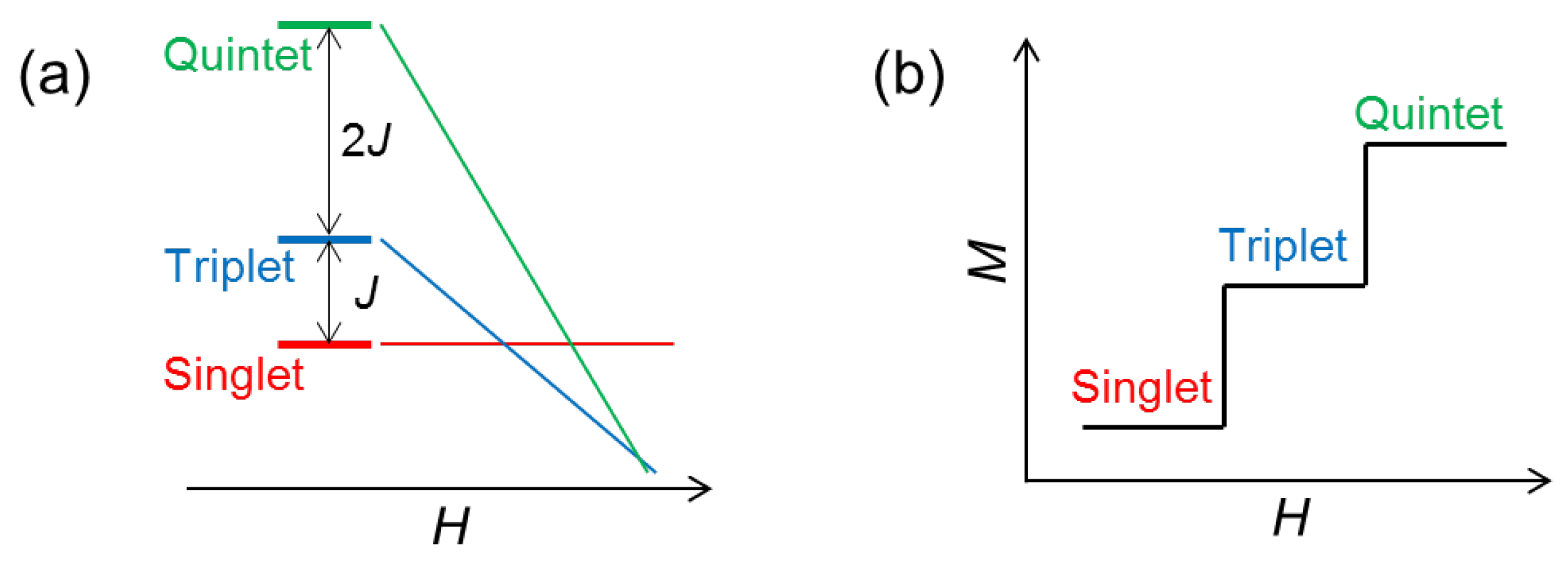
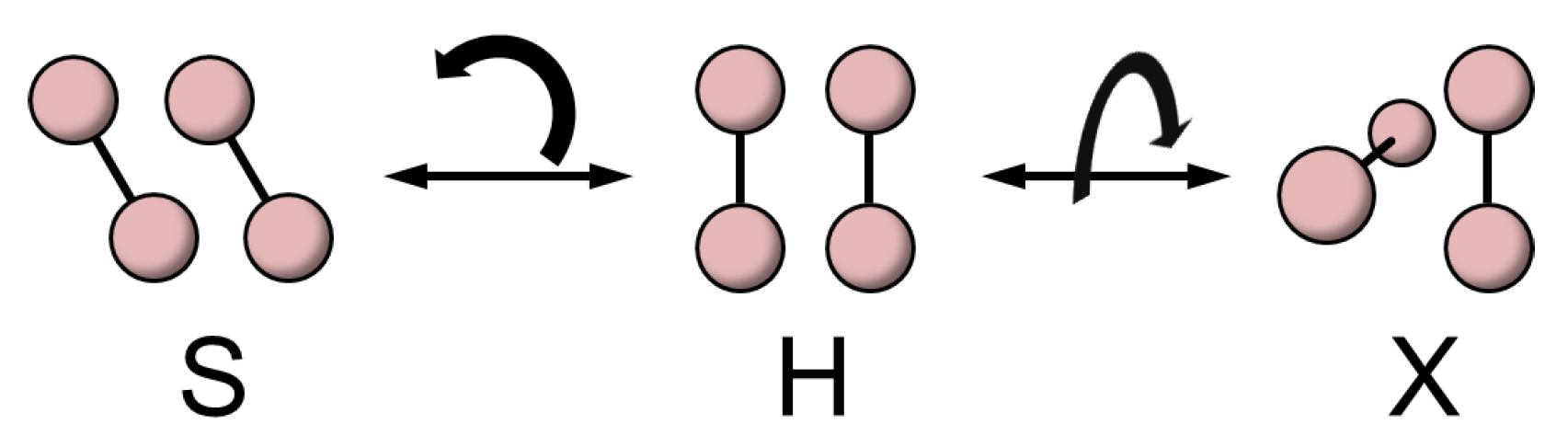
2. The O-O Dimer
3. Solid and Liquid Oxygen
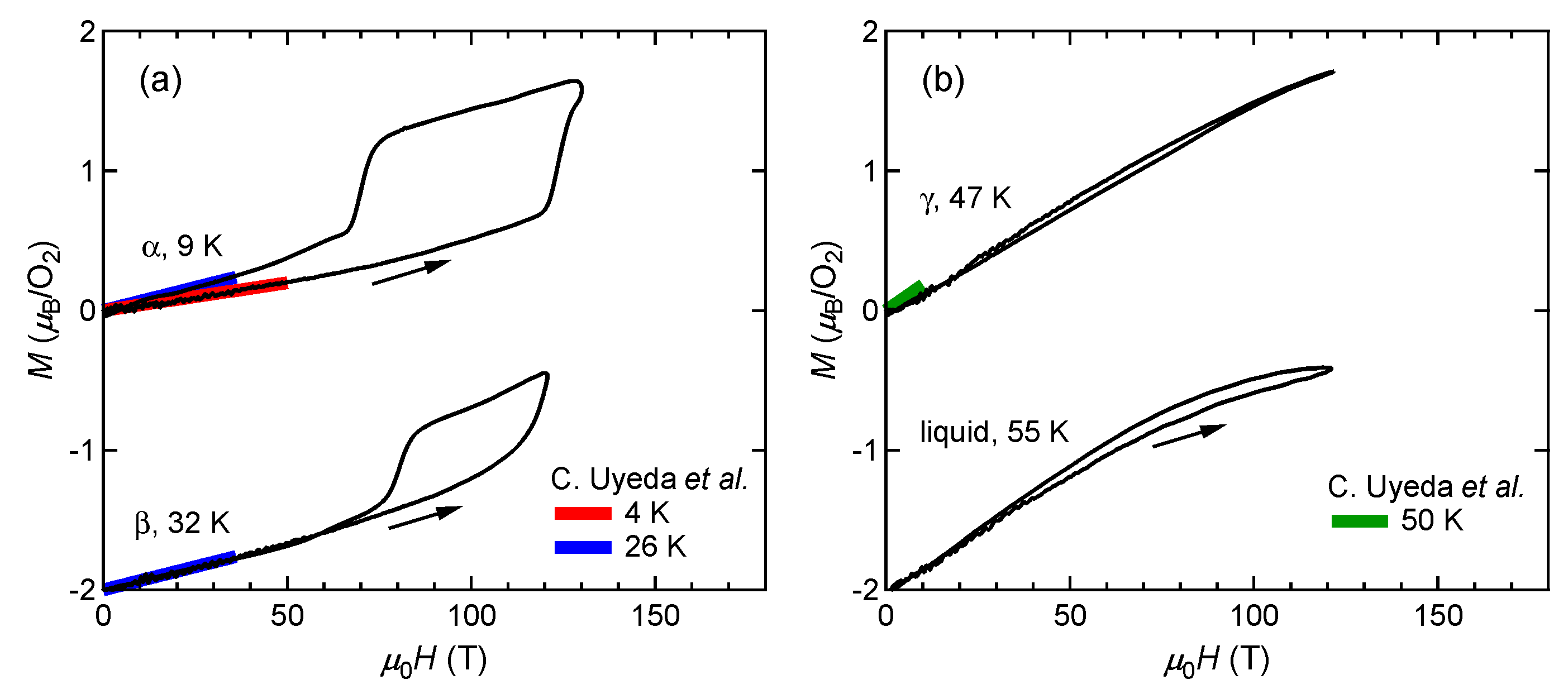
3.1. Magnetization
3.2. Optical Absorption
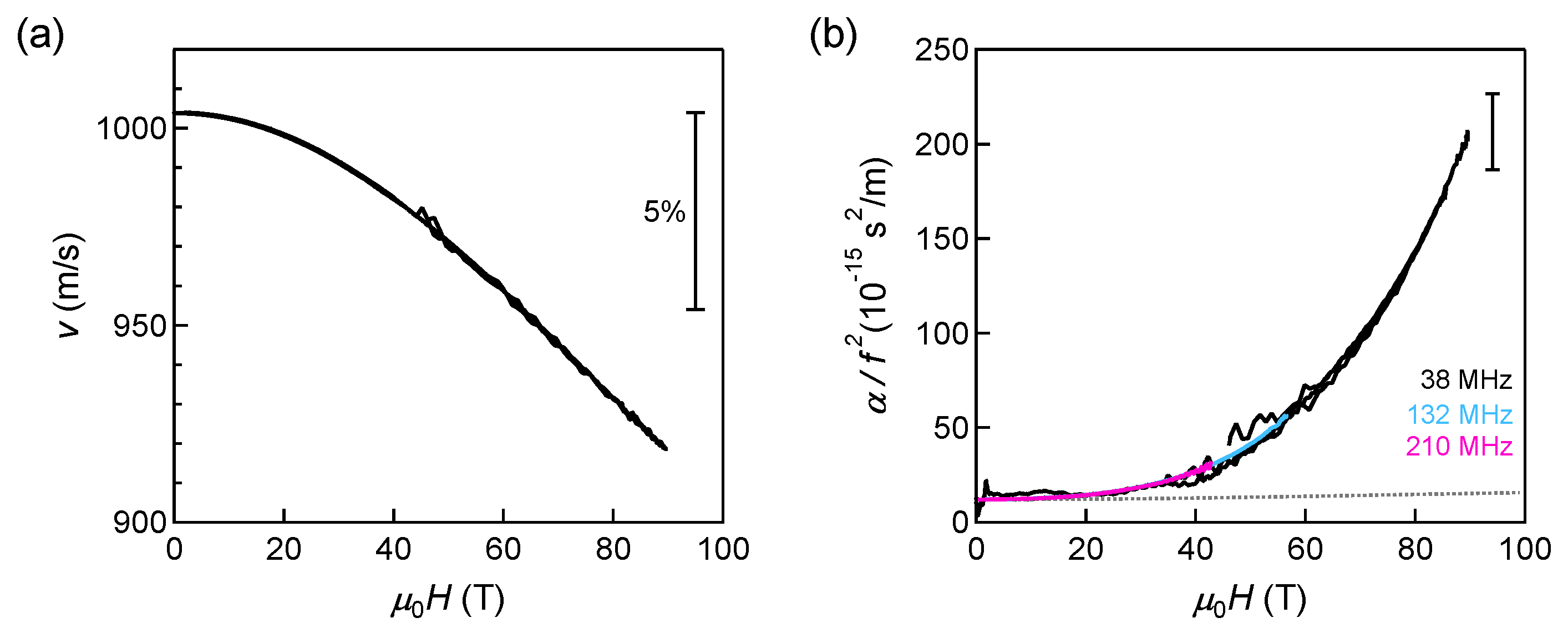
3.3. Magnetocaloric Effect
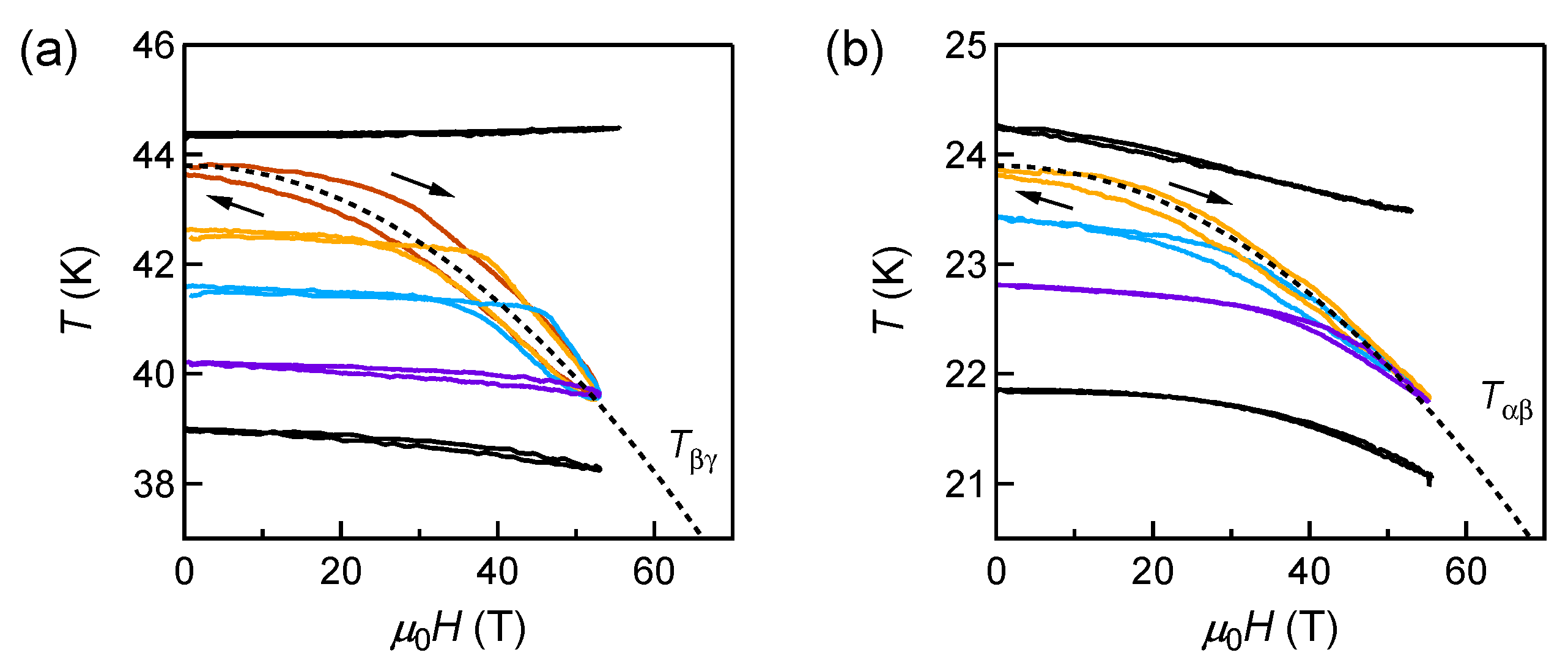
4. Phase Diagram
5. Remaining Issues
5.1. Diffraction Experiment
5.2. High-Field Plastic and Liquid Phases
5.3. High-Pressure and High-Field Study
5.4. Impurity Effect
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Faraday, M. Experimental Researches in Electricity, Vol. 3, Series XXV; Cambridge University Press: Cambridge, UK, 1848. [Google Scholar]
- DeFotis, G.C. Magnetism of solid oxygen. Phys. Rev. B 1981, 23, 4714–4740. [Google Scholar] [CrossRef]
- Freiman, Y.A.; Jodl, H.J. Elementary excitations in solid oxygen (Review). Low Temp. Phys. 2002, 28, 491–504. [Google Scholar] [CrossRef]
- Freiman, Y.; Jodl, H. Solid oxygen. Phys. Rep. 2004, 401, 1–228. [Google Scholar] [CrossRef]
- Freiman, Y.A. Magnetic properties of solid oxygen under pressure (Review Article). Low Temp. Phys. 2015, 41, 847–857. [Google Scholar] [CrossRef]
- Freiman, Y.; Jodl, H.; Crespo, Y. Solid oxygen revisited. Phys. Rep. 2018, 743, 1–55. [Google Scholar] [CrossRef]
- Lewis, G.N. The Magnetism of Oxygen and the Molecule O4. J. Am. Chem. Soc. 1924, 46, 2027–2032. [Google Scholar] [CrossRef]
- Kratky, K.W. Explanation of the magnetic behaviour of oxygen in the liquid state. Acta Phys. Acad. Sci. Hung. 1975, 39, 15–21. [Google Scholar] [CrossRef]
- Fernandez-Alonso, F.; Bermejo, F.J.; Bustinduy, I.; Adams, M.A.; Taylor, J.W. Spin dynamics in liquid and rotationally disordered solid oxygen. Phys. Rev. B 2008, 78, 104303. [Google Scholar] [CrossRef] [Green Version]
- Oda, T.; Pasquarello, A. Noncollinear magnetism in liquid oxygen: A first-principles molecular dynamics study. Phys. Rev. B 2004, 70, 134402. [Google Scholar] [CrossRef]
- Oda, T.; Pasquarello, A. Ab Initio Molecular Dynamics Investigation of the Structure and the Noncollinear Magnetism in Liquid Oxygen: Occurrence of O4 Molecular Units. Phys. Rev. Lett. 2002, 89, 197204. [Google Scholar] [CrossRef]
- Gaididei, Y.B.; Loktev, V.M.; Prikhotko, A.F.; Shanskii, L.I. α-Oxygen doublets. I. Theory. Phys. Status Solidi B 1975, 72, 795–806. [Google Scholar] [CrossRef]
- Gaididei, Y.B.; Loktev, V.M.; Prikhotko, A.F.; Shanskii, L.I. α-Oxygen Doublets II. Experiment. Phys. Status Solidi B 1976, 73, 415–425. [Google Scholar] [CrossRef]
- Litvinenko, Y.G.; Eremenko, V.V.; Garber, T.I. Antiferromagnetic Ordering Effect on the Light Absorption Spectrum by Crystalline Oxygen. Phys. Status Solidi B 1968, 30, 49–60. [Google Scholar] [CrossRef]
- Uyeda, C.; Yamagishi, A.; Date, M. Field-Induced Transparency in Liquid Oxygen by High Magnetic Field. J. Phys. Soc. Jpn. 1986, 55, 468–470. [Google Scholar] [CrossRef]
- Uyeda, C.; Yamagishi, A.; Date, M. Liquid Oxygen under High Magnetic Field. J. Phys. Soc. Jpn. 1988, 57, 3954–3960. [Google Scholar] [CrossRef]
- Fujiwara, T. Optical Absorptions in Solid Oxygen. J. Phys. Soc. Jpn. 1974, 36, 1530–1541. [Google Scholar] [CrossRef]
- Cox, D.E.; Samuelsen, E.J.; Beckurts, K.H. Neutron-Diffraction Determination of the Crystal Structure and Magnetic Form Factor of γ-Oxygen. Phys. Rev. B 1973, 7, 3102–3111. [Google Scholar] [CrossRef]
- Uyeda, C.; Sugiyama, K.; Date, M. High Field Magnetization of Solid Oxygen. J. Phys. Soc. Jpn. 1985, 54, 1107–1115. [Google Scholar] [CrossRef]
- Brodynaskii, A.P.; Freiman, Y.A. γ-oxygen, a quasi-one-dimensional magnetic material. Sov. J. Low Temp. Phys. 1985, 11, 714. [Google Scholar]
- Brodyanskii, A.P.; Freiman, Y.A.; Jezowski, A. The magnetic properties of γ-phase and liquid oxygen. J. Phys. Condens. Matter 1989, 1, 999–1004. [Google Scholar] [CrossRef]
- Meier, R.J.; Schinkel, C.J.; de Visser, A. Magnetisation of condensed oxygen under high pressures and in strong magnetic fields. J. Phys. C: Solid State Phys. 1982, 15, 1015–1024. [Google Scholar] [CrossRef] [Green Version]
- Giauque, W.F.; Johnston, H.L. The Heat Capacity of Oxygen from 12 °K. to its Boiling Point and its Heat of Vaporization. The Entropy from Spectroscopic Data. J. Am. Chem. Soc. 1929, 51, 2300–2321. [Google Scholar] [CrossRef]
- Fagerstroem, C.H.; Hollis Hallett, A.C. The specific heat of solid oxygen. J. Low Temp. Phys. 1969, 1, 3–12. [Google Scholar] [CrossRef]
- Meier, R.J.; Helmholdt, R.B. Neutron-diffraction study of α- and β-oxygen. Phys. Rev. B 1984, 29, 1387–1393. [Google Scholar] [CrossRef] [Green Version]
- Stephens, P.W.; Majkrzak, C.F. Magnetic structure and dynamics in the alpha and β phases of solid oxygen. Phys. Rev. B 1986, 33, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, L.; Szmyrka-Grzebyk, A.; Manuszkiewicz, H. Hysteresis effect in the α-β transition of solid oxygen. Cryogenics 1996, 36, 921–924. [Google Scholar] [CrossRef]
- Steur, P.; Pavese, F. On the double heat capacity peak of oxygen solid-to-solid transition near 23.8 K. Chem. Phys. Lett. 2022, 797, 139598. [Google Scholar] [CrossRef]
- Bhandari, R.; Falicov, L.M. Theory of antiferromagnetism and light absorption in solid oxygen. J. Phys. C: Solid State Phys. 1973, 6, 479–494. [Google Scholar] [CrossRef]
- Nicol, M.; Hirsch, K.; Holzapfel, W.B. Oxygen phase equilibria near 298 K. Chem. Phys. Lett. 1979, 68, 49–52. [Google Scholar] [CrossRef]
- Schiferl, D.; Cromer, D.T.; Schwalbe, L.A.; Mills, R.L. Structure of ‘orange’ 18O2 at 9.6 GPa and 297 K. Acta Crystallogr. B 1983, 39, 153–157. [Google Scholar] [CrossRef]
- Goncharenko, I.N.; Makarova, O.L.; Ulivi, L. Direct Determination of the Magnetic Structure of the Delta Phase of Oxygen. Phys. Rev. Lett. 2004, 93, 055502. [Google Scholar] [CrossRef] [PubMed]
- Klotz, S.; Strässle, T.; Cornelius, A.L.; Philippe, J.; Hansen, T. Magnetic Ordering in Solid Oxygen up to Room Temperature. Phys. Rev. Lett. 2010, 104, 115501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Desgreniers, S.; Vohra, Y.K.; Ruoff, A.L. Optical response of very high density solid oxygen to 132 GPa. J. Phys. Chem. 1990, 94, 1117–1122. [Google Scholar] [CrossRef]
- Akahama, Y.; Kawamura, H.; Häusermann, D.; Hanfland, M.; Shimomura, O. New High-Pressure Structural Transition of Oxygen at 96 GPa Associated with Metallization in a Molecular Solid. Phys. Rev. Lett. 1995, 74, 4690–4693. [Google Scholar] [CrossRef] [PubMed]
- Fujihisa, H.; Akahama, Y.; Kawamura, H.; Ohishi, Y.; Shimomura, O.; Yamawaki, H.; Sakashita, M.; Gotoh, Y.; Takeya, S.; Honda, K. O8 Cluster Structure of the Epsilon Phase of Solid Oxygen. Phys. Rev. Lett. 2006, 97, 085503. [Google Scholar] [CrossRef]
- Lundegaard, L.F.; Weck, G.; McMahon, M.I.; Desgreniers, S.; Loubeyre, P. Observation of an O8 molecular lattice in the ϵ phase of solid oxygen. Nature 2006, 443, 201–204. [Google Scholar] [CrossRef]
- Santoro, M.; Gregoryanz, E.; Mao, H.k.; Hemley, R.J. New Phase Diagram of Oxygen at High Pressures and Temperatures. Phys. Rev. Lett. 2004, 93, 265701. [Google Scholar] [CrossRef] [Green Version]
- Goncharov, A.F.; Subramanian, N.; Ravindran, T.R.; Somayazulu, M.; Prakapenka, V.B.; Hemley, R.J. Polymorphism of dense, hot oxygen. J. Chem. Phys. 2011, 135, 084512. [Google Scholar] [CrossRef]
- Crespo, Y.; Fabrizio, M.; Scandolo, S.; Tosatti, E. Collective spin 1 singlet phase in high-pressure oxygen. Proc. Natl. Acad. Sci. USA 2014, 111, 10427–10432. [Google Scholar] [CrossRef] [Green Version]
- Klotz, S. Magnetism in Solid Oxygen Studied by High-Pressure Neutron Diffraction. J. Low Temp. Phys. 2018, 192, 1–18. [Google Scholar] [CrossRef]
- Katzke, H.; Tolédano, P. Theory of the mechanisms of pressure-induced phase transitions in oxygen. Phys. Rev. B 2009, 79, 140101. [Google Scholar] [CrossRef]
- Shimizu, K.; Suhara, K.; Ikumo, M.; Eremets, M.I.; Amaya, K. Superconductivity in oxygen. Nature 1998, 393, 767–769. [Google Scholar] [CrossRef]
- Eremenko, V.V.; Litvinenko, Y.V. Spectrum of Alpha Oxygen in a Strong Magnetic Field. Sov. Phys. JETP 1968, 26, 350–353. [Google Scholar]
- Kimura, S.; Kindo, K. High field ESR measurements on molecular oxygen. In EPR in the 21st Century; Kawamori, A., Yamauchi, J., Ohta, H., Eds.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; pp. 799–802. [Google Scholar] [CrossRef]
- Kimura, S.; Kindo, K.; Narumi, Y.; Hagiwara, M.; Kikuchi, H.; Ajiro, Y. High Field/High Frequency ESR in Osaka University. J. Phys. Soc. Jpn. 2003, 72, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Nomura, T.; Matsuda, Y.H.; Takeyama, S.; Matsuo, A.; Kindo, K.; Her, J.L.; Kobayashi, T.C. Novel Phase of Solid Oxygen Induced by Ultrahigh Magnetic Fields. Phys. Rev. Lett. 2014, 112, 247201. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T.C.; Nomura, T.; Matsuda, Y.H.; Her, J.L.; Takeyama, S.; Matsuo, A.; Kindo, K. Emergence of novel phase of solid oxygen in ultrahigh magnetic Held. J. Phys. Conf. Ser. 2014, 568, 042018. [Google Scholar] [CrossRef] [Green Version]
- Nomura, T.; Matsuda, Y.H.; Her, J.L.; Takeyama, S.; Matsuo, A.; Kindo, K.; Kobayashi, T.C. Magneto-Absorption in the α Phase of Solid Oxygen at Megagauss Magnetic Fields. J. Low Temp. Phys. 2013, 170, 372–376. [Google Scholar] [CrossRef]
- Nomura, T.; Matsuda, Y.H.; Takeyama, S.; Matsuo, A.; Kindo, K.; Kobayashi, T.C. Phase boundary of θ phase of solid oxygen in ultrahigh magnetic fields. Phys. Rev. B 2015, 92, 064109. [Google Scholar] [CrossRef]
- Nomura, T.; Kohama, Y.; Matsuda, Y.H.; Kindo, K.; Kobayashi, T.C. α-β and β-γ phase boundaries of solid oxygen observed by adiabatic magnetocaloric effect. Phys. Rev. B 2017, 95, 104420. [Google Scholar] [CrossRef] [Green Version]
- Nomura, T.; Matsuda, Y.H.; Kobayashi, T.C. H-T phase diagram of solid oxygen. Phys. Rev. B 2017, 96, 054439. [Google Scholar] [CrossRef] [Green Version]
- Nomura, T.; Ikeda, A.; Gen, M.; Matsuo, A.; Kindo, K.; Kohama, Y.; Matsuda, Y.H.; Zherlitsyn, S.; Wosnitza, J.; Tsuda, H.; et al. Physical properties of liquid oxygen under ultrahigh magnetic fields. Phys. Rev. B 2021, 104, 224423. [Google Scholar] [CrossRef]
- Nomura, T.; Hauspurg, A.; Gorbunov, D.I.; Miyata, A.; Schulze, E.; Zvyagin, S.A.; Tsurkan, V.; Matsuda, Y.H.; Kohama, Y.; Zherlitsyn, S. Ultrasound measurement technique for the single-turn-coil magnets. Rev. Sci. Instrum. 2021, 92, 063902. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Zherlitsyn, S.; Kohama, Y.; Wosnitza, J. Viscosity measurements in pulsed magnetic fields by using a quartz-crystal microbalance. Rev. Sci. Instrum. 2019, 90, 065101. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Matsuda, Y.H.; Takeyama, S.; Kobayashi, T.C. Irreversible Heating Measurement with Microsecond Pulse Magnet: Example of the α–θ Phase Transition of Solid Oxygen. J. Phys. Soc. Jpn. 2016, 85, 094601. [Google Scholar] [CrossRef] [Green Version]
- Nomura, T.; Matsuda, Y.H.; Takeyama, S.; Matsuo, A.; Kindo, K.; Kobayashi, T.C. Orbital Zeeman Effect of Liquid Oxygen in High Magnetic Fields. In Proceedings of the International Conference on Strongly Correlated Electron Systems (SCES2013), Tokyo, Japan, 3–5 August 2013. [Google Scholar] [CrossRef] [Green Version]
- Matsuda, Y.H.; Shimizu, A.; Ikeda, A.; Nomura, T.; Yajima, T.; Inami, T.; Takahashi, K.; Kobayashi, T.C. High magnetic field X-ray diffraction study of the α phase of solid oxygen: Absence of giant magnetostriction. Phys. Rev. B 2019, 100, 214105. [Google Scholar] [CrossRef]
- Kitaura, R.; Kitagawa, S.; Kubota, Y.; Kobayashi, T.C.; Kindo, K.; Mita, Y.; Matsuo, A.; Kobayashi, M.; Chang, H.C.; Ozawa, T.C.; et al. Formation of a One-Dimensional Array of Oxygen in a Microporous Metal-Organic Solid. Science 2002, 298, 2358–2361. [Google Scholar] [CrossRef] [Green Version]
- Hori, A.C.; Kobayashi, T.; Kubota, Y.; Matsuo, A.; Kindo, K.; Kim, J.; Kato, K.; Takata, M.; Sakamoto, H.; Matsuda, R.; et al. Spin-Dependent Molecular Orientation of O2–O2 Dimer Formed in the Nanoporous Coordination Polymer. J. Phys. Soc. Jpn. 2013, 82, 084703. [Google Scholar] [CrossRef]
- Kobayashi, T.C.; Matsuo, A.; Suzuki, M.; Kindo, K.; Kitaura, R.; Matsuda, R.; Kitagawa, S. Magnetic Properties of Molecular Oxygen Adsorbed in Micro-Porous Metal-Organic Solids. Prog. Theor. Phys. Suppl. 2005, 159, 271–279. [Google Scholar] [CrossRef] [Green Version]
- Mori, W.; Kobayashi, T.C.; Kurobe, J.; Amaya, K.; Narumi, Y.; Kumada, T.; Kindo, K.; Katori, H.A.; Goto, T.; Miura, N.; et al. Magnetic Properties of Oxygen Physisorbed in Cu-Trans-1,4-Cyclohexanedicarboxylic Acid. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1997, 306, 1–7. [Google Scholar] [CrossRef]
- Hori, A.; Kobayashi, T.C.; Matsuo, A.; Kindo, K.; Matsuda, R.; Kitagawa, S. High-field magnetization process of O2 adsorbed in a microporous coordination polymer CPL-1 at various temperatures. J. Phys. Conf. Ser. 2010, 200, 022018. [Google Scholar] [CrossRef] [Green Version]
- Soda, M.; Honma, Y.; Takamizawa, S.; Ohira-Kawamura, S.; Nakajima, K.; Masuda, T. Spin Model of O2-Based Magnet in a Nanoporous Metal Complex. J. Phys. Soc. Jpn. 2016, 85, 034717. [Google Scholar] [CrossRef] [Green Version]
- Bussery, B.; Umanskii, S.Y.; Aubert-Frécon, M.; Bouty, O. Exchange interaction between two O2 molecules using the asymptotic method. J. Chem. Phys. 1994, 101, 416–423. [Google Scholar] [CrossRef]
- van Hemert, M.C.; Wormer, P.E.S.; van der Avoird, A. Ab Initio Calculation of the Heisenberg Exchange Interaction between O2 Molecules. Phys. Rev. Lett. 1983, 51, 1167–1170. [Google Scholar] [CrossRef]
- Wormer, P.E.S.; van der Avoird, A. (Heisenberg) exchange and electrostatic interactions between O2 molecules: An ab initio study. J. Chem. Phys. 1984, 81, 1929–1939. [Google Scholar] [CrossRef]
- Bartolomei, M.; Hernández, M.I.; Campos-Martínez, J.; Carmona-Novillo, E.; Hernández-Lamoneda, R. The intermolecular potentials of the O2–O2 dimer: A detailed ab initio study of the energy splittings for the three lowest multiplet states. Phys. Chem. Chem. Phys. 2008, 10, 5374–5380. [Google Scholar] [CrossRef]
- Bussery, B.; Wormer, P.E.S. A van der Waals intermolecular potential for (O2)2. J. Chem. Phys. 1993, 99, 1230–1239. [Google Scholar] [CrossRef]
- Nozawa, K.; Shima, N.; Makoshi, K. Theoretical Study of Structures of Solid Oxygen under High Pressure. J. Phys. Soc. Jpn. 2002, 71, 377–380. [Google Scholar] [CrossRef]
- Miura, N.; Osada, T.; Takeyama, S. Research in Super-High Pulsed Magnetic Fields at the Megagauss Laboratory of the University of Tokyo. J. Low Temp. Phys. 2003, 133, 139–158. [Google Scholar] [CrossRef]
- Uyeda, C.; Yamagishi, A.; Date, M. Magneto-Volume Effect of Liquid Oxygen. J. Phys. Soc. Jpn. 1987, 56, 3444–3446. [Google Scholar] [CrossRef]
- Katsumata, K.; Kimura, S.; Staub, U.; Narumi, Y.; Tanaka, Y.; Shimomura, S.; Nakamura, T.; Lovesey, S.W.; Ishikawa, T.; Kitamura, H. The giant magneto-volume effect in solid oxygen. J. Phys. Condens. Matter 2005, 17, L235–L239. [Google Scholar] [CrossRef]
- Prikhot’ko, A.F.; Ptukha, T.P.; Shanskii, L.I. Splitting of Absorption Lines of Oxygen Crystals in a Magnetic Field. JETP Lett. 1967, 5, 328–330. [Google Scholar]
- Jansen, A.P.J.; van der Avoird, A. Magnetic coupling and dynamics in solid α and β-O2. I. An ab initio theoretical approach. J. Chem. Phys. 1987, 86, 3583–3596. [Google Scholar] [CrossRef] [Green Version]
- Jansen, A.P.J.; van der Avoird, A. Magnetic coupling and dynamics in solid α and β-O2. II. Prediction of magnetic field effects. J. Chem. Phys. 1987, 86, 3597–3601. [Google Scholar] [CrossRef] [Green Version]
- Kihara, T.; Kohama, Y.; Hashimoto, Y.; Katsumoto, S.; Tokunaga, M. Adiabatic measurements of magneto-caloric effects in pulsed high magnetic fields up to 55 T. Rev. Sci. Instrum. 2013, 84, 074901. [Google Scholar] [CrossRef] [PubMed]
- Kasamatsu, S.; Kato, T.; Sugino, O. First-principles description of van der Waals bonded spin-polarized systems using the vdW-DF+U method: Application to solid oxygen at low pressure. Phys. Rev. B 2017, 95, 235120. [Google Scholar] [CrossRef] [Green Version]
- Manzhelii, V.G.; Freiman, Y.A. Physics of Cryocrystals; American Institute of Physics: New York, NY, USA, 1997. [Google Scholar]
- Ikeda, A.; Matsuda, Y.H.; Zhou, X.; Yajima, T.; Kubota, Y.; Tono, K.; Yabashi, M. Single shot X-ray diffractometry in SACLA with pulsed magnetic fields up to 16 T. Phys. Rev. Res. 2020, 2, 043175. [Google Scholar] [CrossRef]
- Ikeda, A.; Matsuda, Y.H.; Zhou, X.; Peng, S.; Ishii, Y.; Yajima, T.; Kubota, Y.; Inoue, I.; Inubushi, Y.; Tono, K.; et al. Generating 77 T using a portable pulse magnet for single-shot quantum beam experiments. Appl. Phys. Lett. 2022, 120, 142403. [Google Scholar] [CrossRef]
- Lüthi, B. Physical Acoustics in the Solid State; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Bhatia, B. Ultrasonic Absorption: An Introduction to the Theory of Sound Absorption and Dispersion in Gases, Liquids, and Solids; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Tanaka, H. Liquid–liquid transition and polyamorphism. J. Chem. Phys. 2020, 153, 130901. [Google Scholar] [CrossRef]
- Anisimov, M.A.; Duška, M.; Caupin, F.; Amrhein, L.E.; Rosenbaum, A.; Sadus, R.J. Thermodynamics of Fluid Polyamorphism. Phys. Rev. X 2018, 8, 011004. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Sakakibara, A.; Inokuchi, H. Magnetic Susceptibilities of Solid Oxygen-Argon Mixtures. Bull. Chem. Soc. Jpn. 1973, 46, 2305–2307. [Google Scholar] [CrossRef] [Green Version]
- Blocker, T.G.; Simmons, C.L.; West, F.G. Magnetic Properties of the Oxygen Molecule in Solid Oxygen-Argon Mixtures. J. Appl. Phys. 1969, 40, 1154–1155. [Google Scholar] [CrossRef]
- Baer, B.J.; Nicol, M. High-pressure binary phase diagram of nitrogen-oxygen at 295 K determined by Raman spectroscopy. J. Phys. Chem. 1990, 94, 1073–1078. [Google Scholar] [CrossRef]
- Sihachakr, D.; Loubeyre, P. O2-N2 mixtures under pressure: A structural study of the binary phase diagram at 295 K. Phys. Rev. B 2004, 70, 134105. [Google Scholar] [CrossRef]
- Akahama, Y.; Maekawa, T.; Sugimoto, T.; Fujihisa, H.; Hirao, N.; Ohishi, Y. High-pressure phase diagram of O2 and N 2 binary system: Formation of kagome-lattice of O2. J. Phys. Conf. Ser. 2014, 500, 182001. [Google Scholar] [CrossRef]
- Kurahashi, M.; Yamauchi, Y. Spin Correlation in O2 Chemisorption on Ni(111). Phys. Rev. Lett. 2015, 114, 016101. [Google Scholar] [CrossRef]
- Kitazawa, K.; Ikezoe, Y.; Uetake, H.; Hirota, N. Magnetic field effects on water, air and powders. Phys. B: Condens. Matter 2001, 294–295, 709–714. [Google Scholar] [CrossRef]
- Pliss, E.M.; Grobov, A.M.; Kuzaev, A.K.; Buchachenko, A.L. Magnetic field effect on the oxidation of organic substances by molecular oxygen. J. Phys. Org. Chem. 2019, 32, e3915. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nomura, T.; Matsuda, Y.H.; Kobayashi, T.C. Solid and Liquid Oxygen under Ultrahigh Magnetic Fields. Oxygen 2022, 2, 152-163. https://doi.org/10.3390/oxygen2020013
Nomura T, Matsuda YH, Kobayashi TC. Solid and Liquid Oxygen under Ultrahigh Magnetic Fields. Oxygen. 2022; 2(2):152-163. https://doi.org/10.3390/oxygen2020013
Chicago/Turabian StyleNomura, Toshihiro, Yasuhiro H. Matsuda, and Tatsuo C. Kobayashi. 2022. "Solid and Liquid Oxygen under Ultrahigh Magnetic Fields" Oxygen 2, no. 2: 152-163. https://doi.org/10.3390/oxygen2020013
APA StyleNomura, T., Matsuda, Y. H., & Kobayashi, T. C. (2022). Solid and Liquid Oxygen under Ultrahigh Magnetic Fields. Oxygen, 2(2), 152-163. https://doi.org/10.3390/oxygen2020013






