Local Normal Approximations and Probability Metric Bounds for the Matrix-Variate T Distribution and Its Application to Hotelling’s T Statistic
Abstract
:1. Introduction
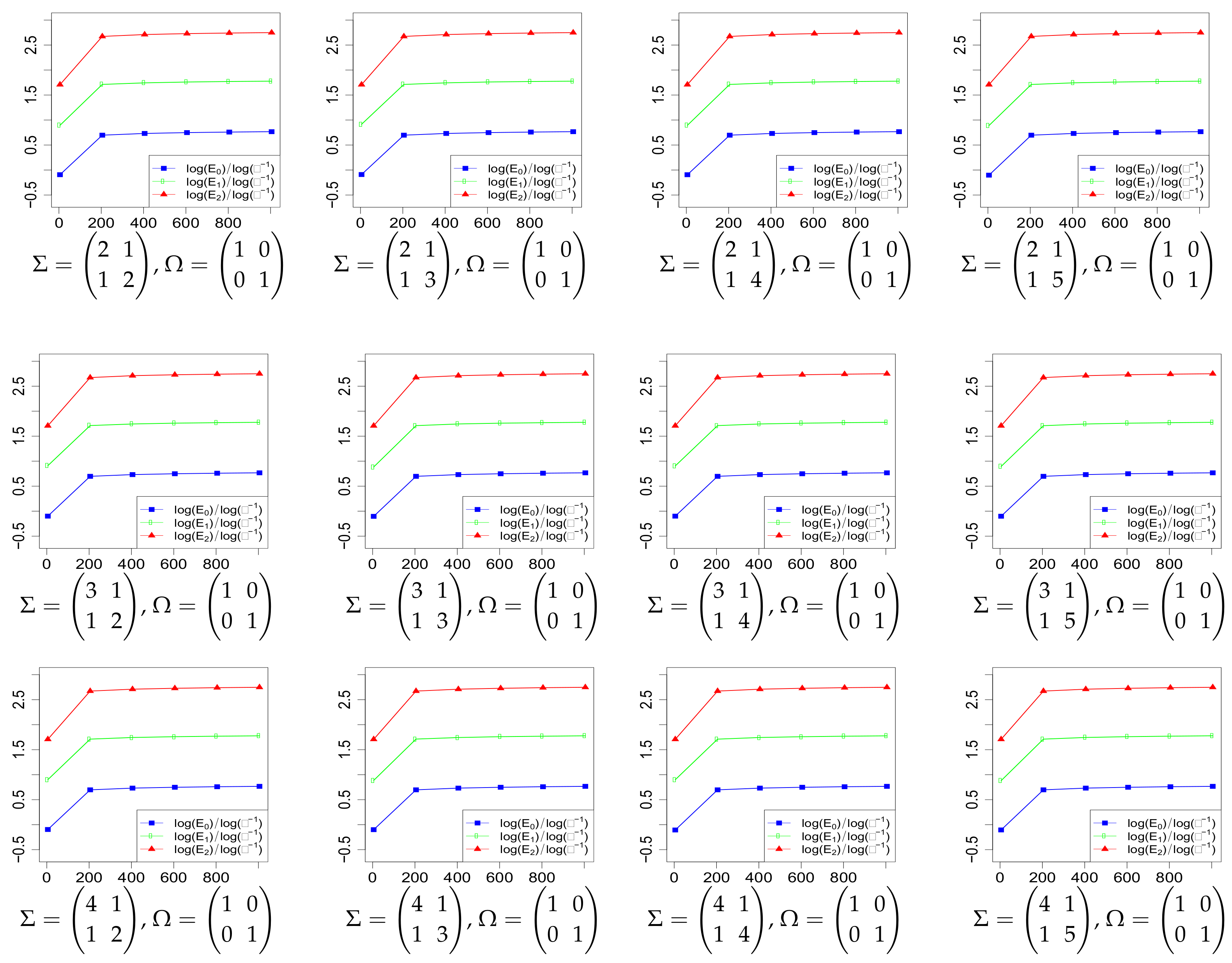
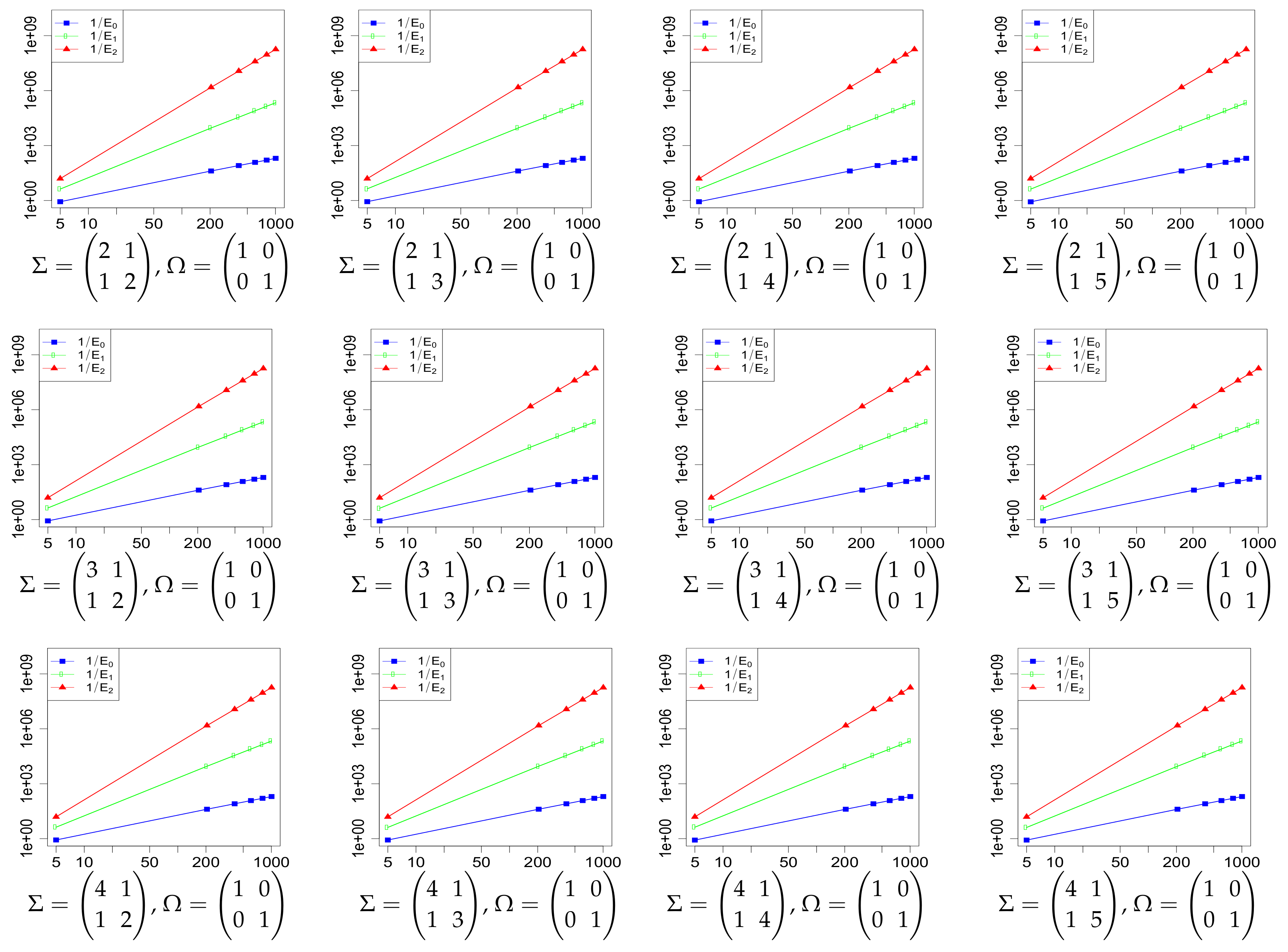
2. Main Results
3. Proofs
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Technical Computations
References
- Gupta, A.K.; Nagar, D.K. Matrix Variate Distributions, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1999; p. 384. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. (Eds.) NIST Handbook of Mathematical Functions; U.S. Department of Commerce, National Institute of Standards and Technology: Washington, DC, USA; Cambridge University Press: Cambridge, UK, 2010; p. xvi+951. [Google Scholar]
- Nagar, D.K.; Roldán-Correa, A.; Gupta, A.K. Extended matrix variate gamma and beta functions. J. Multivar. Anal. 2013, 122, 53–69. [Google Scholar] [CrossRef]
- Pajevic, S.; Basser, P.J. Parametric description of noise in diffusion tensor MRI. In Proceedings of the 7th Annual Meeting of the ISMRM, Philadelphia, PA, USA, 22–28 May 1999; p. 1787. [Google Scholar]
- Basser, P.J.; Jones, D.K. Diffusion-tensor MRI: Theory, experimental design and data analysis—A technical review. NMR Biomed. 2002, 15, 456–467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pajevic, S.; Basser, P.J. Parametric and non-parametric statistical analysis of DT-MRI data. J. Magn. Reson. 2003, 161, 1–14. [Google Scholar] [CrossRef]
- Basser, P.J.; Pajevic, S. A normal distribution for tensor-valued random variables: Applications to diffusion tensor MRI. IEEE Trans. Med. Imaging 2003, 22, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Gasbarra, D.; Pajevic, S.; Basser, P.J. Eigenvalues of random matrices with isotropic Gaussian noise and the design of diffusion tensor imaging experiments. SIAM J. Imaging Sci. 2017, 10, 1511–1548. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alexander, D.C.; Pierpaoli, C.; Basser, P.J.; Gee, J.C. Spatial transformations of diffusion tensor magnetic resonance images. IEEE Trans. Med. Imaging 2001, 20, 1131–1139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schwartzman, A.; Mascarenhas, W.F.; Taylor, J.E. Inference for eigenvalues and eigenvectors of Gaussian symmetric matrices. Ann. Statist. 2008, 36, 2886–2919. [Google Scholar] [CrossRef]
- Mallows, C.L. Latent vectors of random symmetric matrices. Biometrika 1961, 48, 133–149. [Google Scholar] [CrossRef]
- Hu, W.; White, M. A CMB polarization primer. New Astron. 1997, 2, 323–344. [Google Scholar] [CrossRef] [Green Version]
- Vafaei Sadr, A.; Movahed, S.M.S. Clustering of local extrema in Planck CMB maps. MNRAS 2021, 503, 815–829. [Google Scholar] [CrossRef]
- Gallaugher, M.P.B.; McNicholas, P.D. Finite mixtures of skewed matrix variate distributions. Pattern Recognit. 2018, 80, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Ouimet, F. Refined normal approximations for the Student distribution. J. Classical Anal. 2022, 20, 23–33. [Google Scholar] [CrossRef]
- Shafiei, A.; Saberali, S.M. A simple asymptotic bound on the error of the ordinary normal approximation to the Student’s t-distribution. IEEE Commun. Lett. 2015, 19, 1295–1298. [Google Scholar] [CrossRef]
- Govindarajulu, Z. Normal approximations to the classical discrete distributions. Sankhyā Ser. A 1965, 27, 143–172. [Google Scholar]
- Esseen, C.G. Fourier analysis of distribution functions. A mathematical study of the Laplace-Gaussian law. Acta Math. 1945, 77, 1–125. [Google Scholar] [CrossRef]
- Cressie, N. A finely tuned continuity correction. Ann. Inst. Statist. Math. 1978, 30, 435–442. [Google Scholar] [CrossRef]
- Gaunt, R.E. Variance-gamma approximation via Stein’s method. Electron. J. Probab. 2014, 19, 1–33. [Google Scholar] [CrossRef]
- Gaunt, R.E. New error bounds for Laplace approximation via Stein’s method. ESAIM Probab. Stat. 2021, 25, 325–345. [Google Scholar] [CrossRef]
- Gaunt, R.E. Wasserstein and Kolmogorov error bounds for variance-gamma approximation via Stein’s method I. J. Theoret. Probab. 2020, 33, 465–505. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Hotelling, H. The generalization of Student’s ratio. Ann. Math. Statist. 1931, 2, 360–378. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; National Bureau of Standards Applied Mathematics Series, For sale by the Superintendent of Documents; U.S. Government Printing Office: Washington, DC, USA, 1964; Volume 55, p. xiv+1046. [Google Scholar]
- Carter, A.V. Deficiency distance between multinomial and multivariate normal experiments. Ann. Statist. 2002, 30, 708–730. [Google Scholar] [CrossRef]
- de Waal, D.J.; Nel, D.G. On some expectations with respect to Wishart matrices. South African Statist. J. 1973, 7, 61–67. [Google Scholar]
- Letac, G.; Massam, H. All invariant moments of the Wishart distribution. Scand. J. Statist. 2004, 31, 295–318. [Google Scholar] [CrossRef]
- Haff, L.R. An identity for the Wishart distribution with applications. J. Multivar. Anal. 1979, 9, 531–544. [Google Scholar] [CrossRef] [Green Version]
- von Rosen, D. Moments for the inverted Wishart distribution. Scand. J. Statist. 1988, 15, 97–109. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouimet, F. Local Normal Approximations and Probability Metric Bounds for the Matrix-Variate T Distribution and Its Application to Hotelling’s T Statistic. AppliedMath 2022, 2, 446-456. https://doi.org/10.3390/appliedmath2030025
Ouimet F. Local Normal Approximations and Probability Metric Bounds for the Matrix-Variate T Distribution and Its Application to Hotelling’s T Statistic. AppliedMath. 2022; 2(3):446-456. https://doi.org/10.3390/appliedmath2030025
Chicago/Turabian StyleOuimet, Frédéric. 2022. "Local Normal Approximations and Probability Metric Bounds for the Matrix-Variate T Distribution and Its Application to Hotelling’s T Statistic" AppliedMath 2, no. 3: 446-456. https://doi.org/10.3390/appliedmath2030025
APA StyleOuimet, F. (2022). Local Normal Approximations and Probability Metric Bounds for the Matrix-Variate T Distribution and Its Application to Hotelling’s T Statistic. AppliedMath, 2(3), 446-456. https://doi.org/10.3390/appliedmath2030025





