A Computational Fluid Dynamics Study of Flared Gas for Enhanced Oil Recovery Using a Micromodel
Abstract
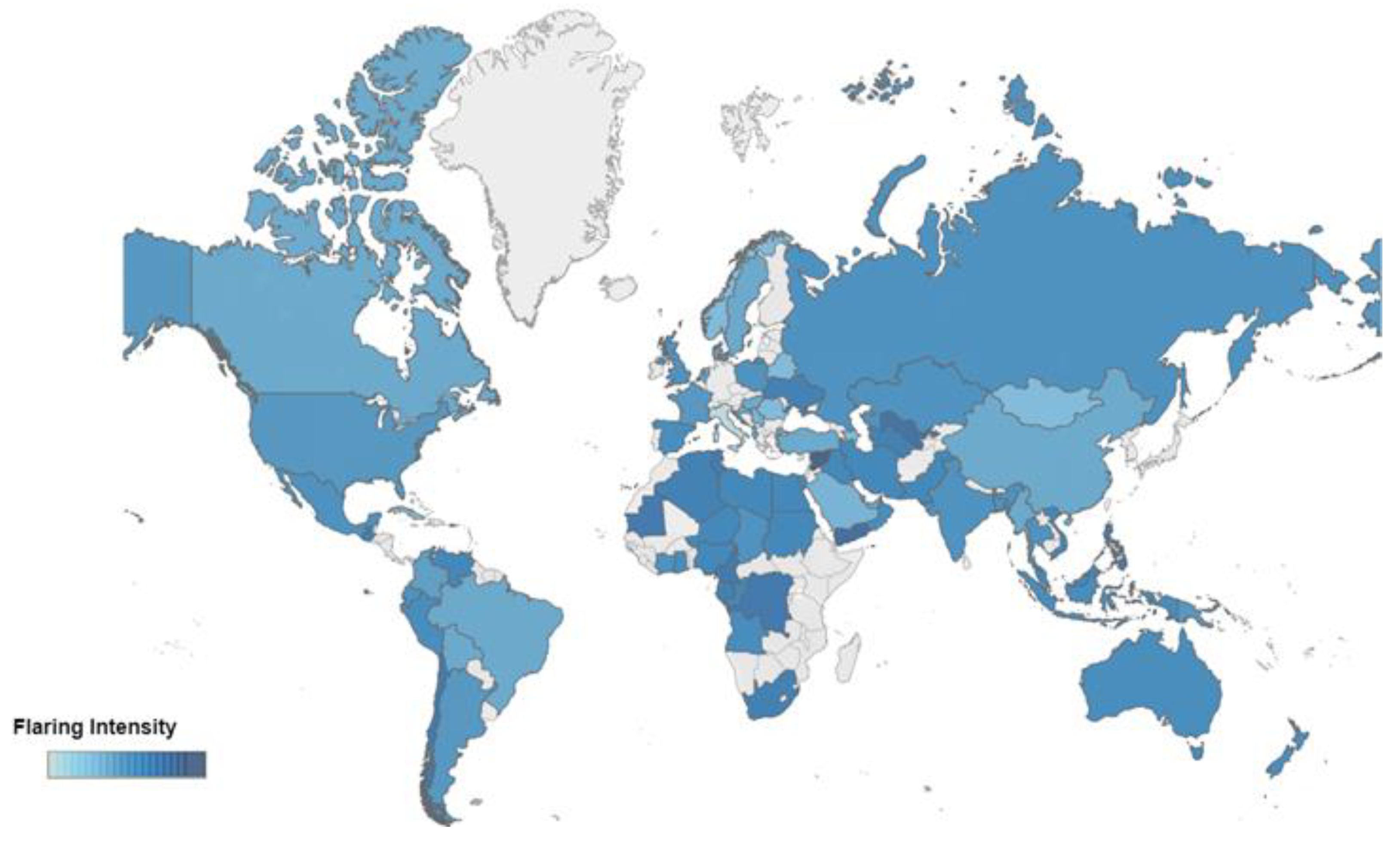
:1. Introduction
2. Methodology
2.1. Geometry
2.2. Mesh Generation
2.3. Boundary Conditions
2.4. Governing Equations
2.5. Viscous Model
2.6. Solution Methods
2.7. Case Studies
3. Results
3.1. Mesh Independence Study
3.2. Model Comparison
3.3. Inlet Pressure Profile
3.4. Oil Displacement
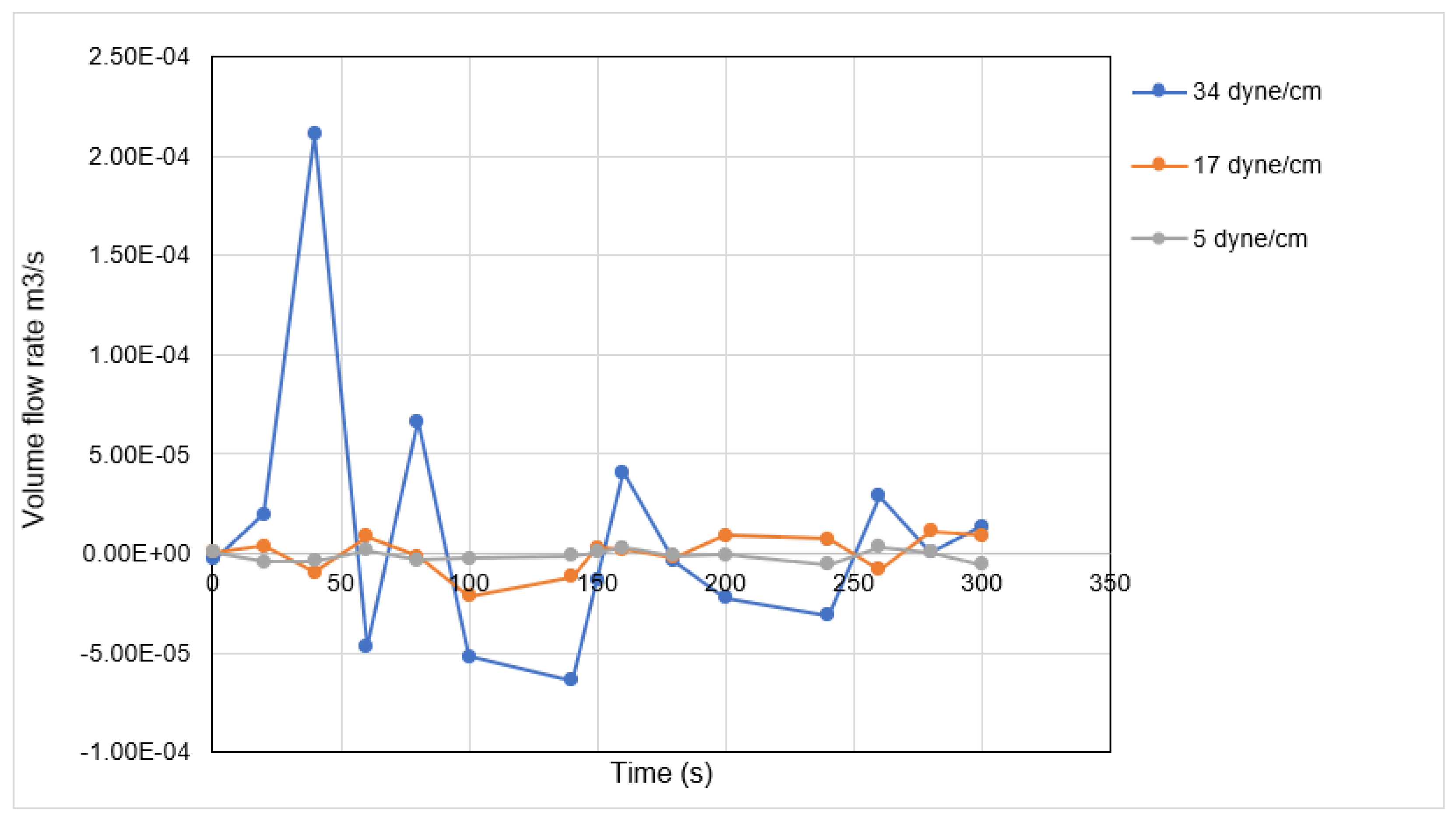
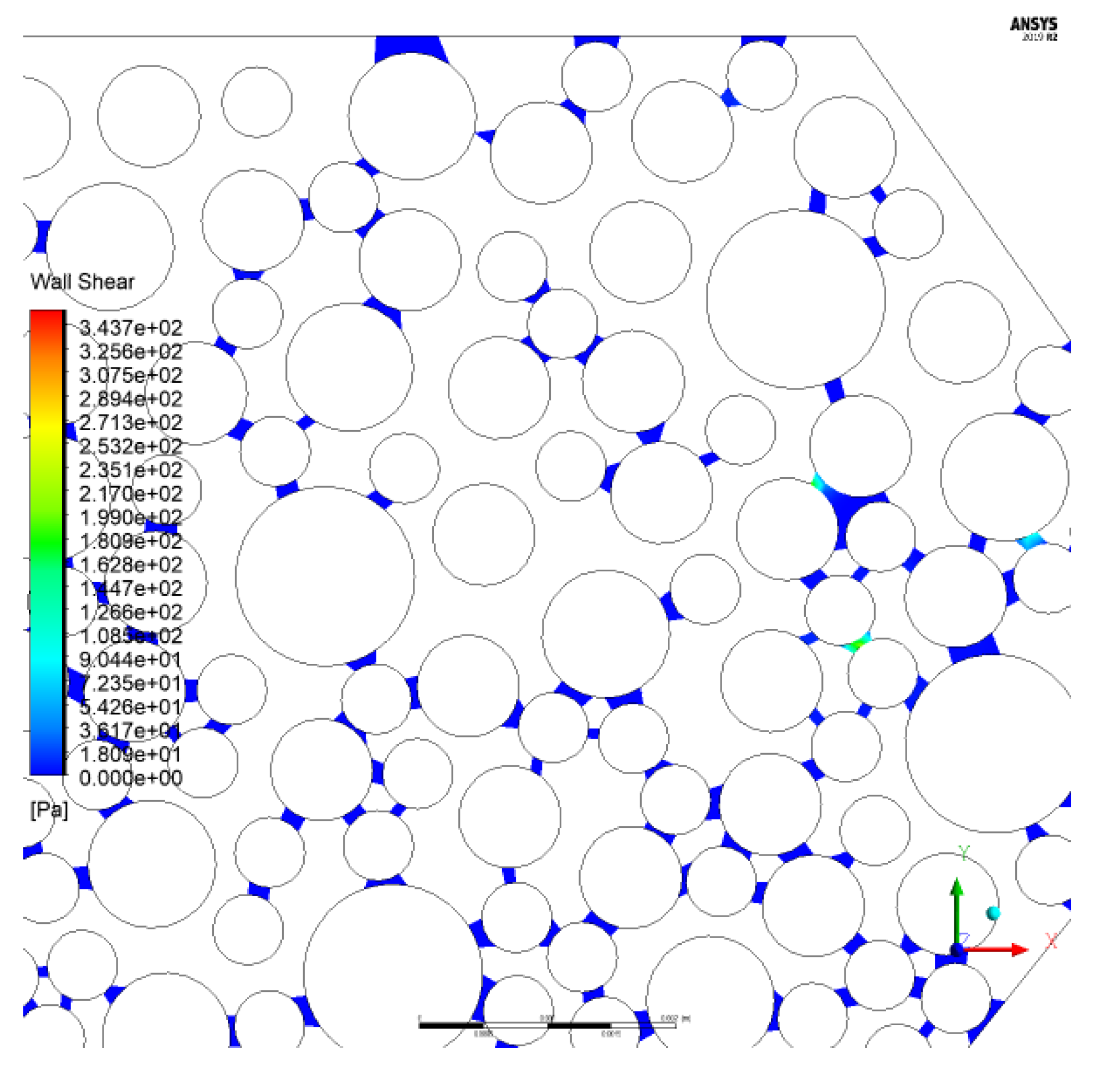
3.5. Pressure and Shear Stress
3.6. Oil Recovery
3.7. Effect of Injection Fluid Velocity
3.8. Discussion
4. Conclusions
5. Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Acronyms
| APG | Associated Petroleum Gas |
| CFD | Computational Fluid Dynamics |
| EOR | Enhanced Oil Recovery |
| GGFP | Global Gas Flaring Partnership |
| IFT | Interfacial tension |
| IRR | Internal Rate of Return |
| VOF | Volume of Fluid |
| OOIP | Original Oil in Place |
| RANS | Reynolds-Averaged Navier–Stokes equation |
| WAG | Water Alternating Gas |
| MMP | Minimum Miscibility Pressure |
References
- U.S. Department of Energy; Office of Oil and Natural Gas. Natural Gas Flaring and Venting: State and Federal Regulatory Overview, Trends, and Impacts; U.S. Department of Energy: Washington, DC, USA, 2019. [Google Scholar]
- Umukoro, G.E.; Ismail, O.S. Modelling Emissions from Natural Gas Flaring. J. King Saud Univ.-Eng. Sci. 2017, 29, 178–182. [Google Scholar] [CrossRef] [Green Version]
- Emam, E.A. GAS Flaring in Industry: An Overview. Pet. Coal 2015, 57, 532–555. [Google Scholar]
- Bamji, Z. Global Gas Flaring Inches Higher for the First Time in Five Years. Available online: https://blogs.worldbank.org/opendata/global-gas-flaring-inches-higher-first-time-five-years (accessed on 7 June 2020).
- Zyryanova, M.M.; Snytnikov, P.V.; Amosov, Y.I.; Belyaev, V.D.; Kireenkov, V.V.; Kuzin, N.A.; Vernikovskaya, M.V.; Kirillov, V.A.; Sobyanin, V.A. Upgrading of Associated Petroleum Gas into Methane-Rich Gas for Power Plant Feeding Applications. Technological and Economic Benefits. Fuel 2013, 108, 282–291. [Google Scholar] [CrossRef]
- Rajović, V.; Kiss, F.; Maravić, N.; Bera, O. Environmental Flows and Life Cycle Assessment of Associated Petroleum Gas Utilization via Combined Heat and Power Plants and Heat Boilers at Oil Fields. Energy Convers Manag. 2016, 118, 96–104. [Google Scholar] [CrossRef]
- Arutyunov, V.S.; Shmelev, V.M.; Sinev, M.Y.; Shapovalova, O.V. Syngas and Hydrogen Production in a Volumetric Radiant Burner. Chem. Eng. J. 2011, 176–177, 291–294. [Google Scholar] [CrossRef]
- Dolinskii, S.E. Economically Attractive Technologies of Deep Conversion of Associated Petroleum Gas. Russ. J. Gen. Chem. 2011, 81, 2574–2593. [Google Scholar] [CrossRef]
- Agboola, O.M.; Nwulu, N.I.; Egelioglu, F.; Agboola, O.P. Gas Flaring in Nigeria: Opportunity for Household Cooking Utilization. Int. J. Therm. Environ. Eng. 2010, 2, 69–74. [Google Scholar] [CrossRef]
- Gur’yanov, A.I.; Evdokimov, O.A.; Piralishvili, S.A.; Veretennikov, S.V.; Kirichenko, R.E.; Ievlev, D.G. Analysis of the Gas Turbine Engine Combustion Chamber Conversion to Associated Petroleum Gas and Oil. Russ. Aeronaut. 2015, 58, 205–209. [Google Scholar] [CrossRef]
- Calderón, A.J.; Pekney, N.J. Optimization of Enhanced Oil Recovery Operations in Unconventional Reservoirs. Appl. Energy 2020, 258, 114072. [Google Scholar] [CrossRef]
- Green, D.W.; Willhite, P.G. Enhanced Oil Recovery, 2nd ed.; Society of Petroleum Engineers: Richardson, TX, USA, 1990; ISBN 9781613994948. [Google Scholar]
- Ahmadi, M.A.; Shadizadeh, S.R. Nano-Surfactant Flooding in Carbonate Reservoirs: A Mechanistic Study; Springer: Berlin/Heidelberg, Germany, 2017; Volume 132, ISBN 9781555633059. [Google Scholar]
- Leach, A.; Mason, C.F.; Van, K. Co-Optimization of Enhanced Oil Recovery and Carbon Sequestration. Resour. Energy Econ. 2011, 33, 893–912. [Google Scholar] [CrossRef] [Green Version]
- Jin, L.; Hawthorne, S.; Sorensen, J.; Pekot, L.; Bosshart, N.; Gorecki, C.; Steadman, E.; Harju, J. Utilization of Produced Gas for Improved Oil Recovery and Reduced Emissions from the Bakken Formation. In Proceedings of the Society of Petroleum Engineers-SPE Health, Safety, Security, Environment, and Social Responsibility Conference-North America, Orleans, LA, USA, 18–20 April 2017; pp. 451–458. [Google Scholar]
- Hoffman, B.T. Comparison of Various Gases for Enhanced Recovery from Shale Oil Reservoirs. In Proceedings of the Improved Oil Recovery Symposium, Tulsa, OK, USA, 14–18 April 2012; pp. 1–8. [Google Scholar]
- Farouq Ali, S.M.; Thomas, S. The Promise and Problems of Enhanced Oil Recovery Methods. J. Can. Pet. Technol. 1996, 35, 57–63. [Google Scholar] [CrossRef]
- Jin, L.; Pekot, L.J.; Hawthorne, S.B.; Salako, O.; Peterson, K.J.; Bosshart, N.W.; Jiang, T.; Hamling, J.A.; Gorecki, C.D. Evaluation of Recycle Gas Injection on CO2 Enhanced Oil Recovery and Associated Storage Performance. Int. J. Greenh. Gas Control 2018, 75, 151–161. [Google Scholar] [CrossRef]
- Srivastava, R.K.; Huang, S.S.; Dong, M. Comparative Effectiveness of CO2, Produced Gas, and Flue Gas for Enhanced Heavy-Oil Recovery. SPE Reserv. Eval. Eng. 1999, 2, 238–247. [Google Scholar] [CrossRef]
- Yin, D.D.; Li, Y.Q.; Zhao, D.F. Utilization of Produced Gas of CO2 Flooding to Improve Oil Recovery. J. Energy Inst. 2014, 87, 289–296. [Google Scholar] [CrossRef]
- Alvarado, V.; Manrique, E. Enhanced Oil Recovery: An Update Review. Energies 2010, 3, 1529. [Google Scholar] [CrossRef]
- Ahmadi, Y.; Eshraghi, S.E.; Bahrami, P.; Hasanbeygi, M.; Kazemzadeh, Y.; Vahedian, A. Comprehensive Water-Alternating-Gas (WAG) Injection Study to Evaluate the Most Effective Method Based on Heavy Oil Recovery and Asphaltene Precipitation Tests. J. Pet. Sci. Eng. 2015, 133, 123–129. [Google Scholar] [CrossRef]
- Yu, H.; Chen, Z.; Lu, X.; Cheng, S.; He, Y.; Shi, L.; Xian, B.; Shi, T. Experimental Study on EOR Performance of Natural Gas Injection in Tight Oil Reservoirs. IOP Conf. Ser. Earth Environ. Sci. 2019, 252, 052021. [Google Scholar] [CrossRef]
- Thomas, F.B.; Holowach, N.; Zhou, X.; Bennion, D.B.; Bennion, D.W. SPE/DOE 27811 Miscible or Near-Miscible Gas Injection, Which Is Better? In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 17–20 April 1994.
- Kamari, E.; Rashtchian, D.; Shadizadeh, S.R. Micro-Model Experimental Study of Fracture Geometrical Effect on Breakthrough Time in Miscible Displacement Process. Iran. J. Chem. Chem. Eng. 2011, 30, 1–7. [Google Scholar]
- Gharibshahi, R.; Jafari, A.; Ahmadi, H. CFD Investigation of Enhanced Extra-Heavy Oil Recovery Using Metallic Nanoparticles/Steam Injection in a Micromodel with Random Pore Distribution. J. Pet. Sci. Eng. 2019, 174, 374–383. [Google Scholar] [CrossRef]
- Sohrabi, M.; Tehrani, D.H.; Danesh, A.; Henderson, G.D. Visualization of Oil Recovery by Water-Alternating-Gas Injection Using High-Pressure Micromodels. SPE J. 2004, 9, 290–301. [Google Scholar] [CrossRef]
- Zhong, H.; Li, Y.; Zhang, W.; Li, D. Study on Microscopic Flow Mechanism of Polymer Flooding. Arab. J. Geosci. 2019, 12, 56. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of Fluid (VOF) Method for the Dynamics of Free Boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hornbrook, J.W.; CastaJnier, L.M.; Pettit, P.A. Observation of Foam/Oil Interactions in a New, High-Resolution Micromodel. In Proceedings of the 66th Annual Technical Conference and Exibition of the Society of Petroleum Engineers, Dallas, TX, USA, 6–9 October 1991; pp. 377–382. [Google Scholar]
- Clemens, T.; Tsikouris, K.; Buchgraber, M.; Castanier, L.; Kovscek, A. Pore-Scale Evaluation of Polymers Displacing Viscous Oil-Computational- Fluid-Dynamics Simulation of Micromodel Experiments. SPE Reserv. Eval. Eng. 2013, 16, 144–154. [Google Scholar] [CrossRef]
- Renardy, Y.; Renardy, M. PROST: A Parabolic Reconstruction of Surface Tension for the Volume-of-Fluid Method. J. Comput. Phys. 2002, 183, 400–421. [Google Scholar] [CrossRef] [Green Version]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling Two-Phase Flow in Porous Media at the Pore Scale Using the Volume-of-Fluid Method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Soh, G.Y.; Yeoh, G.H.; Timchenko, V. A CFD Model for the Coupling of Multiphase, Multicomponent and Mass Transfer Physics for Micro-Scale Simulations. Int. J. Heat Mass Transf. 2017, 113, 922–934. [Google Scholar] [CrossRef] [Green Version]
- Doorwar, S.; Mohanty, K.K. Viscous Fingering during Non-Thermal Heavy Oil Recovery. In Proceedings of the SPE 146841-MS, Proceedings of the SPE Annual Technical Conference and Exibition, Denver, CO, USA, 30 October–2 November 2011. [Google Scholar]
- Ahmadi, P.; Ghandi, E.; Riazi, M.; Malayeri, M.R. Experimental and CFD Studies on Determination of Injection and Production Wells Location Considering Reservoir Heterogeneity and Capillary Number. Oil Gas Sci. Technol. 2019, 74, 4. [Google Scholar] [CrossRef] [Green Version]
- Jafari, A.; Pour, S.E.F.; Gharibshahi, R. CFD Simulation of Biosurfactant Flooding into a Micromodel for Enhancing the Oil Recovery. Int. J. Chem. Eng. Appl. 2016, 7, 353–358. [Google Scholar] [CrossRef] [Green Version]
- UNITROVE Natural Gas Density Calculator. Available online: https://www.unitrove.com/engineering/tools/gas/natural-gas-density (accessed on 4 June 2020).
- Watts, D. Interfacial Tension. Available online: https://petrowiki.org/Interfacial_tension (accessed on 14 December 2022).
- Dalvand, K.; Heydarian, A. Determination of Gas-Oil Interfacial Tension. Energy Sources Part A Recovery Util. Environ. Eff. 2015, 37, 1790–1796. [Google Scholar] [CrossRef]
- Wu, Y.S. Multiphase Fluid Flow in Porous and Fractured Reservoirs; Gulf Professional Publishing: Houston, TX, USA, 2015; ISBN 9780128038482. [Google Scholar]
- Chen, Z.; Huan, G.; Ma, Y. Computational Methods for Multiphase Flows in Porous Media; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2006; Volume 2, ISBN 0898716063. [Google Scholar]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics, 3rd ed.; Springer International Publishing: Stanford, CA, USA, 2002; ISBN 3540420746. [Google Scholar]
- Shahmohammadi, A.; Jafari, A. Application of Different CFD Multiphase Models to Investigate Effects of Baffles and Nanoparticles on Heat Transfer Enhancement. Front. Chem. Sci. Eng. 2014, 8, 320–329. [Google Scholar] [CrossRef]
- Chung, T.J. Computational Fluid Dynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2002; ISBN 9780521595353. [Google Scholar]
- Jafari, A.; Hasani, M.; Hosseini, M.; Gharibshahi, R. Application of CFD Technique to Simulate Enhanced Oil Recovery Processes: Current Status and Future Opportunities. Pet. Sci. 2020, 17, 434–456. [Google Scholar] [CrossRef] [Green Version]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A Continuum Method for Modeling Surface Tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Wood, B.D.; He, X.; Apte, S.V. Modeling Turbulent Flows in Porous Media. Annu. Rev. Fluid Mech. 2020, 52, 171–203. [Google Scholar] [CrossRef] [Green Version]
- Meybodi, H.E.; Kharrat, R.; Ghazanfari, M.H. Effect of Heterogeneity of Layered Reservoirs on Polymer Flooding: An Experimental Approach Using Five-Spot Glass Micromodel. In Proceedings of the 2008 SPE Europec/EAGE Annual Conference and Exibition, Rome, Italy, 9–12 June 2008. [Google Scholar]
- Hauhs, F.; Födisch, H.; Hincapie, R.E.; Ganzer, L. Novel Evaluation of Foam and Immiscible Gas Flooding in Glass-Silicon-Glass Micromodels. In Proceedings of the 80th EAGE Conference and Exhibition, Copenhagen, Denmark, 11–14 June 2018. [Google Scholar]
- Gharibshahi, R.; Jafari, A.; Haghtalab, A.; Karambeigi, M.S. Application of CFD to Evaluate the Pore Morphology Effect on Nanofluid Flooding for Enhanced Oil Recovery. RSC Adv. 2015, 5, 28938–28949. [Google Scholar] [CrossRef]
- Chatzis, I.; Dullien, F.A.L. Dynamic Immiscible Displacement Mechanisms in Pore Doublets: Theory versus Experiment. J. Colloid Interface Sci. 1983, 91, 199–222. [Google Scholar] [CrossRef]
- Mohammadi, S.; Khalili, M.; Mehranfar, M. The Optimal Conditions for the Immiscible Gas Injection Process: A Simulation Study. Pet. Sci. Technol. 2014, 32, 225–239. [Google Scholar] [CrossRef]
- Sohrabi, M.; Danesh, A.; Tehrani, D.H.; Jamiolahmady, M. Microscopic Mechanisms of Oil Recovery by Near-Miscible Gas Injection. Transp. Porous Media 2008, 72, 351–367. [Google Scholar] [CrossRef]
- Firoozabadi, A.; Katz, D.L.; Soroosh, H.; Sajjadian, V.A. Surface Tension of Reservoir Crude-Oil/Gas Systems Recognizing the Asphalt in the Heavy Fraction. SPE Reserv. Eng. (Soc. Pet. Eng.) 1988, 3, 265. [Google Scholar] [CrossRef]
- Shariatpanahi, S.F.; Dastyari, A.; Bashukooh, B.; Haghighi, M.; Sahimi, M.; Ayatollahi, S.S. Visualization Experiments on Immiscible Gas and Water Injection by Using 2D-Fractured Glass Micromodels. In Proceedings of the 14 th SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 12–15 March 2005; pp. 907–915. [Google Scholar]
- Danesh, A.; Krinis, D.; Henderson, G.D.; Peden, J.M. Pore-Level Visual Investigation of Miscible and Immiscible Displacements. J. Pet. Sci. Eng. 1989, 2, 167–177. [Google Scholar] [CrossRef]


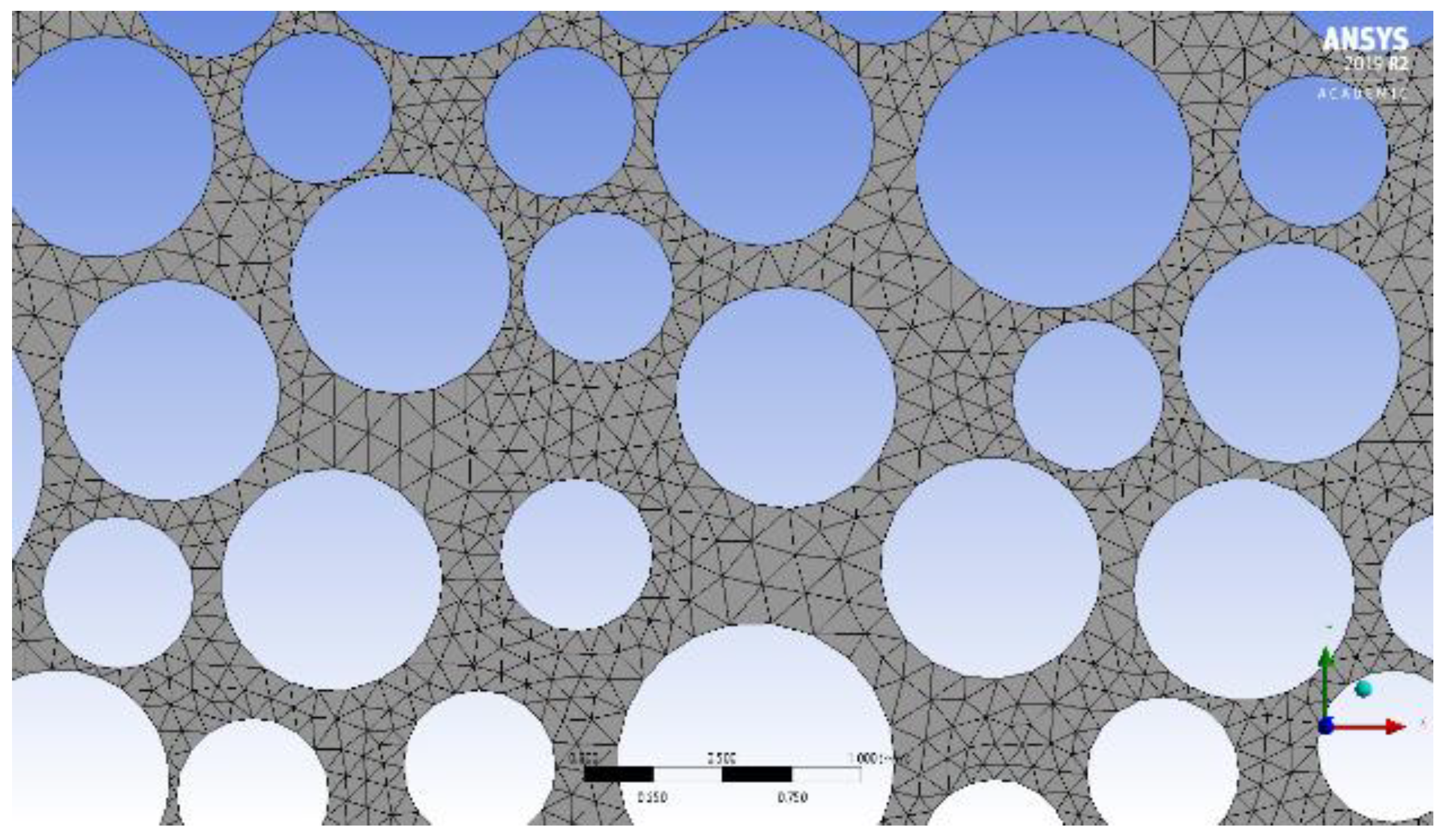
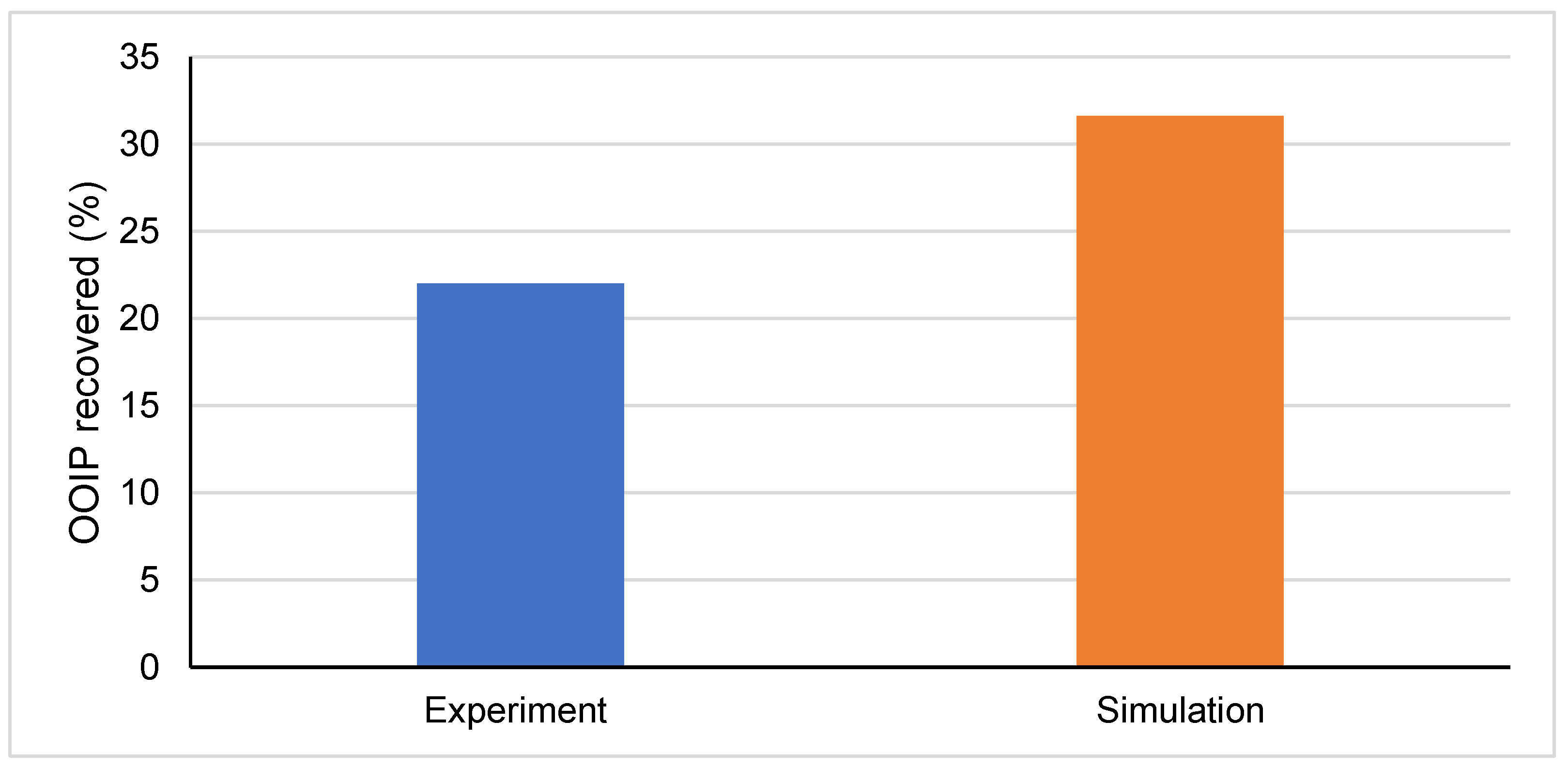










| Diameter (mm) | Number | Percentage Area (%) |
|---|---|---|
| 1.4 | 10 | 35 |
| 1.0 | 19 | 35 |
| 0.8 | 69 | 15 |
| 0.6 | 124 | 15 |
| Case No. | IFT (N/m) | Gas Injection Velocity (m/s) |
|---|---|---|
| 1 | 0.034 | 1 × 10−3 |
| 2 | 0.017 | 1 × 10−3 |
| 3 | 0.005 | 1 × 10−3 |
| 4 | 0.034 | 1 × 10−4 |
| 5 | 0.034 | 1 × 10−6 |
| Grid No. | No. of Cells | DP (Pa) | Relative Error (%) |
|---|---|---|---|
| Grid 1 | 13,950 | 0.2276 | 4.6573 |
| Grid 2 | 17,217 | 0.2382 | |
| 5.2477 | |||
| Grid 3 | 42,210 | 0.2507 |
| Case No. | Injection Rate (m/s) | Oil Recovery (% OOIP) |
|---|---|---|
| Case 1 | 1 × 10−3 | 31.6 |
| Case 4 | 1 × 10−4 | 27.3 |
| Case 5 | 1 × 10−6 | 29.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Were, S.; Nnabuife, S.G.; Kuang, B. A Computational Fluid Dynamics Study of Flared Gas for Enhanced Oil Recovery Using a Micromodel. AppliedMath 2022, 2, 738-757. https://doi.org/10.3390/appliedmath2040044
Were S, Nnabuife SG, Kuang B. A Computational Fluid Dynamics Study of Flared Gas for Enhanced Oil Recovery Using a Micromodel. AppliedMath. 2022; 2(4):738-757. https://doi.org/10.3390/appliedmath2040044
Chicago/Turabian StyleWere, Stephanie, Somtochukwu Godfrey Nnabuife, and Boyu Kuang. 2022. "A Computational Fluid Dynamics Study of Flared Gas for Enhanced Oil Recovery Using a Micromodel" AppliedMath 2, no. 4: 738-757. https://doi.org/10.3390/appliedmath2040044
APA StyleWere, S., Nnabuife, S. G., & Kuang, B. (2022). A Computational Fluid Dynamics Study of Flared Gas for Enhanced Oil Recovery Using a Micromodel. AppliedMath, 2(4), 738-757. https://doi.org/10.3390/appliedmath2040044








