A Sequence of Cohen–Macaulay Standard Graded Domains Whose h-Vectors Have Exponentially Deep Flaws

Abstract

Let $\mathbb{K}$ be a field. In this paper, we construct a sequence of Cohen–Macaulay standard graded $\mathbb{K}$-domains whose h-vectors are non-flawless and have exponentially deep flaws.

1. Introduction

In 1989, Hibi [1] made several conjectures on the h-vectors of Cohen–Macaulay standard graded algebras over a field. In particular, he conjectured that the h-vector of a standard graded Cohen–Macaulay domain is flawless ([1], Conjecture 1.4). The h-vector $(h_0,h_1,\dots ,h_s)$, $h_s\ne 0$, of a Cohen–Macaulay standard graded algebra is flawless if $h_i\le h_{s-i}$ for $0\le i\le \lfloor s/2\rfloor$ and $h_{i-1}\le h_i$ for $1\le i\le \lfloor s/2\rfloor$. Niesi and Robbiano [2] disproved this conjecture by constructing a Cohen–Macaulay standard graded domain whose h-vector is $(1,3,5,4,4,1)$. Further, Hibi and Tsuchiya [3] showed that the Ehrhart rings of the stable-set polytopes of cycle graphs of length 9 and 11 have non-flawless h-vectors by computation using the software Normaliz [4]. Moreover, the present author showed that the Ehrhart ring of the stable-set polytope of any odd cycle graph whose length is at least 9 has non-flawless h-vectors ([5], Theorem 5.2) by proving the conjecture of Hibi and Tsuchiya ([3], Conjecture 1).

However, these examples have the slightest flaws, i.e., there exists i with $0\le i\le \lfloor s/2\rfloor$ and $h_i=h_{s-i}+1$. In this paper, we construct a sequence of standard graded Cohen–Macaulay domains that have h-vectors with exponentially deep flaws, i.e., we show the following.

Theorem 1. 

Let $\mathbb{K}$ be a field and ℓ an integer with $\ell \ge 2$. Then, there exists a standard graded Cohen–Macaulay domain $A^{\langle \ell \rangle }$ over $\mathbb{K}$ such that $dim{A}^{\langle \ell \rangle }=8\ell -3$, $a\left(A^{\langle \ell \rangle }\right)=-4$, and an h-vector $(h_0,h_1,\dots ,h_{s_{\ell }})$, $h_{s_{\ell }}\ne 0$, with $h_{\lfloor s_{\ell }/2\rfloor }=h_{s_{\ell }-\lfloor s_{\ell }/2\rfloor }+2^{2\ell -3}$. In particular, $A^{\langle 2\rangle }$, $A^{\langle 3\rangle }$, …is a sequence of Cohen–Macaulay standard graded domains over $\mathbb{K}$ who have exponentially deep flaws.

This theorem is proved at the end of this paper.

2. Preliminaries

In this section, we establish notation and terminology. For unexplained terminology of commutative algebra and graphy theory we consult [6] and [7], respectively.

In this paper, all rings and algebras are assumed to be commutative with an identity element. Further, all graphs are assumed to be finite, simple and without loops. We denote the set of non-negative integers, the set of integers, the set of rational numbers, the set of real numbers and the set of non-negative real numbers by $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$ and ${\mathbb{R}}_{\ge 0}$, respectively.

For a set X, the cardinality of X is denoted by $\#X$. For sets X and Y, we define $X⧵Y:=\{x\in X\mid x\notin Y\}$. For non-empty sets X and Y, we denote the set of maps from X to Y by $Y^X$. If $Y_1$ is a subset of $Y_2$, then we treat $Y_1^X$ as a subset of $Y_2^X$. If X is a finite set, we identify ${\mathbb{R}}^X$ with the Euclidean space ${\mathbb{R}}^{\#X}$. For f, $f_1$, $f_2\in {\mathbb{R}}^X$ and $a\in \mathbb{R}$, we define maps $f_1\pm f_2$ and $af$ by $(f_1\pm f_2)\left(x\right)=f_1\left(x\right)\pm f_2\left(x\right)$ and $\left(af\right)\left(x\right)=a\left(f\right(x\left)\right)$, for $x\in X$. Let A be a subset of X. We define the characteristic function ${\chi }_A\in {\mathbb{R}}^X$ of A by ${\chi }_A\left(x\right)=1$ for $x\in A$ and ${\chi }_A\left(x\right)=0$ for $x\in X⧵A$. We denote the zero map, i.e., a map which sends all elements of X to 0, by 0. Further, if $X_1$ is a subset of X, then we treat ${\mathbb{R}}^{X_1}$ as a coordinate subspace of ${\mathbb{R}}^X$, i.e., we identify ${\mathbb{R}}^{X_1}$ with $\{f\in {\mathbb{R}}^X\mid f\left(x\right)=0$ for any $x\in X⧵X_1\}$. For a non-empty subset $\mathcal{X}$ of ${\mathbb{R}}^X$, the convex hull (resp. affine span) of $\mathcal{X}$ is denoted by $\mathrm{conv}\mathcal{X}$ (resp. $\mathrm{aff}\mathcal{X}$).

Definition 1. 

Let X be a finite set and $\xi \in {\mathbb{R}}^X$. For $B\subset X$, we set ${\xi }^{+}\left(B\right):={\sum }_{b\in B}\xi \left(b\right)$.

For a field $\mathbb{K}$, the polynomial ring with n variables over $\mathbb{K}$ is denoted by ${\mathbb{K}}^{\left[n\right]}$. Let $R={⨁}_{n\in \mathbb{N}}{R}_n$ be an $\mathbb{N}$-graded ring. We say that R is a standard graded $\mathbb{K}$-algebra if $R_0=\mathbb{K}$ and R is generated by $R_1$ as a $\mathbb{K}$-algebra. Let $R={⨁}_{n\in \mathbb{N}}{R}_n$ and $S={⨁}_{n\in \mathbb{N}}{S}_n$ be $\mathbb{N}$-graded rings with $R_0=S_0=\mathbb{K}$. We denote the Segre product ${⨁}_{n\in \mathbb{N}}{R}_n{\otimes }_{\mathbb{K}}{S}_n$ of R and S by $R\#S$.

Let Y be a finite set. Suppose that there is a family ${\left\{T_y\right\}}_{y\in Y}$ of indeterminates indexed by Y. For $f\in {\mathbb{Z}}^Y$, the Laurent monomial, ${\prod }_{y\in Y}{T}_y^{f\left(y\right)}$, is denoted by $T^f$. A convex polyhedral cone in ${\mathbb{R}}^Y$ is a set C of the form $C={\mathbb{R}}_{\ge 0}{a}_1+\cdots +{\mathbb{R}}_{\ge 0}{a}_r$, where $a_1$, …, $a_r\in {\mathbb{R}}^Y$. If one can take $a_1$, …, $a_r\in {\mathbb{Q}}^Y$, we say that C is rational.

Let C be a rational convex polyhedral cone. For a field $\mathbb{K}$, we define $\mathbb{K}[{\mathbb{Z}}^Y\cap C]$ by $\mathbb{K}[{\mathbb{Z}}^Y\cap C]:={⨁}_{f\in {\mathbb{Z}}^Y\cap C}\mathbb{K}{T}^f$. By Gordon’s lemma, we see that $\mathbb{K}[{\mathbb{Z}}^Y\cap C]$ is a finitely generated $\mathbb{K}$-algebra. In particular, $\mathbb{K}[{\mathbb{Z}}^Y\cap C]$ is Noetherian. Further, by the result of Hochster [8], we see that $\mathbb{K}[{\mathbb{Z}}^Y\cap C]$ is normal and Cohen–Macaulay.

A subspace W of ${\mathbb{R}}^Y$ is rational if there is a basis of W contained in ${\mathbb{Q}}^Y$. Let $W_1$ and $W_2$ be rational subspaces of ${\mathbb{R}}^Y$ with $W_1\cap W_2=\left\{0\right\}$ and $C_i$ be a rational convex polyhedral cone in $W_i$ for $i=1,2$. Then, $C_1+C_2$ is a rational convex polyhedral cone in ${\mathbb{R}}^Y$ that is isomorphic to the Cartesian product $C_1\times C_2$ and $\mathbb{K}[{\mathbb{Z}}^Y\cap (C_1+C_2)]\cong \mathbb{K}[{\mathbb{Z}}^Y\cap C_1]\otimes \mathbb{K}[{\mathbb{Z}}^Y\cap C_2]$.

Let X be a finite set and let $\mathcal{P}$ be a rational convex polytope in ${\mathbb{R}}^X$, i.e., a convex polytope in ${\mathbb{R}}^X$ whose vertices are in ${\mathbb{Q}}^X$. In addition, let $-\infty$ be a new element that is not contained in X. We set $X^{-}:=X\cup \{-\infty \}$. Further, we set $C\left(\mathcal{P}\right):={\mathbb{R}}_{\ge 0}\{f\in {\mathbb{R}}^{X^{-}}\mid f(-\infty )=1$, ${f|}_X\in \mathcal{P}\}$. Then, $C\left(\mathcal{P}\right)$ is a rational convex polyhedral cone in ${\mathbb{R}}^{X^{-}}$. We define the Ehrhart ring $E_{\mathbb{K}}\left[\mathcal{P}\right]$ of $\mathcal{P}$ over a field $\mathbb{K}$ by $E_{\mathbb{K}}\left[\mathcal{P}\right]:=\mathbb{K}[Z^{X^{-}}\cap C\left(\mathcal{P}\right)]$. We define $deg{T}_{-\infty }=1$ and $deg{T}_x=0$ for $x\in X$. Then, $E_{\mathbb{K}}\left[\mathcal{P}\right]$ is an $\mathbb{N}$-graded $\mathbb{K}$-algebra.

Note that if $W_1$ and $W_2$ are rational subspaces of ${\mathbb{R}}^X$ with $W_1\cap W_2=\left\{0\right\}$ and ${\mathcal{P}}_i$ is a rational convex polytope in $W_i$ for $i=1$, 2, then ${\mathcal{P}}_1+{\mathcal{P}}_2$ is a rational convex polytope in ${\mathbb{R}}^X$ that is isomorphic to the Cartesian product ${\mathcal{P}}_1\times {\mathcal{P}}_2$ and $E_{\mathbb{K}}[{\mathcal{P}}_1+{\mathcal{P}}_2]=E_{\mathbb{K}}\left[{\mathcal{P}}_1\right]\#E_{\mathbb{K}}\left[{\mathcal{P}}_2\right]$.

It is known that $dim{E}_{\mathbb{K}}\left[\mathcal{P}\right]=dim\mathcal{P}+1$. Moreover, by the description of the canonical module of a normal affine semigroup ring by Stanley ([9], p. 82), we have the following.

Lemma 1. 

The ideal

$$\underset{f\in {\mathbb{Z}}^{X^{-}}\cap \mathrm{relint}\left(C\left(\mathcal{P}\right)\right)}{⨁}\mathbb{K}{T}^f$$

of $E_{\mathbb{K}}\left[\mathcal{P}\right]$ is the canonical module of $E_{\mathbb{K}}\left[\mathcal{P}\right]$, where $\mathrm{relint}\left(C\right(\mathcal{P}\left)\right)$ denotes the interior of $C\left(\mathcal{P}\right)$ in the topological space $\mathrm{aff}\left(C\right(\mathcal{P}\left)\right)$.

The ideal of the above lemma is denoted by ${\omega }_{E_{\mathbb{K}}\left[\mathcal{P}\right]}$ and is called the canonical ideal of $E_{\mathbb{K}}\left[\mathcal{P}\right]$. Note that the a-invariant (cf. ([10], Definition 3.1.4)), $a\left(E_{\mathbb{K}}\left[\mathcal{P}\right]\right)$, of $E_{\mathbb{K}}\left[\mathcal{P}\right]$ is $-min\{f(-\infty )\mid f\in {\mathbb{Z}}^{X^{-}}\cap \mathrm{relint}\left(C\left(\mathcal{P}\right)\right)\}$.

A stable set of a graph $G=(V,E)$ is a subset S of V whose no two elements are adjacent. We treat the empty set as a stable set.

Definition 2. 

The stable-set polytope $\mathrm{STAB}\left(G\right)$ of a graph $G=(V,E)$ is

$$\mathrm{conv}\{{\chi }_S\in {\mathbb{R}}^V\mid S is a stable set of G\}.$$

Note that ${\chi }_{\left\{v\right\}}\in \mathrm{STAB}\left(G\right)$ for any $v\in V$ and ${\chi }_{\varnothing }\in \mathrm{STAB}\left(G\right)$. In particular, $dim\mathrm{STAB}\left(G\right)=\#V$.

We set

$$\mathrm{TSTAB}\left(G\right):=\{f\in {\mathbb{R}}^V|\begin{array}{l}0\le f(x\mathrm{)}\le 1 \mathrm{for} \mathrm{any} x\in V,f^{+}(e\mathrm{)}\le 1 \mathrm{for} \mathrm{any} e\in E\\ \mathrm{and} f^{+}(C\mathrm{)}\le \frac{\#C-1}{2} \mathrm{for} \mathrm{any} \mathrm{cycle} C\end{array}\}.$$

Then, $\mathrm{TSTAB}\left(G\right)$ is a rational convex polytope in ${\mathbb{R}}^V$ with $\mathrm{TSTAB}\left(G\right)\supset \mathrm{STAB}\left(G\right)$. If $\mathrm{TSTAB}\left(G\right)=\mathrm{STAB}\left(G\right)$, we say that G is t-perfect.

Let $G=(V,E)$ be an arbitrary graph and $n\in \mathbb{Z}$. Set $\mathcal{K}:=\{K\subset V\mid K$ is a clique and $\#K\le 3\}$. We define ${t\mathcal{U}}^{\left(n\right)}\left(G\right)$ by

$${t\mathcal{U}}^{\left(n\right)}\left(G\right):=\{\mu \in {\mathbb{Z}}^{V^{-}}|\begin{array}{l}\mu \left(z\right)\ge n \mathrm{for} \mathrm{any}z\in V,{\mu }^{+}\left(K\right)+n\le \mu (-\infty ) \mathrm{for}\\ \mathrm{any} \mathrm{maximal} \mathrm{element} \mathrm{of} \mathcal{K} \mathrm{and} {\mu }^{+}\left(C\right)+n\le \mu (-\infty ).\\ \frac{\#C-1}{2}\mathrm{for} \mathrm{any} \mathrm{odd} \mathrm{cycle} C \mathrm{without} \mathrm{chord} \mathrm{and} \mathrm{length} \mathrm{at}\\ \mathrm{least}5\end{array}\}.$$

We abbreviate ${t\mathcal{U}}^{\left(n\right)}\left(G\right)$ as ${t\mathcal{U}}^{\left(n\right)}$ if it is clear from the context.

By the definition of $E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G\right)\right]$, we see that

$$E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G\right)\right]=\underset{\mu \in {t\mathcal{U}}^{\left(0\right)}}{⨁}\mathbb{K}{T}^{\mu }.$$

Further, for $\mu \in {\mathbb{Z}}^{V^{-}}$, $\mu \in \mathrm{relint}\left(C\left(E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G\right)\right]\right)\right)$ if and only if $\mu \left(z\right)>0$, ${\mu }^{+}\left(K\right)<\mu (-\infty )$ and ${\mu }^{+}\left(C\right)<\mu (-\infty )·\frac{\#C-1}{2}$, where $z\in V$, K is a maximal element of $\mathcal{K}$ and C is an odd cycle without chords. However, since the values appearing in these inequalities are integers, these inequalities are equivalent to $\mu \left(z\right)\ge 1$, ${\mu }^{+}\left(K\right)+1\le \mu (-\infty )$ and ${\mu }^{+}\left(C\right)+1\le \mu (-\infty )·\frac{\#C-1}{2}$, respectively. Therefore, by Lemma 1, we see that

$${\omega }_{E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G\right)\right]}=\underset{\mu \in {t\mathcal{U}}^{\left(1\right)}}{⨁}\mathbb{K}{T}^{\mu }.$$

3. Construction

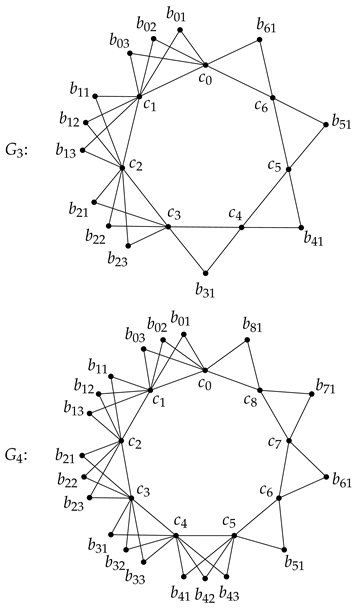
Let $\mathbb{K}$ be a field. In this section, for each integer $\ell \ge 2$, we construct a standard graded Cohen–Macaulay $\mathbb{K}$-algebra, $A^{\langle \ell \rangle }$, which has a non-flawless h-vector. The flaw of the h-vector is computed in the next section.

Let ℓ be an integer with $\ell \ge 2$. We define a graph $G_{\ell }=(V_{\ell },E_{\ell })$ by the following way. Set

$$\begin{array}{ccc}\hfill I_{\ell ,i}& :=& \left\{\begin{array}{cc}\{1,2,3\}\hfill & 0\le i\le 2\ell -4\hfill \\ \left\{1\right\}\hfill & 2\ell -3\le i\le 2\ell \hfill \end{array}\right.,\hfill \\ \hfill C_{\ell }& :=& \{c_0,c_1,\dots ,c_{2\ell }\},\hfill \\ \hfill B_{\ell }& :=& \{b_{ik}\mid 0\le i\le 2\ell ,k\in I_{\ell ,i}\},\hfill \\ \hfill V_{\ell }& :=& C_{\ell }\cup B_{\ell },\hfill \\ \hfill E_{\ell }& :=& \{\{c_i,c_j\}\mid j-i\equiv 1(mod2\ell +1)\}\cup \{\{c_i,b_{ik}\}\mid k\in I_{\ell ,i}\}\hfill \\ & & \cup \{\{c_j,b_{ik}\}\mid j-i\equiv 1(mod2\ell +1),k\in I_{\ell ,i}\}\hfill \\ \hfill \mathrm{and}\\ \hfill G_{\ell }& :=& (V_{\ell },E_{\ell }).\hfill \end{array}$$

The cases where $\ell =3$ and 4 are as follows.

In addition, set

$$A^{\langle \ell \rangle }:=E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G_{\ell }\right)\right]\mathrm{and}{R}^{\langle \ell \rangle }:=E_{\mathbb{K}}\left[\mathrm{TSTAB}\left(G\left(C_{\ell }\right)\right)\right],$$

where $G\left(C_{\ell }\right)$ is the induced subgraph of $G_{\ell }$ by $C_{\ell }$.

In the following, up to the end of the proof of Lemma 5, we fix ℓ and write $G_{\ell }$, $V_{\ell }$, $E_{\ell }$, $C_{\ell }$, $B_{\ell }$, $A^{\langle \ell \rangle }$, $R^{\langle \ell \rangle }$ and $I_{\ell ,i}$ as just G, V, E, C, B, A, R and $I_i$, respectively. Further, we consider the subscripts of $c_i$, $I_i$ and the first subscript of $b_{i,k}$ modulo $2\ell +1$. For example, $c_{2\ell +1}=c_0$, $I_{-2}=I_{2\ell -1}$ and $b_{-3,1}=b_{2\ell -2,1}$.

We set

$$e_i:=\{c_i,c_{i+1}\}\mathrm{and}{K}_{i,k}:=\{c_i,c_{i+1},b_{i,k}\}$$

for $0\le i\le 2\ell$ and $k\in I_i$. We also consider the subscript of $e_i$ and the first subscript of $K_{i,k}$ modulo $2\ell +1$.

We define ${\mu }_i^J\in {\mathbb{Z}}^{V^{-}}$ for $0\le i\le 2\ell$ and $J\subset I_{i-2}$ by

$${\mu }_i^J\left(z\right)=\left\{\begin{array}{cc}1\hfill & z=c_j\mathrm{for} \mathrm{some} j \mathrm{with} j-i\equiv 0,2,\dots ,2\ell -2(mod2\ell +\hfill \\ & 1),z=b_{i-2,k}\mathrm{with}k\in J \mathrm{or}z=-\infty ,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

It is easily verified that ${\mu }_i^J\in {t\mathcal{U}}^{\left(0\right)}$. We also consider the subscript of ${\mu }_i^J$ modulo $2\ell +1$. Note that ${\left({\mu }_i^J\right)}^{+}\left(C\right)=\ell$ and ${\left({\mu }_i^J\right)}^{+}\left(K_{j,k}\right)=1$ if $j\not\equiv i-2(mod2\ell +1)$ or $j\equiv i-2(mod2\ell +1)$ and $k\in J$. Otherwise, ${\left({\mu }_i^J\right)}^{+}\left(K_{j,k}\right)=0$.

First we show the following.

Proposition 1. 

The ring A is a standard graded $\mathbb{K}$-algebra.

Proof. 

Since

$$A=\underset{\mu \in {t\mathcal{U}}^{\left(0\right)}}{⨁}\mathbb{K}{T}^{\mu },$$

it is enough to show that for any $\mu \in {t\mathcal{U}}^{\left(0\right)}$ with $\mu (-\infty )=n>0$ there are ${\mu }_1$, …, ${\mu }_n\in {t\mathcal{U}}^{\left(0\right)}$ with ${\mu }_i(-\infty )=1$ for $1\le i\le n$ and $\mu ={\mu }_1+\cdots +{\mu }_n$ (i.e., $\mathrm{TSTAB}\left(G\right)$ has the integer decomposition property). We prove this fact by induction on n.

The case where $n=1$ is trivial. Suppose that $n>1$. We first consider the case where $\mu \left(c\right)>0$ for any $c\in C$. Since

$$\sum _{i=0}^{2\ell }{\mu }^{+}\left(e_i\right)=2{\mu }^{+}\left(C\right)\le 2\ell n<(2\ell +1)n,$$

we see that there exists j with ${\mu }^{+}\left(e_j\right)<n$. Set $J=\{k\mid \mu \left(b_{j,k}\right)>0\}$. Then, we claim that $\mu -{\mu }_{j+2}^J\in {t\mathcal{U}}^{\left(0\right)}$.

First, since $\mu \left(c\right)>0$ for any $c\in C$ by assumption and $\mu \left(b_{j,k}\right)>0$ for any $k\in J$, we see that $(\mu -{\mu }_{j+2}^J)\left(z\right)\ge 0$ for any $z\in V$.

Next let i be an integer with $0\le i\le 2\ell$ and $k\in I_i$. If $i\not\equiv j(mod2\ell +1)$ or $i\equiv j(mod2\ell +1)$ and $k\in J$, then ${\left({\mu }_{j+2}^J\right)}^{+}\left(K_{i,k}\right)=1$. Thus, ${(\mu -{\mu }_{j+2}^J)}^{+}\left(K_{i,k}\right)\le \mu (-\infty )-1=(\mu -{\mu }_{j+2}^J)(-\infty )$. If $i\equiv j(mod2\ell +1)$ and $k\notin J$, then ${\mu }^{+}\left(e_i\right)<n$ and $\mu \left(b_{i,k}\right)=0$. Therefore, ${(\mu -{\mu }_{j+2}^J)}^{+}\left(K_{i,k}\right)={\mu }^{+}\left(e_i\right)\le n-1=(\mu -{\mu }_{j+2}^J)(-\infty )$.

Finally, ${(\mu -{\mu }_{j+2}^J)}^{+}\left(C\right)={\mu }^{+}\left(C\right)-{\left({\mu }_{j+2}^J\right)}^{+}\left(C\right)\le n\ell -\ell =\ell (\mu -{\mu }_{j+2}^J)(-\infty )$. Therefore, $\mu -{\mu }_{j+2}^J\in {t\mathcal{U}}^{\left(0\right)}$.

Next, suppose that $\mu \left(c_i\right)=0$ for some i. Take $i_0$ with $\mu \left(c_{i_0}\right)=0$. We define ${\mu }^{\prime }\in {\mathbb{Z}}^{V^{-}}$ by the following way.

First, we define ${\mu }^{\prime }\left(c_{i_0+j}\right)$ ($0\le j\le 2\ell$) by induction on j. We define ${\mu }^{\prime }\left(c_{i_0+0}\right)=0$. Suppose that $1\le j\le 2\ell$ and for any $j^{\prime }$ with $0\le j^{\prime }\le j-1$, ${\mu }^{\prime }\left(c_{i_0+j^{\prime }}\right)$ is defined so that ${\mu }^{\prime }\left(c_{i_0+j^{\prime }}\right)\in \{0,1\}$, ${\mu }^{\prime }\left(c_{i_0+j^{\prime }}\right)\le \mu \left(c_{i_0+j^{\prime }}\right)$ for $0\le j^{\prime }\le j-1$, and ${\mu }^{\prime }\left(c_{i_0+j^{\prime }}\right)=1$ implies ${\mu }^{\prime }\left(c_{i_0+j^{\prime }+1}\right)=0$ for $0\le j^{\prime }\le j-2$ (these assumptions are trivially satisfied when $j=1$). We set

$${\mu }^{\prime }\left(c_{i_0+j}\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if} {\mu }^{\prime }\left(c_{i_0+j-1}\right)=0 \mathrm{and} \mu \left(c_{i_0+j}\right)>0,\hfill \\ 0\hfill & \mathrm{if} {\mu }^{\prime }\left(c_{i_0+j-1}\right)=1 \mathrm{or} \mu \left(c_{i_0+j}\right)=0.\hfill \end{array}\right.$$

Then, ${\mu }^{\prime }\left(c_{i_0+j}\right)\in \{0,1\}$, ${\mu }^{\prime }\left(c_{i_0+j}\right)\le \mu \left(c_{i_0+j}\right)$ and ${\mu }^{\prime }\left(c_{i_0+j-1}\right)=1$ implies ${\mu }^{\prime }\left(c_{i_0+j}\right)=0$. Thus, we can continue the induction procedure up to $j=2\ell$. We also set

$$\begin{array}{ccc}\hfill {\mu }^{\prime }\left(b_{i,k}\right)& =& \left\{\begin{array}{cc}1\hfill & \mathrm{if} {\mu }^{\prime }\left(c_i\right)={\mu }^{\prime }\left(c_{i+1}\right)=0 \mathrm{and} \mu \left(b_{i,k}\right)>0,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill {\mu }^{\prime }(-\infty )& =& 1\hfill \end{array}$$

and we define ${\mu }^{\prime }\in {\mathbb{Z}}^{V^{-}}$. Note that $\mathrm{Im}{\mu }^{\prime }\subset \{0,1\}$. Note also that ${\mu }^{\prime }\left(c_i\right)=1$ implies ${\mu }^{\prime }\left(c_{i+1}\right)=0$ and ${\mu }^{\prime }\left(c_i\right)=0$ implies ${\mu }^{\prime }\left(c_{i-1}\right)=1$ or $\mu \left(c_i\right)=0$, for any $i\in \mathbb{Z}$.

Next we prove that ${\mu }^{\prime }\in {t\mathcal{U}}^{\left(0\right)}$.

First since $\mathrm{Im}{\mu }^{\prime }\subset \{0,1\}$, we see that $\mu \left(z\right)\ge 0$ for any $z\in V$.

Next we show that ${\mu }^{\prime }\left(K_{i,k}\right)\le 1$, for any $i\in \mathbb{Z}$ and $k\in I_i$. First consider the case where ${\mu }^{\prime }\left(c_i\right)=1$. Then, ${\mu }^{\prime }\left(c_{i+1}\right)=0$. Further, ${\mu }^{\prime }\left(b_{i,k}\right)=0$ by the definition of ${\mu }^{\prime }$. Therefore, we see that ${\left({\mu }^{\prime }\right)}^{+}\left(K_{i,k}\right)=1$. Next, consider the case where ${\mu }^{\prime }\left(c_i\right)=0$. Since ${\mu }^{\prime }\left(b_{i,k}\right)\le 1$ and ${\mu }^{\prime }\left(c_{i+1}\right)=1$ implies that ${\mu }^{\prime }\left(b_{i,k}\right)=0$, we see that ${\left({\mu }^{\prime }\right)}^{+}\left(K_{i,k}\right)\le 1$.

Finally, since $\mathrm{Im}{\mu }^{\prime }\subset \{0,1\}$ and ${\mu }^{\prime }\left(c_i\right)=1$ implies ${\mu }^{\prime }\left(c_{i+1}\right)=0$ for any $i\in \mathbb{Z}$, we see that ${\left({\mu }^{\prime }\right)}^{+}\left(C\right)\le \ell =\ell {\mu }^{\prime }(-\infty )$. Thus, we see that ${\mu }^{\prime }\in {t\mathcal{U}}^{\left(0\right)}$.

Next, we prove that $\mu -{\mu }^{\prime }\in {t\mathcal{U}}^{\left(0\right)}$.

First, by the definition of ${\mu }^{\prime }$, we see that $\mu \left(z\right)=0$ implies ${\mu }^{\prime }\left(z\right)=0$ for any $z\in V$. Since ${\mu }^{\prime }\left(z\right)\in \{0,1\}$ for any $z\in V$, we see that $(\mu -{\mu }^{\prime })\left(z\right)\ge 0$ for any $z\in V$.

Next, we show that ${(\mu -{\mu }^{\prime })}^{+}\left(K_{i,k}\right)\le (\mu -{\mu }^{\prime })(-\infty )$ for any i and $k\in I_i$. If ${\left({\mu }^{\prime }\right)}^{+}\left(K_{i,k}\right)=1$, then ${(\mu -{\mu }^{\prime })}^{+}\left(K_{i,k}\right)={\mu }^{+}\left(K_{i,k}\right)-1\le \mu (-\infty )-1=(\mu -{\mu }^{\prime })(-\infty )$. Assume that ${\left({\mu }^{\prime }\right)}^{+}\left(K_{i,k}\right)=0$. Then, ${\mu }^{\prime }\left(c_i\right)={\mu }^{\prime }\left(c_{i+1}\right)={\mu }^{\prime }\left(b_{i,k}\right)=0$. Thus, we see that $\mu \left(b_{i,k}\right)=0$ by the definition of ${\mu }^{\prime }$. Since ${\mu }^{\prime }\left(c_{{ı}^{\prime }}\right)=0$ implies ${\mu }^{\prime }\left(c_{{ı}^{\prime }-1}\right)=1$ or $\mu \left(c_{{ı}^{\prime }}\right)=0$, for any ${ı}^{\prime }\in \mathbb{Z}$, we see that $\mu \left(c_{i+1}\right)=0$. If $\mu \left(c_i\right)=0$, then ${(\mu -{\mu }^{\prime })}^{+}\left(K_{i,k}\right)=0\le (\mu -{\mu }^{\prime })(-\infty )$. Suppose that $\mu \left(c_i\right)>0$. Then, ${\mu }^{\prime }\left(c_{i-1}\right)=1$ by the property of ${\mu }^{\prime }$ noted above. Therefore, $\mu \left(c_{i-1}\right)>0$. Since $\mu \left(c_{i-1}\right)+\mu \left(c_i\right)\le {\mu }^{+}\left(K_{i-1,1}\right)\le \mu (-\infty )$, we see that $\mu \left(c_i\right)\le \mu (-\infty )-1$. Therefore, ${(\mu -{\mu }^{\prime })}^{+}\left(K_{i,k}\right)=\mu \left(c_i\right)\le (\mu -{\mu }^{\prime })(-\infty )$.

Finally we show that ${(\mu -{\mu }^{\prime })}^{+}\left(C\right)\le \ell (\mu -{\mu }^{\prime })(-\infty )$. Since $\mu \left(c_{i_0}\right)={\mu }^{\prime }\left(c_{i_0}\right)=0$, we see that

$$\begin{array}{ccc}\hfill {(\mu -{\mu }^{\prime })}^{+}\left(C\right)& =& (\mu -{\mu }^{\prime })\left(c_{i_0}\right)+\sum _{j=1}^{\ell }{(\mu -{\mu }^{\prime })}^{+}\left(e_{i_0+2j-1}\right)\hfill \\ & =& \sum _{j=1}^{\ell }{(\mu -{\mu }^{\prime })}^{+}\left(e_{i_0+2j-1}\right)\hfill \\ & \le & \sum _{j=1}^{\ell }{(\mu -{\mu }^{\prime })}^{+}\left(K_{i_0+2j-1,1}\right)\hfill \\ & \le & \sum _{j=1}^{\ell }(\mu -{\mu }^{\prime })(-\infty )\hfill \\ & =& \ell (\mu -{\mu }^{\prime })(-\infty ).\hfill \end{array}$$

□

Remark 1. 

The functions ${\mu }_{j+2}^J$ and ${\mu }^{\prime }$ in the proof of Proposition 1 are the characteristic function of some stable set of G. Therefore, the above proof shows that G is a t-perfect graph.

4. Structure of the Canonical Module

In this section, we study the generators and the structure of the canonical module of A. First, we set

$$W:=\{f\in {\mathbb{R}}^{V^{-}}\mid f^{+}\left(C\right)=\ell f(-\infty )\}.$$

Then, W is a codimension 1 vector subspace of ${\mathbb{R}}^{V^{-}}$ with $W\supset {\mathbb{R}}^B$. Further, we set

$${t\mathcal{U}}_0^{\left(0\right)}={t\mathcal{U}}_0^{\left(0\right)}\left(G\right):=\{\mu \in {t\mathcal{U}}^{\left(0\right)}\left(G\right)\mid {\mu }^{+}\left(C\right)=\ell \mu (-\infty )\},$$

$${t\mathcal{U}}_0^{\left(0\right)}\left(G\left(C\right)\right):=\{\mu \in {t\mathcal{U}}^{\left(0\right)}\left(G\left(C\right)\right)\mid {\mu }^{+}\left(C\right)=\ell \mu (-\infty )\}$$

and

$$A^{\left(0\right)}:=\underset{\mu \in {t\mathcal{U}}_0^{\left(0\right)}}{⨁}\mathbb{K}{T}^{\mu }.$$

Then, $A^{\left(0\right)}$ is a $\mathbb{K}$-subalgebra of A (we denote this ring by ${\left(A^{\langle \ell \rangle }\right)}^{\left(0\right)}$ when it is necessary to express ℓ). Further, since

$$\mu \in {t\mathcal{U}}_0^{\left(0\right)}{\left(G\right)\iff \mu |}_{C^{-}}\in {t\mathcal{U}}_0^{\left(0\right)}\left(G\left(C\right)\right),$$

for $\mu \in {t\mathcal{U}}^{\left(0\right)}$, we see that

$$R\cap A^{\left(0\right)}=\underset{\mu \in {t\mathcal{U}}_0^{\left(0\right)}\left(G\left(C\right)\right)}{⨁}\mathbb{K}{T}^{\mu }.$$

We denote this ring by $R^{\left(0\right)}$. Note that ${\mu }_i^J\in {t\mathcal{U}}_0^{\left(0\right)}$ for any $i\in \mathbb{Z}$ and $J\subset I_{i-2}$. By ([5], Lemma 4.3) and the argument following the proof of it, we see the following.

Theorem 2. 

The elements ${\mu }_0^{\varnothing }$, ${\mu }_1^{\varnothing }$, …, ${\mu }_{2\ell }^{\varnothing }$ of ${\mathbb{R}}^{V^{-}}$ are linearly independent and

$$R^{\left(0\right)}=\mathbb{K}[T^{{\mu }_0^{\varnothing }},T^{{\mu }_1^{\varnothing }},\dots ,T^{{\mu }_{2\ell }^{\varnothing }}].$$

Further, we see the following.

Lemma 2. 

It holds that

$$A^{\left(0\right)}=\mathbb{K}[T^{{\mu }_i^J}\mid 0\le i\le 2\ell ,J\subset I_{i-2}]=\mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap \left(\sum _{i=0}^{2\ell }\sum _{J\subset I_{i-2}}{\mathbb{R}}_{\ge 0}{\mu }_i^J\right)].$$

Proof. 

It is clear that

$$\mathbb{K}[T^{{\mu }_i^J}\mid 0\le i\le 2\ell ,J\subset I_{i-2}]\subset \mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap \left(\sum _{i=0}^{2\ell }\sum _{J\subset I_{i-2}}{\mathbb{R}}_{\ge 0}{\mu }_i^J\right)]\subset A^{\left(0\right)}.$$

In order to prove the inclusion $A^{\left(0\right)}\subset \mathbb{K}[T^{{\mu }_i^J}\mid 0\le i\le 2\ell ,J\subset I_{i-2}]$, it is enough to show that for any $\mu \in {t\mathcal{U}}_0^{\left(0\right)}$, $T^{\mu }\in \mathbb{K}[T^{{\mu }_i^J}\mid 0\le i\le 2\ell ,J\subset I_{i-2}]$. We prove this fact by induction on $\mu (-\infty )$.

The case where $\mu (-\infty )=0$ is trivial. Let $\mu$ be an arbitrary element of ${t\mathcal{U}}_0^{(0)}$ with $\mu (-\infty )>0$. By the proof of Lemma 4.3 in [5], we see that there is i with $(\mu -{\mu }_i^{\varnothing })(c)\ge 0$ for any $c\in C$ and ${(\mu -{\mu }_i^{\varnothing })}^{+}(e_j)\le (\mu -{\mu }_i^{\varnothing })(-\infty )$ for any j. Set $J=\{k\mid \mu (b_{i-2,k})>0\}$. Then, it holds that $\mu -{\mu }_i^J\in {t\mathcal{U}}_0^{(0)}$.

In fact, $(\mu -{\mu }_i^J)(z)\ge 0$ for any $z\in V$ by the choice of i and the definition of J. If $j\not\equiv i-2(mod2\ell +1)$ or $j\equiv i-2(mod2\ell +1)$ and $k\in J$, then ${({\mu }_i^J)}^{+}(K_{j,k})=1$. Thus, ${(\mu -{\mu }_i^J)}^{+}(K_{j,k})={\mu }^{+}(K_{j,k})-1\le \mu (-\infty )-1=(\mu -{\mu }_i^J)(-\infty )$. If $j\equiv i-2(mod2\ell +1)$ and $k\notin J$, then $\mu (b_{i-2,k})={\mu }_i^J(b_{i-2,k})=0$ by the definition of J. Therefore, by the choice of i, we see that ${(\mu -{\mu }_i^J)}^{+}(K_{j,k})={(\mu -{\mu }_i^J)}^{+}(e_{i-2})={(\mu -{\mu }_i^{\varnothing })}^{+}(e_{i-2})\le (\mu -{\mu }_i^{\varnothing })(-\infty )=(\mu -{\mu }_i^J)(-\infty )$. Finally, ${(\mu -{\mu }_i^J)}^{+}(C)={\mu }^{+}(C)-{({\mu }_i^J)}^{+}(C)=\ell \mu (-\infty )-\ell =\ell (\mu -{\mu }_i^J)(C)$. Thus, we see that $\mu -{\mu }_i^J\in {t\mathcal{U}}_0^{(0)}$.

Since $(\mu -{\mu }_i^J)(-\infty )=\mu (-\infty )-1$, we see, by the induction hypothesis, that

$$T^{\mu -{\mu }_i^J}\in \mathbb{K}[T^{{\mu }_i^{J^{\prime }}}\mid 0\le i\le 2\ell ,J^{\prime }\subset I_{i-2}].$$

Thus, we see that

$$T^{\mu }=T^{{\mu }_i^J}{T}^{\mu -{\mu }_i^J}\in \mathbb{K}[T^{{\mu }_i^{J^{\prime }}}\mid 0\le i\le 2\ell ,J^{\prime }\subset I_{i-2}].$$

□

Since

$${\mathbb{R}}^{V^{-}}={\mathbb{R}}^{C^{-}}\oplus {\mathbb{R}}^{B}andW\supset {\mathbb{R}}^B,$$

we see that

$$W=({\mathbb{R}}^{C^{-}}\cap W)\oplus {\mathbb{R}}^B.$$

Thus, ${\mathbb{R}}^{C^{-}}\cap W$ is a codimension 1 vector subspace of ${\mathbb{R}}^{C^{-}}$. Since $dim{\mathbb{R}}^{C^{-}}=\#C^{-}=2\ell +2$ and ${\mu }_i^{\varnothing }\in {\mathbb{R}}^{C^{-}}\cap W$ for any $0\le i\le 2\ell$, we see, by Theorem 2, that ${\mu }_0^{\varnothing }$, ${\mu }_1^{\varnothing }$, …, ${\mu }_{2\ell }^{\varnothing }$ is a basis of ${\mathbb{R}}^{C^{-}}\cap W$. Set

$$W_i^{\prime }=\sum _{k\in I_{i-2}}\mathbb{R}{\chi }_{\left\{b_{i-2,k}\right\}}\mathrm{and}{W}_i=\mathbb{R}{\mu }_i^{\varnothing }\oplus W_i^{\prime }$$

for $0\le i\le 2\ell$. Then,

$${\mathbb{R}}^B=W_0^{\prime }\oplus W_1^{\prime }\oplus \cdots \oplus W_{2\ell }^{\prime },W=W_0\oplus W_1\oplus \cdots \oplus W_{2\ell }and{W}_i=\sum _{J\subset I_{i-2}}\mathbb{R}{\mu }_i^J$$

for $0\le i\le 2\ell$. Set

$$C_i=\sum _{J\subset I_{i-2}}{\mathbb{R}}_{\ge 0}{\mu }_i^J$$

for $0\le i\le 2\ell$. Then, by Lemma 2, we see that

$$A^{\left(0\right)}=\mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap \left(\sum _{i=0}^{2\ell }{C}_i\right)]\cong \mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap C_0]\otimes \cdots \otimes \mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap C_{2\ell }].$$

It is easily verified that $\mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap C_i]$ is isomorphic to the Ehrhart ring of the unit cube for $2\le i\le 2\ell -2$. Therefore,

$$\mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap C_i]\cong {\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]}$$

for $2\le i\le 2\ell -2$. Further, it is easily verified that

$$\mathbb{K}[{\mathbb{Z}}^{V^{-}}\cap C_i]\cong {\mathbb{K}}^{\left[2\right]}$$

for $i=0$, 1, $2\ell -1$ and $2\ell$. Thus, we see that

$$A^{\left(0\right)}\cong {({\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]})}^{\otimes 2\ell -3}\otimes {\mathbb{K}}^{\left[8\right]}.$$

It is verified by a direct computation, or by Theorem 2.1 in [11], that the Hilbert series of ${\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]}\#{\mathbb{K}}^{\left[2\right]}$ is $\frac{1+4\lambda +{\lambda }^2}{{(1-\lambda )}^4}$. Therefore, the Hilbert series of $A^{\left(0\right)}$ is

$$\frac{{(1+4\lambda +{\lambda }^2)}^{2\ell -3}}{{(1-\lambda )}^{8\ell -4}}.$$

For each integer k with $1\le k\le 2\ell -1$, we define ${\eta }_k\in {\mathbb{Z}}^{V^{-}}$ by

$${\eta }_k\left(z\right)=\left\{\begin{array}{cc}1\hfill & z\in B,\hfill \\ k\hfill & z\in C,\hfill \\ 2k+2\hfill & z=-\infty .\hfill \end{array}\right.$$

It is easily verified that ${\eta }_k\in {t\mathcal{U}}^{\left(1\right)}$ and $\ell {\eta }_k(-\infty )-{\eta }_k^{+}\left(C\right)=2\ell -k$. Further, we see the following.

Lemma 3. 

It holds that $a\left(A\right)=-4$.

Proof. 

Since for any $\eta \in {t\mathcal{U}}^{\left(1\right)}$, $\eta (-\infty )\ge {\eta }^{+}\left(K_{0,1}\right)+1\ge \#K_{0,1}+1=4$ and ${\eta }_1(-\infty )=4$, we see that $a\left(A\right)=-min\{\eta (-\infty )\mid \eta \in {t\mathcal{U}}^{\left(1\right)}\}=-4$. □

Consider the graded A-homomorphism, $\phi :A\to {\omega }_A\left(4\right)$, $T^{\nu }\mapsto T^{\nu +{\eta }_1}$, of degree 0. Then $\mathrm{Im}\phi$ is a submodule of ${\omega }_A\left(4\right)$ generated by $T^{{\eta }_1}$. Further, we have the following.

Lemma 4. 

It holds that

$$\mathrm{Im}\phi (-4)=\underset{\nu \in {t\mathcal{U}}^{\left(1\right)},\ell \nu (-\infty )-{\nu }^{+}\left(C\right)\ge 2\ell -1}{⨁}\mathbb{K}{T}^{\nu }.$$

Further, $\mathrm{Im}\phi$ is a rank-1-free A-module with basis $T^{{\eta }_1}$.

Proof. 

This lemma is proved almost identically to Lemma 4.2 in [5]. □

Set

$$D_k=\underset{\eta \in {t\mathcal{U}}^{\left(1\right)},\ell \eta (-\infty )-{\eta }^{+}\left(C\right)=2\ell -k}{⨁}\mathbb{K}{T}^{\eta }$$

for $2\le k\le 2\ell -1$. Then, the following holds.

Lemma 5. 

$D_k$ is a rank-1-free $A^{\left(0\right)}$-module with basis $T^{{\eta }_k}$ for $2\le k\le 2\ell -1$.

Proof. 

This lemma is proved almost identically to Lemma 4.5 in [5]. □

Now, we prove Theorem 1. First, note that $dim{A}^{\langle \ell \rangle }=\#V_{\ell }^{-}+1=8\ell -3$. Let $(h_0,h_1,\dots ,h_{s_{\ell }})$, $h_{s_{\ell }}\ne 0$, be the h-vector of $A^{\langle \ell \rangle }$. Then,

$$s_{\ell }=dim{A}^{\langle \ell \rangle }+a(A^{\langle \ell \rangle })=8\ell -7\mathrm{and}\lfloor s_{\ell }/2\rfloor =4\ell -4.$$

By the second proof of Theorem 4.1 in [9], we see that

$$H({\omega }_{A^{\langle \ell \rangle }}\left(4\right),\lambda )=\frac{h_{s_{\ell }}+h_{s_{\ell }-1}\lambda +\cdots +h_0{\lambda }^{s_{\ell }}}{{(1-\lambda )}^{8\ell -3}},$$

where $H(M,\lambda )$ denotes the Hilbert series of a graded module M. Since

$$\begin{array}{ccc}\hfill {\omega }_{A^{\langle \ell \rangle }}& =& \underset{\eta \in {t\mathcal{U}}^{\left(1\right)}\left(G_{\ell }\right)}{⨁}\mathbb{K}{T}^{\eta }\hfill \\ & =& \left(\underset{\genfrac{}{}{0pt}{}{\eta \in {t\mathcal{U}}^{\left(1\right)}\left(G_{\ell }\right)}{\ell \eta (-\infty )-{\eta }^{+}\left(C_{\ell }\right)\ge 2\ell -1}}{⨁}\mathbb{K}{T}^{\eta }\right)\oplus \underset{k=2}{\overset{2\ell -1}{⨁}}\left(\underset{\genfrac{}{}{0pt}{}{\eta \in {t\mathcal{U}}^{\left(1\right)}\left(G_{\ell }\right)}{\ell \eta (-\infty )-{\eta }^{+}\left(C_{\ell }\right)=2\ell -k}}{⨁}\mathbb{K}{T}^{\eta }\right),\hfill \end{array}$$

and there is an exact sequence

$$0\to A^{\langle \ell \rangle }\stackrel{\phi }{\to }{\omega }_{A^{\langle \ell \rangle }}\left(4\right)\to \mathrm{Cok}\phi \to 0,$$

we see by Lemmas 4 and 5 that

$$H({\omega }_{A^{\langle \ell \rangle }}\left(4\right),\lambda )=H(A^{\langle \ell \rangle },\lambda )+\sum _{k=2}^{2\ell -1}H({\left(A^{\langle \ell \rangle }\right)}^{\left(0\right)},\lambda ){\lambda }^{2k-2},$$

since $deg{T}^{{\eta }_k}={\eta }_k(-\infty )=2k+2$ for $1\le k\le 2\ell -1$. Therefore,

$$\begin{array}{ccc}& & \frac{(h_{s_{\ell }}-h_0)+(h_{s_{\ell }-1}-h_1)\lambda +\cdots +(h_0-h_{s_{\ell }}){\lambda }^{s_{\ell }}}{{(1-\lambda )}^{8\ell -3}}\hfill \\ & =& \sum _{k=2}^{2\ell -1}\frac{{(1+4\lambda +{\lambda }^2)}^{2\ell -3}{\lambda }^{2k-2}}{{(1-\lambda )}^{8\ell -4}}\hfill \\ & =& \sum _{k=2}^{2\ell -1}\frac{{(1+4\lambda +{\lambda }^2)}^{2\ell -3}({\lambda }^{2k-2}-{\lambda }^{2k-1})}{{(1-\lambda )}^{8\ell -3}}\hfill \\ & =& \frac{{(1+4\lambda +{\lambda }^2)}^{2\ell -3}({\lambda }^2-{\lambda }^3+\cdots +{\lambda }^{4\ell -4}-{\lambda }^{4\ell -3})}{{(1-\lambda )}^{8\ell -3}}.\hfill \end{array}$$

By comparing the coefficient of ${\lambda }^{4\ell -3}$ in the numerators, we see that

$$\begin{array}{lll}& & h_{4\ell -4}-h_{4\ell -3}\hfill \\ & =& \left(\begin{array}{l}\mathrm{the} \mathrm{sum} \mathrm{of} \mathrm{the} \mathrm{coefficients} \mathrm{of} \mathrm{the} \mathrm{odd} \mathrm{powers} \mathrm{of} \lambda \mathrm{of}\\ {(1+4\lambda +{\lambda }^2)}^{2\ell -3}\end{array}\right)\hfill \\ & & -\left(\begin{array}{l}\mathrm{the} \mathrm{sum} \mathrm{of} \mathrm{the} \mathrm{coefficients} \mathrm{of} \mathrm{the} \mathrm{even} \mathrm{powers} \mathrm{of} \lambda \mathrm{of}\\ {(1+4\lambda +{\lambda }^2)}^{2\ell -3}\end{array}\right)\\ & =& {(-1+4-1)}^{2\ell -3}\\ & =& 2^{2\ell -3}\end{array}$$

Since $\lfloor s_{\ell }/2\rfloor =4\ell -4$ and $s_{\ell }-\lfloor s_{\ell }/2\rfloor =4\ell -3$, we see that

$$h_{\lfloor s_{\ell }/2\rfloor }=h_{s_{\ell }-\lfloor s_{\ell }/2\rfloor }+2^{2\ell -3}.$$