SIRS Epidemic Models with Delays, Partial and Temporary Immunity and Vaccination
Abstract
:1. Introduction
2. Materials and Methods
2.1. SIS, SIR and SIRS Models
2.2. Models with Different Immunities
2.3. Models with Loss of Immunity and Two Groups
2.4. Models with Vaccination and Immunity Loss
3. Results
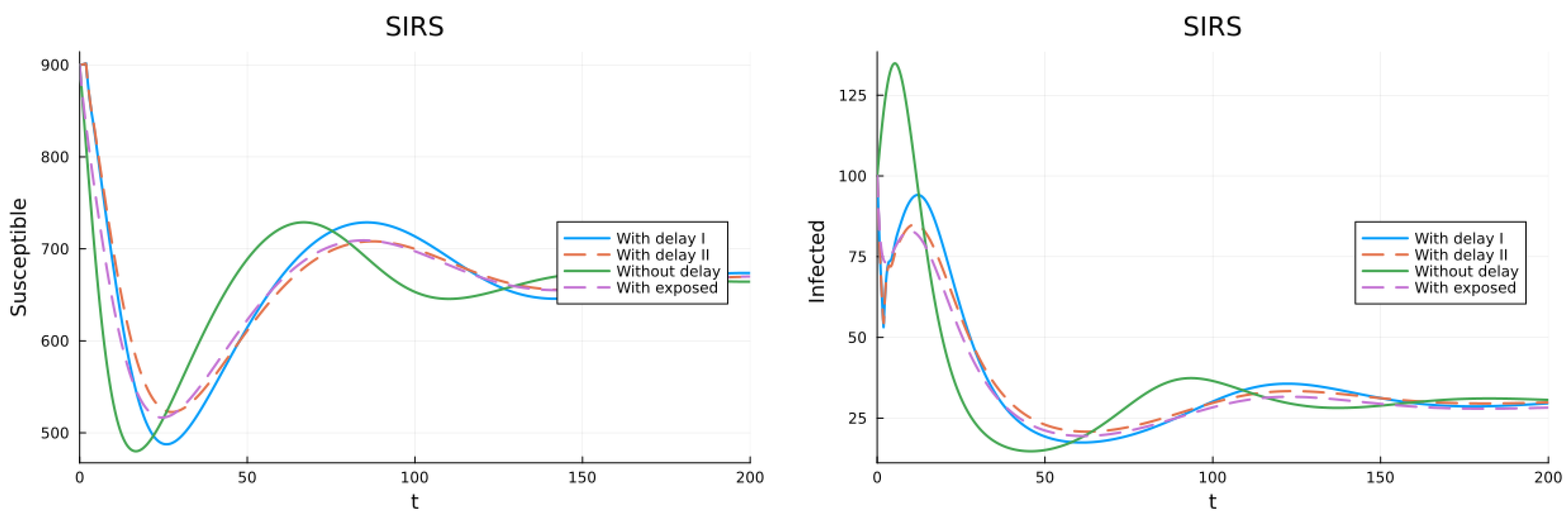
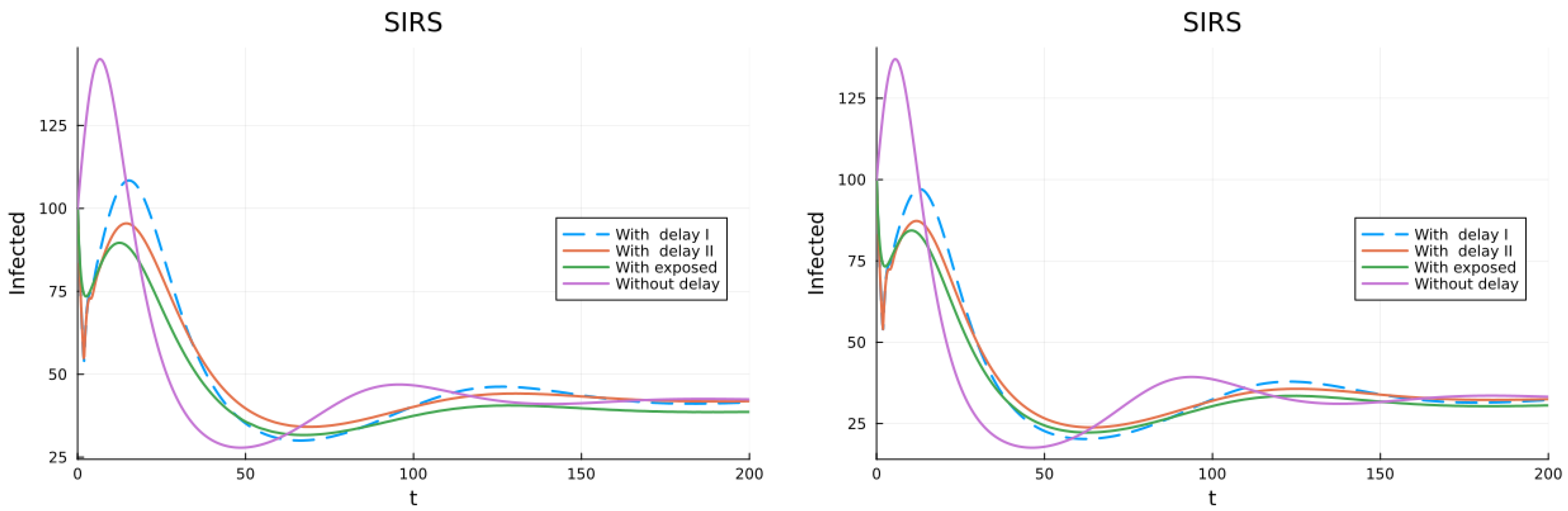
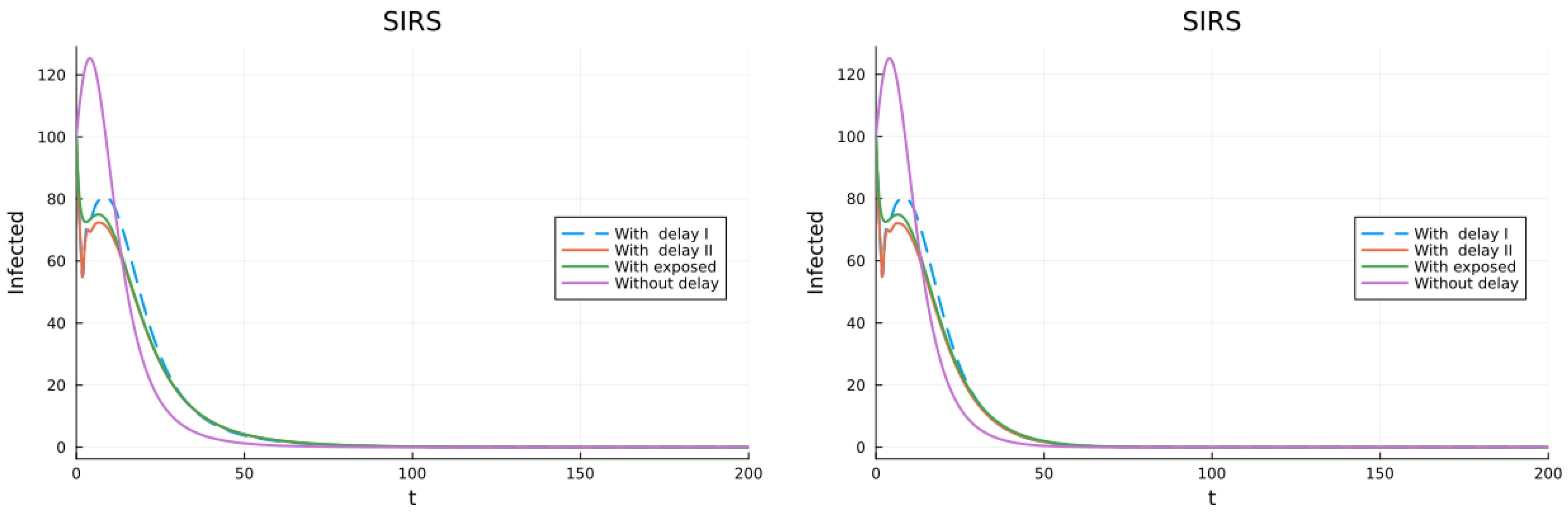
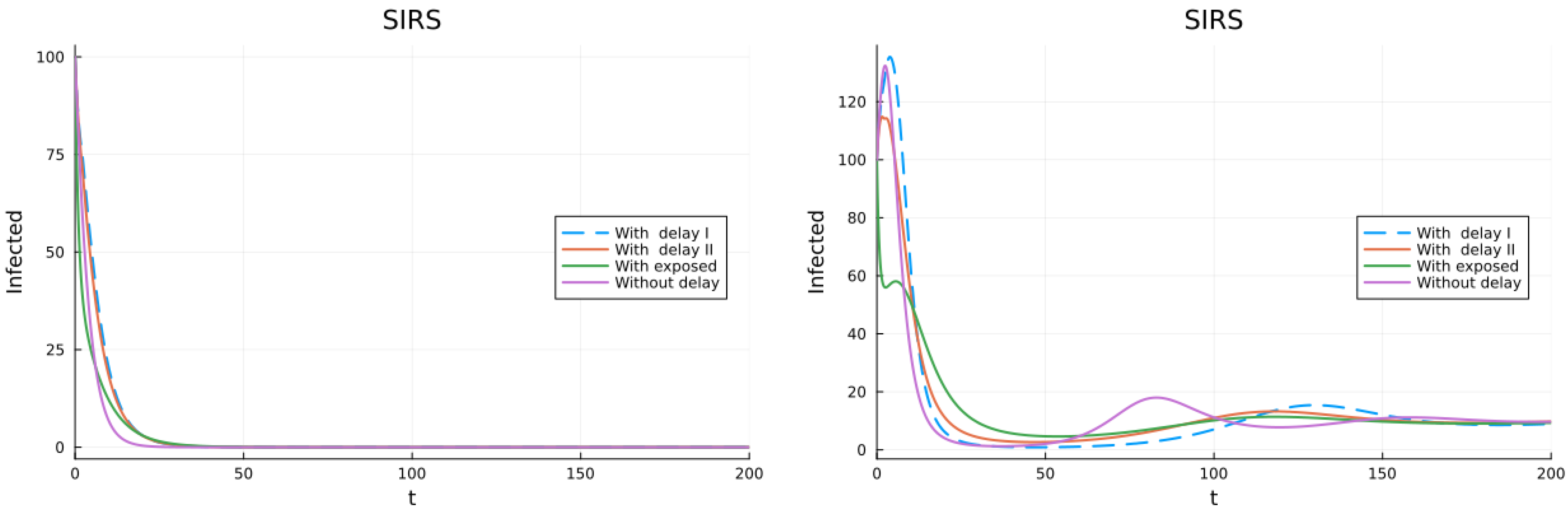
3.1. SIS, SIR and SIRS Models
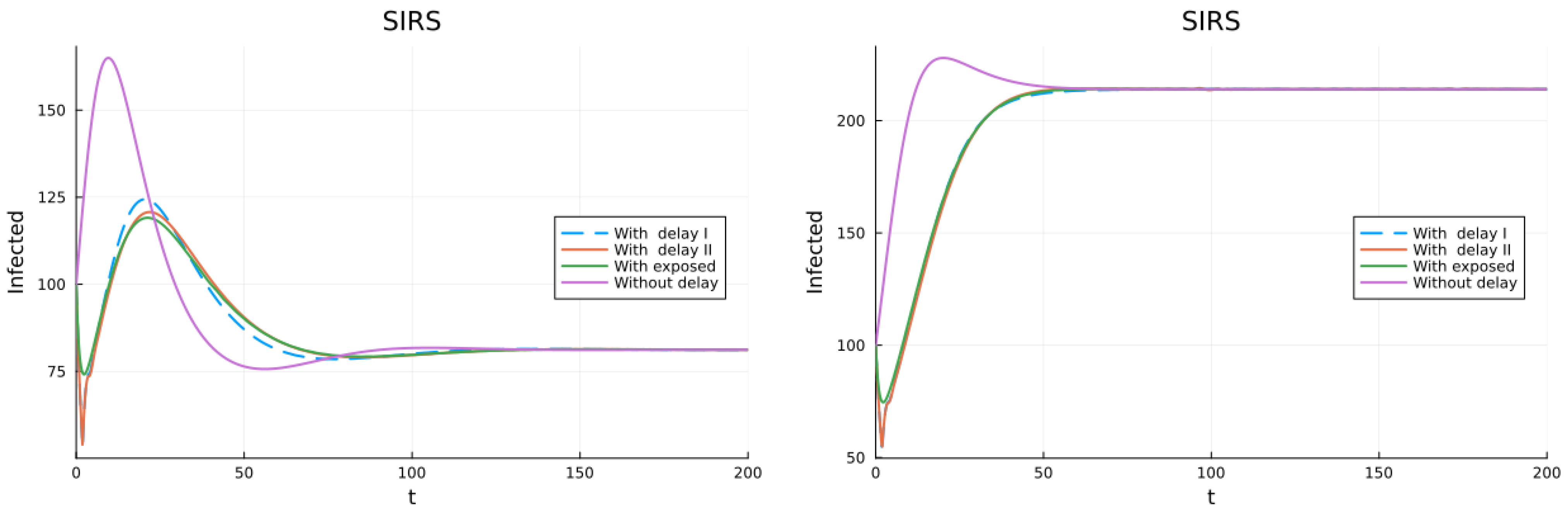
3.2. Models with Different Immunities
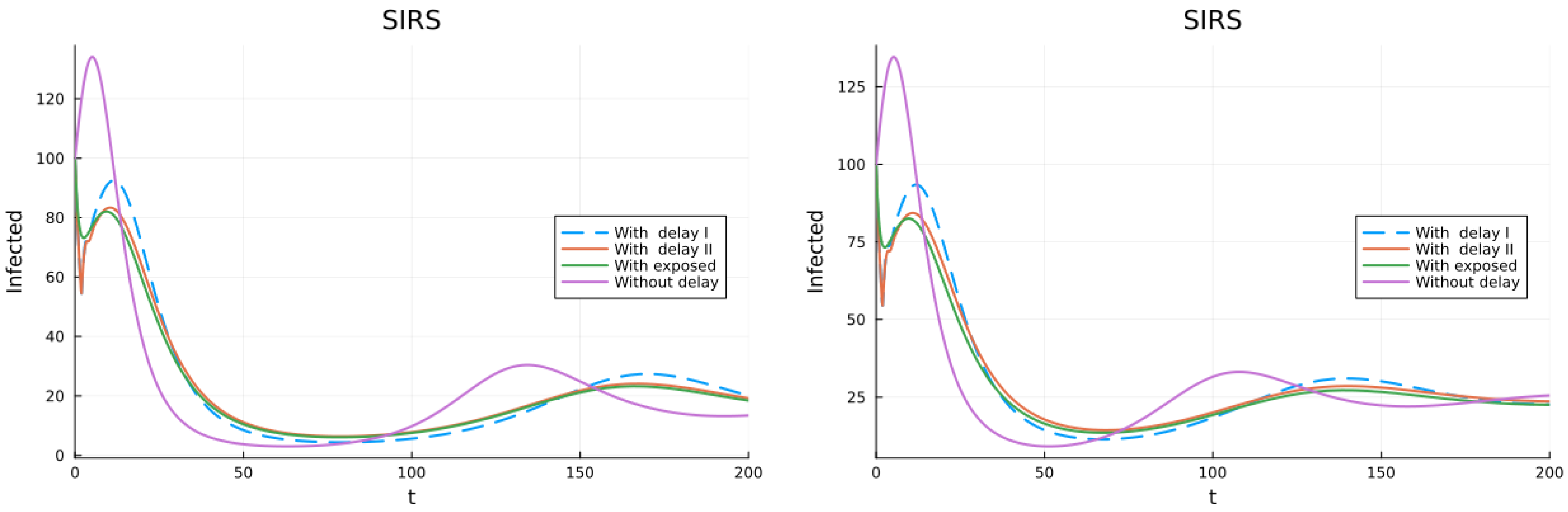
3.3. Models with Loss of Immunity and Two Groups
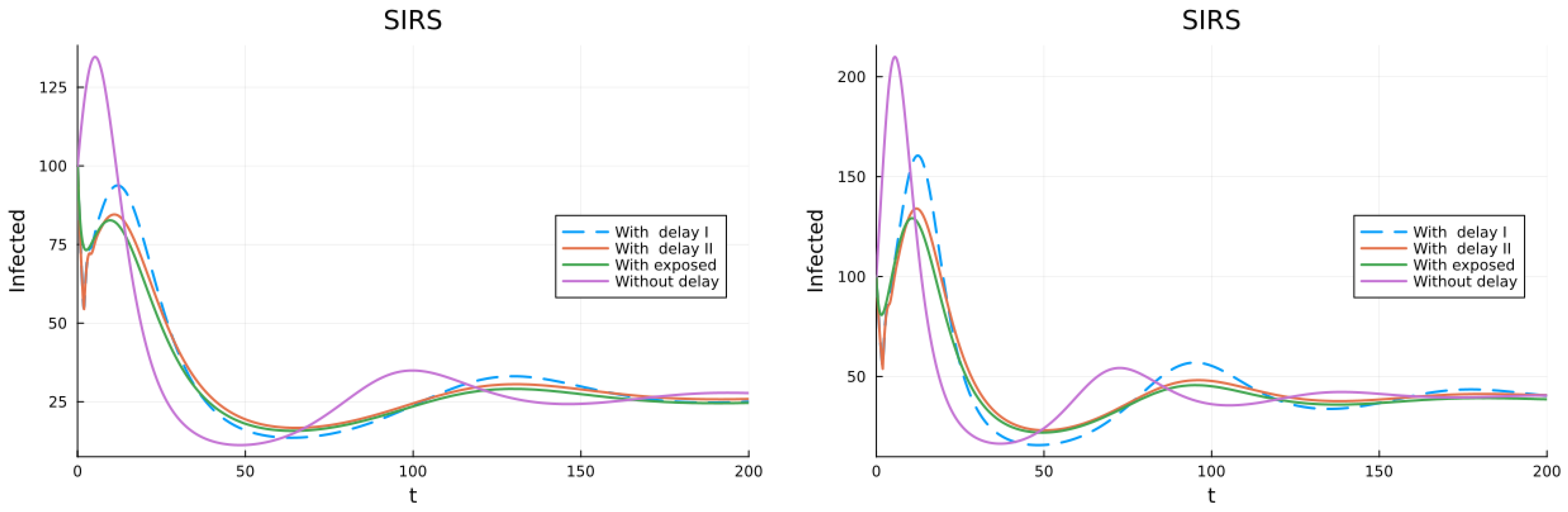
3.4. Models with Vaccination and Immunity Loss
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SIS | Susceptible, infective, susceptible |
| SIR | Susceptible, infective, recovered |
| SIRS | Susceptible, infective, recovered, susceptible |
| ODE | Ordinary differential equation |
| DDE | Delay differential equation |
| DFE | Disease-free equilibrium |
| Basic reproduction number |
References
- Centers for Disease Control. Influenza (Flu). 2024. Available online: https://www.cdc.gov/flu/about/keyfacts.htm#:~:text=Flu%20is%20a%20contagious%20respiratory,a%20flu%20vaccine%20each%20year (accessed on 24 April 2024).
- Centers for Disease Control. Influenza. 2024. Available online: https://www.cdc.gov/nchs/fastats/flu.htm (accessed on 24 April 2024).
- Ross, R.; Hudson, H.P. An application of the theory of probabilities to the study of a priori pathometry—Part III. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1917, 93, 225–240. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Ma, Z. Dynamical Modeling and Analysis of Epidemics; World Scientific: Singapore, 2009. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Singapore, 2021. [Google Scholar]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Edlund, S.; Kaufman, J.; Lessler, J.; Douglas, J.; Bromberg, M.; Kaufman, Z.; Bassal, R.; Chodick, G.; Marom, R.; Shalev, V.; et al. Comparing three basic models for seasonal influenza. Epidemics 2011, 3, 135–142. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Allen, L. An Introduction to Mathematical Biology; Pearson-Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Murray, J.D. Mathematical Biology I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Fages, F.; Soliman, S. On robustness computation and optimization in BIOCHAM-4. In Proceedings of the International Conference on Computational Methods in Systems Biolog, Brno, Czech Republic, 12–14 September 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 292–299. [Google Scholar]
- Cooke, K.L.; Yorke, J.A. Some equations modelling growth processes and gonorrhea epidemics. Math. Biosci. 1973, 16, 75–101. [Google Scholar] [CrossRef]
- Jackson, M.; Chen-Charpentier, B.M. Modeling plant virus propagation with delays. J. Comput. Appl. Math. 2017, 309, 611–621. [Google Scholar] [CrossRef]
- Khan, Q.J.A.; Krishnan, E.V. An Epidemic Model with a Time Delay in Transmission. Appl. Math. 2003, 48, 193–203. [Google Scholar] [CrossRef]
- Al Basir, F.; Takeuchi, Y.; Ray, S.A. Dynamics of a delayed plant disease model with Beddington-DeAngelis disease transmission. Math. Biosci. Eng. 2021, 18, 583–599. [Google Scholar] [CrossRef]
- Huang, G.; Ma, W.; Takeuchi, Y. Global analysis for delay virus dynamics model with Beddington–DeAngelis functional response. Appl. Math. Lett. 2011, 24, 1199–1203. [Google Scholar] [CrossRef]
- Wei, H.M.; Li, X.Z.; Martcheva, M. An epidemic model of a vector-borne disease with direct transmission and time delay. J. Math. Anal. Appl. 2008, 342, 895–908. [Google Scholar] [CrossRef]
- Chan, M.; Johansson, M.A. The incubation periods of dengue viruses. PLoS ONE 2012, 7, e50972. [Google Scholar] [CrossRef] [PubMed]
- Jeger, M.; Madden, L.; Van Den Bosch, F. Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018, 102, 837–854. [Google Scholar] [CrossRef]
- Liu, L. A delayed SIR model with general nonlinear incidence rate. Adv. Differ. Equ. 2015, 2015, 329. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Wang, N.; Fu, Y.; Zhang, H.; Shi, H. An evaluation of mathematical models for the outbreak of COVID-19. Precis. Clin. Med. 2020, 3, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Bjørnstad, O.N.; Shea, K.; Krzywinski, M.; Altman, N. The SEIRS model for infectious disease dynamics. Nat. Methods 2020, 17, 557–559. [Google Scholar] [CrossRef]
- Krammer, F. The human antibody response to influenza A virus infection and vaccination. Nat. Rev. Immunol. 2019, 19, 383–397. [Google Scholar] [CrossRef]
- Patel, M.M.; York, I.A.; Monto, A.S.; Thompson, M.G.; Fry, A.M. Immune-mediated attenuation of influenza illness after infection: Opportunities and challenges. Lancet Microbe 2021, 2, e715–e725. [Google Scholar] [CrossRef]
- Han, A.X.; de Jong, S.P.; Russell, C.A. Co-evolution of immunity and seasonal influenza viruses. Nat. Rev. Microbiol. 2023, 21, 805–817. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Maroto, G.; Atienza-Diez, I.; Ares, S.; Manrubia, S. Vaccination strategies in structured populations under partial immunity and reinfection. J. Phys. A Math. Theor. 2023, 56, 204003. [Google Scholar] [CrossRef]
- Katriel, G. Epidemics with partial immunity to reinfection. Math. Biosci. 2010, 228, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Mondal, B.; Ghosh, U. Dynamical behaviors of an epidemic model with partial immunity having nonlinear incidence and saturated treatment in deterministic and stochastic environments. Chaos Solitons Fractals 2023, 174, 113775. [Google Scholar] [CrossRef]
- Thieme, H.R.; Yang, J. An endemic model with variable re-infection rate and applications to influenza. Math. Biosci. 2002, 180, 207–235. [Google Scholar] [CrossRef] [PubMed]
- Carlsson, R.M.; Childs, L.M.; Feng, Z.; Glasser, J.W.; Heffernan, J.M.; Li, J.; Röst, G. Modeling the waning and boosting of immunity from infection or vaccination. J. Theor. Biol. 2020, 497, 110265. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Adler, F.R. A time since recovery model with varying rates of loss of immunity. Bull. Math. Biol. 2012, 74, 2810–2819. [Google Scholar] [CrossRef]
- Viguerie, A.; Carletti, M.; Silvestri, G.; Veneziani, A. Mathematical Modeling of Periodic Outbreaks with Waning Immunity: A Possible Long-Term Description of COVID-19. Mathematics 2023, 11, 4918. [Google Scholar] [CrossRef]
- Alexander, M.E.; Bowman, C.; Moghadas, S.M.; Summers, R.; Gumel, A.B.; Sahai, B.M. A vaccination model for transmission dynamics of influenza. SIAM J. Appl. Dyn. Syst. 2004, 3, 503–524. [Google Scholar] [CrossRef]
- Sun, C.; Yang, W. Global results for an SIRS model with vaccination and isolation. Nonlinear Anal. Real World Appl. 2010, 11, 4223–4237. [Google Scholar] [CrossRef]
- Sahu, G.P.; Dhar, J. Analysis of an SVEIS epidemic model with partial temporary immunity and saturation incidence rate. Appl. Math. Model. 2012, 36, 908–923. [Google Scholar] [CrossRef]
- Moghadas, S.; Gumel, A. A mathematical study of a model for childhood diseases with non-permanent immunity. J. Comput. Appl. Math. 2003, 157, 347–363. [Google Scholar] [CrossRef]
- Saad-Roy, C.M.; Morris, S.E.; Metcalf, C.J.E.; Mina, M.J.; Baker, R.E.; Farrar, J.; Holmes, E.C.; Pybus, O.G.; Graham, A.L.; Levin, S.A.; et al. Epidemiological and evolutionary considerations of SARS-CoV-2 vaccine dosing regimes. Science 2021, 372, 363–370. [Google Scholar] [CrossRef]
- Goldberg, Y.; Mandel, M.; Bar-On, Y.M.; Bodenheimer, O.; Freedman, L.; Haas, E.J.; Milo, R.; Alroy-Preis, S.; Ash, N.; Huppert, A. Waning immunity after the BNT162b2 vaccine in Israel. N. Engl. J. Med. 2021, 385, e85. [Google Scholar] [CrossRef] [PubMed]
- Turkyilmazoglu, M. An extended epidemic model with vaccination: Weak-immune SIRVI. Phys. A Stat. Mech. Its Appl. 2022, 598, 127429. [Google Scholar] [CrossRef] [PubMed]
- Ho, S.H.; He, D.; Eftimie, R. Mathematical models of transmission dynamics and vaccine strategies in Hong Kong during the 2017–2018 winter influenza season. J. Theor. Biol. 2019, 476, 74–94. [Google Scholar] [CrossRef] [PubMed]
- Reluga, T.C.; Medlock, J. Resistance mechanisms matter in SIR models. Math. Biosci. Eng. 2007, 4, 553–563. [Google Scholar] [PubMed]
- Scherer, A.; McLean, A. Mathematical models of vaccination. Br. Med. Bull. 2002, 62, 187–199. [Google Scholar] [CrossRef] [PubMed]
- Safan, M.; Kretzschmar, M.; Hadeler, K.P. Vaccination based control of infections in SIRS models with reinfection: Special reference to pertussis. J. Math. Biol. 2013, 67, 1083–1110. [Google Scholar] [CrossRef]
- Krithika, B.; Tamilalagan, P. Unveiling the spread of epidemics involving partial immunity and reinfection: Insights from a time-delayed mathematical model. Eur. Phys. J. Spec. Top. 2023, 232, 2657–2673. [Google Scholar] [CrossRef]
- Arif, F.; Majeed, Z.; Rahman, J.U.; Iqbal, N.; Kafle, J. Mathematical modeling and numerical simulation for the outbreak of COVID-19 involving loss of immunity and quarantined class. Comput. Math. Methods Med. 2022, 2022, 3816492. [Google Scholar] [CrossRef] [PubMed]
- Rackauckas, C.; Nie, Q. DifferentialEquations.jl—A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. J. Open Res. Softw. 2017, 5. Available online: https://app.dimensions.aion2019/05/05 (accessed on 24 April 2024). [CrossRef]
- Widmann, D.; Rackauckas, C. DelayDiffEq: Generating Delay Differential Equation Solvers via Recursive Embedding of Ordinary Differential Equation Solvers. arXiv 2022, arXiv:2208.12879. [Google Scholar]
- Colizza, V.; Barrat, A.; Barthelemy, M.; Valleron, A.J.; Vespignani, A. Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions. PLoS Med. 2007, 4, e13. [Google Scholar] [CrossRef]
- Kanyiri, C.W.; Mark, K.; Luboobi, L. Mathematical analysis of influenza A dynamics in the emergence of drug resistance. Comput. Math. Methods Med. 2018, 2018, 2434560. [Google Scholar] [CrossRef]









| Symbol | Parameter Description | Value |
|---|---|---|
| Infection rate | 0.5/d | |
| Recovery rate | 1/3/d | |
| Loss of immunity rate | 1/30/d | |
| Delay in time of infection | 1.9 d | |
| 1/(time of infection) | /d | |
| N | Total population | 1000 |
| Infection rate for partial immunity | ||
| Rate of loss or partial immunity | 1/60/d | |
| Fraction losing immunity at rate | 0.75 | |
| Infection rate for fraction | /d | |
| Infection rate for fraction | /d | |
| Fraction achieving total immunity | 0.5 | |
| r | Vaccination rate | 0.02/d |
| Rate of loss of vaccination immunity | 1/60/d | |
| Infection rate of vaccinated with partial | ||
| Fraction of susceptibles to be vaccinated | 0.2/d | |
| Fraction of vaccinated with permanent immunity | 0.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen-Charpentier, B. SIRS Epidemic Models with Delays, Partial and Temporary Immunity and Vaccination. AppliedMath 2024, 4, 666-689. https://doi.org/10.3390/appliedmath4020036
Chen-Charpentier B. SIRS Epidemic Models with Delays, Partial and Temporary Immunity and Vaccination. AppliedMath. 2024; 4(2):666-689. https://doi.org/10.3390/appliedmath4020036
Chicago/Turabian StyleChen-Charpentier, Benito. 2024. "SIRS Epidemic Models with Delays, Partial and Temporary Immunity and Vaccination" AppliedMath 4, no. 2: 666-689. https://doi.org/10.3390/appliedmath4020036
APA StyleChen-Charpentier, B. (2024). SIRS Epidemic Models with Delays, Partial and Temporary Immunity and Vaccination. AppliedMath, 4(2), 666-689. https://doi.org/10.3390/appliedmath4020036






