A Mathematical Model for Collective Behaviors and Emergent Patterns Driven by Multiple Distinct Stimuli Produced by Multiple Species
Abstract
:1. Introduction
2. Underlying Assumptions Used for Collective Migration
- Unique signal for each type of species. Each individual produces a positive signal unique to its type, centered at its location. In the model, this is denoted by for the ith cell of type j moving in the plane. Note that this signal depends only on the present location of the cell, reflecting the assumption that diffusion of a signal is relatively fast compared to motion and, therefore, past signal emission is ignored. For example, visual signals only tell the present location of the individual being observed, while chemical signals may persist in a region where the individual has left. Marking behaviors leave a long-lasting signal. The example developed here assumes fast dispersion of the signals used. Note also that organisms may produce more than one type of signal which, taken together, are assumed to be a single signal in this paradigm.
- Signal distribution function for a given type. The signal distribution at a given time for the overall signal produced by m individuals of type j is the sum of individual signals. In the model, this is denoted by.In the example developed in this study, signals are represented as two-dimensional Gaussians centered at the location of the individual emitting the signal, although it would be easy to extend the problem to three dimensions. Summing the signals therefore gives greater weight to those near the observing individual. The use of Gaussians approximates the distribution around a point source of a chemical, and makes more sense for cells in water or for olfactory signals. For a visual signal, the Gaussian gives a measure of distance, which can be determined visually, but it is probably not the best representation.
- Close but not too close. Each individual of a given type, k, has a preferred signal strength, , for each species (j). In the case of two individuals, this preferred strength determines their distance from each other at equilibrium, a preferred distance reflecting the desire to be close, but not too close. In the model setup, this preferred signal strength is denoted w. In some cases, such as prey, this assumption could be weakened although it is probably sufficient to make the preferred distance large enough. The response function is constructed to be positive when the signal is less than preferred and negative when the signal is stronger than preferred.
- Motion along the gradient. In the case of a single species, motion is along the signal gradient at the location of the observing individual, until the preferred signal strength is obtained. It is possible, given some boundary conditions and parameters, that equilibrium is never obtained. Anything other than motion along the gradient would imply some kind of strategy on the part of the individual, which is not represented in this model.
- Each individual can distinguish between signals of each species. Most importantly, an individual can distinguish between its own species and other species. Smell, for example, distinguishes prey from predator. Neural crest cells move toward placodal cells because they can distinguish a molecular signal given by those cells. For some examples, this assumption could be weakened, which can be resolved with the model by setting response functions to be the same to both species.
- Motion in the presence of multiple signal types. In this case, the motion of an individual is in the direction of some linear combination of signal gradients for each of the species. Gradients will be weighted in a manner particular to the species of that individual. For example, the urge to be with one’s own kind is balanced against the urge to be with the other species, and that balance is assumed to be different for each species.
3. Model Equations
3.1. Equations of the Motion of Two Types of Cell, N and P
3.2. Signal Distribution
3.3. Response–Magnitude Functions
3.4. Parametrization
3.5. General Framework for Multiple Cell Types in Two or More Spatial Dimensions
4. Numerical Experiments
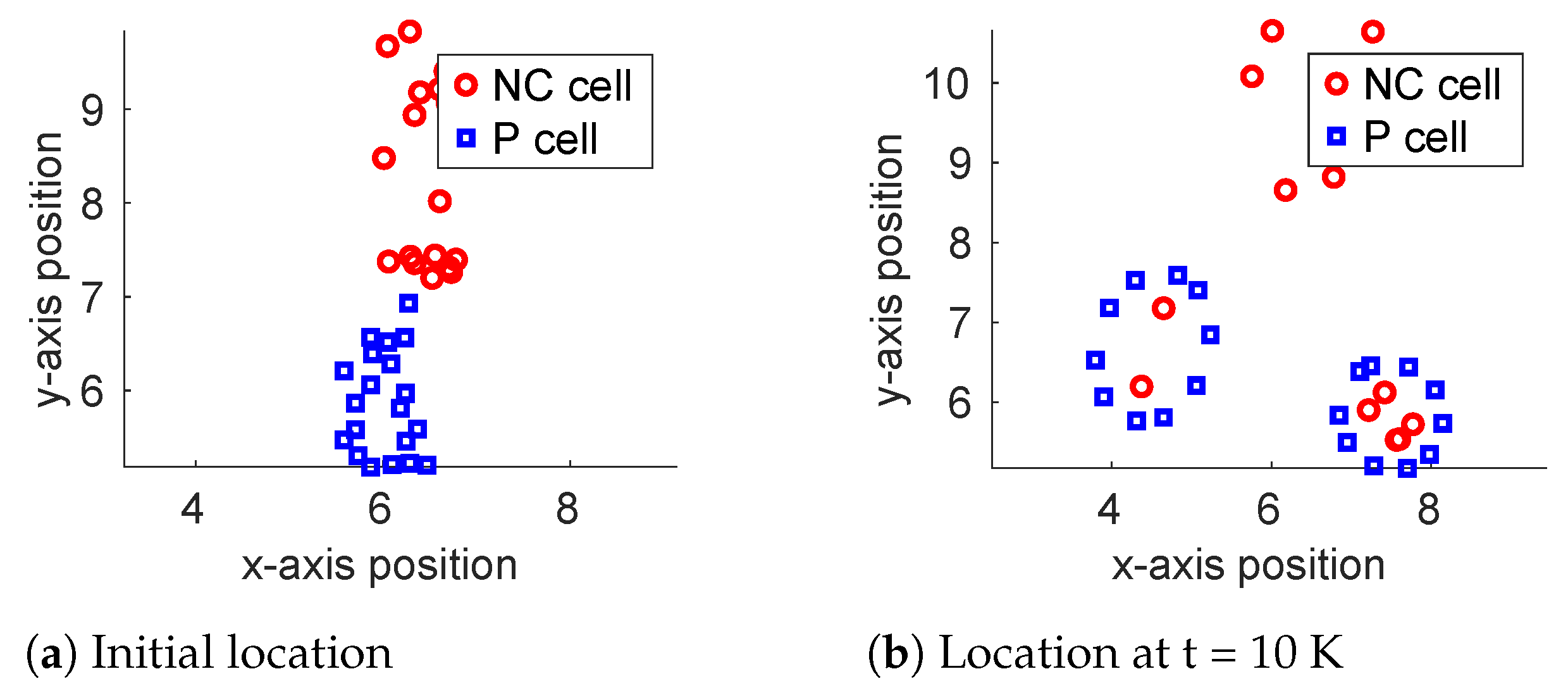
4.1. Two Cells of Different Types Exhibiting Chase-And-Run Behavior
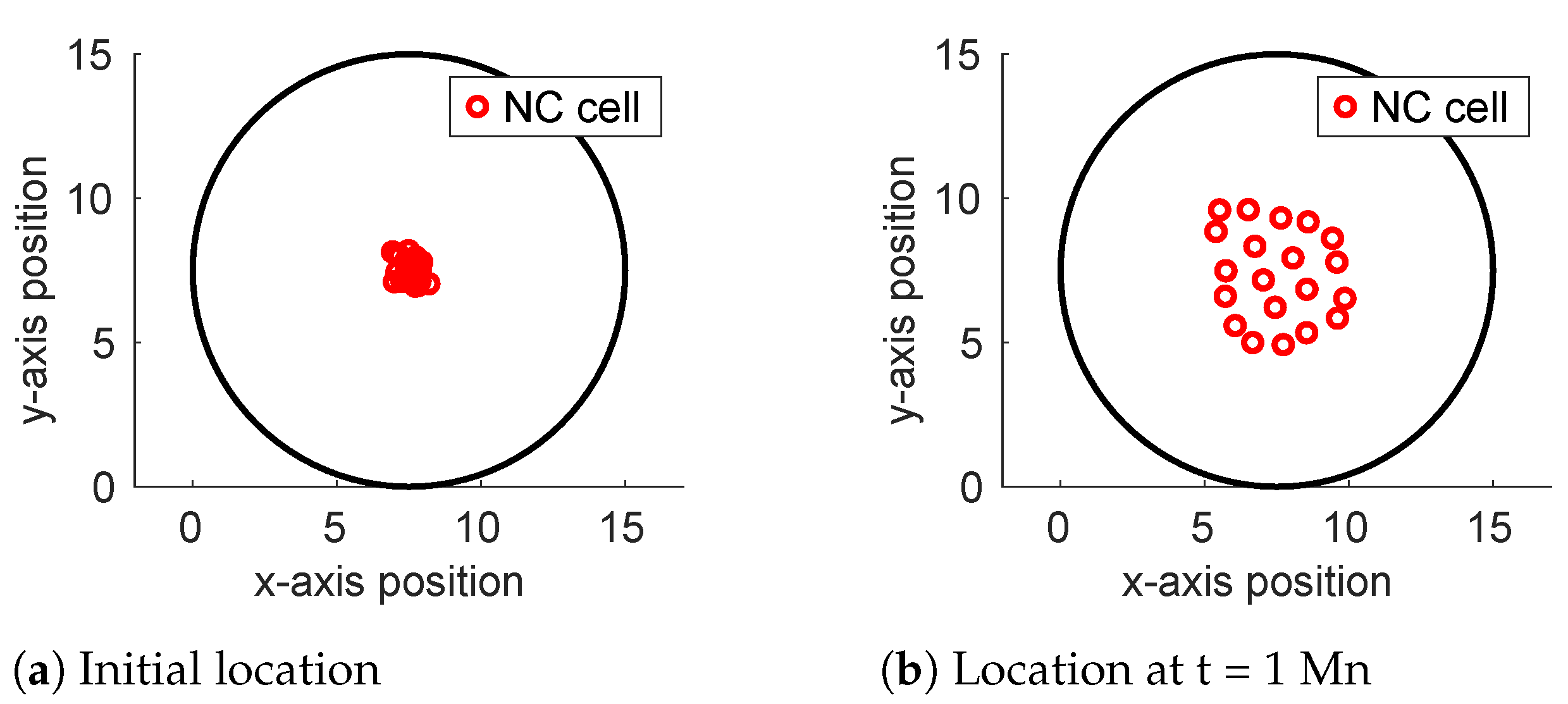
4.2. Multiple Cells of a Single Type in a Disc Congregating in a “Close but Not Too Close” Fashion
4.3. A Heterogeneous Cell Environment in a Rectangular Region Produces Herding and Herd Splitting
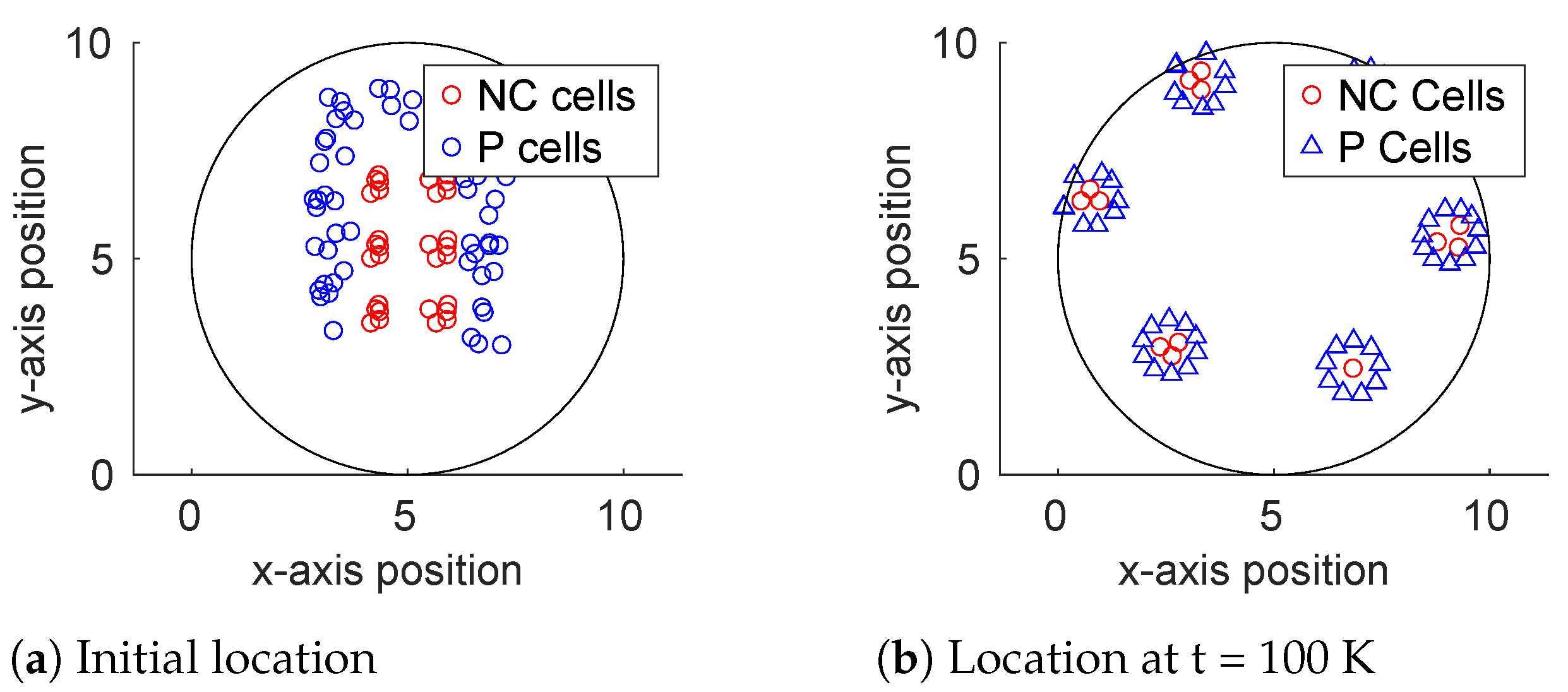
4.4. Heterogeneous Cell Environment on a Disc in Imitation of Neural Crest and Placodal Cell Behavior
5. A Few Theoretical Results
Two Individuals of Different Types
6. Numerical Results: The Example of Neural Crest and Placodal Cells
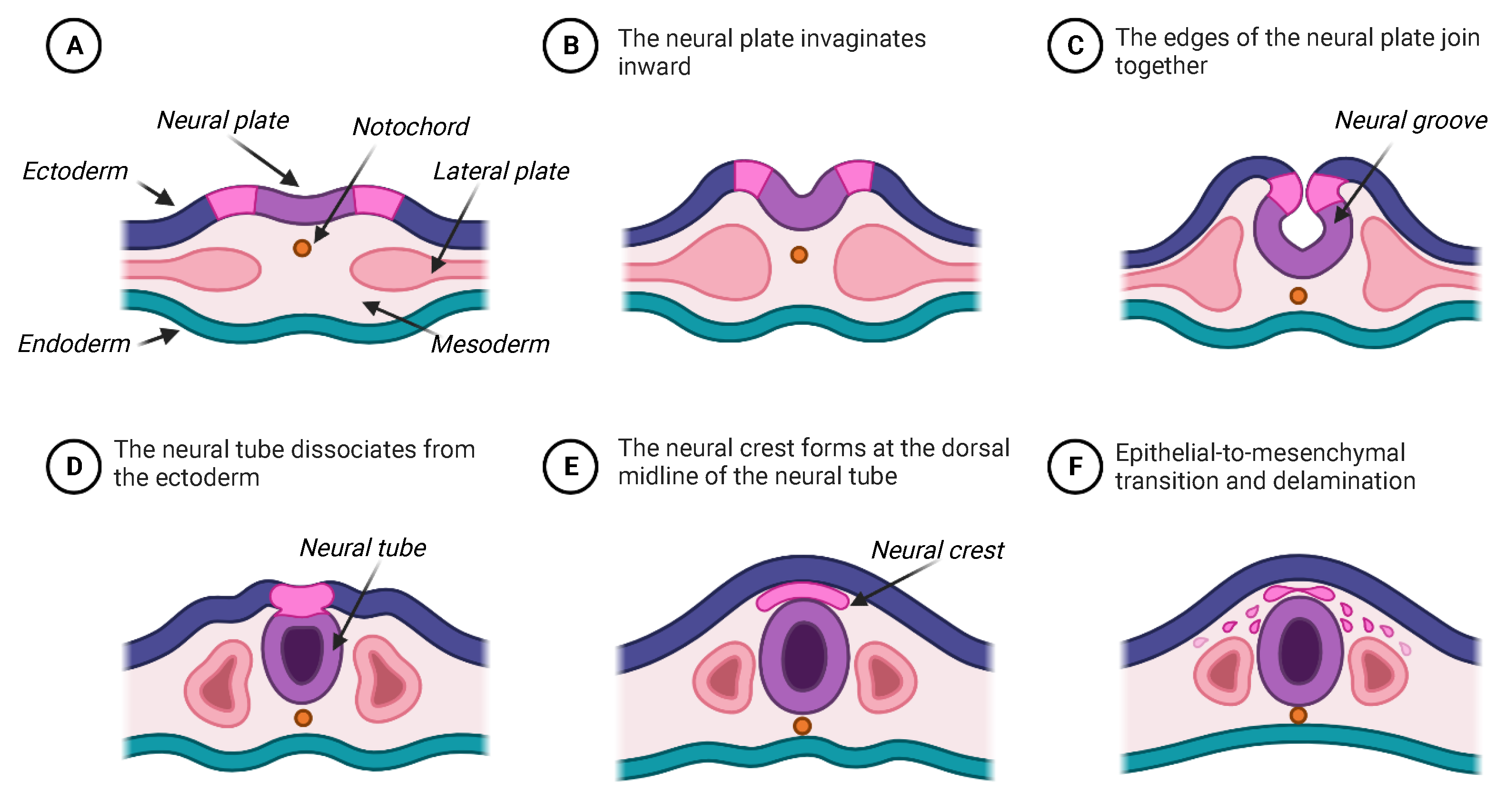
6.1. Mechanisms for Neural Crest Cell Motility and Directed Migration
6.2. Two Individuals in Engaged in “Chase-And-Run” Behavior
6.3. Multiple Cells of a Single Type Flocking or Congregating in a Disc
6.4. Heterogeneous Cell Environment in a Rectangular Region Exhibits Herding and Herd Splitting
6.5. Heterogeneous Cell Environment on a Disc in Imitation of Neural Crest and Placodal Behavior
7. Discussion
7.1. Modeling of Neural Crest and Placodal Collective Cell Migration
7.2. Collective NC Cell Motility
7.3. Directional NC Cell Migration and Emergent Patterns, Herding, and Herd Splitting
7.4. Emergent Self-Organization
7.5. The Functional Response to a Signal
7.6. Expanded Framework for Other Biological Systems
7.7. Limitations of the Study
7.8. Future Work
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cardoso, R.C.; Ferrando, A. A review of agent-based programming for multi-agent systems. Computers 2021, 10, 16. [Google Scholar] [CrossRef]
- Tang, W.; Bennett, D.A. Agent-based modeling of animal movement: A review. Geogr. Compass 2010, 4, 682–700. [Google Scholar] [CrossRef]
- Monga, P.; Sharma, M.; Sharma, S.K. A comprehensive meta-analysis of emerging swarm intelligent computing techniques and their research trend. J. King Saud-Univ.-Comput. Inf. Sci. 2022, 34, 9622–9643. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kar, A.K. Swarm intelligence: A review of algorithms. In Nature-Inspired Computing and Optimization: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2017; pp. 475–494. [Google Scholar]
- Nayyar, A.; Nguyen, N.G. Introduction to swarm intelligence. In Advances in Swarm Intelligence for Optimizing Problems in Computer Science; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 53–78. [Google Scholar]
- Matlab. version 9.10 (R2021a); The MathWorks Inc.: Natick, MA, USA, 2021. [Google Scholar]
- Barriga, E.H.; Theveneau, E. In vivo Neural Crest Cell Migration Is Controlled by “Mixotaxis”. Front. Physiol. 2020, 11, 586432. [Google Scholar] [CrossRef] [PubMed]
- DeAngelis, D.L.; Diaz, S.G. Decision-making in agent-based modeling: A current review and future prospectus. Front. Ecol. Evol. 2019, 6, 237. [Google Scholar] [CrossRef]
- Williams, H.J.; Sridhar, V.H.; Hurme, E.; Gall, G.E.; Borrego, N.; Finerty, G.E.; Couzin, I.D.; Galizia, C.G.; Dominy, N.J.; Rowland, H.M.; et al. Sensory collectives in natural systems. Elife 2023, 12, e88028. [Google Scholar] [CrossRef]
- Stonko, D.P.; Manning, L.; Starz-Gaiano, M.; Peercy, B.E. A mathematical model of collective cell migration in a three-dimensional, heterogeneous environment. PLoS ONE 2015, 10, e0122799. [Google Scholar] [CrossRef]
- Peercy, B.E.; Starz-Gaiano, M. Clustered cell migration: Modeling the model system of Drosophila border cells. Semin. Cell Dev. Biol. 2020, 100, 167–176, Place: England. [Google Scholar] [CrossRef]
- Berez, A.; Peercy, B.E.; Starz-Gaiano, M. Development and Analysis of a Quantitative Mathematical Model of Bistability in the Cross Repression System Between APT and SLBO Within the JAK/STAT Signaling Pathway. Front. Physiol. 2020, 11, 803. [Google Scholar] [CrossRef]
- Boyd, W.A.; Smith, M.V.; Kissling, G.E.; Rice, J.R.; Snyder, D.W.; Portier, C.J.; Freedman, J.H. Application of a mathematical model to describe the effects of chlorpyrifos on Caenorhabditis elegans development. PLoS ONE 2009, 4, e7024. [Google Scholar] [CrossRef]
- Hench, J.; Henriksson, J.; Lüppert, M.; Bürglin, T.R. Spatio-temporal reference model of Caenorhabditis elegans embryogenesis with cell contact maps. Dev. Biol. 2009, 333, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wood, A.J.; Ackland, G.J. Evolving the selfish herd: Emergence of distinct aggregating strategies in an individual-based model. Proc. R. Soc. Biol. Sci. 2007, 274, 1637–1642. [Google Scholar] [CrossRef] [PubMed]
- Setekera, R.; Klar, A. Numerical Simulation for Herding and Flocking Models. LAP LAMBERT Academic Publishing: London, UK, 2010. [Google Scholar]
- Lopez, U.; Gautrais, J.; Couzin, I.D.; Theraulaz, G. From behavioural analyses to models of collective motion in fish schools. Interface Focus 2012, 2, 693–707. [Google Scholar] [CrossRef] [PubMed]
- Katz, Y.; Tunstrøm, K.; Ioannou, C.C.; Huepe, C.; Couzin, I.D. Inferring the structure and dynamics of interactions in schooling fish. Proc. Natl. Acad. Sci. USA 2011, 108, 18720–18725. [Google Scholar] [CrossRef] [PubMed]
- Colombi, A.; Scianna, M.; Painter, K.J.; Preziosi, L. Modelling chase-and-run migration in heterogeneous populations. J. Math. Biol. 2020, 80, 423–456. [Google Scholar] [CrossRef]
- An, L.; Grimm, V.; Turner II, B.L. Meeting grand challenges in agent-based models. J. Artif. Soc. Soc. Simul. 2020, 23. [Google Scholar] [CrossRef]
- An, L.; Grimm, V.; Sullivan, A.; Turner Ii, B.; Malleson, N.; Heppenstall, A.; Vincenot, C.; Robinson, D.; Ye, X.; Liu, J.; et al. Challenges, tasks, and opportunities in modeling agent-based complex systems. Ecol. Model. 2021, 457, 109685. [Google Scholar] [CrossRef]
- Theveneau, E.; Steventon, B.; Scarpa, E.; Garcia, S.; Trepat, X.; Streit, A.; Mayor, R. Chase-and-run between adjacent cell populations promotes directional collective migration. Nat. Cell Biol. 2013, 15, 763–772. [Google Scholar] [CrossRef]
- Kulesa, P.M.; Fraser, S.E. Neural crest cell dynamics revealed by time-lapse video microscopy of whole embryo chick explant cultures. Dev. Biol. 1998, 204, 327–344. [Google Scholar] [CrossRef]
- Martin, P.; Parkhurst, S.M. Parallels between tissue repair and embryo morphogenesis. Development 2004, 131, 3021–3034. [Google Scholar] [CrossRef]
- Olson, H.M.; Nechiporuk, A.V. Using Zebrafish to Study Collective Cell Migration in Development and Disease. Front. Cell Dev. Biol. 2018, 6, 83. [Google Scholar] [CrossRef] [PubMed]
- Prasad, N.G.; Joshi, A. Remarks on the article on life-history traits in Drosophila populations selected for rapid development by Yadav and Sharma. J. Exp. Biol. 2015, 218, 326–327. [Google Scholar] [CrossRef] [PubMed]
- Hintze, M.; Prajapati, R.S.; Tambalo, M.; Christophorou, N.A.D.; Anwar, M.; Grocott, T.; Streit, A. Cell interactions, signals and transcriptional hierarchy governing placode progenitor induction. Development 2017, 144, 2810–2823. [Google Scholar] [CrossRef] [PubMed]
- Steventon, B.; Mayor, R.; Streit, A. Directional cell movements downstream of Gbx2 and Otx2 control the assembly of sensory placodes. Biol. Open 2016, 5, 1620–1624. [Google Scholar] [CrossRef] [PubMed]
- Theveneau, E.; Mayor, R. Collective cell migration of the cephalic neural crest: The art of integrating information. Genesis 2011, 49, 164–176. [Google Scholar] [CrossRef]
- Shellard, A.; Mayor, R. Rules of collective migration: From the wildebeest to the neural crest. Philos. Trans. R Soc. Lond. B Biol. Sci. 2020, 375, 20190387. [Google Scholar] [CrossRef]
- Giniūnaitė, R.; Baker, R.E.; Kulesa, P.M.; Maini, P.K. Modelling collective cell migration: Neural crest as a model paradigm. J. Math. Biol. 2020, 80, 481–504. [Google Scholar] [CrossRef]
- Theveneau, E.; Mayor, R. Neural crest delamination and migration: From epithelium-to-mesenchyme transition to collective cell migration. Dev. Biol. 2012, 366, 34–54. [Google Scholar] [CrossRef]
- Purves, D.; Augustine, G.; Fitzpatrick, D. The Initial Formation of the Nervous System: Gastrulation and Neurulation. In Neuroscience, 2nd ed.; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar]
- DeSesso, J.M.; Williams, A.L. Chapter 10—Periods of Susceptibility: Interspecies Comparison of Developmental Milestones During Ontogenesis of the Central Nervous System. In Handbook of Developmental Neurotoxicology (Second Edition), 2nd ed.; Slikker, W., Paule, M.G., Wang, C., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 113–125. [Google Scholar] [CrossRef]
- York, J.R.; Yuan, T.; McCauley, D.W. Evolutionary and Developmental Associations of Neural Crest and Placodes in the Vertebrate Head: Insights From Jawless Vertebrates. Front. Physiol. 2020, 11, 986. [Google Scholar] [CrossRef]
- Koontz, A. Neural Crest and Placodal Cells Contributions to Cranial Sensory Development. Ph.D Thesis, California Institute of Technology, Pasadena, CA, USA, 2021. [Google Scholar]
- Bronner, M.E. Formation and migration of neural crest cells in the vertebrate embryo. Histochem. Cell Biol. 2012, 138, 179–186. [Google Scholar] [CrossRef]
- Gilbert, S. The Neural Crest. In Developmental Biology, 6th ed.; Sinauer Associates: Sunderland, MA, USA, 2000. [Google Scholar]
- Dincer, Z.; Piao, J.; Niu, L.; Ganat, Y.; Kriks, S.; Zimmer, B.; Shi, S.H.; Tabar, V.; Studer, L. Specification of functional cranial placode derivatives from human pluripotent stem cells. Cell Rep. 2013, 5, 1387–1402. [Google Scholar] [CrossRef] [PubMed]
- Katoh, H.; Shibata, S.; Fukuda, K.; Sato, M.; Satoh, E.; Nagoshi, N.; Minematsu, T.; Matsuzaki, Y.; Akazawa, C.; Toyama, Y.; et al. The dual origin of the peripheral olfactory system: Placode and neural crest. Mol. Brain 2011, 4, 34. [Google Scholar] [CrossRef] [PubMed]
- Inman, K.E.; Caiaffa, C.D.; Melton, K.R.; Sandell, L.L.; Achilleos, A.; Kume, T.; Trainor, P.A. Foxc2 is required for proper cardiac neural crest cell migration, outflow tract septation, and ventricle expansion. Dev. Dyn. 2018, 247, 1286–1296. [Google Scholar] [CrossRef] [PubMed]
- Johnsen, J.I.; Dyberg, C.; Wickström, M. Neuroblastoma-A Neural Crest Derived Embryonal Malignancy. Front. Mol. Neurosci. 2019, 12, 9. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; He, Y.; Zhao, M.; Jiang, J. Collective cell migration: Implications for wound healing and cancer invasion. Burns Trauma 2013, 1, 21–26. [Google Scholar] [CrossRef]
- Carmona-Fontaine, C.; Matthews, H.K.; Kuriyama, S.; Moreno, M.; Dunn, G.A.; Parsons, M.; Stern, C.D.; Mayor, R. Contact inhibition of locomotion in vivo controls neural crest directional migration. Nature 2008, 456, 957–961. [Google Scholar] [CrossRef]
- Roycroft, A.; Mayor, R. Molecular basis of contact inhibition of locomotion. Cell. Mol. Life Sci. 2016, 73, 1119–1130. [Google Scholar] [CrossRef]
- Carmona-Fontaine, C.; Theveneau, E.; Tzekou, A.; Tada, M.; Woods, M.; Page, K.M.; Parsons, M.; Lambris, J.D.; Mayor, R. Complement fragment C3a controls mutual cell attraction during collective cell migration. Dev. Cell 2011, 21, 1026–1037. [Google Scholar] [CrossRef]
- Belmadani, A.; Tran, P.B.; Ren, D.; Assimacopoulos, S.; Grove, E.A.; Miller, R.J. The chemokine stromal cell-derived factor-1 regulates the migration of sensory neuron progenitors. J. Neurosci. 2005, 25, 3995–4003. [Google Scholar] [CrossRef]
- Theveneau, E.; Marchant, L.; Kuriyama, S.; Gull, M.; Moepps, B.; Parsons, M.; Mayor, R. Collective chemotaxis requires contact-dependent cell polarity. Dev. Cell 2010, 19, 39–53. [Google Scholar] [CrossRef]
- McLennan, R.; Schumacher, L.J.; Morrison, J.A.; Teddy, J.M.; Ridenour, D.A.; Box, A.C.; Semerad, C.L.; Li, H.; McDowell, W.; Kay, D.; et al. Neural crest migration is driven by a few trailblazer cells with a unique molecular signature narrowly confined to the invasive front. Development 2015, 142, 2014–2025. [Google Scholar] [CrossRef] [PubMed]
- McLennan, R.; Dyson, L.; Prather, K.W.; Morrison, J.A.; Baker, R.E.; Maini, P.K.; Kulesa, P.M. Multiscale mechanisms of cell migration during development: Theory and experiment. Development 2012, 139, 2935–2944. [Google Scholar] [CrossRef] [PubMed]
- Kulesa, P.M.; Teddy, J.M.; Stark, D.A.; Smith, S.E.; McLennan, R. Neural crest invasion is a spatially-ordered progression into the head with higher cell proliferation at the migratory front as revealed by the photoactivatable protein, KikGR. Dev. Biol. 2008, 316, 275–287. [Google Scholar] [CrossRef] [PubMed]
- Dyson, L.; Holmes, A.; Li, A.; Kulesa, P.M. A chemotactic model of trunk neural crest cell migration. Genesis 2018, 56, e23239. [Google Scholar] [CrossRef]


| Parameter Symbol | Default Value | Description |
|---|---|---|
| a | 2 | Maximum magnitude of Gaussian signal |
| c | 1 | Twice the variance of signal |
| 0.8 | Weight given by N to gradient of signal from P | |
| 0.2 | Weight given by N to gradient of signal from N | |
| 0.8 | Weight given by P to gradient of signal from N | |
| 0.2 | Weight given by P to gradient of signal from P | |
| 0.08 | Root of response of N to signal from P | |
| 0.01 | Root of response of N to signal from N | |
| 0.04 | Root of response of P to signal from N | |
| 0.005 | Root of response of P to signal from P | |
| 1 | Maximum speed of N | |
| 1 | Maximum speed of P |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fox, B.Q.; May, S.; Wallace, D. A Mathematical Model for Collective Behaviors and Emergent Patterns Driven by Multiple Distinct Stimuli Produced by Multiple Species. AppliedMath 2024, 4, 1453-1470. https://doi.org/10.3390/appliedmath4040077
Fox BQ, May S, Wallace D. A Mathematical Model for Collective Behaviors and Emergent Patterns Driven by Multiple Distinct Stimuli Produced by Multiple Species. AppliedMath. 2024; 4(4):1453-1470. https://doi.org/10.3390/appliedmath4040077
Chicago/Turabian StyleFox, Bradley Q., Spencer May, and Dorothy Wallace. 2024. "A Mathematical Model for Collective Behaviors and Emergent Patterns Driven by Multiple Distinct Stimuli Produced by Multiple Species" AppliedMath 4, no. 4: 1453-1470. https://doi.org/10.3390/appliedmath4040077
APA StyleFox, B. Q., May, S., & Wallace, D. (2024). A Mathematical Model for Collective Behaviors and Emergent Patterns Driven by Multiple Distinct Stimuli Produced by Multiple Species. AppliedMath, 4(4), 1453-1470. https://doi.org/10.3390/appliedmath4040077






