Autonomous Drifting like Professional Racing Drivers: A Survey

Abstract

Autonomous drifting is an advanced technique that enhances vehicle maneuverability beyond conventional driving limits. This survey provides a comprehensive, systematic review of autonomous drifting research published between 2005 and early 2025, analyzing approximately 80 peer-reviewed studies. We employed a modified PRISMA approach to categorize and evaluate research across two main methodological frameworks: dynamical model-based approaches and deep learning techniques. Our analysis reveals that while dynamical methods offer precise control when accurately modeled, they often struggle with generalization to unknown environments. In contrast, deep learning approaches demonstrate better adaptability but face challenges in safety verification and sample efficiency. We comprehensively examine experimental platforms used in the field—from high-fidelity simulators to full-scale vehicles—along with their sensor configurations and computational requirements. This review uniquely identifies critical research gaps, including real-time performance limitations, environmental generalization challenges, safety validation concerns, and integration issues with broader autonomous systems. Our findings suggest that hybrid approaches combining model-based knowledge with data-driven learning may offer the most promising path forward for robust autonomous drifting capabilities in diverse applications ranging from motorsports to emergency collision avoidance in production vehicles.

1. Introduction

Drift driving is a high-level skill that involves using a combination of throttle, brakes, and steering inputs to create and maintain controlled high sideslip maneuvers [1]. Compared with traditional driving methods that prioritize grip (Figure 1A), drifting (Figure 1B) can offer significant advantages in various scenarios by enhancing maneuverability and cornering speed. During drifting, the rear wheels lose traction and the vehicle slides sideways through turns.

The fundamental difference between conventional driving and drift driving can be rigorously expressed through their respective vehicle dynamic equations and turning characteristics.

In conventional driving (Figure 1A), the vehicle maintains tire grip with negligible sideslip. The dynamic equations can be expressed as follows:

$$\begin{array}{cc}\hfill \stackrel{·}{x}=vcos\left(\psi \right)& ,\stackrel{·}{y}=vsin\left(\psi \right)\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \stackrel{·}{\psi }={\displaystyle \frac{v}{L}}tan\left({\delta }_1\right)& ,\stackrel{·}{v}={\displaystyle \frac{F_x-F_{\mathrm{drag}}}{m}}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\beta }_1& \approx 0\hfill \end{array}$$

(3)

where $(x,y)$ is the vehicle position, $\psi$ is the heading angle, v is the velocity magnitude, ${\delta }_1$ is the steering angle, L is the wheelbase, $F_x$ is the longitudinal force, $F_{\mathrm{drag}}$ is the aerodynamic drag, m is the vehicle mass, and ${\beta }_1$ is the (negligible) sideslip angle.

The turning curvature for conventional driving follows the Ackermann steering geometry:

$$\begin{array}{c}\hfill {\kappa }_{\mathrm{conv}}={\displaystyle \frac{1}{R}}={\displaystyle \frac{tan\left({\delta }_1\right)}{L}},{\alpha }_1\approx 0\end{array}$$

(4)

where R is the turning radius, ${\kappa }_{\mathrm{conv}}$ is the path curvature, and ${\alpha }_1$ is the difference between the steering angle and velocity direction, which is approximately zero in conventional driving.

During drift driving (Figure 1B), the vehicle maintains a significant sideslip angle with rear wheel traction loss. The dynamic equations are as follows:

$$\begin{array}{cc}\hfill & \stackrel{·}{x}=vcos(\psi +{\beta }_2),\stackrel{·}{y}=vsin(\psi +{\beta }_2),\stackrel{·}{\psi }={\stackrel{·}{\psi }}_2\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & m{\stackrel{·}{v}}_x=m{v}_y{\stackrel{·}{\psi }}_2+F_{xf}cos{\delta }_2-F_{yf}sin{\delta }_2+F_{xr}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & m{\stackrel{·}{v}}_y=-m{v}_x{\stackrel{·}{\psi }}_2+F_{yf}cos{\delta }_2+F_{xf}sin{\delta }_2+F_{yr}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & I_z{\ddot{\psi }}_2=a(F_{yf}cos{\delta }_2+F_{xf}sin{\delta }_2)-b{F}_{yr}\hfill \end{array}$$

(8)

where ${\beta }_2$ is the significant sideslip angle, ${\stackrel{·}{\psi }}_2$ is the yaw rate, $v_x$ and $v_y$ are the longitudinal and lateral velocities in the vehicle-fixed coordinate system, $F_{xf}$, $F_{yf}$, $F_{xr}$, and $F_{yr}$ are the tire forces (which operate in the nonlinear region of the tire characteristic curve), ${\delta }_2$ is the steering angle, a and b are the distances from the center of gravity to the front and rear axles, and $I_z$ is the vehicle’s moment of inertia about the vertical axis.

The turning curvature during drifting differs significantly from conventional driving:

$$\begin{array}{cc}\hfill & {\kappa }_{\mathrm{drift}}={\displaystyle \frac{{\stackrel{·}{\psi }}_2}{vcos\left({\beta }_2\right)}}\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\alpha }_2=arctan\left({\displaystyle \frac{v_y+a{\stackrel{·}{\psi }}_2}{v_x}}\right)-{\delta }_2\ne 0\hfill \end{array}$$

(10)

where ${\kappa }_{\mathrm{drift}}$ is the path curvature during drifting, and ${\alpha }_2$ is the non-zero slip angle at the front wheels.

The key distinction is that drift driving operates with ${\beta }_2>{\beta }_{\mathrm{threshold}}$ where ${\beta }_{\mathrm{threshold}}$ is typically in the range of 5–15 degrees, depending on vehicle characteristics. This significant sideslip enables the characteristic curved trajectory while the vehicle is oriented at an angle to its direction of travel.

In motorsports, proficient drift control is critical for professional racing drivers to achieve optimal lap times, particularly on winding courses and hairpin turns. Rather than decelerating through corners, drifting at high speeds permits drivers to maintain elevated exit velocities, shaving crucial time from their laps. Certain competitions, like drifting events, directly evaluate a driver’s ability to stylishly control prolonged drift maneuvers.

While human drivers require extensive training to master the intricate skill of drift control, autonomous systems can be outfitted with specialized drift controllers that provide them with such capabilities. By utilizing autonomous drift techniques, even untrained operators could navigate racing scenarios optimally and benefit from the time-saving advantages drifting affords over traditional cornering. Moreover, in emergency situations on public roads, controlled drift capabilities could enable advanced driver assistance systems (ADASs) to perform evasive maneuvers and avoid collisions more adeptly than human operators. The lateral translation afforded by drifting allows the vehicle to circumvent obstacles that cannot be navigated through forward driving within the available time and distance. Similarly, autonomous drift control could elevate the performance of self-driving vehicles in safety-critical scenarios.

Furthermore, autonomous drifting presents novel research opportunities for vehicle dynamics. Investigating methods to induce, govern, and recover from low-traction drifting states yields insights into vehicle handling characteristics at the boundaries of adhesion. This understanding could inform control system and stability program designs focused on preventing unintended drift events. Drifting also constitutes an extreme test case for validating motion planning and control algorithms employed by self-driving vehicles.

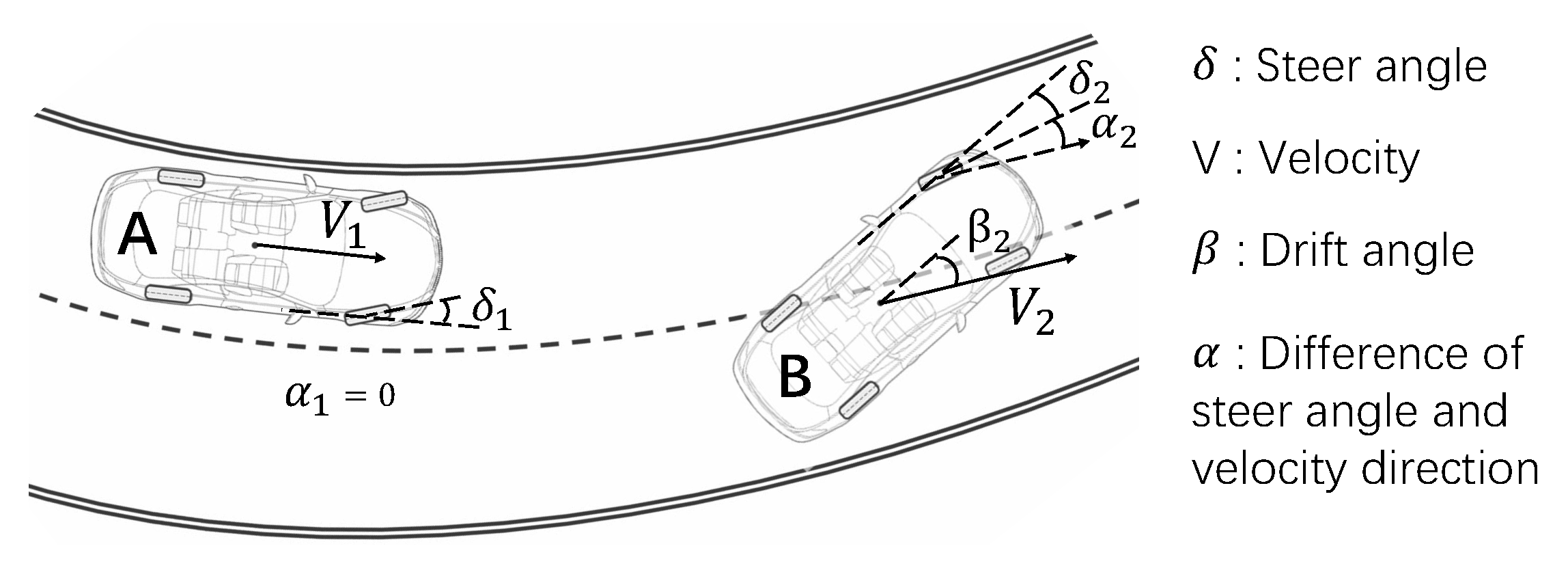
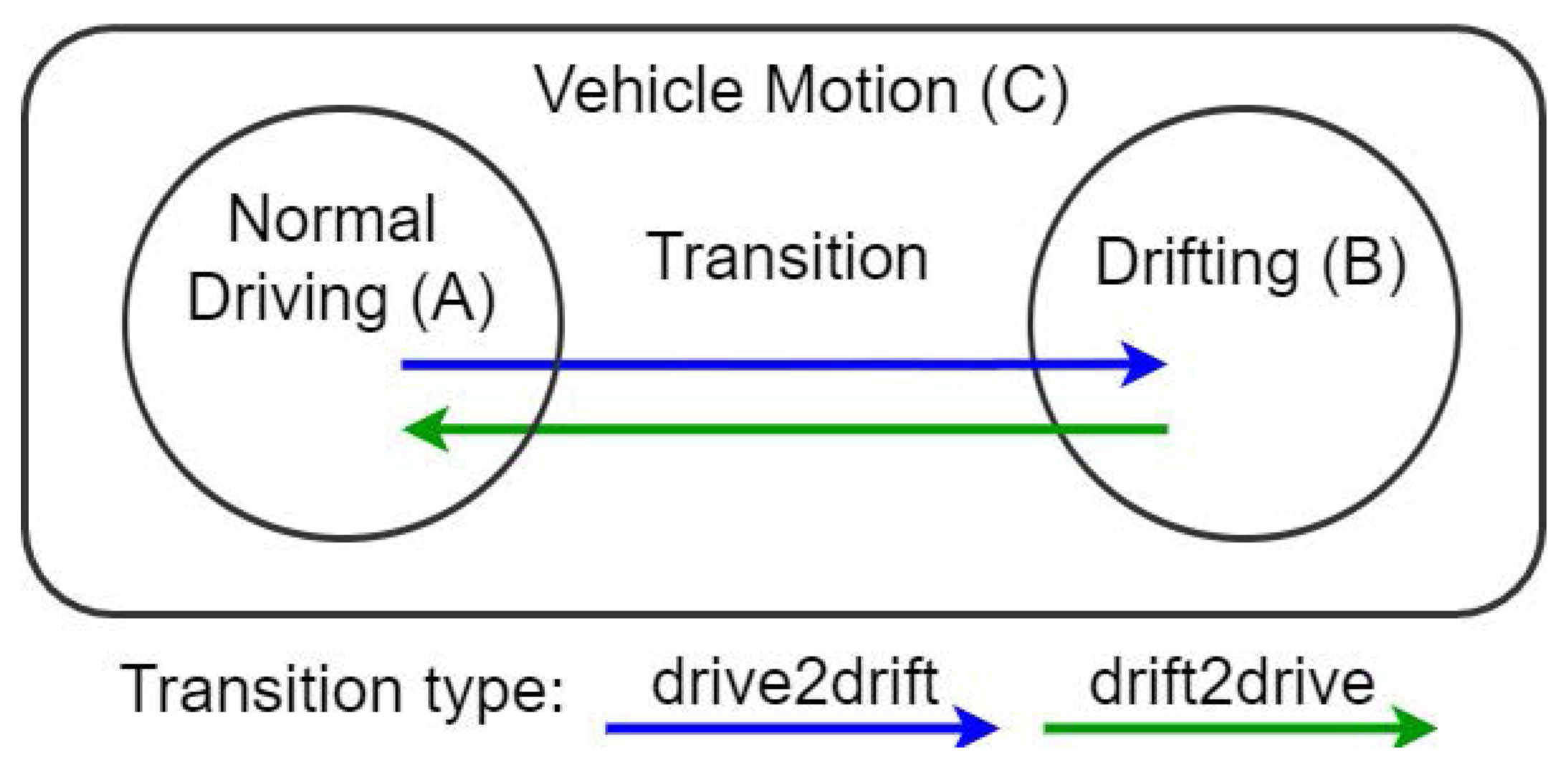
1.1. Drift Process and Techniques

The key to successful drifting is maintaining control of the vehicle while it slides sideways at high speeds. Its process can be divided into three distinct phases, as shown in Figure 2:

(Step 1)

Firstly, the lateral sideslip of the rear wheels must be induced, which is referred to as ‘start drifting’;

(Step 2)

Next, the vehicle’s motion must be controlled during the slip, including the ability to change the lateral slip direction if necessary;

(Step 3)

Finally, the drift must be terminated, and the vehicle must recover to normal driving mode.

There are typically three ways to start drifting [2]: power over, handbrake use, or a clutch kick [3]. Most researchers opt for the first two methods and utilize either rear-wheel-drive (RWD) or all-wheel-drive (AWD) vehicles to start drifting, designing their own controllers for the entire process.

The power-over drift initiation techniques can be formalized as follows:

$$\begin{array}{cc}\hfill \delta \left(t\right)& ={\delta }_{\max }·f_{\delta }(t-t_{\mathrm{init}})\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill T\left(t\right)& =T_{\max }·f_T(t-t_{\mathrm{init}})\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill B\left(t\right)& =0\hfill \end{array}$$

(13)

and handbrake drift initiation:

$$\begin{array}{cc}\hfill \delta \left(t\right)& ={\delta }_{\max }·f_{\delta }(t-t_{\mathrm{init}})\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill T\left(t\right)& =T_{\mathrm{cruise}}\hfill \end{array}$$

(15)

$$B\left(t\right)=\left\{\begin{array}{cc}{B}_{\max },\hfill & \mathrm{if}{t}_{\mathrm{init}}\le t<t_{\mathrm{init}}+\Delta t_{\mathrm{brake}}\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(16)

where $f_{\delta }\left(t\right)$ and $f_T\left(t\right)$ are time-dependent profile functions that define the application patterns of steering and throttle inputs, ${\delta }_{\max }$ is the maximum steering angle, $T_{\max }$ is the maximum drive torque, $T_{\mathrm{cruise}}$ is a constant cruise torque, $B_{\max }$ is the maximum brake pressure (typically applied to the rear wheels only), and $\Delta t_{\mathrm{brake}}$ is the duration of the brake application.

1.2. Research Methodology and Scope

This survey systematically reviews the literature on autonomous drifting following a modified PRISMA 2020 approach [4]. We conducted a comprehensive search across major engineering databases, including IEEE Xplore, ACM Digital Library, Science Direct, and Google Scholar. Search terms included combinations of “autonomous drifting”, “drift control”, “vehicle drift”, “racing control”, and “limit handling control”. We identified approximately 80 relevant studies published between 2005 and early 2025, covering both theoretical developments and experimental implementations.

Studies were included based on several criteria: (1) direct focus on autonomous drifting techniques; (2) presentation of novel control methodologies or experimental results; (3) applications in vehicle dynamics or motion control; and (4) publication in peer-reviewed venues. We excluded studies focused solely on conventional vehicle stability control without explicit drifting objectives.

1.3. Survey Organization

This paper is organized as follows: Section 2 presents various scenarios where autonomous drifting techniques have been applied, including racing, exhibitions, and safety-critical situations. Section 3 categorizes and analyzes the surveyed methods into two main groups: dynamical methods and deep learning approaches, examining their underlying principles, advantages, and limitations. Section 4 provides details on experimental platforms used in autonomous drifting research, including simulators, scaled models, and full-sized vehicles, with particular attention to sensor configurations and computational requirements. Section 5 discusses current challenges, future research directions, and potential applications. Finally, Section 6 concludes the survey with a summary of key findings and insights for researchers and practitioners in the field.

2. Scenarios of Autonomous Drifting Research

Autonomous drift techniques are developed and evaluated across diverse scenarios, each presenting unique challenges and performance requirements. This section categorizes and analyzes the primary application contexts where autonomous drifting has been investigated: competitive racing, exhibition demonstrations, and safety-critical collision avoidance. Understanding these scenarios provides essential context for evaluating the capabilities and limitations of different autonomous drifting approaches.

2.1. Drift in Racing

Racing represents one of the most demanding applications for autonomous drifting, requiring both speed optimization and precise trajectory control. Skilled drifting ability is essential for professional racing drivers to achieve optimal results in many racing events such as the FIA World Rally Championship [5], where controlled slides through corners can significantly reduce lap times.

Researchers have developed autonomous drift controllers specifically optimized for racing [6] and drifting cornering [7] scenarios, as shown in Figure 3. In racing contexts, drift controllers must balance multiple competing objectives: maintaining high exit velocities, minimizing lap times, adapting to variable surface conditions, and ensuring vehicle stability during high-speed maneuvers.

Racing scenarios are particularly valuable for autonomous drifting research. They provide quantifiable metrics for performance evaluation, including lap times, exit velocities, and trajectory adherence. Additionally, the competitive nature of racing creates an objective benchmark for comparing different drifting control strategies across varying track conditions and vehicle configurations.

2.2. Drift Show Scenarios

Drift shows are an effective way to showcase drifting skills in a clear and dramatic manner, while also serving as well-defined benchmarks for comparing different drift control approaches. These scenarios present specific technical challenges that test various aspects of autonomous drift controllers. Many researchers experiment with their drift controllers in the following structured scenarios:

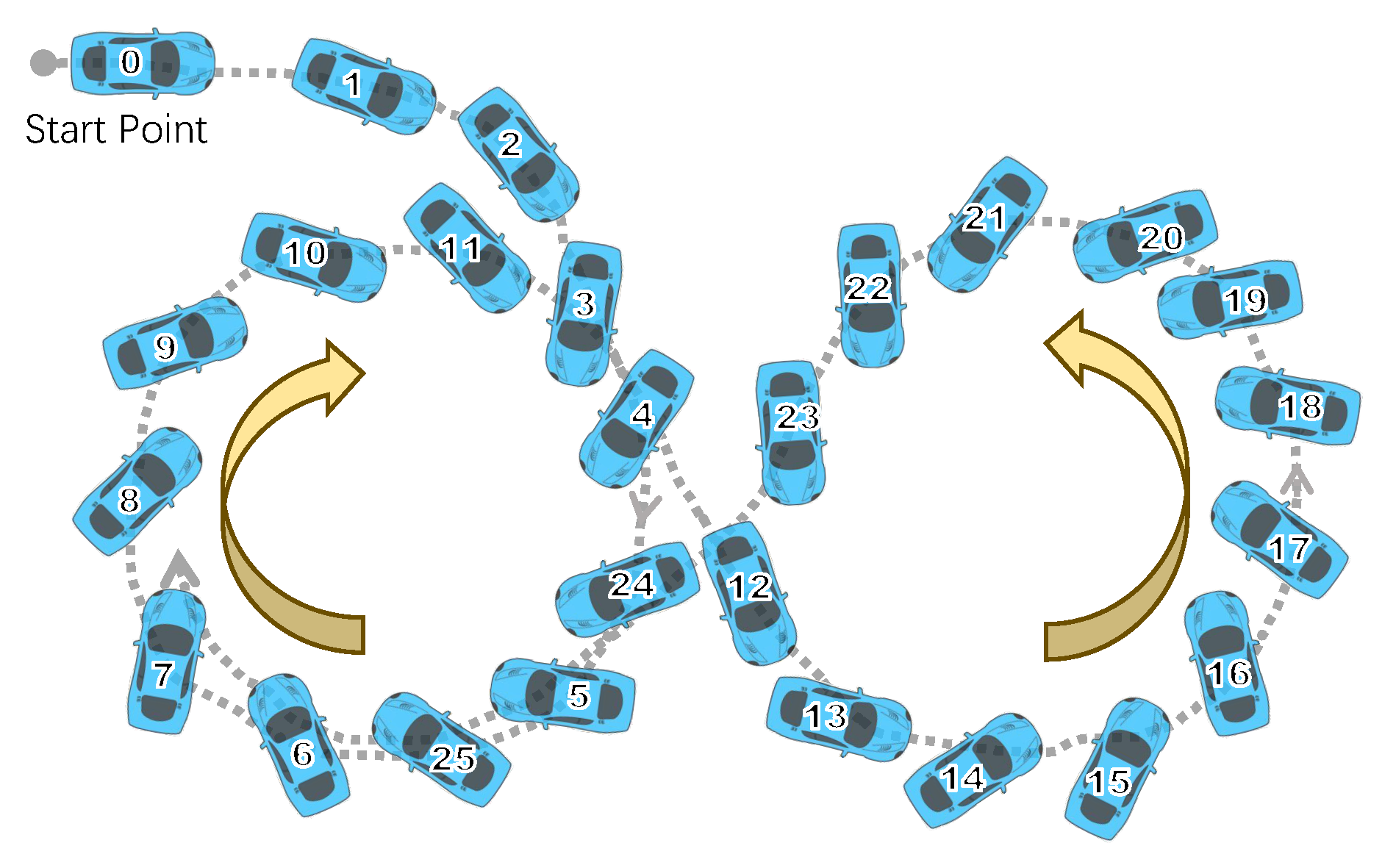
2.2.1. Circle Drift

Circle drift [8,9,10] involves maintaining a constant sideslip angle while following a circular trajectory, as shown in Figure 4. This scenario tests a controller’s ability to maintain a steady-state drift equilibrium, requiring precise balance between steering input and throttle control. MARTY, Stanford’s retrofitted DeLorean, demonstrated impressive performance in this scenario with sustained drifts at speeds up to 12 m/s and yaw rates of 1.25 rad/s [8]. Recent work by Ding et al. [11] has further advanced circle drift capabilities using neural network-based MPC approaches to adapt to unknown tire characteristics.

Circle drift maneuvers can be mathematically formalized as a steady-state drifting equilibrium characterized by the following:

$$\begin{array}{cc}\hfill \stackrel{·}{x}=0,{\stackrel{·}{v}}_x& =0,{\stackrel{·}{v}}_y=0\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \stackrel{·}{r}& =0\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathrm{with}\mathrm{constant}r={\displaystyle \frac{v}{R}}& ,\beta >{\beta }_{\mathrm{threshold}}\hfill \end{array}$$

(19)

where R is the radius of the circular trajectory, r is the constant yaw rate, v is the constant vehicle speed, and $\beta$ is the non-zero sideslip angle maintained throughout the maneuver.

2.2.2. Figure-8 Drift

“Figure-8” drifting [12,13,14] represents a more challenging scenario, where the vehicle must transition between the left and right drifts while following a figure-8 path, as shown in Figure 5. This maneuver tests a controller’s ability to handle drift direction reversals and sideslip angle transitions. Lee et al. [12] addressed the computational challenges of this scenario by developing a DNN-based controller trained on MPC data, achieving real-time performance without sacrificing control quality. Zhou et al. [14] further advanced this approach using adaptive learning-based MPC to achieve smooth transitions between opposite drift directions at speeds up to 17 m/s. Figure-8 drift requires transitioning between left and right drifting states, which can be characterized by the desired trajectory and sideslip angle profile:

$$\begin{array}{cc}\hfill p_{ref}\left(t\right)& =\left[\begin{array}{c}asin\left(\omega t\right)\\ bsin\left(2\omega t\right)\end{array}\right]\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\beta }_{ref}\left(t\right)& ={\beta }_{max}·\mathrm{sign}(sin\left(2\omega t\right))\hfill \end{array}$$

(21)

where $p_{ref}\left(t\right)$ is the reference position at time t, parameters a and b define the figure-8 dimensions, $\omega$ controls the traversal speed, ${\beta }_{max}$ is the maximum desired sideslip angle, and the sign function determines the drift direction.

2.2.3. Open-Loop Drifting

Open-loop drifting [15,16] involves initiating and maintaining a drift through a predefined sequence of control inputs without closed-loop feedback, as illustrated in Figure 6. This scenario evaluates the controller’s understanding of the vehicle dynamics and drift initialization techniques. Acosta and Kanarachos [15] tackled this challenge by using neural networks to learn open-loop control sequences from demonstration data, later incorporating feedforward components into their MPC frameworks to improve performance. This approach bridges the gap between model-based control and learning-based methods, demonstrating how hybrid approaches can leverage the strengths of both paradigms.

To mathematically describe the open-loop drifting trajectory, we can formulate the path and vehicle states as functions of a path parameter. Unlike circle drift, which maintains a constant radius and sideslip angle, open-loop drifting follows a predefined trajectory with varying curvatures and sideslip angles:

$$p_{ref}\left(s\right) = \left[\begin{array}{c}{x}_{ref}\left(s\right)\\ y_{ref}\left(s\right)\end{array}\right] = \left[\begin{array}{c}{\int }_0^{s}cos\left({\theta }_{ref}\left(\sigma \right)\right)d\sigma \\ {\int }_0^{s}sin\left({\theta }_{ref}\left(\sigma \right)\right)d\sigma \end{array}\right]$$

(22)

$$\begin{array}{cc}\hfill {\theta }_{ref}\left(s\right)& ={\int }_0^s{\kappa }_{ref}\left(\sigma \right)d\sigma \hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill {\kappa }_{ref}\left(s\right)& ={\displaystyle \frac{1}{R\left(s\right)}}\hfill \end{array}$$

(24)

where s is the path parameter (arc length), $p_{ref}\left(s\right)$ is the reference position, ${\theta }_{ref}\left(s\right)$ is the path heading angle, ${\kappa }_{ref}\left(s\right)$ is the path curvature, and $R\left(s\right)$ is the radius of curvature at point s.

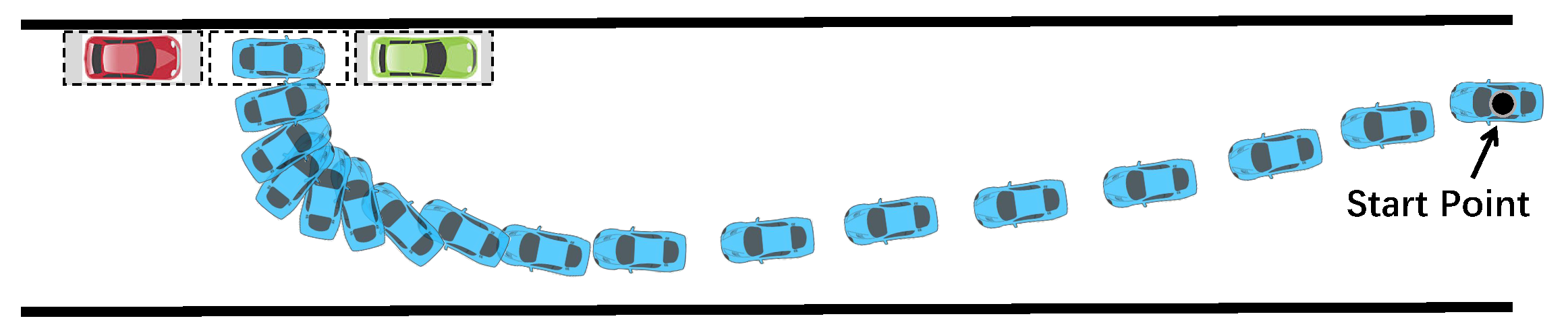
2.2.4. Drift Parking

Drift parking [3,17,18] represents a challenging terminal control problem where the vehicle must perform a high-speed drift maneuver that ends with the vehicle precisely positioned in a parking spot, as shown in Figure 7. This scenario tests not only drift control but also precise planning and estimation capabilities. Kolter et al. [17] pioneered this approach using a mixed open-loop and closed-loop control strategy, successfully executing drift parking maneuvers at speeds of up to 31.29 m/s (70 mph). More recently, Bellegarda and Nguyen [18] developed a nonlinear MPC approach with a fused kinematic–dynamic bicycle model to achieve more reliable drift parking with improved robustness to model uncertainties.

2.3. Drift for Safety in Dangerous Situations

Beyond entertainment and motorsports applications, autonomous drifting techniques have significant potential for enhancing vehicle safety in critical situations. These applications represent the most practical use cases for autonomous drifting technology in production vehicles.

2.3.1. Emergency Collision Avoidance

Car manufacturers have invested significant effort into developing collision avoidance systems that can automatically change lanes to prevent front-end collisions [19]. However, conventional collision avoidance systems have fundamental limitations in extreme scenarios where standard steering or braking maneuvers are insufficient. Recent research has explored using controlled drift maneuvers for emergency collision avoidance [20,21,22,23], as illustrated in Figure 8.

Zhao et al. [20,24] developed the HOTDOG (handling of transition with the docking optimized geometry) controller, which enables smooth transitions between normal driving and drifting modes for effective collision avoidance. Their work demonstrated that controlled drift maneuvers can navigate obstacles that would be impossible to avoid with conventional control approaches. Building upon this foundation, Zhao et al. [23] recently integrated reinforcement learning with reachability analysis to create a safety-aware drift controller that balances performance and safety guarantees—a critical consideration for real-world deployment.

2.3.2. Post-Collision Stabilization

Another important safety application involves stabilizing vehicles after initial collisions to prevent secondary accidents. Researchers have developed controllers for stabilizing a vehicle’s yaw motions after high-speed rear-end collisions [25,26], as shown in Figure 9. Yin et al. [25] employed deep reinforcement learning techniques to develop a self-learning drift controller that can maintain vehicle stability even when the rear tires’ grip is severely compromised after a collision. Their approach demonstrated superior performance compared to traditional stability control systems in these extreme scenarios.

Stano et al. [26] further advanced this concept by developing an integrated autonomous drifting and direct yaw moment control system via nonlinear MPC. Their approach provides enhanced active safety in scenarios where conventional stability control systems would fail, demonstrating the potential for autonomous drifting technology to complement existing safety systems in production vehicles.

2.3.3. Future Safety Applications

Emerging research suggests additional safety applications for autonomous drifting technology. Weng et al. [27] proposed an aggressive cornering framework that combines trajectory planning with drift control, allowing vehicles to navigate sharp turns safely at speeds that would cause conventional controllers to fail. Similarly, Jia et al. [28] developed a nonlinear drift control specifically for sharp turns, demonstrating improved vehicle stability and safety in these challenging scenarios.

The various scenarios discussed in this section highlight the diverse potential applications of autonomous drifting technology. While drifting is commonly associated with motorsports and exhibitions, the ability to induce and control slides can also offer significant advantages for collision avoidance and vehicle stabilization in safety-critical situations on public roads.

As autonomous vehicle technology progresses toward higher levels of autonomy, the ability to handle non-standard driving situations like drifting will become increasingly crucial. The scenarios outlined in this chapter demonstrate the breadth of environments where drift control capabilities could prove advantageous, motivating continued research efforts in this emerging field.

3. Methods in Autonomous Drifting Research

The primary objective of controllable drifting is to track the vehicle’s velocity vector along a given route while stabilizing the lateral slip through the use of yaw acceleration [29]. Some researchers have proposed dynamical methods, which involve analyzing the vehicle’s dynamics and designing controllers based on their understanding of the vehicle’s models. Other researchers have presented deep learning methods to achieve autonomous drifting without a vehicle’s dynamics model.

3.1. Dynamical Methods

Early in 2005, Velenis et al. [30] conducted research on reproducing race-driving behaviors, including drifting. They utilized a half-car model, which is also known as a bicycle model, to analyze the car’s dynamics. This model has since become widely used in many racing car research studies. Through the use of numerical optimization techniques, they were able to achieve realistic drifting behaviors.

The dynamical methods for autonomous drifting predominantly rely on accurate modeling of vehicle dynamics. The most widely adopted model is the bicycle model, where the left and right wheels are lumped together. The nonlinear bicycle model equations of motion can be expressed as follows:

$$\begin{array}{cc}\hfill m{\stackrel{·}{v}}_x& =m{v}_{y}r+F_{xf}cos\delta -F_{yf}sin\delta +F_{xr}\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill m{\stackrel{·}{v}}_y& =-m{v}_{x}r+F_{yf}cos\delta +F_{xf}sin\delta +F_{yr}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill I_z\stackrel{·}{r}& =a(F_{yf}cos\delta +F_{xf}sin\delta )-b{F}_{yr}+M_z\hfill \end{array}$$

(27)

where $v_x$ and $v_y$ are the longitudinal and lateral velocities in the vehicle-fixed coordinate system, r is the yaw rate, $\delta$ is the front wheel steering angle, $F_{xf}$ and $F_{yf}$ are the longitudinal and lateral tire forces at the front wheel, $F_{xr}$ and $F_{yr}$ are the corresponding forces at the rear wheel, a and b are the distances from the center of gravity to the front and rear axles, respectively, $I_z$ is the vehicle’s moment of inertia about the vertical axis, and $M_z$ is any external yaw moment. The vehicle sideslip angle $\beta$ can be calculated as $\beta =arctan(v_y/v_x)$.

In 2010, Voser et al. [31] proposed a relatively simple analytical framework for analyzing the dynamics of drifting. Building upon this work, Zubov et al. [32] developed a drift controller aimed at achieving drift stability. Their controller is capable of drifting and stabilizing an RWD car around an equilibrium state in a simulator using the robot operating system (ROS). They established a mechanical model, tire model, and two-state equilibrium model for the car. The primary objective of the drift controller is to maintain the vehicle in an equilibrium state by controlling the acceleration and steering. The controller was developed by calculating feedback gains and errors in the lateral velocity and yaw rate.

Researchers from Stanford University retrofitted a DeLorean RWD car and used it for drift experiments, naming it “MARTY”. Building upon this work, Goh et al. designed a drift controller to track a reference path [8]. They treated the reference trajectory as a sequence of unstable drifting equilibria and imposed stable dynamics on both look-ahead error and sideslip. Experiments on MARTY showed good tracking performance. Two years later, they proposed a method that does not assume operation near an equilibrium point [29]. They also improved their research by incorporating wheel dynamic control [33], which resulted in significant advantages in control bandwidth and robustness.

Most research on drift control has focused on initiating and maintaining drifting, but Zhao et al. [20] proposed a mode-switching controller for collision avoidance called the HOTDOG control. As shown in Figure 8, the system helps the car move through obstacles while maintaining high maneuverability during drifting. They solved the problems of transitioning from drive to drift, changing drift orientation, and transitioning from drift to drive. As a result, the drift control problem can be simplified to the transition between normal driving mode and drifting mode, as shown in Figure 10. This controller demonstrated good performance in their simulation experiments, particularly when compared with the baseline Stanley controller and MARTY controller.

3.1.1. Models in Dynamical Methods

Some essential models are required in any dynamical methods research:

(a)

Vehicle dynamics model: Commonly used vehicle dynamics models include the bicycle model and its variants [30,31,32], a 3-degree-of-freedom (DOF) vehicle model [34], and a 9-DOF double-track vehicle model [22]. Recent work by Goh et al. [35] has explored fusing kinematic and dynamic models to better handle highly transient drifting states.

(b)

Steering tire force model: Researchers typically rely on the Pacejka tire model [36] as the basis. Other models, such as the nonlinear Fiala tire model [31] and the UniTire model [37], have also been used. Djeumou et al. [38] recently introduced learned tire models that can be trained with minimal data for improved accuracy in extreme slip conditions.

(c)

Driving tire force model: Researchers usually choose the same type of tire model as the steering tire model as the foundation and formulate the driving tire force to analyze the vehicle dynamics.

The accuracy of tire force models is crucial for drift control. The widely used Pacejka Magic Formula tire model characterizes the nonlinear relationship between the tire slip and generated forces:

$$\begin{array}{cc}\hfill F_y\left(\alpha \right)& =D_{y}sin[C_{y}arctan\{B_y\alpha -E_y(B_y\alpha -arctan\left(B_y\alpha \right))\}]\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill F_x\left(\kappa \right)& =D_{x}sin[C_{x}arctan\{B_x\kappa -E_x(B_x\kappa -arctan\left(B_x\kappa \right))\}]\hfill \end{array}$$

(29)

where $\alpha$ is the tire slip angle, $\kappa$ is the longitudinal slip ratio, and the parameters B, C, D, and E define the shape of the curve. Specifically, B is the stiffness factor, C is the shape factor, D is the peak value, and E is the curvature factor.

For drift control applications, the combined slip condition is particularly important, as lateral and longitudinal slips occur simultaneously. The extended Magic Formula for combined slip conditions is as follows:

$$\begin{array}{cc}\hfill F_x(\kappa ,\alpha )& =F_{x0}\left(\kappa \right)·G_{x\alpha }\left(\alpha \right)\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill F_y(\kappa ,\alpha )& =F_{y0}\left(\alpha \right)·G_{y\kappa }\left(\kappa \right)\hfill \end{array}$$

(31)

where $F_{x0}$ and $F_{y0}$ are the pure slip forces, and $G_{x\alpha }$ and $G_{y\kappa }$ are weighting functions that account for the reduction in force capability under combined slip conditions.

Some additional models incorporate more vehicle systems to achieve higher fidelity simulation and control. While the basic models above capture essential dynamics, these supplementary models address specific physical phenomena that become critical during extreme maneuvers. The additional models include the following:

(a)

Roll dynamics model: Considers rollover constraints and lateral load transfer during high-speed cornering [37]. This model captures weight shifts between inner and outer wheels during drift, affecting tire grip and enabling controllers to better predict stability limits during aggressive maneuvers.

(b)

Rear axle differential system model: Considers torque distribution between driving wheels through the vehicle differential system [9]. Stano et al. [26] expanded this to include direct yaw moment control, allowing for enhanced stability during drifting by dynamically adjusting torque between wheels.

(c)

Suspension dynamics model: Considers how the vehicle suspension system affects weight transfer and tire forces during aggressive maneuvers [30]. This model accounts for pitch and heave motions that impact tire-road contact during drift, leading to more realistic behavior prediction.

3.1.2. Controllers in Dynamical Methods

Using the above models, an auto drift controller can be designed, which typically includes path tracking control, sideslip stabilization control, and wheel-speed control. Various methods can be used to build the controller, such as fuzzy-integral sliding-mode controllers (FISMCs) [39], model predictive control (MPC) [18], linear quadratic regulator (LQR) [40], linear matrix inequality (LMI) [41], finite-state machines (FSM) [42], and numerical optimization [7]. Some research also applied equilibrium analysis [43], drive torque control [9], or look-ahead error regulation [8] for better precision in control.

Among the controller designs used for autonomous drifting, model predictive control (MPC) has been particularly effective due to its ability to handle constraints and predict future vehicle states. The general MPC formulation for drift control can be expressed as follows:

$$\begin{array}{cc}\hfill \underset{u_{0:N-1}}{min}& \sum _{k=0}^{N-1}\left[{(x_k-x_{ref,k})}^{T}Q(x_k-x_{ref,k})+u_k^{T}R{u}_k\right]+{(x_N-x_{ref,N})}^{T}P(x_N-x_{ref,N})\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}:& x_{k+1}=f(x_k,u_k),k=0,1,\dots ,N-1\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & x_0=x\left(t\right)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill & x_k\in \mathcal{X},k=0,1,\dots ,N\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & u_k\in \mathcal{U},k=0,1,\dots ,N-1\hfill \end{array}$$

(36)

where $x_k$ is the state vector typically consisting of ${[v_x,v_y,r,\beta ,x,y,\psi ]}^T$, $u_k$ is the control input vector comprising ${[\delta ,T]}^T$ (steering angle and drive/brake torque), $x_{ref,k}$ is the reference state trajectory (including desired drift equilibrium states), $f(x_k,u_k)$ represents the vehicle dynamics, Q, R, and P are weighting matrices, and $\mathcal{X}$ and $\mathcal{U}$ are the feasible state and control input sets, respectively. For drift control, these constraints typically include limits on steering angle, torque, and various stability criteria to ensure controllable drifting.

Recent advances include Tavolo et al.’s [44] integration of rear-wheel steering with nonlinear MPC for enhanced path tracking, Shi et al.’s [45] robust nonlinear MPC formulation for handling model uncertainties, and Jia et al.’s [28] specialized nonlinear drift controller for sharp turns in autonomous vehicles.

3.1.3. Summary and Limitations of Dynamical Methods

Table 1. A summary of dynamical methods for autonomous drifting.

Research	Models and Methods	Experiments Platform	Experiments	Speed (m/s)	Drifting Yaw Rate (Rad/s)
Velenis et al. (2011) [9]	Rear axle differential system model. drive torque control	Simulator: CarSim	Circle drift	up to 8	up to 1.4
Kritayakirana et al. (2012) [10]	LQR	Real car: Shelley, Stanford’s autonomous Audi TTS, an all-wheel drive car	Circle drift	45	0.5
Goh et al. (2020) [33]	Nonlinear model inversion, LQR	Real car: MARTY, a rear-wheel car	Circle drift	up to 12	up to 1.25
Joa et al. (2020) [46]	Vehicle dynamic model, No tire model or road friction coefficient	Real car: an RWD GENESIS car	Circle drift	15.27	0.52
Park et al. (2021) [40]	3-DOF vehicle model. LQR	Model car: A 1:10 scale car	Circle drift	1.1	2.7
Xu et al. (2021) [41]	Nonlinear tire model, UniTire. Robust Control, LMI	Simulator: SimulinkTM	Circle drift	9.5	0.7
Hou et al. (2022) [39]	3-DOF double-track model, Pacejka coupled-slip model. FISMC	Simulator: CarMaker	Circle drift	8.5	0.65
Shi et al. (2023) [45]	3-DOF model. Nonlinear MPC	Simulator: MatlabTM R2015b	Circle drift	20	0.3
Gonzales et al. (2016) [16]	LQR	Simulator: CarSim and model car: 1/10 scale RC vehicle	Open-loop drifting	1.5	1.8
Bellegarda et al. (2021) [18]	Fused kinematic–dynamic bicycle model. MPC	Simulator: Gazebo	Circle drift, drift parking	Up to 4 during drift parking	Up to 3 during drift parking
Kolter et al. (2010) [17]	Closed-loop control in the well-modeled regions, open-loop control in the difficult-to-model regions	Real car	Drift parking	31.29 (70 mph)	N/A
Jakobsen (2011) [13]	Nonlinear two-track vehicle model, linearized vehicle model. Feedback linearizing controller	Simulator: SimulinkTM	“Figure 8” Drifting	3.5	1
Dong et al. (2022) [47]	Real-time drift trajectory tracking controller (DTTC), MPC	Simulator: CarSim	“Figure 8” Drifting	7.5	33
Velenis et al. (2005) [30] (2007) [7]	A bicycle model with suspension dynamics. Numerical optimization	Simulator: CarSim	Drift cornering	13	0.89
Voser et al. (2010) [31]	Two-state bicycle model, nonlinear Fiala tire model	Real car: P1, a rear-wheel drive research platform	Drift cornering	8	0.6
Kritayakirana et al. (2010) [48]	Longitudinal feedforward and feedback control	Real car: P1	Drift cornering	7.3	0.6
Acosta et al. (2016) [42]	Two-track vehicle model, Pacejka tire model. FSM	Simulator: SimulinkTM	Drift cornering	N/A	up to 2.01
Zubov et al. (2018) [32]	Mechanical bicycle model, nonlinear tire model, two-state equilibrium model	Simulator: an all-wheel drive car in Speed Dreams	Drift cornering	14	0.9
You et al. (2018) [49] (2019) [50]	LQR	Simulator: CarSim and model car: 1:15 scale AutoRally platform developed at Georgia Tech	Drift cornering	8.18	0.68
Stano et al. (2023) [26]	Nonlinear MPC	Simulator: CarMaker	Drift cornering	8.9	0.70
Tavolo et al. (2024) [44]	Nonlinear MPC	Real car: A four-wheel-drive electric vehicle	Drift cornering	12.5	2.62
Hindiyeh et al. (2010) [51] (2014) [52]	Three-state bicycle model	Real car: P1	Drifting along given trajectories	6	about 0.6
Beal et al. (2012) [53]	Linear bicycle model, lateral Fiala tire model, affine force input (AFI) model. MPC	Real car: P1	Drifting along given trajectories	10	0.5
Goh et al. (2016) [8] (2018) [29] (2024) [35]	Force-based single-track model	Real car: MARTY	Drifting along given trajectories	6.9 to 12.5	up to 1.2
Laurense et al. (2017) [54] (2018) [55]	Single-track vehicle model. Feedback–feedforward steering control	Real car: Shelley	Drifting along given trajectories	30	N/A
Acosta et al. (2018) [56]	Hierarchical control architecture, MPC	Simulator: CarMaker	Drifting along given trajectories	14	0.35
Goel et al. (2020) [57]	Transform from an underactuated to a fully-actuated system with the use of front-wheel braking	Real car: MARTY	Drifting along given trajectories	about 8.7	up to 11.25
Chen et al. (2023) [43]	Hierarchical dynamic drifting controller (HDDC), MPC, LQR, Equilibrium analysis	ECU hardware-in-the-loop platform	Drifting along given trajectories	8	0.8
Zhang et al. (2017) [58] (2018) [59]	Hybrid rapidly-exploring random trees, rule-based path planning, mixed open-loop and closed-loop control strategy, LQR	Simulator: CarSim and model car: 1/10 scale car	Oval loop race	N/A	N/A
Xu et al. (2022) [37]	Roll dynamics model, UniTire model. MPC	Simulator: SimulinkTM	Oval loop race	15	0.41
Funke et al. (2015) [60]	Four-wheel steering controller and two-wheel steering predictive controller	Real car: Shelley	Lane change obstacle avoidance	20 to 30	up to 0.78
Fors et al. (2020) [22]	Friction-limited particle model, 9DoF double-track vehicle model	Simulator: a Ford Focus in CarMaker	Collision avoidance within safe braking distance on a highway	19.4	up to 0.65
Wurts et al. (2020) [21]	Pacejka tire model, Kreisselmeier–Steinhauser (KS) Aggregation. MPC, IPOPT solver	Simulator	Collision avoidance within safe braking distance on a highway	30	N/A
Chen et al. (2021) [34]	3-DOF vehicle model and tire model. Linear time-varying MPC, nonlinear MPC, receding horizon control (RHC), unscented Kalman filter (UKF) estimator	Simulator: CarSim	Lane change	25	up to 0.8
Zhao et al. (2021) [20]	Tailored optimal control, handling of transition with the docking optimized geometry (HOTDOG) method	Simulator: SimulinkTM	Collision avoidance within safe braking distance on a highway	1	up to 2
Kai et al. (2022) [61]	LQR controller, IPOPT solver	Simulator: an A0 level RWD car	Lane change obstacle avoidance	5.7	up to 1
Zhao et al. (2022) [24,62]	Optimal preview longitudinal control, Stanley lateral control, HOTDOG controller	Simulator: SimulinkTM	Lane change obstacle avoidance	15	0.26
Kehrle et al. (2011) [63]	Pacejka’s Magic Formula tire model. Linear time-varying MPC, nonlinear MPC, receding horizon control (RHC), unscented Kalman filter (UKF) estimator	Simulator: a Porsche 911 club sports car in VDrift	Racing	up to 60	N/A
Kapania et al. (2015) [64]	Feedback–feedforward steering control	Real car: Shelley	Racing	13	1
Liniger et al. (2015) [65,66] (2018) [67]	Nonlinear MPC, hierarchical receding horizon controller (HRHC)	Model car: a 1:43 scale RC cars	Racing with multiple cars	3	N/A
Reiter et al. (2021) [68]	Single-track vehicle model. Multiple-shooting nonlinear program, combinatorial optimization by mixed-integer programming (COMIP)	Simulator: ROS	Racing with obstacles	5	N/A

provides a summary of various research studies that have utilized dynamical methods for auto drift control. These studies have employed different vehicle models, controller designs, and experimental setups to achieve their objectives.

The dynamical methods reviewed in this section rely heavily on accurate vehicle dynamics models and tire force models to design drift controllers. This model-based approach offers some inherent strengths and weaknesses.

A key advantage of dynamical methods is that by explicitly modeling the underlying physics, the controllers can potentially achieve very precise drift control performance when the models accurately represent the real vehicle’s behavior. The use of techniques like MPC, LQR, and numerical optimization allows these controllers to plan and track reference trajectories while respecting the modeled dynamics and constraints.

However, several important limitations emerge from our analysis:

(1)

Model fidelity challenges: Developing sufficiently accurate vehicle and tire models, especially at the limits of handling, remains an ongoing challenge. The fidelity of the models used can significantly impact the controllers’ real-world capabilities. Overly simplistic models like the ubiquitous bicycle model may fail to capture important effects, while excessively complex high-order models can be computationally expensive and difficult to parameterize. Studies by Goh et al. [35] and Tavolo et al. [44] highlight how small inaccuracies in tire models can lead to significant performance degradation during extreme maneuvers.

(2)

Parameter identification complexity: Many dynamical approaches require precise identification of numerous vehicle and tire parameters. As demonstrated by Acosta et al. [15,56], these parameters can be difficult to identify accurately, especially for tire models under combined slip conditions. Moreover, parameters like road friction coefficients can vary dynamically during operation, further complicating model-based approaches.

(3)

Computational burden: Real-time implementation of optimization-based controllers like MPC presents significant computational challenges. Stano et al. [26] reported computational times ranging from 5–20 ms per iteration for their nonlinear MPC implementation, pushing the limits of current automotive-grade hardware. This burden increases with model complexity, creating a tension between model fidelity and computational feasibility.

(4)

Limited environmental adaptability: Dynamical methods may face challenges with generalization to previously unseen environments due to their dependence on specific vehicle models and parameter values. Factors like road material, temperature, and wetness can substantially impact friction characteristics, as noted by Bellegarda et al. [18]. Capturing all possible conditions and circumstances in simulations and models remains difficult.

(5)

Linearization approximations: Many controllers rely on linearization of nonlinear dynamics around operating points, as seen in studies by Zubov et al. [32] and Hou et al. [39]. While this simplifies controller design, it can lead to performance degradation when the system deviates significantly from the linearization points—a common occurrence during aggressive drifting maneuvers.

(6)

State estimation uncertainties: Effective implementation of model-based controllers requires accurate state estimation, including challenging measurements like lateral velocity and tire slip angles. Errors in state estimation can propagate through model-based controllers, potentially destabilizing the system. Hindiyeh and Gerdes [52] specifically addressed this challenge by developing robust estimators for sideslip angles during drift maneuvers.

In summary, while dynamical drift control methods offer high precision when accurately modeling the vehicle, their robustness depends heavily on the fidelity of the underlying models and the accuracy of parameter estimates. Deep learning methods discussed in the next section take an opposing data-driven approach to overcome some of these limitations. The two methodologies have complementary strengths and could potentially be combined in a hybrid framework to leverage the precision of model-based approaches with the adaptability of learning-based methods.

3.2. Deep Learning Methods

Dynamical methods heavily rely on explicit modeling of vehicle dynamics and environments. As a result, these algorithms may be difficult to generalize to other vehicles or roads. To address this, researchers have begun exploring the use of deep learning (DL), particularly reinforcement learning (RL), in autonomous drifting.

Table 2. Some learning methods commonly used for auto drift.

Methods	Full Name	Category
PILCO	Probabilistic inference for learning control	Model-based RL method
DHP	Dual heuristic programming	Model-based RL method
DQN	Deep Q network	Model-free off-policy RL
DDPG	Deep deterministic policy gradients	Model-free on-policy RL
SAC	Soft actor–critic	Model-free on-policy RL
A3C	Asynchronous advantage actor–critic	Model-free on-policy RL
TD3	Twin delayed DDPG	Model-free on-policy RL
LSTM	Long short-term memory	Deep learning method
DNN	Deep neural network	Deep learning method
GPR	Gaussian process regression	Machine learning method

provides a summary of commonly used DL methods in this area.

Reinforcement learning is a method that optimizes decision-making through trial-and-error learning. In this method, an agent learns how to take optimal actions by interacting with the environment and maximizing its long-term cumulative reward. The rewards and punishments that the agent receives from the environment guide it toward taking the right actions and avoiding the wrong ones. By using this method, researchers have been able to develop autonomous drift controllers that can adapt to various road conditions and vehicle types.

Reinforcement learning methods formulate the drift control problem as a Markov decision process (MDP). The objective is to find an optimal policy ${\pi }^{\ast }$ that maximizes the expected cumulative discounted reward:

$$\begin{array}{cc}\hfill {\pi }^{\ast }& =arg\underset{\pi }{max}{\mathbb{E}}_{\tau \sim \pi }\left[\sum _{t=0}^{\infty }{\gamma }^{t}r(s_t,a_t)\right]\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill \mathrm{where}\tau & =(s_0,a_0,s_1,a_1,\dots )\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill a_t& \sim \pi \left(a_t\right|s_t)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill s_{t+1}& \sim P\left(s_{t+1}\right|s_t,a_t)\hfill \end{array}$$

(40)

where $s_t\in \mathcal{S}$ is the state vector at time t (typically including vehicle states and environmental information), $a_t\in \mathcal{A}$ is the control action (steering, throttle, and brake commands), $P:\mathcal{S}\times \mathcal{A}\times \mathcal{S}\to [0,1]$ is the state transition probability, $r:\mathcal{S}\times \mathcal{A}\to \mathbb{R}$ is the reward function, $\gamma \in (0,1)$ is the discount factor, and $\pi :\mathcal{S}\times \mathcal{A}\to [0,1]$ is the policy.

For drift control applications, the reward function typically includes terms for trajectory tracking error, desired sideslip angle maintenance, and control effort penalties:

$$\begin{array}{c}\hfill r(s_t,a_t)=-w_1·\parallel p_t-p_{ref,t}{\parallel }^2-w_2·|{\beta }_t-{\beta }_{ref}|-w_3·{\parallel a_t\parallel }^2+w_4·{\mathbf{I}}_{\mathrm{drift}}\end{array}$$

(41)

where $p_t$ and $p_{ref,t}$ are the current and reference positions, ${\beta }_t$ and ${\beta }_{ref}$ are the current and target sideslip angles, $w_i$ denotes weighting coefficients, and ${\mathbf{I}}_{\mathrm{drift}}$ is an indicator function that rewards maintaining a drifting state.

Some reinforcement learning methods require the modeling of the environment to predict the next stage and reward based on the world model. These methods are called model-based methods, such as PILCO and DHP. In contrast, model-free methods such as DQN, DDPG, SAC, A3C, and TD3 have a wider range of applications. Reinforcement learning methods can also be divided into on-policy and off-policy methods. DQN is an off-policy method, where the training policy is different from the behavior policy. In contrast, DDPG, SAC, A3C, and TD3 are all on-policy methods.

Perot et al. [69] proposed an end-to-end driving approach using the A3C method. They used only images from a front camera as input and trained the network in the WRC 6 simulation environment. The end-to-end driving system was tested for various racing tasks, achieving an overall speed of 91.4 km/h. The system was also capable of learning full control, including the handbrake for drifts. This study demonstrated the potential of using deep reinforcement learning for end-to-end autonomous driving systems.

Cai et al. [6] developed a robust drift controller based on the SAC method. They treated the drift control problem as a trajectory-following task, designing an error-based state and reward system. After training the controller on given maps, it was able to drive and drift the car effectively on new and previously unknown maps. The controller demonstrated much smoother drifting trajectories than other methods. This study highlights the potential of reinforcement learning for developing robust and adaptable drift controllers capable of handling a wide range of environments.

Lee et al. (2022) [12] developed a two-step DNN-based controller to address non-real-time issues with a prior model predictive control (MPC)-based drift controller. The first controller, based on a DNN, controls the steering wheel to drive the vehicle along the desired trajectory during a drift maneuver. The second controller, based on a time-delay neural network (TDNN), maintains the drift state of the vehicle. Simulation results demonstrate that the proposed DNN-based controller has similar tracking performance but a more stable computation time when compared to existing MPC-based controllers. This study highlights the potential of combining deep neural networks with model-based controllers to improve the real-time performance of autonomous drifting systems.

3.2.1. Challenges in Training Data and Generalization

A critical challenge in applying deep learning methods to autonomous drifting lies in the quality and diversity of training data. Several important considerations have emerged from the surveyed literature:

(1)

Sim-to-real transfer gap: Most deep learning approaches are initially trained in simulation environments [6,69,70,71] due to the safety risks and costs associated with collecting real-world drifting data. However, the fidelity gap between simulation and reality—particularly in modeling tire–road interactions during extreme maneuvers—can lead to policies that perform well in simulation but fail when deployed on physical vehicles. Djeumou et al. [72] addressed this challenge by using physics-informed diffusion models to better capture the underlying dynamics, demonstrating improved generalization to physical Toyota Supra and Lexus LC 500 vehicles.

(2)

Data distribution biases: Training data often reflect specific vehicle configurations, road surfaces, and environmental conditions, leading to potential biases. Controllers trained on dry asphalt may fail on wet or low-friction surfaces; similarly, policies optimized for specific vehicle weight distributions or drive configurations may not transfer to different vehicle types. Cai et al. [6,73] attempted to mitigate this through domain randomization techniques, varying vehicle parameters during training to improve robustness.

(3)

Catastrophic forgetting: Sequential learning of different drift maneuvers can lead to performance degradation on previously learned tasks, as observed by Toth et al. [74] when training agents across multiple drift scenarios. This suggests that comprehensive curriculum design is essential for developing versatile drift controllers.

(4)

State representation limitations: The choice of state representation significantly impacts generalization capability. Vision-based approaches [69,70] offer the potential for better environmental adaptation but suffer from sensitivity to lighting and weather conditions. In contrast, state-based methods [6,74,75] may generalize better across visual conditions but require accurate state estimation, which is challenging during high-slip maneuvers.

(5)

Safety verification challenges: A significant limitation of deep learning methods is the difficulty in providing formal safety guarantees. Arab et al. [76] partially addressed this by incorporating safety-guaranteed learning-predictive control for aggressive maneuvers, but comprehensive safety verification remains an open challenge in the field.

These challenges highlight the need for careful consideration of data collection methodologies, validation approaches, and hybrid techniques that combine the strengths of model-based and learning-based methods. The most promising approaches in recent literature [38,72] leverage physics-informed learning to constrain the solution space while maintaining adaptation capabilities.

3.2.2. Summary of Deep Learning Methods

Table 3. A summary of deep learning methods for autonomous drifting.

Research	Input	Methods or Models	Experiments Platform	Experiments	Speed (m/s)
Perot et al. (2017) [69]	RGB image	A3C, End-to-end learning	Simulator: WRC 6	Racing	25.4
Jaritz et al. (2018) [70]	RGB front view image	A3C, End-to-end learning	Simulator: World Rally Championship 6 (WRC 6) racing game	Racing	22.2 in average
Spielberg et al. (2019) [77]	Environment and car state	Two-layer feedforward neural network dynamics model	Real car: Shelley	Racing	42.46
Gucckiran et al. (2019) [78]	Environment and car state	SAC, Rainbow DQN	Simulator: The Open Racing Car Simulation (TORCS)	Racing	52.7
Kabzan et al. (2019) [79]	Car state	Dynamic bicycle model, Pacejka tire model, GPR, MPC	Real car: AMZ driverless vehicle, Gotthard	Racing	15
Cai et al. (2020) [6] (2021) [73]	Environment, car state, and reference trajectory	SAC, DQN, DDPG	Simulator: FWD and AWD vehicles in CARLA and model car: a 1:20 car	Racing	up to 22.0 in corners
Zhao et al. (2024) [80]	Environment and car state	SAC	Simulator: MATLAB and CarSim	Racing	16.67
Arab et al. (2020) [76]	Environment and car state	Nonlinear MPC, polynomial basis (GPPB) method, sum-of-square (SOS)-enhanced safety region estimation	Simulator and model car: a scaled vehicle platform	Racing: oval loop race	N/A
Orgovan et al. (2021) [71]	Environment, car state, and reference trajectory	TD3	Simulator: CARLA	Racing	17.15
Remonda et al. (2021) [81]	Environment and car state	DDPG, LSTM, multi-step targets, prioritized experience replay	Simulator: TORCS	Racing	69
Cutler (2015) [82] (2016) [83]	Simulators	Multi-fidelity RL (MFRL) for learning with multiple simulators, PILCO	Model car: a small robotic car	Circle drift	1.5
Bhattachar et al. (2018) [84]	Environment and car state	double dueling DQN, PILCO	Model car: an RWD radio-controlled car	Circle drift	N/A
Ding et al. (2024) [11]	Car state	Neural Networks MPC	Real car: Lexus LC 500	Circle drift	8
Jiang et al. (2021) [85]	Vehicle dynamics model as prior knowledge	RL, Pacejka tire model, Markov decision process (MDP) model, DHP	Simulator	Circle drift and Drift cornering	10.7
Zhou et al. (2025) [14]	Car state	adaptive learning-based MPC	Simulator: CarSim	“Figure 8” drifting and open-loop drifting	17
Lee et al. (2022) [12]	Environment and car state	Nonlinear MPC, DNN, Brush Tire Model	Model car: a 1:10 scale RC car	Steady-state drift	2
Acosta et al. (2018) [15]	Target body slip angle, target road curvature	MPC, feedforward neural networks	Simulator: CarMaker	Open-loop drifting and Drifting along given trajectories	8
Ji et al. (2018) [86]	Reference path model, dynamics model, and kinematics model of the vehicle	Adaptive neural network (ANN), backstepping variable structure control (BVSC), radial basis function neural network (RBFNN)	Simulator: CarSim and Real car: Brilliance	Drifting along given trajectories	30
Toth et al. (2022) [75] (2024) [87]	Environment and car state	SAC	Simulator: SimulinkTM	Drifting along given trajectories	10
Domberg et al. (2022) [88]	Scoring process of real-life drifting competitions	DNN	Simulator and model car	Open-loop drifting along given trajectories	6.1
Zhou et al. (2022) [89]	Environment and car state	MPC, DNN	Simulator: CarSim and model car: a 1:10 scale RC car	Drifting along given trajectories	24.5
Djeumou et al. (2023) [38] (2024) [72]	Environment and car state	Diffusion models	Real Cars: Toyota Supra and Lexus LC 500	Drifting along given trajectories	16
Lau et al. (2011) [3]	Samples from demonstration, human intuition	Supervised learning	Model car: an AWD radio-controlled car	Drift parking	N/A
Yin et al. (2020) [25]	Random parameterized policy	Multi-layer perception neural network, DDPG	Simulator: a B-class car	stabilizing the vehicle after rear-end collision	22.2
Zhao et al. (2024) [23]	Environment and car state	SAC	Simulator and a scaled vehicle platform	Collision avoidance	8.3
Toth et al. (2022) [74]	Environment and car state	SAC	Simulator: SimulinkTM	Maintain a target drift equilibrium	9

provides a summary of various research studies that have utilized deep learning methods for autonomous drifting. These studies have employed different deep learning architectures, input, and experimental setups to achieve their objectives.

Key implementation details like network architectures, loss functions, and data preprocessing pipelines varied significantly across these deep learning studies based on the specific tasks and input data representations. However, most leveraged the flexibility of deep neural networks and either imitation learning on human demonstrations or reinforcement learning on carefully designed reward functions to learn high-performance drift policies.

A primary advantage of deep learning methods is their ability to directly learn control policies from data, without the need for explicit modeling of complex vehicle dynamics. This provides a path toward greater generalization by learning the drift task directly from real-world data. However, data requirements and sample efficiency remain a challenge, often requiring large and diverse datasets or careful reward shaping to learn generalizable drift controllers. Despite these challenges, deep learning methods complement the dynamical approaches and open up opportunities to develop robust, high-performance autonomous drifting systems.

4. Experiment Platforms

The experimental validation of autonomous drifting controllers occurs across a spectrum of platforms ranging from high-fidelity simulations to full-scale vehicle implementations. This section systematically analyzes the various experimental platforms employed in the surveyed literature, examining their capabilities, limitations, and suitability for different aspects of drifting research.

4.1. Simulation Environments

Simulation environments provide a safe, controllable, and cost-effective platform for the initial development and testing of autonomous drifting algorithms. The most commonly used simulators in the surveyed literature include the following:

(1)

CarSim [90]: Widely used in automotive research [6,10,47,89], CarSim offers high-fidelity vehicle dynamics models with customizable tire models, road surfaces, and environmental conditions. Its ability to simulate the nonlinear dynamics during drift maneuvers makes it particularly valuable for drifting research.

(2)

CARLA [91]: An open-source simulator built on Unreal Engine, CARLA has gained popularity for deep learning applications [6,71] due to its realistic sensor simulation capabilities and integration with machine learning frameworks.

(3)

Gazebo/ROS [92]: Used particularly for robotics-oriented research [18,32], this open-source platform offers flexibility in modeling different vehicle configurations and integrates well with the robot operating system (ROS).

(4)

TORCS [93]: The Open Racing Car Simulator provides a simplified but computationally efficient environment often used for reinforcement learning experiments [78,81].

(5)

Commercial racing games: Some researchers have leveraged commercial racing games like the World Rally Championship (WRC 6) [69,70] for their realistic physics engines and varied environments.

Simulation fidelity is critical for autonomous drifting research, with particular emphasis on accurate tire modeling during high sideslip conditions. The surveyed studies indicate that the fidelity of tire–road interaction models significantly impacts the transferability of simulation-developed controllers to real-world applications.

4.2. Scale Model Vehicles

Scale model vehicles represent an intermediate step between simulation and full-scale implementation, offering physical validation while mitigating cost and safety concerns. Commonly used platforms include the following:

(1)

1:10 Scale RC cars: These commercially available platforms are frequently modified with additional sensors and computational capabilities [12,16,40,89]. A typical configuration includes the following:

• Onboard computing: Nvidia Jetson TX2 or similar embedded systems.
• Sensors: IMU (typically 9-DOF), wheel encoders, camera systems.
• Communication: Wi-Fi or dedicated radio links for telemetry.
• Modifications: Custom motor controllers, reinforced chassis components.

(2)

Custom research platforms: Several studies utilize purpose-built scale vehicles with enhanced sensing and actuation capabilities [65,76]. The Georgia Tech AutoRally platform [49,50] represents one of the most sophisticated systems, featuring the following:

• Full-state estimation through sensor fusion.
• High-torque electric motors with precise control.
• Multiple cameras for visual odometry.
• GPS and IMU integration for localization.
• Onboard computing for real-time control implementation.

Scale vehicle experiments face unique challenges including scaling effects on vehicle dynamics, limited sensor resolution, and environmental control issues. Nevertheless, they provide valuable physical validation of control concepts before full-scale implementation.

4.3. Full-Scale Vehicle Platforms

Full-scale vehicle implementations represent the ultimate validation for drifting controllers, demonstrating real-world applicability. Notable full-scale platforms include the following:

(1)

Stanford’s MART: A modified DeLorean DMC-12 converted to electric drive with steer-by-wire capabilities [8,29,33,35,57]. Key specifications include:

• Dual independent rear electric motors (total 4500 Nm).
• Custom steer-by-wire system with haptic feedback.
• High-precision RTK GPS and IMU integration.
• Onboard computing system with real-time controller implementation.
• External motion capture system for ground truth validation.

(2)

P1 research platform: Used in several studies [31,51,52,53], this rear-wheel drive platform features comprehensive instrumentation:

• Wheel force transducers on all four wheels.
• High-precision IMU and GPS integration.
• CAN bus monitoring and intervention systems.
• Custom hydraulic handbrake system for drift initiation.

(3)

Production vehicle modifications: Several researchers have modified production vehicles like Audi TTS [10], Genesis [46], and Toyota Supra [72] with the following:

• Drive-by-wire throttle, brake, and steering interfaces.
• Real-time computing platforms.
• External state estimation systems.
• Safety override mechanisms.

4.4. Sensor Configurations and Data Processing

The critical importance of accurate state estimation for effective drift control is consistent across all experimental platforms. Typical sensor configurations include the following:

(1)

State estimation sensors:

• Inertial measurement units (IMUs): 6–9 DOF sensors providing acceleration and angular velocity measurements.
• GPS/GNSS systems: Often with RTK corrections for centimeter-level positioning.
• Wheel speed sensors: For slip estimation and longitudinal velocity measurements.
• Optical flow sensors or cameras: For lateral velocity estimation.

(2)

Vehicle dynamic state sensors:

• Steering angle sensors: Potentiometers or encoders measuring steering input.
• Suspension sensors: Linear potentiometers measuring suspension compression.
• Load cells: Measuring forces at tire contact patches (limited to research vehicles).

(3)

Environmental Perception:

• Cameras: For path detection and environmental awareness.
• LiDAR: For precise environmental mapping.
• Infrared sensors: Sometimes used for surface temperature and condition estimation.

4.5. Computational Requirements

The computational demands of autonomous drifting controllers vary significantly based on the methodology employed:

(1)

Dynamical methods: typically require the following:

• Real-time operating systems with deterministic timing.
• Optimization solver implementations (especially for MPC approaches).
• Computation cycles of 10–100 Hz depending on model complexity.
• Hardware platforms ranging from automotive ECUs to dedicated computing systems.

(2)

Deep learning methods: generally demand the following:

• GPU acceleration for inference (especially for vision-based approaches).
• Higher memory requirements for network parameter storage.
• Potential for higher latency if complex network architectures are employed.
• Often implemented on systems like Nvidia Drive PX, Jetson AGX, or custom computing platforms.

The experimental platforms employed in autonomous drifting research reflect the multidisciplinary nature of the field, requiring expertise in vehicle dynamics, control theory, state estimation, and increasingly, machine learning. The progressive validation from simulation to full-scale implementation remains a consistent methodology across the surveyed literature, with each platform offering distinct advantages and limitations.

5. Discussion

Research on autonomous drifting techniques has been ongoing since 2005, resulting in the design of several drift controllers that have demonstrated good performance in limited and constant scenarios. Moreover, with the rapid development of deep learning methods, more DL-based drift controllers have been proposed since 2017, offering better generalization to other vehicles with unknown scenarios or roads. As autonomous drifting techniques have matured, the drift scenarios have also become more challenging, moving beyond simple circle drifting to more complex scenarios such as racing and collision avoidance.

While the surveyed research has made significant strides in achieving autonomous drifting capabilities, several challenges and opportunities remain for future work.

5.1. Real-Time Performance

Many of the current methods, especially those relying on MPC or other optimization-based approaches, can be computationally intensive. Improving the real-time performance of drift controllers is crucial for their deployment in safety-critical scenarios like collision avoidance maneuvers on public roads. Potential avenues include the following:

(1)

Developing more efficient optimization solvers and dynamics models tailored for drifting scenarios.

(2)

Exploring anytime control approaches that can quickly provide suboptimal but safe control inputs under time constraints.

5.2. Generalization Across Environments

Most current methods are evaluated in relatively controlled simulation environments or on specific test vehicles or tracks. Enabling autonomous drift controllers to generalize across diverse real-world conditions remains an open challenge:

(1)

Accounting for variabilities in road surfaces (dry or wet), weather (rain, snow, etc.), vehicle loading, and other environmental factors.

(2)

Developing drift controllers robust to parametric uncertainties and unmodeled dynamics effects.

(3)

Exploring data-driven and transfer learning approaches to adapt drift policies to new environments from limited data.

5.3. Safety Considerations

The high speeds and low-grip situations involved in drifting present unique safety challenges that must be carefully addressed for real-world deployment:

(1)

Formal safety verification and validation of learned or optimized drift policies.

(2)

Ensuring smooth and stable transitions into and out of drifting states.

(3)

Fault-tolerance capabilities to handle actuator or sensor failures during drifts.

5.4. Integration with Autonomous Systems

Autonomous drifting controllers could potentially provide enhanced capabilities when integrated into higher-level autonomous driving systems:

(1)

Incorporating drifting into decision-making and motion-planning frameworks for self-driving vehicles in complex urban environments.

(2)

Combining with perception systems to identify scenarios where drifting may be advantageous for collision avoidance or improved maneuverability.

(3)

Specially designed drift controllers for providing more maneuverable motion in extreme situations could be a supplement to advanced driver assistance systems (ADASs). For example, in cases where a car slides laterally on an unexpectedly slippery road, a drift controller could maintain control of the drift and keep the car on a safe trajectory. Similarly, if an abrupt obstacle appears within the safe steering distance, as shown in Figure 11, drivers or current ADAS systems may not be able to avoid a collision due to their handling limitations. However, drift controllers may provide an opportunity to drift by the obstacle safely.

6. Conclusions

This survey provides a comprehensive overview of the current state-of-the-art in autonomous drifting research. We have categorized the existing methods into two main groups: dynamical model-based methods and emerging deep learning approaches. Each methodology offers distinct advantages and faces unique challenges.

The traditional dynamical methods rely heavily on accurate vehicle dynamics and tire force models to design drift controllers. When the models precisely capture the vehicle’s behavior, these controllers can achieve highly precise drift performance by explicitly respecting the modeled physics and constraints. However, developing sufficiently accurate models, especially at the limits of handling, remains an ongoing challenge. These methods may also struggle with generalization to previously unseen environments due to their dependence on specific vehicle parameters.

In contrast, deep learning techniques like reinforcement learning offer a data-driven approach that can potentially learn drifting policies directly from experience, without requiring explicit modeling of the underlying vehicle dynamics. This could allow for better generalization across different vehicles and environments. However, current deep RL methods still face issues with sample efficiency, safety constraints, and extrapolation to conditions far outside the training distribution.

As autonomous vehicle technology continues advancing toward higher levels of autonomy, the ability to handle extreme driving scenarios like drifting will become increasingly crucial. This emerging field presents numerous exciting research opportunities at the intersection of control theory, vehicle dynamics, and machine learning. Continued innovation in autonomous drifting has the potential to significantly enhance the capabilities, safety, and performance of future self-driving and driver assistance systems.