AI-Assisted Game Theory Approaches to Bid Pricing Under Uncertainty in Construction
Abstract
:1. Introduction
Research Objectives
- Develop an AI-powered framework integrating machine learning (ML), risk modelling, and game theory to optimise bid pricing and strategies;
- Model bidding process for improved success rates by leveraging historical data, competitive dynamics, and uncertainty quantification for strategic bid optimisation;
- Evaluate the model’s effectiveness through a UK case study in the construction sector.
2. Literature Review
2.1. Overview of Traditional Bid-Pricing Methods in Construction
2.2. Key Concepts in Game Theory for Construction Bidding
Utility Function for Payoff Calculation
2.3. Game Theory Applications in Construction Bidding
2.4. The Role of AI in Addressing Uncertainty and Predictive Decision Making
Key AI Techniques for Addressing Uncertainty
2.5. Foundations of AI Applications
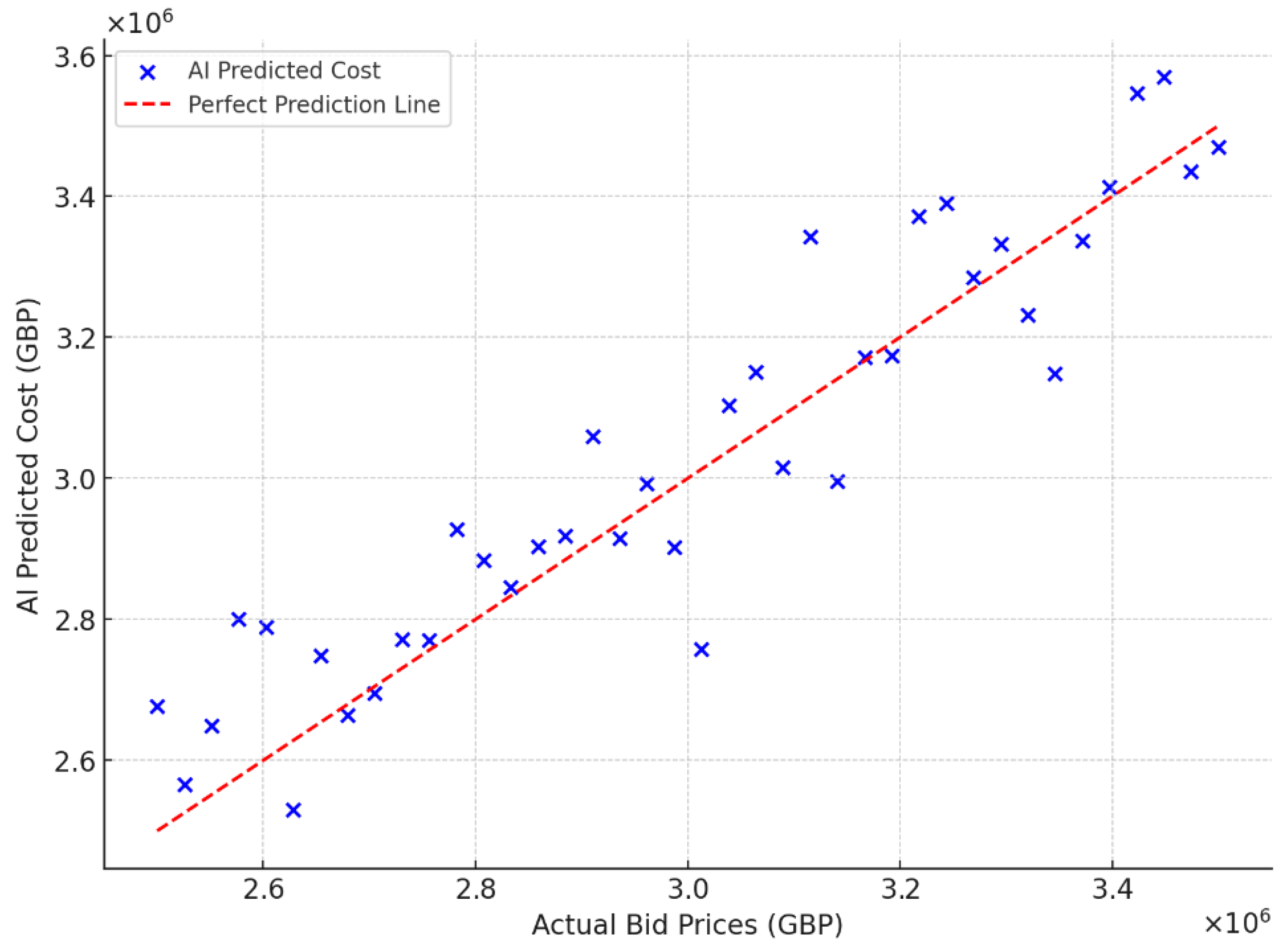
2.5.1. Cost Estimation Using Regression Models
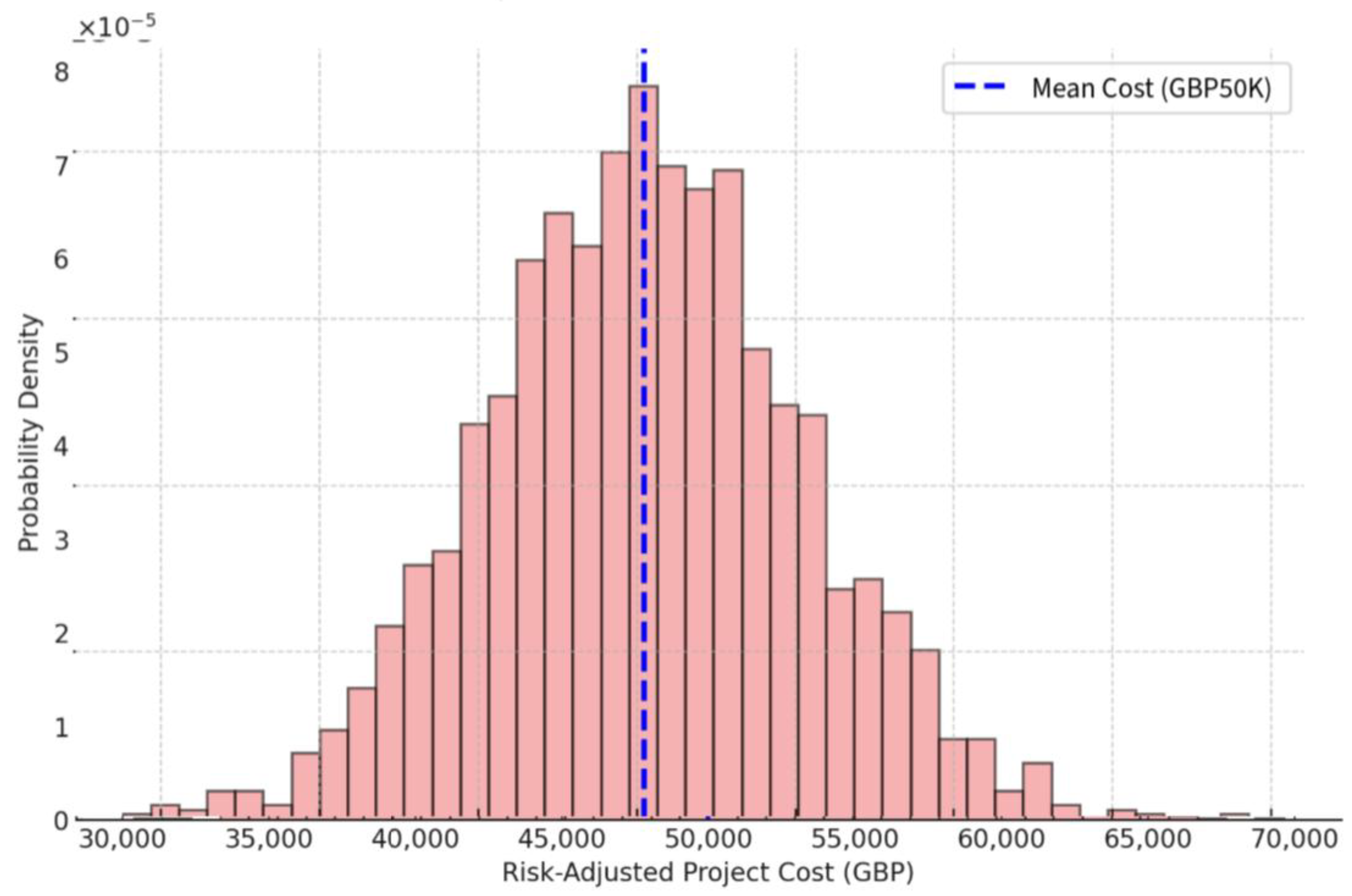
2.5.2. Risk Modelling with Bayesian Networks
2.5.3. Time-Series Forecasting for Market Trends
2.5.4. Competitor Behaviour Prediction Using Classification Models
2.5.5. RL for Adaptive Bidding
2.6. Gaps in Current Research and Justification for the Study
2.6.1. Gaps in Current Research
2.6.2. Justification for the Study
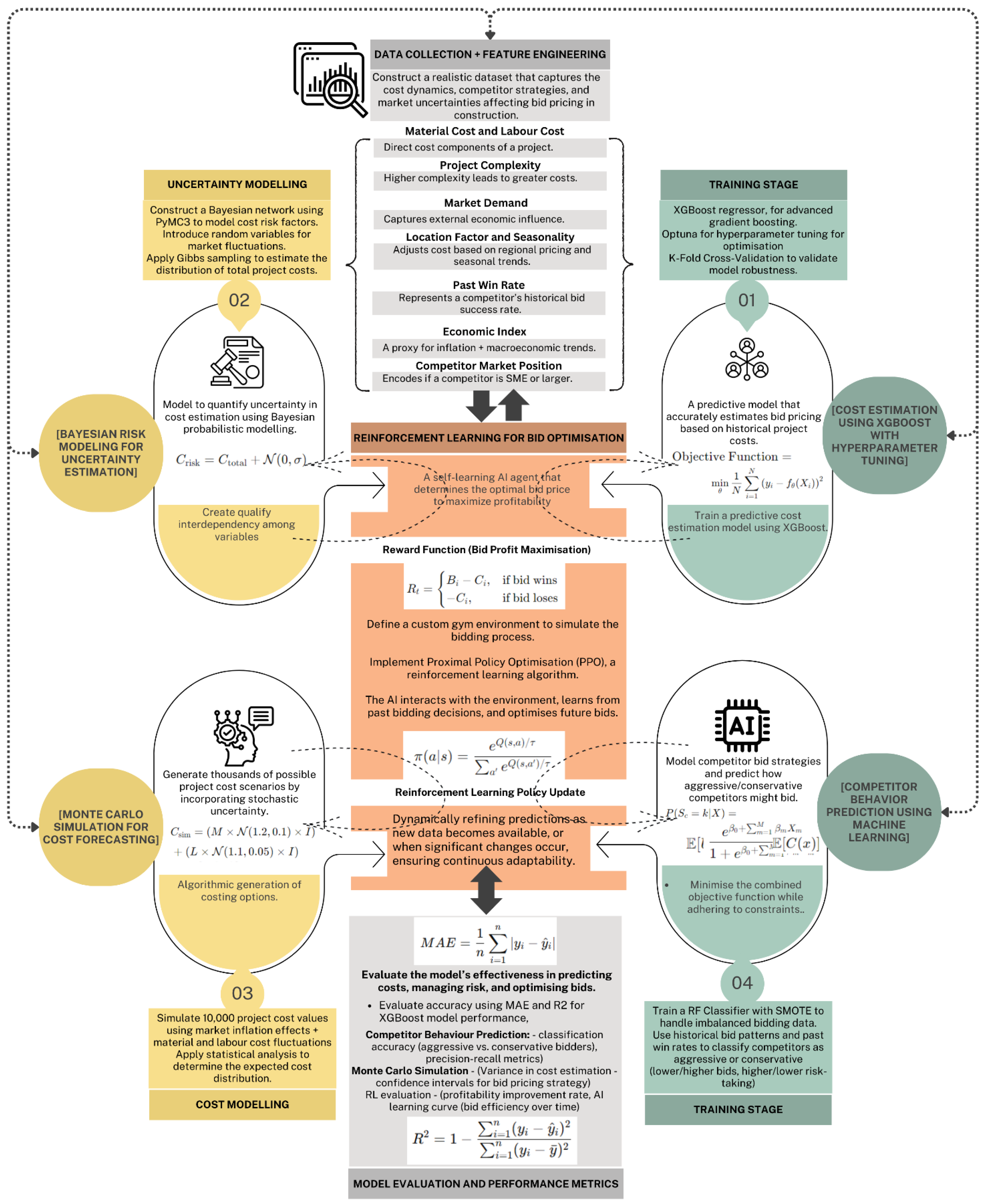
3. Methodology
Case Study and the Assisted Game Theory Model
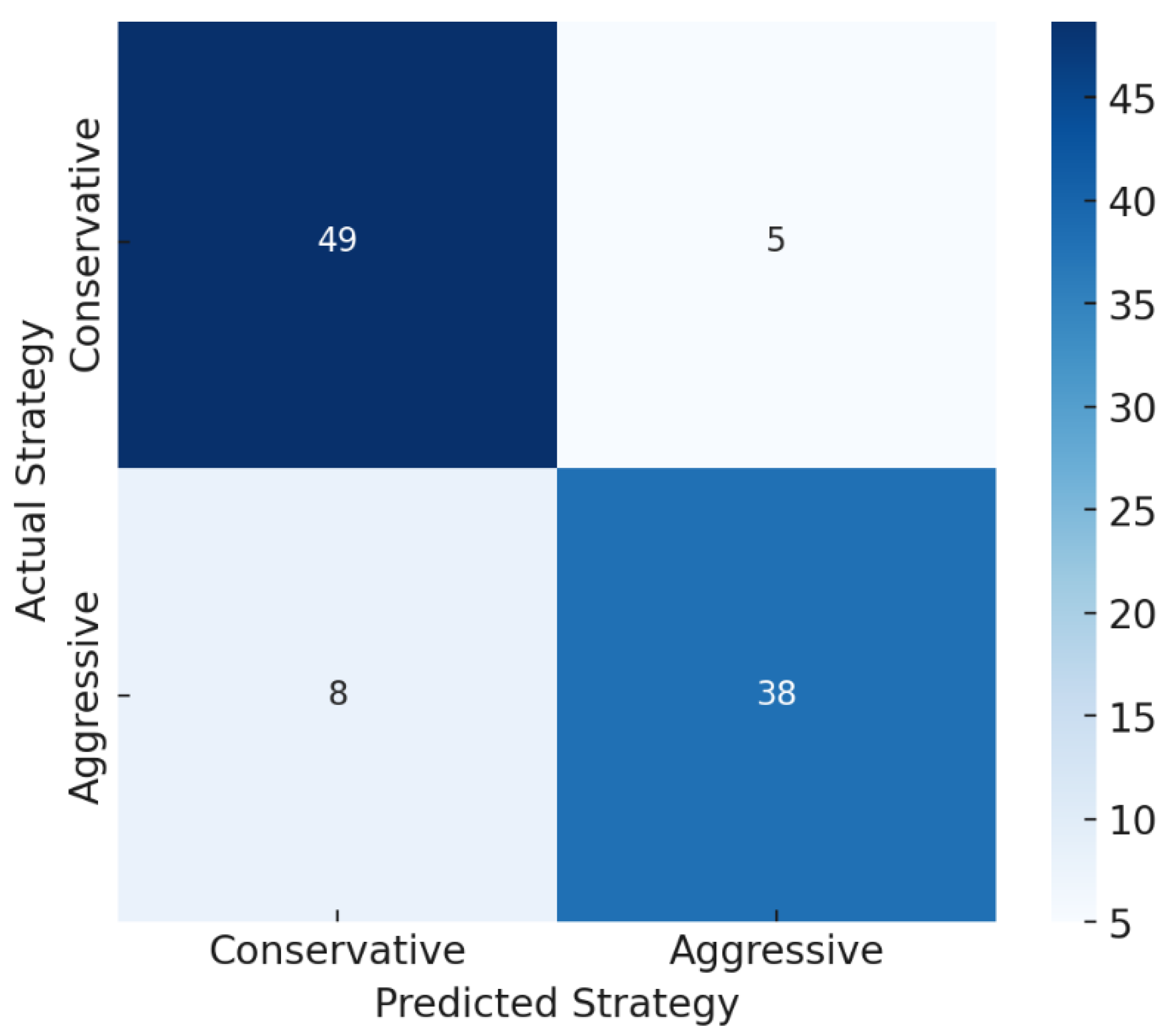
4. Results and Discussion
5. Conclusions and Future Work
5.1. Limitations of the Study
5.2. Future Research
Funding
Data Availability Statement
Conflicts of Interest
References
- Aboseif, E.; Hanna, A.S. Benchmarking of construction projects performance for comparative assessment and performance improvement: A statistical quantitative approach. Eng. Constr. Archit. Manag. 2024, 31, 2829–2851. [Google Scholar]
- Abotaleb, I.S.; El-Adaway, I.H. Construction bidding markup estimation using a multistage decision theory approach. J. Constr. Eng. Manag. 2017, 143, 04016079. [Google Scholar] [CrossRef]
- Afshar, A.; Amiri, H. Risk-based approach to unbalanced bidding in construction projects. Eng. Optim. 2010, 42, 369–385. [Google Scholar] [CrossRef]
- Agrawal, A.; Jaiswal, D. When machine learning meets ai and game theory. Comput. Sci 2012, 2012, 1–5. [Google Scholar]
- Ahmed, M.O.; El-Adaway, I.; Coatney, K.; Eid, M.S. Multi-stage bidding for construction contracts: A game theory approach. In Proceedings of the 5th CSCE International Construction Specialty Conference, Vancouver, BC, Canada, 7–10 June 2015. [Google Scholar]
- Ahmed, M.O.; El-Adaway, I.H. An integrated game-theoretic and reinforcement learning modeling for multi-stage construction and infrastructure bidding. Constr. Manag. Econ. 2023, 41, 183–207. [Google Scholar] [CrossRef]
- Ahmed, M.O.; El-Adaway, I.H.; Caldwell, A. Comprehensive understanding of factors impacting competitive construction bidding. J. Constr. Eng. Manag. 2024, 150, 04024017. [Google Scholar] [CrossRef]
- Ahmed, M.O.; El-Adaway, I.H.; Coatney, K.T. Solving the negative earnings dilemma of multistage bidding in public construction and infrastructure projects: A game theory–based approach. J. Manag. Eng. 2022, 38, 04021087. [Google Scholar] [CrossRef]
- Ahmed, M.O.; El-Adaway, I.H.; Coatney, K.T.; Eid, M.S. Construction bidding and the winner’s curse: Game theory approach. J. Constr. Eng. Manag. 2016, 142, 04015076. [Google Scholar] [CrossRef]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Almuflih, A.S. Extreme gradient boosting-based machine learning approach for green building cost prediction. Sustainability 2022, 14, 6651. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Assaad, R.; Ahmed, M.O.; El-Adaway, I.H.; Elsayegh, A.; Siddhardh Nadendla, V.S. Comparing the impact of learning in bidding decision-making processes using algorithmic game theory. J. Manag. Eng. 2021, 37, 04020099. [Google Scholar]
- Bencomo, N.; Belaggoun, A.; Issarny, V. Bayesian artificial intelligence for tackling uncertainty in self-adaptive systems: The case of dynamic decision networks. In Proceedings of the 2013 2nd International Workshop on Realizing Artificial Intelligence Synergies in Software Engineering (RAISE), San Francisco, CA, USA, 18–26 May 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 7–13. [Google Scholar]
- Bengio, Y. Learning deep architectures for AI. Found. Trends® Mach. Learn. 2009, 2, 1–127. [Google Scholar]
- Blom, H.A.; Stroeve, S.H.; De Jong, H.H. Safety risk assessment by Monte Carlo simulation of complex safety critical operations. Developments in Risk-based Approaches to Safety. In Proceedings of the Fourteenth Safety-Critical Systems Symposium, Bristol, UK, 7–9 February 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 47–67. [Google Scholar]
- Chang, T.; Hwang, B.-G.; Deng, X.; Zhao, X. Identifying political risk management strategies in international construction projects. Adv. Civ. Eng. 2018, 2018, 1016384. [Google Scholar]
- Chapman, C.; Ward, S.; Bennell, J. Incorporating uncertainty in competitive bidding. Int. J. Proj. Manag. 2000, 18, 337–347. [Google Scholar]
- Chou, J.-S.; Lin, C.-W.; Pham, A.-D.; Shao, J.-Y. Optimized artificial intelligence models for predicting project award price. Autom. Constr. 2015, 54, 106–115. [Google Scholar] [CrossRef]
- De Clerck, D.; Demeulemeester, E. Creating a more competitive PPP procurement market: Game theoretical analysis. J. Manag. Eng. 2016, 32, 04016015. [Google Scholar]
- Dozzi, S.; Abourizk, S.; Schroeder, S. Utility-theory model for bid markup decisions. J. Constr. Eng. Manag. 1996, 122, 119–124. [Google Scholar]
- El-Sayegh, S.M.; Abdraboh, T.; Elian, D.; Eljarad, N.; Ahmad, Y. Developing a bi-parameter bidding model integrating price and sustainable construction practices. Int. J. Constr. Manag. 2022, 22, 2191–2198. [Google Scholar]
- Elsayegh, A.; Dagli, C.H.; El-Adaway, I.H. An agent-based model to study competitive construction bidding and the winner’s curse. Procedia Comput. Sci. 2020, 168, 147–153. [Google Scholar]
- Ercan, T.; Koksal, A. Effects of Competitive and Growth Strategy Type on Financial Strategies in Construction Companies. In ICCREM 2013: Construction and Operation in the Context of Sustainability; American Society of Civil Engineers: Reston, VA, USA, 2013. [Google Scholar]
- Ercan, T.; Koksal, A. Competitive Strategic Performance Benchmarking (CSPB) model for international construction companies. KSCE J. Civ. Eng. 2016, 20, 1657–1668. [Google Scholar]
- Fayek, A.; Ghoshal, I.; Abourizk, S. A survey of the bidding practices of Canadian civil engineering construction contractors. Can. J. Civ. Eng. 1999, 26, 13–25. [Google Scholar]
- Feriani, A.; Hossain, E. Single and multi-agent deep reinforcement learning for AI-enabled wireless networks: A tutorial. IEEE Commun. Surv. Tutor. 2021, 23, 1226–1252. [Google Scholar]
- Friedman, L. A competitive-bidding strategy. Oper. Res. 1956, 4, 104–112. [Google Scholar]
- Fu, W.K. The Effect of Experience in Construction Contract Bidding; Hong Kong Polytechnic University: Hong Kong, China, 2004. [Google Scholar]
- Gintis, H. Game Theory Evolving: A Problem-Centered Introduction to Modeling Strategic Behavior; Princeton University Press: Princeton, NJ, USA, 2000. [Google Scholar]
- Gronauer, S.; Diepold, K. Multi-agent deep reinforcement learning: A survey. Artif. Intell. Rev. 2022, 55, 895–943. [Google Scholar]
- Hennebold, C.; Klöpfer, K.; Lettenbauer, P.; Huber, M. Machine learning based cost prediction for product development in mechanical engineering. Procedia CIRP 2022, 107, 264–269. [Google Scholar]
- Heo, C.; Park, M.; Ahn, C.R. Uncovering potential collusive behavior of AI bidders in future construction bidding market. In Computing in Civil Engineering 2023; American Society of Civil Engineers: Reston, VA, USA, 2024. [Google Scholar]
- Holm, L.; Schaufelberger, J.E. Construction Cost Estimating; Routledge: London, UK, 2021. [Google Scholar]
- Hosny, O.; Elhakeem, A. Simulating the winning bid: A generalized approach for optimum markup estimation. Autom. Constr. 2012, 22, 357–367. [Google Scholar]
- Ioannou, P.G. Risk-sensitive competitive bidding model and impact of risk aversion and cost uncertainty on optimum bid. J. Constr. Eng. Manag. 2022, 148, 04021205. [Google Scholar]
- Iyer, S.; Krishna, M.; Arora, S.V. Bidding under uncertainty: Harsh constructions. Emerald Emerg. Mark. Case Stud. 2023, 13, 1–20. [Google Scholar]
- Jang, W.; Lee, J.K.; Lee, J.; Han, S.H. Naive Bayesian classifier for selecting good/bad projects during the early stage of international construction bidding decisions. Math. Probl. Eng. 2015, 2015, 830781. [Google Scholar]
- Ji, S.-H.; Park, M.; Lee, H.-S. Cost estimation model for building projects using case-based reasoning. Can. J. Civ. Eng. 2011, 38, 570–581. [Google Scholar]
- Kabir, S.; Wagner, C.; Ellerby, Z. Toward Handling Uncertainty-At-Source in AI—A Review and Next Steps for Interval Regression. IEEE Trans. Artif. Intell. 2023, 5, 3–22. [Google Scholar] [CrossRef]
- Kembłowski, M.W.; Grzyl, B.; Siemaszko, A. Game theory analysis of bidding for a construction contract. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bangkok, Thailand, 21–23 April 2017; IOP Publishing: Bristol, UK, 2017; p. 062047. [Google Scholar]
- Kempitiya, T.; Sierla, S.; De Silva, D.; Yli-Ojanperä, M.; Alahakoon, D.; Vyatkin, V. An Artificial Intelligence framework for bidding optimization with uncertainty in multiple frequency reserve markets. Appl. Energy 2020, 280, 115918. [Google Scholar] [CrossRef]
- Lan, O.O.B.; Lo, H.P.; Teck-Heng Lim, B. The effect of bidding success in construction bidding. Eng. Constr. Archit. Manag. 2012, 19, 25–39. [Google Scholar] [CrossRef]
- Lan, O.O.B.; Yean Yng Ling, F.; Soo, A. Information feedback and bidders’ competitiveness in construction bidding. Eng. Constr. Archit. Manag. 2014, 21, 571–585. [Google Scholar] [CrossRef]
- Lee, J.-S. Simulating competitive bidding in construction collusive bidding cases. J. Manag. Eng. 2022, 38, 04022050. [Google Scholar] [CrossRef]
- Li, H.; Cao, Y.; Li, S.; Zhao, J.; Sun, Y. XGBoost model and its application to personal credit evaluation. IEEE Intell. Syst. 2020, 35, 52–61. [Google Scholar] [CrossRef]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Mclachlan, S.; Dube, K.; Hitman, G.A.; Fenton, N.E.; Kyrimi, E. Bayesian networks in healthcare: Distribution by medical condition. Artif. Intell. Med. 2020, 107, 101912. [Google Scholar]
- Murtha, J.A. Monte Carlo simulation: Its status and future. J. Pet. Technol. 1997, 49, 361–373. [Google Scholar] [CrossRef]
- Ngai, S.C.; Drew, D.S.; Lo, H.P.; Skitmore, M. A theoretical framework for determining the minimum number of bidders in construction bidding competitions. Constr. Manag. Econ. 2002, 20, 473–482. [Google Scholar] [CrossRef]
- Nguyen, T.A. Digitalized Probabilistic Approach on Construction Bid Pricing: Case example of Vietnam. Int. J. Sustain. Constr. Eng. Technol. 2024, 15, 11–20. [Google Scholar]
- Olawale, S.R.; Chinagozi, O.G.; Joe, O.N. Exploratory research design in management science: A review of literature on conduct and application. Int. J. Res. Innov. Soc. Sci. 2023, 7, 1384–1395. [Google Scholar]
- Palaneeswaran, E.; Kumaraswamy, M. Benchmarking contractor selection practices in public-sector construction—A proposed model. Eng. Constr. Archit. Manag. 2000, 7, 285–299. [Google Scholar]
- Rabin, M. Incorporating fairness into game theory and economics. Am. Econ. Rev. 1993, 83, 1281–1302. [Google Scholar]
- Ren, K.; Zhang, W.; Chang, K.; Rong, Y.; Yu, Y.; Wang, J. Bidding machine: Learning to bid for directly optimizing profits in display advertising. IEEE Trans. Knowl. Data Eng. 2017, 30, 645–659. [Google Scholar]
- Scanagatta, M.; Salmerón, A.; Stella, F. A survey on Bayesian network structure learning from data. Prog. Artif. Intell. 2019, 8, 425–439. [Google Scholar]
- Schelble, B.; Flathmann, C.; Canonico, L.-B.; Mcneese, N. Understanding human-AI cooperation through game-theory and reinforcement learning models. In Proceedings of the Annual Hawaii International Conference on System Sciences, Kauai, HI, USA, 5–8 January 2021. [Google Scholar]
- Serugga, J. Digital Twins and AI Decision Models: Advancing Cost Modelling in Off-Site Construction. Eng 2025, 6, 22. [Google Scholar] [CrossRef]
- Serugga, J.; Kagioglou, M.; Edwards, D.; Talebi, S.; Johns, N. Key influences to cost modelling and analysis in off-site construction: Research trends and GAP analysis. Archit. Eng. Des. Manag. 2023, 20, 1335–1356. [Google Scholar]
- Serugga, J.; Kagioglou, M.; Tzortzopoulos, P. Value generation in front-end design of social housing with qfd and multiattribute utility theory. J. Constr. Eng. Manag. 2020, 146, 04020019. [Google Scholar]
- Sharma, V.; Zaki, M.; Jha, K.N.; Krishnan, N.A. Machine learning-aided cost prediction and optimization in construction operations. Eng. Constr. Archit. Manag. 2022, 29, 1241–1257. [Google Scholar]
- Shen, J.; Yang, C.; Li, T.; Wang, X.; Song, Y.; Guizani, M. Interactive artificial intelligence meets game theory in next-generation communication networks. IEEE Wirel. Commun. 2021, 28, 128–135. [Google Scholar] [CrossRef]
- Shrestha, P.P.; Migliaccio, G.C.; O’connor, J.T.; Gibson, G.E., Jr. Benchmarking of large design–build highway projects: One-to-one comparison and comparison with design–bid–build projects. Transp. Res. Rec. 2007, 1994, 17–25. [Google Scholar] [CrossRef]
- Song, H.; Liu, C.-C.; Lawarrée, J. Nash equilibrium bidding strategies in a bilateral electricity market. IEEE Trans. Power Syst. 2002, 17, 73–79. [Google Scholar] [CrossRef]
- Stebbins, R.A. Exploratory Research in the Social Sciences; Sage: New York, NY, USA, 2001. [Google Scholar]
- Takano, Y.; Ishii, N.; Muraki, M. Determining bid markup and resources allocated to cost estimation in competitive bidding. Autom. Constr. 2018, 85, 358–368. [Google Scholar] [CrossRef]
- Tennenholtz, M. Game theory and artificial intelligence. In Foundations and Applications of Multi-Agent Systems: UKMAS Workshops 1996–2000 Selected Papers; Springer: Berlin/Heidelberg, Germany, 2002; pp. 49–58. [Google Scholar]
- Teo, P.; Bridge, A.; Love, P. Deriving optimal competition in infrastructure procurement. In Proceedings of the International Conference on Construction and Real Estate Management, Luleå, Sweden, 11–18 August 2015. [Google Scholar]
- Van Phan, T.; Nguyen, T.A.; Tran, H.V.V. A Novel Approach for Reducing Risk in Project Bidding Management. Int. J. Sci. Res. Civ. Eng. 2024, 8, 143–160. [Google Scholar]
- Von Neumann, J.; Morgenstern, O. Theory of Games and Economic Behavior, 2nd rev. ed.; Princeton University Press: Princeton, NJ, USA, 1947. [Google Scholar]
- Wang, W.-C.; Wang, S.-H.; Tsui, Y.-K.; Hsu, C.-H. A factor-based probabilistic cost model to support bid-price estimation. Expert Syst. Appl. 2012, 39, 5358–5366. [Google Scholar] [CrossRef]
- Wen, A.; Fu, S.; Moon, S.; El Wazir, M.; Rosenbaum, A.; Kaggal, V.C.; Liu, S.; Sohn, S.; Liu, H.; Fan, J. Desiderata for delivering NLP to accelerate healthcare AI advancement and a Mayo Clinic NLP-as-a-service implementation. NPJ Digit. Med. 2019, 2, 130. [Google Scholar] [CrossRef]
- Xue, Y. Game models of construction project bidding with a composite base price. In ICCREM 2014: Smart Construction and Management in the Context of New Technology; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar]
- Zaqout, I.S.; Islam, M.S.; Hadidi, L.A.; Skitmore, M. Modeling bidding decisions and bid markup size for construction projects: A fuzzy approach. Eng. Appl. Artif. Intell. 2022, 113, 104982. [Google Scholar] [CrossRef]

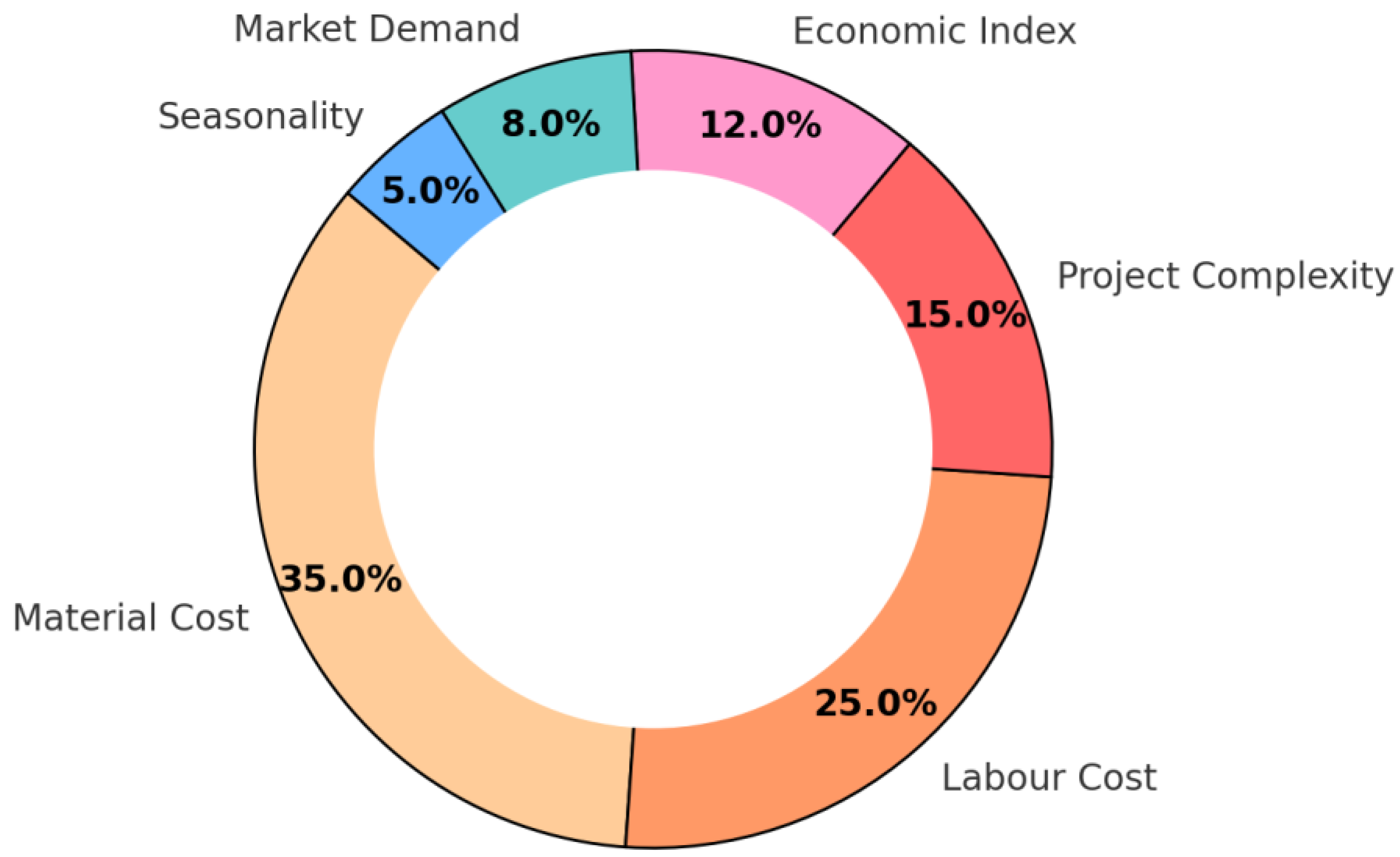
| Feature Name | Description | Why It Matters |
|---|---|---|
| Material Cost | Total cost of raw materials | Major component of total project cost |
| Labour Cost | Total worker wages for the project | Highly variable, depends on location and project type |
| Project Complexity | Scale of difficulty (low/medium/high) | Complex projects require more time and resources |
| Market Demand | Indicator of project demand | High demand raises bid prices |
| Competitor Win Rate | % of past bids won by competitors | Helps AI predict aggressive/conservative bidding |
| Economic Index | Captures inflation, GDP, and bidding environment | Affects material and labour prices |
| Seasonality Factor | Whether the project occurs during the peak or off-peak season | Cost fluctuations due to supply/demand cycles |
| Feature | Mean Value (UK Market) |
|---|---|
| Material Cost | GPB 150,000–600,000 |
| Labour Cost | GPB 100,000–350,000 |
| Project Complexity Score | 1 (Low)–5 (High) |
| Economic Index (UK Inflation) | 105 (Base = 100) |
| Competitor Aggressiveness Score | 0.65 (More Aggressive) |
| Feature | Description |
|---|---|
| Material Cost | Cost of raw materials (steel, cement, etc.) |
| Labour Cost | Total wages for workers |
| Project Complexity | A numerical rating of project difficulty |
| Market Demand | Indicator of how much demand exists for the project type |
| Economic Index | Captures inflation and market stability |
| Competitor Behaviour | Bidding patterns of rival firms |
| Seasonality Factor | Cost variations due to seasonal trends |
| Feature | Description |
|---|---|
| Past Bid Price | The competitor’s last bid amount |
| Market Demand | Economic indicators affecting project bidding |
| Competitor Market Position | Whether the firm is small, medium, or large |
| Past Win Rate | Percentage of bids won by the competitor |
| Project Complexity | Higher complexity may influence bidding behaviour |
| Economic Index | Captures inflation, interest rates, and market stability |
| Statistic | Value (GBP) |
|---|---|
| Predicted Cost | 2.85 M |
| MAE | 100 K |
| R² Score | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serugga, J. AI-Assisted Game Theory Approaches to Bid Pricing Under Uncertainty in Construction. AppliedMath 2025, 5, 39. https://doi.org/10.3390/appliedmath5020039
Serugga J. AI-Assisted Game Theory Approaches to Bid Pricing Under Uncertainty in Construction. AppliedMath. 2025; 5(2):39. https://doi.org/10.3390/appliedmath5020039
Chicago/Turabian StyleSerugga, Joas. 2025. "AI-Assisted Game Theory Approaches to Bid Pricing Under Uncertainty in Construction" AppliedMath 5, no. 2: 39. https://doi.org/10.3390/appliedmath5020039
APA StyleSerugga, J. (2025). AI-Assisted Game Theory Approaches to Bid Pricing Under Uncertainty in Construction. AppliedMath, 5(2), 39. https://doi.org/10.3390/appliedmath5020039





