Mathematical Models of Epidemics with Infection Time

Abstract

After an infectious contact, there is a time lapse before the individual actually becomes infected. In this paper, we present different ways of incorporating this incubation or infection time into epidemic mathematical models. For simplicity, we consider the Susceptible–Infective–Susceptible and the Susceptible–Infective–Recovered–Susceptible models with no demographic effects, so we can concentrate on the infection process. We study the different methods from a modeling point of view to determine their biological validity and find that not all methods presented in the literature are valid. Specifically, the infection part of the model should only move individuals from one compartment to another but should not change the total population. We consider models with no delay, discrete delay, distributed delay, exposed populations, and fractional derivatives. We analyze the methods that are realistic and find their steady solutions, stability, and bifurcations. We also investigate the effect of the duration of the infection time on the solutions. Numerical simulations are conducted and guidelines on how to chose a method are presented.

1. Introduction

Infections take time to develop after an individual has an infectious contact. This is called the infection time or incubation period. For bacterial infections, this time can be as short as a few hours, but for viral infections it usually takes a few days. For influenza, it is between 1 and 3 days, for measles 9 to 12 days, for COVID-19 2 to 14 days, but may take many months or longer for HIV [1,2]. Infection times depend on the individual, especially age and health, and are hard to determine accurately [3,4]. The spread of a disease is a very complicated process: individuals are different and have different lifestyles and numbers of contacts. They can also move, be isolated, live in urban or rural areas, etc. Mathematical models can help predict the development of an epidemic but may have simplifying assumptions like no demographics for short-lived epidemics that cause no or few deaths, homogeneous populations, no dependence on space, and so on. There are different ways of transmission of an infection: direct contact, through a vector, consuming contaminated liquids or foods, and even by blood transfusion or vertical transmission. In this paper, we will only consider infection by direct contact, but similar results can be expected for other transmission forms. Diseases transmitted by direct contact in humans include influenza, small pox, and HIV. The most common simplification used in deriving mathematical models is to consider that the populations are homogeneous, and large enough so they can be thought of as continuous variables, and that there is no spatial dependence. Models based on ordinary differential equations (ODEs) are in this group. The simplest of these models, first proposed in [5], are the SIS (Susceptible–Infective–Susceptible) model, in which a susceptible gets infected by contact with an infective and then recovers with no immunity; the SIR (Susceptible–Infective–Recovered) model, in which a susceptible gets infected by contact but recovers with complete and permanent immunity; and the SIRS (Susceptible–Infective–Recovered–Susceptible) model, in which now the recovered have full but only temporary immunity and then turn back into susceptibles [6,7]. These models assume that the infection is by mass action, that is, proportional to the number of susceptible times the number of infectives (infected). The models can be extended to include vaccination and partial immunity [8,9,10] and quarantined populations (especially for COVID-19) [11,12]. The mass action interactions in the infection and other terms can be modified to be given by saturating functions; see [13] and references therein. These models neglect the effect of the infection times, which cause delays. A first way of introducing a delay is to add an exposed or latent population. A susceptible after contact with an infective converts into an exposed, who after an average time turns into an infective. An SIR (SIRS) model with an infected class is denoted by SEIR (SEIRS) [14,15,16]. See [16] for a history of SEIR models. A second way to incorporate the infection time is to use delay differential equations (DDEs) [17,18]. These equations have different dynamics than ODEs. DDEs consider that each delay has a unique value and is called a discrete delay. There is a vast literature on epidemic models with discrete delays. Some examples are [19,20,21,22]. But infection times have variations. These variations can be included by considering distributed delays [23,24,25,26]. Variations in the delay can also be added by considering the delay to be a random variable [27].

Another common way to introduce dependence on past values is to use fractional derivativesin epidemic models [28,29,30,31,32]. The Caputo form is the most widely used fractional derivative. It has the advantages that its derivative of a constant is zero, and for FDEs, the initial conditions are given in terms of the unknown and, if necessary, integer-order derivatives at the initial point. Exact solutions of FDEs are hard to find. There are several numerical methods [33,34,35,36]. Fractional derivatives are non-local operators that involve the solution from the initial time until the current time. So, the solution at the current time depends on the solution at all previous times, so FDEs incorporate memory. ODEs neglect such effects. In addition, when fitting data, fractional models have more degrees of freedom through the orders of the fractional derivatives compared to ODE models. In fact, many papers that use fractional derivative models for epidemics justify their use by demonstrating superior data fitting compared to ordinary differential equation models. But dependence on the past does not mean that they model infection times.

There are other types of epidemic models: discrete, stochastic, statistical, and more. For reviews, see [37,38,39]. The rest of this paper is organized a follows. In Section 2, the SIS model and SIRS model are introduced first using ODEs, then adding both discrete and distributed delays, and finally adding an exposed population. In Section 3, the equilibrium solutions and their stability are shown, as are numerical simulations under different scenarios. Finally, Section 4 has some discussion and conclusions.

2. Materials and Methods

There are two main groups of models, mechanistic, which use hypotheses based on biology, chemistry, physics, etc. [40], and statistical, which are based on data and are used more for making predictions without considering causality [37,39,41]. Mechanistic models use data to fit parameters that have biological or physical meaning but have either unknown values or values with large variations. See also [42]. Here, we are concerned only with mechanistic models. We will consider that the infection process is short and does not cause a significant number of casualties, so we can assume that the population is constant and that there are no births or deaths. Our main objective is to study how to incorporate the infection time so that the models make sense from a biological point of view and are also simple. We will also study the effect of the duration of the infection time. We will work with the SIS and SIRS models. These models will have the interaction between population compartments given by the law of mass action [43]. The assumption is that both populations are of the same order of magnitude so that saturating interactions such as Holling II [44] or Beddington–Deangelis [45,46] are not necessary. But most the results presented also apply to saturating interactions. For the infection time to be biologically realistic, the infection time needs to be positive, bounded, and have values in a relatively narrow band.

2.1. SIS Model

A simple model consisting of two population compartments, susceptible S and infective I, is the SIS model, which considers that a susceptible gets infected with probability $\beta /N>0$ by contact with an infective, and then recovers with no immunity to susceptible. The flu and influenza are examples of diseases that can be modeled by the SIS model. The total population N is usually considered constant, which assumes that the disease is fast compared with demographic effects or the number of births is equal to the number of deaths with no migration. The SIS model with no demographics is

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}SI+\gamma I\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}SI-\gamma I,\hfill \end{array}$$

(1)

where $\gamma >0$ is the recovery rate and $N>0$ is the total population. More general interactions $f(S,I)$, with f being a positive and monotonically increasing function for $S,I>0$, that satisfies $f(0,I)=f(S,0)=0$, can be used,

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-f(S,I)+\gamma I\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =f(S,I)-\gamma I.\hfill \end{array}$$

(2)

Since the total population is constant, $S\left(t\right)=N-I\left(t\right)$, we can work with only one equation,

$${\displaystyle \frac{dI}{dt}}={\displaystyle \frac{\beta }{N}}(N-I)I-\gamma I.$$

(3)

The SIS model has two equilibrium states, $I^{\ast }=0$ and $I^{\ast }=(1-{\displaystyle \frac{\gamma }{\beta }})N$. The last state makes sense only for ${\displaystyle \frac{\gamma }{\beta }}\le 1$.

Depending on the disease, two delays may be added to the SIS model, ${\tau }_1$, the time in takes the disease to develop in a susceptible individual after being infected by contact with an infective individual, and ${\tau }_2$, the recovery time for a newly infected individual to recover. This second delay gives the minimum time that an individual is infected. Since $\gamma$ is the inverse of the average time an individual is infected, this coefficient needs to be changed if this second delay is used. In this case, the $\gamma$ parameter should be replaced by ${\displaystyle \frac{\gamma }{\gamma \ast {\tau }_2+1}}$ so that the average recovery time is the same as that of the non-delayed model. If the model parameter values are fitted from real data, the fitted $\gamma$ already includes this correction. There are several common assumptions on how to introduce the infection time delay. The first assumption, explained below, leads to the following system of delay differential equations, labeled SIS Delay Model 1:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S(t-{\tau }_1)I(t-{\tau }_1)+{\displaystyle \frac{\gamma }{\gamma {\tau }_2+1}}I(t-{\tau }_2)\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S(t-{\tau }_1)I(t-{\tau }_1)-{\displaystyle \frac{\gamma }{\gamma {\tau }_2+1}}I(t-{\tau }_2).\hfill \end{array}$$

(4)

The model states that contact at time $t-{\tau }_1$ produces a new infective at time t. The model also states that an infective at time $t-{\tau }_2$ recovers at time t. Using $S=N-I$, SIS Delay Model 1 can be simplified to

$${\displaystyle \frac{dI}{dt}}={\displaystyle \frac{\beta }{N}}(N-I(t-\tau ))I(t-\tau )-\gamma I\left(t\right).$$

(5)

As is widely performed, here we have incorporated the delay ${\tau }_2$ into the parameter $\gamma$, and called ${\tau }_1$ simply $\tau$.

The second assumption gives rise to SIS Delay Model 2:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S\left(t\right)I(t-{\tau }_1)+{\displaystyle \frac{\gamma }{\gamma {\tau }_2+1}}I(t-{\tau }_2)\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S\left(t\right)I(t-{\tau }_1)-{\displaystyle \frac{\gamma }{\gamma {\tau }_2+1}}I(t-{\tau }_2).\hfill \end{array}$$

(6)

The assumption is that a new infective takes time ${\tau }_1$ to actually get the disease and be able to infect. So contact at time $t-{\tau }_1$ produces an infective and removes a susceptible at time t. For the recovery delay, the assumption is the same as for SIS Model 1. Again, using $S=N=-I$ and eliminating ${\tau }_2$, we have

$${\displaystyle \frac{dI}{dt}}={\displaystyle \frac{\beta }{N}}(N-I\left(t\right))I(t-\tau )-\gamma I\left(t\right).$$

(7)

Both models conserve the total population and both make biological sense. But if we think of the infection as a reaction between an infective and a susceptible that produces two infectives, the first model makes more sense. But both are widely used.

A third method of introducing the infection time delay is

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S\left(t\right)I\left(t\right)+\gamma I\left(t\right)\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S(t-{\tau }_1)I(t-{\tau }_1)-\gamma I\left(t\right).\hfill \end{array}$$

Here, the assumption is that contact at time $t-{\tau }_1$ increases the infectives at time t, but at the moment of contact the susceptibles decrease. The second delay is not included. Adding the two equations, it can be seen that the total population is not conserved. This assumption is usually used in models with demographics and no constant population ([47] has an SIS model with a varying population and distributed delay). But still, the infection terms create or destroy the population. So these models are not biologically consistent.

This second delay is usually incorporated into the parameter $\gamma$, and we will do the same from here on.

2.2. SIRS Model

Next, we study the SIRS model for epidemics with no demographics [6]. It modifies the SIS by assuming that an infective individual recovers with temporary immunity. It consists of three compartments: susceptible (S), infective (I), and recovered (R). All populations are functions of time t. A susceptible individual moves into the infective compartment with a given probability after contact with an infective. An infective recovers with immunity to the infection at a rate $\gamma$. A recovered loses this immunity at a rate $\nu$ and moves back to the susceptible compartment. Again, we will consider the total population N to be constant, $S\left(t\right)+I\left(t\right)+R\left(t\right)=N$. The infection coefficient will be denoted by $\beta /N$. The SIRS model is described by a system of three ordinary differential equations (ODEs):

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}SI+\nu R\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}SI-\gamma I\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =\gamma I-\nu R.\hfill \end{array}$$

Using that the total population is constant, one population and one equation can be eliminated since $R\left(t\right)=N-S\left(t\right)-I\left(t\right)$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}SI+\nu (N-S-I)\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}SI-\gamma I.\hfill \end{array}$$

(8)

There are three common methods of introducing into the SIRS model the delay in the infection. The first one given by SIRS Model 1 [19,20,22] is

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S(t-\tau )I(t-\tau )+\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S(t-\tau )I(t-\tau )-\gamma I\left(t\right),\hfill \end{array}$$

(9)

where the hypothesis is that an infective has contact with a susceptible at time $t-\tau$ and then it takes time $\tau$ for this susceptible to turn infective. A second delay model is the SIRS Model 2 [21], described by

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S\left(t\right)I(t-\tau )+\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S\left(t\right)I(t-\tau )-\gamma I\left(t\right).\hfill \end{array}$$

(10)

Now, the assumption is that for a susceptible after contact with an infective, a time $\tau$ has to elapse before they move into the infective compartment. So there is a new infective after contact between the susceptible and an individual infected a time ago equal to the delay.

A third way of introducing the infection delay is given by SIRS Model 3, described by

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S\left(t\right)I\left(t\right)+\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S(t-\tau )I(t-\tau )-\gamma I\left(t\right),\hfill \end{array}$$

(11)

where the susceptible after contact with an infective leaves the susceptible population but takes a time $\tau$ to be included in the infective population. It does not conserve the total population, and the infection contact is between individuals at the same time. Since the total population is not conserved, we will not consider this model any further.

Therefore, only two of the above delayed SIRS models make biological sense. The delay has a discrete value $\tau$, which is constant. In Section 2.3, we describe how to introduce variations in the delay.

2.3. Distributed Delay

In practice, it is difficult for an individual to ascertain when the infectious contact happened and when the onset of the infection was. Also, there are variations among individuals, including age and health. Therefore, instead of considering that the infection time has a unique value, it is more realistic to assume that it is given by a probability distribution centered around an accepted value of the delay, such as a uniform, gamma, or normal distribution. Then, one obtains models with distributed delay [23,48,49,50].

It is straight-forward to transform a discrete delay model into a distributed delay one. For example, the SIRS delay models (9) and (10) give the models (12) and (13), respectively, when the discrete delay is replaced by a distributed one with distribution $F\left(u\right)$:

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}{\int }_{-\infty }^{t}F(t-\tau )S\left(\tau \right)I\left(\tau \right)d\tau +\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}{\int }_{-\infty }^{t}F(t-\tau )S\left(\tau \right)I\left(\tau \right)d\tau -\gamma I\left(t\right),\hfill \end{array}$$

(12)

and

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}S\left(t\right){\int }_{-\infty }^{t}F(t-\tau )I\left(\tau \right)d\tau +\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}S\left(t\right){\int }_{-\infty }^{t}F(t-\tau )I\left(\tau \right)d\tau -\gamma I\left(t\right).\hfill \end{array}$$

(13)

Here, the possible delay varies from $-\infty$ to 0. The modification for the SIS delay models is similar.

When the distribution is given by a delta function, $\delta \left({\tau }_0\right)$, we obtain the corresponding discrete delay models with $\tau ={\tau }_0$. Common probability distributions used are beta, normal, log=normal, gamma, and uniform. The gamma distribution,

$$\gamma (x,a,b)={\displaystyle \frac{x^{a-1}{e}^{-bx}{b}^a}{\mathrm{\Gamma }\left(a\right)}},$$

is widely used since then the distributed delay model can be converted into a system of ODEs [51,52,53]. Here, $\mathrm{\Gamma }\left(t\right)$ is the gamma function. For example, for $a=1$, $\gamma (x,1,b)=b{e}^{-bx}$. Taking the SIRS distributed model (12) and letting

$$z\left(t\right)={\int }_{-\infty }^{t}b{e}^{-b(t-s)}S\left(s\right)I\left(s\right)ds,$$

we obtain the system

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}z\left(t\right)+\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}z\left(t\right)-\gamma I\left(t\right)\hfill \\ \hfill {\displaystyle \frac{dz}{dt}}& =b\left(S\right(t\left)I\right(t)-z(t\left)\right),\hfill \end{array}$$

(14)

with $z\left(0\right)=I\left(0\right)S\left(0\right)$. For $\alpha =2$, $\gamma (x,2,b)=b^{2}x{e}^{-bx}$, and letting

$$y\left(t\right)={\int }_{-\infty }^{t}b{e}^{-b(t-s)}S\left(s\right)I\left(s\right)ds,z\left(t\right)={\int }_{-\infty }^t{b}^2(t-s)e^{-b(t-s)}S\left(s\right)I\left(s\right)ds,$$

one obtains the system

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}z\left(t\right)+\nu (N-S\left(t\right)-I\left(t\right))\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\displaystyle \frac{\beta }{N}}z\left(t\right)-\gamma I\left(t\right)\hfill \\ \hfill {\displaystyle \frac{dy}{dt}}& =b\left(S\right(t\left)I\right(t)-by(t\left)\right)\hfill \\ \hfill {\displaystyle \frac{dz}{dt}}& =b\left(y\right(t)-z(t\left)\right).\hfill \end{array}$$

(15)

Proceeding in a similar way, you obtain an additional equation every time a increases by 1. For many infectious diseases, the probability should be fairly narrow, which implies higher $\alpha$. See Figure 1 for plots of the gamma function with the maximum value at $t=10$ for different values of a.

The transformation to a system of ordinary conditions gives a very good method to solve distributed delay equations and can also be used to validate other numerical methods of solution. But due to the high number of equations, it is not so convenient for the analysis, for example, to determine the stability of solutions.

Another common probability distribution used is the normal distribution, which, even though defined from $-\infty$ to ∞, usually has a small negative tail that only introduces small errors. And a uniform distribution is always an option. In the literature, the gamma distribution is commonly used, probably because the distributed delay system can be transformed into an ODE system. Normal distributions are assumed in many applications, and for a given shape of the infection time both the gamma and normal distributions can give similar approximations. But normal distributions require us to solve the integro-differential equations. Uniform distributions are also assumed for their simplicity, but they have the disadvantage that they do not have a peak.

2.4. Random Delay

An alternative method of considering the variations in the values of the delay is to consider that it is a random variable with a given probability distribution. For a given time, the delay has the same value for all the population, but it changes from time to time. Models written using stochastic differential equations to deal with variability and errors have the same assumption. The model given in terms of ODEs is solved for different sampling values of the delay with the given distribution, and the numerical solutions are then averaged. The differences between models with random delay compared with those using distributed delay are given in [27].

2.5. Exposed Population Model

A different modeling assumption that avoids the use of delay differential equations is to introduce an exposed (E) or latent population. This consists of individuals that have been infected but still have not turned infective. The SIS model with an exposed population is

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}SI+\gamma I\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& ={\displaystyle \frac{\beta }{N}}SI-\sigma E\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =\sigma E-\gamma I.\hfill \end{array}$$

(16)

Here, $1/\sigma$ is the average time an individual spends in the compartment, and when comparing with delay models we will take it equal to the delay. This means that the exposed population models have the same average infection time, but the transition from exposed to infective is given by an exponential function instead of a narrow function centered at the infection time. So from a modeling point of view, they are not as good as models given by delay differential equations.

The SIRS model with an exposed population, usually denoted by SEIRS, is

$$\begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =-{\displaystyle \frac{\beta }{N}}SI+\nu R\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& ={\displaystyle \frac{\beta }{N}}SI-\sigma E\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& =\sigma E-\gamma I\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& =\gamma I-\nu R.\hfill \end{array}$$

(17)

The advantages of modeling with (16) or (17) are that they are based on ODEs, so they do not require the previous history of the populations, and their analysis is simpler.

2.6. Fractional Differential Equations

Fractional differential equations (FDEs) offer an alternative approach to account for the infection time. See, among many others [54,55,56,57]. The primary arguments in favor of fractional derivatives are that their models improve the way the available data are adjusted and that, because they are non-local, they have a dependence on historical values. While there are various ways to define fractional derivatives, the most widely used fractional operator in mathematical biology models is the Caputo fractional derivative. One reason is that FDEs based on Caputo derivatives only require that the initial conditions be stated only in terms of ordinary derivatives [54,55]. Consider that the initial time is $t=0$, and the Caputo fractional derivative is

$${}_0{}^{C}D_t^{\alpha }y\left(t\right)={\displaystyle \frac{1}{\mathrm{\Gamma }(m-\alpha )}}{\int }_0^t{(t-\tau )}^{-\alpha -1+m}{\displaystyle \frac{d^m}{d{\tau }^m}}y\left(\tau \right)d\tau ,m-1<\alpha <m,$$

(18)

where $\alpha$ is the order of the derivative. These initial values are given in terms of ordinary derivatives. The initial values for Caputo differential equations are given as

$${}_0{}^{C}D_t^{\alpha }y\left(0\right)=b_{\nu },\nu =1,2,\dots m,$$

with $m-1<\alpha \le m$. In mathematical biology applications, $m=1$. From the definition of the Caputo derivative (18), it is clear that it is a non-local operator over the interval $(0,t)$ and depends only on values for $t\ge 0$. From the kernel of the integral, it can be seen that it is weighted toward the values at time t. When using Caputo derivatives, the population has memory—that is, it is dependent on previous values. However, the precise manner in which it integrates the true dependence on the past is unclear. For our SIS and SIRS models, the dependence on the past is based on the infection time. As a result, at time t, the dependence on the past should be strongly centered at values at $t-\tau$, where $\tau$ represents the infection time. Instead of the Caputo definition, the Grünwald–Letnikov definition of the fractional derivative $D_t^{\alpha }y\left(t\right)$ is commonly used. It is based on taking finite differences at equidistant time steps in $[0,t]$. The Grünwald–Letnikov definition is [34,54]

$$D_t^{\alpha }y\left(t\right)=\underset{\Delta t\to 0}{lim}{\displaystyle \frac{1}{\Delta t^{\alpha }}}{\Delta }_{\Delta t}^{\alpha }y\left(t\right).$$

By applying the Grünwald–Letnikov definition, we obtain the following fractional differential equation:

$${}_0{}^{C}D_t^{\alpha }N\left(t\right)=f\left(N\left(t\right)\right),N\left(0\right)=N_0(0<\alpha <1),$$

(19)

where $N\left(t\right)$ is the exact solution in the interval $[0,T]$. If $N_k$ denotes the approximation of the true solution $N\left(t_k\right)$, then the explicit or implicit Grünwald–Letnikov method solution on a uniform grid is

$$N_{n+1}-\sum _{\nu =1}^{n+1}{c}_{\nu }^{\alpha }{N}_{n+1-\nu }-r_{n+1}^{\alpha }{N}_0=\Delta t^{\alpha }f\left(N_n\right)\mathrm{or}\Delta t^{\alpha }f\left(N_{n+1}\right).$$

Here, $r_{n+1}^{\alpha }={\displaystyle \frac{{(n+1)}^{-\alpha }}{\mathrm{\Gamma }(1-\alpha )}}$, with $\mathrm{\Gamma }$ being the gamma function. By letting $n=0$, the equation for the first step is

$$N_1-c_1^{\alpha }{N}_0-r_1^{\alpha }{N}_0=\Delta t^{\alpha }f\left(N_0\right)\mathrm{or}\Delta t^{\alpha }f\left(N_1\right).$$

As a result, this solution differs from the one found in the initial stage of any standard finite approximation of Equation (19) when a standard finite difference approximation of a regular derivative is used in place of the fractional derivative. In addition to including past values of the solution beginning at initial time $t=0$, the Caputo derivative contains terms that are not found in a standard discrete-time conservation equation. Differential equation-based epidemic models typically begin as discrete time conservation of population models, and the limit is then taken as the time interval approaches zero. The memory given by a fractional derivative is concentrated on the current time, which is not a good model for an infection time, which is concentrated on a finite time in the past. Discrete delay and integrated delay models have this property.

The SIRS fractional model is

$$\begin{array}{cc}\hfill {}_0{}^{C}D_t^{\alpha }S\left(t\right)& =-{\displaystyle \frac{\beta }{N}}SI+\nu R\hfill \\ \hfill {}_0{}^{C}D_t^{\alpha }I\left(t\right)& ={\displaystyle \frac{\beta }{N}}SI-\gamma I\hfill \\ \hfill {}_0{}^{C}D_t^{\alpha }R\left(t\right)& =\gamma I-\nu R.\hfill \end{array}$$

(20)

But due to the fact that fractional derivatives in epidemic models have modeling issues, such as a clear biological interpretation of the fractional derivative in terms of rates of change and the odd dependence on infection times, we will not consider them further. The reason that they adjust better to data is probably due to the presence of an additional parameter, the order of the derivative. But if comparisons are of interest, see [58], where there are simulations for different mathematical models that are described using discrete delay equations, ordinary differential equations with an exposed population, and fractional derivative differential equations with different values of $\alpha$. The results there show that by choosing the $\alpha$ adequately, the simulations are close.

3. Results

Epidemic mathematical models can be used to increase understanding of the processes involved and to make predictions. Important questions are the existence of endemic equilibria and their stability, what is the influence of the infection time length, and what is the time of development and size of the infection. Also, since some of the parameters may have variations or uncertainties in their measurement, what is the influence of changes in their values on the solutions? This section presents the results of the SIS and SIRS models, with their different ways of including the infection time. We will normalize the populations by taking $N=1$.

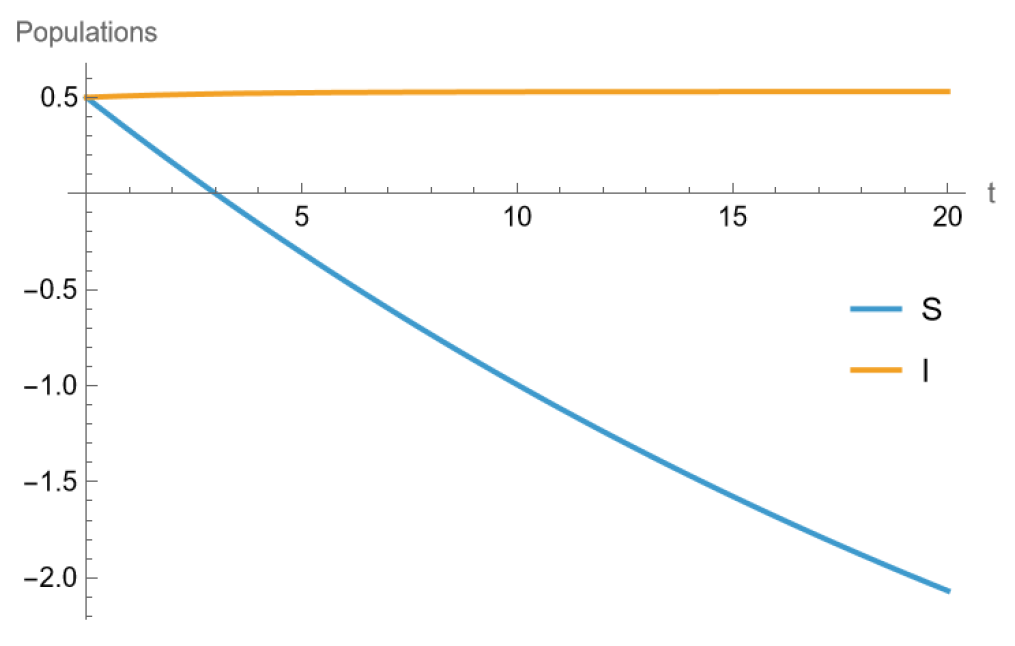
3.1. SIS

3.1.1. ODE Model

The SIS model with no infection time is given by (3). The models have two equilibrium solutions, the disease-free equilibrium (DFE) $S^{\ast }=1,I^{\ast }=0$ and the endemic equilibrium $S^{\ast }=\gamma /\beta ,I^{\ast }=1-\gamma /\beta$. This second equilibrium only makes sense for $\gamma <\beta$. The local stability analysis can be performed by linearizing about an equilibrium point and finding the eigenvalues of the one-dimensional jacobian matrix. The characteristic equation is

$$\lambda =\beta (1-2I^{\ast })-\gamma .$$

(21)

At the DFE, $\lambda =\beta -\gamma$, so the disease-free equilibrium is locally asymptotically stable for $\beta <\gamma$. At the endemic equilibrium, $\lambda =\gamma -\beta$, so it is locally asymptotically stable for $\gamma <\beta$, that is, when the endemic equilibrium makes sense. The stability of the DFE can also be found by calculating the basic reproductive number $R_0$, which can be found by using the next-generation matrix method [26,59]. The equation for the only infective population compartment is

$${\displaystyle \frac{dI}{dt}}=\beta I\left(t\right)-\gamma I\left(t\right)=\mathcal{F}-\mathcal{V}.$$

(22)

Then, let $F={\displaystyle \frac{\partial \mathcal{F}}{dI}}$ and $V={\displaystyle \frac{\partial \mathcal{V}}{dI}}$ so $R_0=F{V}^{-1}=\beta /\gamma$. The DFE is unstable for $R_0>1$, and for this model $R_0=\beta /\gamma$.

The global stability of the equilibrium point $I^{\ast }=0$ using Equation (3) can be established by using the Lyapunov function $V\left(I\right)={\displaystyle \frac{1}{2}}{\left(I\right)}^2$ [60], which is positive definite. Then,

$$\begin{array}{cc}\hfill {\displaystyle \frac{dV\left(t\right)}{dt}}=& {\displaystyle \frac{dV\left(I\right)}{dI}}{\displaystyle \frac{dI}{dt}}={\displaystyle \frac{1}{2}}I(\beta IS-\gamma I)\hfill \\ \hfill =& {\displaystyle \frac{1}{2}}{I}^2(\beta S-\gamma ).\hfill \end{array}$$

Since $S\le 1$ and $\beta <\gamma$${\displaystyle \frac{dV\left(t\right)}{dt}}\le 0$, $I^{\ast }=0$ is globally stable for $\beta <\gamma$.

For the endemic equilibrium $I^{\ast }=1-{\displaystyle \frac{\gamma }{\beta }},S^{\ast }=1-I^{\ast }$, $\beta >\gamma$, using Equation (3) the Lyaponuv function $V\left(I\right)={\displaystyle \frac{1}{2}}{(I-I^{\ast })}^2$ works. We consider Equation (1) and a Lyapunov function based on those presented in [60,61], since similar functions can be used for SIS, SIR, and SIRS models that also include demographics. Let

$$V(S,I)=S-S^{\ast }ln{\displaystyle \frac{S}{S^{\ast }}}+I-I^{\ast }ln{\displaystyle \frac{I}{I^{\ast }}}.$$

Then,

$$\begin{array}{cc}\hfill {\displaystyle \frac{dV}{dt}}=& (1-{\displaystyle \frac{S^{\ast }}{S}})(-\beta SI+\gamma I)+(1-{\displaystyle \frac{I^{\ast }}{I}})(\beta SI-\gamma I)\hfill \\ \hfill =& {\displaystyle \frac{(\gamma -\beta S)(I^{\ast }S-I{S}^{\ast })]}{S}}\hfill \\ \hfill =& -{\displaystyle \frac{{(\beta S-\gamma )}^{2}I}{\beta }}<0.\hfill \end{array}$$

(23)

So the endemic equilibrium is globally stable when the equilibrium is biologically feasible. So for the ODE model there are several alternatives to determine if there will be an epidemic.

As a parameter changes, solutions branches may go through bifurcation. We are only interested in solution branches that are stable. If one of the solutions of the characteristic equations changes sign as the parameter changes, there is an exchange of stability between the two branches at the bifurcation point. We will use the infection rate $\beta$ as the continuation parameter since it has the most variability. At $\beta =\gamma$, both branches intersect and there is an exchange of stability. The DFE is stable for $\beta <\gamma$ and the endemic equilibrium for $\beta >\gamma$.

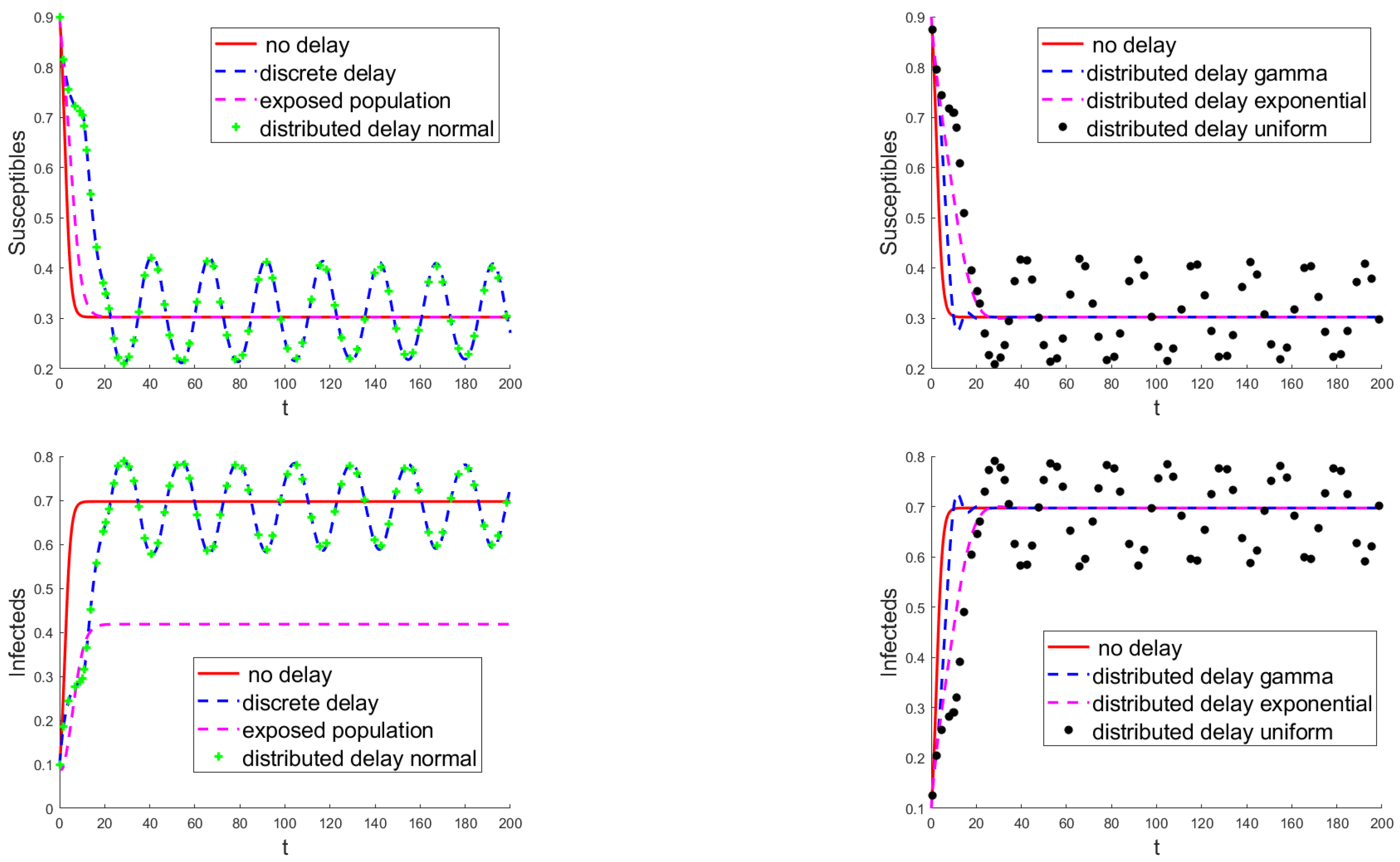
3.1.2. Discrete Delay Models

The two SIS models with discrete delay, (5) and (7), have the same equilibrium points as the ODE model. The local stability of an equilibrium solution $I^{\ast }$ can be determined by letting $I=I^{\ast }+i$. So around the DFE for SIS Model 1, we have the linearized differential equation for i, ${\displaystyle \frac{di}{dt}}=\beta (i(t-\tau )-2I^{\ast }i(t-\tau ))-\gamma i\left(t\right)$. Solutions are obtained by considering $i=exp(-\lambda t)$ and thus obtaining the characteristic equation

$$\lambda =\beta exp(-\lambda \tau )(1-2I^{\ast })-\gamma .$$

(24)

This equation is transcendental and has an infinite number of solutions and no close-form solution. Taking $I^{\ast }=0$, $\lambda >0$, and therefore the DFE is unstable only for $\beta >\gamma$. So we have the same $R_0$ as for the ODE model. At $I^{\ast }=1-\gamma /\beta$, $\lambda <0$ for $\beta >\gamma$. The linearized equation for SIS Model 2 is ${\displaystyle \frac{di}{dt}}=\beta (i(t-\tau )-I^{\ast }i(t-\tau )-I^{\ast }i\left(t\right)-\gamma i\left(t\right)$. The characteristic equation is

$$\lambda =\beta (exp(-\lambda \tau )(1-I^{\ast })-I^{\ast })-\gamma .$$

(25)

At $I^{\ast }=0$, $\lambda >0$ only for $\beta >\gamma$ and at $I^{\ast }=1-\gamma /\beta ,\lambda <0$ for $\beta >\gamma$. This method has been applied to other models by [62,63]. An easier way to determine if there is an infection is to use the next-generation matrix method: Take $S=N=1$; the equation for the infective compartment, for both models (5) and (7), is

$${\displaystyle \frac{dI}{dt}}=\beta I(t-\tau )-\gamma I\left(t\right)=\mathcal{F}-\mathcal{V}.$$

Then, $F={\displaystyle \frac{\partial \mathcal{F}}{dI}}$, $V={\displaystyle \frac{\partial \mathcal{V}}{dI}}$ and $R_0=F{V}^{-1}=\beta /\gamma$.

Global stability of the equilibrium points can be achieved by using Lyapunov functions involving an integral from $t-\tau$ to t [64,65]. But since discrete differential equations can be written as a series of ODEs over time intervals of length equal to the delay [18,66], the methods used for ODEs can be applied piecewise to DDEs.

Bifurcations may happen when there is a change of stability in a branch of solutions. Also, periodic solutions can bifurcate from equilibrium solutions at what is usually called a Hopf bifurcation [67]. Discrete delay differential equations may present Hopf bifurcations. There will be a Hopf bifurcation with respect to a given parameter if the characteristic equation has purely imaginary solutions and the real part of the eigenvalue satisfies a transversality condition. The infection rate $\beta$ is taken as the continuation parameter. For SIS Model 1, let $\lambda =u+iw$ in the characteristic Equation (24) and separate the real and imaginary parts:

$$\begin{array}{cc}\hfill u& =\beta (cos\left(w\tau \right)(1-2I^{\ast }))-\gamma \hfill \\ \hfill w& =\beta (-sin(-w\tau )(1-2I^{\ast })).\hfill \end{array}$$

(26)

There is solution $u=0,w=0$ at $\beta =\gamma$ where the DFE and endemic equilibrium branches intersect and exchange stability. For a periodic solution to bifurcate from the steady solution, it is necessary that there is an eigenvalue $\lambda$ with real part zero, and imaginary part not zero, and no other eigenvalue with real part positive.

For $I^{\ast }=0$, taking $u=0$ and solving for w, $w=\pm \sqrt{{\beta }^2-{\gamma }^2}$. But for $\beta >\gamma$, there is another real positive eigenvalue. So there is no Hopf bifurcation from the DFE branch.

For $I^{\ast }=1-\gamma /\beta$, Equation (26) is

$$\begin{array}{cc}\hfill u& =\beta (cos(w\tau \left)\right(2\gamma /\beta -1\left)\right)-\gamma \hfill \\ \hfill w& =\beta (-sin(-w\tau \left)\right(2\gamma /\beta -1\left)\right).\hfill \end{array}$$

(27)

Solving for w,

$$w=\pm \sqrt{{\left(2\gamma \right)-\beta )}^2-{\gamma }^2}$$

(28)

which makes sense for $\beta >3\gamma$. The value of $\beta$ at the Hopf bifurcation can be found by solving

$$cos\left(w\tau \right)={\displaystyle \frac{\gamma }{2\gamma -\beta }}.$$

(29)

For $\tau =10,\gamma =.333$, the value of $\beta$ is approximately $\beta =1.0$.

For SIS Model 2, the characteristic Equation (25) evaluated at the DFE $I^{\ast }=0$ is the same as that for SIS Model 1, so the same results are true. At the endemic equilibrium $I^{\ast }=1-\gamma /\beta$, the real and imaginary parts of (25) are

$$\begin{array}{cc}\hfill u& =\gamma cos\left(w\tau \right)-\beta \hfill \\ \hfill w& =-\gamma sin(-w\tau ).\hfill \end{array}$$

(30)

$u=w=0$ implies $\beta =\gamma$, which corresponds to the intersection of the DFE with the endemic equilibrium. For a Hopf bifurcation, it is necessary that $u=0,w\ne 0$. But $w^2={\gamma }^2-{\beta }^2$, which implies that the equilibrium $1-\gamma /\beta$ is negative.

3.1.3. Distributed Delay Models

Distributed delay models have the same equilibrium solutions as the corresponding ODE model, independent of the probability distribution of the delay. Models with a gamma probability distribution can be converted to systems of ODEs, as noted in the previous section. However, in many real situations the distribution probability is narrow, which requires systems of many ODEs that are unpractical for the determination of stability. Also, in many cases, the linearization of the distributed delay model does not have solutions of the form $exp\left(rt\right)$. But the next-generation matrix method can be used to determine the stability of the DFE. The infective compartment of (12) is

$${\displaystyle \frac{dI}{dt}}=\beta {\int }_{-\infty }^{t}F(t-\tau )S\left(\tau \right)I\left(\tau \right)d\tau -\gamma I\left(t\right)=\beta {\int }_0^{\infty }F\left(u\right)S(t-u)I(t-u)du-\gamma I\left(t\right).$$

(31)

Evaluate at $S=1$ and let $\mathcal{F}=\beta {\int }_0^{\infty }F\left(u\right)I(t-u)du,\mathcal{V}=-\gamma I$. Then,

$$\begin{array}{cc}\hfill F& ={\displaystyle \frac{\partial \mathcal{F}}{\partial I}}=\beta {\int }_0^{\infty }F\left(u\right)du=\beta \hfill \\ \hfill V& ={\displaystyle \frac{\partial \mathcal{V}}{\partial I}}=\gamma .\hfill \end{array}$$

(32)

Therefore, the basic reproductive number is $R_0=F{V}^{-1}=\beta /\gamma$, which is the same as that of the ODE model. The calculation for the second distributed delay model (13) gives the same $R_0$.

3.1.4. Exposed Population Model

The model with an exposed or latent population to deal with the delay is given by (16). It has two steady solutions, $S^{\ast }=1,I^{\ast }=E^{\ast }=0$ and $S^{\ast }={\displaystyle \frac{\gamma }{\beta }},I^{\ast }={\displaystyle \frac{(\beta -\gamma )\sigma )}{\beta (\gamma +\sigma )}},E^{\ast }=1-S^{\ast }-I^{\ast }$. The second one requires $\beta >\gamma$. The eigenvalues of the linearized model evaluated at the DFE are

$${\lambda }_{1,2}={\displaystyle \frac{-\sigma -\gamma \pm \sqrt{{(\gamma +\sigma )}^2-4\sigma (\gamma -\beta )}}{2}},$$

so one is positive for $\beta >\gamma$. For the endemic equilibrium, they are

$${\lambda }_1={\displaystyle \frac{(-\beta +\gamma )\sigma }{\gamma +\sigma }},{\lambda }_2=-\sigma -\gamma ,$$

so the first one is positive for $\gamma >\beta$. The next-generation matrix method gives $R_0=\sqrt{{\displaystyle \frac{\beta }{\gamma }}}.$ Following either the DFE or the endemic branches, as $\beta$ is varied, there is only an exchange of stability where the two branches cross $\beta =\gamma$.

3.2. Sirs

3.2.1. Ode Model

The SIRS model that has no infection time delay is given by (8). It has two equilibrium solutions, $S^{\ast }=1,I^{\ast }=0$ and $S^{\ast }={\displaystyle \frac{\gamma }{\beta }},I^{\ast }={\displaystyle \frac{(\beta -\gamma )\nu }{\beta (\gamma +\nu )}}$. The characteristic equation is

$${\lambda }^2+\lambda (\gamma +\beta I^{\ast }-\beta S^{\ast }+\nu )+(\beta \gamma I^{\ast }+\beta \nu I^{\ast }-\beta \nu S^{\ast }+\gamma \nu )=0.$$

(33)

At $S^{\ast }=1,I^{\ast }=0$, the eigenvalues are ${\lambda }_1=\beta -\gamma ,{\lambda }_2=-\nu$. Therefore, the DFE is locally asymptotically stable for $\beta <\gamma$ and unstable otherwise. For the endemic equilibrium, rather than determining the sign of the eigenvalues it is easier to look at the characteristic equation:

$${\lambda }^2+\lambda (\nu +{\displaystyle \frac{(\beta -\gamma )\nu }{\gamma +\nu }})=(\gamma -\beta )\nu .$$

(34)

For $\beta >\gamma$, the right-hand side is negative, so $\lambda$ is negative. For the global stability of the DFE, we consider the Lyapunov function $V(S,I)=S+I-S^{\ast }ln{\displaystyle \frac{S}{S^{\ast }}}$. Then, ${\displaystyle \frac{dV}{dt}}=(\beta -\gamma )I$, which is negative for $\beta <\gamma$. For the endemic equilibrium, we take $V(S,I)=S+I-S^{\ast }ln{\displaystyle \frac{S}{S^{\ast }}}-I^{\ast }ln{\displaystyle \frac{I}{I^{\ast }}}$ [60,61]. Also, since the equation for the infective population is the same as that for the SIS ODE model (22), the next-generation matrix method gives that $R_0$ is still $\beta /\gamma$. Finding the $R_0$ is the easiest way of determining the stability of the DFE.

To study the bifurcation of the solution branches as $\beta$ varies, we look at the characteristic Equation (33). For the DFE,

$${\lambda }^2+\lambda (\gamma -\beta +\nu )+(\gamma -\beta )\nu =0,$$

(35)

so $\lambda <0$ for $\beta <\gamma$ and there is a lost of stability at $\beta =\gamma$, which is the intersection with the endemic branch. For the endemic branch, $\lambda <0$ for $\beta >\gamma$. To see if there is a Hopf bifurcation, let $\lambda =iw$ in (35). Separating the real and imaginary parts, the imaginary part is $w=0$. For the endemic branch, the imaginary part is also $w=0$. So there are no Hopf bifurcations.

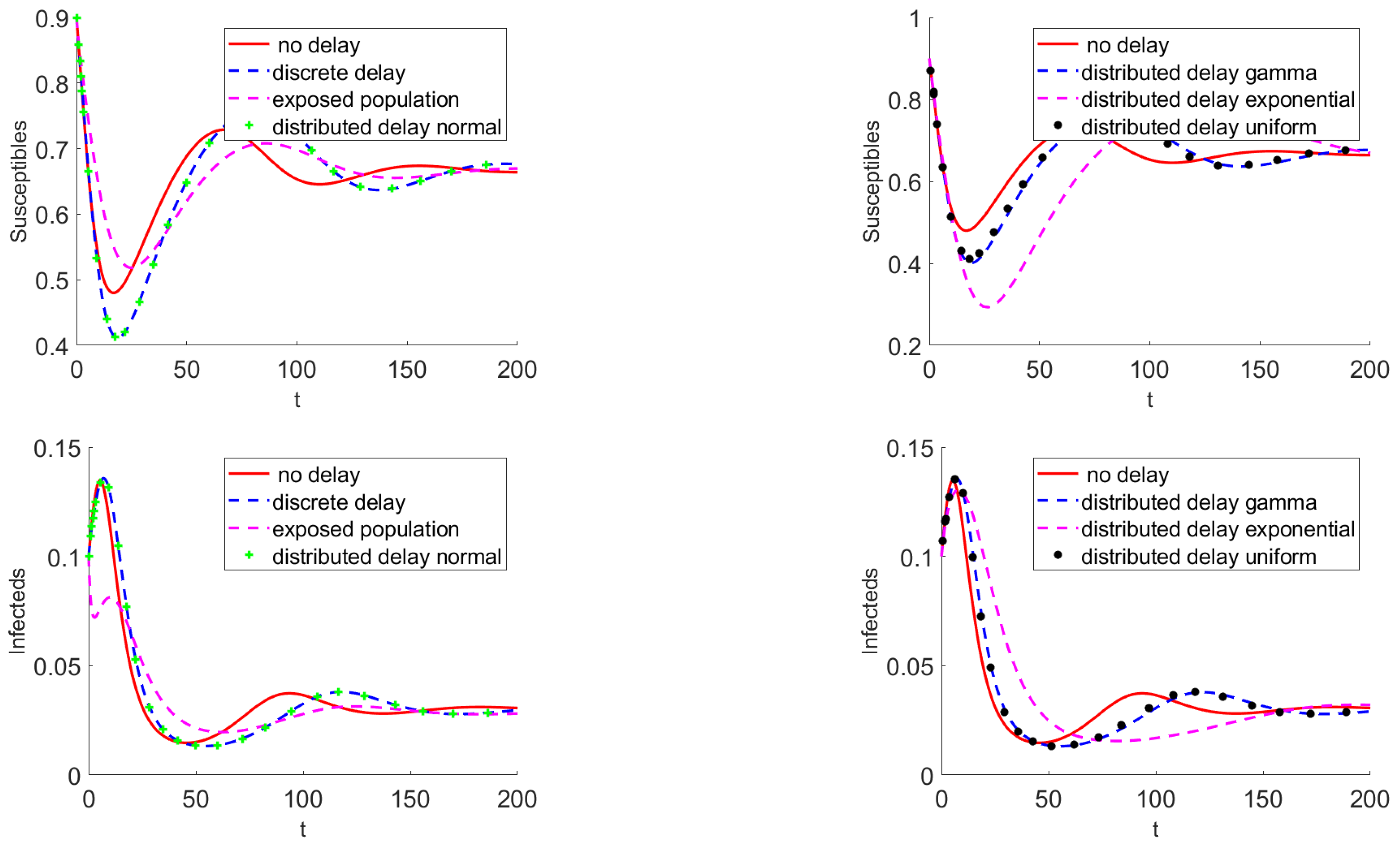
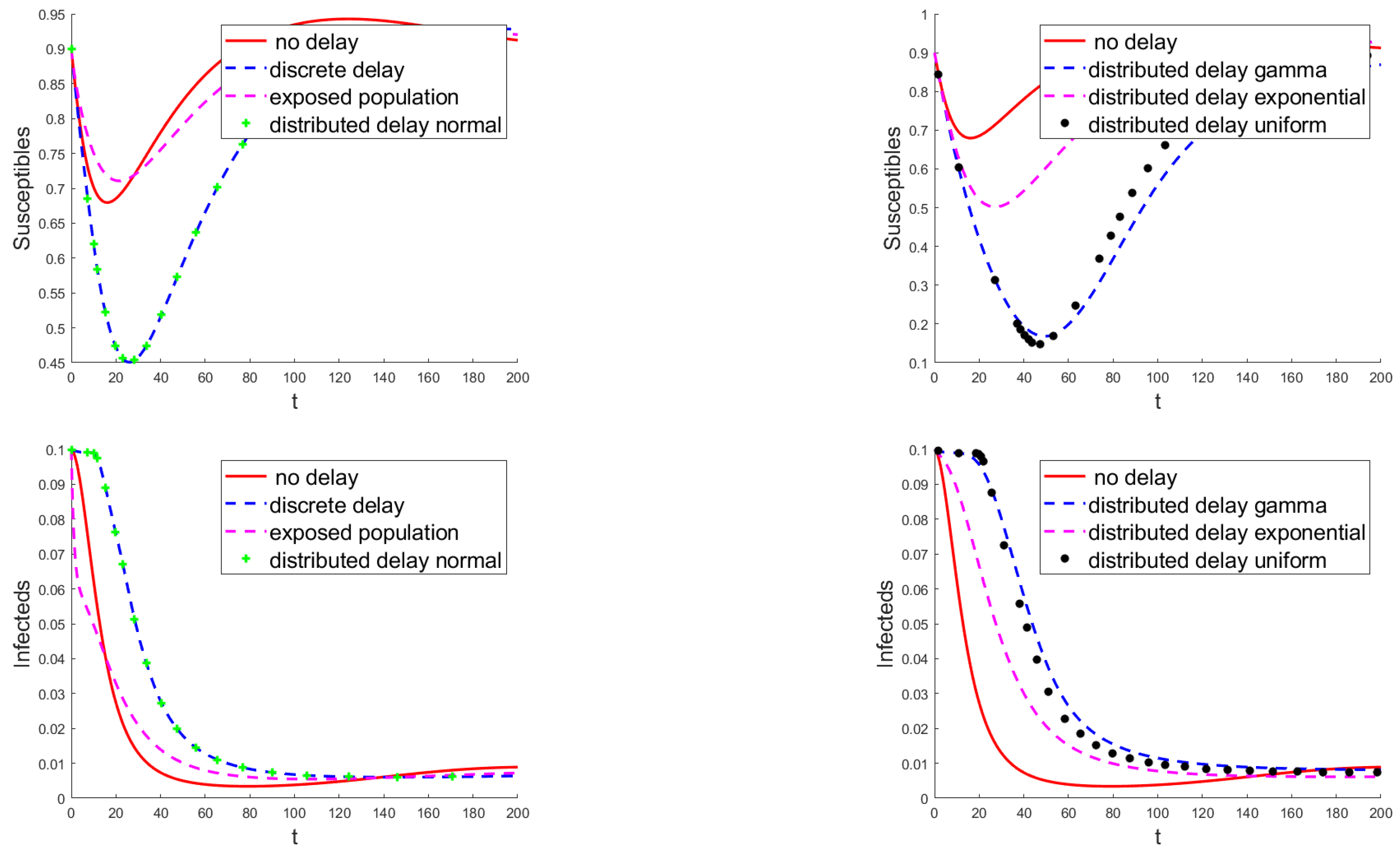
3.2.2. Discrete Delay Models

The discrete delay SIRS Models 1 and 2, (9) and (10), have the same equilibrium points as the ODE model. Letting $I=I^{\ast }+i,S=S^{\ast }+s$, the linearized SIRS Model 1 is

$$\begin{array}{cc}\hfill {\displaystyle \frac{ds}{dt}}=& -\nu (s\left(t\right)+i\left(t\right))-\beta (I\ast s(t-\tau )+S^{\ast }i(t-\tau ))\hfill \\ \hfill {\displaystyle \frac{di}{dt}}=& -nui\left(t\right)+\beta (I\ast s(t-\tau )+S^{\ast }i(t-\tau )).\hfill \end{array}$$

The characteristic equation is

$${\lambda }^2+\lambda (\gamma +\nu +\beta exp(-\lambda \tau )(I^{\ast }-S^{\ast }))+\gamma \nu +\beta exp(-\lambda \tau )(I^{\ast }-S^{\ast })=0.$$

(36)

At $I^{\ast }=0,S^{\ast }=1$,

$${\lambda }^2+\lambda (\gamma -\beta exp(-\lambda \tau )+\nu )+\nu (\gamma -\beta exp(-\lambda \tau )).$$

For $\gamma >\beta$, all coefficients are positive, so $\lambda$ is always negative. At the endemic equilibrium,

$${\lambda }^2+\lambda (\gamma -\gamma exp(-\lambda \tau +\nu +{\displaystyle \frac{exp(-\lambda \tau )(\beta -\gamma )\nu }{\gamma +\nu }})+\gamma \nu -exp(-\lambda \tau )+exp(-\lambda \tau (\beta -\gamma )\nu ).$$

So for $\beta >\gamma$, the endemic equilibrium is locally asymptotically stable. A more straightforward way of determining the stability of the DFE is to calculate the basic reproduction number $R_0$. For both delay models, the next-generation matrix method gives $R_o=\beta /\gamma$.

The DFE and endemic branches intersect at $\beta =\gamma$. To see if there are Hopf bifurcations, write the characteristic Equation (36), as

$${\lambda }^2+\lambda P_1+P_0+exp(-\lambda \tau )(\lambda Q1+Q2)=0,$$

(37)

with

$$P1-\gamma +\nu ,P_0=\gamma \nu ,Q_1=\beta I^{\ast }-\beta S^{\ast },Q_0=\beta \gamma I^{\ast }+\beta I^{\ast }\nu -\beta \nu S^{\ast }.$$

Let $\lambda =1w$ and see if there are positive solutions for w. The real and imaginary parts are

$$\begin{array}{cc}\hfill P_0-w^2=& -Q_{0}cos\left(w\tau \right)+Q_{1}sin\left(w\tau \right)\hfill \\ \hfill P_{1}w=& -Q_{1}wcos\left(w\tau \right)+Q_{0}wsin\left(w\tau \right).\hfill \end{array}$$

Square each equation and add

$$w^4+w^2(P_1^2-Q_1^2-2P_0)+P_0^2-Q_0^2=0.$$

(38)

For a positive w, it is necessary that $P_1^2-Q_1^2-2P_0<0$ and ${(P_1^2-Q_1^2-2P_0)}^2-4(P_0^2-Q_0^2)>0$. For a given epidemic, $\gamma$ and $\nu$ are well determined, but there is a range of variation for $\beta$. As will be presented in the next subsection, for our values there are no Hopf bifurcations.

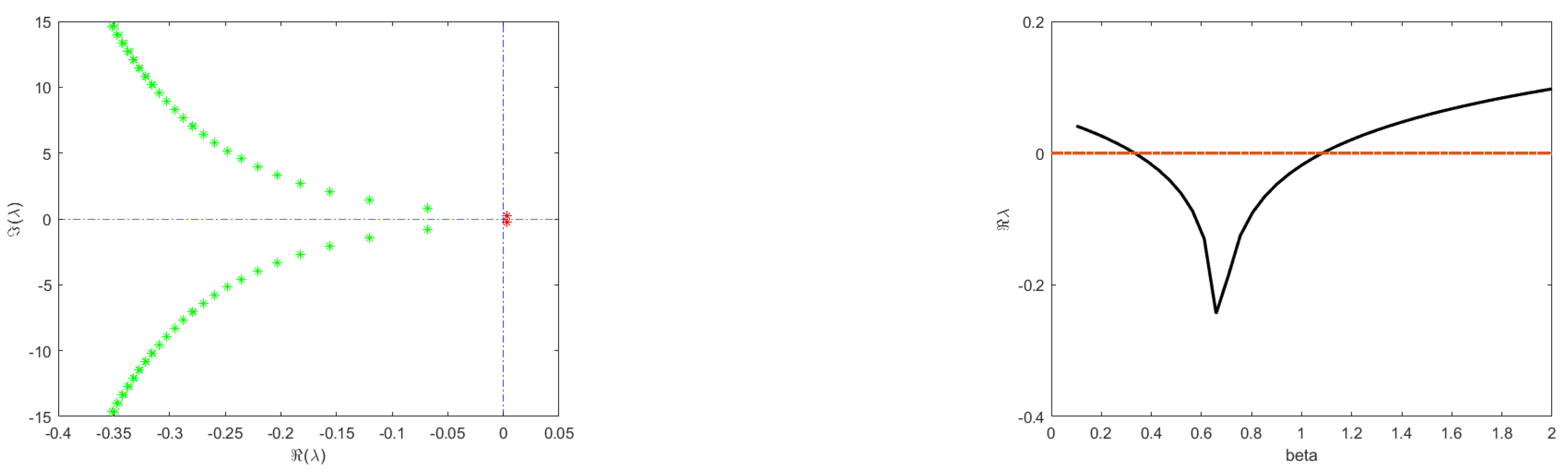
3.2.3. Distributed Delay Models

The SIRS discrete delay models have the same equation for the infected compartment I as the SIS models. Therefore, the $R_0$ calculated using the next-generation matrix method is still $R_0=\beta /\gamma$.

3.2.4. Exposed Population Model

The model with an exposed or latent population to deal with the delay is given by (17). It has two steady solutions, $S^{\ast }=1,I^{\ast }=E^{\ast }=0$ and $S^{\ast }={\displaystyle \frac{\gamma }{\beta }},I^{\ast }={\displaystyle \frac{(\beta -\gamma )\nu \sigma }{\beta \gamma \nu +\beta (\gamma +\nu )}},$$E^{\ast }={\displaystyle \frac{(\beta -\gamma )\gamma \nu }{\beta \gamma \nu +\beta (\gamma +\nu )}},R^{\ast }=1-S^{\ast }-I^{\ast }-E^{\ast }$. The second one requires $\beta >\gamma$. The eigenvalues of the linearized model evaluated at the DFE are

$${\lambda }_1=-\nu ,{\lambda }_{2,3}={\displaystyle \frac{\beta +\sigma \pm \sqrt{{\beta }^2-2\beta \sigma +4\gamma \sigma +{\sigma }^2}}{2}}.$$

For the endemic equilibrium, the expressions are complicated. But the next-generation matrix method gives $R_0={\displaystyle \frac{\sqrt{\beta }}{\sqrt{\gamma }}}$. Following either the DFE or the endemic branches, as $\beta$ is varied, there is only an exchange of stability where the two branches cross at $\beta =\gamma$.

3.3. Numerical Results

For the numerical simulations, the parameter values used are given in

Table 1. This table has the parameter values used in the simulations.

Symbol	Parameter Description	Value
$\beta$	Infection rate	0.3663 /d
$\gamma$	Recovery rate	1/3 /d
$\nu$	Loss-of-immunity rate	1/30 /d
$\tau$	Delay in time of infection	1.9 d
$\sigma$	1/(time of infection)	$1/\tau$ /d
N	Total population	1

. When a different value is used for a particular simulation, it is given in the caption of the corresponding figure. The values of $\beta ,\gamma ,\nu$, and $\tau$ are based on those given in [68] and by the CDC [69] corresponding to seasonal influenza. All the others are estimated. The value of $\beta$ has a large variation depending on the conditions: rural, urban, suburban, high-density work places, etc. The values of the parameters $\beta$ and $\gamma$ used for most simulations give $R_0=1.1$. Reference [70] has similar parameter values for influenza.

The numerical simulations for the ODE models were carried out using the ODE45 routine from matlab [71]. The models with discrete delays were solved using the routine dde23 described in [72]. For the distributed delay models, a routine was written in matlab: In the model given by (12), the integral term ${\displaystyle \frac{\beta }{N}}{\int }_0^{\infty }F\left(\tau \right)S(t-\tau )I(t-\tau )d\tau$ was discretized by dividing the the interval in which the probability distribution was greater than $0.01$ into n equal sub-intervals, and a trapezoidal quadrature rule [73] was used as an approximation. Therefore, the distributed delay equation was approximated by a discrete delay equation depending on $n+1$ delays and solved using dde23. The method was validated by comparing the results with those of solving (14) and (15).

While simulations were carried out with $R_0<1$, only those with $R_0>1$ are shown, since the differences between the different models can be determined more easily.

Figure 2 shows the simulation results for the SIS models. The discrete delay model is Delay Model 1. The difference in the simulations with Delay Model 2 is the time in which a newly infected stops being included as a susceptible. The calculations were performed with $\beta =0.3663$ corresponding to $R_0=1.1$. The discrete delay is $\tau =1.9$. The distributed delay models have the following distributions: uniform in $[\tau -0.1,\tau +0.1]$, approximated using 35 delays; normal centered at $\tau$ with standard deviation $0.5$, and 75 delays; gamma with $a=9,b=\tau /(a-1)$ so it is centered at $\tau$ and 35 delays; and exponential with $a=0.1$. The curves for the discrete delay, normal distribution, and gamma distribution are very similar. Those for the uniform distribution are not so close, due to the fact that the infection time usually has a narrow distribution. For the exponential distribution, since the distribution has its maximum value at the zero delay, it is also not a good approximation for the infection time. It is included for comparison.

To see the differences in the results of using a distributed delay model and a model with a stochastic delay, we ran a distributed delay model with the normal distribution centered at $\tau =10$ and with a standard deviation 0.5 and performed 1000 realizations of the discrete delay model with delay sampled from a normal distribution with the same mean and standard deviation. We started with 500 simulations and took the average, and then performed an additional 500 simulations, and averaged over the 1000 simulations. We found that the difference in the calculations with 500 and 1000 simulations of the average and average +/−1 standard deviation for the infected population over the simulation interval was less than $0.1\%$. Of course, this does not mean that with more simulations the results will not change. $\beta =0.7$ was used for both simulations. Figure 3 shows the results for the infected population for the discrete, distributed with normal distribution, and stochastic models. The differences are very small and are even smaller for $\tau =1.9$.

For the ODE models, there is only an exchange of stability between the DFE and endemic equilibrium branches when $\beta =\gamma$. But for Delay Model 1 (5), there is also a Hopf bifurcation point on the endemic branch. Numerical studies of the bifurcations for Delay Model 1 were carried out using the program dde-biftool [74]. $\beta$ was used as the continuation parameter. Figure 4 shows on the left the dominant eigenvalues close to the Hopf bifurcation point, and on the right the real part of the leading eigenvalue as $\beta$ varies. $\tau$ is equal to 10. The first crossing of the real axis is at the exchange of stability with the DFE branch and the second one at the Hopf bifurcation. Figure 5 shows the same results for Delay Model 2, for which there is no Hopf bifurcation.

To corroborate these results, we conducted simulations for Delay Model 1 on the endemic branch for $\beta =1.1$ and $\tau =10$. Figure 6 shows that there is an oscillatory solution for the discrete delay, normal distributed delay, and uniform delay models, but not for the others. The value of $\beta$ used is very high, higher than the ones observed empirically.

Similar calculations were carried out for SIRS models. Only Delay Model 1 is shown. Simulations for different values of $\tau$ were conducted to see the effect of the size of the delay on the solutions. Figure 7, Figure 8, Figure 9 and Figure 10 have the simulations for $\tau =1.9,10,20,40$, taking $\beta$ = 0.3663 corresponding to $R_0=1.1$. The parameters of the distributions are the same as for the simulations performed with the SIS models. As expected, as $\tau$ increases the difference between the models increases and the length of the transient before reaching the steady state also increases.

To show the difference between the simulations using a distributed delay model and those using a model assuming that the delay is a random variable, we have Figure 11. It is for $\beta =0.7$ and $\tau =5$. The sampling space is the same as that used for the SIS models.

The bifurcation analysis for the discrete delay SIRS models shows that there is only one exchange of stability when the endemic equilibrium and DFE branches cross. To corroborate this result, numerical simulations were conducted using dde-biftool. Figure 12 shows the real part of the dominant eigenvalue for both discrete delay models. $\tau =1.9$ was used.

One disadvantage of using models with discrete or distributed delays is that the history needs to be given. That is, the values of the state variables have to be given in the interval $[-\tau ,0]$. We made the usual assumption that the values of the variables in this interval are constant and equal to the initial conditions, with a small number of infectives. But care needs to be taken since wrong choices can produce negative populations. An example is shown in Figure 13 with $\beta =0.7$. The history was taken starting at $t=0$ as $S=0.5,I=0.5$. If the delay is greater than 3, the solution for $S\left(t\right)$ goes negative.

4. Discussion

Mathematical models are simplifications of reality, but they need to be based on realistic assumptions. For short-duration epidemics that cause no deaths, models with no demographics are valid. If there are no demographics or if the population is assumed constant, the model needs to conserve the total population. Infection processes move individuals from one population group to another but should not change the total population. So even for models with a non-constant total population, these processes should not affect the total population. Also, adding more processes does not necessarily make the model better. The infection time may be modeled by a delay, discrete or distributed, or by adding an exposed or latent population, but not both ways, since this is unnecessary. If the infection time is short, ODE models can be used. Infection times have a narrow distribution, so models that weight the influence of the past more than the present time are not biologically realistic. Models using distributed delays with an exponential distribution fall into this category, as do models using fractional derivatives. Distributed delay models with a realistic distribution are better than models with a discrete delay because there are always variations. An alternative is to consider the delay a random variable. Our results show that in many situations they all produce similar solutions. But the assumptions used for the stochastic model that for any time the delay is the same for all the population and that it changes at every time are weaker. Exposed population models are another alternative. But even though they model the average infection time, the shape of it does not agree with the usual distribution, which is relatively narrowly centered at the average value.

All the models considered have the same basic reproductive number, equilibrium solutions, and stability. The exception is the Hopf bifurcation point for Delay Model 1, but it happens for $R_0>3$. For seasonal influenza, $R_0$ is between 1.2 and 1.4, and for the pandemic strain (2008) between 1.3 and 2 [2]. This corresponds to our $\beta$ between 0.39 and 0.67; therefore, the Hopf bifurcation point is outside the range of interest of $\beta$. So the question is still which method of modeling the infection time is better. One important factor is the ease of analysis and implementation of the model. Models with exposed populations are the simplest since they are based on ODEs and do not require a history. Next come discrete delay models. But epidemic models in general consider more compartments, such as vaccinated, isolated, and partial immunity. Or, they may model epidemics via a vector or with age or spatial distribution. In these cases, the analysis may be very hard or impossible for all models with different hypotheses for the infection time. But since there is reliable software, ease of analysis, in general, is not a factor. It can also be argued that real epidemic data are the decisive factor, since the trajectories produced are different. But the data have large variations and errors, and the simulation curves for the different models are similar for $\tau <2$. For larger infection times, this is definitely an important factor.

The most important factor is to choose the model based on more realistic assumptions. In our case with the SIS and SIRS models, the choices are the distributed delay models with either narrow gamma or normal distributions centered at the average infection time. To decide between the two, there would need to be more data about the actual infection times. Models with a discrete delay may be more appropriate for viruses with a well-defined incubation period (e.g., influenza 1–2 days, acute respiratory disease 5–7 days, and measles 9–12 days [75]), whereas for cases with greater variability (e.g., COVID-19 2–14 days [76], hepatitis A 15–40 days, and mononucleosis 30–50 days [75]), a distributed delay may better capture the dynamics. In this paper, we only dealt briefly with whether to use an SIS or an SIRS model. Of course, it depends on the virus and whether there is recovery with no infection or temporary infection. Another possibility is an SIR model with permanent total immunity. But it may also be necessary to include partial immunity, vaccination, asymptomatic individuals, demographics, etc.