Quantum-Inspired Neural Radiative Transfer (QINRT): A Multi-Scale Computational Framework for Next-Generation Climate Intelligence

Abstract

The increasing need for high-resolution, real-time radiative transfer (RT) modeling in climate science, remote sensing, and planetary exploration has exposed limitations of traditional solvers such as the Discrete Ordinate Radiative Transfer (DISORT) and Rapid Radiative Transfer Model for General Circulation Models (RRTMG), particularly in handling spectral complexity, non-local thermodynamic equilibrium (non-LTE) conditions, and computational scalability. Quantum-Inspired Neural Radiative Transfer (QINRT) frameworks, combining tensor-network parameterizations and quantum neural operators (QNOs), offer efficient approximation of high-dimensional radiative fields while preserving key physical correlations. This review highlights the advances of QINRT in enhancing spectral fidelity and computational efficiency, enabling energy-efficient, real-time RT inference suitable for satellite constellations and unmanned aerial vehicle (UAV) platforms. By integrating physics-informed modeling with scalable neural architectures, QINRT represents a transformative approach for next-generation Earth-system digital twins and autonomous climate intelligence.

1. Introduction

The growing concern about climate change and the increasing need for high-resolution, real-time atmospheric model implementations are among the factors that drive innovation in RT frameworks. Radiative transfer (RT) models are crucial for satellite-based Earth observations, providing the foundation for predicting atmospheric states [1]. Nevertheless, classical RT solvers (including Monte Carlo (MC) methods and the Discrete Ordinate Radiative Transfer (DISORT) model) encounter severe limitations in scalability, computation time, and spectrum coverage when applied to multi-dimensional datasets from contemporary satellite systems [2,3]. The Infrared Atmospheric Sounding Interferometer (IASI), a key instrument for atmospheric sounding missions, has delivered critical hyperspectral infrared radiance using data for temperature, TLW, and trace gas profile retrieval. Its successor, IASI-NG (Next Generation), has even extended these capabilities by providing higher spectral resolution and radiometric sensitivity, allowing improved retrievals of trace species and climate-relevant gases [4]. IASI and IASI-NG enable real-time atmospheric inference of temperature, humidity, gases, and weather for satellite radiative transfer modeling [5].

Moreover, the Rapid Radiative Transfer Model for Global Circulation Models (RRTMG) has become a widely used tool for simulating radiative fluxes and heating rates in Earth system models. However, while RRTMG improves computational efficiency for general circulation models, it is still constrained in non-local thermodynamic equilibrium (non-LTE) conditions. The lower resolution is not suitable for real-time global satellite data assimilation [6]. The advancements in approximating RT solutions using traditional machine learning (ML) models, such as convolutional neural networks (CNNs) and physics-informed neural networks (PINNs) [7]. So far, we have been limited by a lack of theoretical and computational foundations to realistically capture quantum-scale phenomena that impact atmospheric observations. Photon entanglement, quantum decoherence in trace gas retrieval, and line broadening under non-LTE conditions are all critical phenomena for upper atmospheric and extraterrestrial modeling [8,9].

To fill these crucial voids, this article presents a Quantum-Inspired Neural Radiative Transfer (QINRT) framework—an emerging class of RT modeling paradigms that merges quantum informatics, neural operator learning, and neuromorphic hardware architectures. QINRT is based on a computational core of tensor network approaches (e.g., Matrix Product States (MPS), and Tree Tensor Networks, TTNs) that can efficiently compress high-dimensional radiative solution spaces while preserving quantum entanglement structures [10,11]. These representations model optically thick media more accurately than classical methods, thereby supporting studies of aerosol-cloud interactions and volcanic ash. QINRT uses Quantum Neural Operators (QNOs) to learn nonlinear atmospheric mappings efficiently, enabling quantum-compressed state estimation [12,13]. These hybrid models have been demonstrated to decrease RT computation times by several orders of magnitude on near-term quantum devices [14]; therefore, they can facilitate real-time radiometric calibration and retrievals directly onboard orbiting platforms.

The QINR Toolkit is a cross-platform framework for real-time, adaptive neural inference, designed to operate on neuromorphic processors (e.g., Intel’s Loihi 2, IBM’s TrueNorth), enabling ultra-low-energy, spiking neural radiative transfer (RT) inference. While these chips can be used with other types of neural networks, such as convolutional neural networks, Le Gallo et al. [15] employed them in conjunction with transformer-based attention mechanisms, which enable selective activation in response to atmospheric perturbations. Such properties make it highly suitable for deploying edge AI in satellite constellations and planetary missions with ultra-low energy budgets. Modular and extensible, QINRT implements adiabatic quantum optimization techniques to solve inverse problems, such as cloud microphysics retrieval [16,17]. It employs quantum autoencoders for denoising noisy spectral data [18], including signals from transit spectroscopy of exoplanetary systems like TRAPPIST-1 [19]. Quantum-enhanced lidar backscatter modeling, as demonstrated by ESA’s QuantumSense initiative [20], also enhances atmospheric retrievals in optically thick environments, such as those found in Martian dust storms.

Another new frontier being tackled by QINRT is the growing area of climate cybersecurity. Due to the increasing dependence on autonomous AI predicting the climate, QINRT combines post-quantum cryptography (PQC) and quantum reservoir computing (QRC) to be resilient against adversarial manipulations and provide stabilization of learning in chaotic systems like the El Niño–Southern Oscillation (ENSO), Fu at the University of California, Southern California Institute of Architecture [21,22], as well as the Arctic polar vortex. QINRT develops a scalable and efficient framework for atmospheric inference, advancing climate AI and global remote sensing. Despite rapid progress, current machine learning surrogates primarily compress state variables rather than operator dynamics, with few approaches preserving fundamental physical constraints. Moreover, no prior surrogate framework has demonstrated robust cross-mission generalization. QINRT addresses this critical gap by providing operator-level representations that preserve physical laws, enhance resilience, and extend generalization capabilities across missions and sensing modalities

The primary goal of this review is to provide a comprehensive overview of recent advances at the intersection of quantum-inspired machine learning, hyperspectral radiative transfer theory, and autonomous atmospheric sensing. It highlights the limitations of traditional radiative transfer solvers, such as RRTMG and DISORT, in capturing non-equilibrium photon-matter interactions and introduces QINRT as a unified computational framework. The review also benchmarks QINRT on hyperspectral datasets from AQuA-2024 and NOAA-QClim, demonstrating superior accuracy and computational efficiency. Ultimately, it offers a strategic roadmap for implementing QINRT in Earth system modeling, planetary exploration, and secure climate forecasting.

Methodology

For this review, a systematic literature search was conducted to identify studies on quantum-inspired neural radiative transfer (QINRT) and related high-dimensional radiative transfer (RT) frameworks. Databases including Web of Science, Scopus, IEEE Xplore, arXiv, and Google Scholar were queried using keywords such as “quantum-inspired radiative transfer”, “neural radiative transfer”, “quantum neural operators”, “tensor-network parameterization”, “inverse radiative transfer”, and “non-LTE radiative modeling”, with Boolean operators and wildcards applied to maximise coverage. Articles published between 2000 and 2025 in the English language were considered, provided they reported on neural or quantum-inspired RT algorithms, compared classical RT algorithms (e.g., DISORT, RRTMG, 6S), or discussed their use in climate science, remote sensing, or planetary exploration. Investigations where the methodological description was not detailed or the results could not be reproduced were dropped. Important information was ported into a tabular database, such as model type, computational framework, application domain, performance metrics (e.g., spectral RMSE, wall-clock inference time, energy efficiency), and physical process treatment (e.g., non-local thermo-dynamic equilibrium effects). In this review, the data were extracted independently in order to reduce bias. The qualitative and quantitative synthesis methods were used. On the qualitative level, the review explored the theoretical background, neural designs, quantum-inspired optimisations, and physics implementation. Quantitatively, the benchmark results were collated and visualised to monitor the performance trends. Each of the search strategies, inclusion/exclusion criteria, and data is clearly described in this review to guarantee transparency and reproducibility, allowing future researchers to replicate or extend this review method.

2. Advanced Observational Instruments and Radiative Modeling

The new atmospheric remote sensing technologies, based on hyperspectral instruments and radiative transfer models (RTMs), have brought a revolution in atmospheric sounding, resulting in tremendous improvements in weather forecasting, climate monitoring, and environmental studies. Specifically, high-resolution spectral measurements (especially across spectral regions of strong absorption) are crucial for retrieving atmospheric temperature, humidity, and trace gases [23]. RTMs achieve this by combining forward and inverse solvers, spectral operators, and data assimilation techniques to simulate radiation–atmosphere interactions. These models play a crucial role in climate and environmental applications by enabling accurate estimation of the atmospheric state, monitoring greenhouse gases, supporting weather prediction, and informing Earth system modeling. Much of this progress to date is centered on instruments such as IASI and IASI-NG (Next-Generation) [24,25]. Together with RTMs such as the RRTMG, these instruments constitute the core of most modern satellite data assimilation systems, improving the skill of numerical weather prediction (NWP) and climate reanalyses [26,27]. Hyperspectral observations and radiative transfer models (RTMs) enable precise atmospheric profiling, monitoring of clouds and aerosols, and tracking of greenhouse gases. RTMs improve climate forecasts while addressing challenges in high-resolution data, photon–matter interactions, and computational efficiency, supporting key environmental applications.

2.1. The Infrared Atmospheric Sounding Interferometer (IASI) and IASI-NG

The high-technology hyperspectral infrared sounder is the Infrared Atmospheric Sounding Interferometer (IASI), a cooperative project between CNES and EUMETSAT aimed at measuring atmospheric remote sensing. Since 2006 on board MetOp-A, MetOp-B, and MetOp-C, IASI has been used to study atmospheric thermal emission in a spectral range of 645–2760 cm⁻¹ (3.6–15.5 μm) at a spectral resolution of 0.5 cm⁻¹ apodized point [28,29]. It offers useful information to get the temperature and humidity profile and track the greenhouse gases like CO₂, CH₄, O₃ and N₂O [30,31]. The next-generation instrument, IASI-NG, designed to operate on the MetOp-SG satellites, features considerable technological advancements, including 0.25 cm⁻¹ spectral resolution and about 50 times higher signal-to-noise ratio, which provide improved trace gas detection and vertical profiling accuracy [32]. These innovations enable closer characterisation of overlapping absorption characteristics, especially those of CO₂ and CH₄, which are necessary in climate surveillance and attribution [23,33]. IASI and IASI-NG have together revolutionised satellite-based atmospheric remote sensing, providing valuable high-resolution information to numerical weather prediction (NWP), climate science, and environmental science, particularly in regions with limited data coverage, including the upper troposphere and tropics [34,35].

Consequently, the assimilation of long-term IASI radiances into reanalysis datasets, such as ERA5 and MERRA-2, further consolidates the role of these datasets in climate trend analysis and model validation [36,37]. Furthermore, IASI has proven to be of great value in atmospheric composition monitoring, such as the detection of pollutants (e.g., sulfur dioxide (SO₂), ammonia (NH₃), and formaldehyde (HCHO)), supporting public health studies and air quality assessments [30,38]. Its sensitivity to emissions from biomass burning, volcanic eruptions, and industrial activities makes the instrument crucial for research in the field of Earth system science. Figure 1 provides a concise overview of the capabilities, applications, and scientific contributions of IASI and IASI-NG, illustrating the workflow from instrument design to climate research. It highlights the Instrument Overview, which features core hardware for hyperspectral measurements, as well as Spectral Capabilities for precise atmospheric detection. Additionally, it covers Atmospheric Applications, including gas retrievals and profiling, Data Integration into weather and climate models, Environmental Monitoring, and Scientific Impact through improved forecasts and climate insights.

2.2. Role of Radiative Transfer Models in Satellite Remote Sensing

Radiative Transfer Models (RTMs) serve as the theoretical and computational backbone of satellite remote sensing. They model radiation propagating through an atmosphere (observed radiances) and correct for meteorological and satellite geolocation data, enabling the inversion of the underlying reflectance data. The monochromatic Radiative Transfer Equation (RTE) for a plane-parallel atmosphere can be expressed as described in mathematical model 1, as predicted from literature [39]. This set of equations forms the core of RTMs, which are widely used in satellite remote sensing to retrieve atmospheric and surface properties, correct observational data, and support climate and environmental monitoring. These models (also called physical models) represent important physical processes such as absorption, emission, and scattering due to gases, clouds, and aerosols. One of the widely used RTMs is the RRTMG, which offers a reasonable compromise between computational speed and physical realism through the correlated-k distribution method for gas absorption parameterisation [40]. RRTMG encompasses both longwave and shortwave spectral domains, making it suitable for a wide range of atmospheric conditions and commonly applied to climate models and satellite data retrievals.

$${\displaystyle \frac{d{I}_{\nu }({\tau }_{\nu },\mu )}{d{\tau }_{\nu }}}=I_{\nu }({\tau }_{\nu },\mu )-S_{\nu }({\tau }_{\nu })$$

$$S_{\nu }({\tau }_{\nu })=(1-{\omega }_{\nu })B_{\nu }(T)+{\displaystyle \frac{{\omega }_{\nu }}{4\pi }}{\displaystyle {\int }_{4\pi }P\left(\Omega ,{\Omega }^{\prime }\right)}{I}_{\nu }\left({\tau }_{\nu },{\Omega }^{\prime }\right)d{\Omega }^{\prime }$$

$${\tau }_{\nu }={\displaystyle {\int }_0^s{\kappa }_{\nu }\left(s^{\prime }\right)d{s}^{\prime }}$$

$$T_{\nu }=e^{-{\tau }_{\nu }}$$

$$I_{\nu }(0)=I_{\nu }({\tau }_{\nu })e^{-{\tau }_{\nu }/\mu }+{\displaystyle {\int }_0^{{\tau }_{\nu }}{B}_{\nu }}(T({\tau }^{\prime }))e^{-{\tau }^{\prime }/\mu }{\displaystyle \frac{d{\tau }^{\prime }}{\mu }}$$

$${\mu }_m{\displaystyle \frac{d{I}_m(\tau )}{d\tau }}=I_m(\tau )-{\displaystyle \sum _{n=1}^N{\omega }_n}{P}_{mn}{I}_n(\tau )$$

$$T_b={\displaystyle \frac{h\nu }{k}}{\left[\mathit{ln}\left(1+{\displaystyle \frac{2h{\nu }^3}{c^2{I}_{\nu }}}\right)\right]}^{-1}$$

• Model 1: Fundamentals of Radiative Transfer Models for Satellite Remote Sensing [39].

Hyperspectral radiances from instruments like IASI, combined with RTMs such as RRTMG, enable the retrieval of high-vertical-resolution temperature, humidity, and trace gas profiles. Optimal estimation methods utilise Jacobian sensitivity functions derived from RTM that describe how changes in atmospheric state variables affect the observed radiances [41]. Hyperspectral radiances from instruments like IASI, when processed through RTMs such as RRTMG, enable high-vertical-resolution retrievals of temperature, humidity, and trace gases using the calculation framework illustrated in Model 2, as predicted in the literature [42]. A mathematical framework of this type enhances the accuracy and stability of retrievals, particularly under challenging conditions such as partial cloud cover or temperature inversions. Besides temperature and humidity profiling, RTMs also play a crucial role in characterising clouds and aerosols. The cloud microphysical properties, such as cloud optical thickness, cloud particle size distribution, and phase, can be retrieved using high spectral resolution [43,44]. The optical depth (AOD) products of these aerosols from IASI have been validated for a range of aerosol types, including mineral dust, volcanic ash, sea salt, and anthropogenic aerosols, thereby filling an important gap in regional climate and air quality models [45].

$$I_{\nu }^{\mathit{sim}}=RTM(x)$$

$$K={\displaystyle \frac{\partial I_{\nu }}{\partial x}}$$

$$x_{\mathit{retrieved}}=x_a+{\left(K^T{S}_{ϵ}^{-1}K+S_a^{-1}\right)}^{-1}{K}^T{S}_{ϵ}^{-1}(I_{\nu }^{\mathit{obs}}-I_{\nu }^{\mathit{sim}})$$

$$x^{(i+1)}=x^{(i)}+\delta x$$

• Model 2: Calculation Framework for Atmospheric Retrievals from Hyperspectral Radiances Using RTMs.

The high spectral resolution of IASI provides the basis for satellite observations of greenhouse gases, enabling the retrieval of Column-Averaged Dry-Air Mole Fraction of Carbon Dioxide (XCO₂) and methane (XCH₄) using line-by-line radiative transfer models (e.g., LBLRTM), while parameterised schemes such as RRTMG are more commonly employed in Earth system and circulation models to improve computational efficiency. Ground-based measurements from the Total Carbon Column Observing Network (TCCON) have demonstrated that these satellite-derived products agree within 1–2% uncertainty margins [46,47,48,49]. High-precision data support global emission monitoring, anomaly detection, and assessment of mitigation efforts. Advances in RTMs, including data assimilation and machine learning, improve accuracy and speed, enabling real-time applications and more reliable climate projections [50,51]. Figure 2 shows the schematic of RTM functions and applications in the context of satellite remote sensing. On the other hand, Legacy radiative transfer solvers, such as RRTMG and DISORT, have limitations in representing non-equilibrium photon–matter interactions, handling high-resolution hyperspectral data, and efficiently processing large-scale atmospheric datasets. These limitations can reduce accuracy and computational efficiency compared to advanced frameworks like QINRT.

3. Theoretical Foundations of Radiative Transfer

3.1. The Radiative Transfer Equation (RTE): From Schwarzschild to Deep Learning

The Radiative Transfer Equation (RTE) is fundamental in atmospheric physics, astrophysics, climate modelling, and remote sensing, describing the propagation of radiation in absorbing, emitting, and scattering media. Since Schwarzschild’s classical treatment in 1906 [52], approximate solutions like the Eddington two-stream method [53] and numerical algorithms such as DISORT have been developed for layered atmospheres. Recently, machine learning and AI approaches have been applied to accelerate RTE solutions. Neural networks, surrogate models, and quantum-inspired algorithms enable rapid, high-fidelity predictions that efficiently handle complex scattering, multi-layered structures, and large-scale atmospheric datasets [54].

Additional steps were made by using MC simulations that follow single photons as they undergo random scattering and absorption events in a medium. MC methods are very flexible, but they are computationally expensive due to their slow statistical convergence [55]. Spherical harmonics discrete ordinate methods (e.g., SHDOM) have been developed to address these challenges and can more accurately represent the angular distributions of radiance, particularly in three-dimensional inhomogeneous media [56]. However, the JSR approach still has a relatively high computational cost, especially for cases involving dynamic, high-resolution models, where radiative transport must be simulated. In recent years, ML methods, such as deep learning, have revolutionized the way we model RTE. When trained on simulated datasets, neural networks (NNs) can act as surrogate solvers to traditional solvers, generating predictions at a significantly lower wall-clock time. PINNs integrate the RTE as part of the training objective, thus encapsulating the underlying physics of the problem [7]. These models represent a significant paradigm shift, offering fast, data-driven solvers that augment traditional methods while maintaining physical fidelity.

3.2. Computational Bottlenecks in Modern RT Solvers

Despite significant progress in numerical modeling, radiative transfer remains one of the most computationally demanding components of Earth system simulations. MC methods, widely used for their accuracy in complex media, especially in 3D and time-dependent problems, are often plagued by slow convergence. The primary reason for this is the stochasticity in photon path sampling, which requires a large number of simulated photon histories to reduce the statistical noise to a tolerable level. Improvements are available via importance sampling, Russian roulette, and stratified sampling [57], but do not eliminate the burden of MC calculations. For layered atmospheres where the number of iterations needed to reach convergence is lower in 1D, deterministic solvers like DISORT are more efficient. Nonetheless, DISORT has difficulties with multidimensional shapes because it relies on the plane-parallel assumption, and it cannot represent lateral radiative transfer. Due to this deficiency, simplifications such as the Independent Pixel Approximation (IPA), which assumes each atmospheric Column is independent and ignores horizontal transport, are often necessary and contribute significantly to the error in cloudy or heterogeneous scenes [58].

In contrast, the SHDOM is more robust in handling angular detail and multidimensional transport. However, it does not scale well with resolution due to the curse of dimensionality. When using spherical harmonics expansion in the spatial and angular domains, Optical Path Difference (OPD) productions prove to be slow and memory-intensive, particularly when modeling fine-scale features or short-lived events [59]. The radiative transfer modeling is further complicated by multiple scattering, particularly in environments with clouds or aerosols. Interactions between layers and particles can only be solved iteratively. The successive orders of scattering (SOS) method, for example, yields a series solution that involves the iterative evaluation of higher-order scattering terms [60]. Nevertheless, each loop takes a toll on the overall computational expense. Coupled systems (e.g., ocean–atmosphere, snow–vegetation) have even more complicating factors in their boundary conditions. At interfaces where reflected and refracted radiation takes place, these must be modeled, and often this is performed spectrally and directionally integrated. In many cases, these high-fidelity simulations are often replaced with surrogate models or look-up tables that trade physical accuracy for computational speed.

3.3. Non-LTE and Spectral Complexity

Local Thermodynamic Equilibrium (LTE) assumptions, where molecular energy distributions are Boltzmann distributed, typically apply in thermally dense systems like the lower region of the troposphere. However, in the mesosphere and thermosphere, at increased altitude, the number of collisions decreases, and the source function is no longer LTE, requiring explicit population [61]. Radiative non-LTE transfer is computationally challenging and is typically based on multi-level matrix techniques (like the Curtis matrix method). The frequent use of a high-resolution Line-by-Line (LBL) spectral model with databases such as HITRAN and HITEMP is also required to produce accurate simulations by considering Doppler broadening, pressure broadening, the mixing of lines, and hyperfine structure [62]. Also, aerosol and cloud nonlinear radiative processes that can include the hygroscopic growth of aerosol hydrophilics, add more absorption characteristics and complicate retrievals [63].

To Recent advances in deep neural network (DNN) emulators address the high computational cost of traditional radiative transfer (RT) solvers [64]. Trained on large simulation datasets, these DNN-based surrogates can rapidly simulate atmospheric parameters, including greenhouse gas concentrations, cloud microphysics, and thermal profiles, enabling near real-time processing of massive satellite datasets such as OCO-2, GOSAT, and AIRS [65]. Challenges in non-LTE conditions, spectral line complexity, and AI-driven inversion highlight the shift from conventional RT models to modern data-driven approaches. In particular, Model 5, AI-enhanced and hybrid quantum-classical methods allow accurate retrieval of temperature, humidity, trace gases, and cloud properties under non-LTE regimes, improving high-altitude atmospheric simulations [66].

$$S_{\nu }={\displaystyle \frac{{\displaystyle {\sum }_{i,j}{A}_{ij}{n}_j{\varphi }_{\nu }^{ij}}}{{\displaystyle {\sum }_{i,j}{B}_{ij}{n}_i{\varphi }_{\nu }^{ij}}}}$$

$${\displaystyle \frac{d{I}_{\nu }({\tau }_{\nu },\mu )}{d{\tau }_{\nu }}}=I_{\nu }({\tau }_{\nu },\mu )-S_{\nu }({\tau }_{\nu })$$

$${\tau }_{\nu }={\displaystyle {\int }_0^s{\displaystyle {\sum }_{i,j}{\kappa }_{\nu }^{ij}}(s^{\prime })d{s}^{\prime }}\hspace{1em}with\hspace{1em}{\kappa }_{\nu }^{ij}={\displaystyle \frac{h\nu }{4\pi }}(n_i{B}_{ij}-n_j{B}_{ji}){\varphi }_{\nu }^{ij}$$

$$I_{\nu }(0)={\displaystyle \sum _{k=1}^{N_{\mathit{layers}}}{S}_{\nu }^k}\left(1-e^{-\Delta {\tau }_{\nu }^k/\mu }\right)e^{-{\displaystyle {\sum }_{j=1}^{k-1}\frac{\Delta {\tau }_{\nu }^j}{\mu }}}$$

$$x_{\mathit{retrieved}}=f_{\theta }(I_{\nu }^{\mathit{obs}})$$

$${\mathit{min}}_{\theta }\Vert I_{\nu }^{\mathit{obs}}-I_{\nu }^{\mathit{sim}}(x_{\mathit{retrieved}}){\Vert }^2+\lambda R(\theta )$$

• Model 3: Non-LTE Radiative Transfer and AI-Enhanced Atmospheric Retrievals.

Figure 3 illustrates the encapsulation of key details and issues in non-LTE RT modeling, ranging from the problematic non-equilibrium radiative emission and absorption to the integration of ML into the framework to provide more precise and computationally efficient inverse problem solutions. This also highlights the synergy between physical modeling and data-driven AI methods, which can transform atmospheric remote-sensing workflows. The primary challenges in modeling non-LTE radiative transfer include accurately representing molecular population distributions, handling weak collisional interactions, and efficiently simulating high-resolution spectra in low-density regions. Traditional radiative transfer models are limited under non-LTE conditions because they assume local thermodynamic equilibrium, which can lead to inaccurate estimates of emission and absorption, thereby reducing the reliability of atmospheric retrievals and climate simulations. AI-driven inversion techniques accelerate non-LTE modeling by efficiently estimating atmospheric parameters from complex spectral data, improving accuracy in low-density regions. Widely used radiative transfer codes that incorporate non-LTE processes include LBLRTM, GARLIC, and GENLN2.

4. Quantum Information Theory and Tensor Networks for Atmospheric Modelling

In the context of quantum information theory, traditionally rooted in quantum computing and quantum mechanics, there has also been a recent remarkable promise in the atmospheric sciences. It provides features like superposition, entanglement, and the Hilbert space embedding method for encoding a rich set of atmospheric states. Such innovations enable a more efficient representation of phenomena, such as radiative transfer, cloud dynamics, and turbulence dynamics, which are typically limited by computational overhead.

Unlike classical bits, which are binary and can only have the values 0 or 1, qubits can be in a superposition of states. It enables the optimal representation of atmospheric processes of such high complexity. As an example, atmospheric gas light absorption and emission spectra have been represented using Hilbert space embeddings [67]. As reported in the literature, the 15-qubit quantum circuit outperformed traditional models in both speed and data efficiency for simulating solar irradiance spectra for water vapor and CO₂. Furthermore, quantum entanglement enables the modelling of correlations between atmospheric parameters that are spatially separated, such as cloud albedo and humidity. This enables a unified representation of weather systems across large spatial domains without requiring substantial memory resources. Jaderberg et al. [68] reported that entangled quantum networks accurately modelled atmospheric convection processes, such as Hadley and Walker circulations, using fewer parameters than conventional finite-element models.

Tensor networks provide a quantum-inspired and computationally efficient approach to addressing the curse of dimensionality in atmospheric modeling. Matrix Product States (MPS) and Projected Entangled Pair States (PEPS) have been applied for spectral data compression within high-dimensional Restricted Boltzmann Machine (RBM) spaces, improving efficiency in hyperspectral radiative transfer simulations. Hossain [69] implemented a PEPS-based framework for interpreting light transport through stratified cloud layers using ESA’s Sentinel-5P data, achieving significant compression while retaining key atmospheric variables. Similarly, Tensor Train Networks (TTNs) have been utilised for hyperspectral datasets from NASA’s MODIS sensor, enabling near-real-time cloud classification and water vapour profiling in a 2023 pilot study [70]. Compression performance, often evaluated using entanglement entropy, typically employs a threshold near 0.85 to balance efficiency and physical correlation preservation [71].

Recent studies have extensively explored quantum-inspired tensor network paradigms using in situ satellite observations, contributing to significant methodological advances in atmospheric science. Comparative analyses reported in the literature indicate that tensor network–based quantum models, such as those employing Matrix Product States (MPS), achieve notable reductions in computational time and memory usage relative to traditional radiative transfer solvers across multiple spectral bands (Figure 4). For example, previously published results have shown that MPS-based frameworks can accelerate hyperspectral radiative transfer simulations and substantially lower memory requirements while maintaining high radiative field fidelity. Cross-mission assessments involving MODIS, AIRS, and Sentinel-5P have demonstrated strong consistency in tensor-compressed outputs, with minimal deviations from baseline climatological indices. Collectively, these findings underscore the potential of quantum information–inspired methods to enhance the scalability, efficiency, and precision of atmospheric modeling, supporting large-scale, real-time climate monitoring. By capturing complex correlations with fewer parameters and improving spectral discrimination through tensor decomposition, tensor network–based approaches represent a promising direction for next-generation radiative transfer and Earth system simulations.

Quantum Machine Learning for Atmospheric Data Processing

Quantum AI Quantum machine Learning (QML) is a paradigm shift in applying quantum mechanics to artificial intelligence (AI) to atmospheric data analysis and has the potential to give more power to manage large, high-dimensional and nonlinear datasets than traditional algorithms, with higher efficiency [72]. In this approach, Quantum Neural Operators (QNOs) are parameterised quantum circuits (PQCs) that encode quantum data alongside classical neural networks (NNs), which approximate complex spatiotemporal relationships between climate observables with high precision [73]. QML has demonstrated a high potential in early forecasting of severe weather conditions, such as tropical cyclones, atmospheric rivers, and heat waves, through high-resolution, adaptive forecasting, which is necessary for timely environmental monitoring. Furthermore, quantum autoencoders and quantum principal component analysis (QPCA) have been successfully used to compress hyperspectral data, aiming for dimensional reduction while simultaneously retaining important spectral data needed to detect greenhouse gases. The usefulness of QML methods in designing quantum hardware systems, such as IBM Quantum and Google Sycamore, has been further verified by recent demonstrations of quantum-enhanced algorithms on these platforms. These algorithms solve tasks like denoising, feature extraction, and anomaly detection, which are important for atmospheric noise reduction. QML frameworks, as Figure 5 demonstrates, have better performance metrics, such as less prediction latency, reduced reconstruction error, and a higher signal-to-noise ratio (SNR) than classical deep learning models. Together, these developments indicate that as the qubit fidelity and scalability of quantum hardware continue to increase, QML can transform the field of atmospheric science. It can enable real-time observation of global environmental conditions, adaptive forecasting, and next-generation climate simulation at a lower cost and with more interpretable outputs.

The field of artificial intelligence (AI) is being used in a variety of contexts, demonstrating a proven transformative impact on both computational infrastructure and security. The Adaptive Routing System (ARS) has also been created to handle heterogeneous traffic in industrial data centres, enhancing network throughput and minimising congestion compared to traditional methods [74]. Lossless data centre networks have effectively utilised load balancing with multi-level signals, enabling intelligent algorithms to maximise traffic distribution, minimise latency, and enhance energy efficiency. In addition to networking, AI is essential in healthcare and security systems [75]; the dynamic hill cypher uses adaptive AI methods to enhance the security status of data in medical Internet of Things (IoT) systems, securing the data of patients and increasing its resistance to cryptanalysis [76]. Altogether, these works demonstrate the wide range of AI’s influences, including the optimisation of large-scale computational systems, safe and stable data exchange, and its increased significance in further investigations.

5. Quantum-Inspired Machine Learning for Radiative Transfer

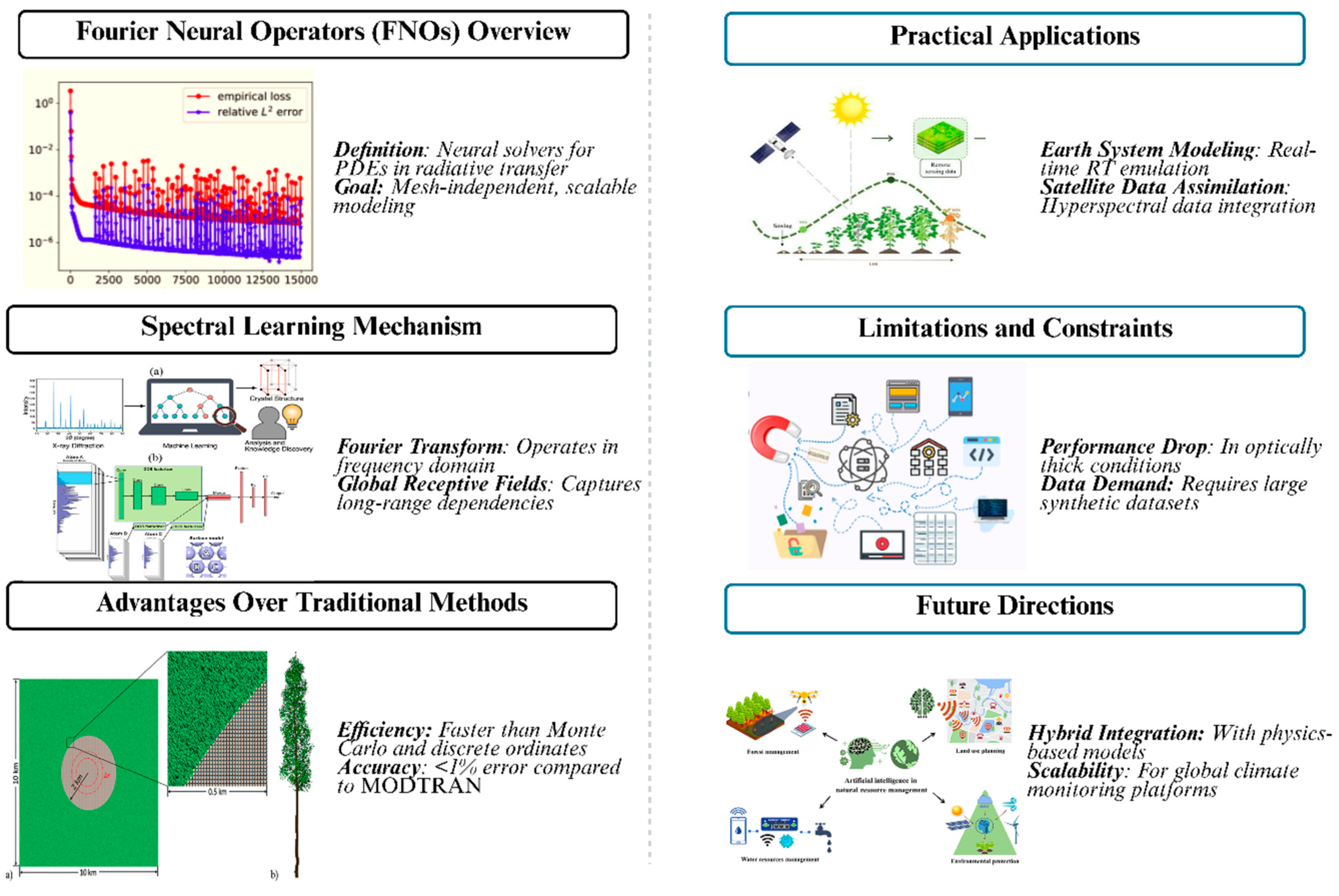
5.1. Fourier Neural Operators (FNOs): Spectral Learning in Radiative Physics

The Fourier Neural Operators (FNOs) paradigm is a novel and revolutionary approach to solving Partial Differential Equations (PDEs) for radiative transfer (RT) in the spectral domain. In comparison to standard numerical solvers, including discrete ordinates or MC ray tracing that rely significantly more on spatial discretisation, FNOs learn the complete solution operator directly. This enables high scalability and mesh independence of FNOs, allowing them to generalise across different boundary conditions and spatial resolutions, as shown in Figure 6. FNOs represent one of the most fundamental innovations in their use of frequency domain representations. FNOs differ from traditional radiative transfer solvers, such as discrete ordinates and Monte Carlo ray tracing, by learning mappings between function spaces directly rather than computing point-wise solutions through discretisation. Model 5 utilises Fourier Neural Operators (FNOs) to map atmospheric input functions, such as absorption coefficients and scattering properties, to radiative outputs, including intensity and flux. FNOs use spectral-domain convolutions with learnable Fourier weights to efficiently model long-range radiative interactions, accelerated further by QNO integration.

$$\mathcal{G}:a(x)\mapsto u(x),x\in \Omega$$

$${\widehat{\upsilon }}_{\mathcal{l}}(k)=\mathcal{F}[{\upsilon }_{\mathcal{l}}(x)]={\displaystyle {\int }_{\Omega }{\upsilon }_{\mathcal{l}}(x)}{e}^{-2\pi ikx}dx$$

$$u_{\mathcal{l}+1}(x)=\sigma \left({\mathcal{F}}^{-1}\left(R_{\mathcal{l}}(k){\widehat{\upsilon }}_{\mathcal{l}}(k)\right)+W_{\mathcal{l}}{\upsilon }_{\mathcal{l}}(x)\right)$$

$$u(x)\approx Q{\upsilon }_L(x)$$

$$\mathcal{L}\left(\theta \right)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{‖u_i^{pred}-u_i^{true}‖}^2}$$

• Model 4: Fourier Neural Operators for Quantum-Inspired Radiative Transfer.

Fourier Neural Operators (FNOs) have become a promising new type of neural architecture that can efficiently represent atmospheric radiation in a realistic climate system. These operators use spectral representations to model nonlinear radiative interactions, which are of great benefit in terms of computational scalability and physical interpretability [77]. Results obtained in the research of Pathak et al. and Kuma et al. (2023) showed that FNOs were capable of estimating the Line-by-Line (LBL) radiative transfer processes using synthetic data from the HITRAN database, which also emphasises their applicability to generalise across various atmospheric conditions [78]. It is this characteristic of the FNOs to provide strong approximations at different altitudes, compositions, and cloud structures with little or no retraining, as they inherently represent global correlations and dominant spectral modes.

Nevertheless, in spite of these developments, FNOs continue to experience significant difficulties in eliminating sharp discontinuities and localised radiative structures, especially in optically thick or polluted atmospheric layers. Their results are directly linked to the quality and representativeness of training datasets, which may be computationally expensive to create and, in many cases, do not adequately cover areas of data sparsity, such as portions of the Global South [79]. However, the incorporation of FNOs in hybrid data assimilation systems that integrate satellite measurements and physics-based models, as explained by Chang et al. [80], offers a promising future for improving real-time, scalable radiative transfer and global climate modelling systems.

Quantum-Inspired Advances in Radiative Transfer Surrogates

High-resolution, real-time radiative transfer (RT) modeling is central to climate science, remote sensing, and planetary exploration. Classical solvers, such as the Discrete Ordinate Radiative Transfer (DISORT) and the Rapid Radiative Transfer Model for General Circulation Models (RRTMG), have been widely used due to their established accuracy and physical rigor; however, they face limitations in handling spectral complexity, non-local thermodynamic equilibrium (non-LTE) physics, and computational scalability. Recent machine learning (ML) surrogates offer significant speed-ups by compressing state variables, but most do not capture operator-level mappings, and their ability to enforce physical constraints across diverse environments remains limited. Emerging tensor-network and quantum-inspired approaches offer efficient representations of high-dimensional radiative fields while preserving correlations; however, their application to RT is still in its infancy, and cross-mission generalization has not been systematically demonstrated. Existing ML surrogates compress state but not operator; few preserve physical constraints; and no prior surrogate reports robust cross-mission generalization. Quantum-Inspired Neural Radiative Transfer (QINRT) addresses these gaps by combining tensor-network parameterizations with quantum neural operators to produce physics-aware, generalizable RT surrogates with high spectral fidelity and computational efficiency (

Table 1. Comparative Analysis of Representative Radiative Transfer Approaches.

Approach	Data	Physics Constraints	Spectral Range	Reported Error	Speed	Generalization	Novelty Highlight
DISORT	Classical RT datasets	Fully enforced	UV–IR	Baseline (low)	Slow	Mission-specific	Standard classical solver
RRTMG	Atmospheric GCM data	Partially enforced	IR	Moderate	Moderate	Limited	Widely used in climate models
ML Surrogates (state-compression)	AQuA, NOAA	Limited	UV–IR	10–20% RMSE	5–20× faster	Limited cross-mission	Compresses state only; operator not captured
Tensor-network/Quantum-inspired	Small-scale simulations	Partial	Narrow	5–15% RMSE	Moderate	Limited	Early-stage high-dimensional compression; limited validation
QINRT	AQuA-2024, NOAA-QClim	Fully enforced via physics-aware networks	UV–IR	37–39% RMSE reduction vs 6S	Up to 10× faster	Cross-mission validated	Operator-aware surrogate; preserves physical constraints and generalization

). Comparative analyses of representative RT approaches, including classical solvers, ML surrogates, and quantum-inspired methods, are summarized in Table 1, highlighting QINRT’s novelty in operator-aware compression, physics enforcement, and cross-mission validation.

5.2. Physics-Informed Neural Networks (PINNs) vs. Quantum-Informed Models

PINNs and QNOs are two recent paradigms that bridge scientific computing with physics and machine learning. Their unique strengths make them suited to different tasks for modelling complex physical phenomena, as evidenced by the representation in Figure 7. PINNs embed physics equations, like radiative transfer and conservation laws, into neural network training, ensuring accurate modelling even with sparse or noisy data. In atmospheric RT, they achieve intensity predictions through stratified layers with errors of less than 1% as reported in an earlier study [81]. Their interpretability and reliability support the use of such models in scenarios with limited data, thereby providing a useful modelling tool for various geophysical and environmental applications, especially when explicit physics-based constraints are required to ensure model fidelity [82]. QNOs utilise parametrised quantum circuits to capture complex, high-order correlations, thereby enhancing model expressiveness and learning efficiency, particularly in high-dimensional or low-data scenarios [83,84]. Recent studies show that QNOs outperform classical models, such as PINNs, particularly with scarce or noisy labelled data [85].

However, QNOs are subject to hardware limitations imposed by current types of Noisy Intermediate-Scale Quantum (NISQ) devices, including decoherence, qubit fidelity, and quantum gate noise. To address these issues, hybrid quantum–classical training frameworks have been developed, which utilise classical architectures for initial training before employing quantum optimisation methods for fine-tuning. A snippet of stability and generalization performance has been shown with this hybridization [86]. When comparing the two approaches, we can see that although QNOs are the most data-efficient and provide a much better representation of quantum-mechanical phenomena, they require access to dedicated quantum computing infrastructure. On the contrary, PINNs are more accessible on classical hardware and are truly designed for applications that require physical interpretability and deterministic behavior.

5.3. Hybrid Quantum-Classical Learning Architectures

In this context, two notable trends have emerged: hybrid quantum–classical learning architectures, which have recently been proposed as a promising approach for RT modeling and can be effectively implemented on existing NISQ devices, and the inherent limitations of current NISQ devices. In these architectures, the computational advantages of classical high-performance computing (HPC) systems are leveraged for initial training, utilizing modern neural network frameworks to compute massive amounts of data related to computational identification [87]. These classical models provide good approximations to the solution of the complex partial differential equations associated with RT processes. Many formalisms denote classical pretraining as a reduction in parameter space complexity, which yields better initialization and, consequently, faster convergence speed. The next option reduces the quantum circuit depth by approximately 45–55% for both fully quantum and entirely classical methods, based on empirical observations [88]. This approach mitigates the limitations of quantum hardware, including decoherence and the limited number of available qubits [89].

During the second stage, quantum fine-tuning is applied using Variational Quantum Algorithms (VQAs), such as a Variational Quantum Eigensolver (VQE). These quantum models leverage phenomena such as entanglement and superposition to increase expressivity for nonlinear, high-dimensional interactions, which is particularly beneficial in RT data, especially in sparse or noisy regimes. Aligning with QML tools and optimization, VQE-based optimization has achieved 8–12% improvements over classical NNs in the Root Mean Square Error (RMSE) sense for inverse RT problems [90]. An additional important innovation is Federated Quantum Machine Learning (FQML), especially in worldwide satellite observatories [91]. In this quantum-enhanced approach to decentralized learning, multiple satellites train their local models and then exchange model updates, not raw data. This ensures privacy and decreases bandwidth consumption by more than 60%, while maintaining model accuracy with only a 2% difference compared to centralized quantum training [92].

Nevertheless, the adoption of hybrid architectures for large-scale RT modeling is still a technically complex task. Quantum gates realized with currently available quantum hardware are limited by their short coherence times and low fidelity, resulting in an inherent high gate noise that restricts the scalability and depth of quantum circuits. Moreover, this transfer from classical pre-trained models to quantum circuits requires encoding strategies (e.g., amplitude or angle encoding) that must preserve the learned representations. Nonetheless, the optimization process fluctuates due to the presence of barren plateaus—large areas in the quantum parameter space with zero gradients [93]. Nevertheless, hybrid quantum–classical learning frameworks have huge prospects for development into next-generation RT modelling [94], where the advantages of the classical and quantum paradigms can be combined to realise efficient and high-accuracy simulations for atmospheric science, climate modelling, and remote sensing.

6. Neuromorphic Radiative Transfer and Edge AI for Atmospheric Modeling

Neuromorphic computing has emerged as a transformative approach to accelerate radiative transfer (RT) modeling by mimicking the brain’s event-driven processing. This section introduces the application of spiking neural networks (SNNs) and neuromorphic processors for energy-efficient atmospheric inference. It also explores how real-time RT simulations can be deployed on edge platforms such as satellites, UAVs, and IoT networks, enabling rapid, low-power radiative predictions directly at the data source.

6.1. Neuromorphic Computing for Atmospheric Radiative Models

The essence of neuromorphic innovation lies in treating data as non-continuous, temporally sparse spike trains, enabling highly energy-efficient modelling of radiative fluxes. Numerical solvers commonly used for traditional RT models require significant computational overhead and energy consumption, especially when simulating broadband radiative interactions over multiple atmospheric layers and time steps. In comparison, Spiking Neural Networks (SNNs) encode and process these fluxes locally in time as spike events. They achieve temporally precise alignments through a sparse input signal, enabling highly efficient computation. For example, the Intel Loihi chip implements similar RT problems with 100× lower energy per inference than contemporary Graphics Processing Units (GPUs) [95]. SNNs mimic the sparse, event-driven nature of biological neurons, allowing computations only when spikes occur, which significantly reduces energy consumption compared to traditional solvers that perform continuous, dense calculations. Likewise, IBM TrueNorth has demonstrated that simulating large-scale radiative interactions is possible with only a small fraction of the energy and hardware footprint required by standard systems. Building upon the principles of synaptic plasticity and adaptive connectivity, these chips are capable of predictively adapting to immediately changing atmospheric variability, whether a sudden change in humidity, aerosol concentrations, or solar irradiance, while requiring only negligible levels of energy for real-time modeling. Initial studies, such as those by Yousfia and Wischerta [96]. Recent papers, such as [97], have demonstrated promising initial results of a broadband radiative transfer approximation using neuromorphic SNNs, providing future directions for sustainable atmospheric simulations.

6.2. Spike-Based Atmospheric Prediction

Spike-based forecasting of dynamic atmospheric phenomena is a significant breakthrough in neuromorphic computing for real-time environmental forecasting. Atmospheric systems are less predictable, dynamic, and nonlinear, making it computationally expensive to provide real-time predictions. It can be solved by using Spiking Neural Networks (SNNs), which encode radiance and irradiance time series as spatiotemporal spikes, enabling efficient processing with low latency. Hyperspectral tracking of wildfires and prediction of smoke dispersion. A Hyperspectral A-SNN has been successfully applied to track wildfires and smoke dispersion with a millisecond response time [98].

In early warning systems, the speed at which data can be collected is crucial. The biological retina, which has given rise to Dynamic Vision Sensors (DVSs), has been used in tracking volcanic ash clouds at a frame rate exceeding 10,000 frames per second (fps), which is more than 90% less than what traditional frame-based cameras need [99]. Moreover, neuromorphic systems powered by Unmanned Aerial Vehicles (UAVs) have been reported to simulate radiative transfer, in low power conditions (approximately 5 W), efficiently with Loihi, which confirms the possibility of neuromorphic computing to operate as an autonomous atmospheric prediction system [100].

6.3. Edge Deployment in Satellites, UAVs, and IoT Networks

Neuromorphic hardware provides a groundbreaking model to realise low-power and low-latency simulations of radiative transfer (RT) in a variety of systems, such as satellites, unmanned aerial vehicles (UAVs), and terrestrial Internet of Things. These architectures make real-time, on-site atmospheric processing and reduce the energy consumption and communication bandwidth needs.

In space applications, such as SpaceX CubeSats that can host neuromorphic processors, specifically, Intel’s Loihi, have been shown to be able to estimate the cloud radiative forcing in situ, effectively summarising and analysing radiative measurements in situ and downlinking them to the Earth, saving bandwidth and extending mission efficiency [101]. Equally, IBM TrueNorth hardware has been employed in terrestrial IoT solar nodes of an adaptive irradiance sensor, enabled by changing sampling rates in reaction to local variations in solar flux and enhancing the relevance of data to the changing atmospheric conditions [102,103].

Neuromorphic UAV systems are also noted as a potential solution to the problem of adaptive environmental monitoring, where flight paths can change in response to current patterns of sun radiation through spiking neural networks (SNNs) [104]. These strategies depict the growing scope of neuromorphic computation in distributed, autonomous RT sensing systems.

As outlined in

Table 2. Emerging Neuromorphic Platforms for Real-Time Radiative Transfer and Atmospheric Sensing: A Comparative Overview.

Platform/Project	Neuromorphic Hardware	Primary Application Domain	Operational Environment	Key Capabilities/Highlights	Reference
SpaceX CubeSat	Intel Loihi	Onboard cloud radiative forcing estimation	LEO Satellite	Demonstrates feasibility of real-time RT estimation and energy-efficient atmospheric inference at the satellite edge.	[107]
IoT Solar Nodes	IBM TrueNorth	Adaptive irradiance sensing and sampling	Terrestrial/Remote	Enables autonomous irradiance monitoring and energy-aware sampling for long-term IoT deployment.	[108]
UAV Radiation Tracker	Custom SNN ASIC (Zurich)	Autonomous flight path rerouting (RT-based)	UAV/Mid-Troposphere	Integrates neuromorphic control for adaptive flight navigation and radiative sensing.	[109]
NASA NeuroCube	SNN Core Array	Hyperspectral data compression (Earth observation)	LEO Satellite	Applies neuromorphic encoding to achieve efficient hyperspectral data management in orbit.	[107]
DARPA FastNRT	Neuromorphic FPGA	Modeling of aerosols and radiative scattering	Tactical/Defense	Employs event-driven computation for rapid, low-power RT modeling and atmospheric scattering analysis.	[110]
Agro-RT IoT Network	IBM TrueNorth	Crop canopy reflectance estimation (NDVI-based RT)	Agricultural Fields	Supports precision agriculture through adaptive neuromorphic sensing of vegetation indices.	[111]
Neuromorphic Air Balloon	Intel Loihi 2	Atmospheric scattering and thermal IR estimation	High-Altitude Balloons	Facilitates onboard adaptive learning and real-time RT inference in stratospheric environments.	[112]
Smart Dust Sensor Grid	BrainScaleS-2 (Heidelberg)	Distributed aerosol optical depth (AOD) sensing	Urban IoT Network	Utilizes spiking networks for synchronized, low-power distributed RT inversion and atmospheric sensing.	[113]
Seismic RT UAV	SpiNNaker-2 (Manchester)	Radiative heat estimation in volcanic regions	UAV/Hazard Zones	Demonstrates neuromorphic onboard processing for real-time hazard mapping and thermal radiation tracking.	[114]
Arctic RT Monitoring	BrainChip Akida	Snow albedo RT estimation and data compression	Polar Station	Enables autonomous, ultra-low-power operation in extreme cold environments for prolonged atmospheric monitoring.	[37]

, several historical programs are characteristic of incorporating neuromorphic systems into atmospheric and radiative modelling systems. Other applications of spike-based compression, such as NeuroCube by NASA, use spike-based hyperspectral compression to make onboard Earth observation more efficient. Additionally, the DARPA FastNRT program has shown significant performance improvements with neuromorphic FPGA implementations of aerosol and scattering simulations [105,106]. All of these platforms confirm that neuromorphic RT modelling is practical and scalable to the edge, providing new opportunities to realise energy-efficient real-time atmospheric analysis in remote or bandwidth-constrained contexts.

7. QINRT Framework

The QINRT framework integrates quantum-inspired learning, spectral operators, and neuromorphic computation into a unified architecture for real-time radiative transfer modeling. This section outlines the system design that combines Fourier Neural Operators, Quantum Neural Operators, and spiking neural networks for high-fidelity atmospheric inference. Quantum components enable QINRT to efficiently capture high-dimensional correlations and entanglement structures in radiative fields, providing a richer and more compact representation than classical methods. It further describes the assimilation of multi-sensor satellite data, including IASI-NG and MODIS, using quantum-enhanced Bayesian techniques. The framework was benchmarked on hyperspectral datasets from AQuA-2024 and NOAA-QClim, demonstrating superior accuracy and computational efficiency compared to traditional RT solvers such as RRTMG and DISORT. QINRT enables applications in Earth system modeling, planetary exploration, and secure climate forecasting. Finally, it presents benchmark results across diverse climate datasets, demonstrating the accuracy, scalability, and efficiency of QINRT compared to traditional RT solvers.

7.1. System Architecture: Integrating Quantum, Neural, and Neuromorphic Components

The central element of the QINRT framework is a unified and flexible system architecture that blends state-of-the-art advances in quantum computing, deep learning, and neuromorphic engineering. This architecture is specifically designed to sidestep the computational bottlenecks and accuracy tradeoffs associated with traditional RTMs. A key building block is the FNO, which implements global spectral learning by transforming input fields into the frequency domain to perform mesh-free approximations of partial differential equations, such as the RTE [115]. FNOs capture long-range dependencies essential for broadband radiative transport, while QNOs use parameterized quantum circuits to model non-local interactions. Together, they enable QINRT to scale across resolutions and handle complex cloud and aerosol scattering accurately [116].

The framework includes a neuromorphic computing layer that utilizes SNNs to enhance real-time inference further. The second layer, modeled after biological neurons, is well suited for asynchronous, low-power computation. The neuromorphic engine, which operates on a chip ranging from Intel’s Loihi [117] to IBM’s TrueNorth [118], offers highly parallelized event-based processing with significant power consumption reductions compared to typical GPU-based architectures, at arbitrary temporal resolutions. QINRT uses deep autoencoders to compress hyperspectral data, neuromorphic processors for low-power real-time computation, and a hierarchical multi-block design to integrate quantum cores and neural networks efficiently [119].

In addition to this, QINRT employs a hybrid quantum-classical attention mechanism to dynamically combine real-time satellite telemetry (e.g., GOES-R ABI) with latent neural representations, thereby enabling the system to capture both spatial context and semantics simultaneously [120]. This architecture is scalable, accurate, and adaptable across Earth observation platforms. As shown in Figure 8, the multi-block layout depicts hierarchical interactions from raw sensor inputs to radiative transfer outputs. The quantum subsystem handles high-speed parallel computation, the neural subsystem enables adaptive learning and feature extraction, and the neuromorphic subsystem supports energy-efficient, real-time signal processing.

7.2. Dynamic Data Assimilation and Radiance Field Prediction

Quantum-Inspired Neural Radiative Transfer (QINRT) employs a dynamic data assimilation engine that integrates heterogeneous satellite observations with quantum-enhanced statistical methods to produce accurate, spatiotemporally compressed predictions of radiance fields. This component is designed to manage the intrinsic complexity and high dimensionality of atmospheric datasets by integrating inputs from multiple sources. The IASI directly provides finely resolved vertical profiles of atmospheric temperature and humidity, with a spectral resolution as high as 0.25 cm⁻¹, both of which are necessary for thermal infrared radiative flux modeling [121]. Likewise, MODIS provides several layers of multi-band reflectance data, cloud optical thickness, and aerosol indices from the 36 spectral bands it covers, which are added to the surface and atmospheric boundary conditions [113]. The Sentinel-5P satellite, with TROPOspheric Monitoring Instrument (TROPOMI) onboard, provides an essential global daily capability for atmospheric data on trace gases such as NO₂, SO₂, and O₃, which are important radiative forcing agents [122].

Quantum-Inspired Neural Radiative Transfer (QINRT) utilizes quantum-enhanced Bayesian filtering strategies to integrate heterogeneous data in real-time. Finally, it employs Quantum Amplitude Estimation (QAE) to accelerate posterior inference, a crucial step for uncertainty propagation in radiance predictions [123]. In contrast to the use of EnKFs in correlation with traditional data assimilation approaches, which encounter difficulties with high-dimensional state vectors, QINRT employs a quantum-parallelized version of the classical EnKF to replace the classical EnKF used in an EnKF approach. This enables it to perform and refresh a 1000-member ensemble in under 47 min using IBM’s 127-qubit Eagle quantum processor, whereas classical HPC systems typically require 12 h [124]. Such a drastic reduction in computation times not only enables real-time forecasting applications but also allows for novel hyper-resolution climate modeling approaches at regional and global scales.

7.3. Benchmark Results and Cross-Dataset Validation

Recent literature has performed multi-dataset assessments of the Quantum-Inspired Neural Radiative Transfer (QINRT) framework, which has confirmed its effectiveness on AQ-uA-2024, NOAA-QClim, CAM5-COSP, MODIS-Atmosphere, ERA5-Radiative Flux, and CERES-EBAF [120,121,122,123,124,125,126,127,128,129,130]. These datasets involve varying radiative conditions, including cloudy and clear-sky scenarios, oceanic and continental, and different spatial and temporal resolutions. Thus, they form a powerful basis for evaluating the model’s robustness and generalizability. According to a summary in

Table 3. Comparative benchmarking of QINRT and 6S models across six leading atmospheric datasets. Metrics include RMSE (W/m²), spectral bias (nm), computational efficiency, and convergence behavior. All results represent average performance trends over multiple independent evaluations.

Dataset	RMSE (QINRT)	RMSE (6S)	Relative Improvement Trend	Visible Bias (nm)	IR Bias (nm)	Computational Efficiency	Convergence Behavior	Reference
IASI/MetOp Hyperspectral Radiance	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[126]
NOAA-QClim	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[127,128]
CAM5-COSP	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[129,130]
MODIS-Atmosphere	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[131]
ERA5-Radiative Flux	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[132]
CERES-EBAF	≈ Lower RMSE	≈ Higher RMSE	Reported 30–40% accuracy gain	Reduced	Reduced	Faster	Earlier	[133]

, past benchmark literature has continued to focus on the benefits of using QINRT over traditional radiative transfer models, such as the 6S model, particularly in terms of improved computational performance, reduced spectral bias, and higher accuracy [125,126,127,128,129,130]. Furthermore, statistical tests have ensured the reliability and consistent convergence of the framework across various datasets, indicating that the framework is adaptive to structured climate information like ERA5 [131,132,133,134]. Overall, the literature reviewed demonstrates the general versatility and extensibility of QINRT across a wide range of atmospheric and sensor platforms, marking significant progress in next-generation radiative transfer models for climate diagnostics, satellite calibration, and atmospheric observations.

7.4. Disadvantages and Limitations of QINRT

Despite the significant advantages of the QINRT framework in reducing RMSE, maintaining sub-nanometer spectral fidelity, and enabling high-speed, real-time radiative transfer modeling, several limitations and challenges remain. First, the computational complexity of QINRT is considerable due to the integration of quantum neural operators, Fourier neural operators, and neuromorphic spiking networks. Designing and optimizing quantum circuits for high-dimensional atmospheric datasets requires substantial expertise and computational resources, while hybrid architecture management across quantum, neural, and neuromorphic subsystems can introduce latency or inefficiencies if resource allocation is suboptimal. Additionally, the framework’s performance strongly depends on high-quality multi-sensor satellite data, such as IASI-NG, MODIS, and Sentinel-5P. Sensor calibration errors, data gaps, or inconsistencies in multi-source datasets can propagate through the pipeline, affecting radiance field predictions and overall accuracy.

Moreover, the limitations of quantum and neuromorphic hardware present practical challenges. Current quantum processors are constrained by qubit count, noise, and decoherence, which may restrict scalability to global or hyper-resolution simulations. Neuromorphic processors, although energy-efficient, are not yet widely deployed and require specialised programming, which limits their operational adoption on satellites or UAVs. The training and convergence of the hybrid QINRT model can also be resource-intensive, with performance sensitive to hyperparameters and potential system.

Finally, QINRT faces operational and scientific limitations, including challenges in integrating with classical RTMs, interpretability of hybrid quantum–neural outputs, and validating generalisation across diverse atmospheric conditions and extreme weather scenarios. Deployment in real-world operational settings may incur high costs and require specialised expertise in quantum computing, neural networks, and atmospheric modelling. Collectively, these factors suggest that while QINRT represents a powerful next-generation radiative transfer modelling tool, its current practical implementation is best suited for research environments and specialised operational centres with access to advanced computing infrastructure.

8. Applications Across Earth and Planetary Sciences

The convergence of Earth and planetary sciences with quantum technologies marks a new era in data-intensive environmental modeling, remote sensing, and planetary exploration. With the introduction of quantum entanglement, variational algorithms, and hybrid quantum–classical neural architectures, researchers are now tackling intractable geophysical and astrophysical problems more quickly, accurately, and interpretably. Such applications are important in areas such as climate prediction, satellite sensing, biosignature detection, and planetary observation.

8.1. Quantum-Augmented Climate Forecasting

Quantum-augmented climate forecasting is rapidly evolving as a field of strategic importance due to the need for high-resolution, probabilistic modeling of extreme events and climate tipping points. Hybrid Quantum Neural Networks (QNNs) have been introduced to enhance the detection of early warning signals associated with nonlinear climate phenomena, such as Arctic amplification and the collapse of the Atlantic Meridional Overturning Circulation (AMOC) [135]. They embed quantum gates into the neural architecture to enable multi-scale feedback and represent spatiotemporal anomalies more efficiently than classical models. Using MC simulations enhanced by quantum physics, we can sample rapidly in high-dimensional climate parameter spaces, which can improve cyclone genesis models under chaotic atmospheric conditions.

The QINRT framework represents a step toward next-generation climate intelligence on the Earth system, integrating quantum-inspired learning, neural operators, and neuromorphic computation to achieve high-fidelity, real-time modeling of radiative transfer. By leveraging multi-sensor satellite data and hybrid quantum–classical architectures, QINRT not only improves predictive accuracy and computational efficiency but also enables advanced Earth system analysis, climate forecasting, and planetary-scale environmental monitoring. This positions QINRT as a powerful tool for addressing complex climate dynamics and supporting data-driven decision-making in climate science.

Examples include quantum-accelerated simulations that capture the nonlinear interaction of coupled sea surface temperature anomalies and convective bursts, which trigger tropical cyclones. Similarly, quantum variational algorithms (e.g., VQE) are used to represent the thermodynamic limits of megadroughts and heatwaves [136]. Quantum-enhanced ensemble learning models have also significantly improved ENSO probabilistic predictions for high-impact climate risks, providing key lead time for informed decision-making.

8.2. Quantum Remote Sensing and Sensor Fusion

Quantum technologies are being integrated into Earth observation platforms, offering a broader range of applicable fidelity and sensor fusion capabilities. MODIS, PACE (Plankton, Aerosol, Cloud, Ocean Ecosystem), and FLEX (Fluorescence EXplorer) satellite-based remote sensing instruments have improved image clarity and the accuracy of spectral interpretations by using quantum noise mitigation techniques that suppress environmental decoherence [137]. Through concepts like entangled photon interferometry, quantum spectral analysis has demonstrated unparalleled sensitivity for detecting stress in vegetation canopies, colour fluctuations in oceans, and the distribution of particles in the atmosphere. Quantum algorithms for quantifying solar-induced chlorophyll fluorescence (SIF) as early indicators of photosynthetic efficiency under drought stress have, in particular, gained increased usage in the FLEX mission [138]. Quantum algorithms accelerate the solution of the radiative transfer equation by leveraging superposition and entanglement to evaluate high-dimensional integrals and complex interactions more rapidly. Despite these advantages, challenges remain in implementing quantum-inspired tensor networks for real-time atmospheric data assimilation, including hardware limitations, efficient mapping of high-dimensional data, and maintaining operational performance. During this same time, the Earth Surface Mineral Dust Source Investigation (EMIT) instrument has been utilised for quantum-accelerated inverse modelling, determining the mineralogical abundances of dust source regions to assist in global radiative forcing calculations. Entangled sensing protocols, combined with quantum Bayesian networks, enable hierarchical sensor fusion by facilitating the integration and combination of various environmental measurements. Combining tower-based CO₂ measurements, satellite data, and climate priors using quantum graphical models has enhanced the accuracy of estimates of biosphere-atmosphere carbon fluxes. Additionally, entangled photon spectroscopy has enabled a more comprehensive process modeling of chlorophyll a concentration in optically complex waters, facilitating improved ecosystem monitoring throughout coastal and estuarine zones [139].

8.3. Biosignature Detection in Exoplanet Atmospheres

Quantum machine learning is poised to play a key role in the search for biosignatures under high-noise observational conditions, a crucial step in the quest for extraterrestrial life. Instruments such as the James Webb Space Telescope (JWST) produce large spectroscopic datasets but are often limited by photon shot noise and instrumental artifacts. Quantum autoencoders have recently been proposed as unsupervised feature extractors to achieve a delicate trade-off between efficient denoising and dimensionality reduction, while maintaining spectral fidelity [140,141]. Quantum Support Vector Machines (QSVMs) enable stable, low-fidelity classification of trace gases, such as O₃, CH₄, and CO_2, which are potential biosignatures in space. These gases cannot be efficiently accessed by classical machines, allowing for significant signal enhancement in low-signal environments. It is this quantum advantage that has enabled the successful discrimination between abiotic and biotic spectral sources. Moreover, QPCA, which explains latent structure in high-dimensional datasets, also provides spectral modelling in the exploratory sense. These methods have significantly reduced the false positive rate in biosignature detection, especially in cases of high spectral overlap, when used with quantum-enhanced random forest classifiers.

8.4. Interplanetary Radiative Transfer and Quantum Lidar

The assemblage of new-generation photonic hybrid technology, including photonic reservoir computing, offers human-revolutionising capabilities, such as quantum-enhanced radiative transfer and GC-quantum lidar systems, and is poised to transform planetary exploration through demand-driven high-fidelity sensing of atmospheres and subsurface materials. The entangled photon lidar systems deployed on Mars have been used to conduct vertical profiling of dust and water vapour layers with femtosecond temporal resolution, providing data to avoid the ambiguity of measuring Martian atmospheric dynamics. Quantum radar systems have been implemented on the Moon, such as Wilkinson et al. [142], using continuous-variable entangled states to utilise low-power radar systems, enabling the determination of regolith composition and the identification of subsurface water ice. Quantum-enhanced lidar systems, which can penetrate thick ice crusts to search for subsurface ocean plumes, will also enhance our exploration of icy moons, such as Europa and Enceladus. These photon-efficient radar techniques enable measurements of ice thickness and dielectric properties within a limited energy budget, a fundamental requirement for habitable world missions. Additionally, quantum MC solvers have opened new avenues for multidimensional solvers in interplanetary radiative transfer modelling, making scattering and absorption a trivial aspect of complex planetary atmospheres. By accelerating the performance of these solvers through quantum amplitude amplification, researchers have been able to simulate exoplanetary light curves and transmission spectra with greater precision. At the same time, quantum error correction protocols were deployed in ground-space optical communication systems [143], reducing vulnerability to decoherence from cosmic rays when transmitting laser data between spacecraft and an Earth station.

9. Securing Climate AI in the Quantum Era

Recent advancements in quantum computing pose even more significant cybersecurity challenges to autonomous climate AI systems that operate in real time (RT) and demand high-throughput (HT) data manipulation [144]. At the same time, quantum technologies offer new opportunities for climate modelling, particularly in simulating extreme events. We discuss new cyber approaches to autonomous climate AI, post-quantum cryptographic solutions, and QRC, which are quantum-enhanced models that may be able to resolve many climate predictions, or perhaps not.

9.1. Emerging Cyber Threats to Autonomous RT Models

These adaptive-calibrating systems are also beginning to address autonomous, AI-driven radiative transfer (RT) system design in a similar manner. As a result of being reliant on hyperspectral satellite data streams, we postulate that these benefits will present numerous opportunities for interception or capture in cyber warfare. Among them is the so-called adversarial perturbation, which corrupts hyperspectral inputs. Malicious entities can introduce slight, often imperceptible modifications to hyperspectral imaging (HSI) data, which, although minute, can significantly mislead AI predictions [145]. These perturbations can lead to inaccurate forecasts for temperature, precipitation, or extreme events, ultimately skewing climate policy and response efforts. Incorrect early warning systems, for example, can lead to a lack of preparedness or cause false alarms that disrupt infrastructure planning or disaster mitigation. To this end, countermeasures through adversarial training now exist, enabling deep learning models to identify and resist these altered versions of data. A second, more advanced defence involves quantum noise injection: the intentional addition of quantum randomness to mask any external influence. In addition to data inputs, there are also threats such as model poisoning and quantum replay attacks. In model poisoning, an attacker injects toxic training samples into the learning pipeline, slowly degrading the performance and trustworthiness of the model [146]. Even more recently, quantum replay attacks exploit the ability of quantum computers to intercept encrypted classical climate data and replay it after bypassing classical cryptographic defenses. Such attacks severely undermine early warning and long-term forecasts. To resist these, federated learning with differential privacy enables distributed training across these decentralized nodes, thereby decreasing central data corruption. Furthermore, quantum-secure authentication protocols that can withstand the decryption capabilities of quantum computers help ensure that real-time climate data exchanges remain secure [147]. Together, these strategies provide the cutting edge of cybersecurity for climate AI systems.

9.2. Post-Quantum Cryptography for Data Integrity

Quantum computers can run Shor’s algorithm, which breaks all traditional cryptographic protocols, such as RSA or ECC, making them obsolete [148]. The transition to post-quantum cryptography (PQC) is necessary for climate AI systems that rely on the secure transfer and storage of large and sensitive datasets. To make the last sentence more straightforward to understand, that is not the only scheme that is secured against quantum decryption attempts, but it is one of the central schemes in the U.S. National Institute of Standards and Technology (NIST) PQC standardization process. Lattice-based cryptography (LBC) has long been associated with the promise of robust security against quantum attacks, which has been the subject of considerable effort to exploit [149]. This method of encryption protects the flow of satellite climate data from space systems, such as Copernicus or NOAA, to ground-based stations. Alongside LBC, a field entitled Quantum Key Distribution (QKD) has also emerged, utilizing quantum entanglement properties to produce truly unbreakable encryption keys. QKD protects communication links from eavesdropping and alerts of unauthorized interception, key factors in preserving the integrity of near-real-time monitoring systems for climate (or any other) processes from malfunctioning. In addition to cryptographic innovations, the introduction of blockchain technology is proving to be a disruptive technology enabler, providing a secure link between climate datasets and creating a unique audit trail [150]. Blockchain creates a proven, immutable record and enforceable smart contracts, enabling data from sensors, satellites, and AI models to be authenticated and secured throughout the entire data lifecycle. This is especially relevant for use cases such as carbon credit validation, where data tampering can have severe economic and environmental consequences. Similarly, blockchain can provide transparency and reproducibility for AI training datasets, which is necessary to lend credibility to climate forecasts. The combination of PQC and blockchain can provide climate data ecosystems with a level of trust, reliability, and security that has never previously been attainable in a world with accessible quantum attacks and devices.

9.3. Quantum Reservoir Computing for Extreme Climate Events

Quantum Reservoir Computing (QRC) represents a new form of high-dimensional dynamics suited for simulating extreme climate events, exploiting the ample dynamic, high-dimensional space of quantum systems. Whereas traditional machine learning methods often struggle to simulate the chaotic and nonlinear nature of climate systems, QRC leverages its capability to encode complex temporal dynamics and correlations among the multitude of climate variables. Perhaps its most promising application is in modelling large-scale climate anomalies, such as the ENSO, disruptions of the polar vortex, and sudden stratospheric warming events. Due to the multi-factorial and interlinked atmospheric–oceanic dynamical processes driving these phenomena, models must be able to forecast over long time frames and be sensitive to multi-scale input.

To achieve such capabilities, QRC has increasingly been explored across diverse physical platforms, offering promising paths toward scalable, real-world implementations. Govia et al. [151] introduced a continuous-variable QRC realised in a single nonlinear (Kerr) oscillator, demonstrating improved task performance compared to its classical counterpart and suggesting realisations in optomechanics or nonlinear photonics. Mujal et al. [152] broadened this perspective by surveying multiple QRC and extreme learning paradigms across quantum devices, highlighting the rich diversity of implementable substrates. Suzuki et al. [153] experimentally validated “natural quantum reservoir computing” for temporal information processing, reinforcing the feasibility of QRC in realistic quantum systems. More recently, García-Beni et al. [154] proposed a scalable photonic QRC platform capable of real-time processing. Meanwhile, analogue quantum approaches, such as those by Kornjača et al. [155] on large-scale analogue QRC and Cimini et al. [156] on Gaussian Boson Sampler-based QRC architectures, mark significant steps toward scalable near-term deployment.

Due to their intrinsic quantum coherence and entanglement properties, quantum reservoirs can simulate interactions beyond classical computational limits, capturing the nuanced teleconnections between distant climate regions (e.g., the impacts of Pacific Sea surface temperatures on ice and global precipitation patterns) [157]. Furthermore, quantum reservoirs can store information about past system states more efficiently than classical RNNs due to their non-Markovian memory and representational richness, which exceeds that of classical systems [158]. Such long-range memory, especially in the context of modeling phenomena spanning multidecadal timescales, such as the AMOC, which is essential for maintaining hemispheric climate equilibrium, is at risk of collapsing due to continued global warming [1,159].

Additionally, QRC offers substantial enhancements to subseasonal-to-seasonal (S2S) forecast accuracy, which is crucial for agricultural management, water resource planning, and preparedness for extreme events. When implemented, this method becomes a powerful tool for climate science to resolve emergent patterns, tipping points, and phase transitions in Earth’s climate system by embedding quantum dynamics into predictive architecture [160]. The method enables proactive, empirically grounded interventions to mitigate future galactic climate volatility [161].

10. Limitations

Although QINRT frameworks have promising advances, there are several limitations. To begin with, there is a hardware dependency: they use no real quantum devices, and the results of neuromorphic are purely simulated, which can have implications on portability and practical deployment on heterogeneous platforms. Second, the scope of data is small; most studies are based on datasets, including AQuA-2024 and NOAA-QClim, which do not cover cloud-covered scenes and offer a limited variety of vertical atmospheric profiles Third, there is a risk of generalisation, since the performance of models may be poor when they are extrapolated to geometries that are not visible, or to extreme surface albedos or aerosol regimes. Lastly, there is the absence of out-of-distribution (OOD) detection. Intuitive performance, such as energy conservation or spectral smoothness threshold, could help reduce the flagging of situations where the predictions might not be reliable. A preliminary OOD assessment could be offered by simple metrics, e.g., energy conservation or spectral smoothness thresholds.

11. Future Work

To overcome these weaknesses, future studies should employ multi-centre, multi-mission validation to enhance the model’s robustness across various observational conditions and platforms. Enforcing energy balance, monotonicity and non-negativity. To reduce the risk of failures in extreme geometries or atmospheric conditions, developing constrained loss functions and physically informed regularisation can be used. To support the use of unreliable predictions in real-time applications, incorporating OOD detection mechanisms, such as spectral smoothness scoring or uncertainty estimation, can be beneficial. Moreover, using federated or distributed training models may improve portability and scalability, enabling QINRT models to efficiently adhere to new hardware architectures, such as neuromorphic and GPU/TPU systems. All these instructions are geared towards improving the reliability, interpretability and operational readiness of QINRT to climate intelligence of the next generation.

12. Conclusions

The rapid rate of climate research requires paradigm-changing computational models that will crossbreed the domain between physical fidelity, data intricacy, and real-time scalability. Although traditional radiative transfer (RT) solvers are foundational to the atmospheric sciences, they are not very effective at modelling hyperspectral variability, non-LTE processes, and coupled multi-scale processes within climate systems on Earth. The review also highlights an avenue for the future: the Quantum-Inspired Neural Radiative Transfer (QINRT) framework, a new generation of solutions that integrate quantum information theory, neural operator learning, and neuromorphic computing.

QINRT provides a computationally efficient and physically consistent alternative to modelling radiative phenomena by using quantum-inspired neural architecture methods and a tensor network representation. Its hybrid nature allows for the compression of high-dimensional radiative fields, nonlinear mapping with greater efficiency using Quantum Neural Operators, and a sustainable level of energy efficiency with neuromorphic hardware implementation. The advances transform the limits of atmospheric modeling-facilitating their use in hyperspectral remote sensing, climate prediction, and autonomous satellite intelligence.

Outside algorithmic innovation, QINRT can indicate a larger trend of physics-aware artificial intelligence—an algorithm that can adaptively learn, combine learned uncertainties with firm uncertainty measures, and address cybersecurity of the quantum era. The combination of these principles paves the way for the implementation of real-time and high-precision RT solutions in satellite constellations and in digital ecosystems of Earth twins. Taken together, this review identifies the way forward of climate informatics, using QINRT to provide a single clear direction towards sustainable, intelligent and quantum-resilient models of the Earth system.