A Quantitative Analysis of the Need for High Conversion Efficiency PV Technologies in Carbon Mitigation Strategies

Abstract

We consider the restrictions on photovoltaic (PV) capacity that are caused by limitations on where panels can be sited and find quantitative evidence for the need for high efficiencies. We define 15% of the UK’s energy consumption as a “significant” contribution and, with London as an exemplar, we perform an idealised calculation that makes the most optimistic possible assumptions about the capabilities of future PV technologies and use published surveys on energy usage, dwelling type and insolation. We find that covering every UK domestic roof with the highest power conversion efficiency (PCE) solar panels currently commercially available could produce up to 9% of the UK’s energy. A 15% contribution would require PV technologies with >37% PCE, more than the theoretical Shockley–Queisser limit. Replacing the idealising assumptions with more realistic estimates increases this by 2–3 times. Alternatively, a solar farm using the currently available PCEs would require a politically challenging ~1200 km² of new land, roughly the area of Greater London, for this 15% contribution. We conclude that PCEs must be driven higher than even the Shockley–Queisser limit for PV to play a significant part in carbon mitigation.

1. Introduction

A significant research effort is being put into making solar cells cheaper and easier to make [1,2,3,4,5,6]. While this is a valuable area of research, making the cells cheaper is, on its own, not necessarily enough to enable photovoltaics (PVs) to contribute significantly to a sustainable carbon mitigation strategy.

These PV approaches use materials which harvest the sun’s energy by using it to promote electrons across a “bandgap” energy step. The energy height of this step depends on the material system, and it has to be matched to the spread of photon energies in sunlight. Too high a value and excessive amounts of the red end of the rainbow are missed, because its photons do not have enough energy to promote the electrons. Too low a value and a large fraction of the energy in the blue end of the rainbow are lost, because the excess energy given to the promoted electrons is lost as heat in the device as they relax back down to the band edges. Even with the bandgap energy perfectly chosen, and even if all the practical engineering issues can be completely solved, this trade-off means that today’s fixed single-junction PV technologies offer a power conversion efficiency (PCE) which is theoretically capped at ~33%, the so-called Shockley–Queisser (S-Q) limit [7,8].

Here, we analyse the practical consequences of this in light of the fact that in the urbanised societies which consume the greater part of the world’s energy, space is a highly valued resource. This is a topic that has been considered by others, but no numerical analysis of the situation has been performed [9]. We first look at the option of mounting solar panels on the roofs of houses and calculate, in an idealised model, the limits to the amount of energy that could be generated using the technology with the best commercially available PCE panels.

For definiteness, we use the term contribution to denote the fraction that PVs could supply of the current total UK energy budget and take 15% as the value at which PVs could be said to contribute “significantly” to a sustainable energy future. We also define the term mPCE to denote the minimum PCE required of a piece of PV technology to generate a given contribution. This is all carried out under the most optimistic assumptions of how well a roof-mounted PV system could be implemented in practice.

Finally, we consider the alternative option, which is both much simpler to model and yet politically much more challenging to implement: that of large-scale solar farms. Again, for discussion purposes, we make similarly generous and optimistic assumptions. We present estimates of the land areas that would be required to generate a significant contribution.

2. Methods

2.1. Description of the Model

Our calculations here were directly impacted by three angles that relate to how solar panels are installed, namely the latitude $\phi$; the angle to the local horizontal at which the panels are mounted $\theta$; and the azimuthal angle of the panels to the meridian $\Psi$. The way the effective PCE is affected by these is derived geometrically in Section 2.4 to find an overall obliquity factor suitably averaged through the day and year and, for roof-mounted arrays, through the random distribution of $\Psi$.

For all calculations involving roof-mounted PVs, the insolation data and statistics on the roof area and energy consumption that have been used are those for the UK or London. The key aspects of the city’s built environment and energy utilisation have been widely and recently surveyed and publicly reported. Also, London typifies the modern mega-city with its high population density. Its temperate climate is fairly typical for the developed world [10], and its latitude is similarly typical of large population centres, resulting in the key obliquity factors that emerge from the analysis outlined above also being representative of the environments where much of the world’s energy is being consumed.

Our calculations are idealised and are intended for discussion purposes. To this end, at all points where assumptions must be made, we do so in a way that would generate an underestimation of the actual PCE required, even if the degree of underestimation this introduces may be quite significant.

We assume that roof coverage is as complete as practically possible (see Section 2.3.2) and that all the panels are mounted on roofs that are optimally inclined to the horizontal plane (Section 2.4.1).

As is discussed more thoroughly in Section 2.3.2, we had to assume that the statistics for flat dwellers should be processed by assuming that all apartment blocks were only 2 storeys high. In reality of course, many are much taller, and the share of the roof area available to each flat dweller is much lower as a result. Thus, this assumption means that our calculations were likely to considerably overestimate the PV generation capacity in cities.

We also assumed that none of the generated energy was lost in either the storage or transmission schemes (see Section 2.2).

These issues are commercially and politically sensitive to the point where accessing reliable, unbiased data for analytical studies is problematic. However, by setting our definition of “significance” to only 15% (i.e., rather less than the 60% used by the non-transport sector), we aimed to sidestep these complications by making our conclusions largely independent of what might happen to the transport sector in the future.

2.2. Factors Surrounding the “Perfect Storage” Assumption

In all our calculations, we assumed that no energy generated by a PV system went to waste. For this idealisation to be the case, it must be possible to store any excess energy with no losses for later use when there is a generation deficit. Using the 15% contribution figure for discussion makes this a more practical proposition if one assumes that the overall energy-generating system contains flexible elements whose generating capacity can be switched in and out as the generating capacity of the PV component fluctuates. However, the issue would become progressively more challenging if PVs were to aim for higher contribution levels.

This issue is quantified in the Supplementary Materials, where we show that a PV system able to generate a 15% contribution annually may be limited over winter to a contribution as low as ~3% but become >30% at times over summer. This means other sources would need to provide up to 97% in winter but only ~70% in summer.

At higher assumed contribution values, storage issues become relevant because the installed capacity required could, in principle, generate more energy in summer than the UK could consume. The excess could be exported or stored. If one assumes that the latter is performed with today’s best battery technology, lithium-ion, then the recovery efficiency is ~80% [11,12], and there is a loss due to self-discharging of ~3% per month [13]. Taking these effects into account, storing enough energy for six months to cope with seasonal variations would increase the corresponding mPCEs by a factor of 1.5. This is a combination of a 1.25 factor due to the finite energy efficiency and a further factor of 1.2 to account for six months of self-discharge at 3% per month.

2.3. Data Collection

Wherever possible, the data used in the calculations were sourced from official documents such as government reports and statistical tables, and uncertainties were taken from standard deviations or estimated from the data available. To be able to perform the analysis, we required data for the insolation that reached the surface of Earth, the energy consumption of the UK (as a whole and for individual households), and the available rooftop area that could be used to mount solar panels.

2.3.1. Energy: Insolation and Consumption

Insolation data were sourced from NASA’s Projection Of Worldwide Energy Resources (POWER) [14], which provides insolation data at a given location to 0.5° precision in terms of both latitude and longitude. The data were a daily average for each calendar month of all sky insolation on a horizontal surface using solar climatological datasets which covered the period from July 1983 to June 2005 [14].

Data for the total annual energy consumption in the UK were taken from the Department for Business, Energy & Industrial Strategy’s (DBEIS’s) Energy Consumption in the UK (ECUK) 2018, using 2017 data [15]. For calculations that separated homes by the type of dwelling, we used the average annual household consumption from ECUK [15] and scaled it using electricity data taken from the Household Electricity Survey [16].

2.3.2. Available Roof Area

The available roof area was taken from the Energy Saving Trust (EST) [17], which provides values for a selection of different types of homes. The values given by the EST use dwelling footprints from a report by the BRE Group on behalf of the Department of the Environment, Transport and the Regions [18] and then assume each has a pitched roof with a slope of 30°, meeting in the middle. They assumed that solar panels can be mounted on only one half of the roof, with a further 20% of it being unsuitable. This is shown in Figure 1. We adjusted the resulting areas quoted by the EST by a factor of $\mathrm{c}\mathrm{o}\mathrm{s}(30°)$ to find the horizontal cross-sectional area (HCSA), which is the cross-sectional area as viewed from directly above. This could then be used in conjunction with the insolation data from NASA POWER, which are for a horizontal surface [14].

The roof area provided by the EST for a flat was 28 m² (giving an HCSA of 24.2 m²) and was for a “top floor flat” [17]. We took half that value, as the term “top floor” implies the existence of at least one flat below this one, and the available roof area should be split equally between them. As such, we estimated an increased uncertainty in the HCSA for the flat relative to the other types of homes. In the absence of any further information, for discussion purposes, we must assume that only one flat exists below the top floor, but this means that all the estimates of roof areas available to flat dwellers are likely to be significant overestimates, and the calculations would be strongly biased in favour of lower mPCE estimates.

Flats make up a large fraction of all households in large cities (~44% in London in 2011 [19]), and any overestimate in the roof area estimates for a flat will translate to an overestimate by a factor of around half as much for the roof area values for an average home. With blocks of flats often standing at more than three storeys and tower blocks having storeys in the double figures, the roof area per flat was probably quite significantly less than the calculation assumed, but this would be offset by the fact that the calculation ignored the roof areas that might have been available on commercial properties (see Section 3.1).

2.3.3. Solar Farms and Today’s PCEs

Further data that we researched included the locations of existing solar farms in the UK. We considered the five largest by declared net capacity [20]. The coordinates for each were taken from Google Maps [21,22,23,24,25] using the addresses provided by Ofgem [20]. We input these coordinates into NASA POWER [14] and used the location of that which received the highest annual insolation for our calculations of a theoretical solar farm.

Finally, in order to estimate the capability of the solar technology that is currently available, we used six independent web pages that purport to list the most efficient solar panels on the market. The highest reported PCEs ranged from 21.5% to 23.8% [26,27,28,29,30,31]. In this investigation, we took the highest value of 23.8%, as this provided the most optimistic results for today’s technology and therefore challenged our hypothesis most strongly. This value of 23.8% is hereafter referred to as PCE_NOW.

2.4. Geometrical Factors

2.4.1. The Obliquity Factor from Solar Panel Orientation

The theoretically ideal orientation of a solar panel—assuming its orientation is fixed—is to mount it at an angle to the horizontal that is equal to the latitude of its location and to have it aligned meridionally, facing the equator. This would mean that the incident solar rays, on average over the course of the year, are normally incident on the panel, and thus the cross-sectional area of the panel is maximised. However, this is not always practical. Especially for roof-mounted solar panels, the angle to the horizontal, and indeed the azimuthal angle to the meridian, are generally fixed by the slope of the roof and the orientation of the house, respectively.

For a solar panel at a location with latitude $\phi$, the average angle to the horizontal of incoming solar rays over the course of the year is ($90°-\phi$). On top of this, the cross-sectional area of the solar panel that collects sunlight also depends upon the angle of the panels to the horizontal θ and the azimuthal angle to the meridian $\Psi$. Figure 2 illustrates this. By taking the inner product of the vectors labelled $\stackrel{⃑}{A_0}$ and $\stackrel{⃑}{\gamma }$ in Figure 2—the normal to the surface of the panel and the average trajectory of incident sunlight, respectively—the cross-sectional area seen by incident sunlight was found to be multiplied by an obliquity factor $f_{Obl}(\phi ,\theta ,\Psi )$, given by

$$\begin{array}{ll}{f}_{Obl}\left(\phi ,\theta ,\Psi \right)& =\stackrel{⃑}{A_0}·\stackrel{⃑}{\gamma }\\ & =\mathrm{s}\mathrm{i}\mathrm{n}\left(\phi \right)\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\Psi \right)+\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right).\end{array}$$

(1)

In this study, we assumed that the orientations of houses in the UK were randomly distributed, and thus we averaged this over the appropriate range of azimuthal angles (i.e., $\Psi \in [0,\frac{\pi }{2}]$). The obliquity factor that emerged is then given by

$$f_{tilt}\left(\phi ,\theta \right)=\frac{\frac{2}{\pi }\sin \left(\phi \right)\sin \left(\theta \right)+\cos \left(\phi \right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right)}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)},$$

(2)

where the $\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)$ in the denominator is a normalisation factor such that $f_{tilt}\left(\phi ,0\right)=1$, meaning the cross-sectional area of the panels when lying flat is unchanged by the obliquity factor. Taking the latitude of London to be $\phi =$51.5072° [32], the obliquity factor $f_{tilt}(\phi ,\theta )$—and therefore the insolation received—was maximised to a value of 1.281 for a roof incline of 39°.

If it is possible to align the azimuthal angle directly with the meridian—as would be the case for a free-standing array of solar panels in a solar farm—then the normalised obliquity factor relative to a flat panel is given instead by

$$f_{tilt}^{\Psi =0}\left(\phi ,\theta \right)=\frac{\mathrm{c}\mathrm{o}\mathrm{s}(\phi -\theta )}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)},$$

(3)

which peaks when $\theta =\phi$, giving a value of $f_{tilt}^{\Psi =0}\left(\phi \right)=\frac{1}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)}.$

2.4.2. Separation of Rows of Solar Panels

Figure 3 illustrates the effect of tilting solar panels in rooftop and free-standing solar arrays, also highlighting the effect on the space needed between rows of solar panels in a farm. In large-scale solar arrays that have multiple rows of solar panels, tilting the panels at a steeper angle means they must be spaced further apart in order to minimise the shadows cast by one row of panels on the next (Figure 3c). This is not a problem for roof-mounted arrays, which generally comprise just one row, meaning shadows cast by the panels are irrelevant (Figure 3b).

For a solar farm, the value of the panel spacing is labelled $x$ in Figure 3c. When the panels are laid flat (i.e., at $\theta =0$), this is simply equal to the length of the panels $D$. However, when setting $\theta =\phi$ in order to minimise the amount of material needed (see Supplementary Materials), the separation $x$ is changed by a factor $f_{sep}\left(\phi \right)$, given by

$$\begin{array}{cc}\hfill f_{sep}\left(\phi \right)& =\frac{x}{D}\hfill \\ \hfill & =\cos \left(\phi \right)+\frac{\sin \left(\phi \right)}{\tan \left(90°-\phi \right)}\hfill \\ \hfill f_{sep}\left(\phi \right)& =\frac{1}{\mathrm{c}\mathrm{o}\mathrm{s}\left(\phi \right)} \equiv f_{tilt}^{\Psi =0}\left(\phi \right),\hfill \end{array}$$

(4)

as illustrated in Figure 3c. This shows that the factor by which the necessary separation of successive rows increases $f_{sep}\left(\phi \right)$ is the same as the factor by which received insolation increases $f_{tilt}^{\Psi =0}\left(\phi \right)$. This result means that tilting the panels in a solar farm does not affect the amount of land area needed to generate a given amount of energy. The spatial efficiency—a measure of the amount of flat land area required to generate a given amount of power for a fixed PCE and fixed insolation on a horizontal surface of an array of consecutive rows of solar panels—is independent of the angle at which the solar panels are tilted to the horizontal.

Note that due to the integral nature of the number of rows of solar panels in a solar farm, this result is not always exact, but the variations for large numbers of rows are small; variations are <1% at all latitudes < 69° for ≥250 rows. With 99% of the world’s population living within 60° of the equator [33] and the areas involved in these calculations necessitating many rows, this formula is considered to be exact in this paper. More details on the exact variations are given in the Supplementary Materials.

2.5. Weighted Mean Energy Consumption per Unit Area by House Type

Despite the 28 m² given by the EST [17], the roof area that corresponds to a single flat is likely to be smaller even than the 14 m² used here, as blocks of flats are often several stories high, especially in crowded cities. The 2011 census showed that almost half of all households in London were flats at that time [19], meaning the data for flats are especially important in reaching the value for the average home.

Indeed, we calculated the values for an average home in the UK using a weighted mean consumption per unit HCSA, as shown in

Table 1. Calculating the weighted mean total annual energy consumption for homes in London. The energy consumption of each home type has been upscaled to account for all sectors, rather than just the domestic sector. (The total value is not upscaled, as the weighted fractional value is simply the sum of the constituent parts).

House Type	Number in London (2011) [19]	Upscaled Energy Consumption (kWh/m2)	Weighted Fractional Consumption (kWh/m2/yr)
Terrace	756,988	2730	740
Semi-detached	617,647	3400	750
Detached	205,422	2490	180
Flat	1,219,534	3570	1560
—Total—	2,799,591	—	3229 ± 1004

.

The energy consumptions found for different types of homes using the HES [16] and the ECUK [15] gave values for domestic energy use. The domestic sector makes up ~30% of the total energy consumption in the UK [15], and in order to account for the total energy needs of the UK, these values are upscaled using the ratio of the UK’s total annual energy consumption in all sectors (141 ktoe [15]) to that in the domestic sector (40 ktoe [15]). The upscaled value is that which is included in Table 1.

We then divided the upscaled consumption values by the HCSA for each type of dwelling and weighted them using the number of households of each type, as given by the Census Information Scheme for the 2011 census [19]. The resulting values were then summed to find a weighted mean annual energy consumption per unit of HCSA.

The same method was used to calculate a weighted mean HCSA for the calculation in Section 3.2 of the amount of solar panel material that would be needed to install panels on every domestic rooftop in the UK.

3. Results and Discussion

3.1. Contribution from Today’s Best Roof-Mounted Solar Panels

We considered first a scenario with solar panels covering the roofs of every home in the country in order to achieve a grid-level generation capacity that produced a significant contribution. We did not consider commercial and industrial rooftops, as these buildings are generally not only more densely built (using a smaller area per occupant) but also generally have more storeys, and their roofs are often used to site plant. These issues all result in a small available roof area per occupant. For rooftop calculations, we used the obliquity factor $f_{tilt}(\phi ,\theta )$ from Equation (2) to multiply the insolation data from NASA POWER [14] and took $\phi$ = 51.5° from [32].

We supposed that all domestic roofs were covered as fully as possible with solar panels of PCE equal to PCE_NOW. We calculated the power that could be generated by the different classes of dwelling, which gave a contribution scaled with the average consumption of each type of home. We then calculated the contribution for an average home by taking a weighted mean of the annual consumption per unit area (as detailed in Section 2.5).

The results by type of home and for the average home are shown in

Table 2. The contribution, calculated separately for each dwelling type, that could be generated by roof-mounted solar panels of the highest efficiency that was available to buy at the time of writing (23.8% [26,27,28,29,30,31]). Values are given for an optimal 39° roof incline, and we assumed that all the energy generated could be used without any losses. Uncertainties were propagated using the standard deviation or estimated errors from the sources. Note that the available data did not record the storey heights of apartment blocks, and thus the values for the flat were calculated by assuming that the total roof area was only divided by two. This is the most optimistic possible estimate of the contribution and is likely to be a considerable overestimate.

House Type	Contribution Available from Panels with 23.8% PCE
Terrace	11 ± 2%
Semi-detached	9 ± 2%
Detached	12 ± 2%
Bungalow	14 ± 3%
Flat	9 ± 4%
Average Home	9 ± 3%

, where we assumed the roof pitch to be the optimal 39° (see Section 2.4.1) for the latitude of London.

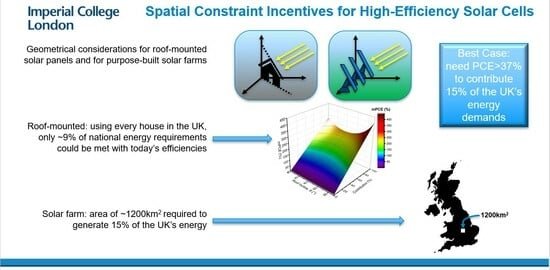
These contributions show that, in this idealisation, the average home could generate a contribution of up to ~9%. This is likely to be a considerable overestimate due to all the assumptions that we made favouring high contributions. We estimated that on average, the effective available roof area per flat might have been another factor of two (i.e., corresponding to a mean block height of four floors), lower than the 14 m² used here. This would mean a 50% change in the values for the average home. Combining this with the assumptions of perfect storage and an optimal roof incline, we believe that the contribution for PCE_NOW was more likely to be ⪅5%.

3.2. mPCEs for Roof-Mounted PVs to Provide a 15% Contribution

We repeated the calculations above, first constraining the contribution and then determining the corresponding mPCEs that would be required to achieve them. The results for the average home are shown in Figure 4a as a function of both the roof pitch and contribution. Figure 4b shows a cross-section of this at a fixed roof pitch of 39°, the angle corresponding to the lowest mPCEs. The shaded region in Figure 4b shows the uncertainty.

In this case, we can see that to generate a contribution of 15%, a PCE of ~37% would be required, which is in excess of the S-Q limit of ~33%. If the PCE were equated to the S-Q limit, then a contribution of ~13% might be generated. However, these values again correspond to the highly optimistic idealised case, with the additional assumption here that all roofs were optimally pitched.

In order to gauge the feasibility of mounting solar panels on all domestic roofs in the UK, we should also consider the quantity and area of the solar panel material that would be needed. The mean available roof area weighted by the number of dwelling types was found to be ~15 m². This is the HCSA, while the area of the material actually depends on the absolute area of the inclined roof. Assuming a pitch of 39°, this was ~19.5 m². Taking the number of households in the UK to be 28 million (according to a recent government report [15]), this gave a total panel area of ~550 km².

Clearly, this would be a major undertaking. One would hope that there would be quite significant economies of scale, and because of this, present day comparisons based on cost-per-watt estimates for PV technologies must be treated with extreme caution. There is the risk that premature costing exercises could unwittingly rule out research into high-PCE approaches that in fact have the better long-term likelihood of producing a significant contribution to carbon mitigation.

3.3. The Area Needed for a Single Solar Farm in the UK

An alternative to roof-mounted solar arrays is to construct a number of large-scale solar farms. Here, we calculate the land area that would have to be dedicated to a solar farm as a function of contribution using solar panels of PCE_NOW. In this calculation, we supposed that the panels, if tilted, were built facing meridionally south ($\Psi =0$). We therefore used the obliquity factor $f_{tilt}^{\Psi =0}(\phi ,\theta )$ from Equation (3) in Section 2.4.1. The results are shown in Figure 5, where the shaded area represents an estimate of uncertainty, the main source of which in this case is the energy consumption data.

The calculation was straightforward, with the result being that over 1200 km² of new land area would have to be dedicated to solar panels to produce enough energy to fulfil 15% of the energy needs of the UK. As a percentage of the nation’s area, this is small, yet it corresponds to a land area that is comparable to the size of Greater London [34] and would most likely be impossible to implement either politically or logistically. That said, in this scenario, even small improvements in PCE correspond to large savings in land area. For example, if the PCE were raised from PCE_NOW by one percentage point (from 23.8% to 24.8%), the area needed for a 15% contribution would decrease by ~50 km², roughly the size of a large county town in the UK.

These land area values were unaffected by the tilt of the solar panels according to the constant nature of the spatial efficiency, a concept discussed in Section 2.4.2. If the panels were laid flat, then the area of the solar panel material would be the same as the land area (i.e., ~1200 km²). However, if they were tilted at 52° to the south, this would be reduced by a factor of ~38%, meaning ~750 km² of panel material would be needed for the 1200 km² farm that would be capable of generating a 15% contribution.

This is ~250 km² more material than would be needed to cover all the UK’s domestic roofs, and this difference arose from two factors. First, this calculation assumed that the farm was in fact large enough to generate a 15% contribution, whereas there was only enough roof area to generate a ~9% contribution using the same PCE. Secondly, the obliquity factors were different for the two cases because the orientation of the panels $\Psi$ could be optimised in the farm but was dictated by the spread of house orientations for the rooftop case. There are further details on this calculation in the Supplementary Materials.

4. Conclusions

Here, we attempted to calculate the fraction of the UK’s energy consumption that could be generated by the best PV technology currently available, factoring in the key consideration of where the panels could realistically be deployed.

This calculation was, necessarily, highly idealised, and it certainly overestimated the possible contribution that today’s PV technology could make. A separate version of this study with more realistic considerations could be of interest in the future. We found that the most efficient solar panels available today, if installed on every domestic roof in the UK, would be able to produce up to ~9% of the UK’s energy. Due to the assumptions made in this analysis, particularly the assumption regarding the roof area available to every flat dweller, we believe that a more realistic figure is less than ~5%.

Using the same generous assumptions, we found that the PCE would need reach values of at least ~37% for roof-mounted solar PVs to contribute 15% of the UK’s energy needs. The same caveats over the available roof area of apartment buildings apply as above, and the real PCEs needed would likely be rather larger still. This already exceeds the Shockley–Queisser theoretical limit of 33% and will only become possible with so-called “third-generation” PV technologies.

Many such technologies employ multi-bandgap and other quantum engineering approaches to circumvent the shortcomings of the single-junction devices that were considered in calculating this limit [5,35,36,37,38,39,40,41,42,43,44,45]. Alternative approaches include hot carrier devices, which increase the photovoltage by harvesting charge carriers before they can thermalise [46,47], and the use of concentrator modules to increase the amount of light collected by a solar converter, which can lead to the required efficiencies but comes at increased cost and complexity, and it causes the devices to operate at high temperatures [48,49,50]. All such devices and systems are in the research stage and require further investigation and development to be brought to commercial realisation.

We determined that approximately 1200 km², an area comparable to the size of Greater London, would be needed for a solar farm to generate 15% of the UK’s energy using the most efficient solar panels currently available.

Our broad conclusion is that independent of the commonly used “dollar-per-watt” economic metric, if solar PVs are to become a significant part of any carbon mitigation strategy, then research and development programmes must target a raw increase in PCEs. Not only are values required that are beyond those currently available, but they are also well beyond the Shockley–Queisser limit of single-bandgap approaches.