Limits of Harmonic Stability Analysis for Commercially Available Single-Phase Inverters for Photovoltaic Applications
Abstract
:1. Introduction
2. The State of the Art
2.1. Low-Voltage Network Model
2.2. Inverter Model
2.2.1. White-Box Model
2.2.2. Gray-Box Model
2.2.3. Black-Box Model
2.2.4. Measurement-Based Identification
2.3. Harmonic Stability Analysis
3. Limits of Harmonic Stability Assessment
3.1. Theoretic Considerations
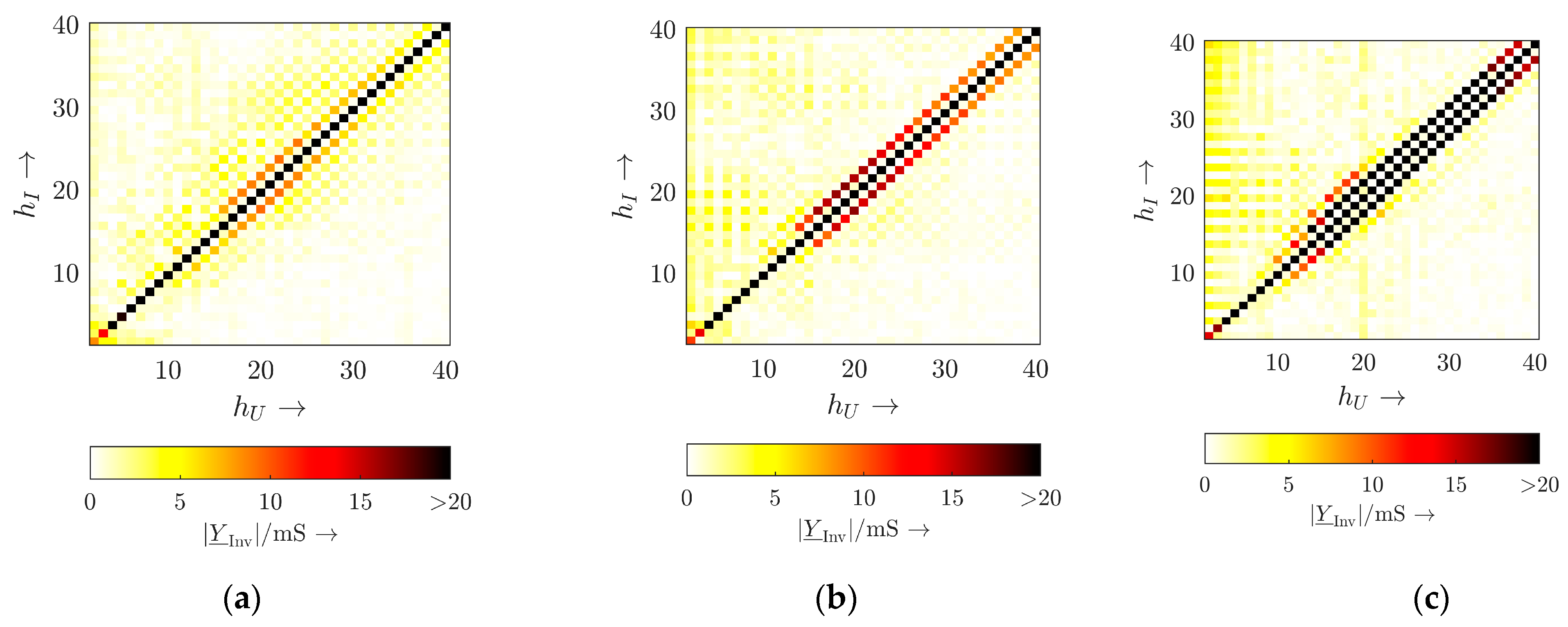
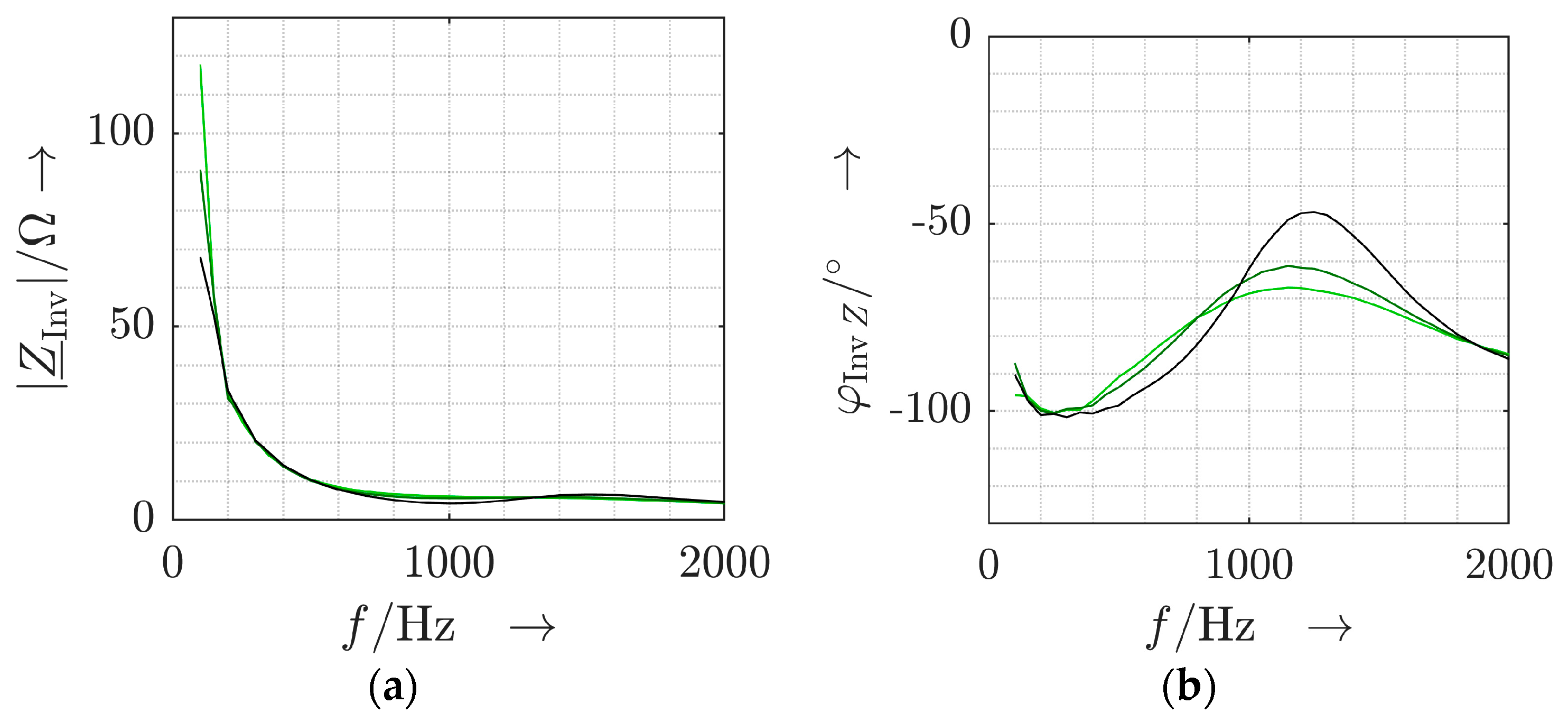
3.2. Measurement-Based Identification of Small-Signal Characteristics
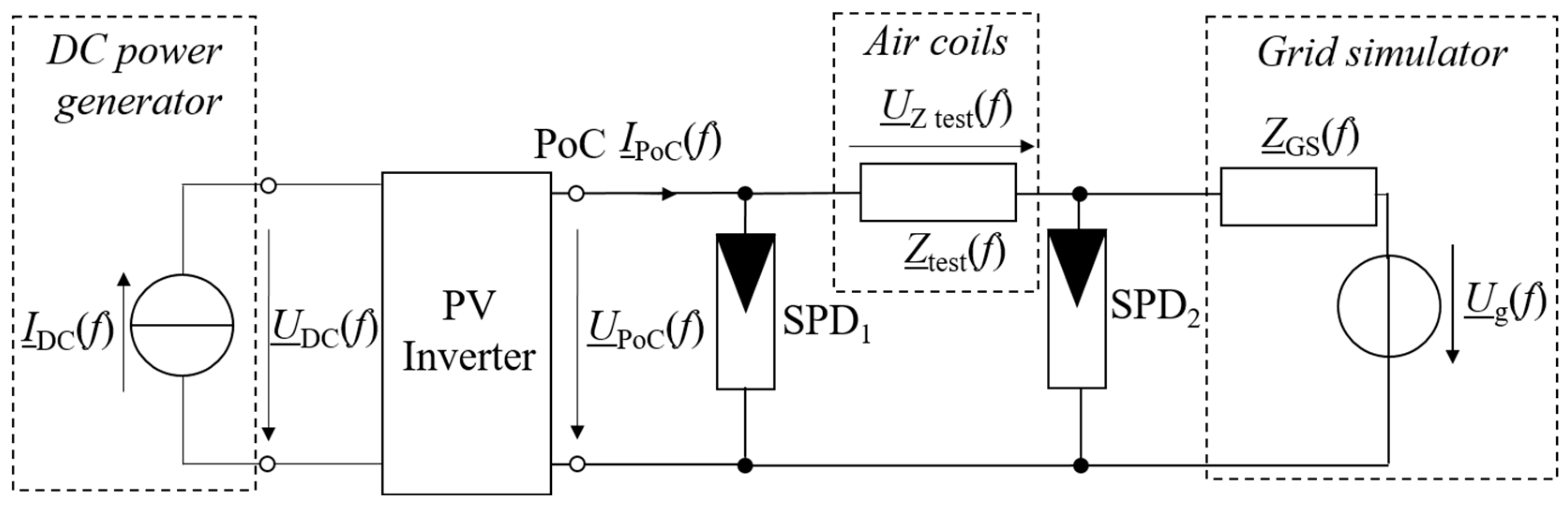
3.2.1. Measurement Setup
3.2.2. Measurement Results
3.3. Measurement-Based Evaluation of Stable Operation
3.3.1. Measurement Setup
Test Stand Configuration
Measurement Scenarios
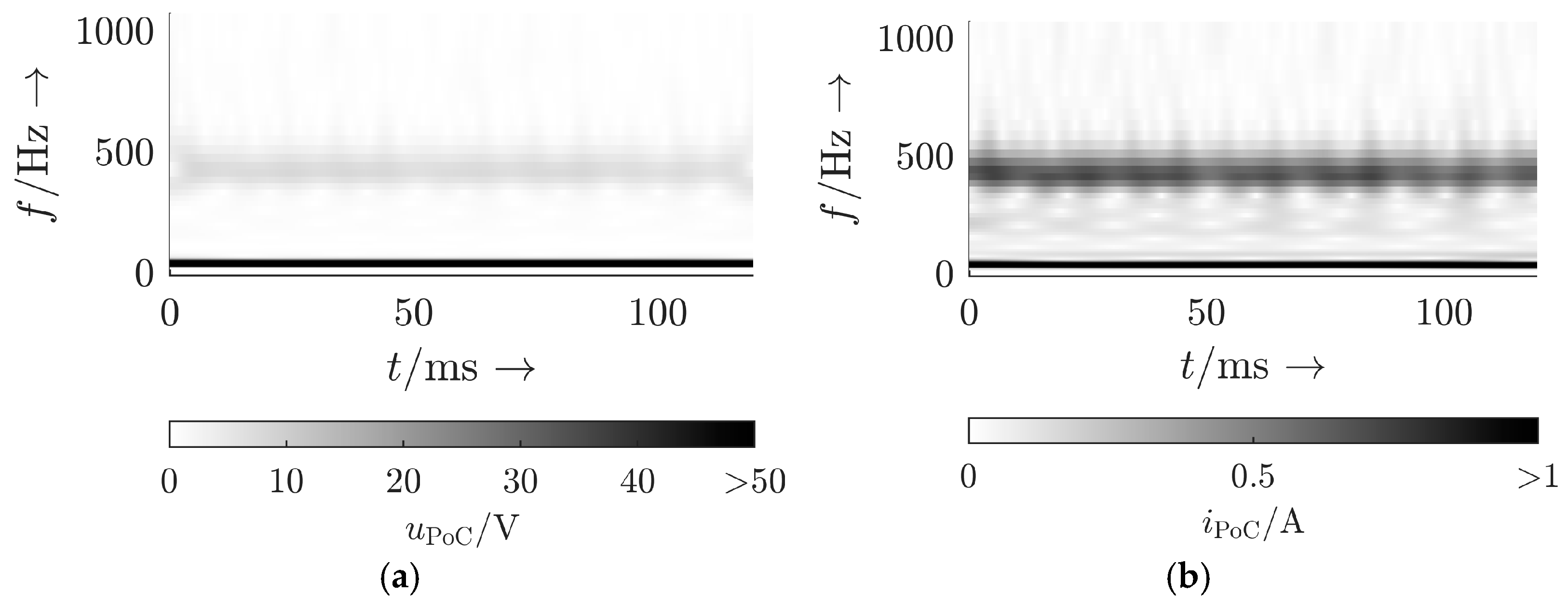
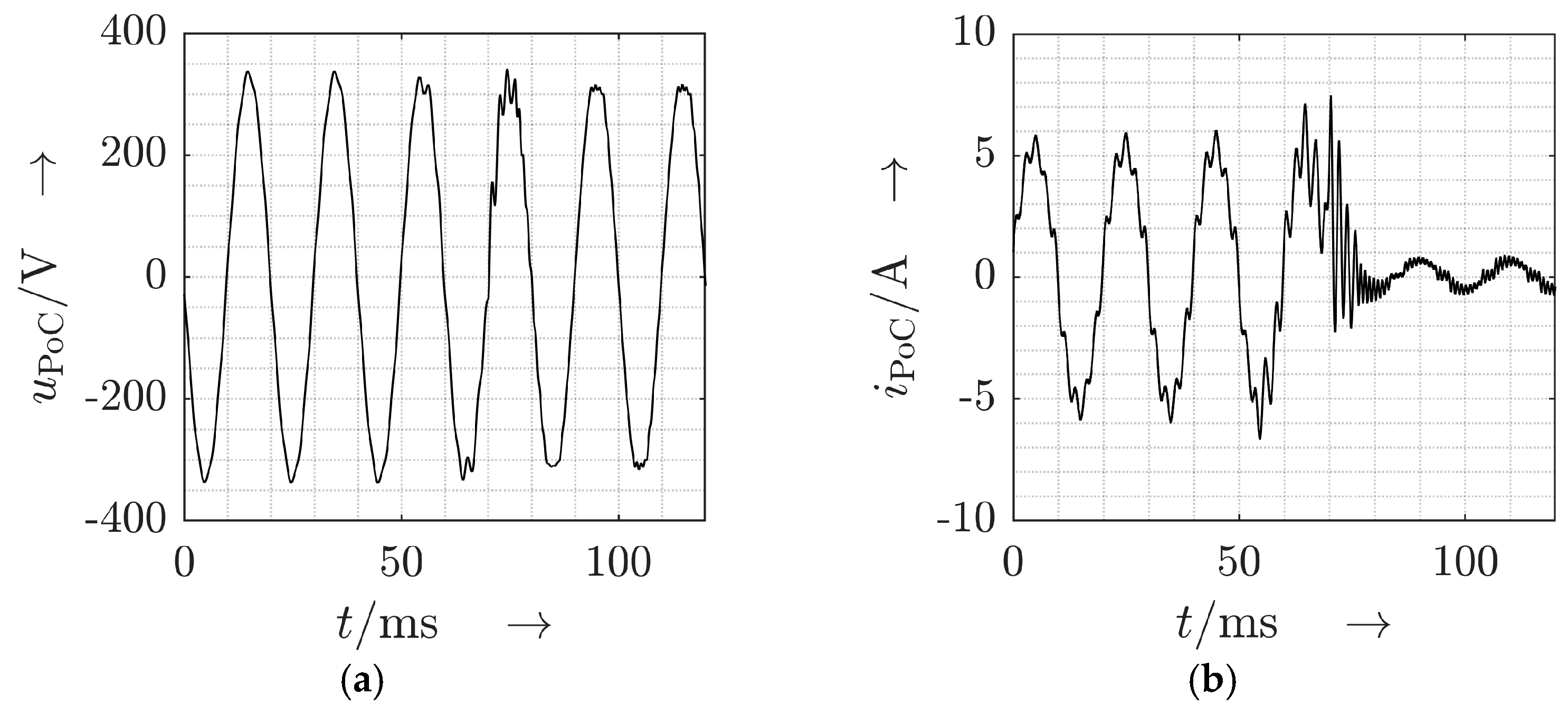
3.3.2. Measurement Results
3.3.3. Measurement Result Categorization
3.3.4. Measurement Evaluation
4. Discussion
4.1. Network Impedance
4.2. Background Distortion
4.3. General Assessment Framework
5. Conclusions
5.1. Summary
5.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- REN21 Renewables 2022 Global Status Report 2022. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2022_Full_Report.pdf (accessed on 14 July 2024).
- IEC 61000-3-2:2018; Electromagnetic Compatibility (EMC)—Part 3-2: Limits—Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A per Phase). IEC: Geneva, Switzerland, 2018.
- IEC 61000-3-12:2011; Electromagnetic Compatibility (EMC)—Part 3-12: Limits—Limits for Harmonic Currents Produced by Equipment Connected to Public Low-Voltage Systems with Input Current > 16 A and ≤ 75 A per Phase. IEC: Geneva, Switzerland, 2011.
- IEC TS 61000-3-16:2023; Electromagnetic Compatibility (EMC)-Part 3-16: Limits—Limits for Harmonic Currents Produced by the Inverter of Inverter-Type Electrical Energy-Supplying Equipment, with a Reference Current Less than or Equal to 75 A per Phase. IEC: Geneva, Switzerland, 2023.
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Möllerstedt, E.; Bernhardsson, B. Out of Control Because of Harmonics-an Analysis of the Harmonic Response of an Inverter Locomotive. IEEE Control Syst. 2000, 20, 70–81. [Google Scholar] [CrossRef]
- Enslin, J.H.R.; Heskes, P.J.M. Harmonic Interaction Between a Large Number of Distributed Power Inverters and the Distribution Network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Höckel, M.; Gut, A.; Arnal, M.; Schild, R.; Steinmann, P.; Schori, S. Measurement of Voltage Instabilities Caused by Inverters in Weak Grids. CIRED-Open Access Proc. J. 2017, 2017, 770–774. [Google Scholar] [CrossRef]
- Moghbel, M.; Glenister, S.; Calais, M.; Shahnia, F.; Carter, C.; Edwards, D.; Stephens, D.; Jones, L.; Trinkl, P. Fluctuations in the Output Power of Photovoltaic Systems Distributed Across a Town with an Isolated Power System Using High-Resolution Data. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, Australia, 10–12 December 2019; pp. 1–5. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Lin, B.H.; Tsai, J.T.; Lian, K.L. A Non-Invasive Method for Estimating Circuit and Control Parameters of Voltage Source Converters. IEEE Trans. Circuits Syst. I Regul. Pap. 2019, 66, 4911–4921. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Schegner, P. Black-Box Identification of Grid-Side Filter Circuit for Improved Modelling of Single-Phase Power Electronic Devices for Harmonic Studies. Electr. Power Syst. Res. 2021, 199, 107421. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Schegner, P. Transient Response of Single-Phase Photovoltaic Inverters to Step Changes in Supply Voltage Distortion. In Proceedings of the 2020 19th International Conference on Harmonics and Quality of Power (ICHQP), Dubai, United Arab Emirates, 6–7 July 2020; IEEE: Dubai, United Arab Emirates, 2020; pp. 1–6. [Google Scholar]
- Gabor, D. Theory of Communication. Part 1: The Analysis of Information. J. Inst. Electr. Eng.-Part III Radio Commun. Eng. 1946, 93, 429–441. [Google Scholar] [CrossRef]
- Kaufhold, E.; Grandl, S.; Meyer, J.; Schegner, P. Feasibility of Black-Box Time Domain Modeling of Single-Phase Photovoltaic Inverters Using Artificial Neural Networks. Energies 2021, 14, 2118. [Google Scholar] [CrossRef]
- Patcharaprakiti, N.; Kirtikara, K.; Chenvidhya, D.; Monyakul, V.; Muenpinij, B. Modeling of Single Phase Inverter of Photovoltaic System Using System Identification. In Proceedings of the 2010 Second International Conference on Computer and Network Technology, Bangkok, Thailand, 23–25 April 2010; pp. 462–466. [Google Scholar]
- Wiesermann, L.M. Developing a Transient Photovoltaic Inverter Model in Opendss Using the Hammerstein-Wiener Mathematical Structure. Ph.D. Thesis, University of Pittsburgh, Pittsburgh, PA, USA, 2017. [Google Scholar]
- Hall, S.R.; Wereley, N.M. Generalized Nyquist Stability Criterion for Linear Time Periodic Systems. In Proceedings of the 1990 American Control Conference, San Diego, CA, USA, 23–25 May 1990; pp. 1518–1525. [Google Scholar]
- Cobben, S.; Kling, W.; Myrzik, J. The Making and Purpose of Harmonic Fingerprints. In Proceedings of the 19th International Conference on Electricity Distribution, Vienna, Austria, 21–24 May 2007; pp. 21–24. [Google Scholar]
- Fauri, M. Harmonic Modelling of Non-Linear Load by Means of Crossed Frequency Admittance Matrix. IEEE Trans. Power Syst. 1997, 12, 1632–1638. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Myrzik, J.; Schegner, P. Harmonic Stability Assessment of Commercially Available Single-Phase Photovoltaic Inverters Considering Operating-Point Dependencies. Solar 2023, 3, 473–486. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill, Inc.: New York, NY, USA, 1994; p. 1176. [Google Scholar]
- Salis, V.; Costabeber, A.; Cox, S.M.; Zanchetta, P. Stability Assessment of Power-Converter-Based AC Systems by LTP Theory: Eigenvalue Analysis and Harmonic Impedance Estimation. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1513–1525. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Salis, V.; Costabeber, A.; Cox, S.M.; Tardelli, F.; Zanchetta, P. Experimental Validation of Harmonic Impedance Measurement and LTP Nyquist Criterion for Stability Analysis in Power Converter Networks. IEEE Trans. Power Electron. 2019, 34, 7972–7982. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Schegner, P. Impact of Grid Impedance and Their Resonance on the Stability of Single-Phase PV-Inverters in Low Voltage Grids. In Proceedings of the 2020 IEEE 29th International Symposium on Industrial Electronics (ISIE), Delft, The Netherlands, 17–19 June 2020; pp. 880–885. [Google Scholar]
- Kaufhold, E.; Meyer, J.; Müller, S.; Schegner, P. Probabilistic Stability Analysis for Commercial Low Power Inverters Based on Measured Grid Impedances. In Proceedings of the 2019 9th International Conference on Power and Energy Systems (ICPES), Perth, Australia, 10–12 December 2019; pp. 1–6. [Google Scholar]
- Langella, R.; Testa, A.; Meyer, J.; Moller, F.; Stiegler, R.; Djokic, S.Z. Experimental-Based Evaluation of PV Inverter Harmonic and Interharmonic Distortion Due to Different Operating Conditions. IEEE Trans. Instrum. Meas. 2016, 65, 2221–2233. [Google Scholar] [CrossRef]
- IEC 61000-4-13:2002; Electromagnetic Compatibility (EMC)—Part 4-13: Testing and Measurement Techniques—Harmonics and Interharmonics Including Mains Signalling at a.c. Power Port, Low Frequency Immunity Tests. IEC: Geneva, Switzerland, 2002.
- EN 50160:2022; Voltage Characteristics of Electricity Supplied by Public Electricity Networks. Cenelec: Brussels, Belgium, 2022.
- IEC 61000-2-2:2002; Electromagnetic Compatibility (EMC)—Part 2-2: Einvironment—Compatibility Levels for Low-Frequency Conducted Disturbances and Signalling in Public Low-Voltage Power Supply Systems. IEC: Geneva, Switzerland, 2002.
- Kaufhold, E.; Duque, C.A.; Meyer, J.; Schegner, P. Measurement-Based Black-Box Harmonic Stability Assessment of Single-Phase Power Electronic Devices Based on Air Coils. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Kaufhold, E.; Meyer, J.; Myrzik, J.; Schegner, P. Framework to Assess the Stable Operation of Commercially Available Single-Phase Inverters for Photovoltaic Applications in Public Low Voltage Networks. Renew. Energy Power Qual. J. 2023, 21, 214–219. [Google Scholar] [CrossRef]



| Operating Power | Inductance Value @1 kHz | Operation Status | |
|---|---|---|---|
| Sinusoidal Voltage | Flat-Top Voltage (and Pointed-Top) | ||
| 1 kW | 3785 µH | Stable | Stable |
| 3943 µH | Stable | Instable | |
| 4112 µH | Instable | - | |
| 2.5 kW | 3785 µH | Stable | Stable |
| 3943 µH | Instable | - | |
| 4112 µH | Instable | - | |
| 4.5 kW | 1625 µH | Stable | Stable |
| 1908 µH | Stable | Instable | |
| 2385 µH | Instable | - | |
| Cate-Gory | Stability Statement | Type of Instability | Voltage Waveform | Specifications | |
|---|---|---|---|---|---|
| 1 | Stable | - | Sinusoidal | - | |
| Flat-top | - | ||||
| Pointed-top | - | ||||
| 2 | A | Instable | Steady state | Sinusoidal | - |
| Flat-top | - | ||||
| B | Instable | Transient | Sinusoidal to flat-top | Shut down when changing the background voltage | |
| C | Instable | Unspecified | Sinusoidal | Not reaching the intended operating point before shutting down | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaufhold, E.; Meyer, J.; Myrzik, J.; Schegner, P. Limits of Harmonic Stability Analysis for Commercially Available Single-Phase Inverters for Photovoltaic Applications. Solar 2024, 4, 387-400. https://doi.org/10.3390/solar4030017
Kaufhold E, Meyer J, Myrzik J, Schegner P. Limits of Harmonic Stability Analysis for Commercially Available Single-Phase Inverters for Photovoltaic Applications. Solar. 2024; 4(3):387-400. https://doi.org/10.3390/solar4030017
Chicago/Turabian StyleKaufhold, Elias, Jan Meyer, Johanna Myrzik, and Peter Schegner. 2024. "Limits of Harmonic Stability Analysis for Commercially Available Single-Phase Inverters for Photovoltaic Applications" Solar 4, no. 3: 387-400. https://doi.org/10.3390/solar4030017







