Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN †
Abstract
:1. Motivating Precise Energy Scale Calibration in LArTPCs
2. Cosmic Muons as a Standard Candle
2.1. Uncertainties on the Energy Scale
3. Energy Scale Calibration Procedure
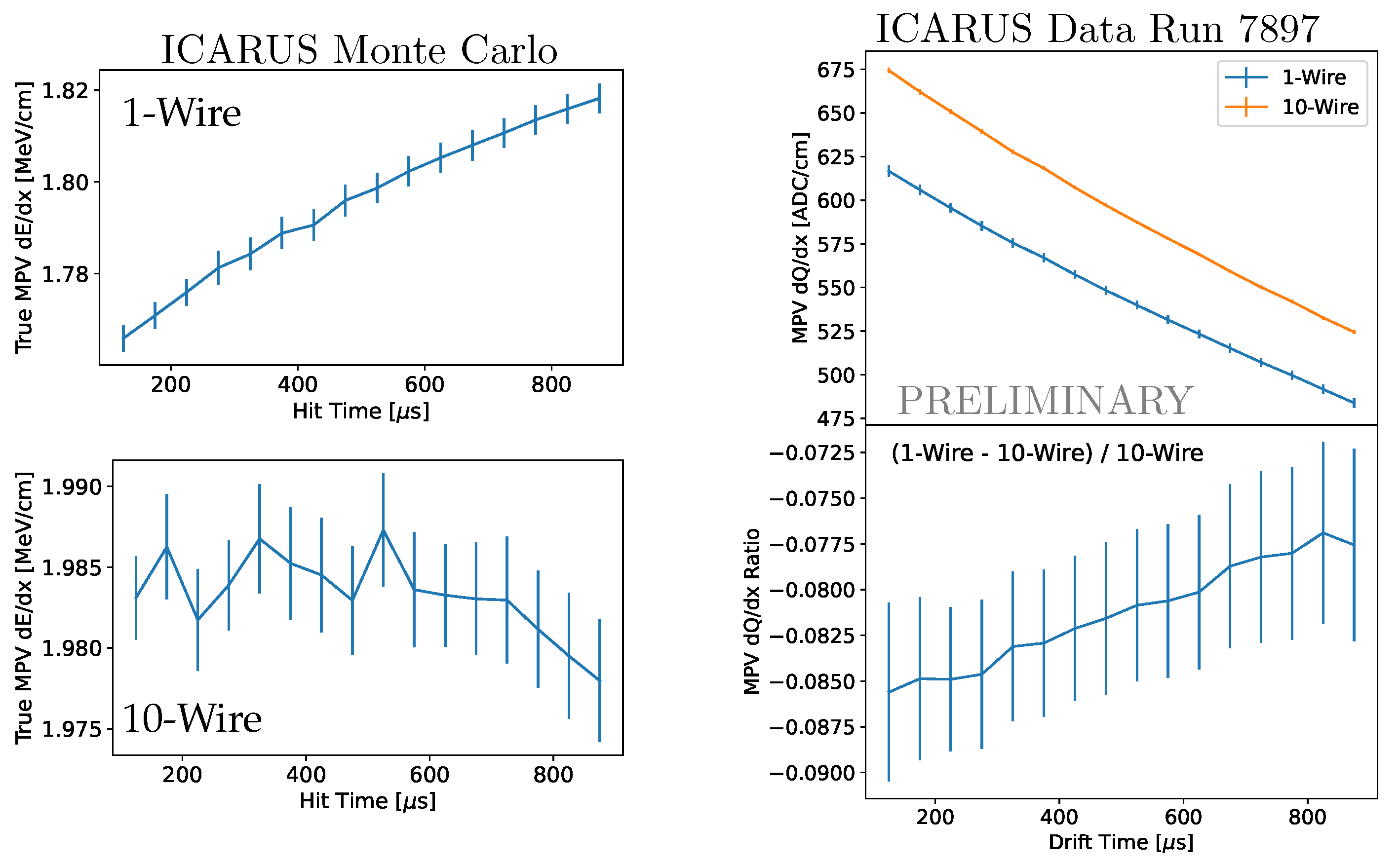
3.1. Charge Normalization in the Drift Direction
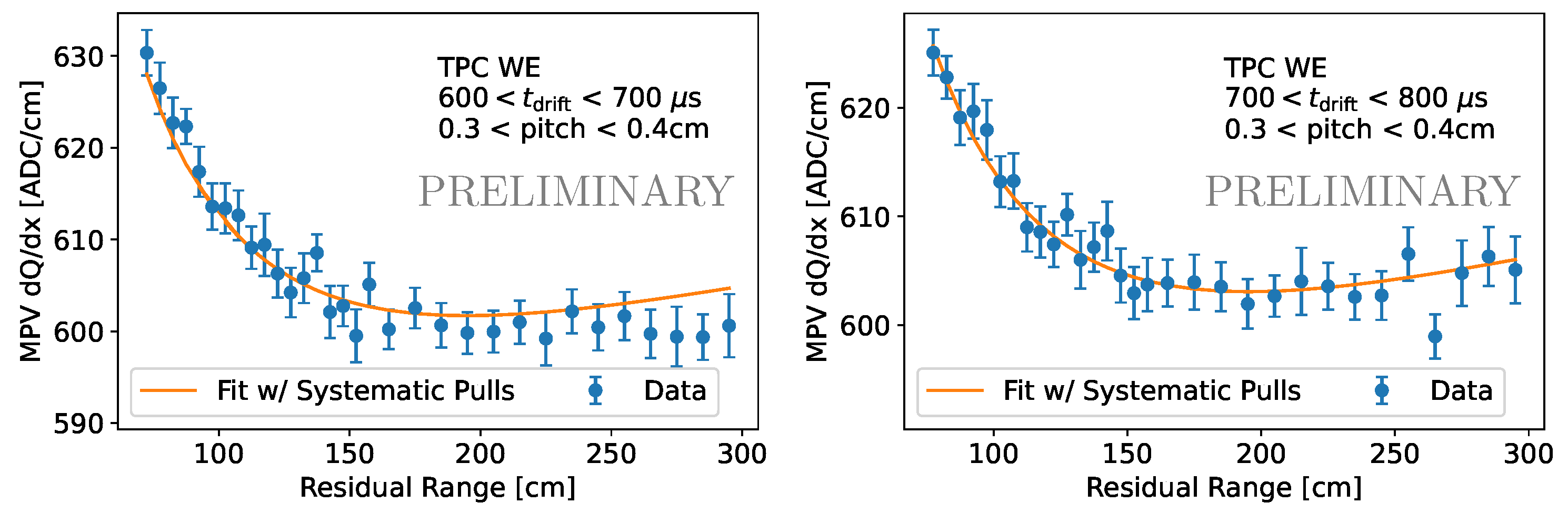
3.2. Gain Measurement
4. Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acciarri, R.; Adams, C.; An, R.; Andreopoulos, C.; Ankowski, A.M.; Antonello, M.; Asaadi, J.; Badgett, W.; Bagby, L.; Baibussinov, B.; et al. A Proposal for a Three Detector Short-Baseline Neutrino Oscillation Program in the Fermilab Booster Neutrino Beam. arXiv 2015, arXiv:1503.01520. [Google Scholar]
- Machado, P.A.; Palamara, O.; Schmitz, D.W. The Short-Baseline Neutrino Program at Fermilab. Ann. Rev. Nucl. Part. Sci. 2019, 69, 363–387. [Google Scholar] [CrossRef] [Green Version]
- Abi, B.; Acciarri, R.; Acero, M.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume IV: Far Detector Single-phase Technology. JINST 2020, 15, T08010. [Google Scholar] [CrossRef]
- Acciarri, R.; Adams, C.; Asaadi, J.; Baller, B.; Bolton, T.; Bromberg, C.; Cavanna, F.; Church, E.; Edmunds, D.; Ereditato, A.; et al. Demonstration of MeV-Scale Physics in Liquid Argon Time Projection Chambers Using ArgoNeuT. Phys. Rev. D 2019, 99, 012002. [Google Scholar] [CrossRef] [Green Version]
- Caratelli, D.; Foreman, W.; Friedland, A.; Gardiner, S.; Gil-Botella, I.; Karagiorgi, G.; Kirby, M.; Miotto, G.L.; Littlejohn, B.R.; Mooney, M.; et al. Low-Energy Physics in Neutrino LArTPCs. arXiv 2022, arXiv:2203.00740. [Google Scholar]
- Thomas, J.; Imel, D.A.; Biller, S. Statistics of charge collection in liquid argon and liquid xenon. Phys. Rev. A 1988, 38, 5793–5800. [Google Scholar] [CrossRef] [PubMed]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamov, G.; Adams, D.; Adinolfi, M.; Ahmad, Z.; Ahmed, J.; Alion, T.; Monsalve, S.A.; et al. introduction to DUNE. J. Instrum. 2020, 15, T08008. [Google Scholar] [CrossRef]
- Bethe, H. Zur Theorie des Durchgangs schneller Korpuskularstrahlen durch Materie. Annalen der Physik 1930, 397, 325–400. [Google Scholar] [CrossRef]
- Landau, L. On the energy loss of fast particles by ionization. J. Phys. (USSR) 1944, 8, 201–205. [Google Scholar]
- Vavilov, P.V. Ionization losses of high-energy heavy particles. Sov. Phys. JETP 1957, 5, 749–751. [Google Scholar]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.-J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. (Particle Data Group) Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 2020, 083C01. [Google Scholar] [CrossRef]
- Putnam, G.; Schmitz, D.W. Effect of diffusion on the peak value of energy loss observed in a LArTPC. JINST 2022, 17, P10044. [Google Scholar] [CrossRef]
- Lister, A.; Stancari, M. Investigations on a fuzzy process: Effect of diffusion on calibration and particle identification in Liquid Argon Time Projection Chambers. JINST 2022, 17, P07016. [Google Scholar] [CrossRef]
- Berger, M.; Inokuti, M.; Anderson, H.; Bichsel, H.; Dennis, J.; Powers, D.; Seltzer, S.; Turner, J. ICRU Report 37: Stopping Powers for Electroncs and Positrons. Rep. Int. Comm. Radiat. Units Meas. 1984, 4, 15–22. [Google Scholar] [CrossRef]
- Abratenko, P.; An, R.; Anthony, J.; Asaadi, J.; Ashkenazi, A.; Balasubramanian, S.; Baller, B.; Barnes, C.; Barr, G.; Basque, V.; et al. Measurement of the longitudinal diffusion of ionization electrons in the MicroBooNE detector. JINST 2021, 16, P09025. [Google Scholar] [CrossRef]
- Atrazhev, V.M.; Timoshkin, I.V. Transport of electrons in atomic liquids in high electric fields. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 450–457. [Google Scholar] [CrossRef]
- Li, Y.; Tsang, T.; Thorn, C.; Qian, X.; Diwan, M.; Joshi, J.; Kettell, S.; Morse, W.; Rao, T.; Stewart, J.; et al. Measurement of Longitudinal Electron Diffusion in Liquid Argon. Nucl. Instrum. Meth. A 2016, 816, 160–170. [Google Scholar] [CrossRef]
- Wannier, G.H. Motion of gaseous ions in strong electric fields. Bell Syst. Tech. J. 1953, 32, 170–254. [Google Scholar] [CrossRef]
- Thomas, J.; Imel, D.A. Recombination of electron-ion pairs in liquid argon and liquid xenon. Phys. Rev. A 1987, 36, 614–616. [Google Scholar] [CrossRef]
- Acciarri, R.; Adams, C.; Asaadi, J.; Baller, B.; Bolton, T.; Bromberg, C.; Cavanna, F.; Church, E.; Edmunds, D.; Ereditato, A.; et al. A Study of Electron Recombination Using Highly Ionizing Particles in the ArgoNeuT Liquid Argon TPC. JINST 2013, 8, P08005. [Google Scholar] [CrossRef] [Green Version]
- Amoruso, S.; Antonello, M.; Aprili, P.; Arneodo, F.; Badertscher, A.; Baiboussinov, B.; Ceolin, M.B.; Battistoni, G.; Bekman, B.; Benetti, P.; et al. Study of electron recombination in liquid argon with the ICARUS TPC. Nucl. Instrum. Meth. A 2004, 523, 275–286. [Google Scholar] [CrossRef]
- Abratenko, P.; An, R.; Anthony, J.; Arellano, L.; Asaadi, J.; Ashkenazi, A.; Balasubramanian, S.; Baller, B.; Barnes, C.; Barr, G.; et al. Search for an Excess of Electron Neutrino Interactions in MicroBooNE Using Multiple Final-State Topologies. Phys. Rev. Lett. 2022, 128, 241801. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Prior | Posterior |
|---|---|---|
| Recombination [20] | ||
| Recombination [cm/g][cm/kV] [20] | ||
| Transverse Diffusion Constant [cm/s] [15] | ||
| Mean Excitation Energy [eV] [14] | ||
| Gain TPC EE [e/ADC] | – | |
| Gain TPC EW [e/ADC] | – | |
| Gain TPC WE [e/ADC] | – | |
| Gain TPC WW [e/ADC] | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putnam, G., on behalf of the ICARUS Collaboration. Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN. Phys. Sci. Forum 2023, 8, 15. https://doi.org/10.3390/psf2023008015
Putnam G on behalf of the ICARUS Collaboration. Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN. Physical Sciences Forum. 2023; 8(1):15. https://doi.org/10.3390/psf2023008015
Chicago/Turabian StylePutnam, Gray on behalf of the ICARUS Collaboration. 2023. "Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN" Physical Sciences Forum 8, no. 1: 15. https://doi.org/10.3390/psf2023008015
APA StylePutnam, G., on behalf of the ICARUS Collaboration. (2023). Calibrating for Precision Calorimetry in LArTPCs at ICARUS and SBN. Physical Sciences Forum, 8(1), 15. https://doi.org/10.3390/psf2023008015






