Online Machine-Learning-Based Event Selection for COMET Phase-I ^†

Abstract

In many modern particle physics experiments, high-rate data handling is one of the most critical challenges due to the increase in particle intensity required to achieve higher statistics. We will tackle the challenge in the COMET experiment by developing the sub-microseconds ultra-fast machine learning (ML) algorithm implemented inside FPGAs to search for the lepton flavour violation process, a $\mu$-e conversion, using the world’s most intense muon beam. Our previous study showed that a trigger algorithm based on a gradient-boosted decision tree will realise the sufficient trigger performance within 3.2 $\mathsf{\mu }$s with a cut-based event classification. In this paper, we further investigated neural network algorithms as event classifications. For the feasibility test, a multi-layer perceptron (MLP) model was implemented inside the FPGA, and the preliminary results are presented.

1. Introduction

A COMET (COherent Muon to Electron Transition) experiment searches for a muon to electron (μ-e) conversion in a field of aluminium nuclei [1,2]. This process is extremely suppressed in the standard model of particle physics with a minimal extension, including neutrino masses. However, many new physics models predict the conversion rate enhancement around the level of ${10}^{-15}$ due to the presence of new particles mediating the flavour-changing neutral current [3]. The COMET experiment aims for an upper limit sensitivity of $3\times {10}^{-15}$ to investigate the new physics in Phase-I. To achieve the target sensitivity, the experiment will collect more than ${10}^{16}$ muons stopped inside an aluminium target with the world’s highest intensity muon beam, available at Japan Proton Accelerator Research Complex (J-PARC), with 150 days of data collection. Figure 1 shows the detector configuration in the COMET Phase-I physics measurement. Due to the high-intensity muon beam, an extremely high particle hit rate is expected in both a Cylindrical Drift Chamber (CDC) and a Cylindrical Trigger Hodoscope (CTH). To significantly suppress accidental coincidence, the coincidence of four neighbouring hits is required in CTH counters to generate the primary trigger signal. After taking the four-fold coincidence (also referred as a “CTH Trigger”), a fake trigger rate is dominated by the electrons and positrons induced by gamma rays coming from the muon-stopping target with relatively high energy, such that they can penetrate the multiple counters. The rate is calculated to be 100 kHz based on the simulation study, and this rate is still an order of magnitude higher than the maximum trigger rate available of 13 kHz. Most of those electrons and positrons have a momentum smaller than 50 MeV/c; hence, they create fewer hits inside the CDC volume compared to the μ-e conversion electrons. To suppress the fake trigger rate due to such low-momentum particles, we introduce the CDC hit information into an entire trigger system, called a “CDC trigger”, in addition to the four-fold CTH trigger. The entire CyDet trigger system, called “COTTRI” (COmeT TRIgger) [4], is based on the field-programmable gate arrays (FPGAs) and high-speed data transfer protocol between multiple boards. To realise high-efficiency fast trigger signal processing, machine learning (ML)-based algorithms are being developed. The R&D status and preliminary results of the CyDet trigger system will be presented in this paper.

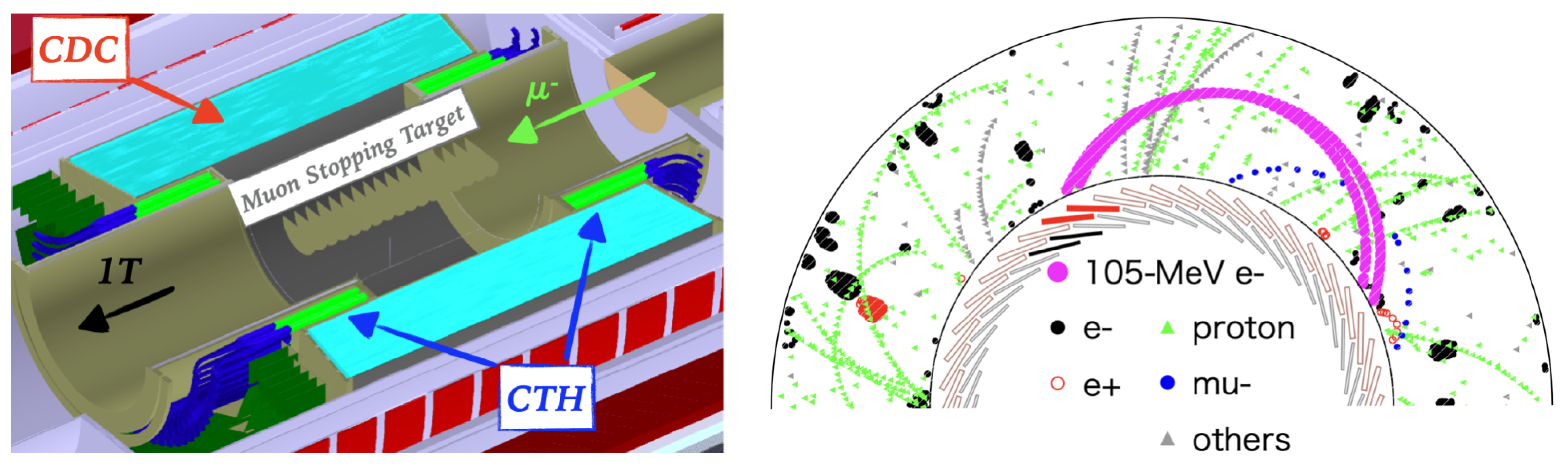
2. The COTTRI System

Figure 2 shows the entire structure of the CyDet trigger system, including the central trigger system. To summarise all CDC and CTH readout channels without having boundaries, both CDC and CTH trigger systems have front-end trigger-info processing boards (FE) and signal merger boards (MB). The FE boards and MBs are connected via copper cables with DisplayPort (DP) connectors, and a multi-gigabit data transfer protocol (Aurora8B10B, 2.4 Gbps) is adopted for inter-board communication. Due to the limited online event buffer size available in the CDC readout system, the trigger decision should be made and distributed to all readout systems within 7.5 $\mathsf{\mu }$s. For the COTTRI CDC MB and CDC FE boards, each board has one commercial FPGA (Xilinx, xc7k355t-2ffg901) as a main processor, allowing one board to have 10 DP connections and two optical links or one optical link plus an additional DP connection, respectively.

3. The Event Classification

In a previous study [5], we developed a hit classification to distinguish signal-like hits based on a gradient-boosted decision tree (GBDT) and combined this with a cut-based event classification. The result showed a 96% trigger efficiency while keeping the fake trigger rate less than 13 kHz with a delayed measurement time window of [700, 1170] ns after the pulse timing of muons. Instead of the cut-based event classification, it is possible to implement a pattern matching algorithm into FPGAs to further improve the trigger performance, enabling us to increase the time window, for instance, to [500, 1170] ns. Due to nature of muons in terms of their exponential decay, a 200 ns wider time window will increase signal events by more than 70%. However, it is known that the calculation for conventional pattern-matching algorithms such as a Hough transformation requires resources and time, as pointed out in [6], and the expected latency is unacceptably large. Another approach is to implement the software trigger inside the data acquisition computers, commonly used in collider-based experiments [7,8]. This approach requires intensive computing resources, high-throughput data transfer devices, and/or temporary long buffer data storage. Instead, it is possible to construct a neural network (NN) model trained offline, and implement it into an FPGA chip as a machine learning interface. This may result in significantly shorter processing time without requiring resource-intensive calculations, except for the activation functions, which can be extremely simplified equations based on either look-up tables (LUTs) or random access memories (RAMs) inside an FPGA. Since the processing of LUTs or RAMs only takes one or two clock cycles, the whole calculation time of NNs can be significantly shorter than that of conventional methods. However, there are a few key challenges which should be solved to realise the integration of NN algorithms into FPGAs, as follows:

• Limited FPGA resources for large-sized neural networks, such as a convoluted neural networks.
• The complexity of converting NN models into FPGA firmware using hardware-level synthesis (HLS) language.

These are common challenges in modern high-intensity particle physics experiments since it is a common goal to make a fast online trigger with high accuracy, and it is a natural way to use NN-based algorithms. Recently, an open-source software called hls4ml was developed by the community [9]. This tool can automatically convert deep learning models into HLS files, enabling almost seamless studies ranging from model construction and optimisation based on the standard ML software such as TensorFlow to firmware implementation. This results in the easier and faster optimisation of model structure, in terms of accuracy, network size, and latency. The procedure enables efficient node reduction by identifying the less effective nodes, making a sparse network, changing the precision of calculations by interfacing QKeras, and allowing some layers to be reused multiple times. Owing to these factors, the two challenges above have been solved by hls4ml (more details in [9]).

For the feasibility test, we constructed a simple NN model based on the “Quantized” Multilayer Perceptron (QMLP). The model consists of one 6-bit × 40 inputs layer, four hidden layers with a 4-bit rectifier linear unit as an activation function, and one output layer. Some of the hyper-parameters such as the number of layers were optimised using Bayesian optimisation in Keras before the final training.

4. The Performance Test

Although the QMLP model described in the previous section was not fully optimised, we performed a preliminary firmware implementation to check the feasibility of whether the current FPGA chip (Kintex-7, xc7k355t-2ffg901) is capable of accommodating NN models with reasonable classification accuracy.

For training and testing the model, we produced 20,000 random uniform background events in a 2D field and equally split them. Half of these events were mixed with a pseudo-signal trajectory in the form of an arch pattern, as shown in Figure 3. The dataset was randomly split into training (50%), validation (10%), and testing (40%) datasets. The categorical cross entropy loss function is minimised with $L^1$ regularisation [10] of the weights using the Adam optimiser [11]. The batch size is set to 32, and the training proceeds for 20 epochs.

To fit the data into the QMLP model, we flatten and compress the data into one-dimensional 6-bit 40 arrays. The consistency between hls4ml model prediction and an actual HLS converted model was checked using the Vivado simulation test bench tool [12]. The hardware test was performed using one COTTRI MB with the QMLP module implemented, and validation data were sent from COTTRI FE through the DP cable. Output scores were obtained using the Vivado ILA debug tool [13] through the JTAG cable and compared with the offline model.

5. Results

We found that the current QMLP model fits our baseline FPGA chip comfortably with a latency of 26 clock cycles, corresponding to 130 ns with a 200 MHz clock speed, as shown in

Table 1. Estimations of resource usage for xc7k355t-2ffg901 and the latency reported by hls4ml.

BRAM Usage (%)	DSP Usage (%)	FF Usage (%)	LUT Usage (%)	Latency
0	0	5	32	26 clock cycles

, which was reported by hls4ml. The latency value was also confirmed by the Vivado test bench simulation.

As shown in Figure 4a, the signal classifier showed consistent performance against the same validation data. The classification performance was as high as 96% at a BG rejection of 80%, as can be seen in Figure 4b.

6. Discussion

We found that the compact QMLP model can comfortably fit inside our baseline FPGA chip with a short latency of 130 ns, which meets the requirement. The firmware including this QMLP module was successfully generated and tested with a set of COTTRI MB and COTTRI FE. Therefore, we concluded that it is possible for us to utilise an online NN-based event classification algorithm on middle-class FPGA in the COMET Phase-I trigger system, in terms of both cost and performance. This study was conducted using only pseudo-data, namely, both signal-events and BG events were produced based on toy models. As a next step, we will use more realistic input data for both signal and BG events, together with further optimisations for NN models to improve the performance.