Abstract
Rotor and stator support structures of significant size and mass are required to withstand the considerable loads that direct-drive wind turbine electrical generators face to maintain an air-gap clearance that is open and stable. With the increase of scale, reducing the weight and environmental impact of these support structures is believed to be one of the key components to unlocking the true potential of direct-drive generators. An investigation on the electrical generator rotor structure of the IEA 15 MW offshore reference wind turbine was conducted. An integrated approach that considered the environmental impact, including the manufacturing energy usage and CO2 footprint, as well as the financial repercussions of structural parameter modifications as they are optimised was followed, making use of distinct commercial pieces of software. The rotor structure was parametrically optimised, and its operating loading conditions were evaluated at various size scales. The study determined that the effect of thermal loading is significant, which forces the designer to augment the mass to comply with the imposed structural requirements. The ensuing life-cycle assessment showed an increase in the environmental impact due to the consideration of this particular load, whose effect in structural deflection and stress has been typically underestimated.
1. Introduction
Capturing wind energy through wind turbines is widely considered as one of the key technological tools that we can use to help transition to sustainable energy production and thus work to reverse the effects of climate change. The IPCC AR6 Synthesis Report released in Q1 2023 summarised this clearly for global policymakers, even stating that the cost of wind generation has fallen below fossil fuel costs over the past 20 years [1].
However, even as costs are falling, there is still room for improvement. The maintenance and servicing of a typical large-scale wind energy project is one of the largest contributors among the major cost elements in the levelized cost of energy—LCOE, at 18.9%—approximately GBP 50,000 per Megawatt (MW), with GBP 33,000 per MW of that coming from turbine maintenance and service alone [2]. It has been determined that the traditional gearbox has the highest cost per failure compared to the other components (GBP~177,000), with a high major replacement failure rate and repair time and requiring a high number of technicians (~17) for major replacements [3].
In this investigation, the direct-driven alternative to using traditional geared powertrains is presented. A detailed analysis of the IEA 15 MW Offshore Reference Wind Turbine Electrical Generator Rotor supporting structure, including loads that have been traditionally underestimated along with a parametric optimisation for mass reduction, and taking into consideration financial costs, is carried out. Trends are identified, with the aim of understanding the structural matters that will arise as designers modify the size of the machines. Much of the structural optimisation of these machines is being actively researched and developed. With 15 MW turbines expected to start commercial operations as soon as 2024, it is clear that turbines will only grow bigger [4]. Sustainability issues during the manufacturing stage are also taken into account, making use of a life-cycle analysis that presents the full environmental impact.
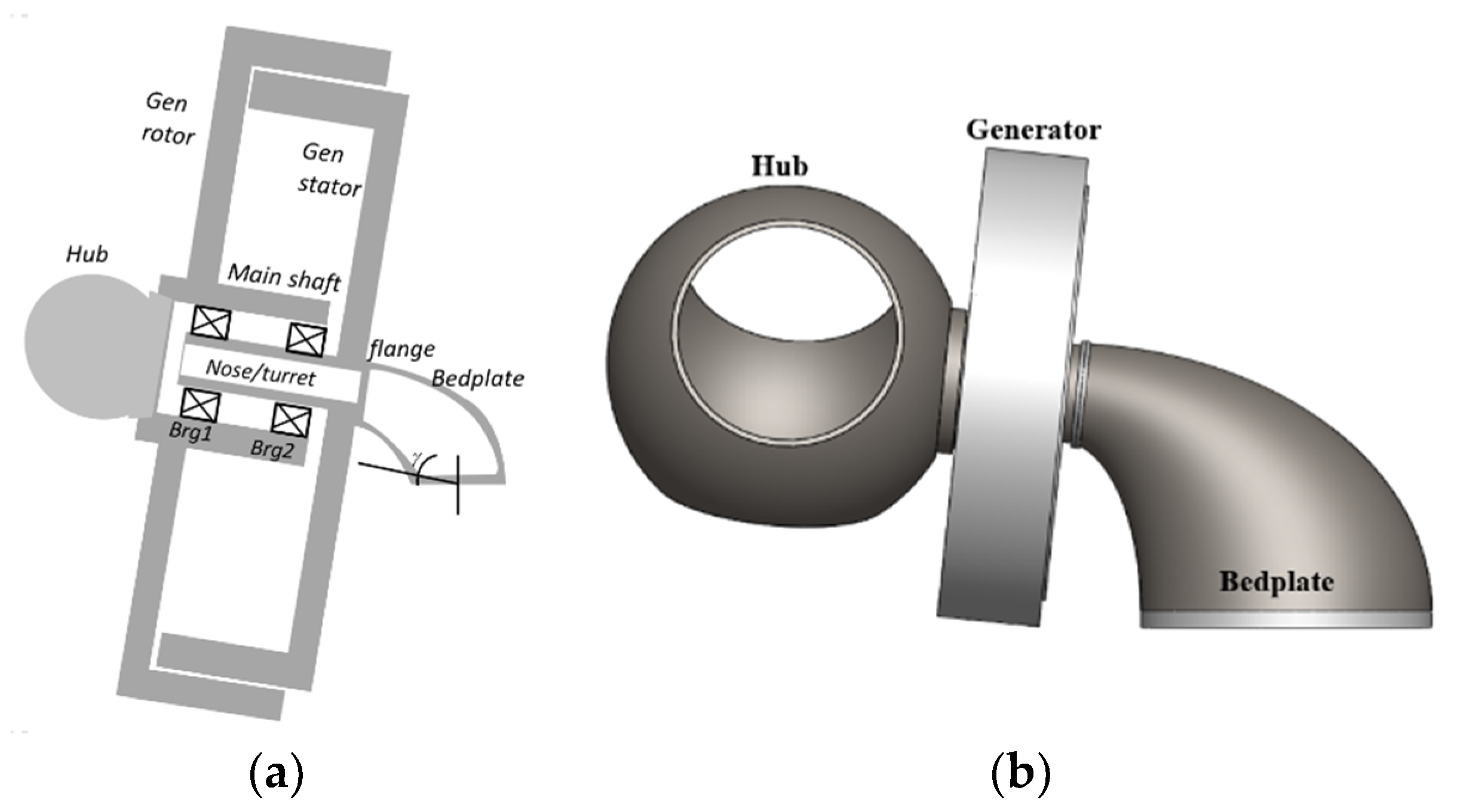
Direct-drive wind turbines eliminate the gearbox completely from their powertrain. This helps to increase the machine’s availability, reliability, and serviceability, as well as generating a more compact design, especially in the axial direction [5]. However, this results in the generator taking on the full loads and stresses; this does not represent a major concern if the machine is appropriately designed. Recent investigations have revealed that this type of machine suffers from larger average stops and average downtime per year than expected [6]. As a result, the addition of mass to combat the increased loading conditions leads to increased costs; thus, optimising the supporting structures of these machines is key to unlocking their full potential. Without a gearbox, this type of turbine operates at very low rotational speeds, which forces the designer to increase the generator size to develop high torques [7]. Figure 1 depicts the IEA 15 MW reference turbine powertrain.
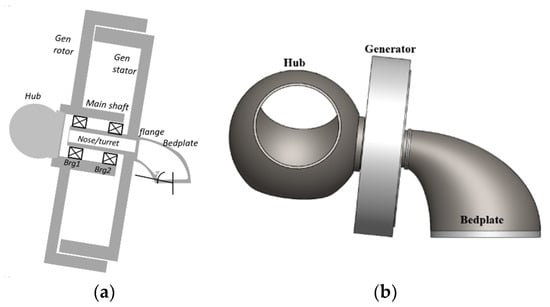
Figure 1.
IEA 15 MW Offshore Reference Wind Turbine powertrain: (a) Sketch view; (b) CAD view [8].
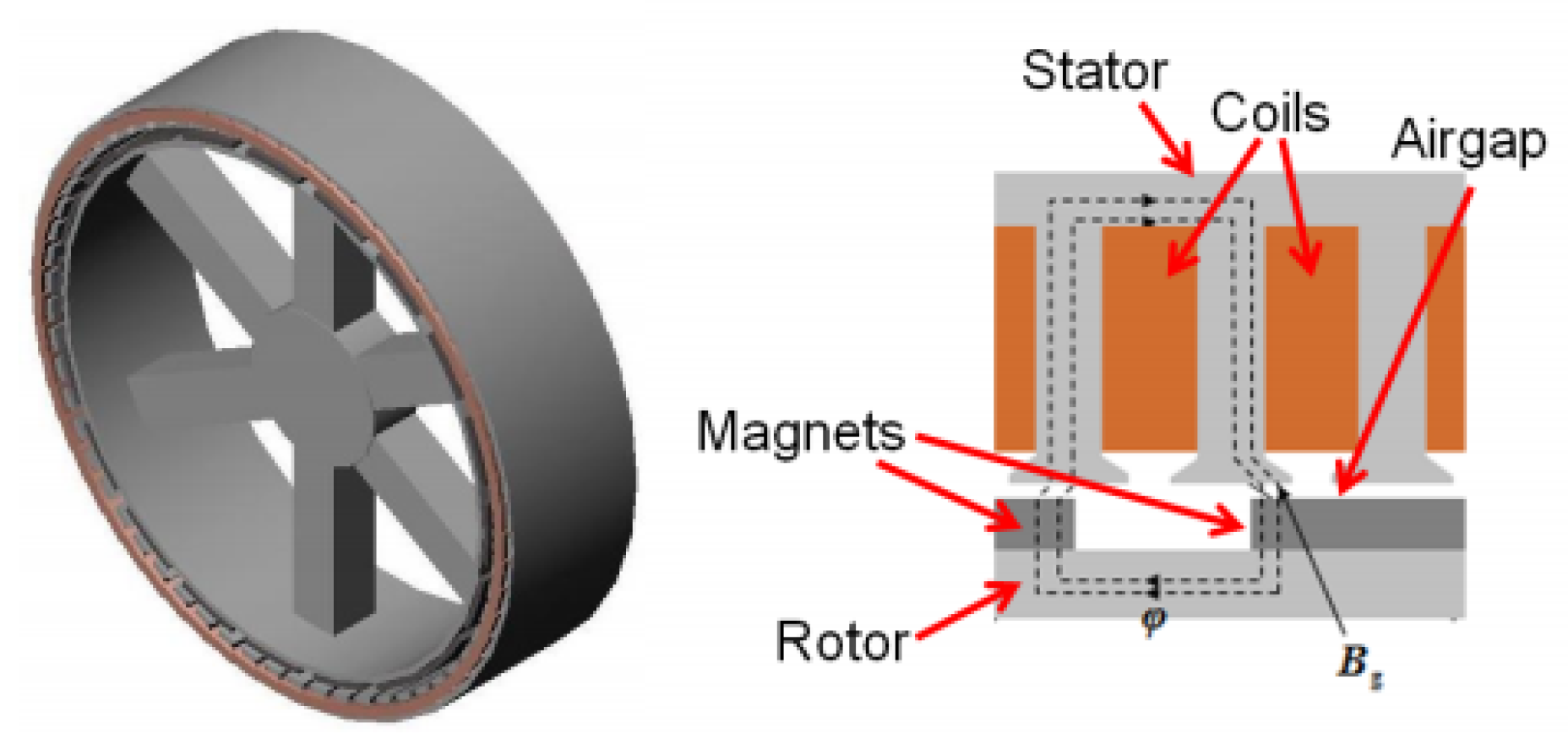
This particular machine has a permanent magnet (PM) AC synchronous electrical generator. An AC electrical machine can be permanent-magnet-excited or electrically excited. Switch reluctance generators are electrical machines in which only the stator is electrically excited. Due to its demonstrated higher efficiency and reliability, permanent magnet machines are considered superior to their electrically excited counterparts. This has resulted in a rapid increase in their use for commercial and military applications over the last decade [5]. Permanent magnet machines are often characterised by the orientation of the magnetic flux as it crosses the airgap. There are three different topologies: radial flux, axial flux, and transverse flux. Considering that a large number of manufacturers are looking at radial flux permanent magnet machines for their offshore wind turbines, the authors have centred their attention on these machines. Figure 2 represents a radial flux permanent magnet electrical generator, highlighting its main components.
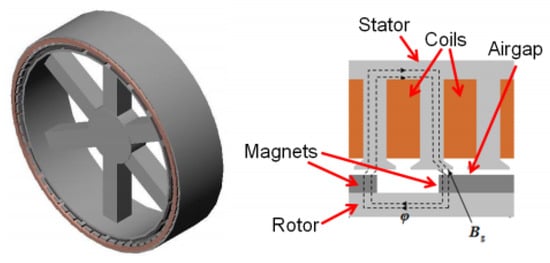
Figure 2.
A typical radial flux PM generator, showing its main components [5].
As observed, there is a clearance between the rotor and the stator structures, known as the air gap. This is where the electromagnetic field is generated; therefore, it needs to be continuously open and stable. However, there are a number of loads present during installation, operation, and transportation that can close this gap and that must be considered during the design stage.
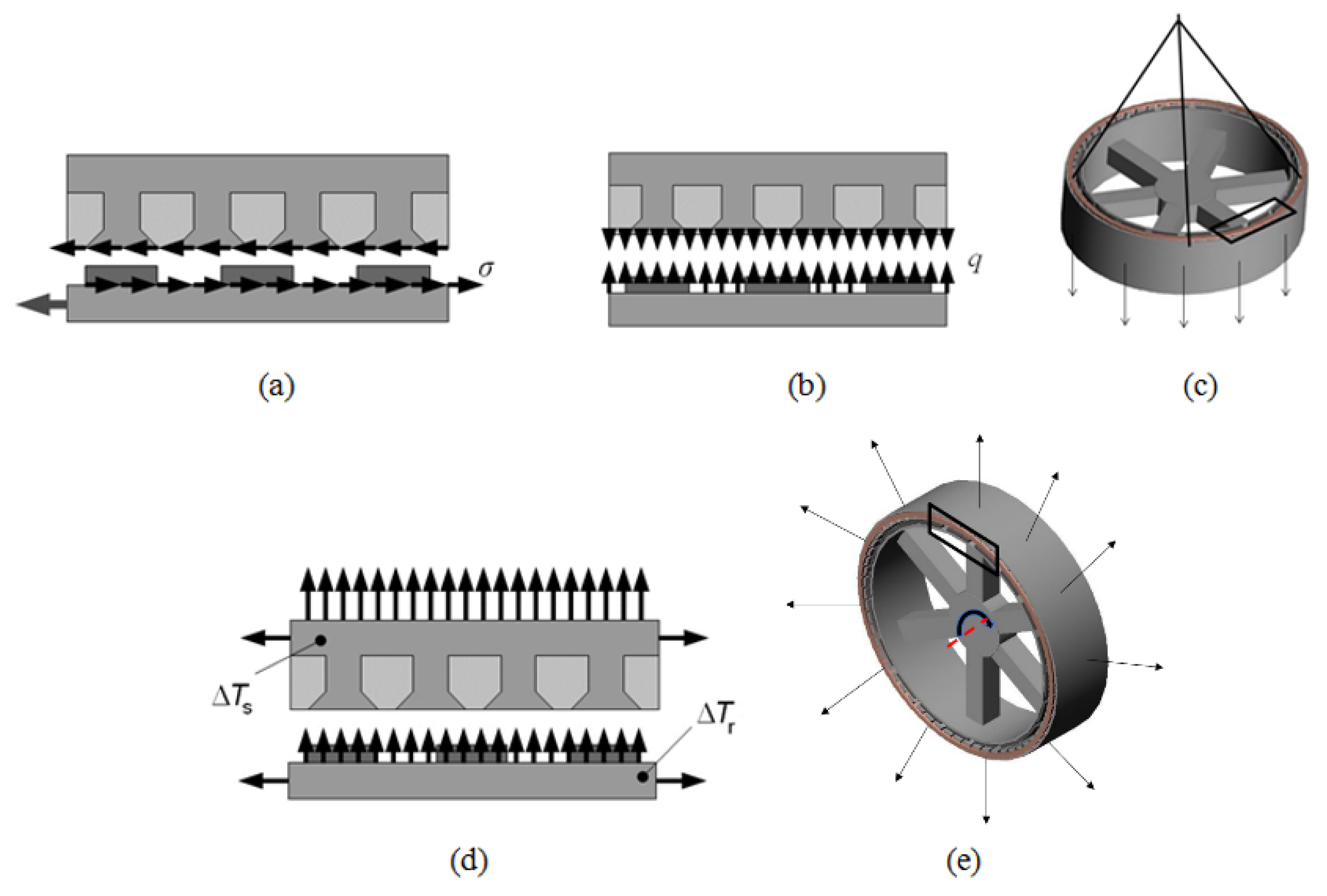
In Figure 3, the loads that need to be taken into consideration are introduced. The magnetic loading, shown in Figure 3b, produced by the magnetic attraction between the PM and the metallic stator structure, also known as Maxwell stress, is widely thought to be the most critical [9], but this can change as the size of the turbines increases. Figure 3a shows the tangential loading due to the shear stress caused by the magnetic interaction between the magnets mounted onto the surface of the rotor and the metallic structure of the back iron of the stator. Gravitational and centrifugal loading are shown in Figure 3c,e, respectively. Note that for the centrifugal loading, the axis of rotation, which coincides with the machine’s axis of rotation, is highlighted using a red dashed line and that the arrow showing the direction of rotation is in the isometric plane of the rotor. Thermal loading, which has been typically underrated, is given in Figure 3d and can be applied by assuming a constant operating temperature across the whole supporting structure. The structural topological configuration also has an important role to play, as with different geometries it is possible to spread the stresses, with a consequent reduction in deformation. This opens the door to further and more ambitious mass, material, and manufacturing cost reductions. Figure 4 depicts typical rotor supporting structures.
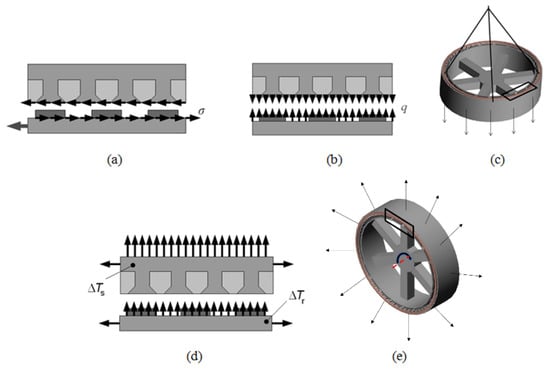
Figure 3.
Loads at play: (a) shear loading; (b) magnetic loading; (c) gravitational loading; (d) thermal loading; (e) centrifugal/centripetal loading [10].

Figure 4.
Typical radial flux PM generator rotor structures [11].
This investigation is focused on the analysis and optimisation of the electrical machine rotor supporting structure of the IEA 15 MW Offshore Reference Wind turbine. Other authors have attempted this task from distinct perspectives, on smaller-scale wind turbines and using other techniques and pieces of software. In [12], Zhang et al. demonstrated that most of the mass and cost of large-scale electrical generators corresponds to the supporting structure, also known as “inactive material”, using numerical methods and a genetic algorithm. Employing polynomial modelling, McDonald found that the structural mass of the stator of a 5 MW generator is greater than that of the rotor and that, when combined, they account for at least 82% of the total mass. In this investigation, the author also concluded that normal stress, also known as Maxwell stress, has the greatest influence on the inactive material mass [13]. An optimal strategy for the structural mass reduction of permanent magnet direct drive electrical generators was proposed by Zavvos in [14], considering machines with the same power rating and size. Making use of simplified models of the traditionally used structures, deflection and fatigue levels generated by the imposed loads were estimated. Then, optimisation tools were utilised to minimise the mass while complying with the structural requirements.
Jaen-Sola explored different structural configurations in [5], and with the use of finite element (FE) static simulation studies, the author demonstrated that disc-supporting structures were more effective without the addition of stiffeners, due to the limited increase in frequency that the stiffeners provided compared to the added weight. In the same study, Jaen-Sola also investigated the structural geometries from a dynamic perspective using modal studies and determined that conical supporting structures have superior performance to disc structures, needing less mass and having natural frequencies nearly twice those of the disc structure. This can be attributed to the inclusion of a new parameter, the cone angle, which makes the optimization process more flexible for the designer.
Topology optimisation was also investigated by Jaen-Sola in [5], in an attempt to have more control over a typically manual parametric optimisation process, with the aim of reducing the structural mass of a machine of the same power rating and size subjected to Maxwell stress, shear stress, and gravitational loading. This resulted in a significant reduction of mass for 3 MW disc geometries of 15% and 38% for small and large scale disc structure models, respectively. Also in [5], contour plots were established as a method to make reasonable estimations of the weight and frequencies of the structure to be produced. Jaen-Sola also notes the need for further study and comparison between structures of a direct-drive machine made of different materials, such as conventional structural steel and carbon-fibre-reinforced composite, particularly with a focus on thermal properties, since the thermal expansion properties in composite structures could be tailored to meet the needs of the structure. Moreover, benefits like lower heat conductivity and density should be taken into consideration.
In [4], Tartt et al. parametrically optimised the rotor structure of the 15 MW Reference Turbine and added holes to reduce its mass, as well as stiffeners with the aim of modifying the natural frequencies of the structure. An overall mass reduction of 20% was reported under uniform loading conditions, whereas 34% was achieved for a non-uniform loading scenario.
Approaching the task from a more applied point of view, Hayes et al. proposed additive manufacturing techniques as a means to develop more ambitious and complex lightweight structural topologies for a 5 MW PMDD generator, which would be impossible to produce using conventional methods [15,16]. According to their study, a potential mass reduction of 34% can be achieved through finite element analysis, and it is possible to scale up the technique for larger electrical generators. Gonzalez-Delgado et al. employed generative design techniques, implementing an artificial intelligence–controlled process to generate a series of iterations of structural geometric models, following a fitting algorithm based on control parameters and initial specifications [17]. A parametric study linked to topology optimisation analysis was presented in [18], where a conical supporting structure was proposed for a 3 MW PMDD generator. Through finite element analysis (FEA), the authors demonstrated that the structure satisfied static and dynamic working conditions. Considering loads such as those derived from operating thermal conditions and the worst-case loading scenario, it was demonstrated that the rotor structural mass needed to be 6.5 times higher than the mass for a rotor working under the typical static loading conditions. The authors also emphasised the impact of the material selection on the dynamic response of the structure.
In most of the papers cited herein, the thermal loading conditions were not considered during the optimisation process. Structural configurations and shapes were proposed assuming that the response of the structure would be similar despite changes in the scale of the machine. It is important to remember that there is a clear trend towards larger-scale machines. Therefore, it is imperative to estimate the influence of this load on the behaviour of a large-scale structure and establish a theory that describes its effects on machines of different scales. Environmental impact is a factor that was not considered in any of the cited studies. Thus, we aim to shed some light on these important aspects.
In the following section, the authors will introduce the reader to the methodology followed to accomplish this research. The characteristics of the machine in question will be presented first, followed by the steps taken during the optimisation and the consequent analyses. The obtained results are given in Section 3, and the conclusions drawn are presented in Section 4.
2. Methodology
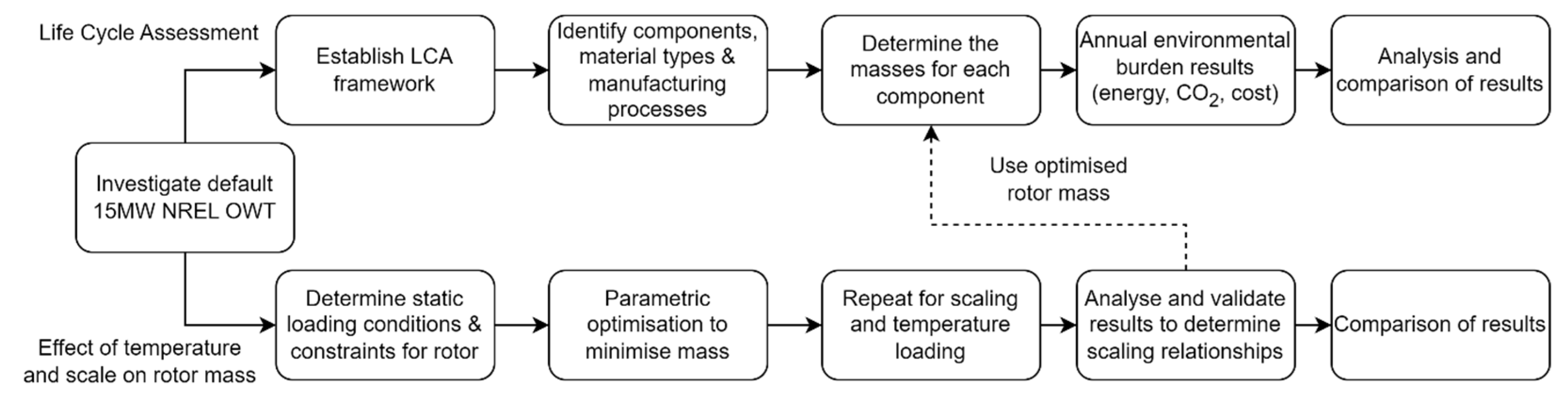
In this section, the proposed methodology for investigating the rotor structure regarding temperature loading, scaling, and environmental impact is described. As can be seen in Figure 5, an initial evaluation of the rotor structure was carried out. With this stage completed, the authors proceeded to investigate the effects of introducing an underestimated loading condition, such as the temperature, in 2 different types of analyses that were run in parallel. One looked at how the structure would behave with and without this load applied and as its size changed, and one looked at the environmental impact as the machine size is modified with and without the load applied, for a clear visualization of its influence.
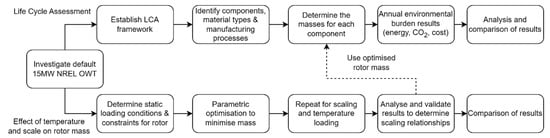
Figure 5.
Flowchart detailing research methodology.
2.1. Initial Rotor Evaluation
Before any analysis can be completed, first a rotor design must be selected, modelled, and analysed to use as the base case.
For this project, the model selected is the IEA 15-Megawatt Offshore Turbine, developed by the National Renewable Energy Laboratory (NREL), the Technical University of Denmark (DTU), and the University of Maine [8]. This open-source model was selected for its relevance in the current stage of technological development. Tartt et al. also studied this reference turbine in [4]. Details about the structural design include the following:
- Airgap length: 10.16 mm;
- Rotor rim thickness: 63.69 mm;
- Rotor disc thickness: 81.75 mm;
- Total rotor structural steel mass: 86.2 tons;
- Structural material: plain carbon steel.
Table 1 lists the properties of the material used in the structural design of the machine.

Table 1.
Plain carbon steel material properties [19].
Using this model as the base case, the authors generated a design table in SolidWorks Design [19], with the aim of automating the parametric optimization process through finite element analysis (FEA). Design tables allow the user to parametrise the problem and use the same simulation set-up for all the iterations defined within a particular range. The parameters to be optimised are converted into design variables first to set the objective, which in this case corresponds to minimizing the structural mass while keeping the radial deflection of the rotor to a limit of 20% of the air-gap length, i.e., 2.032 mm, and 200 MPa of equivalent stress [4]. It is worth noting that a preliminary FE analysis was run in order to ensure that the model complied with the requirements before starting with the optimisation. Prior to commencing with the finite element analysis, a mesh independence study was conducted to ensure that the results were of the highest accuracy. For the default IEA 15 MW model dimensions, a high-quality tetrahedral mesh of 32,752 nodes and 16,127 elements was defined by using a 240 mm element size with a tolerance of 12 mm. As can be observed in Figure 1, the generator was tilted by 6°; therefore, the component in the vertical direction needed to be calculated. For the initial static structural simulation study, the rotor was fixed at the shaft, and the following loading conditions were imposed: g is gravity at 9.81 m/s2, θ is the shaft tilt angle at 6°, v is maximum nominal tip speed at 95 m/s, and r is the rotor blade radius at 120 m. The distributed mass represents the “active material”, corresponding to the rotor back iron and permanent magnets. After performing the preliminary static analysis, it was noticed that the structure did not comply with the deflection limit under typical operating conditions, as shown in Table 2. Tartt et al. reported the same finding in [4]. Bearing this in mind, the optimization process had to be slightly modified. The initial idea was to optimise the mass of the whole structure, considering the effect of the thermal loading in the design and quantifying its influence when increasing the size of the machines and in the life cycle analysis. However, it was clear that more material was going to be needed regardless, as the structure did not pass the initial test. Making use of the mentioned design table tool, a suitable structure was found. A view of the reference turbine electrical generator rotor supporting structure that was able to comply with the traditionally imposed requirements is given in Figure 6.

Table 2.
Structural study loading conditions [4].
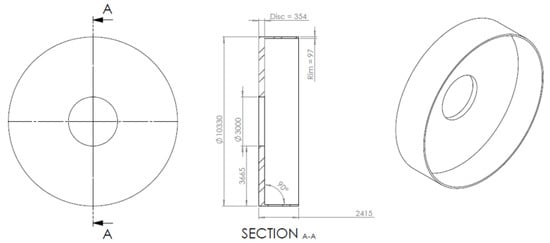
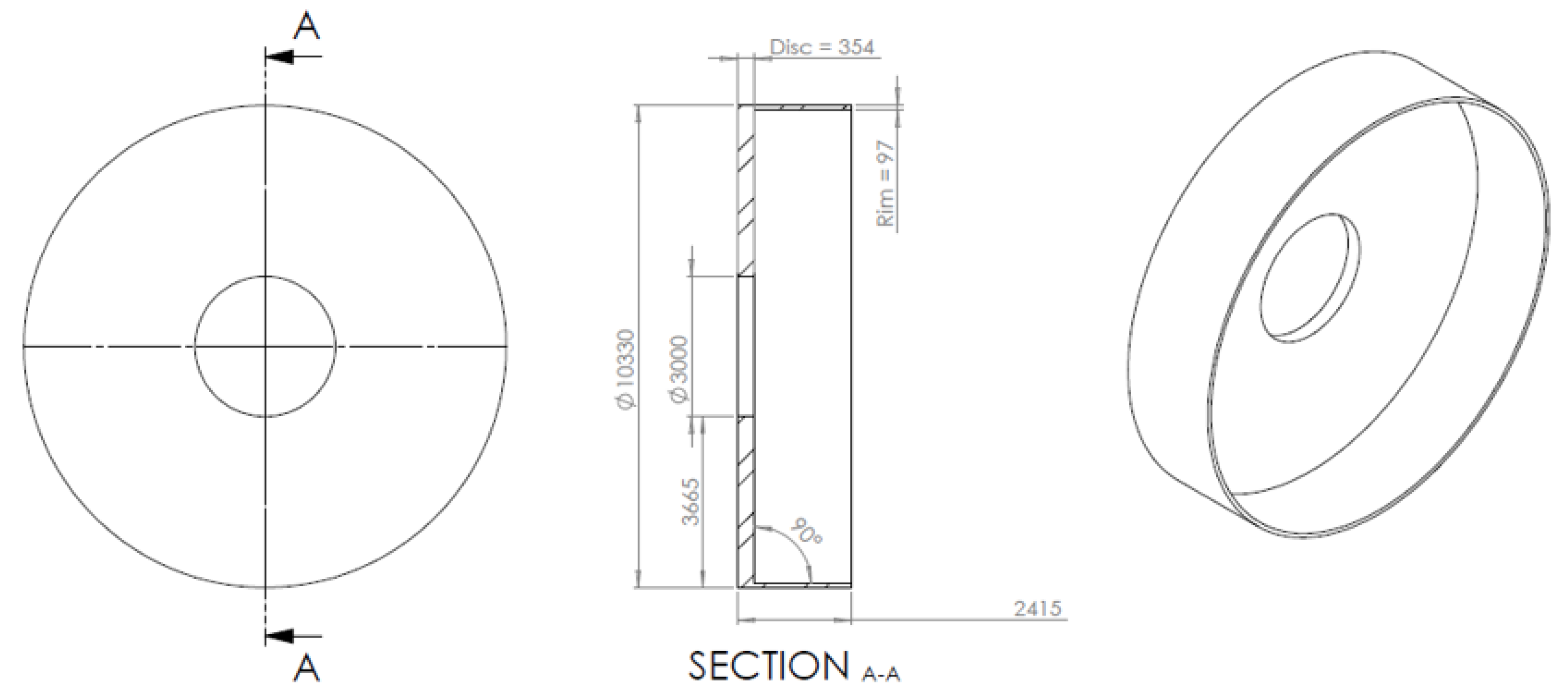
Figure 6.
A view of the parametrically optimised 15 MW electrical generator rotor structure, highlighting dimensions in millimetres.
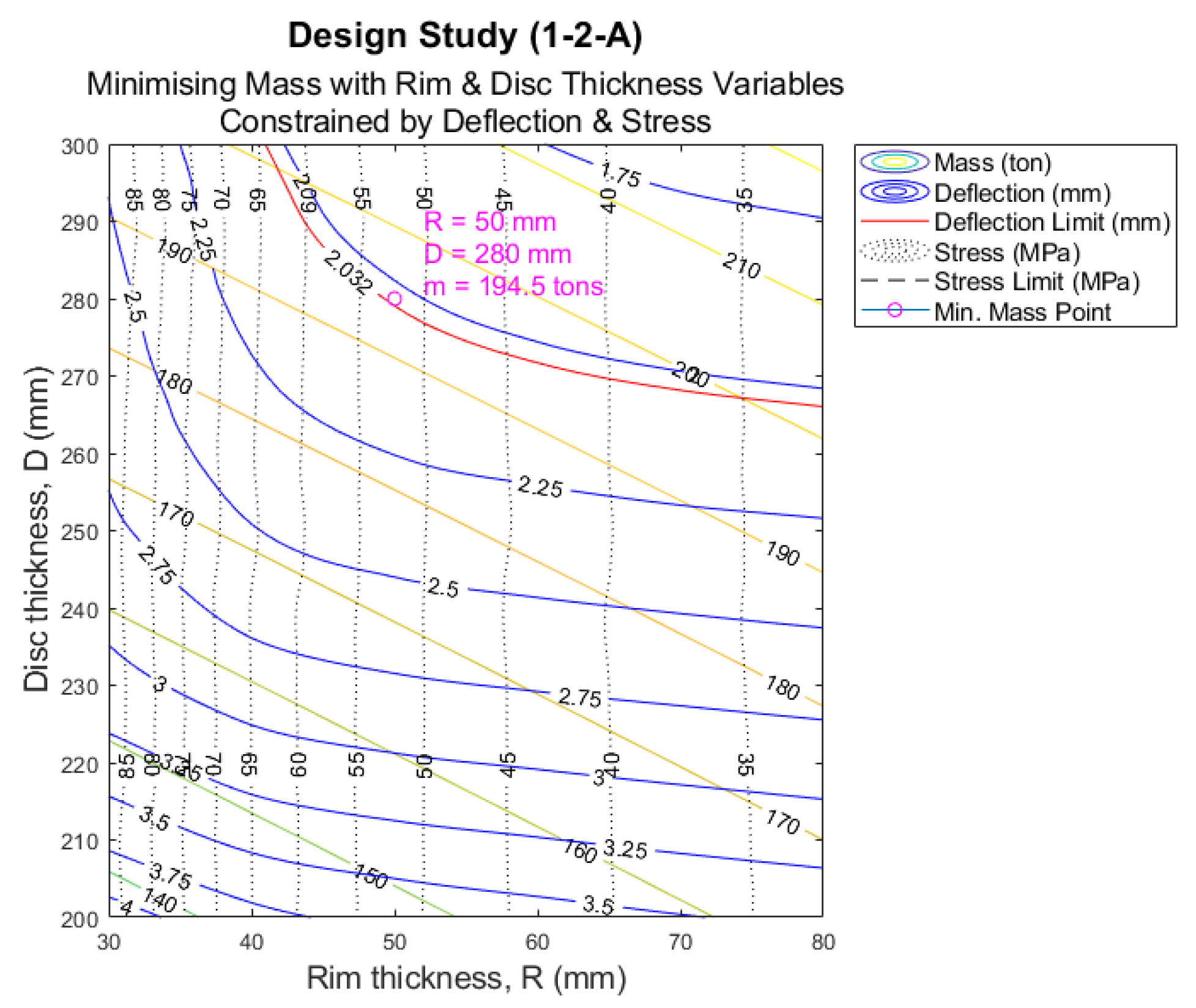
As one can see, the rim thickness increased from 63.69 mm to 97 mm, whereas the disc thickness had to increase to 354 mm from 81.75 mm, with the consequent increase in mass. Even though the preliminary analysis delivered unexpected results, which forced the authors to increase the seeking range, it was found that the data generated during the process were of interest. Using contour plots, it was possible to identify trends that would help save considerable amounts of time when trying to define the optimization ranges for the parameters of structures of different sizes. The contours were generated in MATLAB R2018a using the ‘griddata’ function to interpolate between points. Each point found using the design study tool was identified by a tick, with the query points in between interpolated. A cubic interpolation method was used for the three scattered datasets (mass, deflection, and stress). An analysis of the contour plot was completed by outlining a rectangular box and identifying the suitable range that should be further investigated. This was done visually. In basic terms, each rectangular box identified the area that should be ‘zoomed-in’ on; the magnification was essentially narrowing down the seeking range and increasing the number of defined points until the rim and disc axis units reached single millimetres. An example of a contour plot is shown for the default case of the NREL 15 MW model in Figure 7.
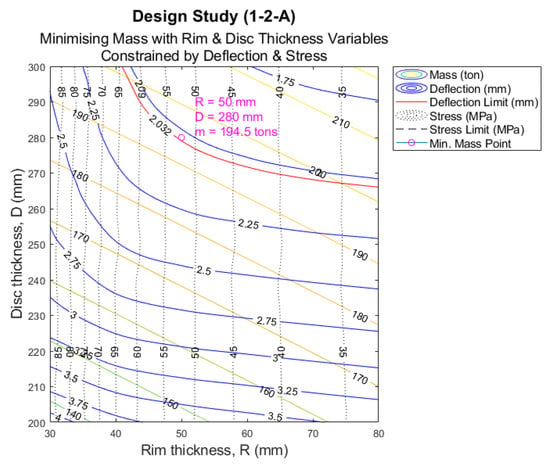
Figure 7.
Base case initial contour plot.
As the aim is to reduce the mass, the contour plot provides a clear visual of the relationship among the rim and disc thicknesses, the structural limits, and the rotor mass itself. The identified range for the disc and rim thicknesses is thus used in the next iteration of the design study—keeping range steps as reasonable as possible. Using this method of analysis allows for a much more efficient and accurate analysis of the parametric optimization, as rather than running a large study that would take much longer, smaller studies can be run, and interesting data pinpointed for examination in order to refine the model. Once a refined design is found, thermal mass can be included in a separate design study. By using the design table, a new configuration is easily made. In this paper, temperature or thermal loading of the rotor is defined as thermal expansion of the rotor in normal operating conditions. A temperature load of 55.69 °C (~56 °C) is applied to the entire rotor, which was extracted from the SCADA data provided by [20], showing the same values for long periods of time. Thermal stress due to unsteady thermal loading is not considered in this investigation as a result. The entire parametric optimization process can then be repeated. Note that the mesh is kept consistent.
2.2. Scaling Considerations
Due to the amount of data collected, a clear naming convention is needed to establish consistency and avoid errors. Table 3 below provides a description of what each character indicates. For example, the design study labelled 1–3 indicates that this is the 1.0 scale model being parametrically optimised, including temperature loading. The result 1-3-C thus indicates the final optimised version.

Table 3.
Naming convention.
To scale the rotor correctly, each value must be calculated by the appropriate method. For the dimensions, this is done simply by multiplying each measurement by the base case scale. To be more accurate during the design study range identification step (see Section 2.1), the actual values used to multiply the disc and rim are optimised with temperature figures, i.e., using study 1-3-C values. The scaled rotor dimensions are shown in Table 4. These remain consistent throughout the optimization process, with only the rim and disc changing. These data can thus be inputted into the design table to progress with the scaling analysis. Note that the dimensions given in the first row of Table 4 correspond to those given in [21].

Table 4.
Initial 15 MW rotor dimensions for each scale.
The five loads discussed in Table 2 are scaled similarly to the dimensions. Note that the rotor blade radius r is scaled (default 120 m) instead of the centrifugal force, which is instead calculated using the previously defined equation in Table 2—centripetal loading. This is because the centrifugal force will decrease with scale, assuming the tip speed remains constant (at 95 m/s). For the studies including temperature loading, the temperature remains constant, as do the yield strength and deflection constraints. Mesh independence studies were again first conducted before each scale was parametrically optimised. Note that two mesh independence studies were conducted for the 1.0 scale rotor—one at default IEA 15 MW model dimensions and one following all optimizations, including the impact of temperature loading. The second study validated the usage of the 240 mm element size plus a tolerance of 12 mm, despite the significant change in rim and disc dimensions (described later), and resulted in a high-quality tetrahedral mesh of 41,346 nodes and 22,738 elements. Studies were also conducted for the 0.9, 1.1, and 1.2 scale rotors, which defined a 280 mm element size with 14 mm tolerance for the upscaled models. It was thus determined that the model downscaled 10% used the same 240 mm element size and 12 mm tolerance. In total, five mesh independence studies were conducted.
Parametric optimization thus occurred for the 1.1, 1.2, and 0.9 scale rotors, following the steps outlined in Section 2.1. In order to determine relationships between rotor scaling, graphs were created to analyse trends. Multiple trendlines were investigated. By visually examining the fit of the trendline and comparing the R2, or Coefficient of Determination values, the most suitable trendline type was selected. The generated trendlines showed the relationship between rim or disc width and scaling.
Once the most suitable trendline was established for each scaling relationship, i.e., a static study including and excluding temperature loading, validation through FEA could be done. This was done by using the trendline equations to plot points that were then simulated. The two points investigated were scaling the rotor to 1.05 and 1.15 times the default IEA 15 MW rotor. Whilst the rim and disc thicknesses were calculated through the equation, the other dimension and load variables were determined normally through the same process used for the initial scaled structures. A comparison between different fitting trendline equations could be made as well, which was particularly important for the temperature loaded rotors due to their uniquely disordered contour charts. See Section 3 for the obtained results.
When the resulting rim and disc thicknesses were checked using an equation to determine whether they met the constraints, a design study was conducted to identify the actual optimised solution. This validation methodology was completed for both the 1.05 and 1.15 scaled rotors, both including and excluding temperature loading. Finally, updated trendlines could be developed including these values, in order to further refine the equations. Using the data collected, a comparison could be made to investigate the effect temperature as the scale increased. This was done by plotting a bar chart, with variances included to determine bigger-picture trends.
2.3. LCA Framework
The goal of a Life Cycle Analysis (LCA) is to provide a high-level environmental assessment of a product, standardised via the framework in ISO14040:2006 [22]. By establishing a Life Cycle Inventory (LCI) using the Bill of Materials (BOM) presented in Appendix A and the information provided in Appendix B, a Life Cycle Impact Assessment, (LCIA) could be completed. Initially, the Eco-Indicator 99 method was explored as a viable option to conduct the LCA; however, further investigation resulted in the Ansys Granta EcoAudit+ tool [23] determined to be a more modern and viable method. This advanced tool must be used with a Level 3 database, so the Level 3 Sustainability Database with the MaterialUniverse subset was selected. First, however, the scope of the LCA was defined.
The goal of this LCA was to establish an approximate assessment of the distribution of environmental burdens, including energy and CO2 emissions as well as cost over the life of the IEA 15 MW Reference Wind Turbine. The ‘life cycle’ is defined in this case from the point of assembly, i.e., where all the components come together to make the product, to the end-of-life, which assumes 100% recycling, including the turbine blades and miscellaneous mass. To complete the Ansys Granta EcoAudit+, some key assumptions must be made. First, a scenario must be defined in order to identify the distances. In Scotland, it is known that the Seagreen site is the largest offshore wind farm, with 114 wind turbines currently under construction off the coast of Angus [24]. There is also the current—as of late 2021—proposal to expand the farm under a project called Seagreen 1A, which aims to build the remaining 36 approved turbines [25]. These turbines are known to have an indicative capacity of 16 MW, and the proposed size range includes the current IEA 15 MW reference wind turbine (e.g., maximum rotor diameter: 167 m to 242 m (NREL is 240 m); maximum hub height above LAT: 126.2 m to 165 m (NREL is 150 m)) [8]. Thus, it is a valid site on which to base this LCA.
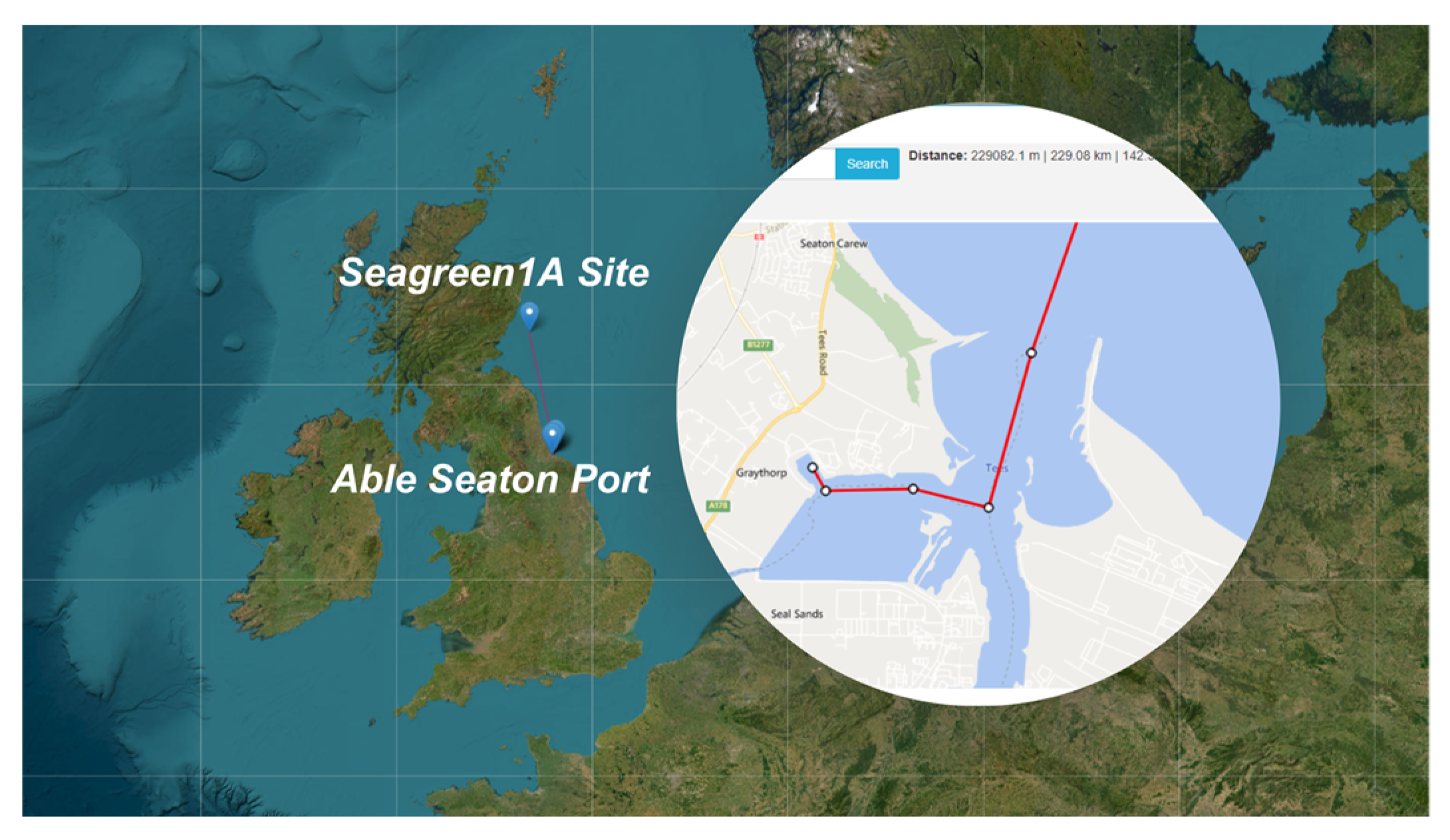
With the knowledge that the Seagreen1A project is planned to be constructed at the coordinates Latitude: 56°36′39.5″ and Longitude: −1°49′15.5″, and that the Able Seaton Port in the Northeast of England is used for marshalling operations for the Seagreen site, a diagram can be made to determine the distance between the two [26,27]. The distance totals 229 km. See Figure 8.
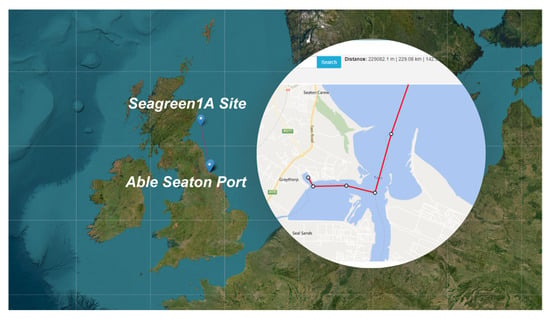
Figure 8.
Able Seaton Port to Seagreen 1A distance [26].
All components, material types, and manufacturing processes are defined in Appendix A and Appendix B. The study is repeated for each optimised rotor scale, both with and without temperature loading. Most other components are scaled directly—those which are not are noted in Appendix A and Appendix B. Once the results are outputted from the EcoAudit+ report, the data can be analysed and compiled. Graphs can be created to study the impacts with relation to scale. Annual energy and CO2 burdens can be evaluated with regard to scale of the entire wind turbine as well as with the cost involved. Finally, an evaluation of just the rotor can be completed.
3. Results and Discussion
In this section, the authors present the results obtained during the optimization process of the base case electrical generator structure, using contour plots. Contour plots for models 0.9, 1.1, and 1.2 were also obtained and are available on demand. The three iterations showing how the optimization ranges—dimensions in horizontal and vertical axes—varied until finding the optimal values are depicted in Figure 9. As explained, the initial structure was scaled up and down, employing design tables for automating the process, and analysed under typical loading conditions, first excluding thermal loading and then adding it to the simulation. A comparison of the achieved data is given. Scaling relationships were derived by fitting trendlines and validating the retrieved equations with further FE studies. Models were also evaluated from an environmental point of view, with the aim of determining the impact of including the thermal loading into the machine’s design. Results at a turbine level and at generator-only level are presented.

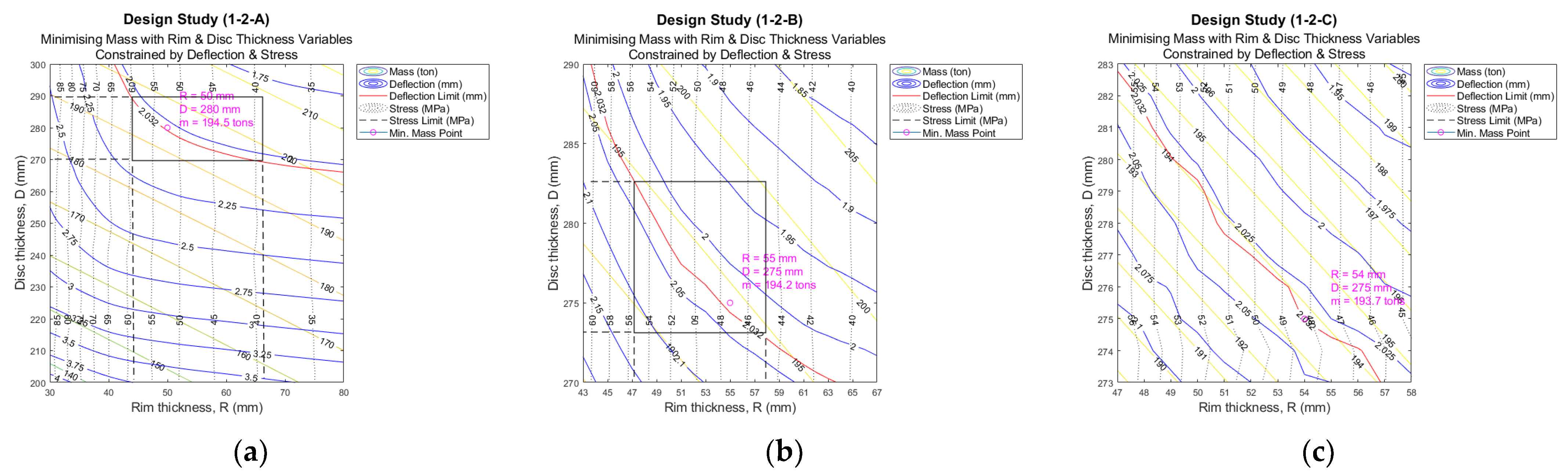
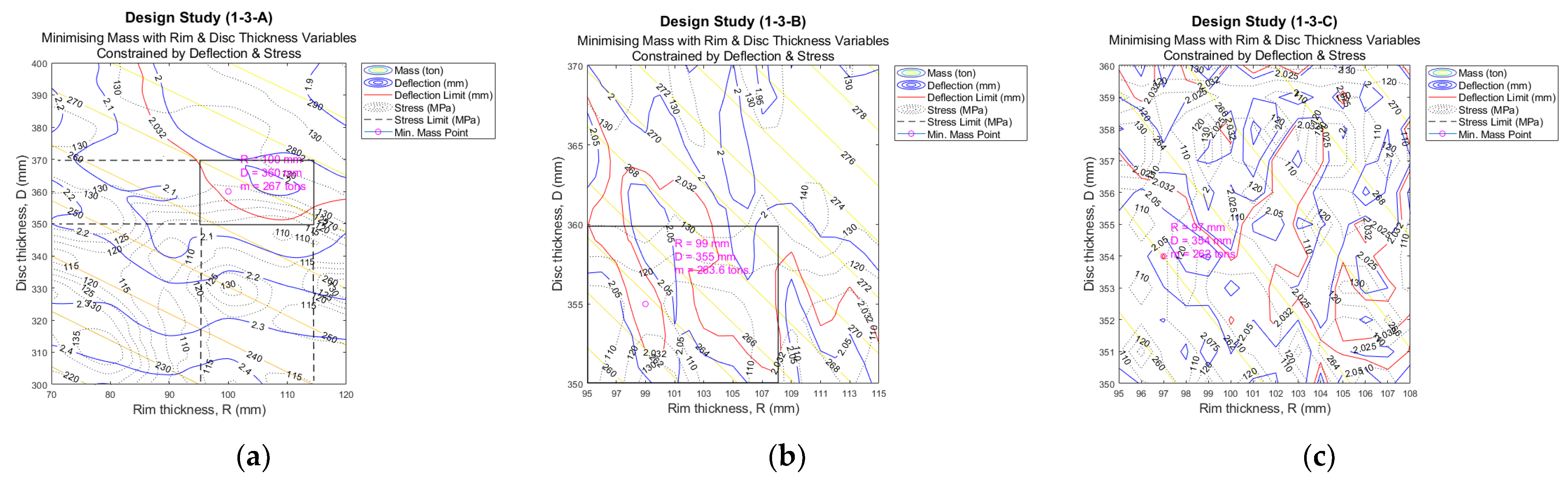
Figure 9.
Design study 1-2 (1.0 scale of the 15 MW reference turbine) contour plots, excluding thermal loading: (a) initial iteration of parametric optimization; (b) second iteration of parametric optimization; (c) final iteration of parametric optimization.
3.1. Comparison between Structures Using Contour Plots
As one can see in Figure 9, with contour plots, it is easy to identify patterns and areas of interest. By highlighting the deflection (in red) and stress limits (in dotted black), a potential zone can be differentiated. Utilizing the data available, a point where both design variables, disc thickness in mm in the vertical axis and rim thickness in mm in the horizontal axis, are optimised. See the values in purple. It is important to highlight the fact that the contour plots shown here show clear trends for the structural mass (in yellow) and deflection (in blue), which facilitates the manual/visual selection of potential candidates.
However, the introduction of the thermal loading has a significant effect, which can be observed in Figure 10.

Figure 10.
Design study 1-3 (1.0 scale of the 15 MW reference turbine) contour plots, including thermal loading: (a) initial iteration of parametric optimization; (b) second iteration of parametric optimization; (c) final iteration of parametric optimization.
A much less predictable behaviour is seen when the loading is introduced. Although mass (in yellow) maintains a similar trend, the deflection is very volatile. It is even worse as the model is refined (1-3-C according to naming convention). Selecting a point in a visual manner becomes more difficult, as deflection and stress limits are unpredictable. It is clear that the dimensions of the rotor disc and rim thicknesses need to be considerably increased when considering the operating temperature, to comply with the imposed deflection and stress requirements. Comparing the values from Figure 9c and Figure 10c, it can be noted that thicknesses increases from 54 and 275 mm for the rim and the disc, respectively, with a total mass of 193.7 tons, to 97 mm for the rim thickness and 354 mm for the disc thickness, with a total mass of 262 tons. This is an increment in the required mass of more than 26%. An increase in stress is also noticeable, from maximum values of around 50 MPa without the load to values of around 100 MPa and over when temperature is included, which must be considered when estimating the structure working life. Nonetheless, the authors believe that the temperature influence needs to be further analysed, as the increment in size presents additional considerations for the designer, as a thicker structure is able to store more heat.
Across all eight design studies, an average of 77.5 FE scenarios were generated in order to develop each contour plot, with each design study scenario taking anywhere between 20 s and 2 min to calculate.
3.2. Deriving Validated Scaling Rules
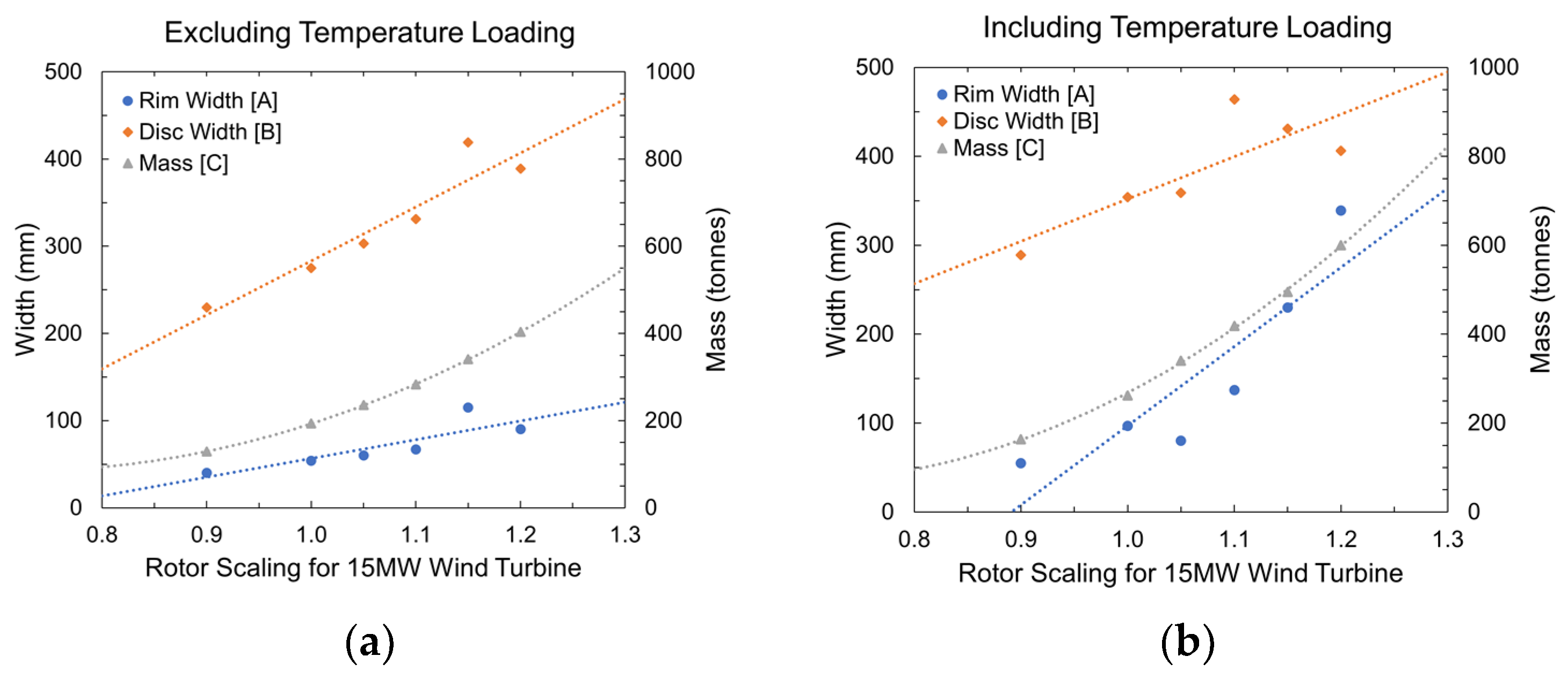
In Figure 11, graphs showing the behaviour of both disc and rim thicknesses plus the total mass for different model scales are plotted for comparison. As described, four models were simulated first, so a trendline could be fitted and an equation found. Then, the equation was validated and refined, picking points within the trendline and simulating them under the specified characteristics. These graphs are obtained from scrutinizing six models of different sizes. Taking the 15 MW machine as the base case, its scale was reduced by 10% (corresponding to 0.9 model) and increased by 5, 10, 15, and 20% (corresponding to models 1.05, 1.1, 1.15, and 1.2). As observed, the slope of the mass [C] trendline is much steeper in Figure 11b, mainly due to the influence of the rim width [A], which, for last two models, needed masses of nearly 500 and 600 tons, respectively. A difference of about 150 and 200 tons exists if compared with the data given in Figure 11a, which reflects the total mass. Although the behaviour of the disc changes, it plays a less important role in the development of the total mass of the models.
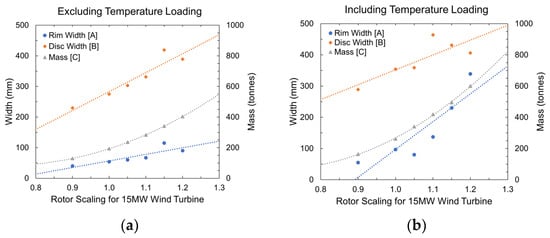
Figure 11.
Validated scaling relationships: (a) excluding temperature loading; (b) including temperature loading.
Fitted equations and R2 values are listed in Table 5 for disc, rim, and total mass for the models, with and without thermal loading. Good correlation was observed for the models. The values for the rim width [A] and disc width [B] in Figure 11b show volatility; however, this can be attributed to the outliers created when including the temperature loading, as demonstrated in the contour plot in Figure 10c. A higher R2 value could be achieved for these fitted equations if the outliers were ignored; however, the minimisation of mass was instead prioritised. The mass [C] fitted equations in Figure 11a,b demonstrate this, with a high R2 value. Ultimately, the equations are a quick tool to estimate mass or rim and disc thicknesses for a rotor of approximately 15 MW. Further data would help refine these equations.

Table 5.
Disc, rim and mass scaling equations.
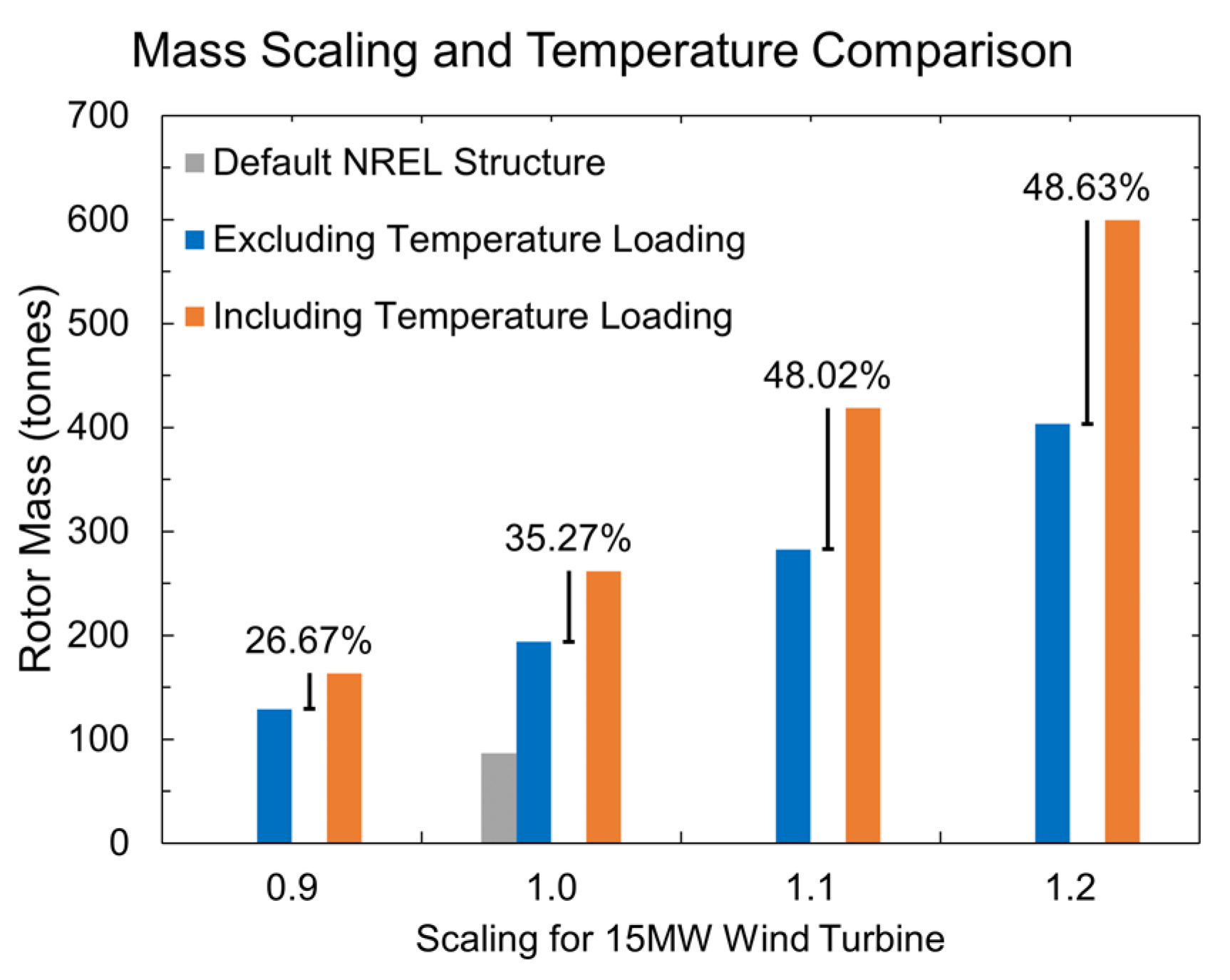
Figure 12 depicts the total mass needed when scaling the electrical generator as well as the difference between the models including the temperature and the models excluding it.
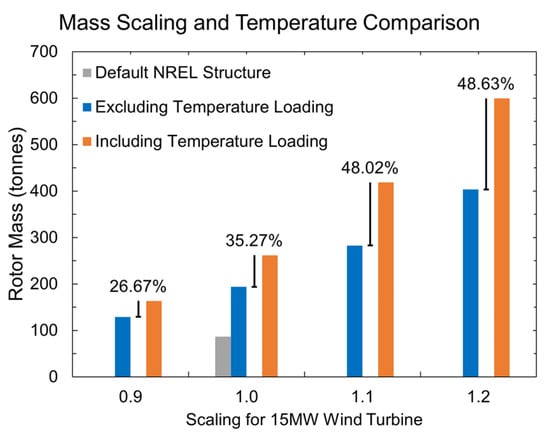
Figure 12.
Mass scaling and temperature comparison.
As one can see, 35.27% more mass is required for the base case when temperature is considered. This figure increases as the size of the models increases, being more than 48% when scaling up by 10 and 20%. This has a significant influence in the turbine’s environmental impact and cost, as explained in the following sub-section. Note that the default NREL structure, in grey, did not comply with the typical operating structural requirements and that its mass had to be almost doubled, as shown in Figure 12.
3.3. LCA—Turbine and Electrical Generator Rotor
In this sub-section, the authors compare the environmental impact caused by the machines at different scales, as well as their costs, at a full-turbine level and at an electrical-generator-rotor level only.
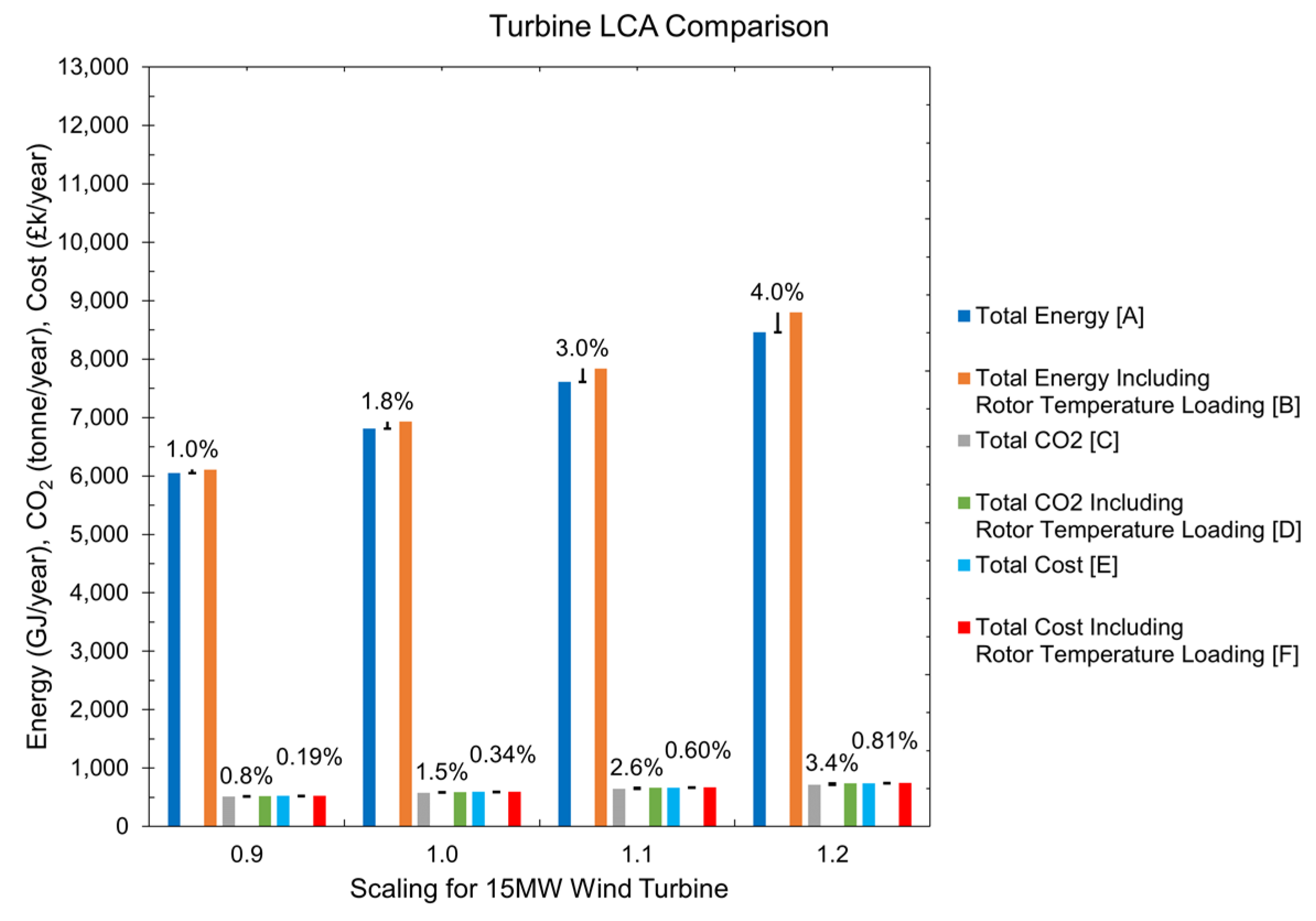
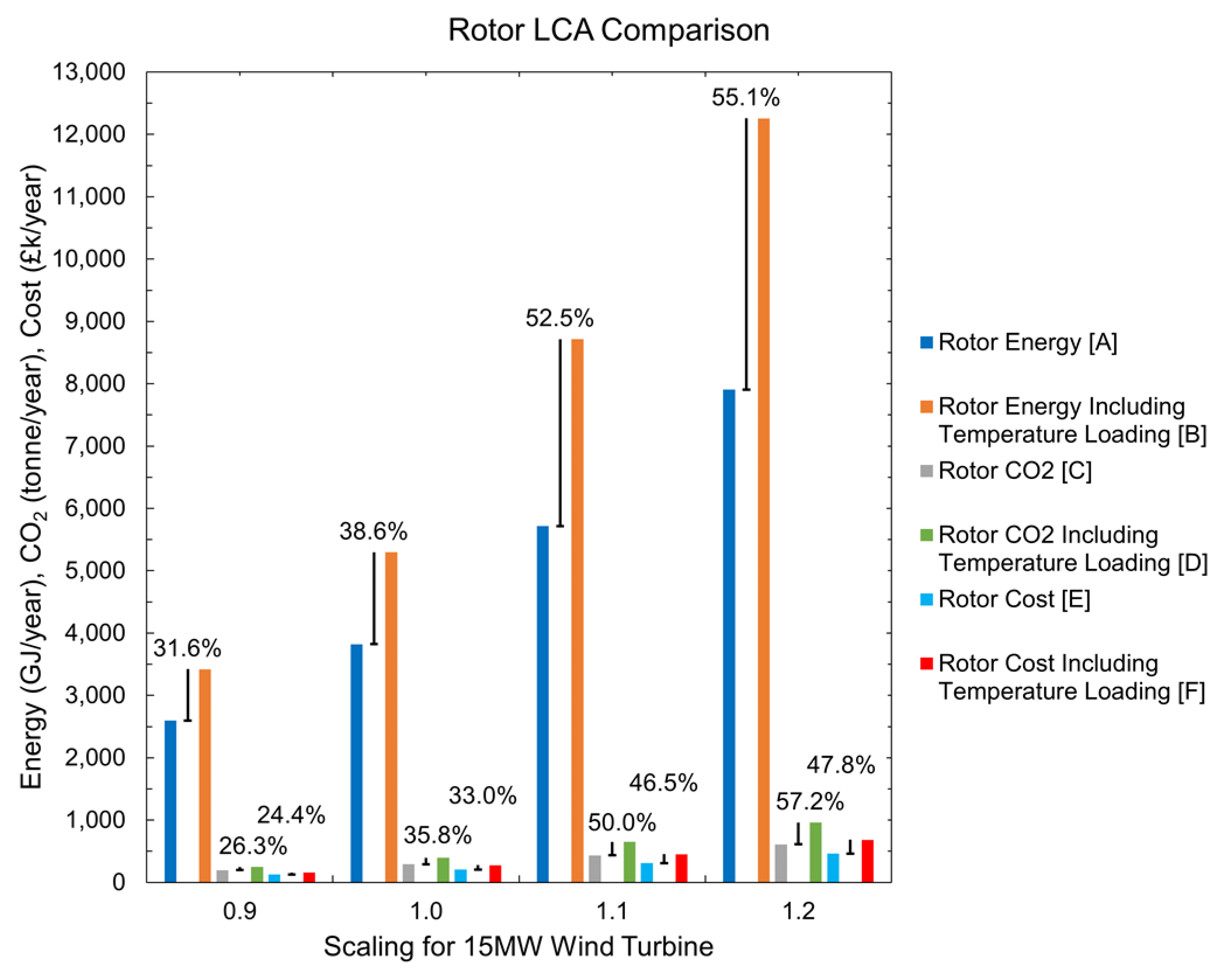
In Figure 13, three indicators—annual energy burden, CO2 footprint, and cost per year—are shown for comparison. These include material, manufacturing, transport, use, disposal, and End-of-Life (EoL) potential, averaged over 25-year product life. Values seem to be small at first sight, but it must be remembered that the data given here correspond to considering a load in a particular mechanical component, like the supporting structure of the electrical generator rotor. By looking at the total energy for the 1.0 model, a difference of 1.8% can be observed. At the same time, CO2 emissions increase by 1.5%, and the total cost for the turbine increases by 0.34%. Similar trends are seen in the other models. Figure 14 gives a clear picture of the environmental impact at the electrical-generator-rotor level only.
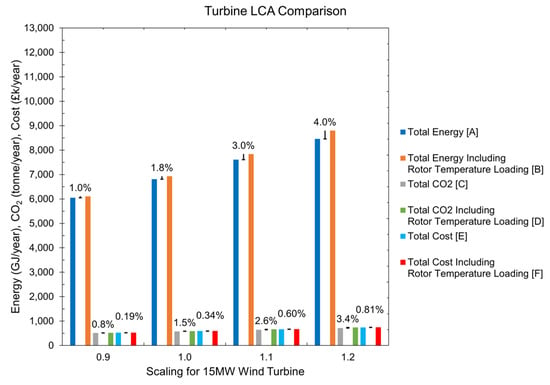
Figure 13.
Full turbine LCA comparison showing energy, CO2 emissions, and costs per year.
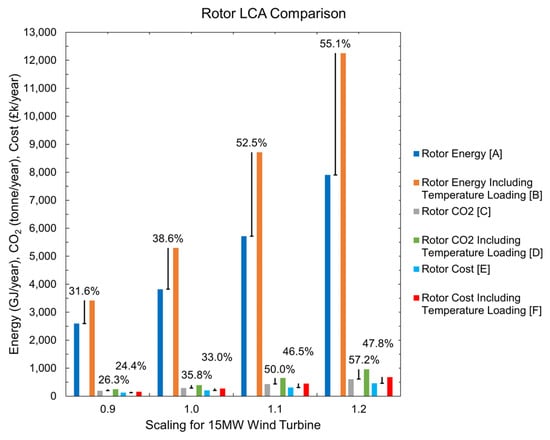
Figure 14.
Electrical generator rotor LCA comparison showing energy, CO2 emissions, and costs per year.
The LCA results show the impact that the rotor has on the environment. Extracted from the overall EcoAudit+, the data show how temperature loading creates a significant impact for both the annual energy burden, from 31.6% to 55.1%, and CO2 footprint, ranging from 26 to 57%, as well as in the annual cost, from 24 to 49%. Looking at the 1.0 model, an increment of 38.6% in total energy is observed. CO2 emissions and cost increase by 35.8% and 33%, respectively. Differences can be easily spotted at a machine level, giving the reader the opportunity to understand the consequences of considering this load from distinct perspectives.
4. Conclusions
This investigation is centred on the analysis and optimization of the 15 MW Offshore Reference Wind Turbine Electrical Generator Rotor supporting structure. As demonstrated, the structure initially analysed did not comply with the traditionally imposed deflection and equivalent stress limitations under typical working conditions. This work corroborates the findings of other authors in this sense. Bearing this in mind, the authors augmented the search range during the optimization process. The introduction of more mass than initially anticipated plus the mass required to withstand the thermal loading increased the mass of the supporting structure considerably—by more than 26%—with the consequent rise in cost. The optimised model, capable of complying with the structural requirements, was then scaled up and down with the aim of finding the scaling rules governing this process through the use of finite element techniques. Scaling equations were proven to be a viable method to estimate the approximate disc and rim thicknesses necessary for the desired scale for this rotor design configuration. The addition of temperature loading had a significant impact on mass. Thus, in the design of the load-bearing structure, the temperature loading of the rotor must be accounted for, particularly with increased scale.
The rotor had a significant percentage impact on the overall life cycle, regardless of whether temperature was included, from 1 to 4% for both the energy burden and CO2 footprint, and from 0.34 to 0.81% for the cost. Considering that these changes are generated by the inclusion of one load in the supporting structure of a particular component of the turbine powertrain, the authors believe that it is of relevance and needs to be considered, especially as turbines’ size increases. The results from the rotor structure for LCA comparison only showed a much more profound change for electrical generator manufacturers.
The obtained data demonstrated a more pragmatic consideration of the impact of the added mass from temperature loading. Further investigation is needed into the scaling equations, as more data will ensure further accuracy. Temperature loading is particularly fickle, as shown by the contour plots, and the authors recommend further research in this area. It is expected that temperature changes during long periods of high and low rotational speeds will introduce a fluctuating stress, whose amplitude will need to be added to the current estimated amplitudes, which that do not consider this load; this will determine the real level of fatigue experienced by the structure and its working lifetime. Increasing the mass with the aim of making the structure capable of withstanding the loads also has an important disadvantage. Since the conventionally employed structural materials have high heat conductivity coefficients, the more mass that is added, the more room there is for thermal heat to store. Finding the optimum point between preventing high deformation and heat storage limits could be an interesting area of research.
Author Contributions
Conceptualization, L.T. and P.J.S.; methodology, P.J.S.; resources, P.J.S.; software, L.T.; formal analysis, L.T.; investigation, L.T.; data curation, L.T.; writing—original draft preparation, P.J.S. and L.T.; writing—review and editing, P.J.S. and E.O.; supervision, P.J.S. and E.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Bill of Materials
Due to the sustainability aspect, the Level 3 Sustainability Database was selected, but this required more specific material selections. The result of this was the “BoM” included below (see Table A1), which is expanded further in Appendix B for use in the LCA.

Table A1.
Bill of Materials (BoM) [23].
Table A1.
Bill of Materials (BoM) [23].
| Component | Material Spec. | 1st Manuf. Process | 2nd Manuf. Process | Mass (tons) | Mass (%) |
|---|---|---|---|---|---|
| Yaw System | Low alloy steel, AISI 4140, normalised | Casting | Fine machining | 100 | 3.04 |
| Turret Nose | Cast iron, nodular graphite, EN GJS 400 18 LT | Casting | Grinding | 11.394 | 0.35 |
| Total Rotor Structural Steel Mass | Low alloy steel, AISI 4140, normalised | Casting | Coarse machining | 86.2 | 2.62 |
| Total Stator Structural Steel Mass | Low alloy steel, AISI 4140, normalised | Casting | Coarse machining | 71.1 | 2.16 |
| Iron | Air melted magnetic iron | Forging | Fine machining | 180.95 | 5.49 |
| Copper | Copper, C12200, hard (phosphorous deoxidised arsenical h.c. copper) | Wire drawing | Cutting and trimming | 9.01 | 0.27 |
| Permanent Magnet | Neodynium magnet N40UH | Casting | Fine machining | 24.2 | 0.73 |
| Shaft | Low alloy steel, AISI 4140, normalised | Roll forming | Grinding | 15.734 | 0.48 |
| Hub | Cast iron, nodular graphite, EN GJS 400 18 LT | Casting | Grinding | 190 | 5.77 |
| Bedplate | Low alloy steel, AISI 4140, normalised | Casting | Coarse machining | 70.329 | 2.13 |
| Flange | Structural Steel, S355J | Forging | Fine machining | 3.946 | 0.12 |
| Misc. Equipment | N/A | N/A | N/A | 50 | 1.52 |
| Tapered Double Outer Ring | Low alloy steel, AISI 4140, normalised | Casting | Fine machining | 2.23 | 0.07 |
| Spherical Roller Bearing | Low alloy steel, AISI 4140, normalised | Casting | Fine machining | 5.664 | 0.17 |
| Blades (x3) | *** PVC cross-linked foam (rigid, closed cell, AC 0.090) | Polymer moulding | Cutting and trimming | 195.75 | 5.94 |
| Monopile—75 m | Structural Steel, S355J | Roll forming | Cutting and trimming | * 1318 | 40.01 |
| Tower—135 m | Structural Steel, S355J | Roll forming | Cutting and trimming | * 860 | 26.1 |
| Transition piece—15 m | Structural Steel, S355J | Roll forming | Cutting and trimming | ** 100 | 3.04 |
| Total Structural Mass | 3294.507 | 100 |
* Note that the mass is increased by 7% for outfitting mass. ** The transition piece is assumed to be separate from the monopile and tower at 100 tons. *** The rotor blades may require further development, as they are made from a variety of materials, which are not simple to identify in the Ansys Granta database.
Appendix B. LCA Details
The information provided in Figure A1 is a summary of all the quantities that are needed to perform the LCA, which are scaled appropriately.
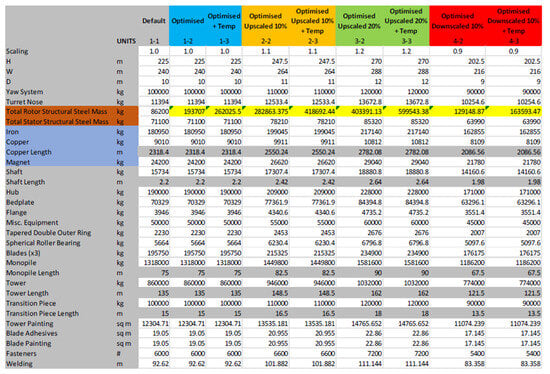
Figure A1.
LCA details.
Figure A1.
LCA details.
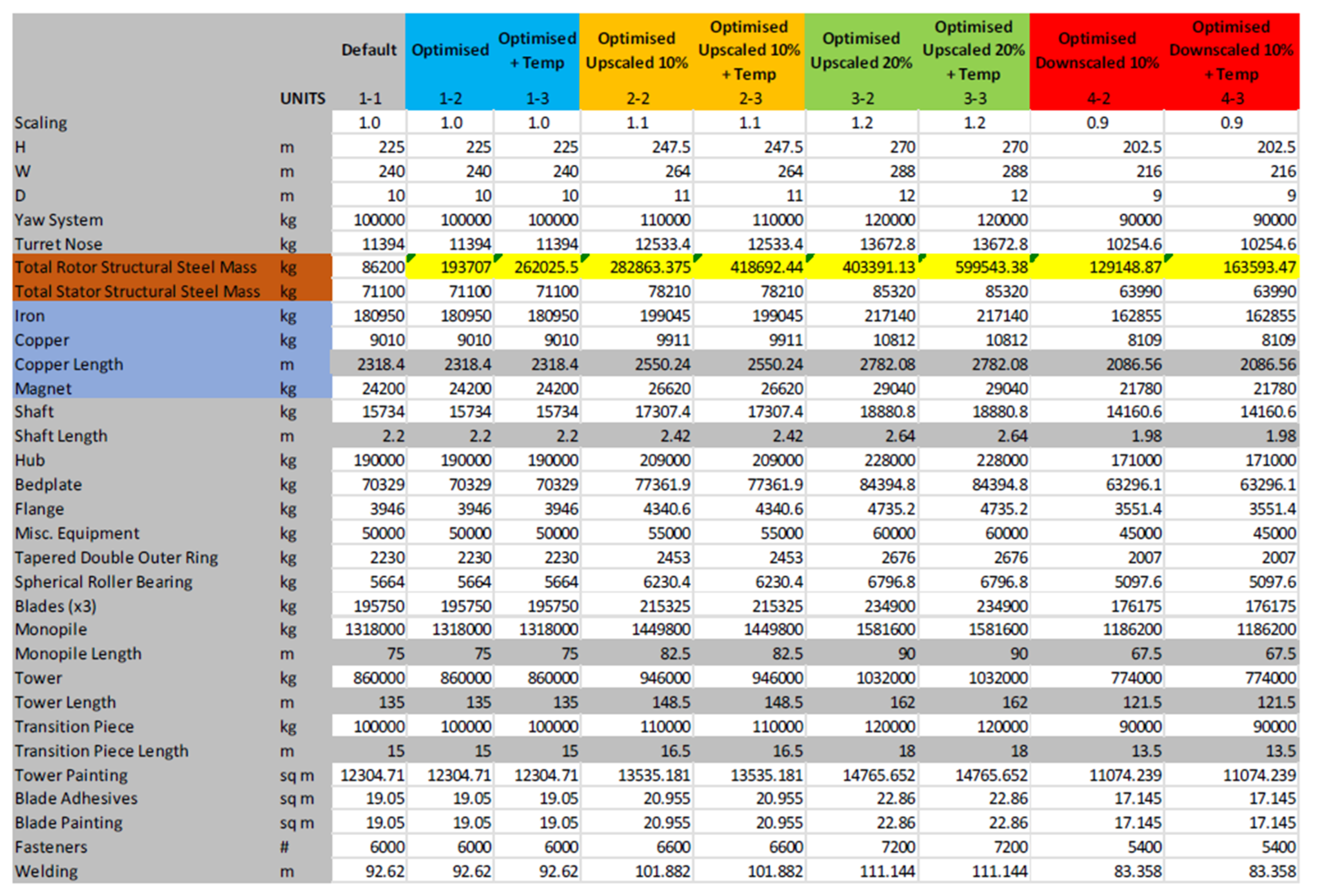
- Number of fasteners, 6000 [28];
- Tower Painting, Blade Painting, and Adhesives—surface areas found using IEA
15 MW Reference Turbine CAD model in SolidWorks [21];
12,304.71 m and (3 × 6.35 m);
- Welding length found by adding all circumference connection points in the tower, found using IEA 15 MW Reference Turbine CAD model in SolidWorks [21]: 92.62 m = 3.25 + 2.4 + 6.5 + 6.5 + 6.57 + 6.75 + 6.91 + 7.39 + 8.15 + 8.83 + 9.44 + 9.93 + 10.
References
- IPCC. AR6 Synthesis Report: Climate Change 2023—IPCC. 2023. Available online: https://www.ipcc.ch/report/sixth-assessment-report-cycle/ (accessed on 5 July 2023).
- BVG Associates. Wind Farm Costs–Guide to an Offshore Wind Farm. The Crown Estate and the Offshore Renewable Energy Category, January. 2019. Available online: https://guidetoanoffshorewindfarm.com/wind-farm-costs (accessed on 5 July 2023).
- Carroll, J.; McDonald, A.; McMillan, D. Failure rate, repair time and unscheduled O&M cost analysis of offshore wind turbines: Reliability and maintenance of offshore wind turbines. Wind Energy 2016, 19, 1107–1119. [Google Scholar]
- Tartt, K.; Amiri, A.K.; McDonald, A.; Jaen-Sola, P. Structural optimisation of offshore direct-drive wind turbine generators including static and dynamic analyses. J. Phys. Conf. Ser. 2021, 2018, 012040. [Google Scholar] [CrossRef]
- Turnbull, A.; McKinnon, C.; Carrol, J.; McDonald, A. On the Development of Offshore Wind Turbine Technology: An Assessment of Reliability Rates and Fault Detection Methods in a Changing Market. Energies 2022, 15, 3180. [Google Scholar] [CrossRef]
- Mueller, M.; Polinder, H. Electrical Drives for Direct Drive Renewable Energy Systems; Woodhead Publishing Limited: Sawston, UK, 2013. [Google Scholar]
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.E.; Abbas, N.J.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. Definition of the IEA 15 MW Offshore Reference Wind Turbine. Golden, CO. 2020. Available online: https://www.nrel.gov/docs/fy20osti/75698.pdf%0ANRE (accessed on 5 July 2023).
- Jaen-Sola, P. Advanced Structural Modelling and Design of Wind Turbine Electrical Generators. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2017. [Google Scholar]
- Chen, H.; Zuo, Y.; Chau, K.T.; Zhao, W.; Lee, C.H.T. Modern electric machines and drives for wind power generation: A reviewof opportunities and challenges. IET Renew. Power Gener. 2021, 15, 1864–1887. [Google Scholar] [CrossRef]
- McDonald, A.; Mueller, M.; Polinder, H. Structural Mass in Direct-Drive Permanent Magnets Electrical Generators. IET Renew. Power Gener. 2008, 2, 3–15. [Google Scholar] [CrossRef]
- Stander, J.N.; Venter, G.; Kamper, M.J. Review of direct-drive radial flux wind turbine generator mechanical design. Wind Energy 2012, 15, 459–472. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, A.; Matveev, A.; Nilssen, R.; Nysveen, A. High Power Generators for Offshore Wind Turbines. Energy Procedia 2013, 35, 52–61. [Google Scholar] [CrossRef]
- McDonald, A.S. Structural Analysis of Low Speed, High Torque Electrical Generators for Direct Drive Renewable Energy Converters. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2008. [Google Scholar]
- Zavvos, A. Structural Optimisation of Permanent Magnet Direct Drive Generators for 5MW Wind Turbines. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2013. [Google Scholar]
- Hayes, A.; Sethuraman, L.; Dykes, K.; Fingersh, L.J. Structural Optimization of a Direct-Drive Wind Turbine Generator Inspired by Additive Manufacturing. Procedia Manuf. 2018, 26, 740–752. [Google Scholar] [CrossRef]
- Hayes, A.C.; Whiting, G.L. Reducing the Structural Mass of Large Direct Drive Wind Turbine Generators through Triply Periodic Minimal Surfaces Enabled by Hybrid Additive Manufacturing. Clean Technol. 2021, 3, 227–242. [Google Scholar] [CrossRef]
- Gonzalez-Delgado, D.; Jaen-Sola, P.; Oterkus, E. Design and optimisation of multi-MW offshore direct-drive wind turbine electrical generator structures using generative design techniques. Ocean Eng. 2023, 280, 114417. [Google Scholar] [CrossRef]
- Jaen-Sola, P.; Oterkus, E.; McDonald, A.S. Parametric lightweight design of a direct-drive wind turbine electrical generator 574 supporting structure for minimising dynamic response. Ships Offshore Struct. 2021, 16 (Suppl. S1), 266–274. [Google Scholar] [CrossRef]
- SolidWorks. SolidWorks Academic Research. SolidWorks. 2021. Available online: https://www.solidworks.com/ (accessed on 13 April 2023).
- ORE Catapult. 7 MW Levenmouth Demonstration Turbine—ORE. Available online: https://ore.catapult.org.uk/what-we-do/testing-validation/levenmouth/ (accessed on 5 July 2023).
- Gaertner, E.; Rinker, J.; Sethuraman, L.; Zahle, F.; Anderson, B.; Barter, G.E.; Abbas, N.J.; Meng, F.; Bortolotti, P.; Skrzypinski, W.; et al. IEAWindTask37/IEA-15-240-RWT: 15MW Reference Wind Turbine Repository. Available online: https://github.com/IEAWindTask37/IEA-15-240-RWT (accessed on 5 July 2023).
- BS EN ISO 14040:2006+A1:2020; Environmental Management—Life Cycle Assessment—Principles and Framework. BSI Standards Publication: London, UK, 2006.
- ANSYS. ANSYS GRANTA Academic Research; ANSYS: Canonsburg, PA, USA, 2022. [Google Scholar]
- SeagreenWindEnergy. Seagreen Wind Energy—Home. Available online: https://www.seagreenwindenergy.com (accessed on 5 July 2023).
- SSE Seagreen 1A. Available online: https://www.seagreen1a.com (accessed on 5 July 2023).
- Seagreen. Seagreen (United-Kingdom)—Wind Farms—Online Access—The Wind Power. Available online: https://www.thewindpower.net/windfarm_en_16768_seagreen.php (accessed on 5 July 2023).
- Compass Handbooks. Marshalling Underway at Largest Offshore Wind Farm. UK Ports. 12 November 2021. Available online: https://uk-ports.org/marshalling-underway-at-largest-offshorewind-farm/ (accessed on 5 July 2023).
- Conlong, M. Optimal Way to Measure Bolt Tension in Wind Turbine in Service: Most Accurate, Quickest and Cost-Efficient? Moller International. Available online: https://mollerint.com/news/press-releases/number-of-bolts-in-a-wind-turbine/ (accessed on 5 July 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).