Anomalous Work Hardening Behavior of a Single Crystalline Co-Base Superalloy
Abstract
:1. Introduction
2. Materials and Methods
3. Results
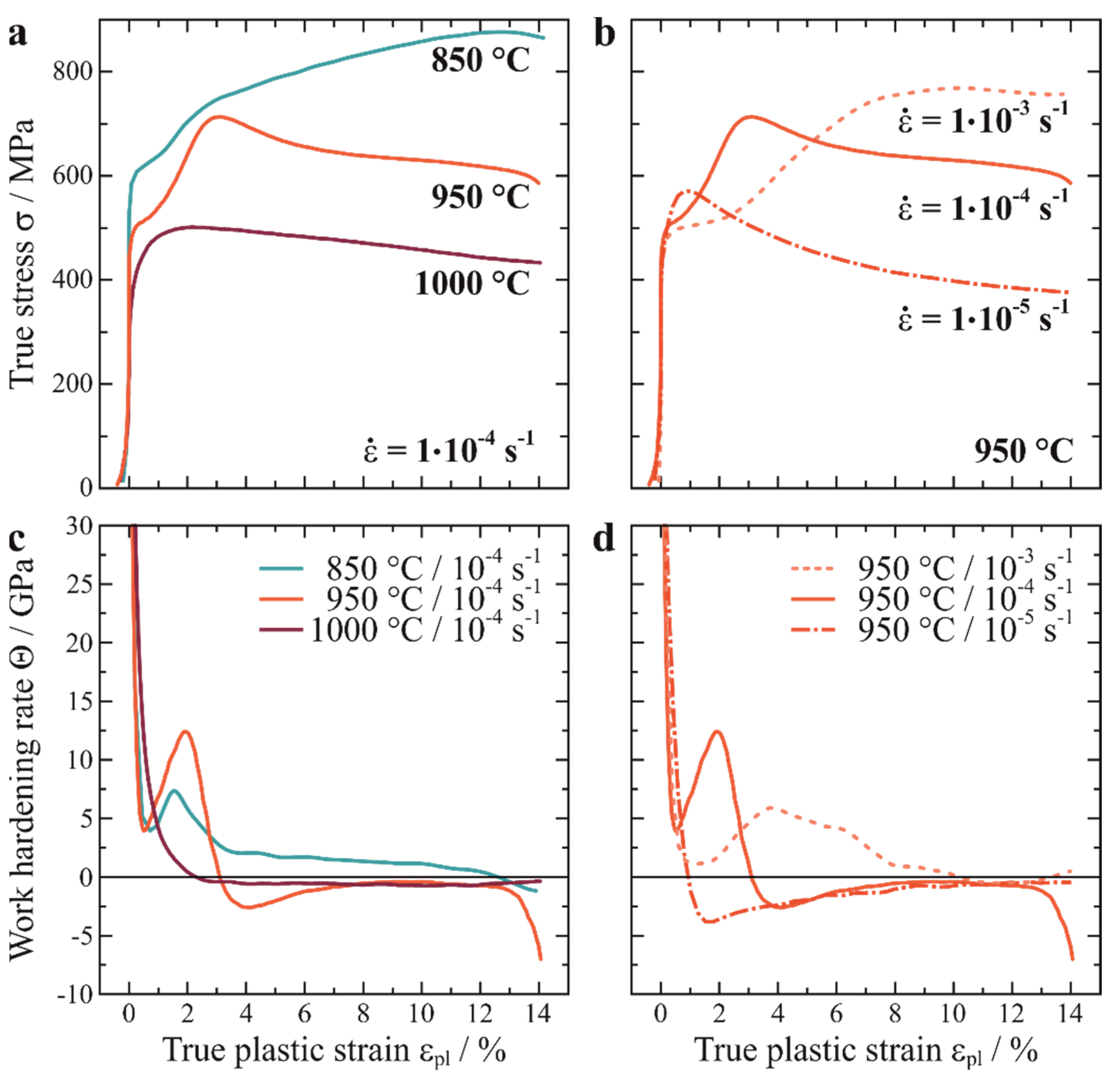
3.1. Mechanical Properties and Deformation Behavior
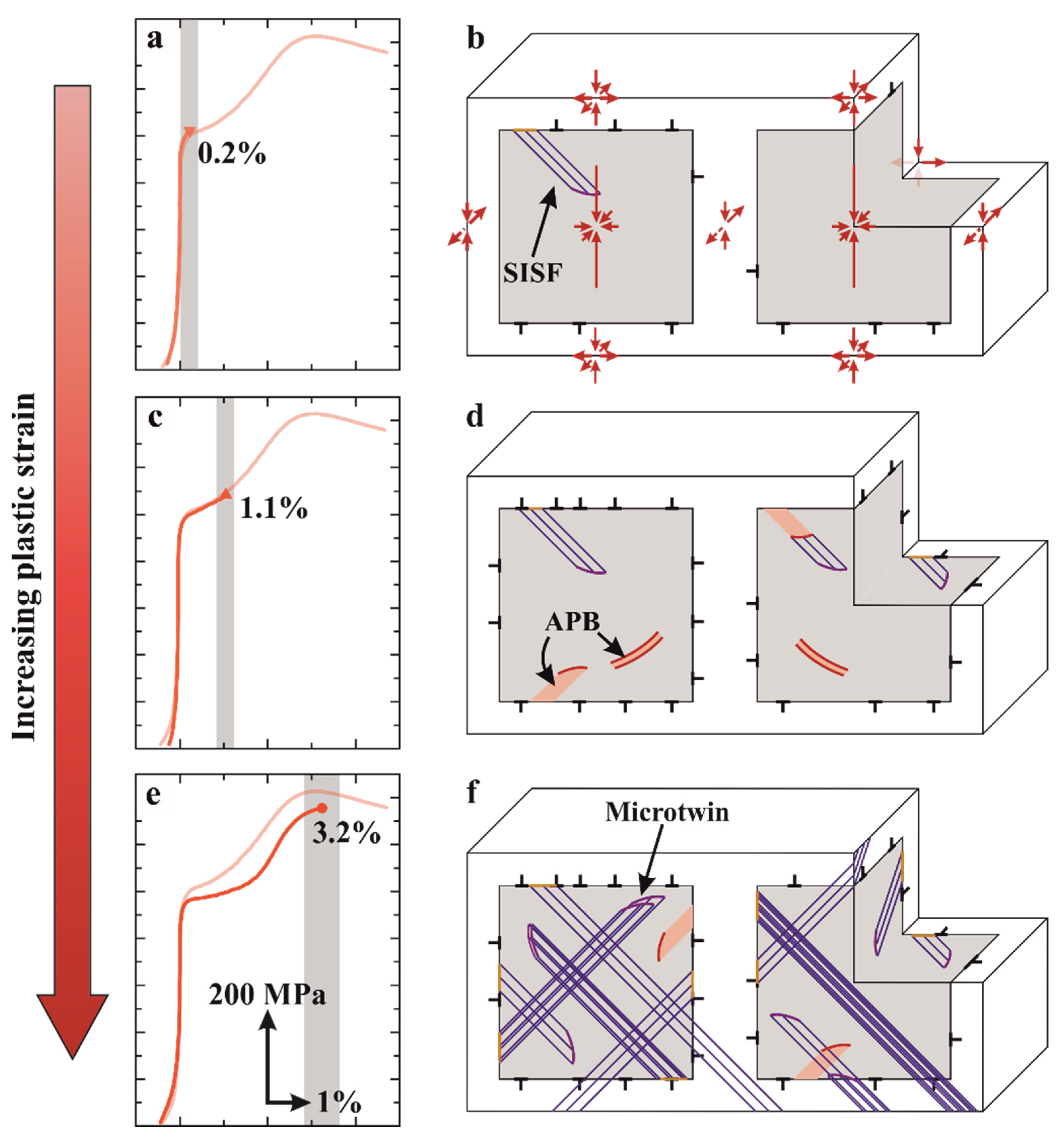
3.2. Microstructure and Deformation Mechanisms
4. Discussion
5. Conclusions
- The anomalous work hardening behavior at 950 °C and a strain-rate of 10−4 s−1 with a strength increase of approximately 200 MPa within only 3% plastic deformation are due to a change in deformation mechanism from dislocation motion in the γ matrix to extensive stacking fault formation in the γ′ precipitates, which then interact with each other and thus increase the strength.
- Since shearing of dislocations into the γ′ precipitates is facilitated by segregation, diffusion plays an important role. The significant increase in the work hardening rate and the corresponding maximum stress is reached at lower plastic strains at both higher temperatures and lower strain-rates, since segregation can occur more quickly in each case.
- At lower temperatures (850 °C) or higher temperatures (1000 °C) no (distinct) intermediate increase in the work hardening behavior occurs. While diffusion is either too slow so that the segregation of alloying elements may be less pronounced or take too much time at lower temperatures, the situation is reversed at too high temperatures as segregation occurs too quickly, weakening the hardening contribution of stacking faults, increasing the dislocation velocity, and facilitating microtwinning and microstructural degradation processes.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sato, J.; Omori, T.; Oikawa, K.; Ohnuma, I.; Kainuma, R.; Ishida, K. Cobalt-Base High-Temperature Alloys. Science 2006, 312, 90–91. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; DeNolf, G.C.; Pollock, T.M. Flow stress anomalies in γ/γ′ two-phase Co–Al–W-base alloys. Scr. Mater. 2007, 56, 385–388. [Google Scholar] [CrossRef]
- Suzuki, A.; Pollock, T.M. High-temperature strength and deformation of γ/γ′ two-phase Co–Al–W-base alloys. Acta Mater. 2008, 56, 1288–1297. [Google Scholar] [CrossRef]
- Bauer, A.; Neumeier, S.; Pyczak, F.; Göken, M. Microstructure and creep strength of different γ/γ′-strengthened Co-base superalloy variants. Scr. Mater. 2010, 63, 1197–1200. [Google Scholar] [CrossRef] [Green Version]
- Klein, L.; Shen, Y.; Killian, M.S.; Virtanen, S. Effect of B and Cr on the high temperature oxidation behaviour of novel γ/γ′-strengthened Co-base superalloys. Corros. Sci. 2011, 53, 2713–2720. [Google Scholar] [CrossRef]
- Xue, F.; Wang, M.; Feng, Q. Alloying Effects on Heat-Treated Microstructure in Co-Al-W-Base Superalloys at 1300 °C and 900 °C. In Superalloys 2012; TMS: Warrendale, PA, USA, 2012; pp. 813–821. ISBN 978-1-118-51643-0. [Google Scholar]
- Titus, M.S.; Suzuki, A.; Pollock, T.M. Creep and directional coarsening in single crystals of new γ–γ′ cobalt-base alloys. Scr. Mater. 2012, 66, 574–577. [Google Scholar] [CrossRef]
- Meher, S.; Yan, H.-Y.; Nag, S.; Dye, D.; Banerjee, R. Solute partitioning and site preference in γ/γ′ cobalt-base alloys. Scr. Mater. 2012, 67, 850–853. [Google Scholar] [CrossRef]
- Klein, L.; Killian, M.S.; Virtanen, S. The effect of nickel and silicon addition on some oxidation properties of novel Co-based high temperature alloys. Corros. Sci. 2013, 69, 43–49. [Google Scholar] [CrossRef]
- Bezold, A.; Volz, N.; Lenz, M.; Zenk, C.H.; Spiecker, E.; Mills, M.; Göken, M.; Neumeier, S. Yielding behavior of a single-crystalline γ’-strengthened Co-Ti-Cr superalloy. Scr. Mater. 2021, 200, 113928. [Google Scholar] [CrossRef]
- Bezold, A.; Volz, N.; Lenz, M.; Karpstein, N.; Zenk, C.H.; Spiecker, E.; Göken, M.; Neumeier, S. Quantification of the temperature-dependent evolution of defect structures in a CoNi-base superalloy. Acta Mater. 2022, 227, 117702. [Google Scholar] [CrossRef]
- Cao, B.X.; Xu, W.-W.; Yu, C.Y.; Wu, S.W.; Kong, H.J.; Ding, Z.Y.; Zhang, T.L.; Luan, J.H.; Xiao, B.; Jiao, Z.B.; et al. L12-strengthened multicomponent Co-Al-Nb-based alloys with high strength and matrix-confined stacking-fault-mediated plasticity. Acta Mater. 2022, 229, 117763. [Google Scholar] [CrossRef]
- Xue, F.; Zhou, H.J.; Shi, Q.Y.; Chen, X.H.; Chang, H.; Wang, M.L.; Feng, Q. Creep behavior in a γ′ strengthened Co–Al–W–Ta–Ti single-crystal alloy at 1000 °C. Scr. Mater. 2015, 97, 37–40. [Google Scholar] [CrossRef]
- Titus, M.S.; Mottura, A.; Babu Viswanathan, G.; Suzuki, A.; Mills, M.J.; Pollock, T.M. High resolution energy dispersive spectroscopy mapping of planar defects in L12-containing Co-base superalloys. Acta Mater. 2015, 89, 423–437. [Google Scholar] [CrossRef]
- Zhou, H.J.; Chang, H.; Feng, Q. Transient minimum creep of a γ′ strengthened Co-base single-crystal superalloy at 900 °C. Scr. Mater. 2017, 135, 84–87. [Google Scholar] [CrossRef]
- Lu, S.; Antonov, S.; Li, L.; Feng, Q. Two Steady-State Creep Stages in Co-Al-W-Base Single-Crystal Superalloys at 1273 K/137 MPa. Metall. Mater. Trans. A 2018, 49, 4079–4089. [Google Scholar] [CrossRef]
- Lu, S.; Antonov, S.; Li, L.; Liu, C.; Zhang, X.; Zheng, Y.; Fraser, H.L.; Feng, Q. Atomic structure and elemental segregation behavior of creep defects in a Co-Al-W-based single crystal superalloys under high temperature and low stress. Acta Mater. 2020, 190, 16–28. [Google Scholar] [CrossRef]
- Zhou, H.; Li, L.; Antonov, S.; Feng, Q. Sub/micro-structural evolution of a Co–Al–W–Ta–Ti single crystal superalloy during creep at 900 °C and 420 MPa. Mater. Sci. Eng. A 2020, 772, 138791. [Google Scholar] [CrossRef]
- Viswanathan, G.B.; Shi, R.; Genc, A.; Vorontsov, V.A.; Kovarik, L.; Rae, C.M.F.; Mills, M.J. Segregation at stacking faults within the γ′ phase of two Ni-base superalloys following intermediate temperature creep. Scr. Mater. 2015, 94, 5–8. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.M.; Esser, B.D.; Antolin, N.; Viswanathan, G.B.; Hanlon, T.; Wessman, A.; Mourer, D.; Windl, W.; McComb, D.W.; Mills, M.J. Segregation and η phase formation along stacking faults during creep at intermediate temperatures in a Ni-based superalloy. Acta Mater. 2015, 100, 19–31. [Google Scholar] [CrossRef]
- Eggeler, Y.M.; Müller, J.; Titus, M.S.; Suzuki, A.; Pollock, T.M.; Spiecker, E. Planar defect formation in the γ′ phase during high temperature creep in single crystal CoNi-base superalloys. Acta Mater. 2016, 113, 335–349. [Google Scholar] [CrossRef]
- Barba, D.; Pedrazzini, S.; Vilalta-Clemente, A.; Wilkinson, A.J.; Moody, M.P.; Bagot, P.A.J.; Jérusalem, A.; Reed, R.C. On the composition of microtwins in a single crystal nickel-based superalloy. Scr. Mater. 2017, 127, 37–40. [Google Scholar] [CrossRef] [Green Version]
- Makineni, S.K.; Kumar, A.; Lenz, M.; Kontis, P.; Meiners, T.; Zenk, C.; Zaefferer, S.; Eggeler, G.; Neumeier, S.; Spiecker, E.; et al. On the diffusive phase transformation mechanism assisted by extended dislocations during creep of a single crystal CoNi-based superalloy. Acta Mater. 2018, 155, 362–371. [Google Scholar] [CrossRef]
- He, J.; Zenk, C.H.; Zhou, X.; Neumeier, S.; Raabe, D.; Gault, B.; Makineni, S.K. On the atomic solute diffusional mechanisms during compressive creep deformation of a Co-Al-W-Ta single crystal superalloy. Acta Mater. 2020, 184, 86–99. [Google Scholar] [CrossRef]
- Volz, N.; Xue, F.; Zenk, C.H.; Bezold, A.; Gabel, S.; Subramanyam, A.P.A.; Drautz, R.; Hammerschmidt, T.; Makineni, S.K.; Gault, B.; et al. Understanding creep of a single-crystalline Co-Al-W-Ta superalloy by studying the deformation mechanism, segregation tendency and stacking fault energy. Acta Mater. 2021, 214, 117019. [Google Scholar] [CrossRef]
- Barba, D.; Alabort, E.; Pedrazzini, S.; Collins, D.M.; Wilkinson, A.J.; Bagot, P.A.J.; Moody, M.P.; Atkinson, C.; Jérusalem, A.; Reed, R.C. On the microtwinning mechanism in a single crystal superalloy. Acta Mater. 2017, 135, 314–329. [Google Scholar] [CrossRef]
- Reichstein, S.; Kraft, S.; Mughrabi, H. Sequence of distinct microyielding stages of the monocrystalline nickel-base superalloy CMSX-6 at high temperatures. Int. J. Mater. Res. 2009, 100, 494–499. [Google Scholar] [CrossRef]
- Mughrabi, H. Microstructural aspects of high temperature deformation of monocrystalline nickel base superalloys: Some open problems. Mater. Sci. Technol. 2009, 25, 191–204. [Google Scholar] [CrossRef]
- Xue, F.; Zenk, C.H.; Freund, L.P.; Hoelzel, M.; Neumeier, S.; Göken, M. Double minimum creep in the rafting regime of a single-crystal Co-base superalloy. Scr. Mater. 2018, 142, 129–132. [Google Scholar] [CrossRef]
- Xue, F.; Zenk, C.H.; Freund, L.P.; Neumeier, S.; Göken, M. Understanding raft formation and precipitate shearing during double minimum creep in a γ′-strengthened single crystalline Co-base superalloy. Philos. Mag. 2021, 101, 326–353. [Google Scholar] [CrossRef]
- Bezold, A.; Volz, N.; Xue, F.; Zenk, C.H.; Neumeier, S.; Göken, M. On the Precipitation-Strengthening Contribution of the Ta-Containing Co3(Al,W)-Phase to the Creep Properties of γ/γ′ Cobalt-Base Superalloys. Metall. Mater. Trans. A 2020, 51, 1567–1574. [Google Scholar] [CrossRef]
- Volz, N.; Xue, F.; Bezold, A.; Zenk, C.H.; Fries, S.G.; Schreuer, J.; Neumeier, S.; Göken, M. Design of a Co–Al–W–Ta Alloy Series with Varying γ′ Volume Fraction and Their Thermophysical Properties. Metall. Mater. Trans. A 2021, 52, 3931–3944. [Google Scholar] [CrossRef]
- Heckl, A.; Rettig, R.; Singer, R.F. Solidification Characteristics and Segregation Behavior of Nickel-Base Superalloys in Dependence on Different Rhenium and Ruthenium Contents. Metall. Mater. Trans. A 2010, 41, 202. [Google Scholar] [CrossRef]
- Smith, T.M.; Esser, B.D.; Antolin, N.; Carlsson, A.; Williams, R.E.A.; Wessman, A.; Hanlon, T.; Fraser, H.L.; Windl, W.; McComb, D.W.; et al. Phase transformation strengthening of high-temperature superalloys. Nat. Commun. 2016, 7, 13434. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bezold, A.; Volz, N.; Xue, F.; Göken, M.; Neumeier, S. Anomalous Work Hardening Behavior of a Single Crystalline Co-Base Superalloy. Alloys 2022, 1, 243-253. https://doi.org/10.3390/alloys1030015
Bezold A, Volz N, Xue F, Göken M, Neumeier S. Anomalous Work Hardening Behavior of a Single Crystalline Co-Base Superalloy. Alloys. 2022; 1(3):243-253. https://doi.org/10.3390/alloys1030015
Chicago/Turabian StyleBezold, Andreas, Nicklas Volz, Fei Xue, Mathias Göken, and Steffen Neumeier. 2022. "Anomalous Work Hardening Behavior of a Single Crystalline Co-Base Superalloy" Alloys 1, no. 3: 243-253. https://doi.org/10.3390/alloys1030015
APA StyleBezold, A., Volz, N., Xue, F., Göken, M., & Neumeier, S. (2022). Anomalous Work Hardening Behavior of a Single Crystalline Co-Base Superalloy. Alloys, 1(3), 243-253. https://doi.org/10.3390/alloys1030015