Modelling Microstructure in Casting of Steel via CALPHAD-Based ICME Approach
Abstract
:1. Introduction
2. Theory and Methods
2.1. Thermodynamic and Kinetic Calculation for Solidification
2.2. Thermal Model
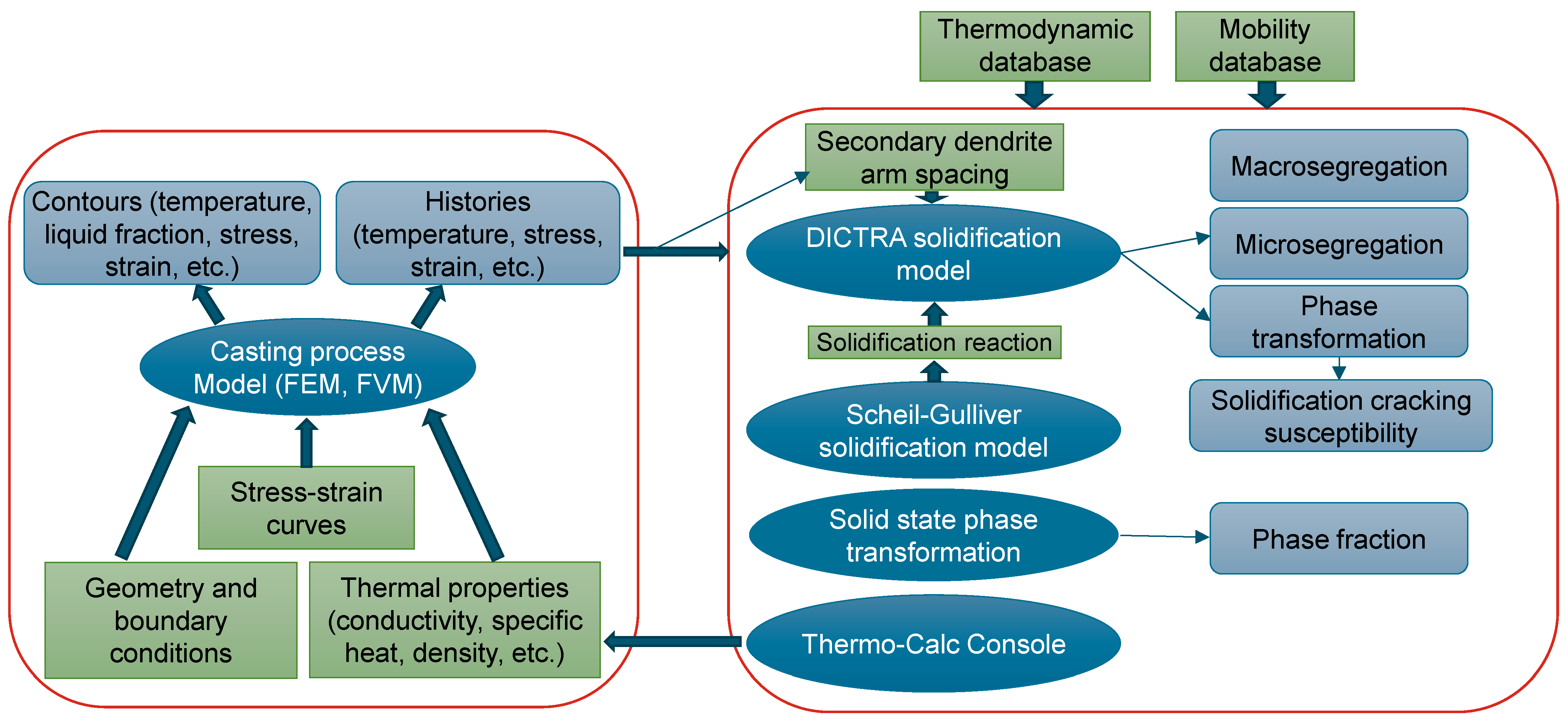
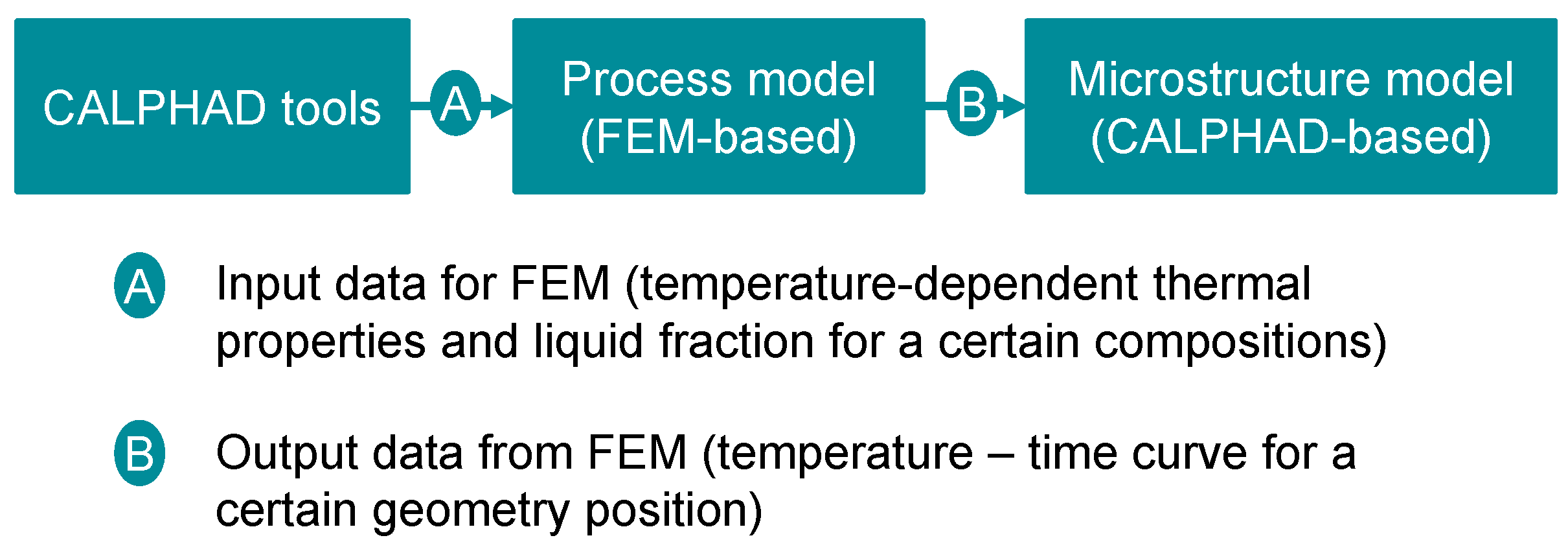
2.3. Model Integration
3. Results and Discussions
3.1. General Solidification
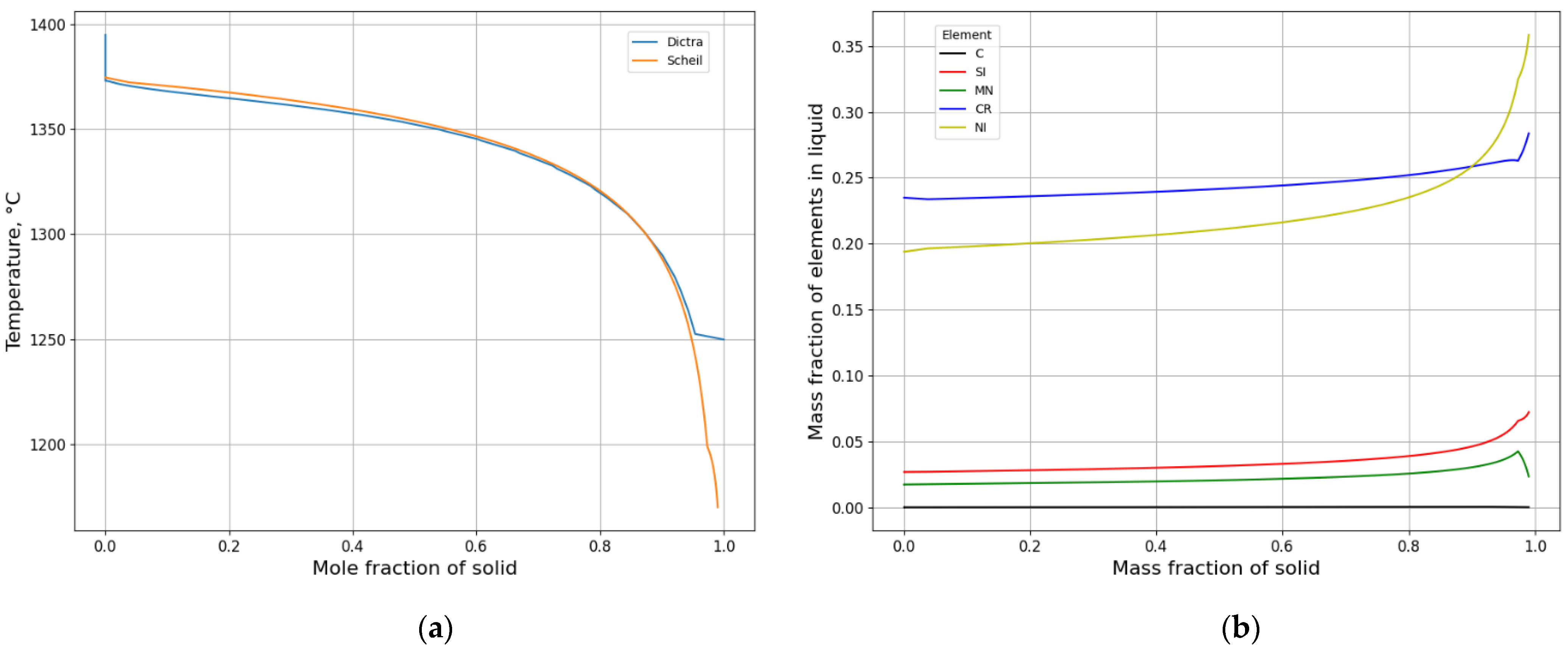
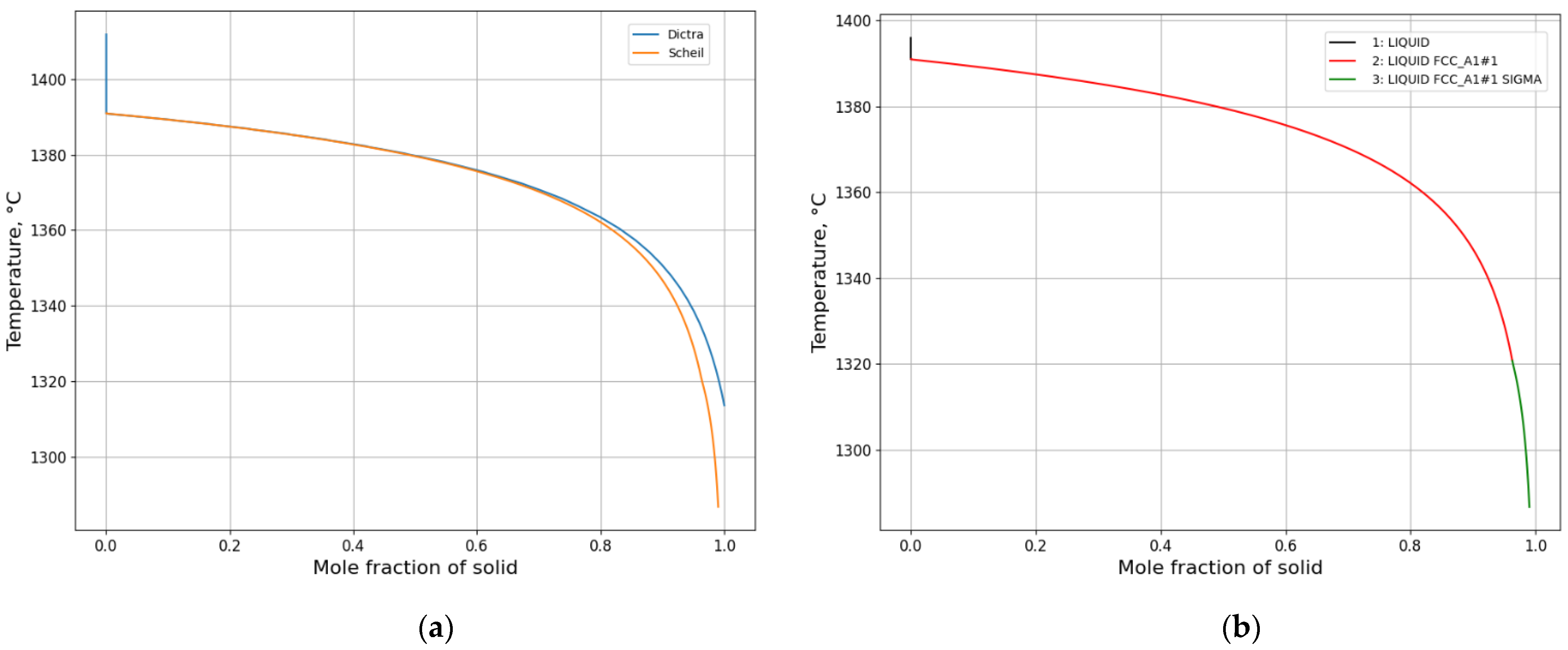
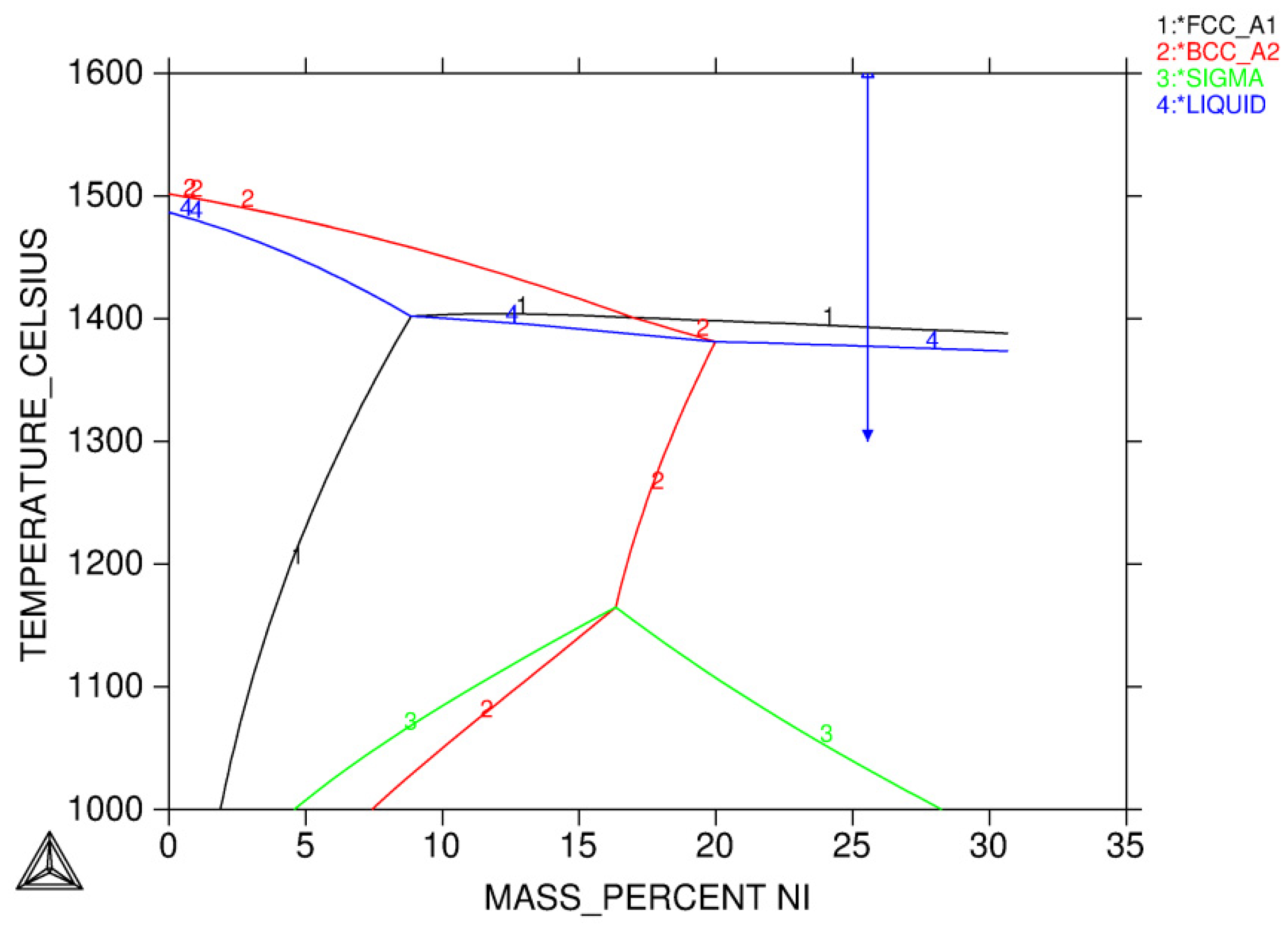
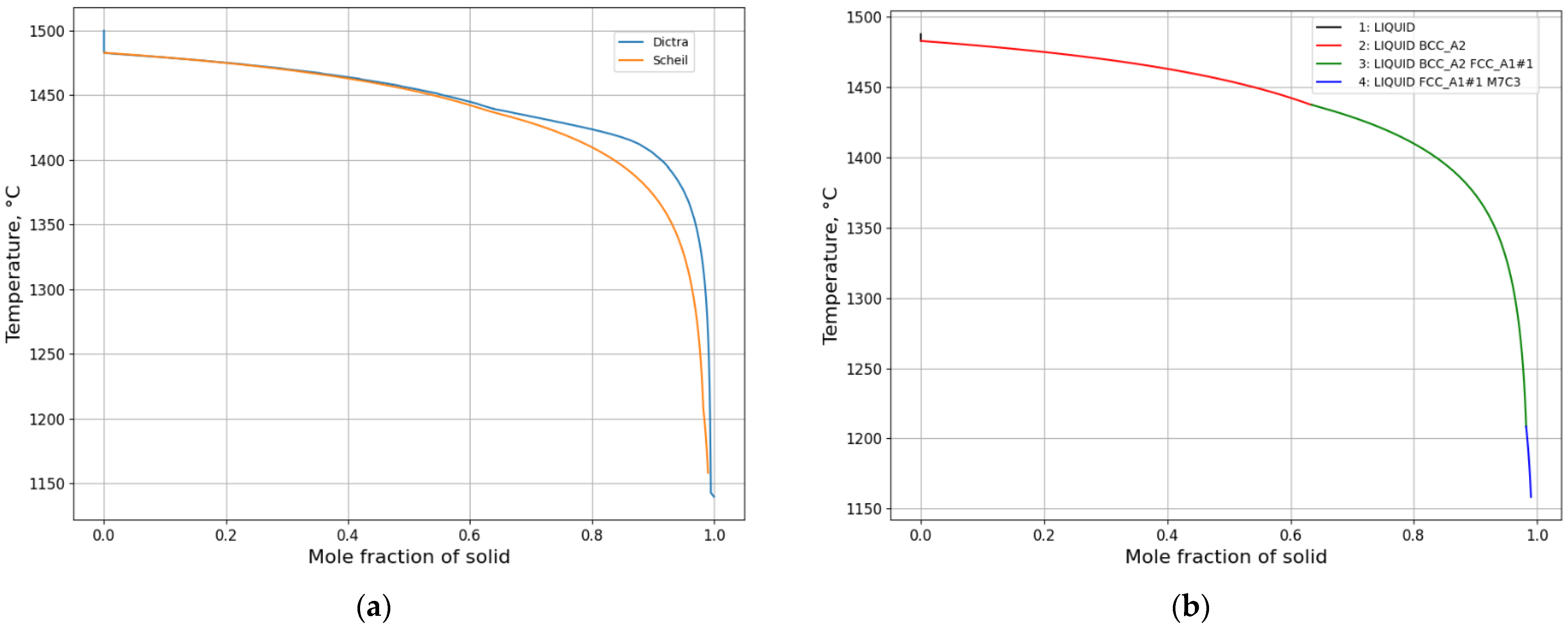
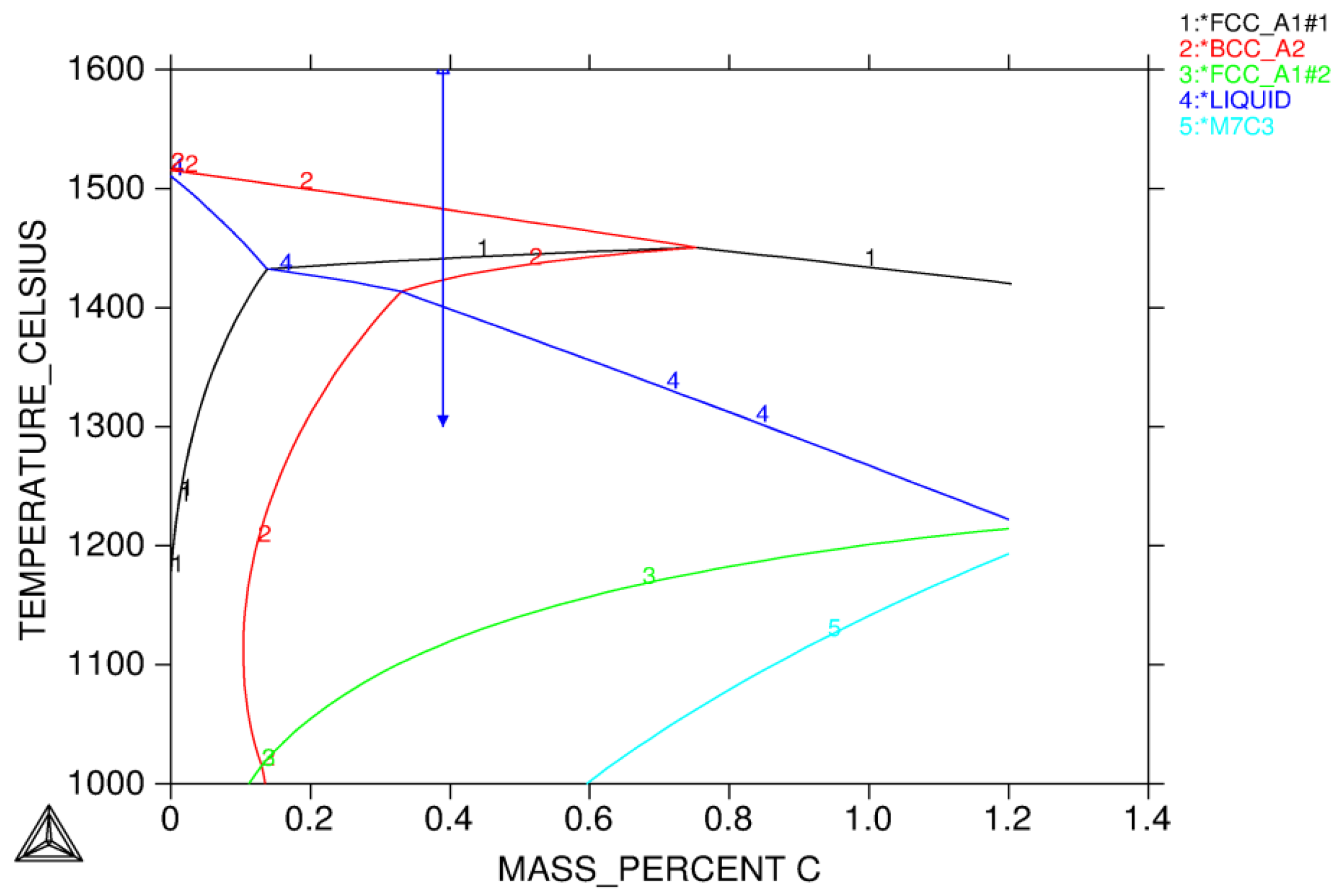
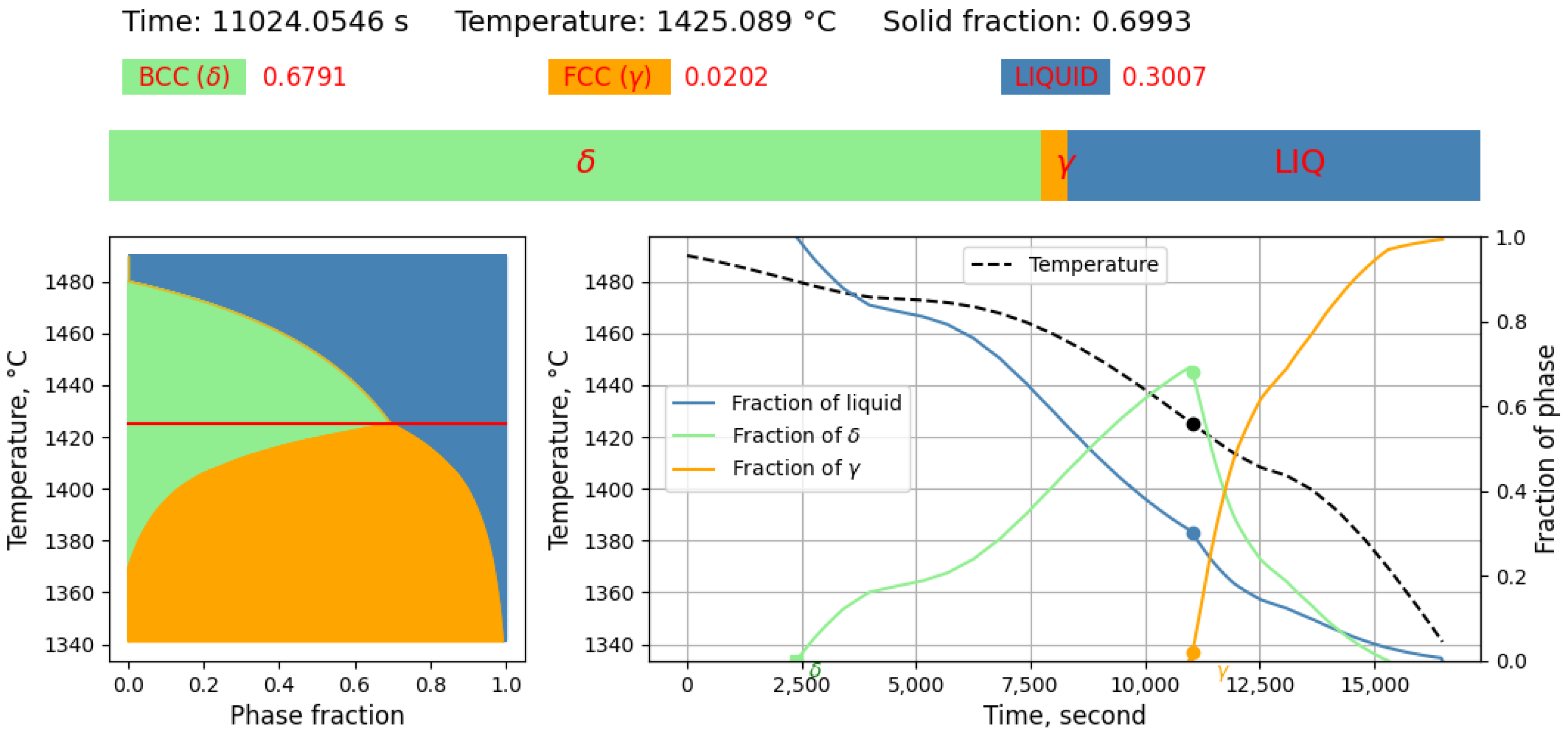
3.1.1. Solidification Path Diagram
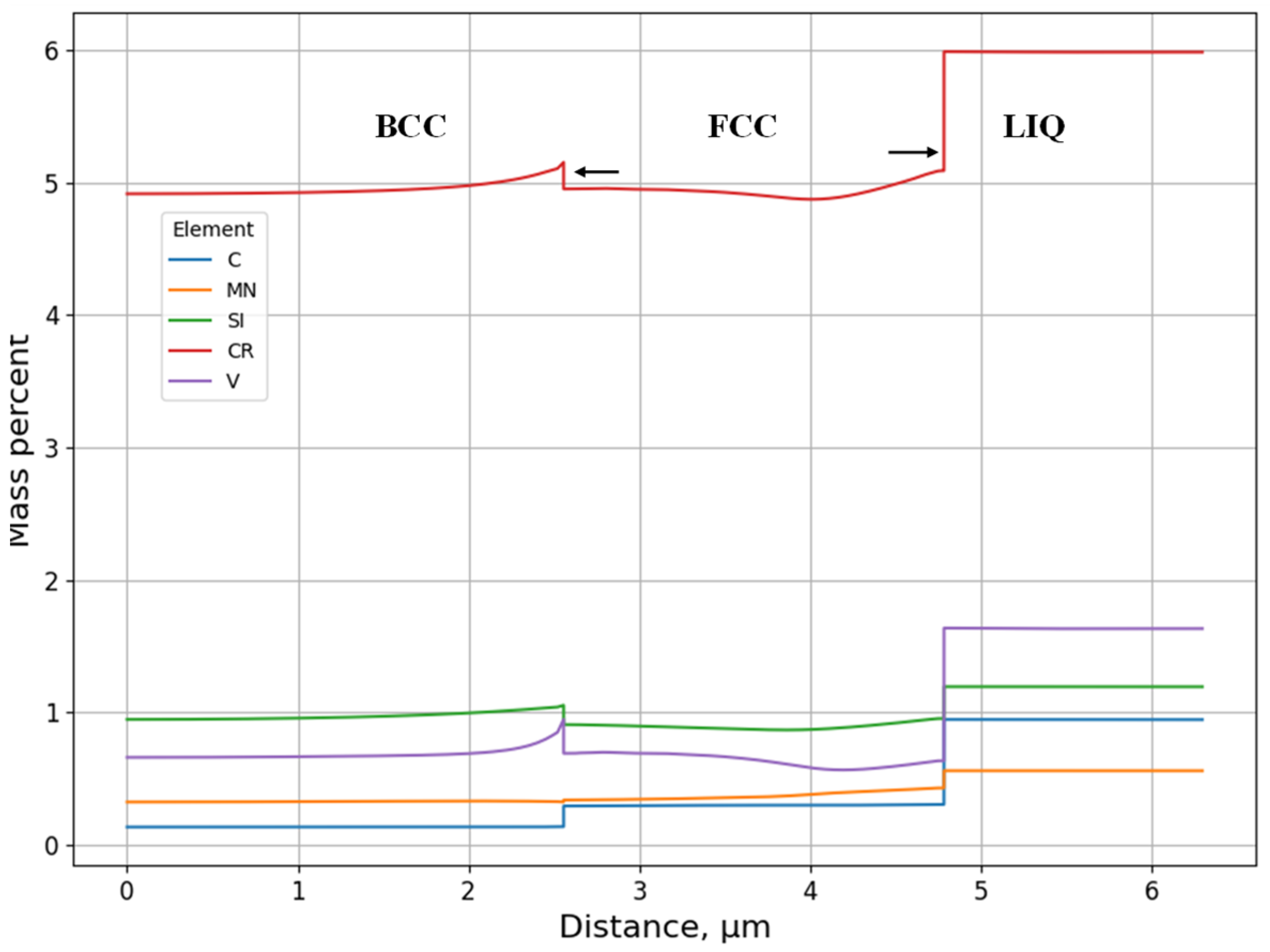
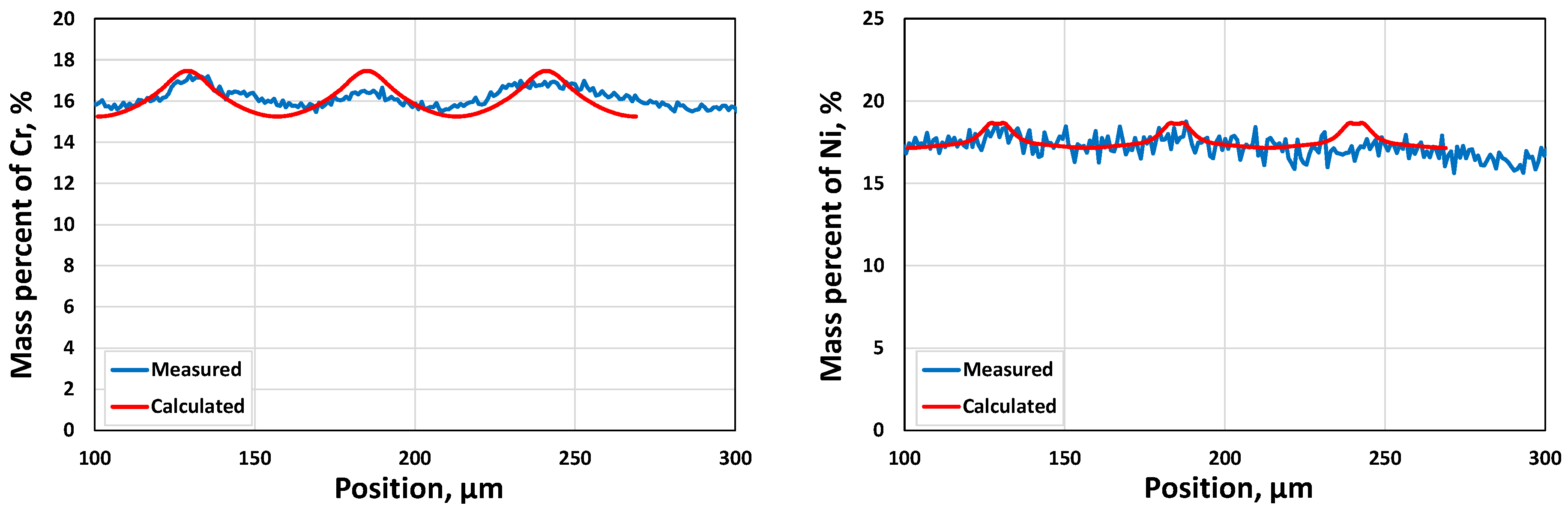
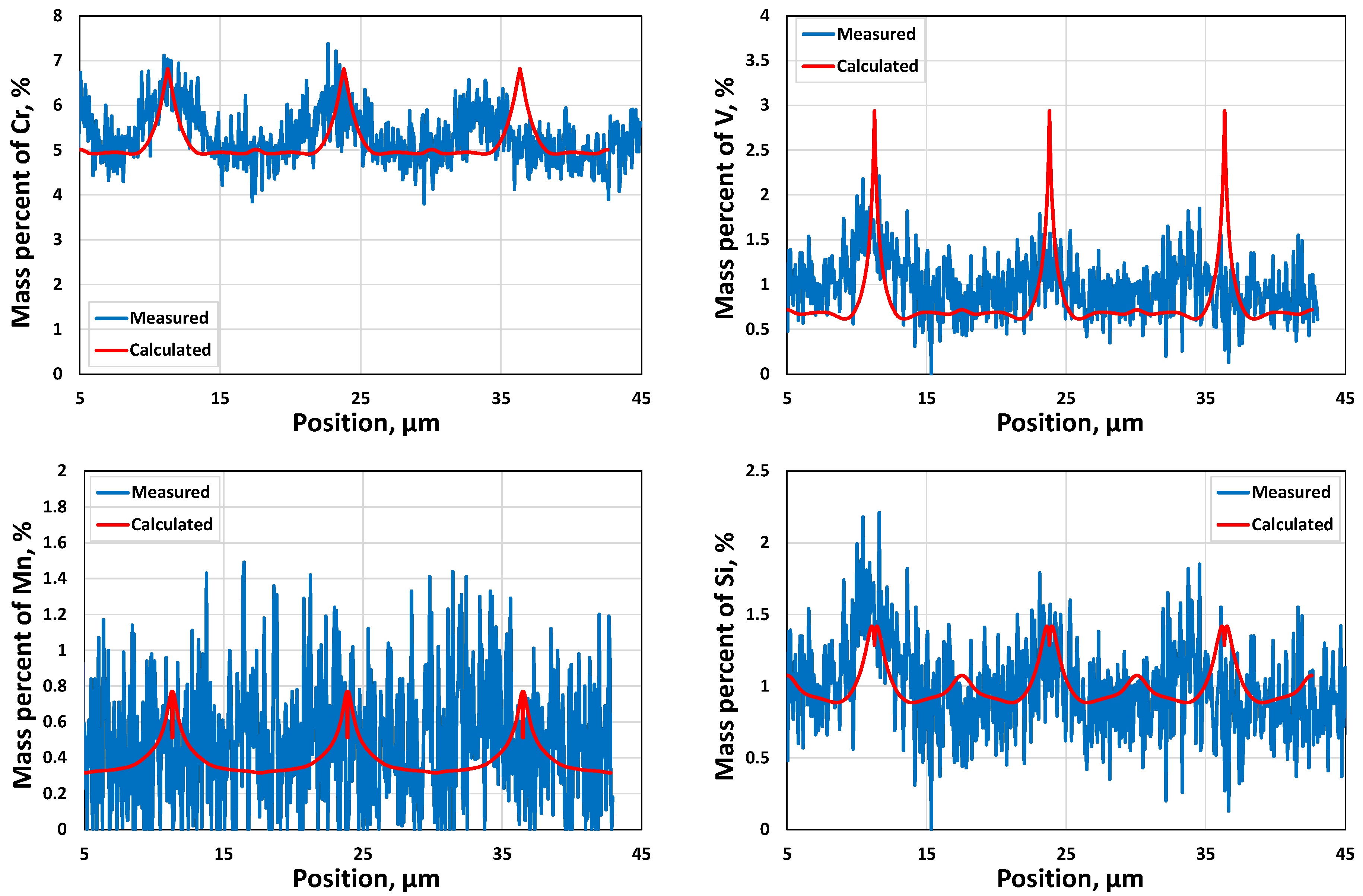
3.1.2. Microsegregation during Solidification
- (1)
- Equilibrium calculations using Thermo-Calc should be performed first to determine knowledge of possible phases over a reasonable range of temperatures. It also gives a picture regarding possible solidification reaction. An isopleth phase diagram provides basic information on equilibrium solidification path.
- (2)
- A Scheil calculation is carried out to obtain an overview of segregation of all elements quickly and possible phases during solidification.
- (3)
- A DICTRA setup model is created based on the information regarding phases and temperatures from both the equilibrium calculation and Scheil calculation as well as a calculation of domain size. DICTRA calculation is performed according to the specified cooling rate or given temperature–time curve.
- (4)
- A comparative analysis of experimental and calculated microsegregation is conducted.
- (A)
- L ⇒ L + δ ⇒ δ ⇒ γ + δ
- (B)
- L ⇒ L + δ ⇒ L + γ + δ ⇒ γ + δ
- (C)
- L ⇒ L + δ ⇒ L + γ + δ ⇒ γ
- (D)
- L ⇒ L + γ ⇒ L + γ + σ
3.2. Solidification for Industrial Casting Process
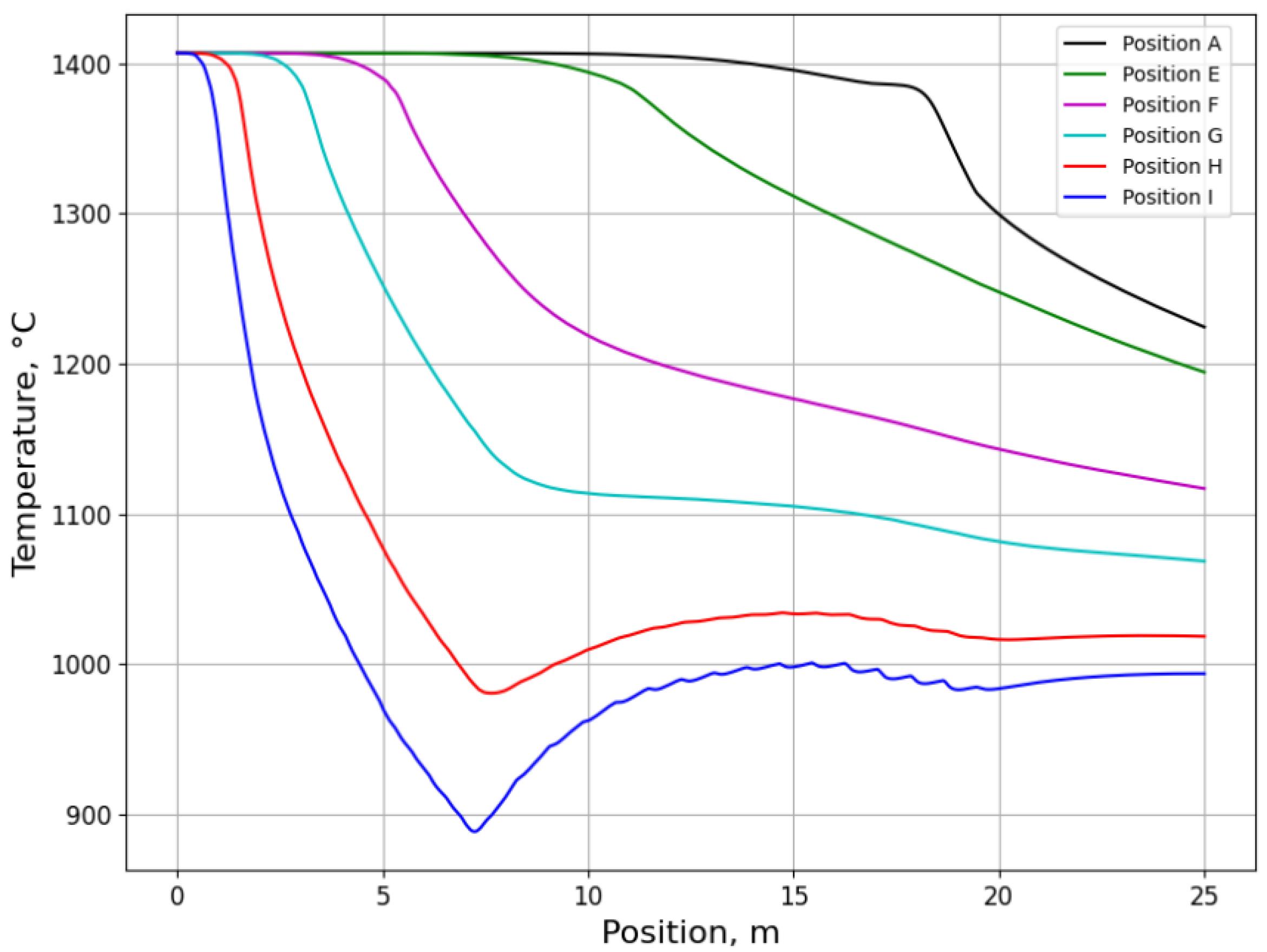
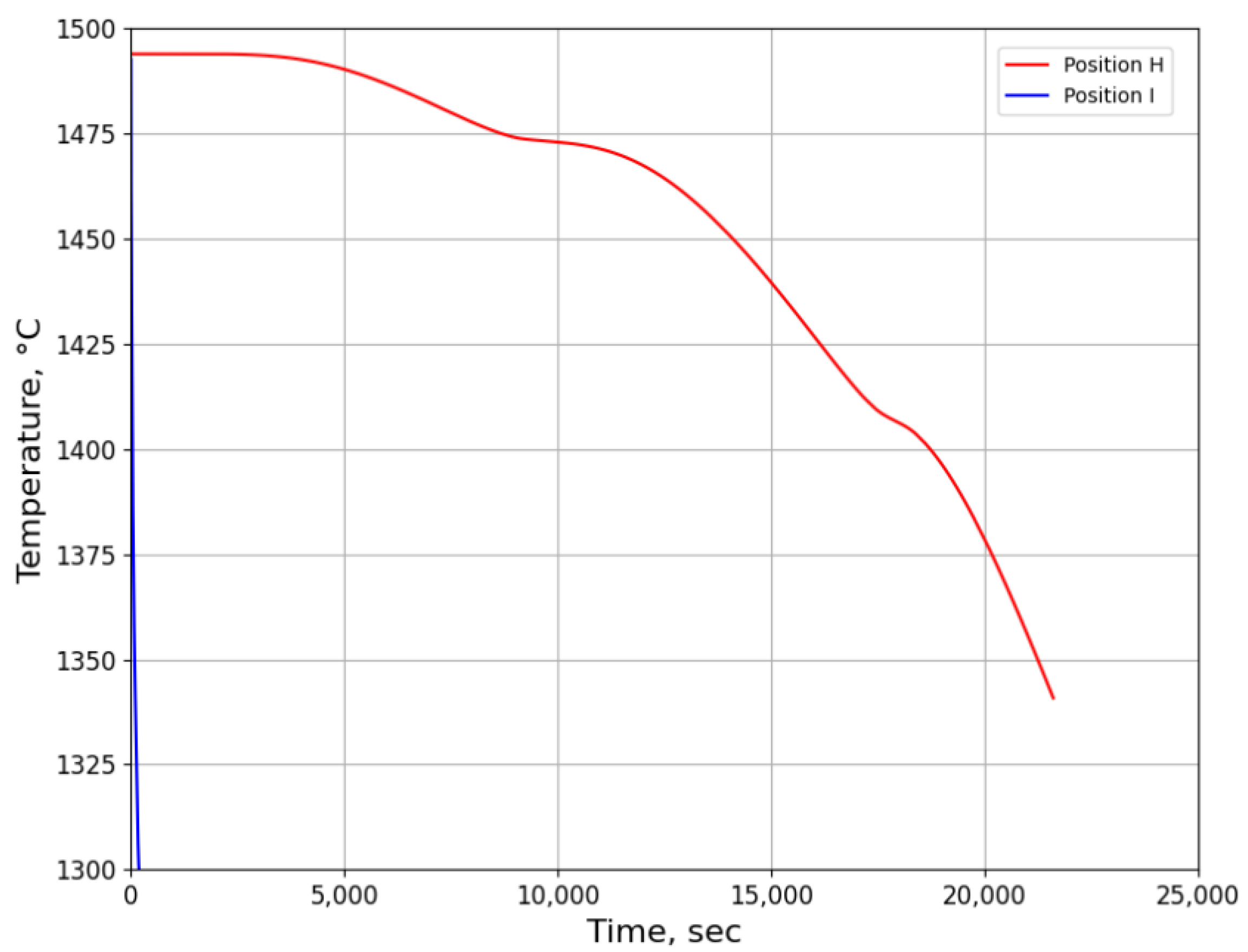
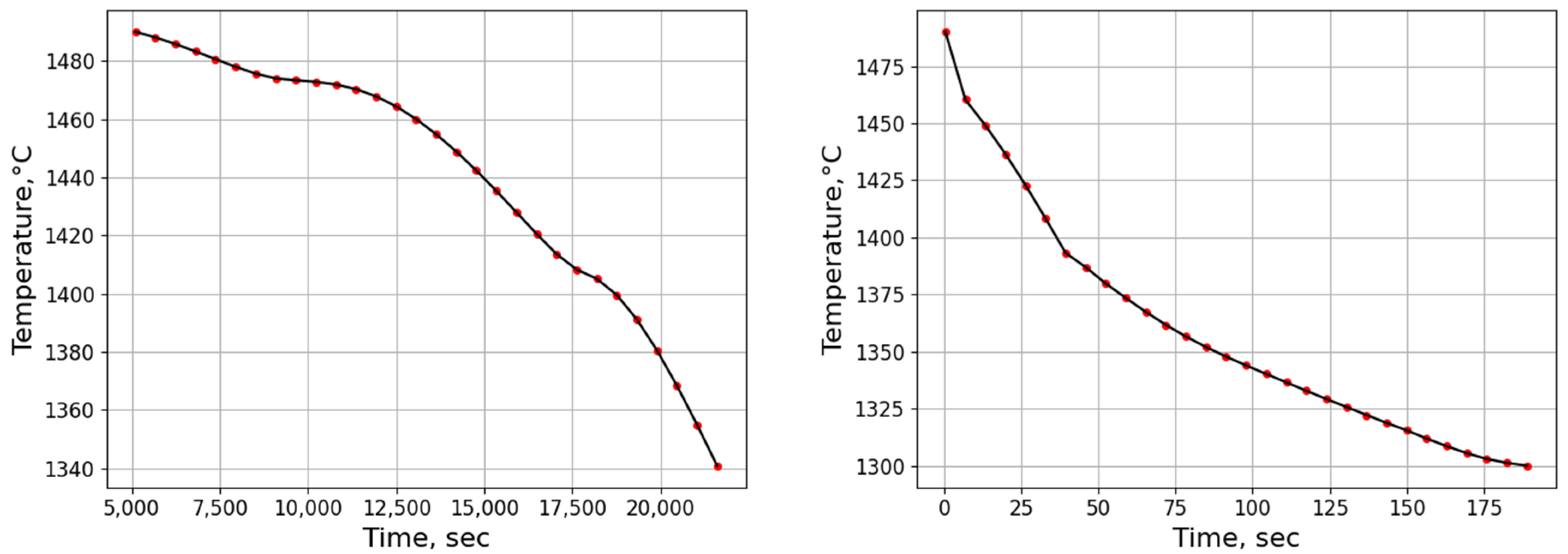
3.2.1. Temperature History from Process Simulation
3.2.2. Microsegregation Using Temperature History Data
- (1)
- For continuous casting, what factors cause the biggest changes in the metallurgical length of the strand and the shell thickness under the mold?
- (2)
- For ingot casting, what factors cause the changes of full solidified time?
- (3)
- In which positions do the most pronounced microsegregation occur? How does it effectively trace the temperature history of the interested positions from the center to the surface below the meniscus?
- (1)
- The temperature distributions and histories in continuous casting and ingot casting of steels were calculated using in-house finite-element code integrated in MICAST.
- (2)
- The predicted temperature history from the casting process simulation was exported as input data for the DICTRA simulation of solidification.
- (3)
- The resulting microsegregation by the DICTRA simulation will be compared with the measured ones if available. The measured microsegregation values at the specified locations are missing in the current paper and will be carried out in future work.
4. Conclusions
- (1)
- Integrated computational materials engineering (ICME) of the industrial casting process can be achieved by incorporating macroscopic models (finite element-based thermal models) and microscopic models (CALPHAD-based microstructural models), building an industry-oriented computational tool (MICAST) for casting of steels. MICAST delivers a user-friendly interface which allows industrial users to start quickly.
- (2)
- Two case studies were performed for solidification simulations of tool steel and stainless steel by using the CALPHAD approach (Thermo-Calc package and CALPHAD database). The predicted microsegregation results agree with the measured ones. From the results in Section 3.1, feasible procedures are proposed to complete a general solidification analysis.
- (3)
- Two case studies were performed for process simulations (continuous casting and ingot casting) with selected steel grades, mold geometry and process conditions using the finite element method. The temperature distributions and histories in continuous casting and ingot casting of steels were calculated using in-house finite-element code integrated in MICAST. The predicted temperature history from the casting process simulation was exported as input data for the DICTRA simulation of solidification. The resulting microsegregation by the DICTRA simulation reflects the microstructure evolution in the real casting process. Current computational practice demonstrates that CALPHAD-based material models can be directly linked with casting process models to predict location-specific microstructures for smart material processing.
- (4)
- The animation of solidification sequence plus other outputs could be used as good pedagogical tools.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flemings, M.C. Solidification Processing; McGraw-Hill Book Company: New York, NY, USA, 1974. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans Tech Publications: Aedermannsdorf, Switzerland, 1998. [Google Scholar]
- Fredriksson, H.; Ulla, A. Materials Processing during Casting; Wiley: Chichester, UK, 2006; Volume 210. [Google Scholar]
- Dantzig, J.A.; Rappaz, M. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Cabrera-Marrero, J.M.; Carreno-Galindo, V.; Morales, M.; Chavez-Alcala, F. Macro-micro modeling of the dendritic microstructure of steel billets processed by continuous casting. ISIJ Int. 1998, 50, 812–821. [Google Scholar] [CrossRef]
- Celentano, D.J.; Dardati, P.M.; Godoy, L.A.; Boeri, R.E. Computational simulation of microstructure evolution during solidification of ductile cast iron. Int. J. Cast Met. Res. 2008, 21, 416–426. [Google Scholar] [CrossRef]
- Bellon, B.; Boukellal, A.K.; Isensee, T.; Wellborn, O.M.; Trumble, K.P.; Krane, M.J.M.; Titus, M.S.; Tourret, D.; Llorca, J. Multiscale prediction of microstructure length scales in metallic alloy casting. Acta Mater. 2021, 207, 116686. [Google Scholar] [CrossRef]
- Cusato, N.; Nabavizadeh, S.A.; Eshraghi, M. A Review of Large-Scale Simulations of Microstructural Evolution during Alloy Solidification. Metals 2023, 13, 1169. [Google Scholar] [CrossRef]
- Chen, Z.; Li, Y.; Zhao, F.; Li, S.; Zhang, J. Progress in numerical simulation of casting process. Meas. Control. 2022, 55, 257–264. [Google Scholar] [CrossRef]
- Wu, M.; Ludwig, A.; Kharicha, A. Simulation of As-Cast Steel Ingots. Steel Res. Int. 2018, 89, 1700037. [Google Scholar] [CrossRef]
- Thomas, B.G. Review on modeling and simulation of continuous casting. Steel Res. Int. 2017, 89, 1700312. [Google Scholar] [CrossRef]
- Miłkowska-Piszczek, K.; Falkus, J. Control and design of the steel continuous casting process based on advanced numerical models. Metals 2018, 8, 591. [Google Scholar] [CrossRef]
- Demay, C.; Ferrand, M.; Belouah, S.; Robin, V. Modeling and simulation of ingot solidification with the open-source software Code_Saturne. IOP Conf. Ser. Mater. Sci. Eng. 2020, 861, 012033. [Google Scholar] [CrossRef]
- Khan, M.A.A.; Sheikh, A.K. A comparative study of simulation software for modelling metal casting processes. Int. J. Simul. Model. 2018, 17, 197–209. [Google Scholar] [CrossRef]
- Kamal, M.; Sahai, Y. Modeling of melt flow and surface standing waves in a continuous casting mold. Steel Res. Int. 2005, 76, 44–52. [Google Scholar] [CrossRef]
- Hepp, E.; Bernbeck, P.; Schäfer, W.; Senk, D. New Developments for Process Modelling of the Continuous Casting of Steel. In SteelSim 2007; Graz: Seggau, Austria, 2007; p. 203. [Google Scholar]
- Li, W.M.; Jiang, Z.H.; Li, H.B. Simulation and Calculation to Segregation of High Nitrogen Steels Solidification Process Based on PROCAST Software. Adv. Mater. Res. 2011, 217, 1185–1190. [Google Scholar] [CrossRef]
- Burbelko, A.; Falkus, J.; Kapturkiewicz, W.; Sołek, K.; Drożdż, P.; Wróbel, M. Modeling of the grain structure formation in the steel continuous ingot by CAFE method. Arch. Metall. Mater. 2012, 57, 379–384. [Google Scholar] [CrossRef]
- Patil, P.; Puranik, A.; Balachandran, G.; Balasubramanian, V. Improvement in Quality and Yield of the Low Alloy Steel Ingot Casting Through Modified Mould Design. Trans. Indian Inst. Met. 2017, 70, 2001–2015. [Google Scholar] [CrossRef]
- Zhang, C.; Shahriari, D.; Loucif, A.; Jahazi, M.; Lapierre-Boire, L.P.; Tremblay, R. Effect of segregated alloying elements on the high strength steel properties: Application to the large size ingot casting simulation. In TMS 2017 146th Annual Meeting & Exhibition Supplemental Proceedings; Springer International Publishing: Cham, Switzerland, 2017; pp. 491–500. [Google Scholar]
- Fang, Q.; Ni, H.; Zhang, H.; Wang, B.; Liu, C. Numerical study on solidification behavior and structure of continuously cast U71Mn steel. Metals 2017, 7, 483. [Google Scholar] [CrossRef]
- Kotásek, O.; Kurka, V.; Vindyš, M.; Jonšta, P.; Noga, R.; Dobiáš, M. Comparison of casting and solidification of 12 ton steel ingot using two different numerical software. In Proceedings of the 30th Anniversary International Conference on Metallurgy and Materials, Brno, Czech Republic, 26–28 May 2021; pp. 147–152. [Google Scholar]
- CALPHAD. Available online: https://en.wikipedia.org/wiki/CALPHAD (accessed on 23 November 2023).
- Sarreal, J.A.; Abbaschian, G.J. The effect of solidification rate on microsegregation. Metall. Trans. A 1986, 17, 2063–2073. [Google Scholar] [CrossRef]
- Won, Y.M.; Thomas, B.G. Simple model of microsegregation during solidification of steels. Metall. Mater. Trans. A 2001, 32, 1755–1767. [Google Scholar] [CrossRef]
- Poirier, D.R.; Heinrich, J.C. Modeling of Microsegregation and Macrosegregation, Casting; ASM Handbook; ASM International: Materials Park, OH, USA, 2008; Volume 15, pp. 445–448. [Google Scholar]
- Natsume, Y.; Shimamoto, M.; Ishida, H. Numerical modeling of microsegregation for Fe-base multicomponent alloys with peritectic transformation coupled with thermodynamic calculations. ISIJ Int. 2010, 50, 1867–1874. [Google Scholar] [CrossRef]
- Zhang, D. Characterisation and Modelling of Segregation in Continuously Cast Steel Slab. Ph.D. Thesis, University of Birmingham, Birmingham, UK, 2015. Available online: https://etheses.bham.ac.uk/id/eprint/6256/ (accessed on 23 November 2023).
- Kobayashi, Y.; Todoroki, H.; Mizuno, K. Problems in solidification model for microsegregation analysis of Fe–Cr–Ni–Mo–Cu alloys. ISIJ Int. 2019, 59, 277–282. [Google Scholar] [CrossRef]
- Zhang, C.; Jahazi, M.; Isabel Gallego, P. On the Impact of Microsegregation model on the thermophysical and solidification behaviors of a large size steel ingot. Metals 2020, 10, 74. [Google Scholar] [CrossRef]
- Thermo-Calc Application Example: Microsegregation during Solidification. Available online: https://thermocalc.com/showcase/application-examples/microsegregation-during-solidification/ and https://thermocalc.com/wp-content/uploads/Application_Examples/Microsegregation_Solidification/analysis-of-microsegregation-during-solidification.pdf (accessed on 23 November 2023).
- ICME. Available online: https://en.wikipedia.org/wiki/Integrated_computational_materials_engineering (accessed on 23 November 2023).
- Luo, A.A. Material design and development: From classical thermodynamics to CALPHAD and ICME approaches. Calphad 2015, 50, 6–22. [Google Scholar] [CrossRef]
- Zhang, C.; Miao, J.; Chen, S.; Zhang, F.; Luo, A.A. CALPHAD-Based Modeling and Experimental Validation of Microstructural Evolution and Microsegregation in Magnesium Alloys During Solidification. J. Phase Equilibria Diffus. 2019, 40, 495–507. [Google Scholar] [CrossRef]
- Luo, C.; Antonsson, K.H.; Shahbazian, F. An Industry Oriented Computational Tool for Modelling Microstructure in Continuous Casting of Steel (MICAST I), Swerea KIMAB AB internal report; Stockholm, Sweden, 2017.
- Luo, C.; Shahbazian, F.; Antonsson, K.H.; Song, Z.; Karlsson, L.; Ågren, D.; Persson, E.; Cederholm, F.; Xuan, C.; Ejnermark, S. An Industry Oriented Computational Tool for Modelling Microstructure in Casting of Steel (MICAST II), Swerim AB report (No. MEF21181); Stockholm, Sweden, 2021.
- Kaufman, L.; Bernstein, H. Computer Calculation of Phase Diagrams; Academic Press: New York, NY, USA, 1970; ISBN 0-12-402050-X. [Google Scholar]
- CALPHAD. Available online: https://CALPHAD.org.
- Gulliver, G.H. The quantitative effect of rapid cooling upon the constitution of binary alloys. J. Inst. Met. 1913, 9, 120–157. [Google Scholar]
- Scheil, E. Remarks on the crystal layer formation. Z. Metallkd. 1942, 34, 70. [Google Scholar]
- Thermo-Calc Software. Available online: https://thermocalc.com/.
- Schematic of Scheil–Gulliver model. Available online: https://en.wikipedia.org/wiki/Scheil_equation (accessed on 23 November 2023).
- Ågren, J. Numerical treatment of diffusional reactions in multicomponent alloys. J. Phys. Chem. Solids 1982, 43, 385–391. [Google Scholar] [CrossRef]
- Miettinen, J.; Louhenkilpi, S.; Kytönen, H.; Laine, J. IDS: Thermodynamic–kinetic–empirical tool for modelling of solidification, microstructure and material properties. Math. Comput. Simul. 2010, 80, 1536–1550. [Google Scholar] [CrossRef]
- Jernkontoret. A Guide to the Solidification of Steels; Jernkontoret, Stockholm, Sweden. 1977. Available online: https://www.phase-trans.msm.cam.ac.uk/2007/Solidification/solidification.html (accessed on 23 November 2023).
- Mao, M.; Guo, H.; Wang, F.; Sun, X. Effect of cooling rate on the solidification microstructure and characteristics of primary carbides in H13 steel. ISIJ Int. 2019, 59, 848–857. [Google Scholar] [CrossRef]
- Hao, Y.; Cao, G.; Li, C.; Liu, W.; Li, J.; Liu, Z.; Gao, F. Solidification structures of Fe–Cr–Ni–Mo–N super-austenitic stainless steel processed by twin-roll strip casting and ingot casting and their segregation evolution behaviors. ISIJ Int. 2018, 58, 1801–1810. [Google Scholar] [CrossRef]








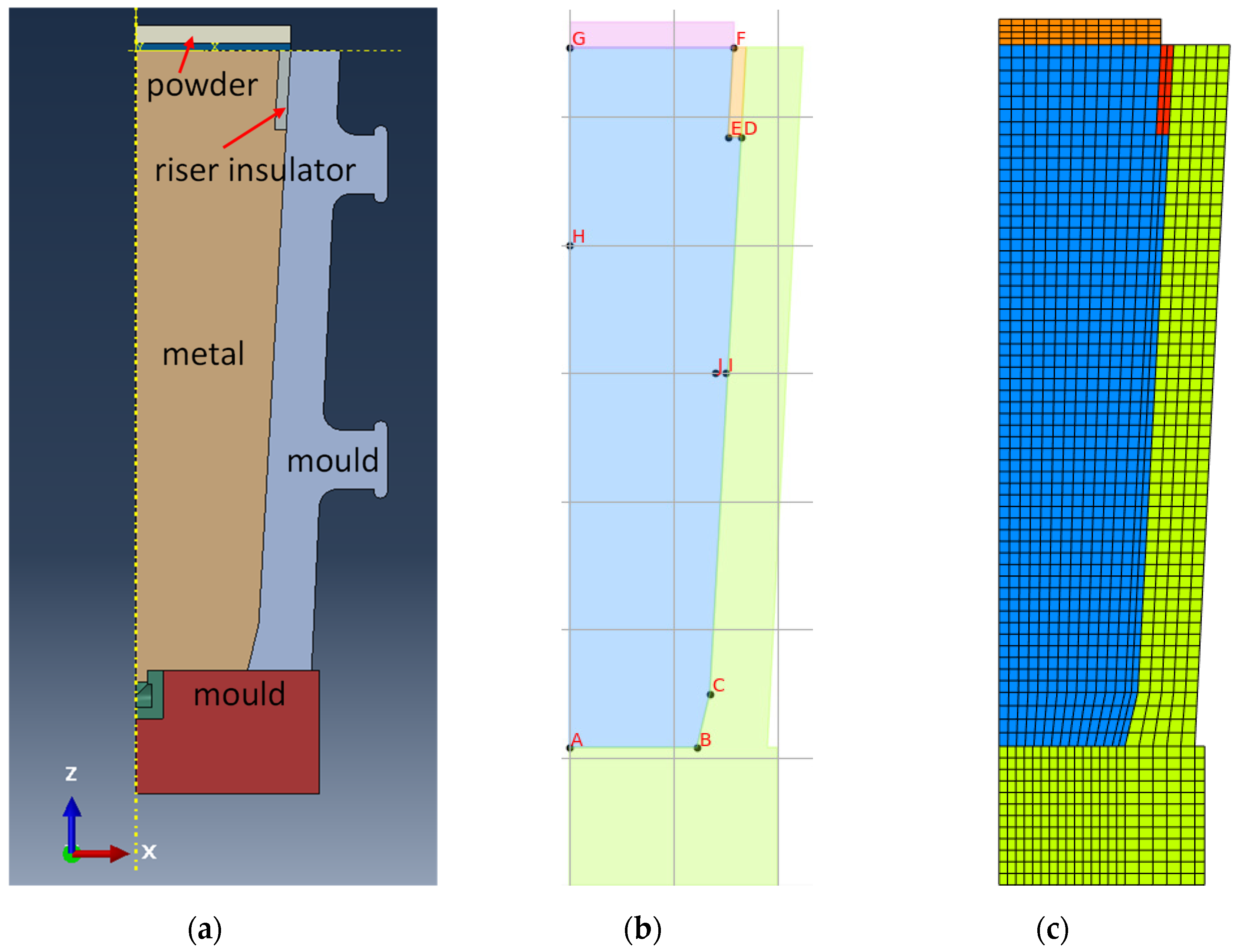
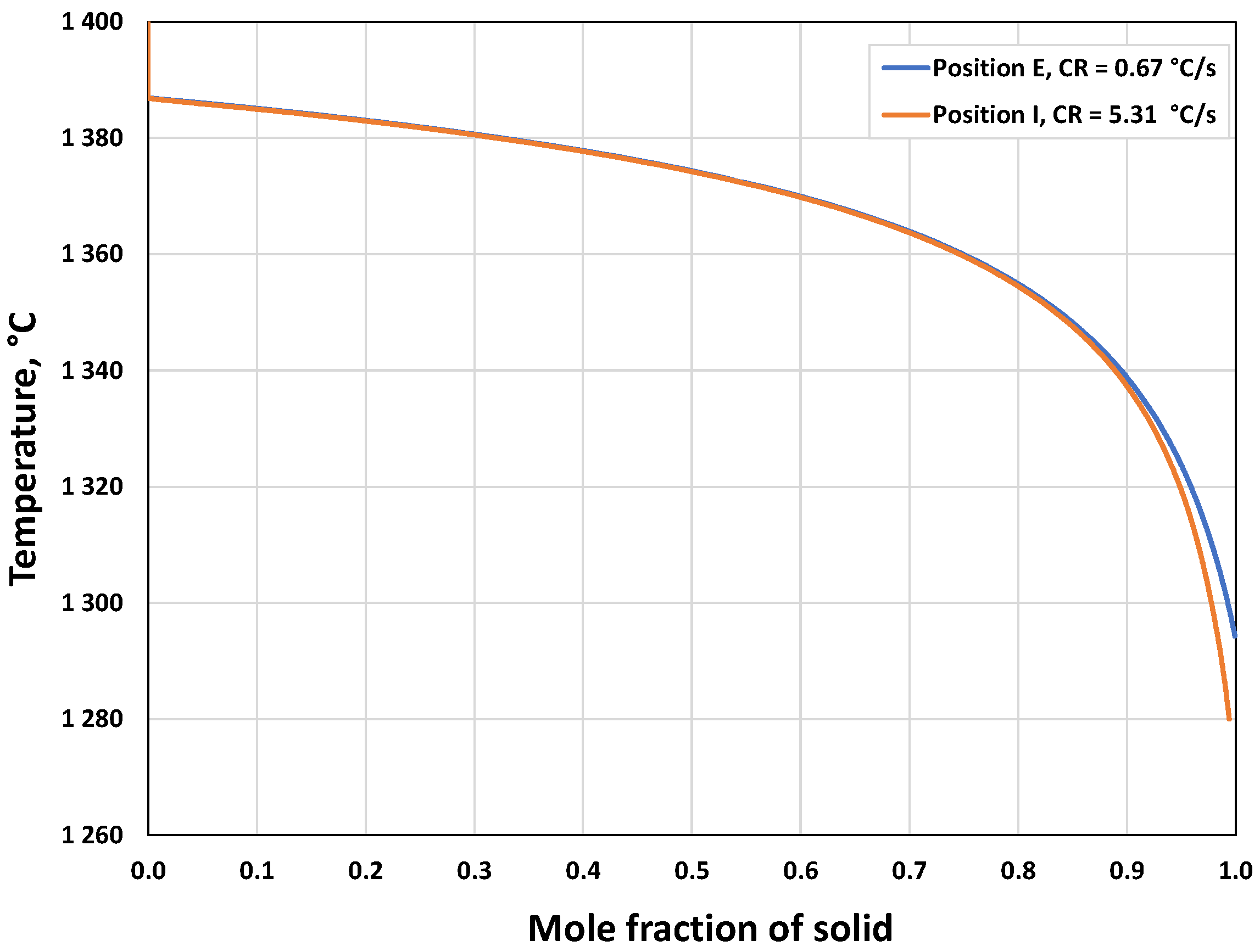
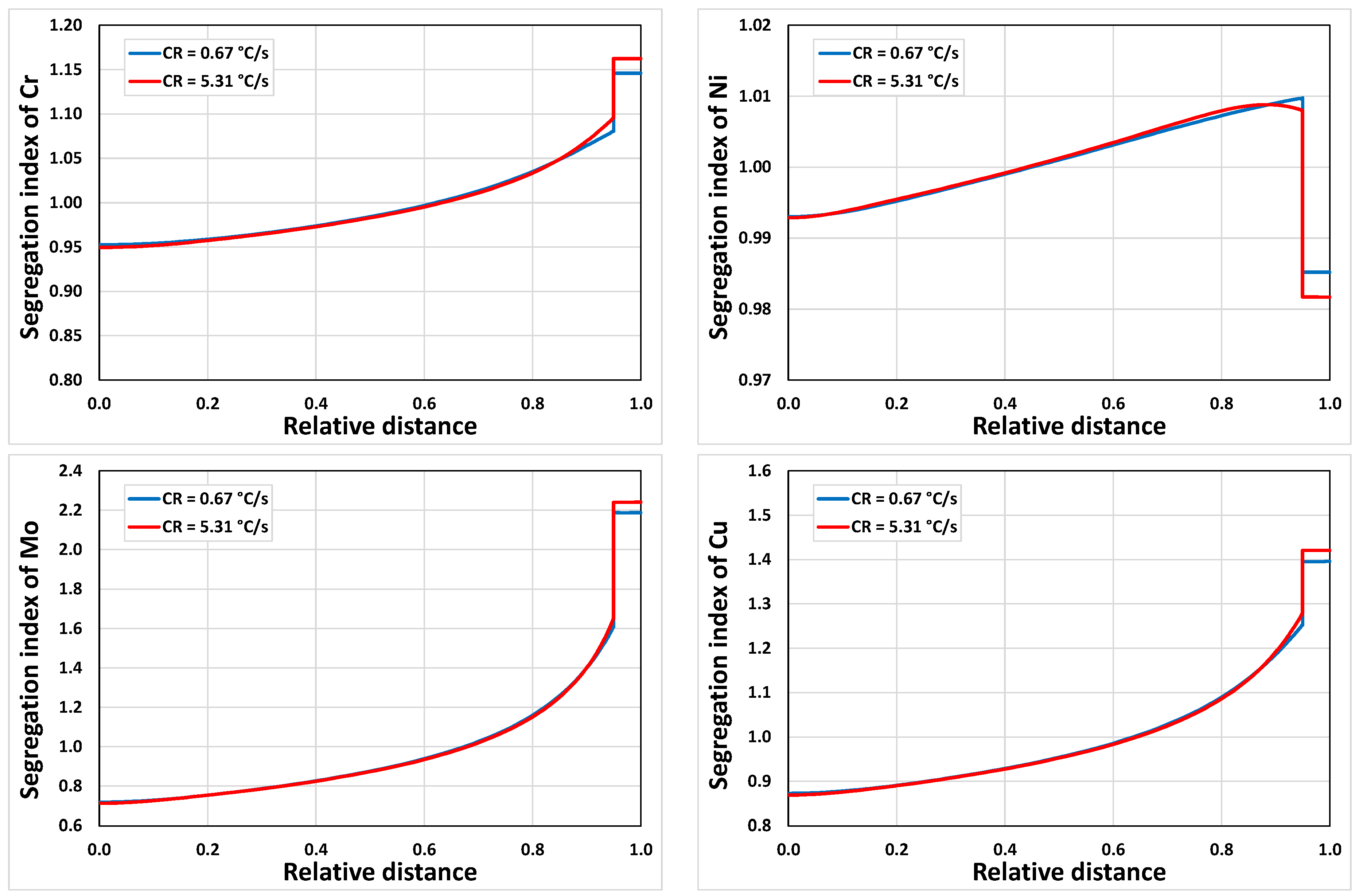

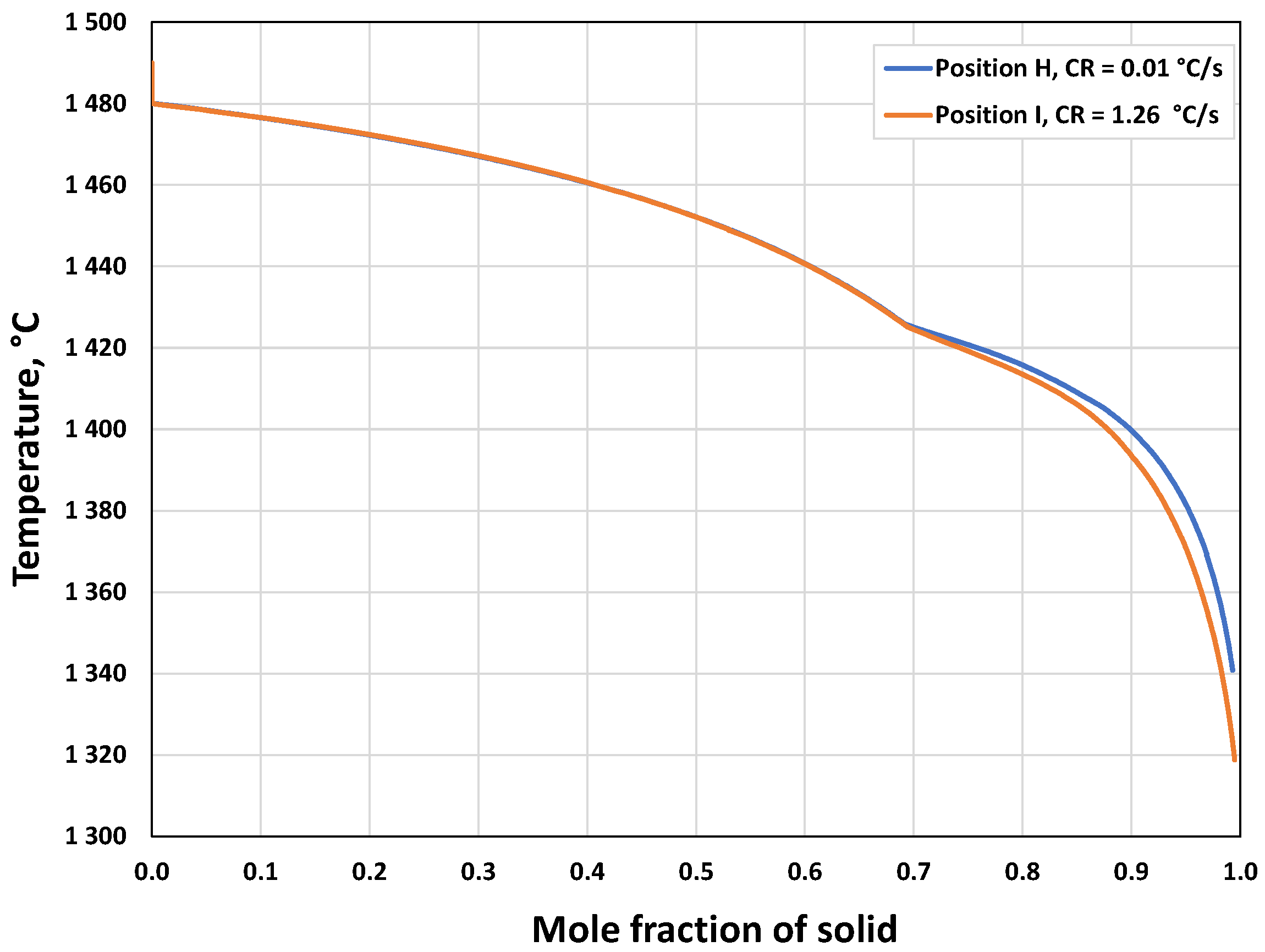
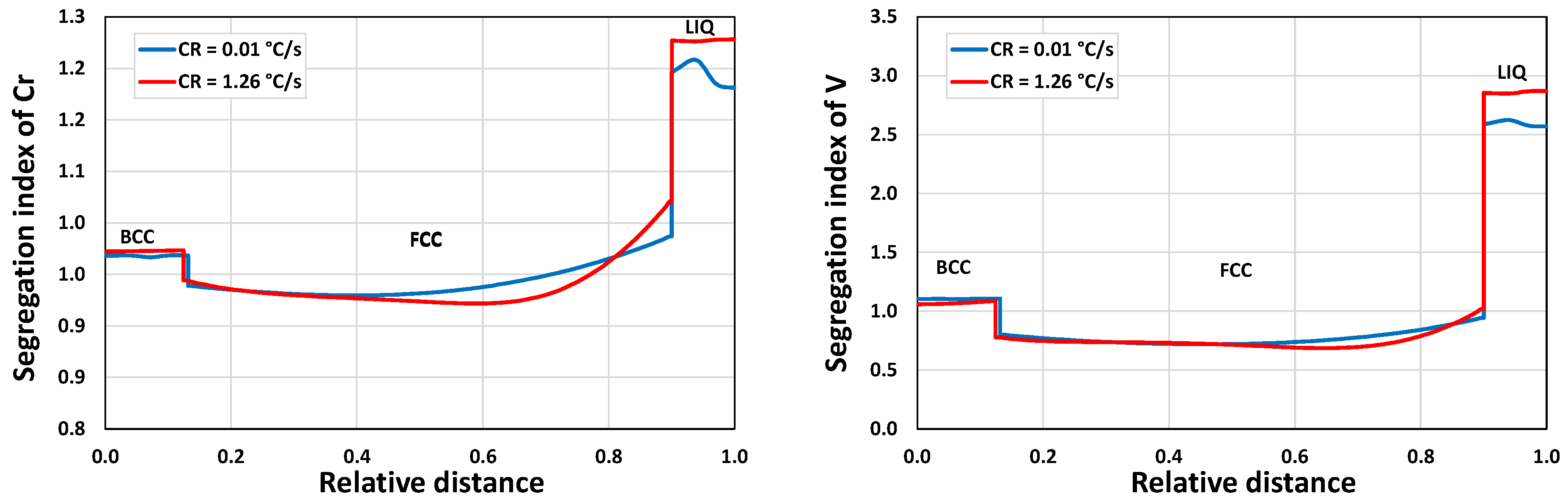
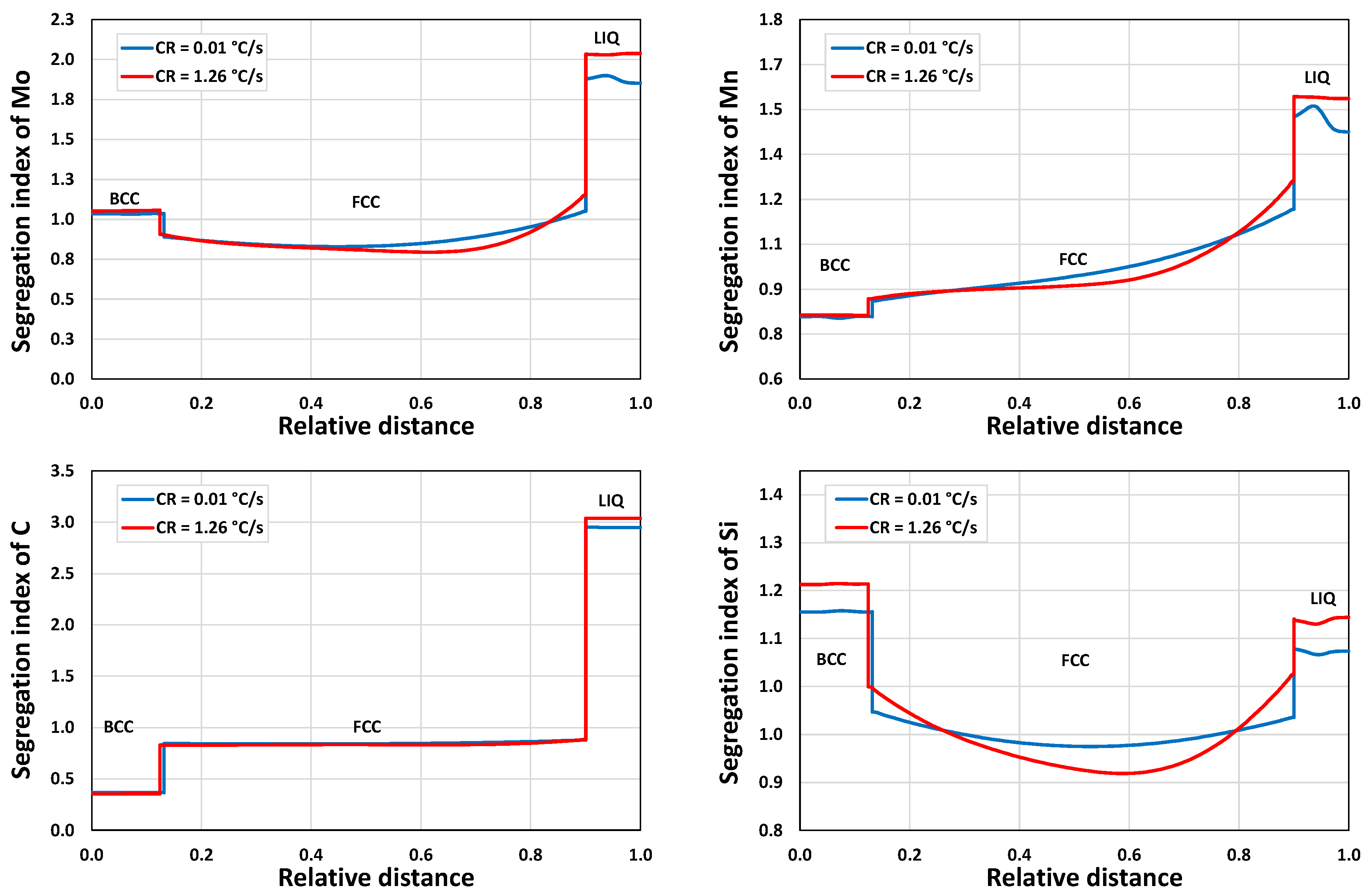

| Position | Average Cooling Rate (°C/s) | Dendrite Arm Spacing (μm) |
|---|---|---|
| E | 0.67 | 74 |
| I | 5.31 | 44 |
| Position | Average Cooling Rate (°C/s) | Dendrite Arm Spacing (μm) |
|---|---|---|
| H | 0.01 | 206 |
| I | 1.26 | 44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Hansson, K.; Song, Z.; Ågren, D.; Persson, E.S.; Cederholm, F.; Xuan, C. Modelling Microstructure in Casting of Steel via CALPHAD-Based ICME Approach. Alloys 2023, 2, 321-343. https://doi.org/10.3390/alloys2040021
Luo C, Hansson K, Song Z, Ågren D, Persson ES, Cederholm F, Xuan C. Modelling Microstructure in Casting of Steel via CALPHAD-Based ICME Approach. Alloys. 2023; 2(4):321-343. https://doi.org/10.3390/alloys2040021
Chicago/Turabian StyleLuo, Chunhui, Karin Hansson, Zhili Song, Debbie Ågren, Ewa Sjöqvist Persson, Fredrik Cederholm, and Changji Xuan. 2023. "Modelling Microstructure in Casting of Steel via CALPHAD-Based ICME Approach" Alloys 2, no. 4: 321-343. https://doi.org/10.3390/alloys2040021
APA StyleLuo, C., Hansson, K., Song, Z., Ågren, D., Persson, E. S., Cederholm, F., & Xuan, C. (2023). Modelling Microstructure in Casting of Steel via CALPHAD-Based ICME Approach. Alloys, 2(4), 321-343. https://doi.org/10.3390/alloys2040021