Oxidation Kinetics of FeCr and FeCrAl Alloys: Influence of Secondary Processes (Continuation)
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
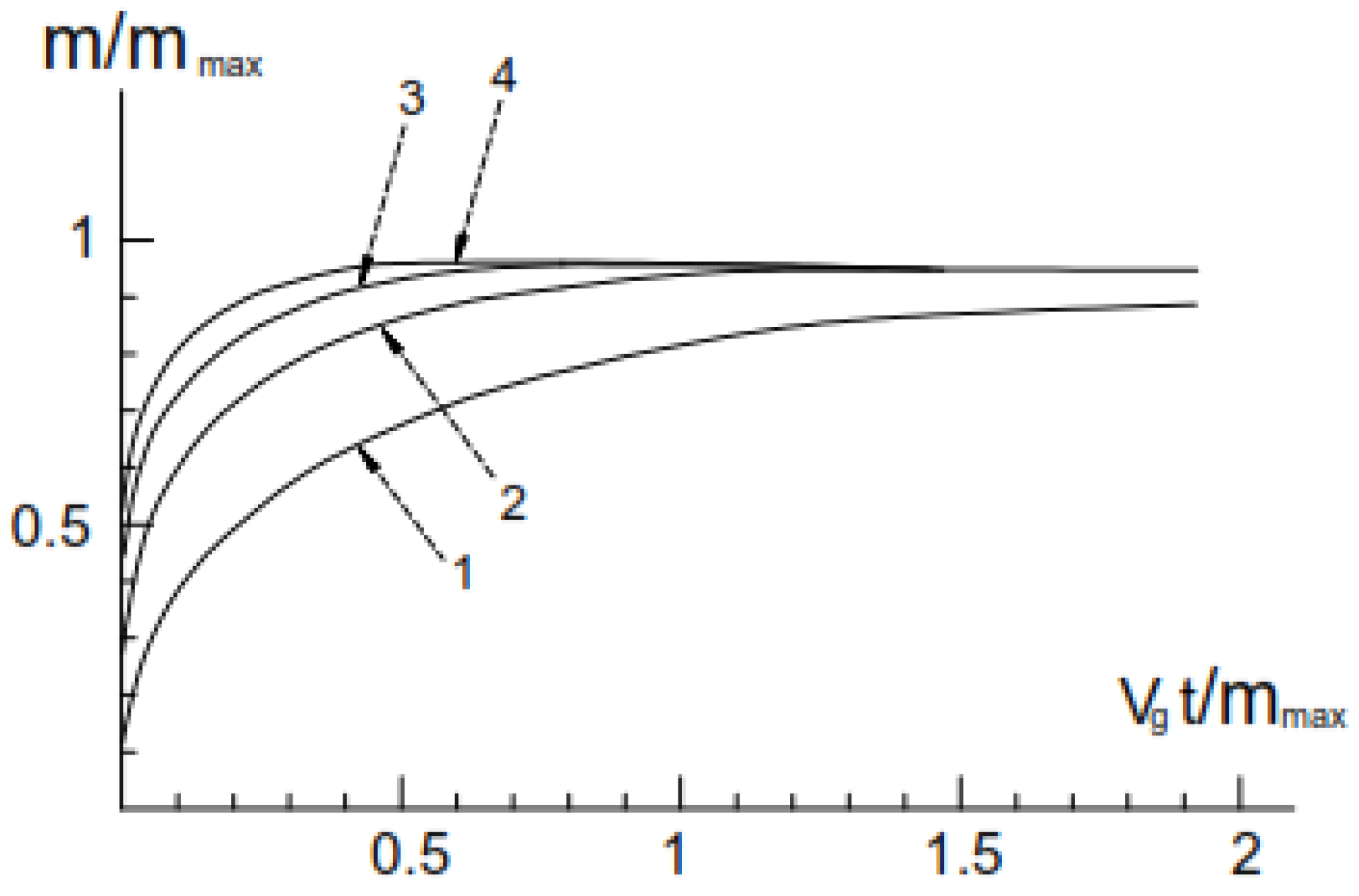
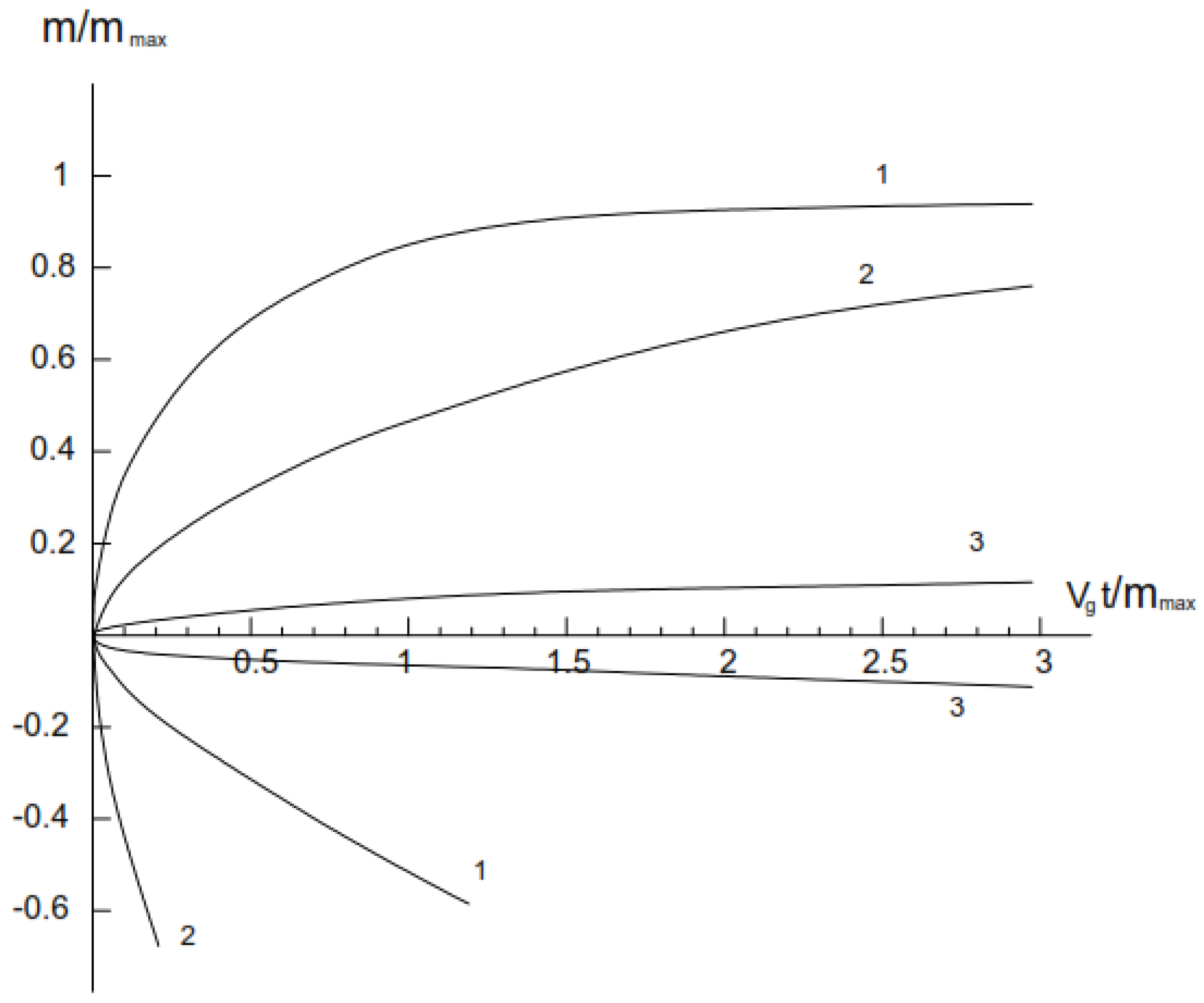
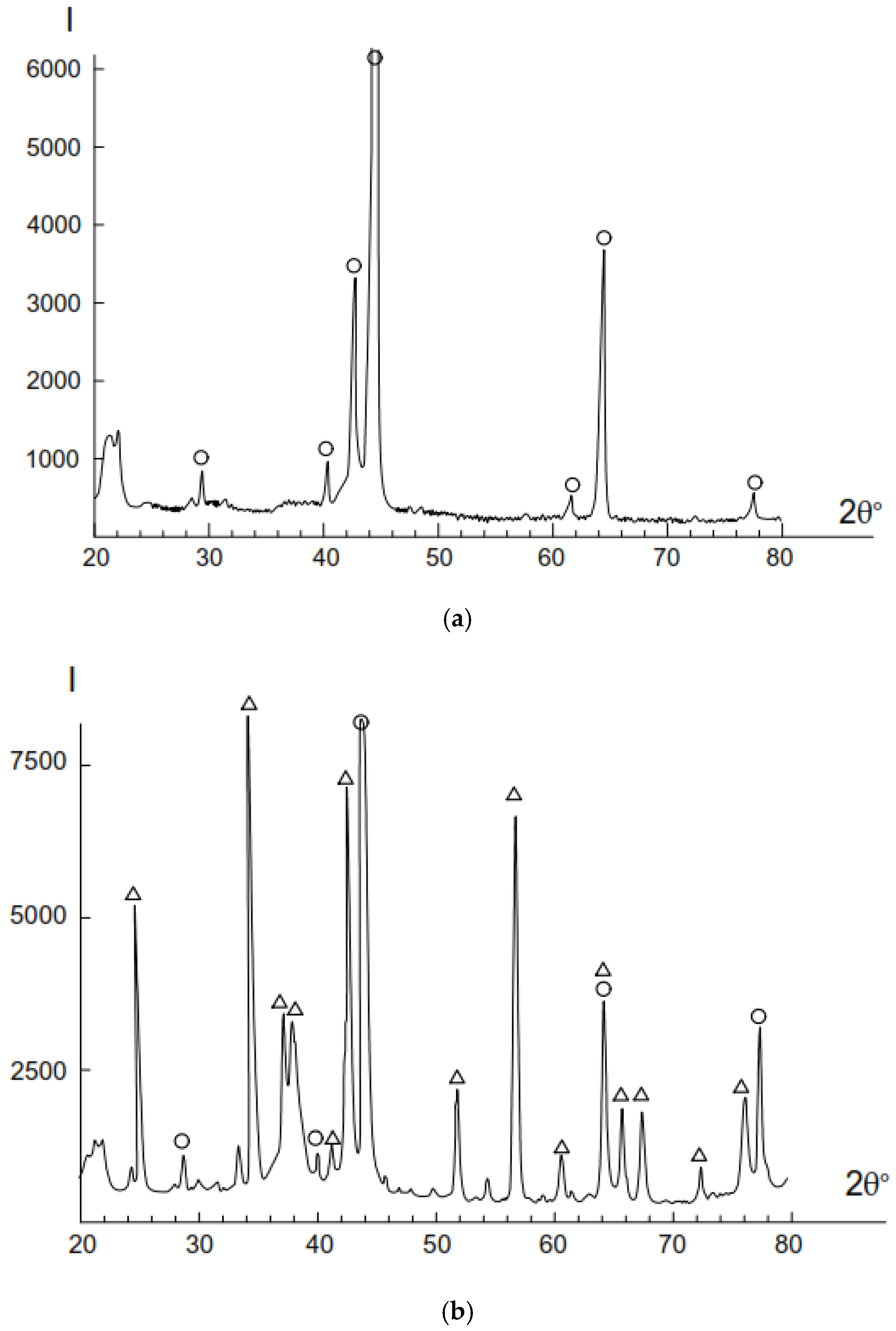
3.1. Oxidation Kinetic of Alumina-Forming Alloy in Air
3.2. Oxidation Kinetic of Chromia-Forming Alloy in Air
- t ≈ 4.04 [e1.99m (1.99m − 1) + 1] + 0.77 (e1.99m − 1);
- t ≈ 4.04 [1 − φ−1ln(eφ)] + 0.77 (φ−1 − 1) for alumina-forming alloy at 1200 °C;
- t ≈ 4.04 [e1.99m (1.99m − 1) + 1];
- t ≈ 4.04 [1 – φ−1ln(eφ)] for chromia-forming alloy at 1200 °C (t is in hours, m is in mg/cm2).
4. Conclusions
5. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Yan, X.; Wang, J.; Li, H.; Wang, S. Microstructure evolution and oxidation resistance properties of oxide dispersion strengthened FeCrAl alloys at 1100 °C. Vacuum 2024, 227, 113371. [Google Scholar] [CrossRef]
- Ibrahim, O.M.; Alazemi, A.A.; Naji, L.B. Multistage heat treatment and the development of a protective oxide-scale layer on the surface of FeCrAl sintered-metal-fibers. Sci. Rep. 2021, 11, 797. [Google Scholar] [CrossRef]
- Umretiya, R.V.; Qu, H.; Yin, L.; Jurewicz, T.B.; Gupta, V.K.; Drobnjak, M.; Knussman, M.P.; Hoffman, A.K.; Rebak, R.B. Corrosion behavior of additively manufactured FeCrAl in out-of-pile light water reactor environments. NPJ Mater. Degrad. 2024, 8, 88. [Google Scholar] [CrossRef]
- Kanthal, I.; Fedorova, I.; Alleima, D.; Karlsson, D. Oxidation behavior of additively manufactured Ti-added FeCrAl alloys. High Temp. Corros. Mater. 2024, 101, 1155–1165. [Google Scholar]
- Okoro, V.U.; Daub, K.; Nordin, H.; Persaud, S.Y. Comparing the oxidation of FeCrAl alloys in isothermal and cyclic high-temperature steam environments. Nucl. Mater. 2024, 589, 154843. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Huang, X. Exploring the impact of microstructure refinement on high temperature steam oxidation behavior of FeCrAl alloy. Nucl. Mater. 2025, 603, 155372. [Google Scholar] [CrossRef]
- Kim, C.; Tang, C.; Grosse, M.; Maeng, Y.; Jang, C.; Steinbrueck, M. Oxidation mechanism and kinetics of nuclear-grade FeCrAl alloys in the temperature range of 500–1500 °C in steam. Zeitschriftenaufsatz 2022, 564, 1000145733. [Google Scholar] [CrossRef]
- Wang, P.; Qi, W.; Yang, K.; Qiao, Y.; Wang, X.; Zheng, T.; Bai, C.; Liu, Z.; Zhang, X. Systematic investigation of the oxidation behavior of Fe-Cr-Al cladding alloys in high-temperature steam. Corros. Sci. 2022, 207, 110595. [Google Scholar] [CrossRef]
- Qi, W.; Yang, K.; Wang, P.; Du, S.; Bai, C.; Wang, X.; Qiao, Y.; Zheng, T.; Zhang, L.; Zhang, X. High-temperature steam oxidation behavior of an FeCrAl alloy with controlled addition of Mo. J. Mater. Sci. 2022, 57, 20909–20927. [Google Scholar] [CrossRef]
- Raiman, S.S.; Field, K.G.; Rebak, R.B.; Yamamoto, Y.; Terrani, K.A. Hydrothermal corrosion of 2nd generation FeCrAl alloys for accident tolerant fuel cladding. Nucl. Mater. 2020, 536, 152221. [Google Scholar] [CrossRef]
- Hou, P.Y.; Shui, Z.R.; Chuang, G.Y.; Stringer, J. Effect of reactive element oxide coatings on the high temperature oxidation behavior of a FeCrAl alloy. Electrochem. Soc. 1992, 139, 1119. [Google Scholar] [CrossRef]
- Othman, N.K.; Jalar, A.; David Young, D. Effects of lanthanum on Fe-25Cr alloys under cyclic oxidation. Adv. Mater. Res. 2010, 97–101, 1212–1215. [Google Scholar] [CrossRef]
- Mikadze, O.; Kandelaki, A. Influence of cerium additives on high-temperature corrosion of chromium. Bull. Georgian Acad. Sci. 2010, 4, 66–69. [Google Scholar]
- Qi, W.; Qiao, Y.; Ru, W.; Wang, X.; Zhang, X.; Zheng, T.; Du, S.; Wang, P.; Yang, K. High-temperature steam oxidation and surface microstructure evolution of Fe13Cr6Al(1–4)Mo0.15Y alloys. Metals 2024, 14, 1229. [Google Scholar] [CrossRef]
- Zhang, S.; Hayashi, S.; Ukai, C. High-temperature oxidation of oxide-dispersion-strengthened FeCrAl alloys: Influences of Al, Co and Y concentration on the mechanism of oxide scale growth. Mater. Res. Technol. 2024, 30, 9196–9204. [Google Scholar] [CrossRef]
- Evans, U.R. An introduction to Metallic Corrosion; Edward Arnold Ltd.: London, UK, 1981; p. 302. [Google Scholar]
- Tavadze, F.N.; Mikadze, O.I.; Keshelava, N.P.; Bulia, B.P. High-temperature corrosion of dilute chromium-lanthanum alloys. Oxid. Met. 1986, 25, 335–350. [Google Scholar] [CrossRef]
- Nakhutsrishvili, I. Oxidation kinetics of FeCr and FeCrAl alloys: Influence of secondary processes. Johns. Matthey Technol. Rev. 2025, 69, 1–12. [Google Scholar]
- Mikadze, O.; Dzindzibadze, T.G.; Bulia, B.P.; Rukhadze, L.N. Chemical-thermal treatment of low-alloyed chromium. Georgian Eng. News 2000, 1, 92–93. [Google Scholar]
- Mikadze, O.; Tsurtsumia, O.; Bulia, B. Improvement in Corrosion Resistance of Low-Alloyed Chromium by Thermo-Chemical Treatment; Congress Junior Euromat: Lausanne, Switzerland, 2006. [Google Scholar]
- Mikadze, O.; Bulia, B. Scientific principles of chromium matrix heat resistant alloing. Bull. Georgian Acad. Sci. 2001, 163, 495–597. [Google Scholar]
- Gussev, M.N.; Field, K.G.; Yamamoto, Y. Design, properties, and weldability of advanced oxidation-resistant FeCrAl alloys. Mater. Des. 2017, 129, 227–238. [Google Scholar] [CrossRef]
- Gurevich, L.M.; Pronichev, D.V.; Slautin, O.V.; Tikhaeva, V.V. Corrosion resistance of Fe-Cr-Al intermetallic coatings obtained by aluminizing. Metals 2023, 13, 1883. [Google Scholar] [CrossRef]
- Mikadze, O.I.; Nakhutsrishvili, I.G.; Dzigrashvili, T.A.; Maisuradze, N.I.; Mikadze, G.O. Calculation of oxidation kinetic parameters for heat—Resistant alloys with the decreasing effective diffusion area. Metallofiz. I Noveyshiye Tekhnologii (Met. Adv. Technol.) 2010, 32, 543–548. [Google Scholar]
- Smialek, J.L. Simplified paralinear oxidation analyses. High Temp. Corros. Mater. 2023, 99, 1–27. [Google Scholar] [CrossRef]
- Nakhutsrishvili, I.; Sepashvili, N. Analisys of kinetic curves of mass change during the interaction of active gases with the surface of certain metals and compounds with simultaneous evaporation of the product of reaction. 2025; in press. [Google Scholar]
- Tedmon, C.S. The effect of oxide volatilization on the oxidation kinetics of Cr and Fe-Cr alloys. Electrochem. Soc. 1966, 113, 766. [Google Scholar] [CrossRef]
- Yamamura, K.; Uehara, T.; Tanaka, S.; Yasuda, N. Oxidation behavior of Fe-Cr ferritic alloy for SOFC interconnects ZMG232G10 in air and H2/H2O. Electrochem. Soc. 2013, 57, 2177. [Google Scholar] [CrossRef]
- Guo, T.; He, C.; Liang, Z.; Zhao, Q. Molecular dynamics study on the initial oxidation behavior of FeCr alloys in supercritical H2O and supercritical CO2 with O2. Supercrit. Fluids 2024, 204, 106110. [Google Scholar] [CrossRef]
- Hu, Q.; Lyu, Z.-Y.; Xing, L.-D.; Gu, C.; Bao, Y.-P. Initial oxidation of Fe-Cr alloys at different temperatures and atmospheric conditions: A ReaxFF molecular dynamics approach. ISIJ Int. 2024, 64, 1967–1975. [Google Scholar] [CrossRef]
- Chyrkin, A.; Froitzheim, J.; Quadakkers, W.J. Transition from internal to external oxidation in binary Fe-Cr alloys around 900 °C. 2024; preprint. [Google Scholar] [CrossRef]
- Caplan, D.; Cohen, M. The volatilization of chromium oxide. Electrochem. Soc. 1961, 108, 438. [Google Scholar] [CrossRef]
- Yamauchi, A.; Kurokawa, K.; Takahashi, H. Evaporation of Cr2O3 in atmospheres containing H2O. Oxid. Met. 2003, 59, 517–527. [Google Scholar] [CrossRef]
- Zhang, K.; El-kharouf, A.; Caykara, T.; Steinberger-Wilckens, R. Effect of temperature and water content on the xidation behaviour and Cr evaporation of high-Cr alloys for SOFC cathode air preheaters. High Temp. Corros. Mater. 2023, 100, 1–25. [Google Scholar]
- Chen, Y.; Tan, T.; Chen, H. Oxidation companied by scale removal: Initial and asymptotic kinetics. Nucl. Sci. Technol. 2008, 45, 662–667. [Google Scholar] [CrossRef]
- Krejčí, J.; Vrtílková, V.; Gajdoš, P.; Rada, D. Proposal of new oxidation kinetics for sponge base E110 cladding tubes material. Nucl. Sci. Technol. 2017, 3, 18. [Google Scholar] [CrossRef]
- Stringer, J. The functional form of rate curves for high-temperature oxidation of dispersioncontaining alloys forming Cr2O3 scales. Oxid. Met. 1972, 5, 49–58. [Google Scholar] [CrossRef]
- Yong, Y.; Benton, B.E.; Howell, M.; Bell, G. High-temperature oxidation kinetics of sponge-based E110 cladding alloy. Nucl. Mater. 2018, 499, 595–612. [Google Scholar]
- Smeltzer, W.W.; Haering, R.R.; Kirkaldy, J.S. Oxidation of metals by short circuit and lattice diffusion of oxygen. Acta Metall. 1969, 9, 880–885. [Google Scholar] [CrossRef]
- Atkinson, H.V. A review of the role of short-circuit diffusion in the oxidation of nickel, chromium, and nickel-chromium alloys. Oxid. Met. 1985, 24, 177–197. [Google Scholar] [CrossRef]
- Waber, J.T. On the cubic law of oxidation. Chem. Phys. 1952, 20, 734–735. [Google Scholar] [CrossRef]
- Sadique, S.E.; Mollah, A.H.; Islam, M.S.; Ali, M.M.; Megat, M.H.H.; Basri, S. High-temperature oxidation behavior of iron–chromium–aluminum alloys. Oxid. Met. 2000, 54, 385–400. [Google Scholar] [CrossRef]
- Piatkowski, J.; Przeliorz, R.; Jabłońska, B. Oxidation kinetics of NiAl, FeAl and TiAl alloys. Solid State Phenom. 2013, 203–204, 431–434. [Google Scholar] [CrossRef]
- Li, H.; Zhang, H.; Zheng, W. Study on oxidation kinetics of three kinds of candidate superalloys for VHTR under air ingress accident. Ann. Nucl. Energy 2023, 189, 109844. [Google Scholar] [CrossRef]
- Kopec, M.; Mierzejewska, I.; Gorniewicz, D.; Sitek, R.; Jóźwiak, S. High-temperature oxidation behaviour of additively manufactured and wrought HAYNES 282. Mater. Sci. 2024, 37, 17647–17665. [Google Scholar] [CrossRef]
- Nakhutsrishvili, I. Study of growth and sublimation of germanium nitride using the concept of Tedmon’s kinetic model. Orient. J. Chem. 2020, 36, 850–854. [Google Scholar] [CrossRef]
- Carrette, F.; Guinard, L.; Pieraggi, B. Kinetics of corrosion products release from nickel-base alloys corroding in primary water conditions a new modeling of release. In Proceedings of the International Conference Water Chemistry in Nuclear Reactor Systems, Avignon, France, 22–26 July 2022; pp. 1–32. [Google Scholar]
- Liu, T.-K.; Bautista, R.G. Prediction of the global volatilization rate of gas-metal-alloy reaction systems—Method of calculation. Oxid. Met. 1981, 16, 243–252. [Google Scholar] [CrossRef]



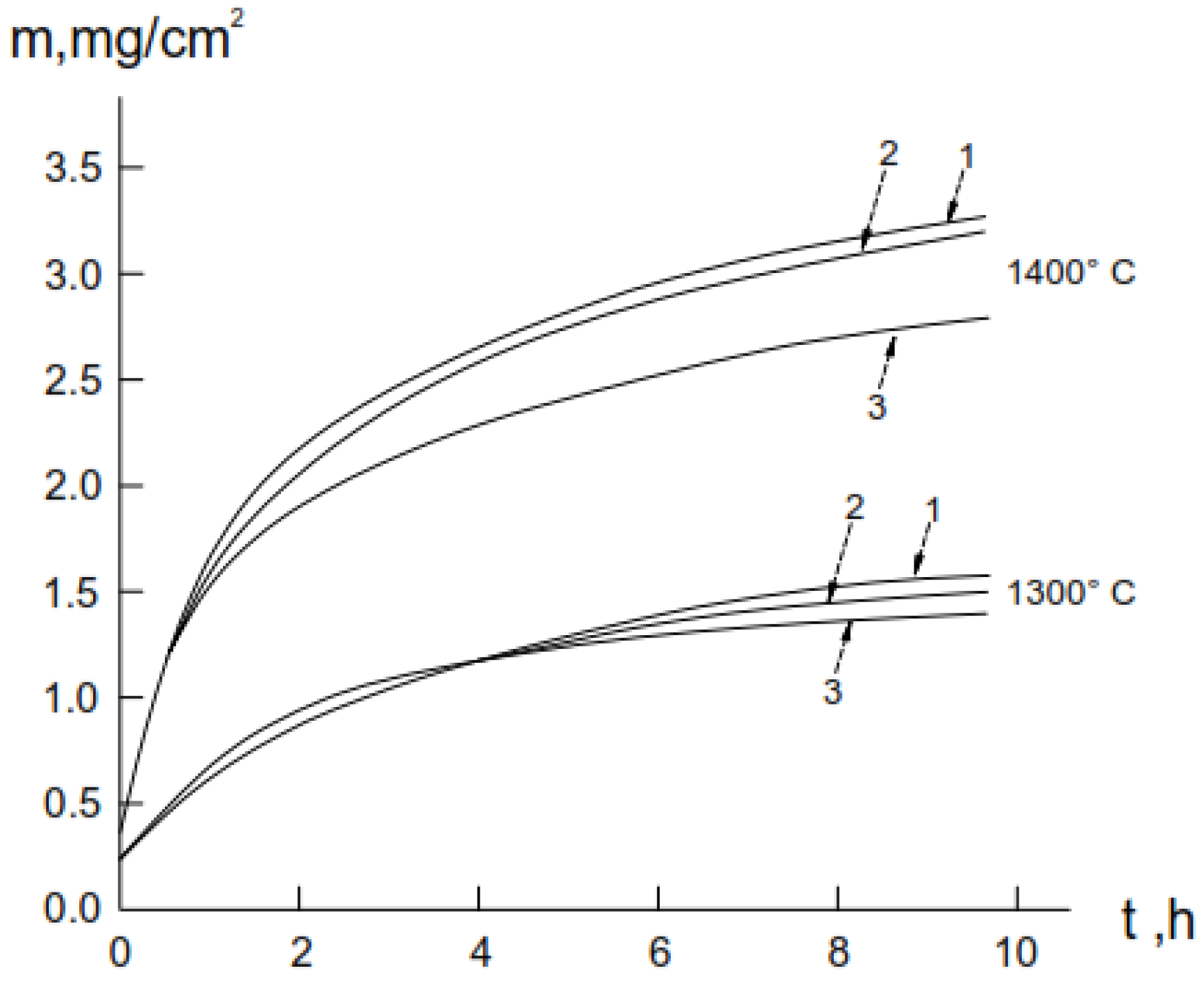
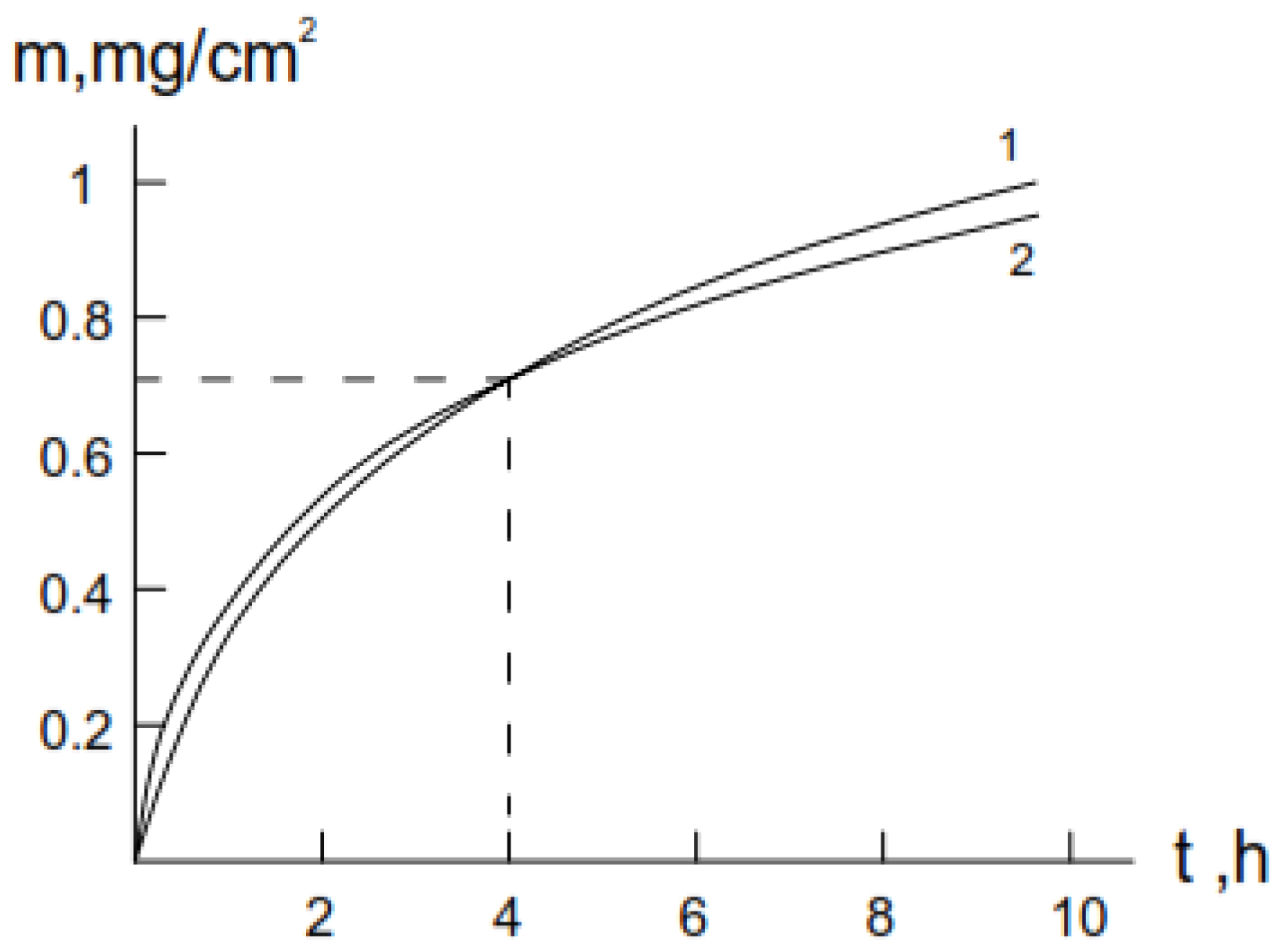
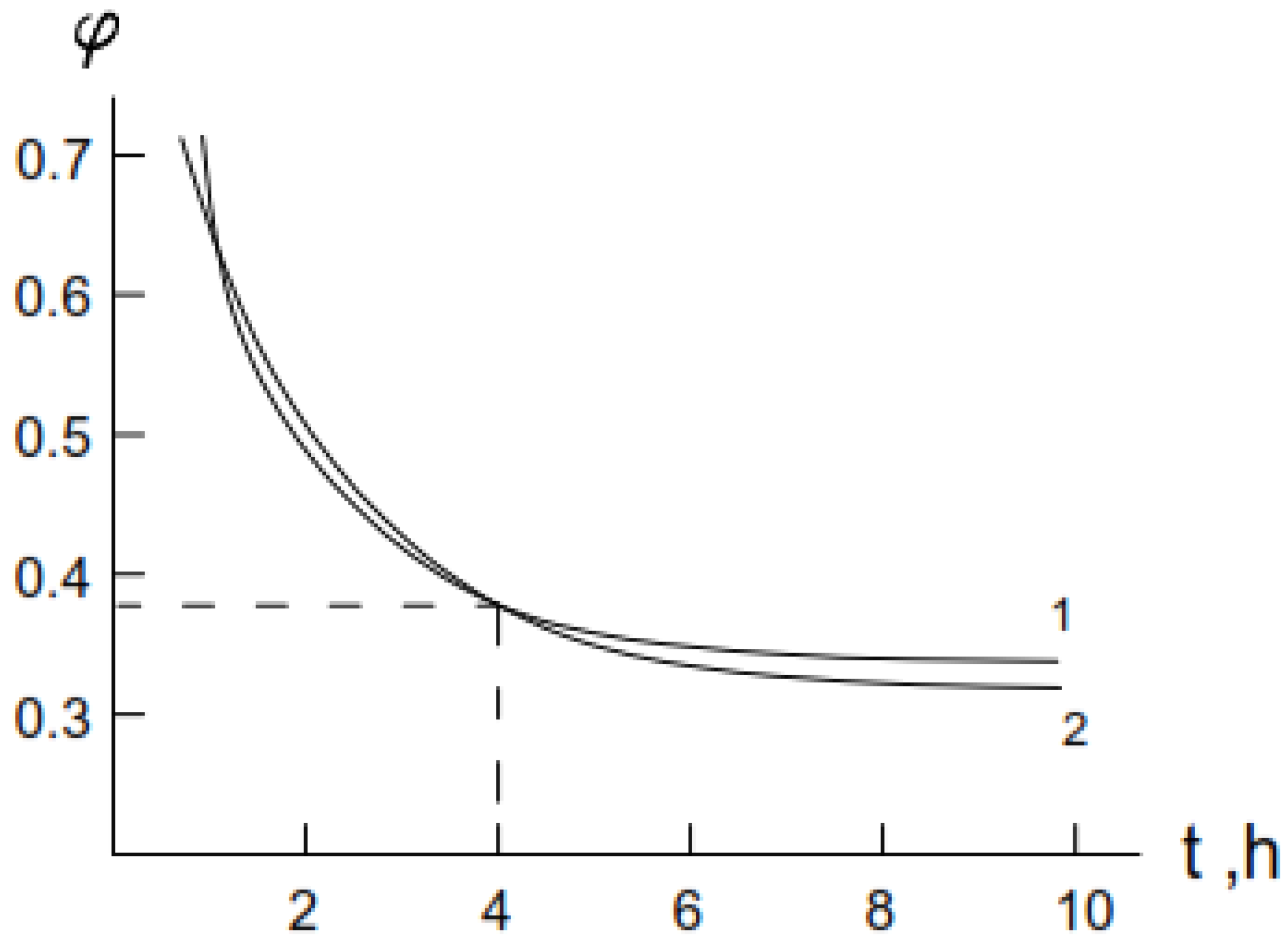
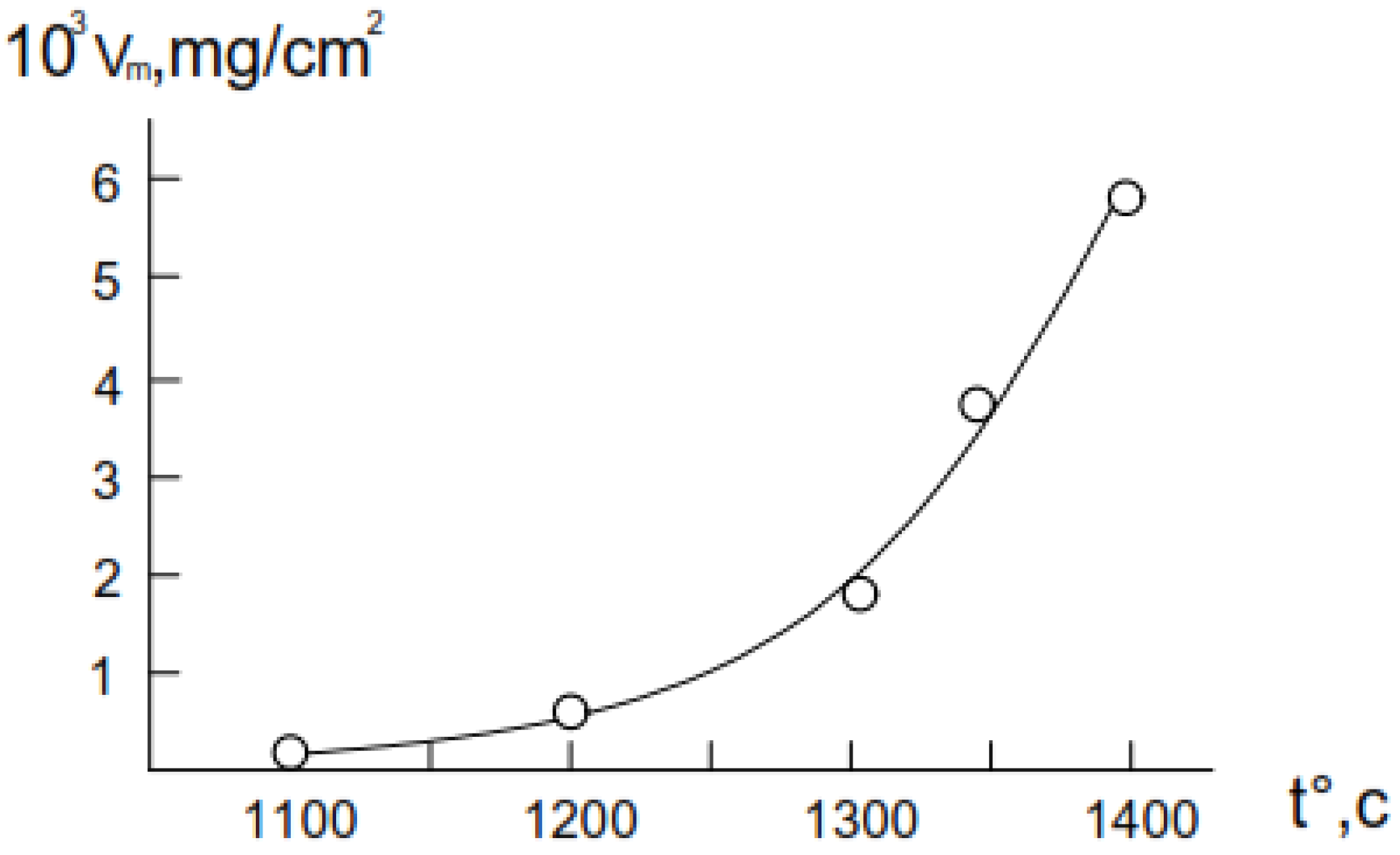

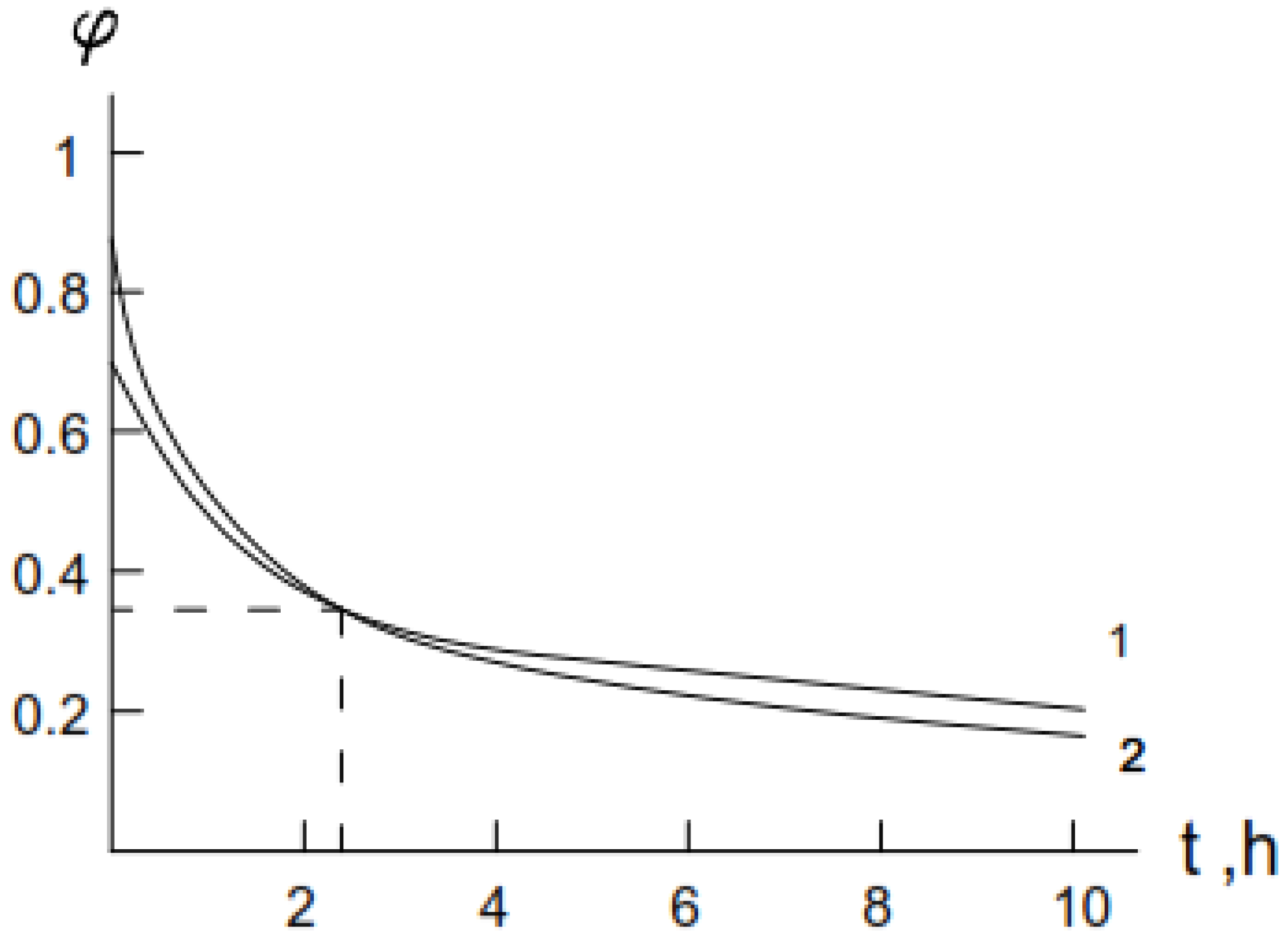
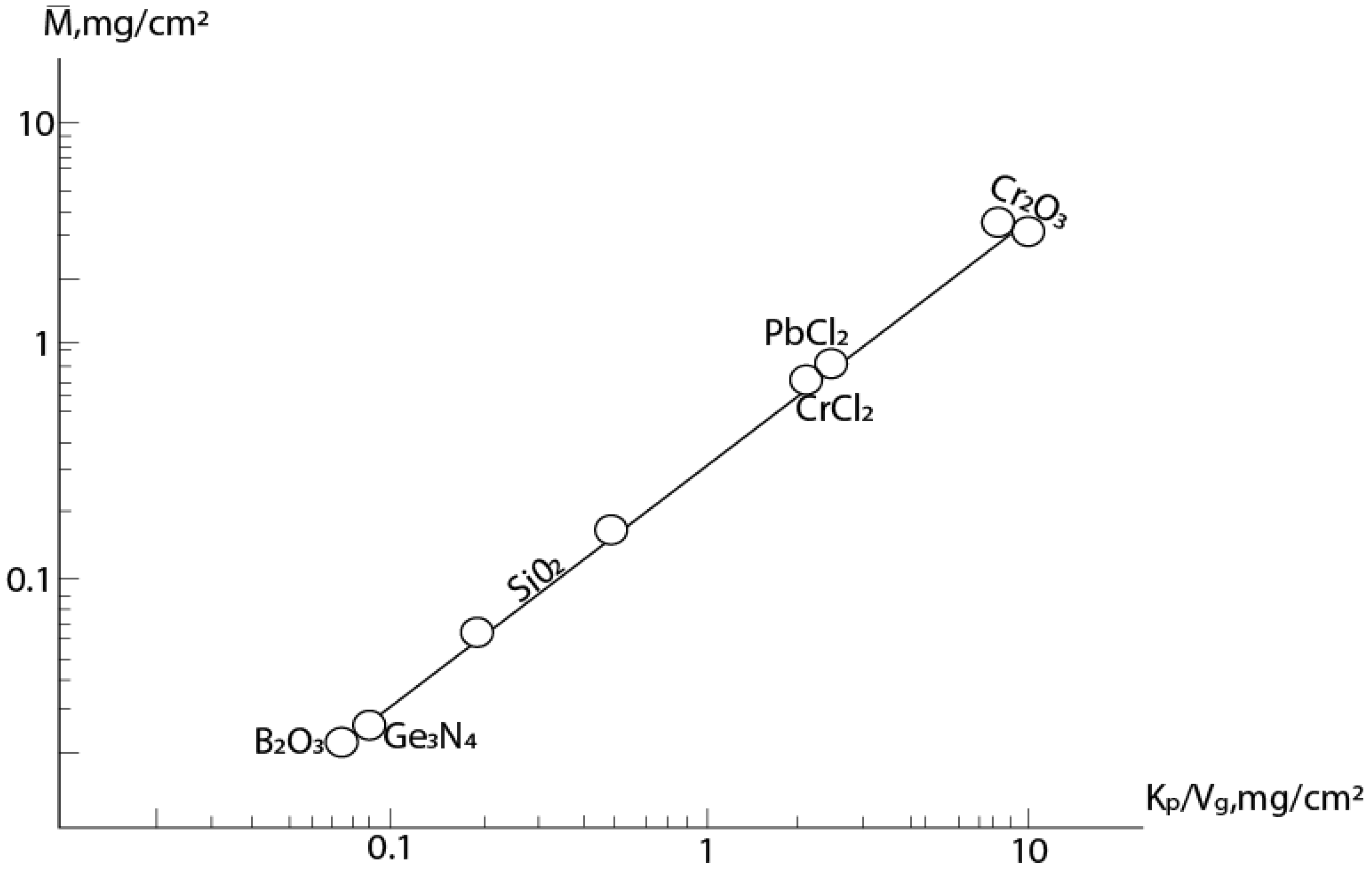

| Parameters | Temperature, °C | ||
|---|---|---|---|
| 1200 | 1250 | 1300 | |
| k, cm2/mg | 1.99 | 1.68 | 1.46 |
| kr, mg/cm2·h | 0.65 | 0.78 | 0.95 |
| kp, mg2/cm4·h | 0.12 | 0.27 | 0.59 |
| mA, mg/cm2 | 0.4 | 0.5 | 0.7 |
| tA, h | 4 | 2.7 | 2.4 |
| φA, relat. units | 0.45 | 0.43 | 0.36 |
| Parameters | Temperature, °C | ||
|---|---|---|---|
| 1100 | 1200 | 1300 | |
| k, cm2/mg | 2.32 | 1.55 | 0.69 |
| kr, mg/cm2·h | 18.9 | 0.28 | 1.07 |
| kp, mg2/cm4·h | 3.85 | 3.6 | 3.93 |
| mA, mg/cm2 | 0.4 | 0.7 | 1.5 |
| tA, h | 4 | 4 | 4 |
| φA, relat. units | 0.39 | 0.37 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nakhutsrishvili, I.; Tevzadze, R. Oxidation Kinetics of FeCr and FeCrAl Alloys: Influence of Secondary Processes (Continuation). Alloys 2025, 4, 2. https://doi.org/10.3390/alloys4010002
Nakhutsrishvili I, Tevzadze R. Oxidation Kinetics of FeCr and FeCrAl Alloys: Influence of Secondary Processes (Continuation). Alloys. 2025; 4(1):2. https://doi.org/10.3390/alloys4010002
Chicago/Turabian StyleNakhutsrishvili, Irakli, and Revaz Tevzadze. 2025. "Oxidation Kinetics of FeCr and FeCrAl Alloys: Influence of Secondary Processes (Continuation)" Alloys 4, no. 1: 2. https://doi.org/10.3390/alloys4010002
APA StyleNakhutsrishvili, I., & Tevzadze, R. (2025). Oxidation Kinetics of FeCr and FeCrAl Alloys: Influence of Secondary Processes (Continuation). Alloys, 4(1), 2. https://doi.org/10.3390/alloys4010002