Long Short-Term Memory Network for Predicting Exchange Rate of the Ghanaian Cedi
Abstract
:1. Introduction
- (i)
- Enhancement can be achieved in exchange rate predictability using information fusion from historical microeconomic data and public search queries (Google Trends).
- (ii)
- The long short-term memory offers a better prediction accuracy than the traditional statistical models.
2. Related Works
| Ref. | Algorithm | Data Source | Evaluation Metric | Study Origin |
|---|---|---|---|---|
| [22] | PPP, Random walk, Monetary model, interest parity | GT | MSPE | NS |
| [5] | PLSSEM | MV | R2, f2, Q2 and SGT | Ghana |
| [28] | Multivariate GARCH DCC and BEKK models using | MV | Correlation | Ghana |
| [1] | ARIMA | MV | RMSE, MAE, MPE, MAPE | Nigeria |
| [12] | Neural Network | MV | RMSE | NS |
| [10] | Morlet wavelet transform | MV | Mean, variance, skewness, kurtosis | Ghana |
| [30] | ARIMA | MV | MAPE, RMSE | Ghana |
| [13] | SVAR | MV | UK | |
| [11] | Taylor rules fundamentals, yield curve factors | MV | MSE | NS |
| [4] | FFVAR, Bayesian vector auto-regression | MV | MSE | US |
| [31] | ARIMA and Random walk | MV | Correlation | Ghana |
| [38] | Neural network | MV | MSE, MAPE | Indian |
| [9] | MV | Skewness, p-value, Kurtosis | Ghana | |
| [39] | RNN and CNN | MV | RMSE | China |
| [40] | SVM, ANN and LSTM | MV | Accuracy | India |
| [37] | LSTM | MV | RMSE, accuracy | NS |
| [41] | Public sentiments | RMSE, MAE | Korea | |
| [24] | Extreme Learning Machines (ELMs) and the Jaya optimisation technique | MV | MAPE, Theil’s U, ARV, and MAE | India |
| Proposed model | LSTM | GT + MV | RMSE, MAE, Accuracy | Ghana |
3. Materials and Methods
3.1. Study Framework
3.1.1. Data Download and Integration
3.1.2. Data Pre-Processing and Partitioning
3.1.3. Machine-Learning Model
3.2. Theoretical Background of Benchmark Models
3.2.1. Support Vector Regressor
3.2.2. Back-Propagation Neural Network (BPNN)
3.2.3. Evaluation Metrics
4. Results and Discussions
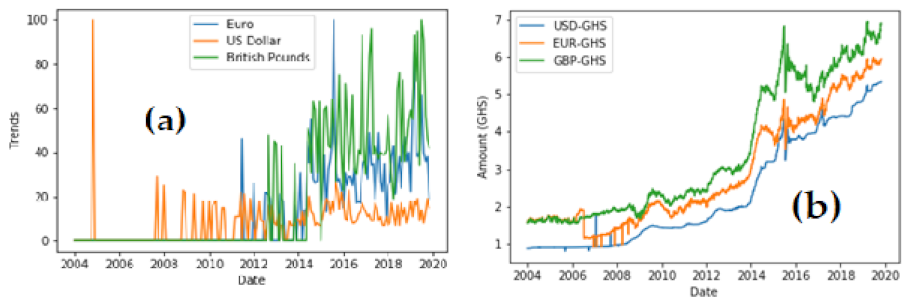
4.1. Dataset Visualisation
4.2. Model Performance Measure
4.2.1. Automatic Feature Selection
4.2.2. Prediction with Macroeconomic Variables
4.2.3. Prediction with Macroeconomic Variables and Google Trend
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| S/N | MACROECONOMIC VARIABLES | Abbreviation |
|---|---|---|
| MONTHLY MONETARY SURVEY | ||
| 1. | Net Foreign Assets | NFA |
| 2. | BOG | BOG |
| 3. | DMBs | DMB |
| 4. | Net Domestic Assets | NDA |
| 5. | Claims on Gov’t | CoG |
| 6. | Govt. Deposits | GD |
| 7. | Claims on private sector | CPS |
| 8. | Other Items (net) | OI |
| 9. | Total Assets | TA |
| 10. | Currency outside banks | COB |
| 11. | Demand deposits | DD |
| 12. | Savings & Time deposits | STD |
| 13. | Foreign currency deposits | FCD |
| 14. | Total Liabilities | TL |
| 15. | Reserve Money (RM) | RM |
| 16. | Narrow Money (M1) | M1 |
| 17. | Broad Money (M2) | M2+ |
| 18. | Total Liquidity (M2+) | TLM2+ |
| MONTHLY INTEREST RATES | ||
| 19. | Monetary Policy Rate | MPR |
| 20. | 91-Day Treasury Bill Interest Rate Equivalent | 91-Tbill |
| 21. | Inter-Bank Weighted Average | IBWA |
| 22. | Average Commercial Banks Lending Rate | ACBLR |
| 23. | Average Savings Deposits Rate | ASDR |
| 24. | Average Time Deposits Rate (3-Month) | ATD |
| COMMODITY PRICES MONTHLY | ||
| 25. | International Cocoa Price (US$/Tonne) | CP |
| 26. | International Gold (US$/fine ounce) | GP |
| 27. | International Brent Crude Oil (US$/Barrel) | BCOP |
| INFLATION | ||
| 28. | Headline Inflation | HF |
| 29. | Food Inflation | FI |
| 31. | Non-Food Inflation | NFI |
| 32. | Bank of Ghana Composite Index of Economic Activity (Nominal Growth) | BGCIEA_NG |
| 33. | Bank of Ghana Composite Index of Economic Activity (Real Growth) | BGCIEA_RG |
References
- Nyoni, T. Modeling and Forecasting Naira/USD Exchange Rate in Nigeria: A Box-Jenkins ARIMA Approach; MPRA Paper No 88622; Munich Personal RePEc Archive, 2018; pp. 6–25. Available online: https://mpra.ub.uni-muenchen.de/88622/ (accessed on 27 February 2020).
- Auclert, A. Monetary policy and the redistribution channel. Am. Econ. Rev. 2019, 109, 2333–2367. [Google Scholar] [CrossRef] [Green Version]
- Mueller, P.; Tahbaz-Salehi, A.; Vedolin, A. Exchange Rates and Monetary Policy Uncertainty. J. Financ. 2017, 72, 1213–1252. [Google Scholar] [CrossRef] [Green Version]
- Abbate, A.; Marcellino, M. Point, interval and density forecasts of exchange rates with time varying parameter models. J. R. Stat. Soc. Ser. A Stat. Soc. 2018, 181, 155–179. [Google Scholar] [CrossRef] [Green Version]
- Adusei, M.; Gyapong, E.Y. The impact of macroeconomic variables on exchange rate volatility in Ghana: The Partial Least Squares Structural Equation Modelling approach. Res. Int. Bus. Financ. 2017, 42, 1428–1444. [Google Scholar] [CrossRef]
- Byrne, J.P.; Korobilis, D.; Ribeiro, P.J. On the Sources of Uncertainty in Exchange Rate Predictability. Int. Econ. Rev. (Phila.) 2018, 59, 329–357. [Google Scholar] [CrossRef] [Green Version]
- Samanhyia, S.; Oware, K.M.; Anisom-yaansah, F. Financial Distress and Bankruptcy Prediction: Evidence from Ghana. Expert J. Financ. 2016, 4, 52–65. [Google Scholar]
- Ernest, K.; Theophilus, A.-K.; Amoah, P.; Emmanuel, B.B. Identifying key economic indicators influencing tender price index prediction in the building industry: A case study of Ghana. Int. J. Constr. Manag. 2019, 19, 106–112. [Google Scholar] [CrossRef]
- Sarpong, S. Estimating the probability distribution of the exchange rate between Ghana Cedi and American dollar. J. King Saud Univ.-Sci. 2019, 31, 177–183. [Google Scholar] [CrossRef]
- Owusu, P.J.; Tweneboah, G.; Adam, A.M. Interdependence of Major Exchange Rates in Ghana: A Wavelet Coherence Analysis. J. Afr. Bus. 2019, 20, 407–430. [Google Scholar] [CrossRef]
- Cheung, Y.-W.; Chinn, M.D.; Pascual, A.G.; Zhang, Y. Exchange rate prediction redux: New models, new data, new currencies. J. Int. Money Financ. 2019, 95, 332–362. [Google Scholar] [CrossRef] [Green Version]
- Shahbazi, N.; Memarzadeh, M.; Gryz, J. Forex Market Prediction Using NARX Neural Network with Bagging. MATEC Web Conf. 2016, 68, 19001. [Google Scholar] [CrossRef] [Green Version]
- Forbes, K.; Hjortsoe, I.; Nenova, T. The shocks matter: Improving our estimates of exchange rate pass-through. J. Int. Econ. 2018, 114, 255–275. [Google Scholar] [CrossRef] [Green Version]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A systematic review of fundamental and technical analysis of stock market predictions. Artif. Intell. Rev. 2019, 53, 3007–3057. [Google Scholar] [CrossRef]
- Rezaee, M.J.; Jozmaleki, M.; Valipour, M. Integrating dynamic fuzzy C-means, data envelopment analysis and artificial neural network to online prediction performance of companies in stock exchange. Phys. A Stat. Mech. Appl. 2018, 489, 78–93. [Google Scholar] [CrossRef]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. Random Forest Based Feature Selection of Macroeconomic Variables for Stock Market Prediction. Am. J. Appl. Sci. 2019, 16, 200–212. [Google Scholar] [CrossRef]
- Agarwal, S.; Kumar, S.; Goel, U. Stock market response to information diffusion through internet sources: A literature review. Int. J. Inf. Manag. 2019, 45, 118–131. [Google Scholar] [CrossRef]
- Pandurang, G.D.; Kumar, K. Ensemble Computations on Stock Market: A Standardized Review for Future Directions. In Proceedings of the 2019 IEEE International Conference on Electrical, Computer and Communication Technologies (ICECCT), Coimbatore, India, 20–22 February 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nguyen, T.; Yoon, S. A Novel Approach to Short-Term Stock Price Movement Prediction using Transfer Learning. Appl. Sci. 2019, 9, 4745. [Google Scholar] [CrossRef] [Green Version]
- Thakkar, A.; Chaudhari, K. Fusion in stock market prediction: A decade survey on the necessity, recent developments, and potential future directions. Inf. Fusion 2021, 65, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A novel multi-source information-fusion predictive framework based on deep neural networks for accuracy enhancement in stock market prediction. J. Big Data 2021, 8, 17. [Google Scholar] [CrossRef]
- Bulut, L. Google Trends and the forecasting performance of exchange rate models. J. Forecast. 2018, 37, 303–315. [Google Scholar] [CrossRef]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. Predicting Stock Market Price Movement Using Sentiment Analysis: Evidence from Ghana. Appl. Comput. Syst. 2020, 25, 33–42. [Google Scholar] [CrossRef]
- Das, S.R.; Mishra, D.; Rout, M. A hybridized ELM-Jaya forecasting model for currency exchange prediction. J. King Saud Univ.-Comput. Inf. Sci. 2020, 32, 345–366. [Google Scholar] [CrossRef]
- Picasso, A.; Merello, S.; Ma, Y.; Oneto, L.; Cambria, E. Technical analysis and sentiment embeddings for market trend prediction. Expert Syst. Appl. 2019, 135, 60–70. [Google Scholar] [CrossRef]
- Chen, W.; Xu, H.; Jia, L.; Gao, Y. Machine learning model for Bitcoin exchange rate prediction using economic and technology determinants. Int. J. Forecast. 2021, 37, 28–43. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H. Insights into lstm fully convolutional networks for time series classification. IEEE Access 2019, 7, 67718–67725. [Google Scholar] [CrossRef]
- Nortey, E.N.N.; Ngoh, D.D.; Doku-Amponsah, K.; Ofori-Boateng, K. Modeling inflation rates and exchange rates in Ghana: Application of multivariate GARCH models. Springerplus 2015, 4, 86. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meese, R.; Rogoff, K.S. The Out-of-Sample Failure of Empirical Exchange Rate Models: Sampling Error or Misspecification? National Bureau of Economic Research: Cambridge, MA, USA, 1982; Volume 1982, ISBN 0226262502. [Google Scholar]
- Adetunde, I.A.; Appiah, S.T. Forecasting Exchange Rate Between the Ghana Cedi and the Us Dollar Using Time Series Analysis. Afr. J. Basic Appl. Sci. 2011, 3, 255–264. [Google Scholar]
- Ayekple, Y.E.; Harris, E.; Frempong, N.K.; Amevialor, J. Time Series Analysis of the Exchange Rate of the Ghanaian Cedi to the American Dollar. J. Math. Res. 2015, 7, 46–53. [Google Scholar] [CrossRef] [Green Version]
- Caiani, A.; Godin, A.; Caverzasi, E.; Gallegati, M.; Kinsella, S.; Stiglitz, J.E. Journal of Economic Dynamics & Control Agent based-stock flow consistent macroeconomics: Towards a benchmark model. J. Econ. Dyn. Control. 2016, 69, 375–408. [Google Scholar] [CrossRef] [Green Version]
- Bisoi, R.; Dash, P.K. A hybrid evolutionary dynamic neural network for stock market trend analysis and prediction using unscented Kalman filter. Appl. Soft Comput. J. 2014, 19, 41–56. [Google Scholar] [CrossRef]
- Galeshchuk, S. Neural networks performance in exchange rate prediction. Neurocomputing 2016, 172, 446–452. [Google Scholar] [CrossRef]
- Galeshchuk, S.; Mukherjee, S. Deep networks for predicting direction of change in foreign exchange rates. Intell. Syst. Account. Financ. Manag. 2017, 24, 100–110. [Google Scholar] [CrossRef]
- Galeshchuk, S.; Mukherjee, S. Deep Learning for Predictions in Emerging Currency Markets. In Proceedings of the 9th International Conference on Agents and Artificial Intelligence, Porto, Portugal, 24–26 February 2017; Volume 2: NO. ICAART. SCITEPRESS—Science and Technology Publications: Setúbal, Portugal, 2017; pp. 681–686. [Google Scholar] [CrossRef]
- Qu, Y.; Zhao, X. Application of LSTM Neural Network in Forecasting Foreign Exchange Price. J. Phys. Conf. Ser. 2019, 1237, 042036. [Google Scholar] [CrossRef]
- Singh, U.P.; Jain, S. Optimization of neural network for nonlinear discrete time system using modified quaternion firefly algorithm: Case study of Indian currency exchange rate prediction. Soft Comput. 2018, 22, 2667–2681. [Google Scholar] [CrossRef]
- Ni, L.; Li, Y.; Wang, X.; Zhang, J.; Yu, J.; Qi, C. Forecasting of Forex Time Series Data Based on Deep Learning. Proced. Comput. Sci. 2019, 147, 647–652. [Google Scholar] [CrossRef]
- Nagpure, A.R. Prediction of multi-currency exchange rates using deep learning. Int. J. Innov. Technol. Explor. Eng. 2019, 8, 316–322. [Google Scholar]
- Yasir, M.; Durrani, M.Y.; Afzal, S.; Maqsood, M.; Aadil, F.; Mehmood, I.; Rho, S. An intelligent event-sentiment-based daily foreign exchange rate forecasting system. Appl. Sci. 2019, 9, 2980. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Tang, L.; Zhang, S.; Wang, H. Predicting the direction of stock markets using optimized neural networks with Google Trends. Neurocomputing 2018, 285, 188–195. [Google Scholar] [CrossRef]
- Fan, M.-H.; Chen, M.-Y.; Liao, E.-C. A deep learning approach for financial market prediction: Utilization of Google trends and keywords. Granul. Comput. 2021, 6, 207–216. [Google Scholar] [CrossRef]
- Maneejuk, P.; Yamaka, W. Predicting Contagion from the US Financial Crisis to International Stock Markets Using Dynamic Copula with Google Trends. Mathematics 2019, 7, 1032. [Google Scholar] [CrossRef] [Green Version]
- Bock, J. Quantifying Macroeconomic Expectations in Stock Markets Using Google Trends. SSRN Electron. J. 2018, 1805.00268. Available online: https://ssrn.com/abstract=3218912 (accessed on 22 March 2018).
- Ito, T.; Masuda, M.; Naito, A.; Takeda, F. Application of Google Trends-based sentiment index in exchange rate prediction. J. Forecast. 2021, 40, 1154–1178. [Google Scholar] [CrossRef]
- Wilcoxson, J.; Follett, L.; Severe, S. Forecasting Foreign Exchange Markets Using Google Trends: Prediction Performance of Competing Models. J. Behav. Financ. 2020, 21, 412–422. [Google Scholar] [CrossRef]
- Appiah, A.Y.; Zhang, X.; Ayawli, B.B.K.; Kyeremeh, F. Long Short-Term Memory Networks based Automatic Feature Extraction for Photovoltaic Array Fault Diagnosis. IEEE Access 2019, 7, 30089–30101. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support vector method for function approximation, regression estimation, and signal processing. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 281–287. [Google Scholar]
- Nawi, N.M.; Khan, A.; Rehman, M.Z. A new back-propagation neural network optimized with cuckoo search algorithm. In Computational Science and Its Applications–ICCSA 2013; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7971 LNCS, Part 1; pp. 413–426. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Qian, Y.; Bai, Q.; Liu, W. Exploration on the financing risks of enterprise supply chain using Back Propagation neural network. J. Comput. Appl. Math. 2020, 367, 112457. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Techie Quaicoe, M.; Twenefour, F.B.K.; Baah, E.M.; Nortey, E.N.N. Modeling variations in the cedi/dollar exchange rate in Ghana: An autoregressive conditional heteroscedastic (ARCH) models. Springerplus 2015, 4, 329. [Google Scholar] [CrossRef] [Green Version]
- Nti, I.K.; Adekoya, A.F.; Weyori, B.A. A comprehensive evaluation of ensemble learning for stock-market prediction. J. Big Data 2020, 7, 20. [Google Scholar] [CrossRef]












| Hyperparameter | Value |
|---|---|
| Input time steps | 20 |
| Input feature dimension | 10 |
| Learning rate | 0.002 |
| Adam optimiser | |
| Batch size | 128 |
| # Epochs | 100 |
| # nodes in LSTM input layer | 34 |
| # nodes in LSTM output layer | 1 |
| Output layer | single value prediction |
| USD–GH₵ | EUR–GH₵ | GBP–GH₵ | |
|---|---|---|---|
| Mean | 2.321627451 | 2.901645 | 3.434115 |
| Standard Error | 0.02308252 | 0.023675 | 0.02839 |
| Median | 1.5859 | 2.1533 | 2.4558 |
| Mode | 0.9122 | 1.9176 | 1.7076 |
| Standard Deviation | 1.446484115 | 1.483602 | 1.779061 |
| Sample Variance | 2.092316295 | 2.201076 | 3.165059 |
| Kurtosis | −1.09615245 | −1.05057 | −1.37613 |
| Skewness | 0.671644346 | 0.661981 | 0.541371 |
| Range | 4.5275 | 5.0625 | 5.4178 |
| Minimum | 0.8124 | 0.922 | 1.5343 |
| Maximum | 5.3399 | 5.9845 | 6.9521 |
| Sum | 9117.031 | 11,394.76 | 13,485.77 |
| Confidence Level (95.0%) | 0.045254859 | 0.046416 | 0.05566 |
| Currency | Models | MAE | MSE | RMSE | R2 | RMSLE | MAPE |
|---|---|---|---|---|---|---|---|
| EUR | LSTM | 0.0327 | 0.0035 | 0.0551 | 0.9983 | 0.0129 | 0.0121 |
| BPNN | 0.0433 | 0.0056 | 0.0688 | 0.9974 | 0.0172 | 0.0168 | |
| SVR | 0.0508 | 0.0051 | 0.0683 | 0.9973 | 0.0191 | 0.0241 | |
| USD | LSTM | 0.0805 | 0.0172 | 0.1208 | 0.9939 | 0.0218 | 0.0218 |
| BPNN | 0.0973 | 0.0217 | 0.1406 | 0.9916 | 0.0274 | 0.0287 | |
| SVR | 0.095 | 0.0238 | 0.146 | 0.9911 | 0.0275 | 0.0269 | |
| GBP | LSTM | 0.0634 | 0.0096 | 0.0923 | 0.9953 | 0.0268 | 0.0257 |
| BPNN | 0.0794 | 0.0139 | 0.1135 | 0.993 | 0.0329 | 0.0328 | |
| SVR | 0.0928 | 0.0172 | 0.1255 | 0.9914 | 0.0333 | 0.0362 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adekoya, A.F.; Nti, I.K.; Weyori, B.A. Long Short-Term Memory Network for Predicting Exchange Rate of the Ghanaian Cedi. FinTech 2022, 1, 25-43. https://doi.org/10.3390/fintech1010002
Adekoya AF, Nti IK, Weyori BA. Long Short-Term Memory Network for Predicting Exchange Rate of the Ghanaian Cedi. FinTech. 2022; 1(1):25-43. https://doi.org/10.3390/fintech1010002
Chicago/Turabian StyleAdekoya, Adebayo Felix, Isaac Kofi Nti, and Benjamin Asubam Weyori. 2022. "Long Short-Term Memory Network for Predicting Exchange Rate of the Ghanaian Cedi" FinTech 1, no. 1: 25-43. https://doi.org/10.3390/fintech1010002
APA StyleAdekoya, A. F., Nti, I. K., & Weyori, B. A. (2022). Long Short-Term Memory Network for Predicting Exchange Rate of the Ghanaian Cedi. FinTech, 1(1), 25-43. https://doi.org/10.3390/fintech1010002






