First-Order Decay Models for the Estimation of Methane Emissions in a Landfill in the Metropolitan Area of Oaxaca City, Mexico
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Climatology
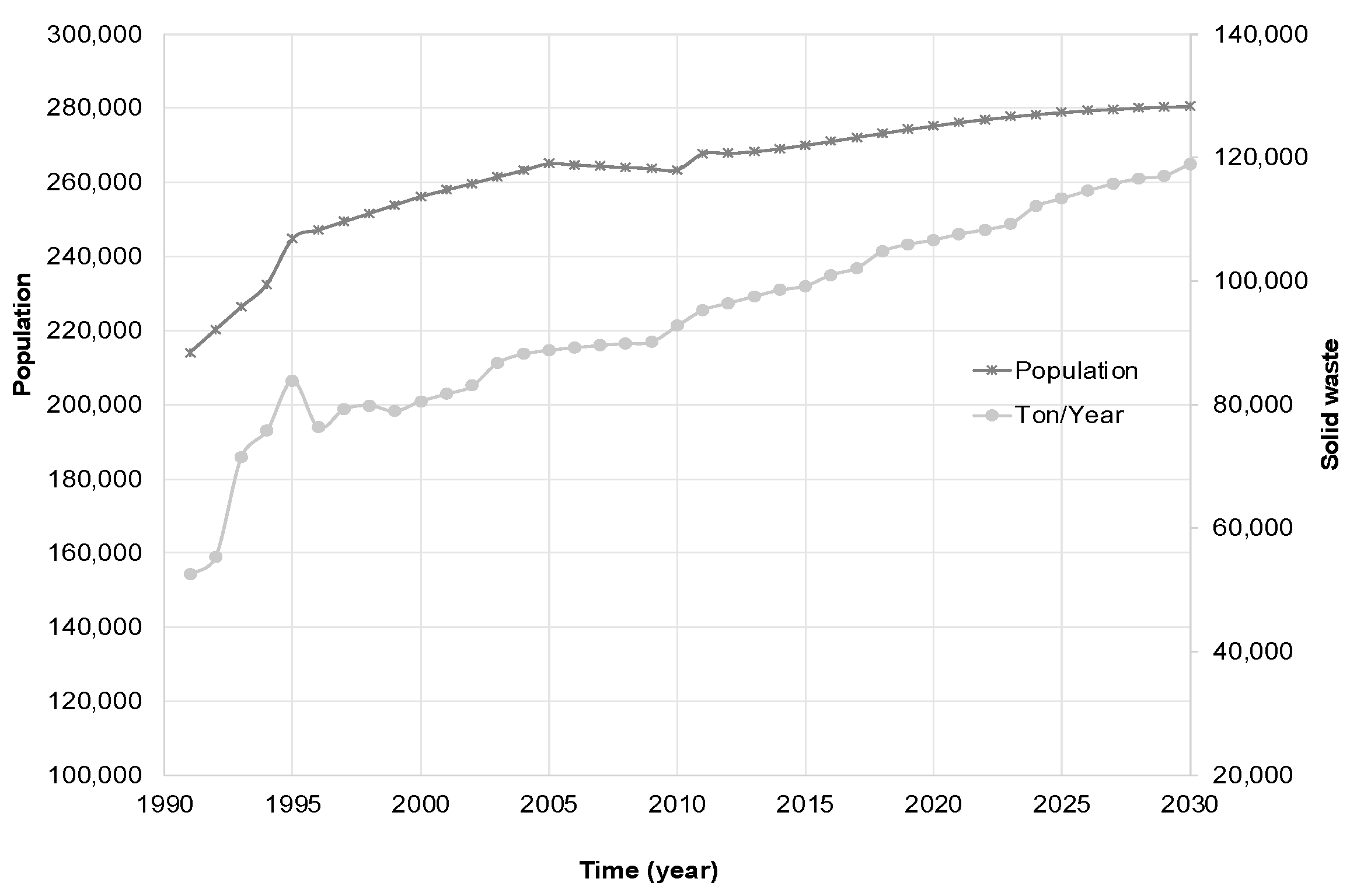
2.3. Population and Generation of Waste in the City of Oaxaca
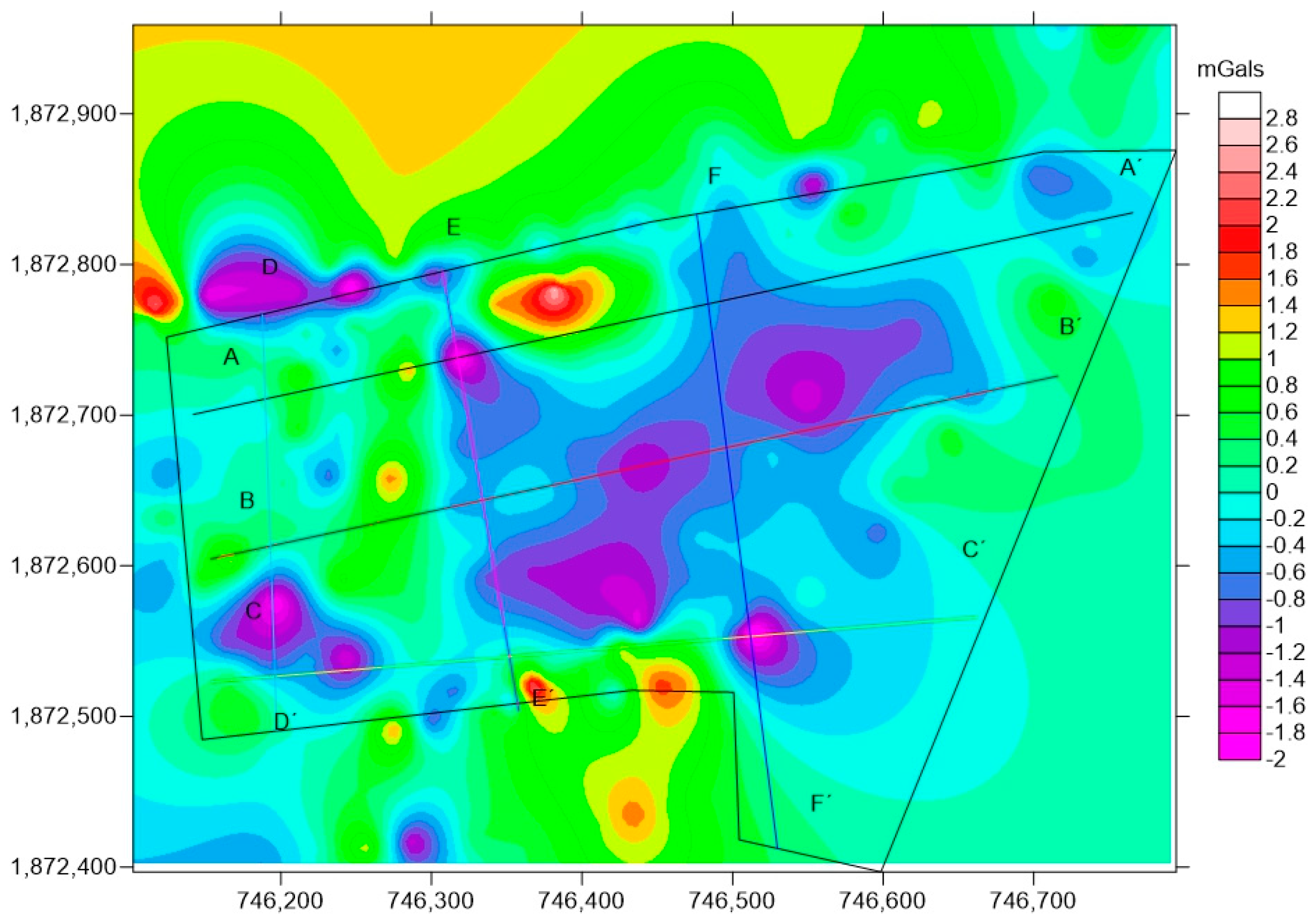
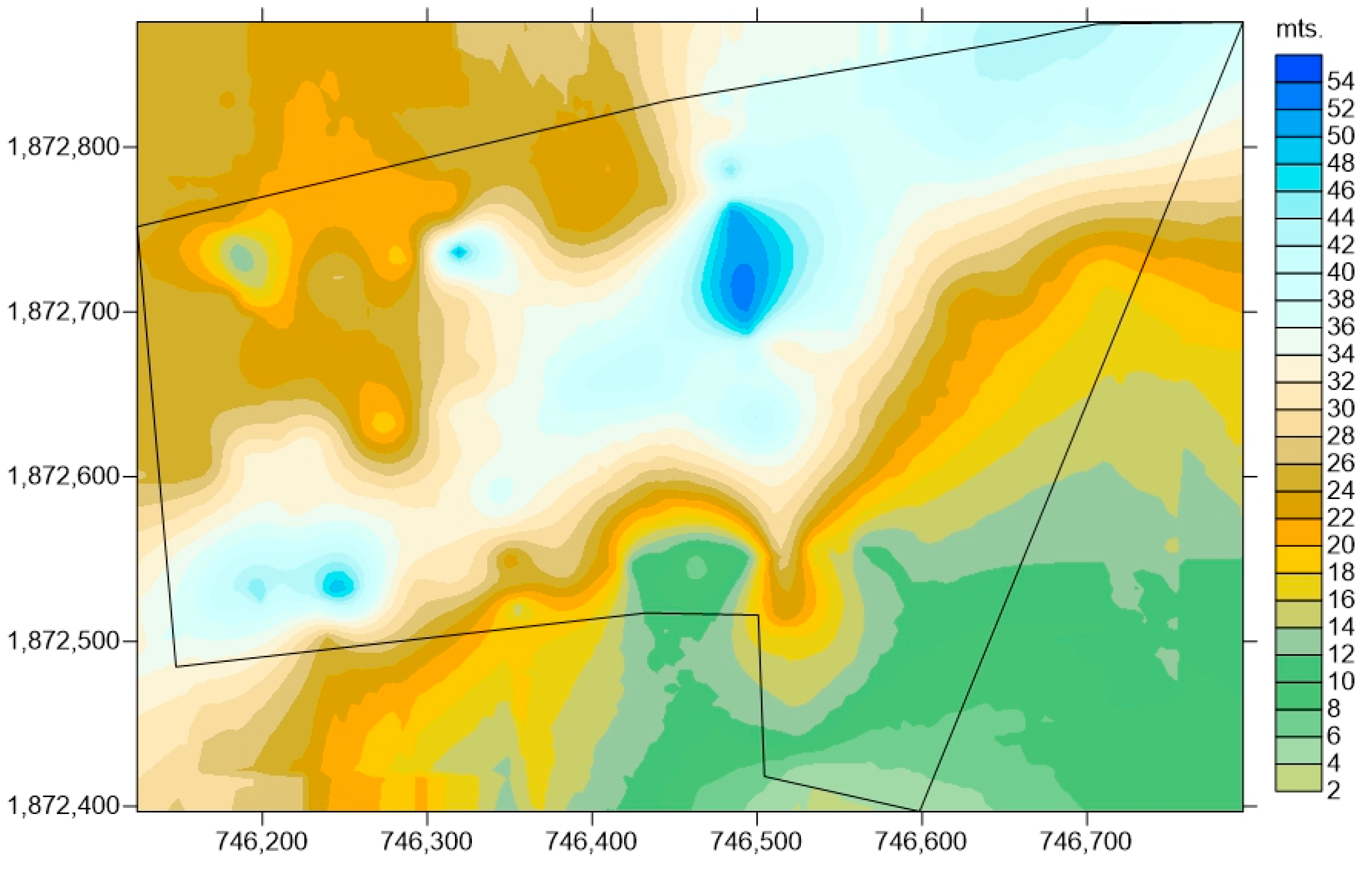
2.4. Volume of Waste
2.5. Composition of Solid Waste
2.6. Mathematical Models for Methane Emissions
2.7. Input Parameters of the Models
2.7.1. Degradable Organic Carbon (DOC)
2.7.2. Fraction of CH4 in Biogas
2.7.3. Ratio of Molecular Weight
2.7.4. Methane Correction Factor (MCF)
3. Results
3.1. Volume of Waste
3.2. Parameters k and L0
3.3. Modeling Solid Waste Generation
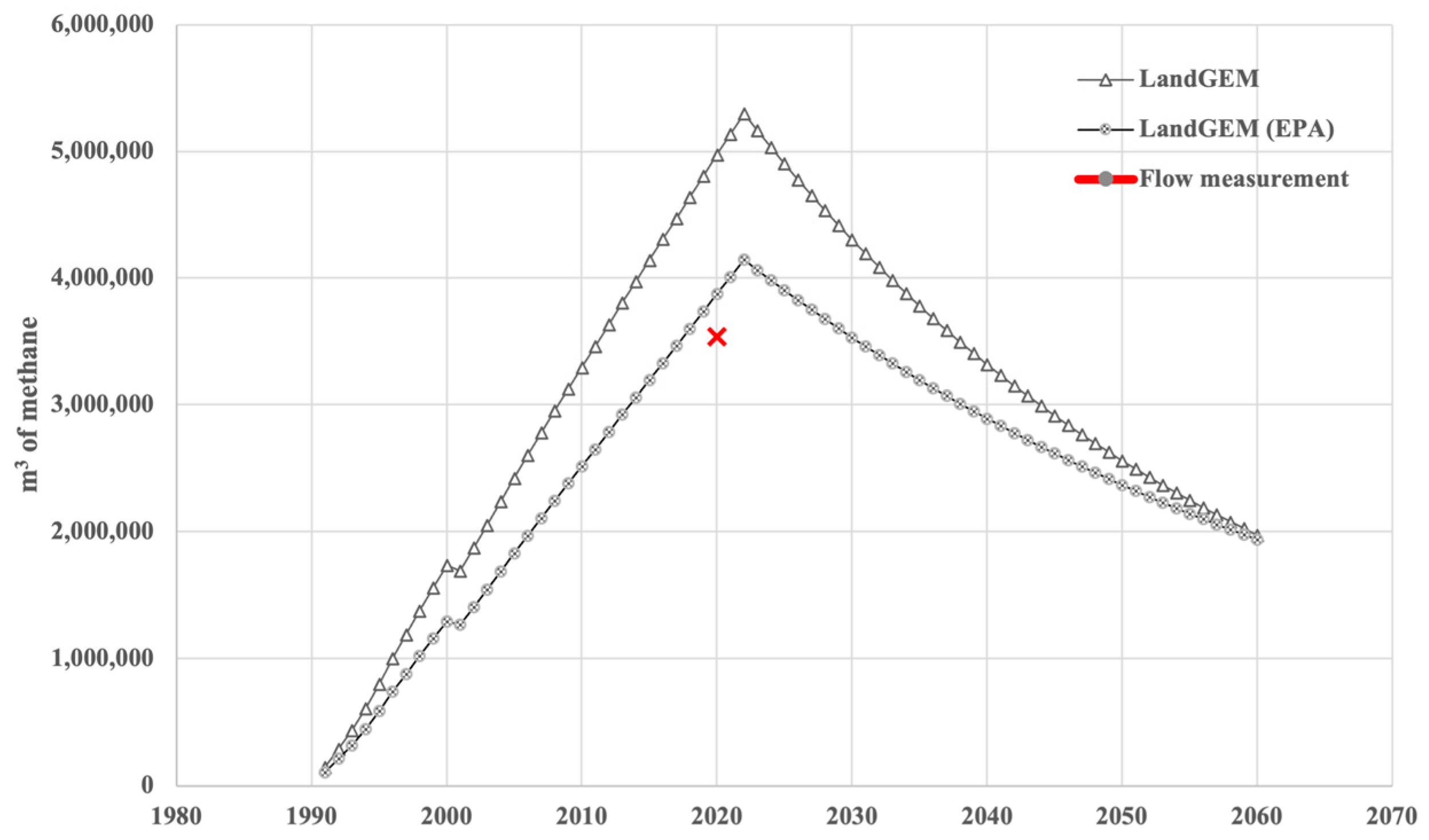
3.4. Modeling the Generation of Methane
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Loganath, R.; Mohammed Bin Zacharia, K.; Kumar, A.; Singh, E.; Varma, V.S.; Sharma, D. System optimization models for solid waste management. In Current Developments in Biotechnology and Bioengineering; Elsevier: Amsterdam, The Netherlands, 2021; pp. 349–371. ISBN 978-0-12-821009-3. [Google Scholar] [CrossRef]
- Kaza, S.; Yao, L.C.; Bhada-Tata, P.; Van Woerden, F. What a Waste 2.0: A Global Snapshot of Solid Waste Management to 2050; World Bank: Washington, DC, USA, 2018; ISBN 978-1-4648-1329-0. [Google Scholar] [CrossRef]
- Kua, H.W.; He, X.; Tian, H.; Goel, A.; Xu, T.; Liu, W.; Yao, D.; Ramachandran, S.; Liu, X.; Tong, Y.W.; et al. Life cycle climate change mitigation through next-generation urban waste recovery systems in high-density Asian cities: A Singapore Case Study. Resour. Conserv. Recycl. 2022, 181, 106265. [Google Scholar] [CrossRef]
- Paes, M.X.; De Medeiros, G.A.; Mancini, S.D.; Gasol, C.; Pons, J.R.; Durany, X.G. Transition towards eco-efficiency in municipal solidwaste management to reduce GHG emissions: The case of Brazil. J. Clean. Prod. 2020, 263, 121370. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.P. Estimation of GHG emission and energy recovery potential from MSW landfill sites. Sustain. Energy Technol. Assess. 2014, 5, 50–61. [Google Scholar] [CrossRef]
- Gobierno del Estado de Oaxaca. Resumen Ejecutivo del Programa Estatal Para la Prevención y Gestión Integral de los Residuos Sólidos Urbanos y de Manejo Especial en el Estado de Oaxaca; Secretaria de Medio Ambiente Energías y Desarrollo Sustentable, Oaxaca: Oaxaca, Mexico, 2013; Available online: https://www.oaxaca.gob.mx/semaedeso/wp-content/uploads/sites/59/2022/08/Resumen-Ejecutivo-PEPGIRSUME.pdf (accessed on 25 November 2024).
- SEMARNAT. Diagnóstico Básico Para la Gestión Integral de los Residuos Sólidos. Mexico, 2020. Secretaria de Medio Ambiente y Recursos Naturales, México. 2020. Available online: https://www.gob.mx/cms/uploads/attachment/file/554385/DBGIR-15-mayo-2020.pdf (accessed on 25 November 2024).
- Rueda-Avellaneda, J.F.; Rivas-García, P.; Gomez-Gonzalez, R.; Benitez-Bravo, R.; Botello-Álvarez, J.E.; Tututi-Avila, S. Current and prospective situation of municipal solid waste final disposal in Mexico: A spatio-temporal evaluation. Renew. Sustain. Energy Transit. 2021, 1, 100007. [Google Scholar] [CrossRef]
- Kumar, S.; Nimchuk, N.; Kumar, R.; Zietsman, J.; Ramani, T.; Spiegelman, C.; Kenney, M. Specific model for the estimation of methane emission from municipal solid waste landfills in India. Bioresour. Technol. 2016, 216, 981–987. [Google Scholar] [CrossRef]
- Molina, L.; Puentes, A.; Ortuzar, F.; Zirath, S.; Islas, I.; Gonzalez, R.; Masera, O.; Bickel, J.; Ortinez, A.; Castelan-Ortega, O.; et al. Avances y Oportunidades en la Reducción de Contaminantes Climáticos de Vida Corta en América Latina y el Caribe; UN Environment: Nairobi, Kenya, 2018. [Google Scholar]
- Malmir, T.; Lagos, D.; Eicker, U. Optimization of landfill gas generation based on a modified first-order decay model: A case study in the province of Quebec, Canada. Environ. Syst. Res. 2023, 12, 6. [Google Scholar] [CrossRef]
- MathWorks What Is the Genetic Algorithm? Available online: https://la.mathworks.com/help/gads/what-is-the-genetic-algorithm.html?lang=en (accessed on 25 November 2024).
- Mir, A.A.; Mushtaq, J.; Dar, A.Q.; Patel, M. A quantitative investigation of methane gas and solid waste management in mountainous Srinagar city-A case study. J. Mater. Cycles Waste Manag. 2023, 25, 535–549. [Google Scholar] [CrossRef]
- Pheakdey, D.V.; Noudeng, V.; Xuan, T.D. Landfill Biogas Recovery and Its Contribution to Greenhouse Gas Mitigation. Energies 2023, 16, 4689. [Google Scholar] [CrossRef]
- Amini, H.R.; Reinhart, D.R.; Niskanen, A. Comparison of first-order-decay modeled and actual field measured municipal solid waste landfill methane data. Waste Manag. 2013, 33, 2720–2728. [Google Scholar] [CrossRef]
- Thompson, S.; Sawyer, J.; Bonam, R.; Valdivia, J.E. Building a better methane generation model: Validating models with methane recovery rates from 35 Canadian landfills. Waste Manag. 2009, 29, 2085–2091. [Google Scholar] [CrossRef]
- Colomer Mendoza, F.J.; García Darás, F.; Esteban Altabella, J.; Robles Martínez, F.; Aranda, G. Emisiones gaseosas de un relleno sanitario en México. Comparación con modelos de generación de biogás. Rev. Int. Contam. Ambie. 2016, 32, 113–122. [Google Scholar] [CrossRef]
- Córdoba, V.; Blanco, G.; Santalla, E.M. Modelado de la generación de biogás en rellenos sanitarios. Av. En Energías Renov. Y Medio Ambiente 2009, 13, 69–76. [Google Scholar]
- NOAA Global Monitoring Laboratory—Carbon Cycle Greenhouse Gases. Available online: https://gml.noaa.gov/ccgg/trends_ch4/ (accessed on 27 July 2023).
- Kuylenstierna, J.C.; Michalopoulou, E.; Malley, C. Global Methane Assessment: Benefits and Costs of Mitigating Methane Emissions. Available online: http://www.unep.org/resources/report/global-methane-assessment-benefits-and-costs-mitigating-methane-emissions (accessed on 14 February 2024).
- Bouyakhsass, R.; Souabi, S.; Bouaouda, S.; Taleb, A.; Kurniawan, T.A.; Liang, X.; Goh, H.H.; Anouzla, A. Adding value to unused landfill gas for renewable energy on-site at Oum Azza landfill (Morocco): Environmental feasibility and cost-effectiveness. Trends Food Sci. Technol. 2023, 142, 104168. [Google Scholar] [CrossRef]
- Chandrasekaran, R.; Busetty, S. Estimating the methane emissions and energy potential from Trichy and Thanjavur dumpsite by LandGEM model. Environ. Sci. Pollut. Res. 2022, 29, 48953–48963. [Google Scholar] [CrossRef] [PubMed]
- Vogt, W.G.; Augenstein, D. Comparison of Models for Predicting Landfill Methane Recovery; Final Report(NREL/SR--430-26041); Institution for Environmental Management: Palo Alto, CA, USA, 1997; p. 314088. [Google Scholar] [CrossRef]
- Da Silva, N.F.; Schoeler, G.P.; Lourenço, V.A.; De Souza, P.L.; Caballero, C.B.; Salamoni, R.H.; Romani, R.F. First order models to estimate methane generation in landfill: A case study in south Brazil. J. Environ. Chem. Eng. 2020, 8, 104053. [Google Scholar] [CrossRef]
- Nzotungicimpaye, C.-M.; MacIsaac, A.J.; Zickfeld, K. Delaying methane mitigation increases the risk of breaching the 2 °C warming limit. Commun. Earth Environ. 2023, 4, 250. [Google Scholar] [CrossRef]
- United Nations Environment Program Methane Emissions are Driving Climate Change. Here’s How to Reduce Them. Available online: https://www.unep.org/news-and-stories/story/methane-emissions-are-driving-climate-change-heres-how-reduce-them (accessed on 21 November 2024).
- Secretaria de Relaciones Exteriores México se Adhirió al Compromiso Global de Metano en la COP26, gob.mx. Available online: http://www.gob.mx/sre/prensa/mexico-se-adhirio-al-compromiso-global-de-metano-en-la-cop26?state=published (accessed on 21 November 2024).
- Observatorio Mexicano de Emisiones de Metano Petróleo y Gas, Observatorio Mexican. Available online: https://www.obmem.mx/sector-petroleo-y-gas-mx (accessed on 21 November 2024).
- Escamilla-García, P.E.; Jiménez-Castañeda, M.E.; Fernández-Rodríguez, E.; Galicia-Villanueva, S. Feasibility of energy generation by methane emissions from a landfill in southern Mexico. J. Mater. Cycles Waste Manag. 2020, 22, 295–303. [Google Scholar] [CrossRef]
- Garrido, P.A.L.; Gómez, J.S. Saneamiento del tiradero de la ciudad de Oaxaca de Juárez. In Revista AIDIS de Ingeniería y Ciencias Ambientales. Investigación, Desarrollo y Práctica; Instituto de Ingeniería, Universidad Nacional Autónoma de México: Mexico City, Mexico, 2006; Available online: https://www.revistas.unam.mx/index.php/aidis/article/view/14440 (accessed on 6 February 2024).
- CCKP World Bank Climate Change Knowledge Portal. Available online: https://climateknowledgeportal.worldbank.org/ (accessed on 14 February 2024).
- CONAGUA Climogramas 1981–2010. Available online: https://smn.conagua.gob.mx/es/climatologia/informacion-climatologica/climogramas-1981-2010 (accessed on 8 February 2024).
- INEGI Banco de Indicadores. Available online: https://www.inegi.org.mx/app/indicadores/ (accessed on 30 December 2023).
- OECD Waste—Municipal Waste. Available online: http://data.oecd.org/waste/municipal-waste.htm (accessed on 30 December 2023).
- Brockwell, P.J.; Davis, R.A. Introduction to Time Series and Forecasting; Springer Texts in Statistics; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-29852-8. [Google Scholar] [CrossRef]
- Dickey, D.; Fuller, W. Distribution of the Estimators for Autoregressive Time Series With a Unit Root. JASA J. Am. Stat. Assoc. 1979, 74, 427–431. [Google Scholar] [CrossRef]
- Dickey, D.G. Dickey-Fuller Tests. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 385–388. ISBN 978-3-642-04898-2. [Google Scholar] [CrossRef]
- Hinze, W.J.; Von Frese, R.R.B.; Saad, A.H. Gravity and Magnetic Exploration: Principles, Practices, and Applications; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-0-521-87101-3. [Google Scholar]
- LaCoste & Romberg Instruction Manual; Micro g LaCoste: Lafayette, CO, USA, 2004; Available online: https://microglacoste.com/support/product-manuals/ (accessed on 17 April 2024).
- SGM Carta Geológico-Minera Zaachila E14-12, Oaxaca, Esc. 1:250,000. Available online: https://mapserver.sgm.gob.mx/Cartas_Online/metadatos_geol/100_GL_zaachila.html (accessed on 5 January 2024).
- Tchobanoglous, G.; Theissen, H.; Eliassen, R. Desechos Sólidos Principios de Ingeniería y Administración. in Ambiente y los Recursos Naturales Renovables, no. AR-16. Venezuela, 1982. Available online: https://www.passeidireto.com/es/content/115360937/desechos-solidos-principios-de-ingenieria-y-administracion-2 (accessed on 28 July 2023).
- Talwani, M.; Worzel, J.L.; Landisman, M. Rapid gravity computations for two-dimensional bodies with application to the Mendocino submarine fracture zone. J. Geophys. Res. (1896–1977) 1959, 64, 49–59. [Google Scholar] [CrossRef]
- İşseven, T.; Aydın, N.G.; Arslan, M.S. 2D modelling the depth of the southeastern Thrace Basin by using Bouguer gravity anomalies. Acta Geophys. 2024, 72, 849–860. [Google Scholar] [CrossRef]
- Mohammed, M.A.A.; Mohammed, S.H.; Szabó, N.P.; Szűcs, P. Geospatial modeling for groundwater potential zoning using a multi-parameter analytical hierarchy process supported by geophysical data. Discov. Appl. Sci. 2024, 6, 121. [Google Scholar] [CrossRef]
- IPCC Directrices del IPCC de 2006 Para los Inventarios Nacionales de Gases de Efecto Invernadero 3.1. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/spanish/vol5.html (accessed on 28 July 2023).
- Amini, H.R.; Reinhart, D.R.; Mackie, K.R. Determination of first-order landfill gas modeling parameters and uncertainties. Waste Manag. 2012, 32, 305–316. [Google Scholar] [CrossRef]
- Machado, S.L.; Carvalho, M.F.; Gourc, J.-P.; Vilar, O.M.; do Nascimento, J.C.F. Methane generation in tropical landfills: Simplified methods and field results. Waste Manag. 2009, 29, 153–161. [Google Scholar] [CrossRef] [PubMed]
- Park, J.-K.; Chong, Y.-G.; Tameda, K.; Lee, N.-H. Methods for Determining the Methane Generation Potential and Methane Generation Rate Constant for the FOD Model: A Review. Waste Manag. Research 2018, 36, 200–220. [Google Scholar] [CrossRef]
- EPA Visualización de Documentos|NEPIS|EPA de EE. UU. Available online: https://nepis.epa.gov/Exe/ZyNET.exe/P1009C8L.txt?ZyActionD=ZyDocument&Client=EPA&Index=2016%20Thru%202020%7C1991%20Thru%201994%7C2011%20Thru%202015%7C1986%20Thru%201990%7C2006%20Thru%202010%7C1981%20Thru%201985%7C2000%20Thru%202005%7C1976%20Thru%201980%7C1995%20Thru%201999%7CPrior%20to%201976%7CHardcopy%20Publications&Docs=&Query=600r05047&Time=&EndTime=&SearchMethod=2&TocRestrict=n&Toc=&TocEntry=&QField=&QFieldYear=&QFieldMonth=&QFieldDay=&UseQField=&IntQFieldOp=0&ExtQFieldOp=0&XmlQuery=&File=D%3A%5CZYFILES%5CINDEX%20DATA%5C00THRU05%5CTXT%5C00000026%5CP1009C8L.txt&User=ANONYMOUS&Password=anonymous&SortMethod=h%7C-&MaximumDocuments=15&FuzzyDegree=0&ImageQuality=r85g16/r85g16/x150y150g16/i500&Display=hpfr&DefSeekPage=x&SearchBack=ZyActionL&Back=ZyActionS&BackDesc=Results%20page&MaximumPages=1&ZyEntry=1&SeekPage=x (accessed on 7 January 2024).
- Faour, A.A.; Reinhart, D.R.; You, H. First-order kinetic gas generation model parameters for wet landfills. Waste Manag. 2007, 27, 946–953. [Google Scholar] [CrossRef] [PubMed]
- EPA Background Information Document for Updating AP42 Section 2.4 for Estimating Emissions from Municipal Solid Waste Landfills|Science Inventory|US EPA. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?Lab=NRMRL&dirEntryId=198363 (accessed on 27 July 2023).
- IPCC Good Practice Guidance and Uncertainty Management in National Greenhouse Gas Inventories. Available online: https://www.ipcc-nggip.iges.or.jp/public/gp/english/index.html (accessed on 8 June 2024).
- Coskuner, G.; Jassim, M.S.; Nazeer, N.; Damindra, G.H. Quantification of landfill gas generation and renewable energy potential in arid countries: Case study of Bahrain. Waste Manag. Res. 2020, 38, 1110–1118. [Google Scholar] [CrossRef] [PubMed]
- Mantlík, F.; Matias, M.; Lourenço, J.; Grangeia, C.; Tareco, H. The use of gravity methods in the internal characterization of landfills—A case study. J. Geophys. Eng. 2009, 6, 357–364. [Google Scholar] [CrossRef]
- Vu, H.L.; Ng, K.T.W.; Richter, A. Optimization of first order decay gas generation model parameters for landfills located in cold semi-arid climates. Waste Manag. 2017, 69, 315–324. [Google Scholar] [CrossRef]
- Krause, M.J.; Chickering, G.W.; Townsend, T.G.; Reinhart, D.R. Critical review of the methane generation potential of municipal solid waste. Crit. Rev. Environ. Sci. Technol. 2016, 46, 1117–1182. [Google Scholar] [CrossRef]
- Krause, M.J.; Chickering, G.W.; Townsend, T.G. Translating landfill methane generation parameters among first-order decay models. J. Air Waste Manag. Assoc. 2016, 66, 1084–1097. [Google Scholar] [CrossRef]
- Kayaba, H.; Issoufou, O.; Téré, D.; Abdoulaye, C.; Oumar, S.; Antoine, B.; Jean, K. Estimation of Landfill Gas and Its Renewable Energy Potential from the Polesgo Controlled Landfill Using First-Order Decay (FOD) Models. J. Environ. Prot. 2024, 15, 975–993. [Google Scholar] [CrossRef]
- Singh, C.K.; Kumar, A.; Roy, S.S. Quantitative analysis of the methane gas emissions from municipal solid waste in India. Sci. Rep. 2018, 8, 2913. [Google Scholar] [CrossRef] [PubMed]
- Andreottola, G.; Cossu, R.; Ritzkowski, M. 9.1—Landfill Gas Generation Modeling. In Solid Waste Landfilling; Cossu, R., Stegmann, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 419–437. ISBN 978-0-12-818336-6. [Google Scholar]
- El-Fadel, M.; Findikakis, A.N.; Leckie, J.O. Gas simulation models for solid waste landfills. Crit. Rev. Environ. Sci. Technol. 1997, 27, 237–283. [Google Scholar] [CrossRef]



| Approximate Thickness (m) | Density (gr/cm3) | Reference | ||
|---|---|---|---|---|
| SDF Zaachila | Compacted mixed waste | 6–64 | 0.445 | [41] |
| Sedimentary | Sandstones–shales | 15–78 | 2.1 | [38] |
| Metamorphic | Gneiss | 250 | 2.7 | [38] |
| Classification of Waste | Percentage (%) | |
|---|---|---|
| Organic | Food waste | 32.0 |
| Landscaping waste | 10.2 | |
| Paper | 4.0 | |
| Rag | 3.5 | |
| Cardboard | 2.1 | |
| Cotton | 1.0 | |
| Wood | 0.1 | |
| Inorganic | Disposable diapers | 11.4 |
| Fine residue | 9.5 | |
| Others | 9.2 | |
| Plastic | 8.8 | |
| Glass | 3.4 | |
| Rubber | 1.6 | |
| Tetrapack | 1.1 | |
| Cans | 0.8 | |
| Earthenware and ceramics | 0.4 | |
| Leather | 0.2 | |
| Iron | 0.2 | |
| Synthetic fibers | 0.2 | |
| Aluminum | 0.1 | |
| Model | Equation | Index of Symbols |
|---|---|---|
| Simple of first order | (1) [23] | G = Generation of methane (m3/year) W = Mass of waste (Tons) L0 = Potential of generation of methane (m3/Ton) t = Time after waste placement (years) ti = Lag time (between placement and the start of generation k = First-order rate constant (year−1) |
| Simple of first order modified | (2) [23] | G = Generation of methane (m3/year) W = Mass of waste (Tons) L0 = Potential of generation of methane (m3/Ton) t = Time after waste placement (years) ti = Lag time (between placement and the start of generation k = First-order rate constant (year−1) s = Constant of the phase of first order |
| Multiphase model | (3) [23] | kr = Constant of decomposition of first order for rapidly decomposable waste ks = Constant of decomposition of first order for slowly decomposable waste Fr = Fraction of rapidly decomposable waste Fs = Fraction of slowly decomposable waste |
| LandGEM | (4) [49] | QCH4 = Annual methane generation in the year of calculation (m3/year) n = (Year of the calculation)—(initial year of waste acceptance) i = 1 year time increment j = 0.1-year time increment k = Methane generation rate (year−1) L0 = Potential methane generation capacity (m3/Mg) Mi = Mass of waste accepted in the ith year (Mg) tij = Age of the jth section of waste mass accepted in the ith year (decimal of year) |
| IPCC | (4) (5) (6) (7) (8) [45] | CH4 Emissions = CH4 emitted in the year T, Gg T = Inventory year X = Waste category or type/material RT = Recovered CH4 in year T, Gg OXT = Oxidation factor in year T (fraction) F = Fraction of CH4, by volume, in generated landfill gas (fraction) 16/12 = Ratio of molecular weight of CH4/C DDOCma(T) = DDOCm accumulated at the end of year T, Gg DDOCma(T-1) = DDOCm accumulated at the end of year (T-1), Gg DDOCmd(T) = DDOCm deposited in year T, Gg DDOCm decompT = DDOCm decomposed in the SWDS in year T, Gg k = Reaction constant (year—1) DDOCm = Total mass of degradable organic carbon (DDOC) in the year T W = Mass of waste deposited (Gg) DOC = Degradable organic carbon in the year of deposition, fraction, Gg C/Gg waste DOCf = Fraction of DOC that can decompose (fraction) MFC = CH4 correction factor for aerobic decomposition in the year of deposition (fraction) |
| Type of Site | Default Values of MCF |
|---|---|
| Managed—anaerobic | 1.0 |
| Managed—semiaerobic | 0.5 |
| Not managed—deep (>5 m of waste and/or high-water table) | 0.8 |
| Not managed—shallow (<5 m of waste) | 0.4 |
| No category | 0.6 |
| Data | Values |
|---|---|
| Degradable organic carbon (DOC) | 0.129 |
| Fraction of degradable organic carbon DOCf | 0.77 |
| Fraction of CH4 in biogas | 0.5 |
| Ratio of molecular weight | 1.33 |
| Methane correction factor (MFC) | 1 |
| Density of methane at constant temperature | 0.627 kg/m3 |
| Model | m3/Year of CH4 in Year 2020 | Relative Error (%) |
|---|---|---|
| Simple of first order | 3.50 × 106 | 1.0 |
| Simple of first order modified | 3.76 × 106 | 6.3 |
| Multiphase model | 3.09 × 106 | 12.6 |
| LandGEM | 4.97 × 106 | 40.7 |
| IPCC | 3.19 × 106 | 9.7 |
| Flow measurement (experimental) | 3.53 × 106 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merab, P.B.N.; Sadoth, S.T.; Isidro, B.J.S. First-Order Decay Models for the Estimation of Methane Emissions in a Landfill in the Metropolitan Area of Oaxaca City, Mexico. Waste 2025, 3, 14. https://doi.org/10.3390/waste3020014
Merab PBN, Sadoth ST, Isidro BJS. First-Order Decay Models for the Estimation of Methane Emissions in a Landfill in the Metropolitan Area of Oaxaca City, Mexico. Waste. 2025; 3(2):14. https://doi.org/10.3390/waste3020014
Chicago/Turabian StyleMerab, Pérez Belmonte Nancy, Sandoval Torres Sadoth, and Belmonte Jiménez Salvador Isidro. 2025. "First-Order Decay Models for the Estimation of Methane Emissions in a Landfill in the Metropolitan Area of Oaxaca City, Mexico" Waste 3, no. 2: 14. https://doi.org/10.3390/waste3020014
APA StyleMerab, P. B. N., Sadoth, S. T., & Isidro, B. J. S. (2025). First-Order Decay Models for the Estimation of Methane Emissions in a Landfill in the Metropolitan Area of Oaxaca City, Mexico. Waste, 3(2), 14. https://doi.org/10.3390/waste3020014






