Wavelet Entropy for Efficiency Assessment of Price, Return, and Volatility of Brent and WTI During Extreme Events
Abstract
:1. Introduction
2. Related Literature
3. Methods
3.1. Wavelet Entropy
- (a)
- The signal y is decomposed by applying the continuous wavelet transform given by the following:
- (b)
- Given the number of translation coefficients N at scale aj, the wavelet coefficients are normalized to obtain the wavelet energy density:
- (c)
- Finally, the wavelet entropy (WE) is then calculated as the Shannon entropy of the wavelet energy density at scale M, as follows:
3.2. EGARCH Model
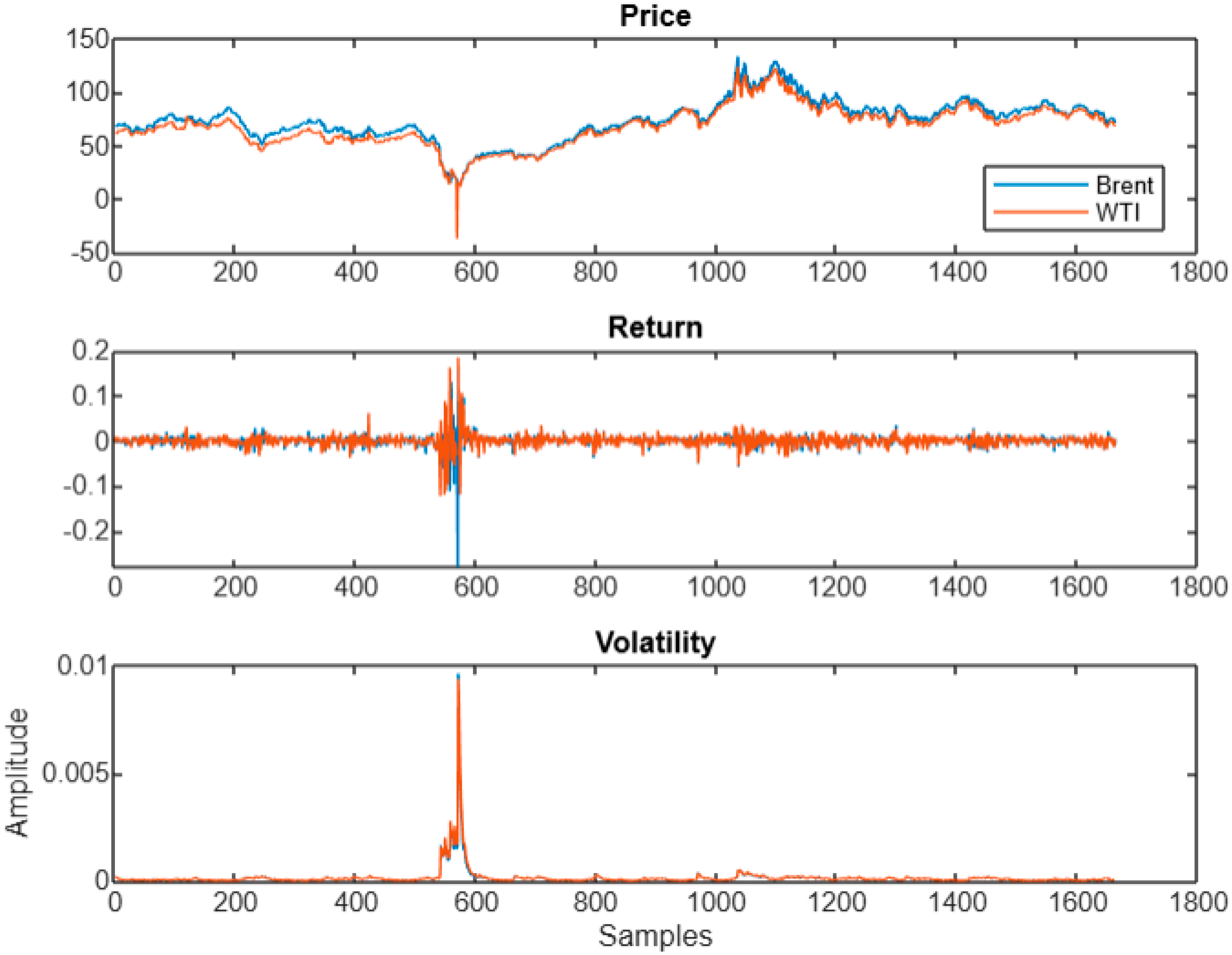
4. Results
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fama, E. Efficient capital markets: A review of theory and empirical work. J. Financ. 1970, 25, 383–417. [Google Scholar] [CrossRef]
- Časta, M. Inflation, interest rates and the predictability of stock returns. Financ. Res. Lett. 2023, 58, 104380. [Google Scholar] [CrossRef]
- Salisu, A.A.; Tchankam, J.P. US Stock return predictability with high dimensional models. Financ. Res. Lett. 2022, 45, 102194. [Google Scholar] [CrossRef]
- Pham, Q.T.T. Stock Return Predictability: Evidence Across US Industries. Financ. Res. Lett. 2021, 38, 101531. [Google Scholar] [CrossRef]
- Rehman, M.Z.; Tiwari, A.K.; Samontaray, D.P. Directional predictability in foreign exchange rates of emerging markets: New evidence using a cross-quantilogram approach. Borsa Istanb. Rev. 2022, 22, 145–155. [Google Scholar] [CrossRef]
- Azzam, I.; El-Masry, A.A.; Yamani, E. Foreign exchange market efficiency during COVID-19 pandemic. Int. Rev. Econ. Financ. 2023, 86, 717–730. [Google Scholar] [CrossRef]
- Lee, N.; Choi, W.; Pae, Y. Market efficiency in foreign exchange market. Econ. Lett. 2021, 205, 109931. [Google Scholar] [CrossRef]
- Keles, D.; Genoese, M.; Möst, D.; Fichtner, W. Comparison of extended mean-reversion and time series models for electricity spot price simulation considering negative prices. Energy Econ. 2012, 34, 1012–1032. [Google Scholar] [CrossRef]
- Olmstead, D.E.H.; Yatchew, A. Alberta’s electricity futures market: An empirical analysis of price formation. Energy Econ. 2025, 143, 108284. [Google Scholar] [CrossRef]
- Haugom, E.; Ullrich, C.J. Market efficiency and risk premia in short-term forward prices. Energy Econ. 2012, 34, 1931–1941. [Google Scholar] [CrossRef]
- Zhang, F.; Gao, H.; Yuan, D. The asymmetric effect of G7 stock market volatility on predicting oil price volatility: Evidence from quantile autoregression model. J. Commod. Mark. 2024, 35, 100409. [Google Scholar]
- Zhu, B.; Tian, C.; Wang, P. Exploring the relationship between Chinese crude oil futures market efficiency and market micro characteristics. Energy Econ. 2024, 134, 107577. [Google Scholar]
- Ren, X.; Xiao, Y.; Duan, K.; Urquhart, A. Spillover effects between fossil energy and green markets: Evidence from informational inefficiency. Energy Econ. 2024, 131, 107317. [Google Scholar]
- Charles, A.; Darné, O.; Kim, J.H. Will precious metals shine? A market efficiency perspective. Int. Rev. Financ. Anal. 2015, 41, 284–291. [Google Scholar]
- Adewuyi, A.O.; Wahab, B.A.; Adeboye, O.S. Stationarity of prices of precious and industrial metals using recent unit root methods: Implications for markets’ efficiency. Resour. Policy 2020, 65, 101560. [Google Scholar]
- Cagli, E.C.; Taskin, D.; Mandaci, P.E. The short- and long-run efficiency of energy, precious metals, and base metals markets: Evidence from the exponential smooth transition autoregressive models. Energy Econ. 2019, 84, 104540. [Google Scholar]
- Lazzarino, M.; Berrill, J.; Šević, A. The importance of distinguishing between precious and industrial metals when investing in mining stocks. Resour. Policy 2022, 78, 102802. [Google Scholar]
- Batten, J.A.; Lucey, B.M.; McGroarty, F.; Peat, M.; Urquhart, A. Does intraday technical trading have predictive power in precious metal markets? J. Int. Financ. Mark. Inst. Money 2018, 52, 102–113. [Google Scholar]
- Papenfuß, P.; Schischke, A.; Rathgeber, A. Factors of predictive power for metal commodities. N. Am. J. Econ. Financ. 2025, 76, 102309. [Google Scholar]
- Byrne, J.P.; Fazio, G.; Fiess, N. Primary commodity prices: Co-movements, common factors and fundamentals. J. Dev. Econ. 2013, 101, 16–26. [Google Scholar] [CrossRef]
- Budinski-Petković, L.; Lončarević, I.; Jakšić, Z.K.; Vrhovac, S.B. Fractal properties of financial markets. Physica A 2014, 410, 43–53. [Google Scholar] [CrossRef]
- Zhuang, X.-T.; Huang, X.-Y.; Sha, Y.-L. Research on the fractal structure in the Chinese stock market. Physica A 2004, 333, 293–305. [Google Scholar]
- Lahmiri, S. Long memory in international financial markets trends and short movements during 2008 financial crisis based on variational mode decomposition and detrended fluctuation analysis. Physica A 2015, 437, 130–138. [Google Scholar] [CrossRef]
- Vogl, M.; Kojić, M.; Mitić, P. Dynamics of green and conventional bond markets: Evidence from the generalized chaos analysis. Physica A 2024, 633, 129397. [Google Scholar]
- Nie, C.-X. Correlation dimension of financial market. Physica A 2017, 473, 632–639. [Google Scholar]
- Lahmiri, S. A study on chaos in crude oil markets before and after 2008 international financial crisis. Physica A 2017, 466, 389–395. [Google Scholar]
- Alvarez-Ramirez, J.; Rodriguez, E. A singular value decomposition entropy approach for testing stock market efficiency. Physica A 2021, 583, 126337. [Google Scholar]
- Gao, Y.-C.; Tan, R.; Fu, C.-J.; Cai, S.-M. Revealing stock market risk from information flow based on transfer entropy: The case of Chinese A-shares. Physica A 2023, 624, 128982. [Google Scholar]
- Lahmiri, S. Randomness in denoised stock returns: The case of Moroccan family business companies. Phys. Lett. A 2018, 382, 554–560. [Google Scholar]
- Zunino, L.; Bariviera, A.F.; Belén Guercio, M.; Martinez, L.B.; Rosso, O.A. Monitoring the informational efficiency of European corporate bond markets with dynamical permutation min-entropy. Physica A 2016, 456, 1–9. [Google Scholar]
- Heinlein, R.; Legrenzi, G.D.; Mahadeo, S.M.R. Crude oil and stock markets in the COVID-19 crisis: Evidence from oil exporters and importers. Q. Rev. Econ. Financ. 2021, 82, 223–229. [Google Scholar] [CrossRef]
- Alqahtani, A.; Selmi, R.; Ouyang, H. The financial impacts of jump processes in the crude oil price: Evidence from G20 countries in the pre- and post-COVID-19. Resour. Policy 2021, 72, 102075. [Google Scholar]
- Chen, Y.; Xu, J.; Miao, J. Dynamic volatility contagion across the Baltic dry index, iron ore price and crude oil price under the COVID-19: A copula-VAR-BEKK-GARCH-X approach. Resour. Policy 2023, 81, 103296. [Google Scholar]
- Zhang, H.; Hong, H.; Guo, Y.; Yang, C. Information spillover effects from media coverage to the crude oil, gold, and Bitcoin markets during the COVID-19 pandemic: Evidence from the time and frequency domains. Int. Rev. Econ. Financ. 2022, 78, 267–285. [Google Scholar]
- Gharib, C.; Mefteh-Wali, S.; Serret, V.; Ben Jabeur, S. Impact of COVID-19 pandemic on crude oil prices: Evidence from Econophysics approach. Resour. Policy 2021, 74, 102392. [Google Scholar]
- Zhang, W.; Hamori, S. Crude oil market and stock markets during the COVID-19 pandemic: Evidence from the US, Japan, and Germany. Int. Rev. Financ. Anal. 2021, 74, 101702. [Google Scholar]
- Mensi, W.; Al-Yahyaee, K.H.; Vo, X.V.; Kang, S.H. COVID-19 and time-frequency spillovers between oil and sectoral stocks and portfolio implications: Evidence from China and US economies. Int. Econ. 2024, 180, 100554. [Google Scholar]
- He, Z.; Dong, T.; Qian, W.; Xu, W. Dynamic interactions among trade policy uncertainty, climate policy uncertainty, and crude oil prices. Int. Rev. Econ. Financ. 2024, 95, 103479. [Google Scholar]
- Faisal, S.M.R.; Ebrahimi Salari, T.; Adibian, M.S. What is the effect of the 2008 economic crisis and the COVID-19 pandemic crisis on oil consumption in selected OECD countries? Energy Policy 2024, 188, 114055. [Google Scholar]
- Peng, L.; Liang, C. Sustainable development during the post-COVID-19 period: Role of crude oil. Resour. Policy 2023, 85, 103843. [Google Scholar]
- Lahmiri, S. Multifractals and multiscale entropy patterns in energy markets under the effect of the COVID-19 pandemic. Decis. Anal. J. 2023, 7, 100247. [Google Scholar]
- Foroutan, P.; Lahmiri, S. Connectedness of cryptocurrency markets to crude oil and gold: An analysis of the effect of COVID-19 pandemic. Financ. Innov. 2024, 10, 68. [Google Scholar]
- Lahmiri, S. The nexus between fossil energy markets and the effect of the COVID-19 pandemic on clustering structures. Energy Nexus 2024, 16, 100344. [Google Scholar]
- Lahmiri, S. Price disorder and information content in energy and gold markets: The effect of the COVID-19 pandemic. Energy Nexus 2024, 16, 100343. [Google Scholar]
- Xu, Y.; Liu, T.; Du, P. Volatility forecasting of crude oil futures based on Bi-LSTM-Attention model: The dynamic role of the COVID-19 pandemic and the Russian-Ukrainian conflict. Resour. Policy 2024, 88, 104319. [Google Scholar] [CrossRef]
- Pan, Q.; Sun, Y. Changes in volatility leverage and spillover effects of crude oil futures markets affected by the 2022 Russia-Ukraine conflict. Financ. Res. Lett. 2023, 58, 104442. [Google Scholar]
- Ohikhuare, O.M. How geopolitical risk drives spillover interconnectedness between crude oil and exchange rate markets: Evidence from the Russia-Ukraine war. Resour. Policy 2023, 86, 104282. [Google Scholar] [CrossRef]
- Guo, X.; Lu, X.; Mu, S.; Zhang, M. New roles for energy and financial markets in spillover connections: Context under COVID-19 and the Russia-Ukraine conflict. Res. Int. Bus. Financ. 2024, 71, 102403. [Google Scholar]
- Ye, Y.; Lin, B.; Que, D.; Cai, S.; Wang, C. COVID-19, the Russian-Ukrainian conflict and the extreme spillovers between fossil energy, electricity, and carbon markets. Energy 2024, 311, 133399. [Google Scholar]
- Zhou, E.; Wang, X. Dynamics of systemic risk in European gas and oil markets under the Russia–Ukraine conflict: A quantile regression neural network approach. Energy Rep. 2023, 9, 3956–3966. [Google Scholar]
- Cui, J.; Maghyereh, A. Higher-order moment risk connectedness and optimal investment strategies between international oil and commodity futures markets: Insights from the COVID-19 pandemic and Russia-Ukraine conflict. Int. Rev. Financ. Anal. 2023, 86, 102520. [Google Scholar] [CrossRef]
- Maneejuk, P.; Kaewtathip, N.; Yamaka, W. The influence of the Ukraine-Russia conflict on renewable and fossil energy price cycles. Energy Econ. 2024, 129, 107218. [Google Scholar] [CrossRef]
- Vo, D.H.; Phuoc-Bao Tran, M. Volatility spillovers between energy and agriculture markets during the ongoing food & energy crisis: Does uncertainty from the Russo-Ukrainian conflict matter? Technol. Forecast. Soc. Chang. 2024, 208, 123723. [Google Scholar]
- Guntu, R.K.; Yeditha, P.K.; Rathinasamy, M.; Perc, M.; Marwan, N.; Kurths, J.; Agarwal, A. Wavelet entropy-based evaluation of intrinsic predictability of time series. Chaos 2020, 30, 033117. [Google Scholar] [CrossRef]
- Bentes, S.R.; Menezes, R. Entropy: A new measure of stock market volatility? J. Phys. Conf. Ser. 2012, 394, 012033. [Google Scholar] [CrossRef]
- Sheraz, M.; Dedu, S.; Preda, V. Entropy measures for assessing volatile markets. Procedia Econ. Financ. 2015, 22, 655–662. [Google Scholar] [CrossRef]
- Ahn, K.; Lee, D.; Sohn, S.; Yang, B. Stock market uncertainty and economic fundamentals: An entropy-based approach. Quant. Financ. 2019, 19, 1151–1163. [Google Scholar] [CrossRef]
- Niu, H.; Hu, Z. Information transmission and entropy-based network between Chinese stock market and commodity futures market. Resour. Policy 2021, 74, 102294. [Google Scholar] [CrossRef]
- Wang, X. Efficient markets are more connected: An entropy-based analysis of the energy, industrial metal and financial markets. Energy Econ. 2022, 111, 106067. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S.; Bezzina, F. Complexity analysis and forecasting of variations in cryptocurrency trading volume with support vector regression tuned by Bayesian optimization under different kernels: An empirical comparison from a large dataset. Expert Syst. Appl. 2022, 209, 118349. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Renyi entropy and mutual information measurement of market expectations and investor fear during the COVID-19 pandemic. Chaos Solitons Fractals 2020, 139, 110084. [Google Scholar]
- Lahmiri, S.; Bekiros, S. The impact of COVID-19 pandemic upon stability and sequential irregularity of equity and cryptocurrency markets. Chaos Solitons Fractals 2020, 138, 109936. [Google Scholar] [CrossRef]
- Lahmiri, S.; Bekiros, S. Randomness, informational entropy, and volatility interdependencies among the major world markets: The role of the COVID-19 pandemic. Entropy 2020, 22, 833. [Google Scholar] [CrossRef]
- Karagiannis, R.; Karagiannis, G. Nonparametric estimates of price efficiency for the Greek infant milk market: Curing the curse of dimensionality with Shannon entropy. Econ. Model. 2023, 121, 106202. [Google Scholar] [CrossRef]
- Neto, D. Examining interconnectedness between media attention and cryptocurrency markets: A transfer entropy story. Econ. Lett. 2022, 214, 110460. [Google Scholar]
- Yin, J.; Zhu, Y.; Fan, X. Correlation analysis of China’s carbon market and coal market based on multi-scale entropy. Resour. Policy 2021, 72, 102065. [Google Scholar]
- Liu, X.; Zhou, X.; Zhu, B.; He, K.; Wang, P. Measuring the maturity of carbon market in China: An entropy-based TOPSIS approach. J. Clean. Prod. 2019, 229, 94–103. [Google Scholar]
- Zhang, L.; Zhang, S.; Ling, T.; Huang, F. Biorthogonal wavelet energy entropy method with different time windows for strong interference processing of GPR signals. J. Appl. Geophys. 2023, 216, 105158. [Google Scholar]
- Mazumder, B.; Khan, M.S.I.; Mohi Uddin, K.M. Biorthogonal wavelet based entropy feature extraction for identification of maize leaf diseases. J. Agric. Food Res. 2023, 14, 100756. [Google Scholar] [CrossRef]
- Xia, Q.; Tang, H.; Fu, L.; Tan, J.; Guo, Y. A drought stress-sensing technique based on wavelet entropy of chlorophyll fluorescence excited with pseudo-random binary sequence. Comput. Electron. Agric. 2023, 210, 107933. [Google Scholar]
- Ali, H.; Zhang, Z.; Gao, F. Multiscale monitoring of industrial chemical process using wavelet-entropy aided machine learning approach. Process Saf. Environ. Prot. 2023, 180, 1053–1075. [Google Scholar]
- Zhuang, J.; Peng, Q.; Wu, F.; Guo, B. Multi-component attention-based convolution network for color difference recognition with wavelet entropy strategy. Adv. Eng. Inform. 2022, 52, 101603. [Google Scholar]
- Valverde, E.R.; Clemente, G.V.; Arini, P.D.; Vampa, V. Wavelet-based entropy and complexity to identify cardiac electrical instability in patients post myocardial infarction. Biomed. Signal Process. Control 2021, 69, 102846. [Google Scholar]
- Xu, P.; Hu, X.; Yao, D. Improved wavelet entropy calculation with window functions and its preliminary application to study intracranial pressure. Comput. Biol. Med. 2013, 43, 425–433. [Google Scholar] [CrossRef]
- Gu, R.; Shao, Y. How long the singular value decomposed entropy predicts the stock market?—Evidence from the Dow Jones Industrial Average Index. Physica A 2016, 453, 150–161. [Google Scholar]
- Fan, X.; Li, S.; Tian, L. Complexity of carbon market from multi-scale entropy analysis. Physica A 2016, 452, 79–85. [Google Scholar]
- Mastroeni, L.; Mazzoccoli, A.; Quaresima, G. Effects of the climate-related sentiment on agricultural spot prices: Insights from Wavelet Rényi Entropy analysis. Energy Econ. 2025, 142, 108146. [Google Scholar]
- Tang, L.; Lv, H.; Yu, L. An EEMD-based multi-scale fuzzy entropy approach for complexity analysis in clean energy markets. Appl. Soft Comput. 2017, 56, 124–133. [Google Scholar]
- Wang, J.; Wang, X. COVID-19 and financial market efficiency: Evidence from an entropy-based analysis. Financ. Res. Lett. 2021, 42, 101888. [Google Scholar]
- Efremidze, L.; Stanley, D.J.; Kownatzki, C. Entropy trading strategies reveal inefficiencies in Japanese stock market. Int. Rev. Econ. Financ. 2021, 75, 464–477. [Google Scholar]
- Nelson, D.B. Conditional Heteroskedasticity in Asset Returns: A New Approach. Econometrica 1991, 59, 347–370. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar]
| Parameter | Value | t-Statistic | p-Value |
|---|---|---|---|
| ω | −0.30952 | −4.479 | 7.499 × 10−6 |
| β | 0.96644 | 129.19 | 0.0000 |
| γ | 0.19674 | 6.793 | 1.098 × 10−11 |
| α | −0.085366 | −4.9498 | 7.4271 × 10−7 |
| Parameter | Value | t-Statistic | p-Value |
|---|---|---|---|
| ω | −0.1959 | −3.278 | 0.0010455 |
| β | 0.97888 | 152.65 | 0.0000 |
| γ | 0.20043 | 7.4821 | 7.3136 × 10−14 |
| α | −0.059715 | −3.6685 | 0.00024396 |
| Before | Pandemic | War | |
|---|---|---|---|
| Price | |||
| Brent | 0.2719 | 0.2418 | 0.8166 |
| WTI | 0.8116 | 0.3144 | 0.2878 |
| Return | |||
| Brent | 0.8319 | 0.5348 | 0.8625 |
| WTI | 0.8053 | 0.6256 | 0.8413 |
| Volatility | |||
| Brent | 0.1 | 0.2259 | 0.695 |
| WTI | 0.7669 | 0.4653 | 0.7003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lahmiri, S. Wavelet Entropy for Efficiency Assessment of Price, Return, and Volatility of Brent and WTI During Extreme Events. Commodities 2025, 4, 4. https://doi.org/10.3390/commodities4020004
Lahmiri S. Wavelet Entropy for Efficiency Assessment of Price, Return, and Volatility of Brent and WTI During Extreme Events. Commodities. 2025; 4(2):4. https://doi.org/10.3390/commodities4020004
Chicago/Turabian StyleLahmiri, Salim. 2025. "Wavelet Entropy for Efficiency Assessment of Price, Return, and Volatility of Brent and WTI During Extreme Events" Commodities 4, no. 2: 4. https://doi.org/10.3390/commodities4020004
APA StyleLahmiri, S. (2025). Wavelet Entropy for Efficiency Assessment of Price, Return, and Volatility of Brent and WTI During Extreme Events. Commodities, 4(2), 4. https://doi.org/10.3390/commodities4020004







