Geometry Change of 1,3-Dicyanobenzene upon Electronic Excitation from a Franck–Condon Fit of Several Fluorescence Emission Spectra †
Abstract
:1. Introduction
2. Computational Methods
2.1. Quantum Chemical Calculations
2.2. Franck–Condon Fits
3. Experimental Methods
4. Results and Discussion
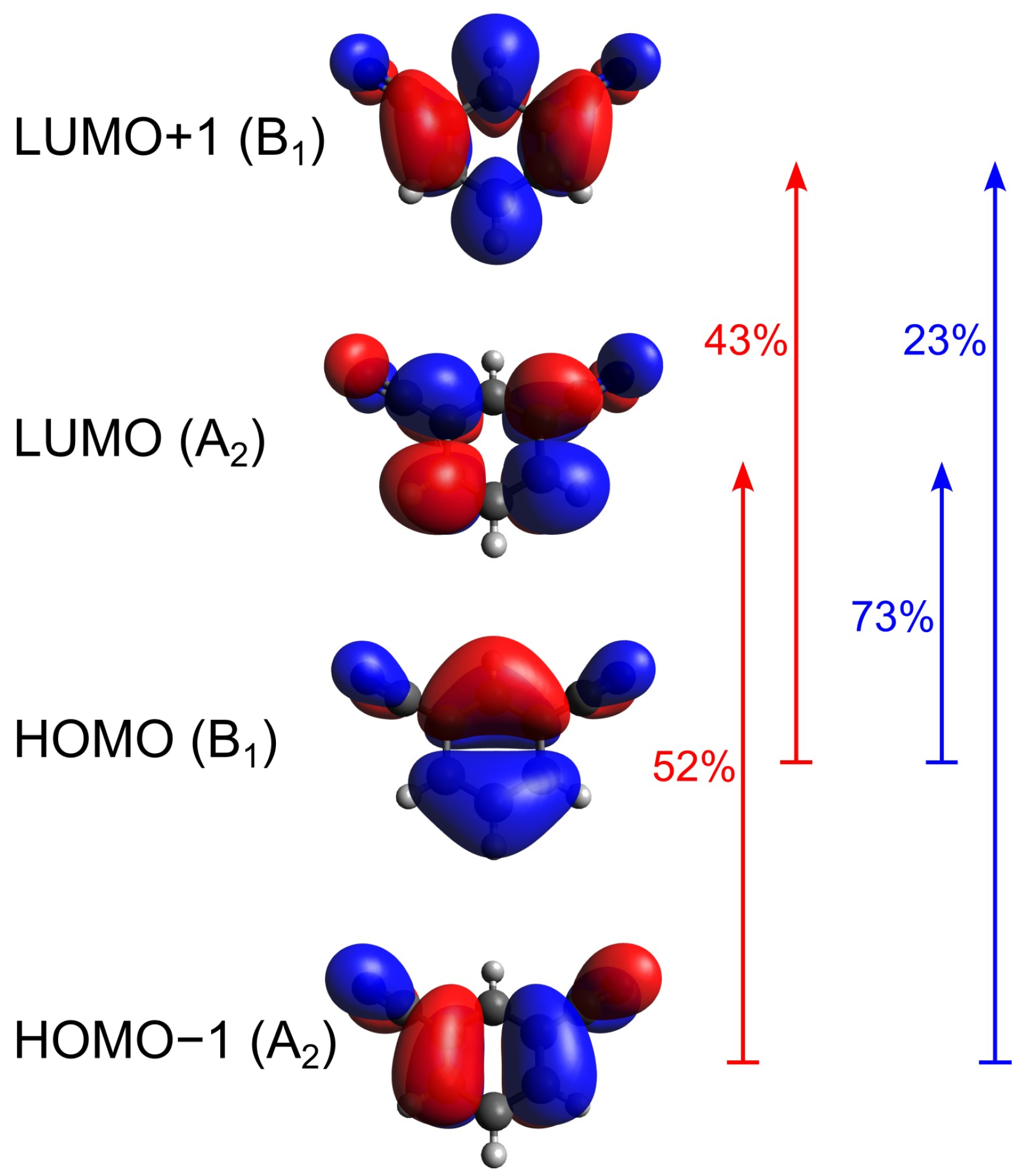
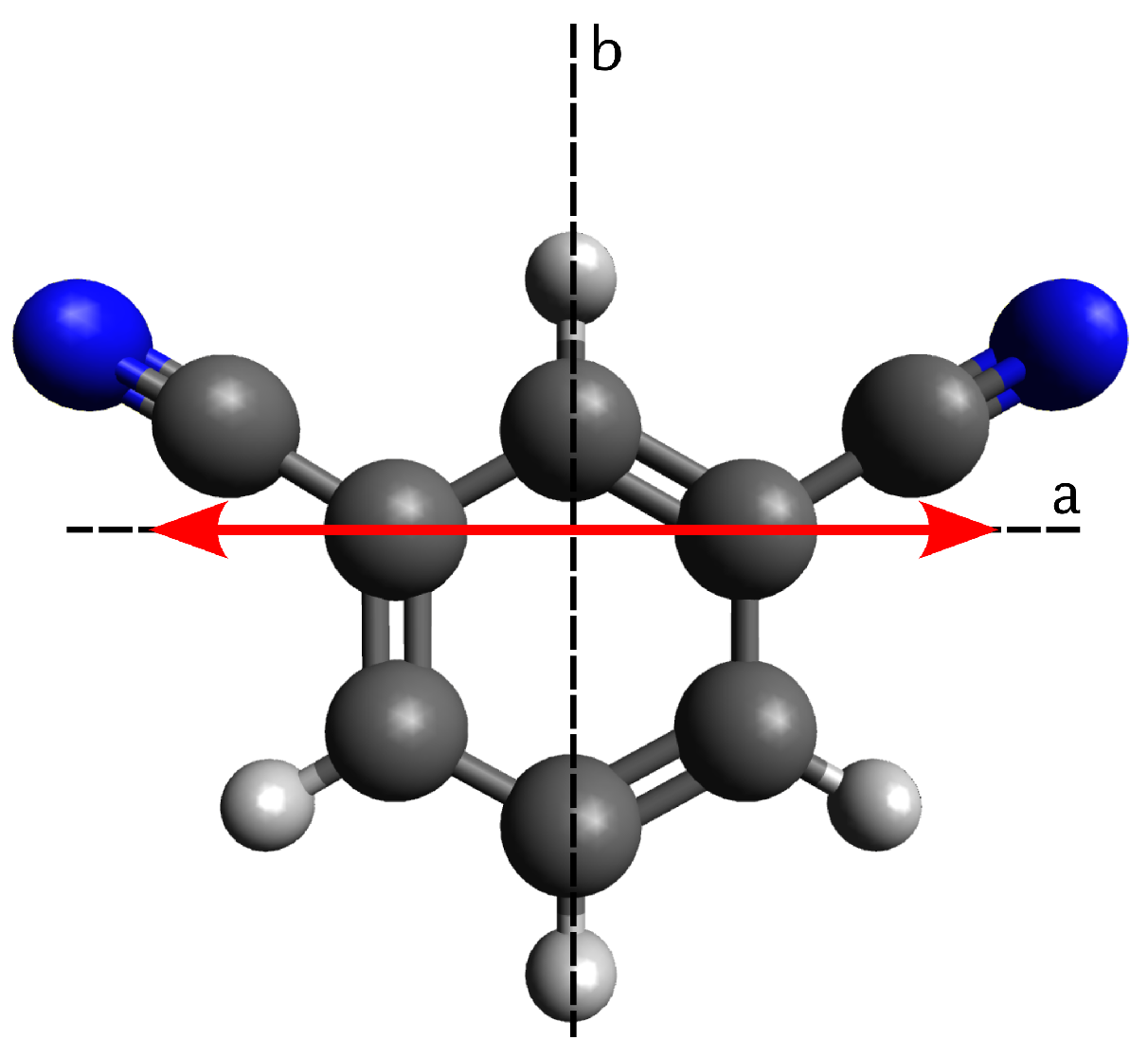
4.1. Computational Results
4.2. Experimental Results
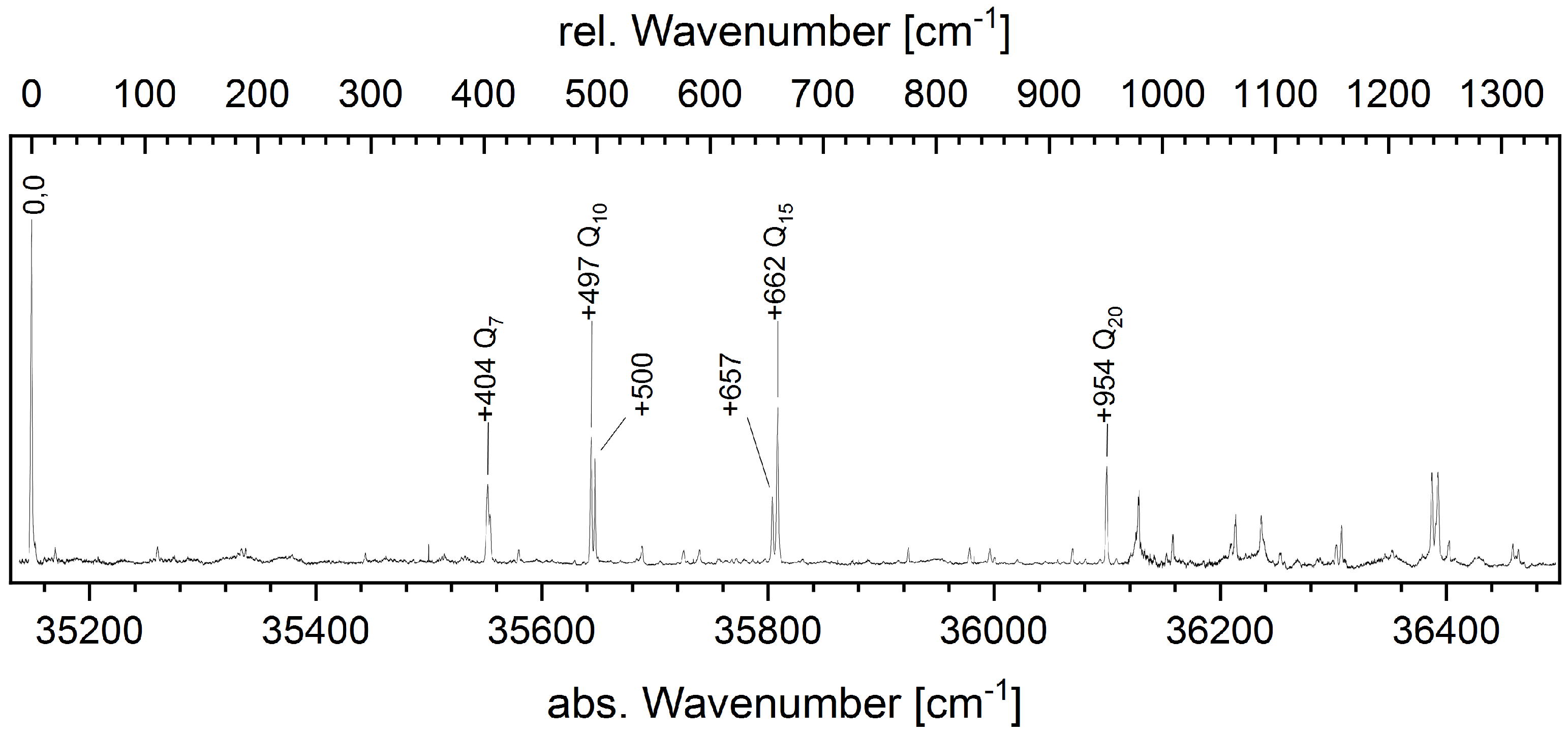
4.2.1. The LIF Spectrum of 1,3-Dicyanobenzene
4.2.2. Fluorescence Emission
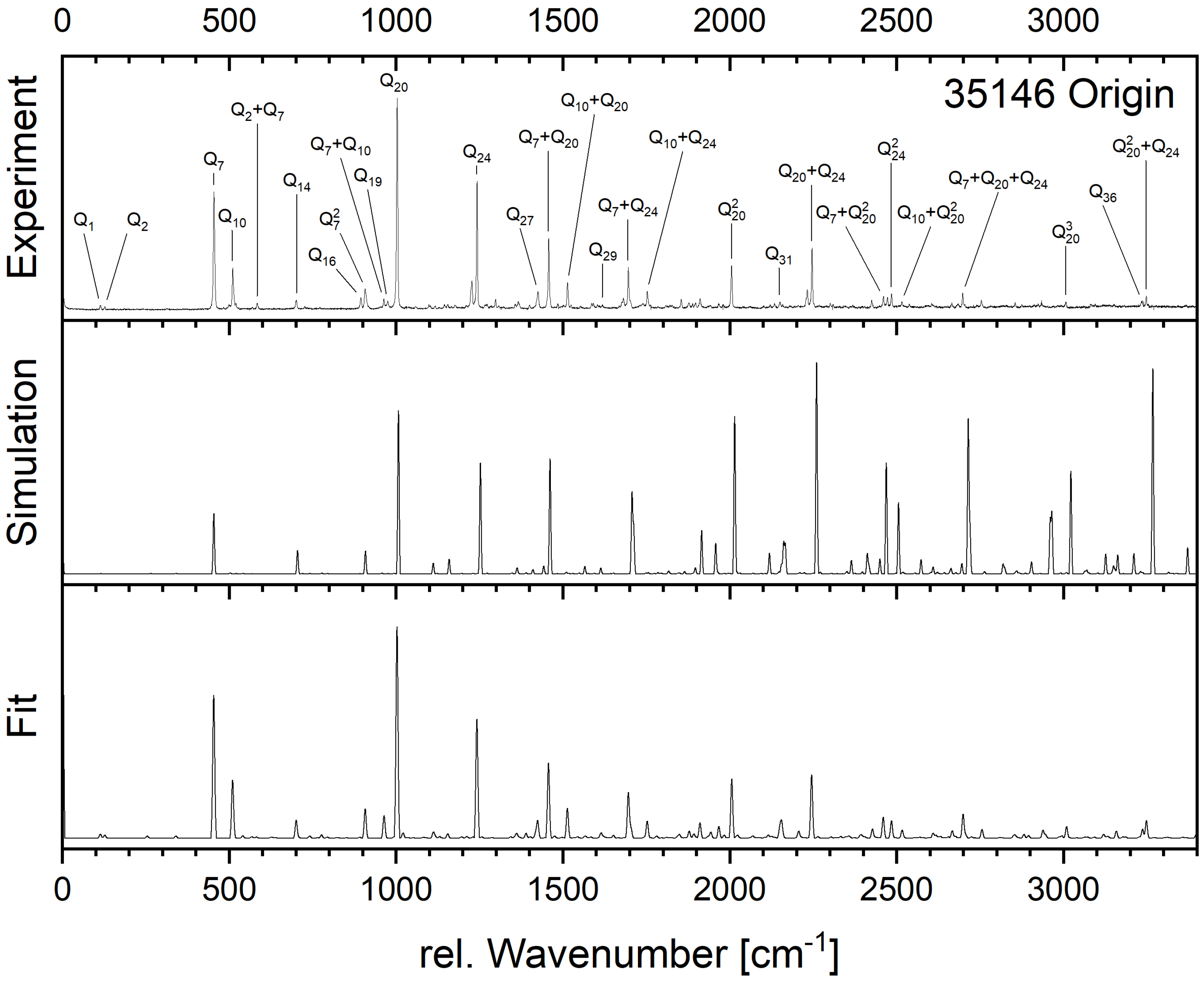
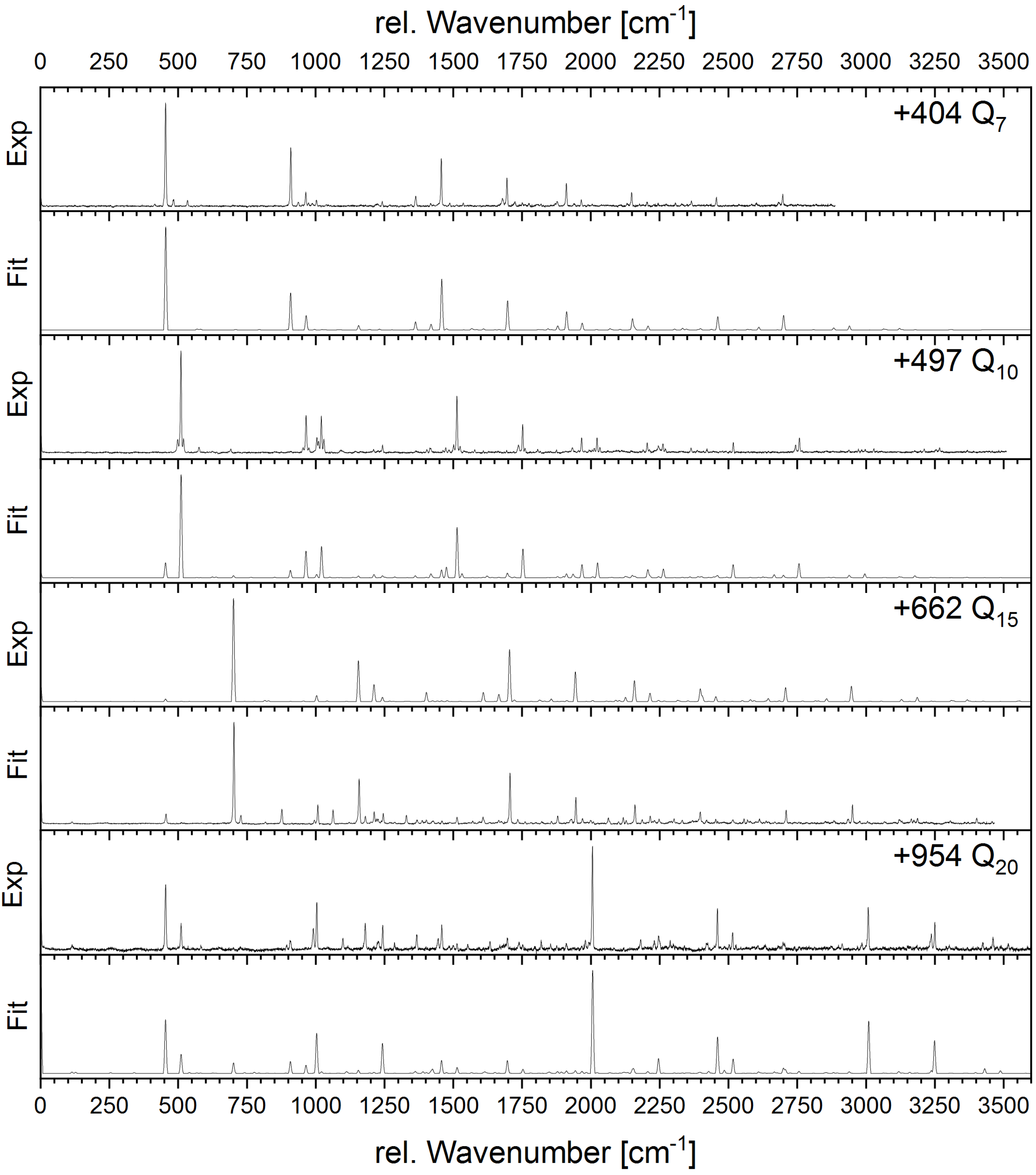
4.3. Franck–Condon Fit of Geometry Changes upon Electronic Excitation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karle, J.; Mark, H.; Hargittai, I. Stereochemical Applications of Gas-Phase Electron Diffraction; Hargittai, I., Hargittai, M., Eds.; VCH: Deerfield Beach, FL, USA, 1988. [Google Scholar]
- Küpper, J.; Stern, S.; Holmegaard, L.; Filsinger, F.; Rouzée, A.; Rudenko, A.; Johnsson, P.; Martin, A.V.; Adolph, M. X-ray Diffraction from Isolated and Strongly Aligned Gas-Phase Molecules with a Free-Electron Laser. Phys. Rev. Lett. 2014, 112, 083002. [Google Scholar] [CrossRef]
- Majewski, W.A.; Meerts, W.L. Near UV spectra with fully resolved structure of naphthalene and perdeurated naphthalene. J. Mol. Spec. 1984, 104, 271–281. [Google Scholar] [CrossRef]
- Majewski, W.A.; Plusquellic, D.F.; Pratt, D.W. The rotationally resolved fluorescence excitation spectrum of 1-fluoronaphthalene. J. Chem. Phys. 1989, 90, 1362–1367. [Google Scholar] [CrossRef]
- Felker, P.M. Rotational coherence spectroscopy: Studies of the geometries of large gasphase species by picosecond time-domain methods. J. Phys. Chem. 1992, 96, 7844–7857. [Google Scholar] [CrossRef]
- Riehn, C. High-resolution pump-probe rotational coherence spectroscopy - rotational constants and structure of ground and electronically excited states of large molecular systems. Chem. Phys. 2002, 297, 283. [Google Scholar] [CrossRef]
- Williamson, J.; Dantus, M.; Kim, S.; Zewail, A. Ultrafast diffraction and molecular structure. Chem. Phys. Lett. 1992, 196, 529–534. [Google Scholar] [CrossRef]
- Bohm, M.; Tatchen, J.; Krügler, D.; Kleinermanns, K.; Nix, M.G.D.; LeGreve, T.A.; Zwier, T.S.; Schmitt, M. High-resolution and Dispersed Fluorescence Examination of Vibronic bands of Tryptamine: Spectroscopic signatures for La/Lb mixing near a conical intersection. J. Phys. Chem. A 2009, 113, 2456–2466. [Google Scholar] [CrossRef] [PubMed]
- Speckmeier, E.; Fischer, T.G.; Zeitler, K. A Toolbox Approach To Construct Broadly Applicable Metal-Free Catalysts for Photoredox Chemistry: Deliberate Tuning of Redox Potentials and Importance of Halogens in Donor-Acceptor Cyanoarenes. J. Am. Chem. Soc. 2018, 140, 15353–15365. [Google Scholar] [CrossRef] [PubMed]
- Geon Hyeong Lee, D.Y.K.; Kim, Y.S. High-Efficiency Dicyanobenzene-Based Organic Light-Emitting Diodes Exhibiting Thermally Activated Delayed Fluorescence. Mol. Cryst. Liq. Cryst. 2015, 621, 1–7. [Google Scholar]
- McGuire, B.A.; Loomis, R.A.; Burkhardt, A.M.; Lee, K.L.K.; Shingledecker, C.N.; Charnley, S.B.; Cooke, I.R.; Cordiner, M.A.; Herbst, E.; Kalenskii, S.; et al. Detection of two interstellar polycyclic aromatic hydrocarbons via spectral matched filtering. Science 2021, 371, 1265–1269. [Google Scholar] [CrossRef]
- McGuire, B.A.; Burkhardt, A.M.; Kalenskii, S.; Shingledecker, C.N.; Remijan, A.J.; Herbst, E.; McCarthy, M.C. Detection of the aromatic molecule benzonitrile (C6H5CN) in the interstellar medium. Science 2018, 359, 202–205. [Google Scholar] [CrossRef] [PubMed]
- Chitarra, O.; Lee, K.L.K.; Buchanan, Z.; Melosso, M.; McGuire, B.A.; Goubet, M.; Pirali, O.; Martin-Drumel, M.-A. Hunting the relatives of benzonitrile: Rotational spectroscopy of dicyanobenzenes. Astron. Astrophys 2021, 652, A163. [Google Scholar] [CrossRef]
- Zajonz, M.; Oberkirch, T.; Hebestreit, M.-L.; Lindic, M.M.; Hättig, C.; Schmitt, M. Excited state dipole moments of two dicyanobenzene isomers from thermochromic shifts and ab initio calculations. J. Photochem. Photobiol. A Chem. 2024, 452, 115589. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Bär, M.; Häser, M.; Horn, H.; Kölmel, C. Electronic Structure Calculations onWorkstation Computers: The Program System TURBOMOLE. Chem. Phys. Lett. 1989, 162, 165–169. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Hättig, C.; Weigend, F. CC2 excitation energy calculations on large molecules using the resolution of the identity approximation. J. Chem. Phys. 2000, 113, 5154–5161. [Google Scholar] [CrossRef]
- Hättig, C.; Kohn, A. Transition moments and excited-state first-order properties in the coupled cluster model CC2 using the resolution-of-the-identity approximation. J. Chem. Phys. 2002, 117, 6939–6951. [Google Scholar] [CrossRef]
- Hättig, C. Geometry optimizations with the coupled-cluster model CC2 using the resolution-of-the-identity approximation. J. Chem. Phys. 2002, 118, 7751–7761. [Google Scholar] [CrossRef]
- Hellweg, A.; Grün, S.; Hättig, C. Benchmarking the performance of spin-component scaled cc2 in ground and electronically excited states. Phys. Chem. Chem. Phys. 2008, 10, 1159–1169. [Google Scholar] [CrossRef] [PubMed]
- Deglmann, P.; Furche, F.; Ahlrichs, R. An efficient implementation of second analytical derivatives for density functional methods. Chem. Phys. Lett. 2002, 362, 511–518. [Google Scholar] [CrossRef]
- Spangenberg, D.; Imhof, P.; Kleinermanns, K. The S1 state geometry of phenol determined by simultaneous Franck–Condon and rotational constants fits. Phys. Chem. Chem. Phys. 2003, 5, 2505–2514. [Google Scholar] [CrossRef]
- Brause, R.; Schmitt, M.; Spangenberg, D.; Kleinermanns, K. Determination of the excited state structure of 7-azaindole using a Franck–Condon analysis. Mol. Phys. 2004, 102, 1615–1623. [Google Scholar] [CrossRef]
- Doktorov, E.V.; Malkin, I.A.; Man’ko, V.I. Dynamical symmetry of vibronic transitions in polyatomic molecules and the Franck-Condon principle. J. Mol. Spec. 1975, 56, 1–20. [Google Scholar] [CrossRef]
- Doktorov, E.V.; Malkin, I.A.; Man’ko, V.I. Dynamical symmetry of vibronic transitions in polyatomic molecules and the Franck-Condon principle. J. Mol. Spec. 1977, 64, 302–326. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. Meth. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.D. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Schmitt, M.; Henrichs, U.; Müller, H.; Kleinermanns, K. Intermolecular vibrations of the phenol dimer revealed by spectral hole burning and dispersed fluorescence spectroscopy. J. Chem. Phys. 1995, 103, 9918–9928. [Google Scholar] [CrossRef]
- Roth, W.; Jacoby, C.; Westphal, A.; Schmitt, M. A study of 2H- and 2D-benzotriazole in their lowest electronic states by UV-laser double-resonance spectroscopy. J. Phys. Chem. A 1998, 102, 3048–3059. [Google Scholar] [CrossRef]
- Palmer, M.H.; Moyes, W.; Spiers, M. The Electronic Structure of Substituted Benzenes: Ab Initio Calculations and Photoelectron Spectra for Benzonitrile, the Tolunitriles, Ffluorobenzonitriles, Dicyanobenzenes and Ethynybenzene. J. Mol. Struct. 1980, 62, 165–167. [Google Scholar] [CrossRef]
- Wilson, E.B. The Normal Modes and Frequencies of Vibration of the Regular Plane Hexagon Model of the Benzene Molecule. Phys. Rev. 1934, 45, 706. [Google Scholar] [CrossRef]
- Varsanyi, G. Assignments for Vibrational Spectra of 700 Benzene Derivatives; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Mulliken, R.S. Report on Notation for the Spectra of Polyatomic Molecules. J. Chem. Phys. 1955, 23, 1997–2011. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure, III. Electronic Spectra and Electronic Structure of Polyatomic Molecules; van Nostrand Reinhold Company: New York, NY, USA, 1966. [Google Scholar]
- Kemp, D.J.; Tuttle, W.D.; Jones, F.M.; Gardner, A.M.; Andrejeva, A.; Wakefield, J.C.; Wright, T.G. Consistent assignment of the vibrations of symmetric and asymmetric meta-disubstituted benzenes. J. Mol. Spec. 2018, 346, 46–59. [Google Scholar] [CrossRef]
| SCS-CC2/cc-pVTZ | Experiment | FCFit | |
|---|---|---|---|
| /MHz | 2706.7 | 2723.018609(46) 1 | 2706.7 2 |
| /MHz | 899.9 | 906.419893(21) 1 | 899.9 2 |
| /MHz | 675.4 | 679.859840(15) 1 | 675.4 2 |
| /amu Å2 | 0.0 | 0.207 | 0.0 |
| ()/MHz | 2632.9 | - | 2618.3 |
| ()/MHz | 885.9 | - | 884.3 |
| ()/MHz | 662.9 | - | 661.1 |
| () /amu Å2 | 0.0 | - | −0.014 |
| A(-)/MHz | −73.8 | - | −88.4 |
| B(-)/MHz | −14.0 | - | −15.6 |
| C(-)/MHz | −12.5 | - | −14.3 |
| () /∘ | 0.0 | - | - |
| () / | 35,958.0 | 35,146 3 | - |
| State | S0 | S1 | (S1-S0) | |||
|---|---|---|---|---|---|---|
| Method | SCS-CC2 | FCFit | SCS-CC2 | FCFit | SCS-CC2 | FCFit |
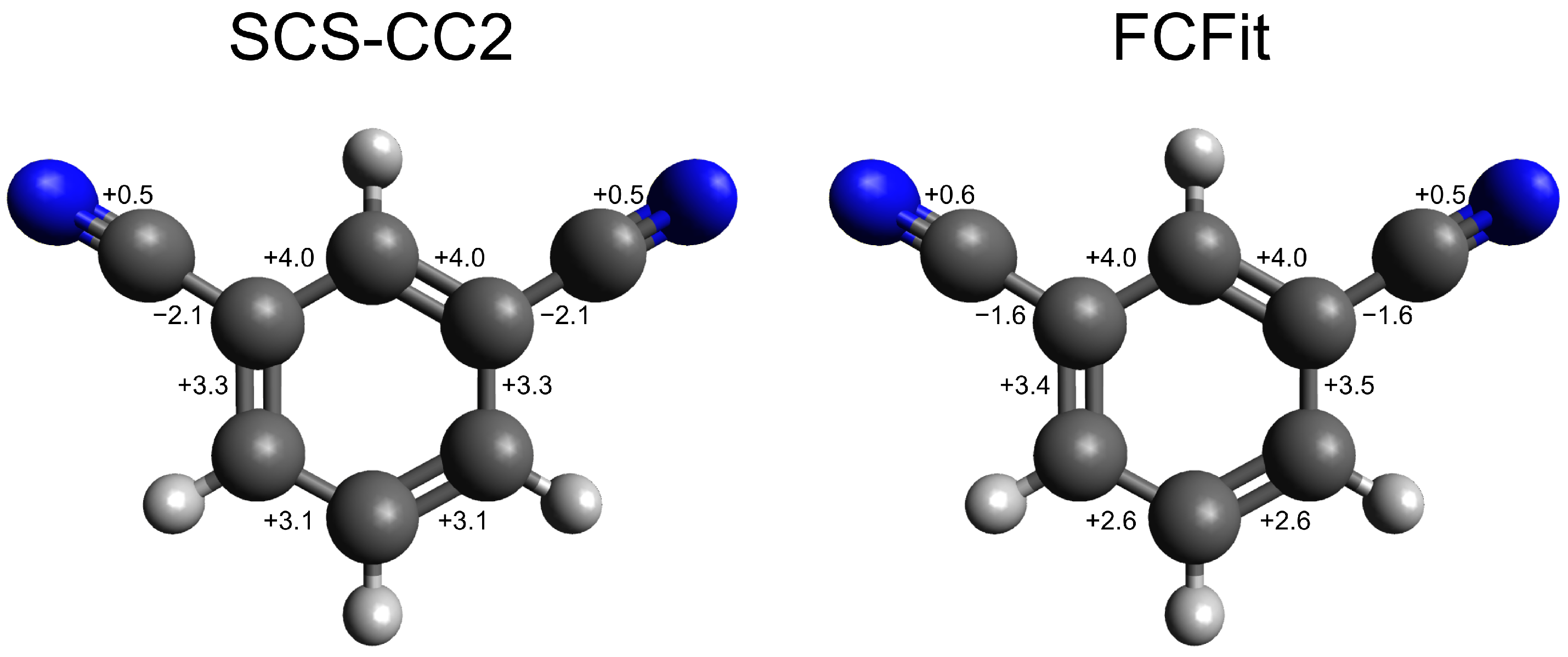
| C1-C2 | 139.4 | 139.4 | 142.5 | 142.0 | +3.1 | +2.6 |
| C2-C3 | 140.2 | 140.2 | 143.5 | 143.7 | +3.3 | +3.5 |
| C3-C4 | 139.9 | 139.9 | 143.9 | 143.9 | +4.0 | +4.0 |
| C4-C5 | 139.9 | 139.9 | 143.9 | 143.9 | +4.0 | +4.0 |
| C5-C6 | 140.2 | 140.2 | 143.5 | 143.6 | +3.3 | +3.4 |
| C6-C1 | 139.4 | 139.4 | 142.5 | 142.0 | +3.1 | +2.6 |
| C3-C8 | 143.8 | 143.8 | 141.7 | 142.2 | −2.1 | −1.6 |
| C8-N2 | 117.6 | 117.6 | 118.1 | 118.1 | +0.5 | +0.5 |
| C5-C7 | 143.8 | 143.8 | 141.7 | 142.2 | −2.1 | −1.6 |
| C7-N1 | 117.6 | 117.6 | 118.1 | 118.2 | +0.5 | +0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martini, J.; Amar, S.; Schmitt, M. Geometry Change of 1,3-Dicyanobenzene upon Electronic Excitation from a Franck–Condon Fit of Several Fluorescence Emission Spectra. Spectrosc. J. 2025, 3, 4. https://doi.org/10.3390/spectroscj3010004
Martini J, Amar S, Schmitt M. Geometry Change of 1,3-Dicyanobenzene upon Electronic Excitation from a Franck–Condon Fit of Several Fluorescence Emission Spectra. Spectroscopy Journal. 2025; 3(1):4. https://doi.org/10.3390/spectroscj3010004
Chicago/Turabian StyleMartini, Jascha, Simran Amar, and Michael Schmitt. 2025. "Geometry Change of 1,3-Dicyanobenzene upon Electronic Excitation from a Franck–Condon Fit of Several Fluorescence Emission Spectra" Spectroscopy Journal 3, no. 1: 4. https://doi.org/10.3390/spectroscj3010004
APA StyleMartini, J., Amar, S., & Schmitt, M. (2025). Geometry Change of 1,3-Dicyanobenzene upon Electronic Excitation from a Franck–Condon Fit of Several Fluorescence Emission Spectra. Spectroscopy Journal, 3(1), 4. https://doi.org/10.3390/spectroscj3010004






